A&A 386, 1160-1171 (2002)
DOI: 10.1051/0004-6361:20020297
F. Boone
LERMA, Observatoire de Paris, 61 Av. de l'Observatoire, 75014 Paris, France
Received 8 October 2001 / Accepted 26 February 2002
Abstract
This paper is complementary to (Boone 2001) in which an optimization method was introduced. An analysis is developed in order to define the distributions of
uv-plane samples that should be used as targets in the optimization of an array. The aim is to determine how should be distributed the uv-plane samples of a given interferometer array in order to allow imaging with the maximum of sensitivity at a given resolution and with a given level of side-lobes. A general analysis is developed taking into account the levels of interpolation and extrapolation that can be achieved in the uv-plane and the loss of sensitivity implied by an imperfect distribution. For a given number of antennas and a given antenna diameter two characteristic instrument sizes are introduced. They correspond to the largest size allowing single configuration observations and to the largest size allowing imaging with the full sensitivity of the instrument. The shape of the distribution of uv-plane samples minimizing the loss of sensitivity is derived for intermediate sizes and when a Gaussian beam is wanted. In conclusion it is shown that the shape of the distribution of samples and therefore of the array itself is entirely determined by a set of five parameters specifying the work (interpolation and extrapolation) that can be demanded to the imaging process, the level of side-lobes and the resolution at a given wavelength.
It is also shown that new generation interferometers such as ALMA and ATA will be able to make clean images without deconvolution algorithms and with the full sensitivity of the instrument provided that the short spacings problem is solved.
Key words: instrumentation: interferometers - methods: analytical
The aim of this paper is to determine the distributions of uv-plane samples that should be taken as targets when optimizing an array. The choice of a target distribution depends upon the scientific goals purchased. In the present analysis we concentrate on the case where the goal is to make a reliable clean image of the source. The same problem was addressed in Holdaway (1996) and it was found that in many cases a centrally condensed distribution of uv-plane samples is better than a uniform coverage. Here, we would like to derive an exact and general description of the ideal distribution. More precisely, the question that is addressed is the following: how should be distributed the uv-plane samples of a given interferometer array in order to allow reliable imaging with the maximum of sensitivity at a given resolution and with a given level of side-lobes? Note that the notion of reliability is subjective. For the following we will state that reliable imaging is performed when the visibility function is estimated everywhere in the uv-domain of interest with an error not much greater than the noise level in the measurements.
This paper is complementary to (Boone 2001, hereafter Paper I) which covers the optimization issue. Together, these two papers cover the problem of interferometric array design for imaging: the model distributions derived from the analysis developed here can be used as targets in the optimization method introduced in Paper I. This complete approach of the array design is applied to the ALMA project in Boone (2002) which can be referred to for illustration.
To be complete, the analysis should take into account the possibility of interpolating and extrapolating in the uv-plane. Indeed, a great effort has been made since the beginning of interferometry to compensate for incomplete Fourier coverage and widely used algorithms such as CLEAN or MEM have proven their efficiency. The specification on the distribution of samples should be eased accordingly. However, evaluating the performance of each existing algorithm is a complex task (it also depends upon the kind of source observed as described in Cornwell et al. 1999) which is beyond the scope of this paper. Instead, two parameters are defined which represent the level of interpolation and extrapolation that can be achieved. All the results are therefore very general: they can be adapted to any real situation by adjusting the parameters appropriately.
Note that the purpose of this analysis is different from the one of Woody (2001). In the latter reference a precise and thorough statistical analysis of the relationship between the sidelobes and the distribution of uv-plane samples of real arrays (pseudo-random arrays) was developed. Here, idealized distributions only are considered i.e. distributions that are not associated with any real array. They are only ideal solutions to which the real distributions should tend. Moreover, the aim is to define how they should be for some specifications on the clean map (i.e. after deconvolution) and the aspect of the dirty map is not considered. The main argument for this omission is, that the new generation arrays will provide high densities of samples (higher than Nyquist in most of the uv-plane). It will therefore be possible to remove the sidelobes due to small scale bumps in the distribution by adjusting appropriately the weights of the data and at a low expense in sensitivity. Also, it is probable that linear algorithms (e.g. Non Negative Least Squares), which are well adapted to complete coverage, will be more widely used (this was also suggested by Briggs 1995), and such algorithms are less sensitive to the problem of sidelobes in the dirty map.
The structure of the paper is the following: in Sect. 2 the parameters characterizing the process of image reconstruction (i.e. the level of interpolation and of extrapolation that can be achieved and the loss of sensitivity) are introduced. In Sect. 3, the number of uv-plane samples required to allow a distribution of samples equal to the Fourier transform of the wanted clean beam is computed. It is shown in Sect. 4 that when there are less samples than this limit the sampling constraint imposes a distribution of samples implying a loss of sensitivity. The relationship between the shape of the distribution minimizing the loss of sensitivity and the number of samples is derived. The feasibility of such distributions is also studied by means of simulations. In Sect. 5 it is shown that, for given imaging specifications, the choice of the distribution is actually driven by the size of the instrument (i.e. the length of the largest baseline). Two characteristic array sizes are introduced and computed for various existing and future arrays. The conclusions are drawn in Sect. 6.
As seen from Fourier plane, the image reconstruction process consists in the estimation of the visibility function from the measurements and in the weighting of this function according to the Fourier transform of the clean beam. In this section some definitions are given and some assumptions are made to allow a simplified description of the various processes involved. Two parameters are introduced to characterize the levels of interpolation and extrapolation that can be achieved in the uv-plane. The loss of sensitivity implied by the imperfection of the distribution of samples is also derived. All the notations defined along the paper are gathered in Appendix A.
Let us first define the density of samples at a point (u,v) in the Fourier plane and considered at the scale ![]() as the number of samples situated in the disc
as the number of samples situated in the disc
![]() of center (u,v) and of radius
of center (u,v) and of radius
![]() ,
divided by the area of the disc:
,
divided by the area of the disc:
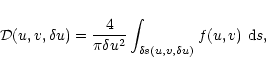 |
(1) |
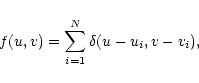 |
(2) |
A region ![]() is said well sampled at
is said well sampled at ![]() scale when there exists a regular grid of step
scale when there exists a regular grid of step ![]() such that, for each knot of the grid in
such that, for each knot of the grid in ![]() ,
there is a sample at a distance less or equal
,
there is a sample at a distance less or equal
![]() .
In terms of density it is equivalent to:
.
In terms of density it is equivalent to:
We shall assume in the following that interpolation, i.e. the use of the neighboring data for estimation of the visibility function at some coordinates in a uv-region ![]() ,
is possible with a reasonable precision (i.e. with an error close to the noise level) if and only if
,
is possible with a reasonable precision (i.e. with an error close to the noise level) if and only if ![]() is well sampled at
is well sampled at
![]() scale i.e. if and only if
scale i.e. if and only if
![]() .
In the absence of prior knowledge
.
In the absence of prior knowledge
![]() is the Shannon interpolation interval (aka Nyquist sampling interval). More generally, the value of
is the Shannon interpolation interval (aka Nyquist sampling interval). More generally, the value of
![]() depends on the prior knowledge of the source observed, on the performance of the algorithm used for interpolation (which is generally based itself on a priori properties of the astronomical sources) and whether a mosaic is made or not.
depends on the prior knowledge of the source observed, on the performance of the algorithm used for interpolation (which is generally based itself on a priori properties of the astronomical sources) and whether a mosaic is made or not.
![]() will be called the sampling accuracy required for interpolation. For Shannon interpolation, which can be used when the size of the source
will be called the sampling accuracy required for interpolation. For Shannon interpolation, which can be used when the size of the source ![]() is the only information available, we have
is the only information available, we have
![]() .
The justification of this requirement is emphasized by some simulations in Appendix B.
.
The justification of this requirement is emphasized by some simulations in Appendix B.
This assumption is a simplification that allows to consider image reconstruction independently of the method used. It is mostly inspired by the error behavior in Shannon interpolation but it is also based on the postulate that, to allow estimation of the brightness distribution at a given scale and along a given direction, a minimum of information is required on the structure of the source at nearby scales and along nearby directions. It is therefore believed that for any method used there is a condition that can be written like Eq. (3). For some interpolation techniques
![]() might be variable in the uv-plane but this would not change the results of the analysis developed here: the distributions considered in the following are all decreasing functions of the radius in the uv-plane and the limit
might be variable in the uv-plane but this would not change the results of the analysis developed here: the distributions considered in the following are all decreasing functions of the radius in the uv-plane and the limit
![]() actually concerns the density of samples at the edges only. (This can however alter the value of the sensitivity loss calculated below.)
actually concerns the density of samples at the edges only. (This can however alter the value of the sensitivity loss calculated below.)
Estimation of the data outside the largest region ![]() that is well sampled at
that is well sampled at
![]() scale is defined as extrapolation. Then, from the definition of
scale is defined as extrapolation. Then, from the definition of
![]() even if some data are present outside
even if some data are present outside ![]() they cannot be used to estimate the visibility function, they are "lost''. In the following we will assume that we always want a circularly symmetric beam and we will therefore only consider circular regions:
they cannot be used to estimate the visibility function, they are "lost''. In the following we will assume that we always want a circularly symmetric beam and we will therefore only consider circular regions:
![]() will refer to the radius of the largest well sampled region
will refer to the radius of the largest well sampled region ![]() and
and
![]() will refer to the radius up to which the visibility function can be extrapolated. Note that extrapolation is considered as forbidden by some theoretical approaches. For example in the deterministic approach of Lannes et al. (1994), a condition for the stability of the solution is that the data outside the sampled uv-region be set to zero.
will refer to the radius up to which the visibility function can be extrapolated. Note that extrapolation is considered as forbidden by some theoretical approaches. For example in the deterministic approach of Lannes et al. (1994), a condition for the stability of the solution is that the data outside the sampled uv-region be set to zero.
Let us then define two parameters ![]() and
and ![]() representing the level of interpolation and respectively extrapolation that can be achieved:
representing the level of interpolation and respectively extrapolation that can be achieved:
The constraint on the sampling accuracy is
![]() .
Setting
.
Setting ![]() to a value greater than one implies that at least one of the following conditions is fulfilled: an effective algorithm can be used, some prior information on the source are available (e.g. the source size), a mosaic of the source is made. Mosaicing technique (see e.g., Cornwell 1988; Cornwell et al. 1993) can indeed allow to recover information at distances up to
to a value greater than one implies that at least one of the following conditions is fulfilled: an effective algorithm can be used, some prior information on the source are available (e.g. the source size), a mosaic of the source is made. Mosaicing technique (see e.g., Cornwell 1988; Cornwell et al. 1993) can indeed allow to recover information at distances up to
![]() around the samples. This implies that the samples can be separated by
around the samples. This implies that the samples can be separated by
![]() and therefore
and therefore ![]() .
Note that when the source size is known to be half of the field of view we also have
.
Note that when the source size is known to be half of the field of view we also have ![]() .
.
The next important assumption made is that the accuracy on the estimate of the visibility function at some point in uv-plane depends on the number of samples n(u,v) situated at a distance less than
![]() from this point. This assumption is actually related to the first one that concerned the sampling accuracy required: the maximum gap allowed is close to
from this point. This assumption is actually related to the first one that concerned the sampling accuracy required: the maximum gap allowed is close to
![]() and it implies that the samples separated by such a distance are more or less independent. We will also assume for simplicity that all measurements are made with the same level of noise
and it implies that the samples separated by such a distance are more or less independent. We will also assume for simplicity that all measurements are made with the same level of noise ![]() .
More precisely it will be assumed that the error,
.
More precisely it will be assumed that the error,
![]() ,
on the estimate of the visibility function at (u,v) follows:
,
on the estimate of the visibility function at (u,v) follows:
| |
Figure 1:
The solid lines show the radial profile of the model distribution of samples, |
| Open with DEXTER | |
In the following it will be assumed that the N uv-samples can be distributed arbitrarily, whereas in fact there are only
![]() degrees of freedom.
The characteristics of an ideal distribution of samples allowing to reconstruct images without loss of sensitivity are dictated by three independent considerations:
degrees of freedom.
The characteristics of an ideal distribution of samples allowing to reconstruct images without loss of sensitivity are dictated by three independent considerations:
The parameter, ![]() ,
imposes the uv-disc to be well sampled at
,
imposes the uv-disc to be well sampled at
![]() scale. It constrains the distribution according to Eq. (3) with
scale. It constrains the distribution according to Eq. (3) with
![]() .
But we are now looking for idealized distributions of samples to be used as model for the optimization. We can therefore assume a perfectly smoothed distribution of samples and this condition reduces to:
.
But we are now looking for idealized distributions of samples to be used as model for the optimization. We can therefore assume a perfectly smoothed distribution of samples and this condition reduces to:
![]() .
It follows that the model distribution should not decrease smoothly to zero at the edges but should rather be truncated when the density
.
It follows that the model distribution should not decrease smoothly to zero at the edges but should rather be truncated when the density
![]() is reached: the information gathered by samples distributed at a lower density would be useless (for the reliability of the map) as mentioned in the previous section. The factor,
is reached: the information gathered by samples distributed at a lower density would be useless (for the reliability of the map) as mentioned in the previous section. The factor, ![]() ,
determines the radius up to which data can be extrapolated (
,
determines the radius up to which data can be extrapolated (
![]() )
and therefore the shape of the distribution allowing to achieve the beam specifications within this radius.
)
and therefore the shape of the distribution allowing to achieve the beam specifications within this radius.
The SNR of the data gives another constraint on the minimum density of samples in the case where an individual sample is too noisy to be usable. In this case more than one sample per
![]() area is necessary and the minimum density is
area is necessary and the minimum density is
![]() .
In general this is not the case and in the following
.
In general this is not the case and in the following
![]() will refer to
will refer to
![]() .
.
From now on it is supposed that the wanted beam is Gaussian but all the calculations can be made in a similar way for any other function. Then, the clean weighting function is also a Gaussian of FWHM
![]() such that
such that
![]() that is:
that is:
The distribution of samples is ideal (the loss of sensitivity is minimum) when
![]() ,
but the density at the edges (at radius
,
but the density at the edges (at radius
![]() )
should be greater than
)
should be greater than
![]() .
This condition can be satisfied when the number of samples is greater than
.
This condition can be satisfied when the number of samples is greater than
![]() given by:
given by:
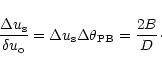 |
(11) |
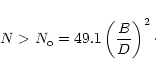 |
(13) |
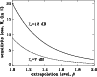 |
Figure 2:
Loss of sensitivity due to the weighting of the estimated visibility function in the clean map when the initial distribution of samples is uniform (
|
| Open with DEXTER | |
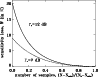 |
Figure 3:
Sensitivity loss as a function of the number of samples in the case where |
| Open with DEXTER | |
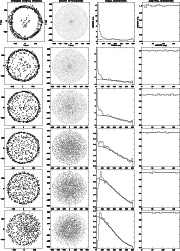 |
Figure 4:
Optimization of 10 configurations of 64 antennas for
|
| Open with DEXTER | |
If the number of samples is less than
![]() all the specifications cannot be satisfied and some of them have to be relaxed. However, one should stick as long as possible to the sampling condition for imaging and use a model distribution with a density higher than
all the specifications cannot be satisfied and some of them have to be relaxed. However, one should stick as long as possible to the sampling condition for imaging and use a model distribution with a density higher than
![]() .
Breaking this condition would imply the lack of some essential information and would prevent any reliable image reconstruction. The minimum number of samples required for the uv-disc to be well sampled at
.
Breaking this condition would imply the lack of some essential information and would prevent any reliable image reconstruction. The minimum number of samples required for the uv-disc to be well sampled at
![]() scale is:
scale is:
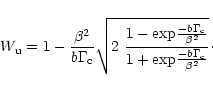 |
(15) |
When
![]() the ideal distribution is not attainable but the sampling constraint can be fulfilled and the
the ideal distribution is not attainable but the sampling constraint can be fulfilled and the
![]() samples can be distributed in a way that minimizes the inevitable loss of sensitivity. It can be shown from the calculus of variations that the integral
samples can be distributed in a way that minimizes the inevitable loss of sensitivity. It can be shown from the calculus of variations that the integral
![]() in Eq. (8) is minimized when
w2(u,v)/n(u,v) is a Gaussian function. Therefore, if w(u,v) is a Gaussian, the loss of sensitivity is minimized when n(u,v) is itself a Gaussian, i.e. when the distribution of samples is Gaussian. Let us write
in Eq. (8) is minimized when
w2(u,v)/n(u,v) is a Gaussian function. Therefore, if w(u,v) is a Gaussian, the loss of sensitivity is minimized when n(u,v) is itself a Gaussian, i.e. when the distribution of samples is Gaussian. Let us write
![]() the FWHM of such a distribution. Its value is imposed by the requirement that the density of samples be greater or equal
the FWHM of such a distribution. Its value is imposed by the requirement that the density of samples be greater or equal
![]() at the edges and that the integral of the distribution be equal N. Hence,
at the edges and that the integral of the distribution be equal N. Hence,
![]() is solution of:
is solution of:
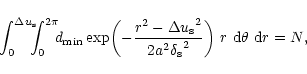 |
(16) |
Equation (17) has been solved for
![]() and the loss computed according to Eq. (18). The loss is plotted versus the number of samples in Fig. 3 for
and the loss computed according to Eq. (18). The loss is plotted versus the number of samples in Fig. 3 for ![]() (no extrapolation),
(no extrapolation),
![]() dB and
dB and
![]() dB.
dB.
For a given uv-disc radius, the less the number of samples the greater the FWHM of the Gaussian distribution. More generally, whatever the kind of model distribution chosen, as the number of samples decreases and tends to
![]() ,
it should tend to be uniform to ensure the density to be higher than
,
it should tend to be uniform to ensure the density to be higher than
![]() everywhere. However, as mentioned in Paper I it is not possible to get a uniform distribution of samples. Furthermore, for a number of samples close to the minimum required,
everywhere. However, as mentioned in Paper I it is not possible to get a uniform distribution of samples. Furthermore, for a number of samples close to the minimum required,
![]() ,
non-uniformity implies necessarily under sampling of some regions. The number of samples actually required to ensure the uv-disc to be well sampled is therefore greater than
,
non-uniformity implies necessarily under sampling of some regions. The number of samples actually required to ensure the uv-disc to be well sampled is therefore greater than
![]() as given Eq. (14).
In order to evaluate the largest ratio
as given Eq. (14).
In order to evaluate the largest ratio
![]() (i.e. the maximum flatness of the distribution) allowing the sampling requirement to be fulfilled, and the corresponding number of samples required
(i.e. the maximum flatness of the distribution) allowing the sampling requirement to be fulfilled, and the corresponding number of samples required
![]() ,
10 configurations have been optimized for various ratios
,
10 configurations have been optimized for various ratios
![]() .
The optimizations have been performed using the APO software introduced in Paper I. The results for
.
The optimizations have been performed using the APO software introduced in Paper I. The results for
![]() ,
2, 1.6, 1.4, 1.2 and 1 are drawn Fig. 4. From these simulations, the highest ratio
,
2, 1.6, 1.4, 1.2 and 1 are drawn Fig. 4. From these simulations, the highest ratio
![]() allowing the density of samples to be greater than
allowing the density of samples to be greater than
![]() everywhere is estimated to be around 2. From Eq. (17) it can be shown that the number of samples required,
everywhere is estimated to be around 2. From Eq. (17) it can be shown that the number of samples required,
![]() ,
for such a model distribution to be feasible is:
,
for such a model distribution to be feasible is:
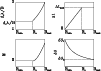 |
Figure 5:
The FWHM of the model distribution in uv-disc radius units,
|
| Open with DEXTER | |
| array | D |
|
|
|
|
|
|
| PdB | 15 m | 6 | 37 m | 8 m | 19 m | 52 m | 3960 s |
| BIMA | 6 m | 9 | 18 m | 8 m | 18 m | 50 m | 1650 s |
| VLA | 25 m | 27 | 130 m | 330 m | 750 m | 2.0 km | 169 s |
| ALMA | 12 m | 64 | 100 m | 910 m | 2.1 km | 5.6 km | 29.5 s |
| ATA | 4 m | 350 | 75 m | 9.2 km | 21 km | 57 km | 1.0 s |
In the previous section it was shown that for a given uv-disc radius the shape of the distribution of samples (i.e. the FWHM for a Gaussian distribution) is determined by the number of samples available. But the radius of the uv-disc depends on the size of the instrument (i.e. the largest projected baseline of the instrument) and the number of samples depends on the size of the instrument and on the duration of the observation. Therefore, for a given duration of observation the shape of the distribution of samples is entirely determined by the size of the instrument. If the size of the array is less or equal a value
![]() ,
there are enough samples for the distribution to be ideal: its FWHM can be the same as that of the clean weighting function. For greater sizes the FWHM has to be adapted for the sampling constraint to be fulfilled everywhere. For a size greater than a value
,
there are enough samples for the distribution to be ideal: its FWHM can be the same as that of the clean weighting function. For greater sizes the FWHM has to be adapted for the sampling constraint to be fulfilled everywhere. For a size greater than a value
![]() the sampling constraint cannot be fulfilled anymore. In this section the two characteristic baselines
the sampling constraint cannot be fulfilled anymore. In this section the two characteristic baselines
![]() and
and
![]() are computed and the value of the FWHM as a function of the size of the instrument B is derived for
are computed and the value of the FWHM as a function of the size of the instrument B is derived for
![]() .
.
The number of samples depends on the number of antennas,
![]() ,
the duration of the observation,
,
the duration of the observation, ![]() ,
and the averaging time interval,
,
and the averaging time interval, ![]() .
This last parameter has a specific meaning in the present context. Indeed, it was assumed that the density of samples could reach the minimum value
.
This last parameter has a specific meaning in the present context. Indeed, it was assumed that the density of samples could reach the minimum value
![]() at the edges of the uv-disc. Then,
at the edges of the uv-disc. Then, ![]() should be such that neighbor samples measured with the same antenna pair be separated by
should be such that neighbor samples measured with the same antenna pair be separated by
![]() (note that it is a theoretical constraint on the way to count the samples, and not on the way to effectively perform the measurements). During an observation a baseline describes an elliptical track in uv-plane (e.g., Thompson et al. 2000). When the source is at the north or south pole the curve is a circle and the rotation velocity is:
(note that it is a theoretical constraint on the way to count the samples, and not on the way to effectively perform the measurements). During an observation a baseline describes an elliptical track in uv-plane (e.g., Thompson et al. 2000). When the source is at the north or south pole the curve is a circle and the rotation velocity is:
![]() rd hour-1. But most of the time the track is not circular and the linear velocity of the baseline is less than
rd hour-1. But most of the time the track is not circular and the linear velocity of the baseline is less than
![]() .
This linear velocity is difficult to evaluate in a general way as it depends upon the source position, the latitude of the array site and the baseline orientation. However it is sufficient for the following analysis to use an average velocity,
.
This linear velocity is difficult to evaluate in a general way as it depends upon the source position, the latitude of the array site and the baseline orientation. However it is sufficient for the following analysis to use an average velocity,
![]() .
Then
.
Then ![]() is given in hour by:
is given in hour by:
Finally, the shape of the model distribution of samples for an interferometer array of a given size, B, is determined as follows:
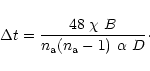 |
(28) |
The baseline lengths
![]() ,
,
![]() and
and
![]() are given in Table 1 for some existing or future interferometers and when reliance upon deconvolution is minimized (
are given in Table 1 for some existing or future interferometers and when reliance upon deconvolution is minimized (
![]() ). The values show that imaging with instruments like PdB or BIMA with only one configuration, even if optimally designed, is generally paid by a loss of sensitivity (
). The values show that imaging with instruments like PdB or BIMA with only one configuration, even if optimally designed, is generally paid by a loss of sensitivity (
![]() )
if no efficient deconvolution algorithms are used (i.e. if we are not in the case where
)
if no efficient deconvolution algorithms are used (i.e. if we are not in the case where ![]() and/or
and/or ![]() ). The VLA could in principle produce a Gaussian beam with the Fourier plane sampled at Nyquist accuracy for baselines up to 1 km. Clearly, for new generation interferometers such as ALMA and ATA, the possibility of imaging without deconvolution and loss of sensitivity will become a reality for baseline lengths up to respectively 3 km and 30 km.
). The VLA could in principle produce a Gaussian beam with the Fourier plane sampled at Nyquist accuracy for baselines up to 1 km. Clearly, for new generation interferometers such as ALMA and ATA, the possibility of imaging without deconvolution and loss of sensitivity will become a reality for baseline lengths up to respectively 3 km and 30 km.
For a limited duration of observation, the shape of the distribution of samples that should be taken as target is determined by the size of the instrument. For an array of
![]() antennas of diameter D two characteristic sizes independent of the observing wavelength were introduced:
antennas of diameter D two characteristic sizes independent of the observing wavelength were introduced:
![]() and
and
![]() given by Eqs. (24) and (25) respectively. Their value depend on the effort that can be demanded to the interpolation (sampling accuracy required) and
given by Eqs. (24) and (25) respectively. Their value depend on the effort that can be demanded to the interpolation (sampling accuracy required) and
![]() also depends on the level of extrapolation allowed and on the level of side-lobes specified (or the truncation level of the clean weighting function). For an instrument smaller than
also depends on the level of extrapolation allowed and on the level of side-lobes specified (or the truncation level of the clean weighting function). For an instrument smaller than
![]() it is possible to achieve a distribution of samples implying no (or a little in practice) loss of sensitivity. For a size between
it is possible to achieve a distribution of samples implying no (or a little in practice) loss of sensitivity. For a size between
![]() and
and
![]() the sampling requirement imposes a distribution of samples which shape induces a loss of sensitivity. For a Gaussian clean beam the sensitivity loss is minimized when the distribution of samples is Gaussian. The FWHM of the distribution is solution of Eq. (29). The closer the size of the array to
the sampling requirement imposes a distribution of samples which shape induces a loss of sensitivity. For a Gaussian clean beam the sensitivity loss is minimized when the distribution of samples is Gaussian. The FWHM of the distribution is solution of Eq. (29). The closer the size of the array to
![]() the flatter the distribution (the higher the ratio of the FWHM by the sampled uv-disc radius). In terms of array shapes it implies that the larger the array the more it should resemble a ring (see Fig. 4). On the contrary the smaller the array the more the configuration should be centrally condensed. For sizes greater than
the flatter the distribution (the higher the ratio of the FWHM by the sampled uv-disc radius). In terms of array shapes it implies that the larger the array the more it should resemble a ring (see Fig. 4). On the contrary the smaller the array the more the configuration should be centrally condensed. For sizes greater than
![]() imaging with a single configuration is in principle not possible. This gives a limit to the imaging resolution attainable with a single configuration,
imaging with a single configuration is in principle not possible. This gives a limit to the imaging resolution attainable with a single configuration,
![]() ,
given by Eq. (31) when the duration of observation is limited to eight hours.
,
given by Eq. (31) when the duration of observation is limited to eight hours.
This result may appear opposite to the conclusion of Woody (2001) or Holdaway (1997), namely, that large arrays should be filled or centrally condensed and arrays made of a small number of antennas should be ring-like. Actually, both conclusions are in agreement: in our conclusion above a fixed number of antennas was considered and the array size was the free parameter. But the values of
![]() and
and
![]() are proportional to the square of the number of antennas. Therefore, increasing the number of antennas implies the possibility of getting a Gaussian distribution with good coverage up to large configurations (precisely up to
are proportional to the square of the number of antennas. Therefore, increasing the number of antennas implies the possibility of getting a Gaussian distribution with good coverage up to large configurations (precisely up to
![]() )
i.e. the configurations can be filled or centrally condensed. When the number of antennas is small,
)
i.e. the configurations can be filled or centrally condensed. When the number of antennas is small,
![]() is small and for configurations larger than
is small and for configurations larger than
![]() the distribution should be more uniform, i.e. the configuration more ring-like.
the distribution should be more uniform, i.e. the configuration more ring-like.
The size, B, of the array to be designed depends on the resolution wanted
![]() through Eq. (30).
Finally, from the expressions of B,
through Eq. (30).
Finally, from the expressions of B,
![]() ,
,
![]() and the equation giving the FWHM (Eq. (29)), the shape of the distribution of samples, and therefore the shape of the array itself, is entirely determined by a set of 5 specifications:
and the equation giving the FWHM (Eq. (29)), the shape of the distribution of samples, and therefore the shape of the array itself, is entirely determined by a set of 5 specifications:
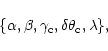 |
(32) |
It was also shown that for new generation interferometers such as ALMA or ATA the maximum size allowed for imaging without demanding any effort to interpolation and with a single configuration was of several kilometers (5.6 km for ALMA and 56 km for ATA). Even
![]() ,
the size below which it is possible to image without losing any sensitivity, is large (see Table 1). It implies the possibility of performing images in a way comparable to optical imaging systems (e.g. optical telescopes): without particular algorithm of image reconstruction and with the full sensitivity of the instrument. For example, with ALMA it will be possible to get a Gaussian distribution of samples truncated at 10 dB up to 2.1 km (Table 1) which corresponds to a resolution of 0.23 arcsec at 1 mm (Eq. (30)).
,
the size below which it is possible to image without losing any sensitivity, is large (see Table 1). It implies the possibility of performing images in a way comparable to optical imaging systems (e.g. optical telescopes): without particular algorithm of image reconstruction and with the full sensitivity of the instrument. For example, with ALMA it will be possible to get a Gaussian distribution of samples truncated at 10 dB up to 2.1 km (Table 1) which corresponds to a resolution of 0.23 arcsec at 1 mm (Eq. (30)).
It should however be noted that the so called short spacings problem was ignored throughout the analysis. It was assumed that a real distribution of samples can follow a Gaussian distribution down to the center of the uv-plane. Due to the physical size of the antennas this assumption is obviously never verified: the distribution necessarily decreases around the center and reaches zero at a radius greater or equal
![]() ,
where x is the minimum spacing required between the sides of neighboring antennas. But there exist some solutions such as mosaicing technique, or the use of complementary observations from a single dish telescope or another array of smaller antennas. Then, the great potentiality of the new generation arrays as depicted here requires at least one of these solutions to be applied.
,
where x is the minimum spacing required between the sides of neighboring antennas. But there exist some solutions such as mosaicing technique, or the use of complementary observations from a single dish telescope or another array of smaller antennas. Then, the great potentiality of the new generation arrays as depicted here requires at least one of these solutions to be applied.
Acknowledgements
I am grateful to the referee J. Moran for recommendations that helped to improve the clarity of this paper. I thank F. Viallefond for constructive comments and suggestions. I also thank J. Conway for the numerous and fruitful exchanges we had about the sampling accuracy required. Finally I am grateful to J. Lequeux, M. de Oliveira and F. Rozados-Frota for careful reading of the manuscript and useful suggestions.
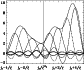 |
Figure B.1:
Illustration of Eq. (B.2) when only the 8 sinc functions the closest to a point
|
 |
Figure B.2:
|
This appendix is aimed at illustrating the effect of the sampling on the accuracy of Shannon interpolation in Fourier plane. It shows the correctness of the assumption made in Sect. 2, namely, that for Shannon interpolation
![]() .
For simplicity, one dimension only is considered. Then, if the source size is known to be
.
For simplicity, one dimension only is considered. Then, if the source size is known to be ![]() it can be shown that the Fourier transform of the source brightness distribution can be expanded as a sum of sinc functions:
it can be shown that the Fourier transform of the source brightness distribution can be expanded as a sum of sinc functions:
The sinc functions that are centered on points situated at a distance larger than a given limit from
![]() can be considered as having a negligible influence on the value of
can be considered as having a negligible influence on the value of
![]() .
Let n be the number of sinc functions that are close enough to affect the value of
.
Let n be the number of sinc functions that are close enough to affect the value of
![]() and let us assume that the measurements made outside the corresponding domain have a negligible influence on the accuracy of the estimate of
and let us assume that the measurements made outside the corresponding domain have a negligible influence on the accuracy of the estimate of
![]() .
We will also assume that the parameters outside the domain are known to be zero. These assumptions simplify the following error computation without changing significantly the results. Let us suppose that m measurements are made to estimate the value of the relevant ai parameters with
.
We will also assume that the parameters outside the domain are known to be zero. These assumptions simplify the following error computation without changing significantly the results. Let us suppose that m measurements are made to estimate the value of the relevant ai parameters with ![]() .
Each sample has a value yi measured at a position ui with an uncertainty
.
Each sample has a value yi measured at a position ui with an uncertainty ![]() .
Then, the data can be modelized by the linear equations:
.
Then, the data can be modelized by the linear equations:
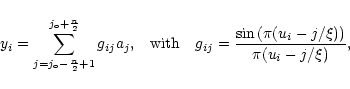 |
(B.3) |
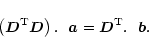 |
(B.4) |
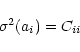 |
(B.5) |
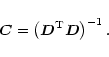 |
(B.6) |
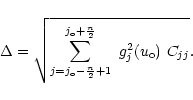 |
(B.7) |
In one dimension the condition for the support ![]() to be well sampled at
to be well sampled at ![]() scale is (Eq. (3)):
scale is (Eq. (3)):