A&A 386, 865-868 (2002)
DOI: 10.1051/0004-6361:20020321

Dusty haloes of galaxies at intermediate redshifts

P. Teerikorpi

Tuorla Observatory, 21500 Piikkiö, Finland

Received 10 January 2002 / Accepted 20 February 2002

Abstract
The presence and amount of dust in the halo matter producing narrow metal line absorption systems is still uncertain. We consider the parameter $\Sigma_{\rm a} = \sum (1+z_{\rm a})$, summed over the detected aborption line system redshifts $z_{\rm a}$, and ask whether radio-loud quasars at z < 2 and with a large value of the parameter $\Sigma _{\rm a}$ are redder in the B-V colour than those with a smaller $\Sigma _{\rm a}$. This is anticipated if the absorption lines originate in sites which contain "normal'' dust causing selective extinction. The answer is positive, and a mean intrinsic reddening e0 per halo is consistent with $\approx$0.05, or about 0.2 B-mag extinction, roughly as expected.

Key words: quasars: absorption lines - galaxies: haloes - ISM: dust


1 Introduction

Massive galaxy haloes are generally thought to consist of some non-baryonic dark matter, with at least a minor component of baryonic gas. Dark matter is observed via its gravitational effect. The gas has been detected via narrow metal absorption lines in the spectra of background quasars, and absorptions appear to originate in chemically enriched gas haloes of typical galaxies having a wide range of luminosities and a gas halo radius about 100 h-1kpc (Chen et al. 2001).

The presence and amount of dust, and the dust/gas ratio, in the intermediate redshift halo matter producing narrow metal line absorption systems is still an uncertain issue, the best direct evidence being the marginal detection of the 2175 Å dust feature in the composite spectrum of MgII absorbers (Malhotra 1997; but cf. Pitman et al. 2000). There is evidence (Fall et al. 1989) for some dust in another kind of absorption system: damped Lyman-$\alpha$ lines, thought to be associated with metal-poor progenitor galaxies, in the form of slightly redder absorption line quasars as compared to quasars with no such systems. This kind of compelling evidence is here presented for the narrow metal line systems, especially those containing CIV absorption, using radio-loud quasars at redshifts <2 as test objects, and readily available data.

We consider the parameter $\Sigma_{\rm a} = \sum (1+z_{\rm a})$, summed over the detected aborption line system redshifts $z_{\rm a}$, and ask whether the quasars with a large value of the parameter $\Sigma _{\rm a}$ are redder in the B-V colour than those with a smaller $\Sigma _{\rm a}$. This is expected if the absorption lines originate in sites which contain "normal'' cosmic dust causing selective extinction.

2 The expected amount of reddening

Ostriker et al. (1990) concluded that a typical absorption line system (with a rest frame equivalent width of $\approx$0.6 Å for CIV) may have dust corresponding to intrinsic $E(B-V) \approx 0.06{-}0.12$, if the dust-to-gas ratio in these high-z objects is similar to that locally. Because of redshift and the extinction curve, the observed reddening and extinction are larger.

The extinction-to-reddening ratio $R_V = A_V/E(B-V) \approx 3.3$varies little with redshift for typical quasar spectra, if the dust is in our Galaxy (Teerikorpi 1981). If the dust lies at some redshift $z_{\rm dust}$between a quasar and us, one again does not expect a large influence on RV, though similar absorbers with an intrinsic extinction $A_V ({\rm int})$at different z will cause significantly different effects on the radiation received at z = 0 (Ostriker et al. 1990). The idealized extinction curve with the $1/\lambda$ dependence leads to an especially simple result (Teerikorpi 2000):

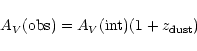\begin{displaymath}A_V ({\rm obs}) = A_V ({\rm int}) (1+z_{\rm dust}) \end{displaymath} (1)

and RV does not depend on $z_{\rm dust}$. Though the $1/\lambda$-law is not exact, the formula (1) is a useful quick estimate.
   
Table 1: Radio quasars with metal line absorption.
name z V B-V $N_{\rm a}$ $\Sigma _{\rm a}$
0024+2225 1.118 16.6 0.33 1 2.109
0029-4124 0.896 17.8 0.57 1 1.781
0402-3613 1.417 17.2 0.15 1 1.797
0420-0127 0.915 17.8 0.58 1 1.633
0454-2204 0.534 16.1 0.06 1 1.475
0454+0356 1.345 16.5 0.23 2 4.013
0637-7513 0.651 15.8 0.33 1 1.152
0725+1443 1.382 18.9 0.43 1 2.388
0809+4822 0.871 17.8 0.57 2 3.308
0812+0204 0.402 17.1 0.18 2 2.728
0827+2421 0.939 17.3 0.36 1 1.524
0835+5805 1.534 17.6 0.48 3 7.512
0856+1703 1.449 17.9 0.40 2 4.848
0952+1757 1.472 17.2 0.08 1 1.238
0955+3238 0.530 15.8 0.10 2 2.518
0957+0019 0.907 17.6 0.47 1 1.672
1019+3056 1.316 17.5 0.27 1 1.346
1038+0625 1.270 16.8 0.16 1 1.441
1049+6141 0.422 16.5 0.10 2 2.618
1055-0434 1.428 17.8 0.07 1 2.256
1148+3842 1.303 17.0 0.18 1 1.213
1206+4356 1.400 18.4 0.58 3 6.185
1213-0630 1.410 17.7 0.20 1 1.789
1218+3359 1.519 18.6 0.19 1 2.500
1229-0207 1.038 16.8 0.48 1 1.395
1308+3236 0.997 15.2 0.37 1 1.879
1327-2040 1.169 17.0 0.63 3 4.724
1328+3045 0.849 17.3 0.26 1 1.692
1354+1933 0.720 16.0 0.18 1 1.456

This means that a single low- $z_{\rm abs}$ system is expected to show little reddening, while quasars with several $z_{\rm abs}$ systems including high $z_{\rm abs}$ should be significantly reddened, if there is dust. In fact, if each absorption redshift system is accompanied by some average intrinsic (rest-frame) reddening e0, then Eq. (1) leads one to expect

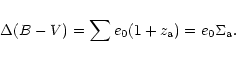\begin{displaymath}\Delta(B-V) = \sum e_0 (1+z_{\rm a}) = e_0\Sigma_{\rm a}. \end{displaymath} (2)

The sum is over the absorption systems, one for each halo.

3 A direct approach to the reddening question


   
Table 2: Continuation of Table 1.
name z V B-V $N_{\rm a}$ $\Sigma _{\rm a}$
1416+0642 1.440 16.8 0.33 4 9.526
1421+1213 1.611 18.0 0.14 1 2.360
1510-0854 0.361 16.5 0.20 1 1.351
1511+1022 1.546 18.1 0.03 1 1.437
1602-0011 1.625 17.1 0.15 1 2.325
1622+2352 0.927 17.5 0.44 4 6.680
1704+6048 0.371 15.3 0.13 2 2.385
1821+1042 1.360 17.3 0.39 3 5.297
1912-5500 0.398 16.5 0.09 1 1.401
2020-3705 1.048 17.5 0.33 1 1.029
2128-1220 0.501 16.0 0.13 1 1.430
2135-1446 0.200 15.5 0.10 1 1.200
2142-7550 1.139 17.3 0.49 1 1.960
2145+0643 0.990 16.5 0.41 1 1.791
2201+3131 0.298 16.0 0.39 1 1.282
2223-0512 1.404 18.4 0.44 1 1.847
2326-4746 1.299 16.8 0.25 1 2.261
0002+0507 1.899 16.2 0.35 2 4.600
0058+0155 1.959 17.2 0.32 2 4.077
0119-0437 1.969 16.9 0.46 6 14.706
0802+1023 1.954 18.4 0.25 2 5.300
1023+0642 1.703 18.3 0.54 3 8.053
1148-0007 1.979 17.6 0.17 2 5.453
1157+0128 1.986 17.7 0.49 4 11.558
2044-1650 1.937 17.4 0.19 3 7.806
2120+1651 1.805 18.0 0.22 2 5.360
2249+1832 1.758 18.4 0.12 3 6.654
2354+1429 1.816 18.2 0.14 1 2.576

Naturally, several problems can hinder a detection of the dust effect predicted by Eq. (2). Here we adopt a simple approach to the reddening question, which allows us to use readily-available data.

1) In order to see the dependence of reddening on $\Sigma _{\rm a}$ one needs accurate photometry and, in particular, quasars with intrinsically similar colours. B-V naturally varies with redshift, due to the K effect, but this may be taken into account.

2) Fortunately, there is now evidence for intrinsically rather stable (at the level of $\approx$$\pm 0.05$ mag) B-V colours for radio loud quasars (Teerikorpi 1981, 2000, 2001; Teerikorpi & Kotilainen 1989). This evidence has emerged from our work on the bright end of the optical luminosity function of radio quasars. The z-limit 1.65 was adopted in these studies in which Galactic reddening corrections were derived from $\delta (B-V)$. At higher redshifts the scatter in B-Vincreases. In fact, a large part of this scatter, even starting around $z \approx 1$, appears to be due to intervening halos, as will be seen.

3) Furthermore, being radio-detected there is little colour bias in a sample of radio quasars and also less bias towards small extinctions, a main motive when we initially came up with B-V as a Galactic reddening indicator.

4) It is difficult to gather a genuine comparison sample of "clean'' quasars with no absorption line systems. This problem is possible to bypass using quasars with $\geq$1 reported system: to have $N_{\rm a} = 1$ means that the quasar spectrum was at some level inspected for absorption lines.

5) It is known that at higher resolution individual absorption systems divide into subcomponents, apparently revealing clouds in a halo. For the present purpose, in the calculation of $\Sigma _{\rm a}$ one should use data refering to entire haloes. The method of Eq. (2) breaks down if absorption systems emerging at high resolutions are counted, in addition to those of low resolution. On the other hand, the colour effect searched for is so strong that the scatter due to undetected independent weak absorption systems (which may correspond to smaller haloes and reddening) will not conceal the effect, if e0 is large enough.

4 ${\vec{B-V}}$ vs. ${\vec z}$ for different $\mathsf{\Sigma(1+{\vec z}_{a})}$

In order to see whether there is a signal indicative of reddening as predicted, we use a sample containing radio-loud quasars with reliable narrow line $z_{\rm a}$ systems (Tables 1-2). It was collected from the basic catalog by Junkkarinen et al. (1991), with a few additional objects from Steidel & Sargent (1992), having UBV photometry and z < 2. We take V and B-V from Veron-Cetty & Veron (1993). For each quasar we calculated the parameter $\sum (1+z_{\rm a})$. In this collection the absorption systems generally seem to refer to individual haloes.

First we show, in Fig. 1, B-V vs. redshift for our sample and indicate separately those narrow absorption line objects for which the normalized[*] quantity $\sum (1+z_{\rm a})/(1+z) $ is smaller than 1, between 1 and 2, or larger than 2. The curve (cf. Teerikorpi 2000) describes the lower envelope for radio quasars in general. For z > 1 the three categories are clearly segregated in the sense expected. Those with $\Sigma _{\rm a}/(1+z) <1$ (usually having one $z_{\rm a} < z$) are mostly found close to the lower envelope, while those with more absorption systems are systematically higher.

Though the sample of absorption line quasars is not homogeneous, as regards detection probabilities of absorption systems, it is difficult to think about some selection effect which would cause the pattern in Fig. 1.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS2258f1.eps} \end{figure} Figure 1: B-V vs. z for radio loud absorption line quasars in the redshift range 0.2-2.0. The curve describes the lower envelope for radio quasars in general. Dot: $\Sigma _{\rm a}/(1+z) <1$; triangle: $1<\Sigma _{\rm a}/(1+z) < 2$; open circle: $2 < \Sigma _{\rm a}/(1+z)$.
Open with DEXTER

5 The value of the intrinsic reddening $\mathsf{{\vec e}_0}$

In order to see a typical value of the intrinsic reddening e0accompanying an absorption line system, we experimented with different e0, and show in Fig. 2a the $(B-V)_{\rm cor}$ vs. z diagram, in which from each colour we subtracted $e_0 \Sigma_{\rm a}$, with e0 = 0.045. Now the quasars follow rather well a common colour vs. redshift relation. In Fig. 2b we have excluded the faintest quasars with V > 18 mag.

  \begin{figure} \par\includegraphics[width=7.2cm,clip]{MS2258f2.eps} \end{figure} Figure 2: a) Corrected colours $(B-V)_{\rm c} = (B-V) - e_0 \sum (1+z_{\rm a})$, with the intrinsic reddening/halo e0 = 0.045. b) As in a), but for bright quasars $V \leq 18$.
Open with DEXTER

Figure 3 shows the colour residuals $\delta (B-V)$, as B-V minus the low envelope curve (Fig. 1), versus the parameter $\Sigma _{\rm a}$ for z>1. Possibly, among the fainter quasars some absorption systems have gone undetected or are reddened in our Galaxy. In Fig. 4a, for the objects fainter than V = 18 mag, we have denoted quasars according to the presence of MgII and CIV in their spectra: those with MgII, but no CIV, those with CIV, but no MgII, and the rest, all containing CIV. The MgII and CIV objects have quite different distributions of $\Sigma _{\rm a}$(MgII usually observed at $z_{\rm a} < 1$), though their emission $z_{\rm e}$'s are rather similar. Nevertheless, the deviations $\delta (B-V)$from the common envelope follow the same expected relation.

We have also checked the diffuse Galactic reddening, from the dust IR emission maps of Schlegel et al. (1998). Almost all predicted B-V reddenings are small, between 0.03 and 0.10 mag. We show in Fig. 4b the diagram of Fig. 4a as corrected for Schlegel et al. reddenings.

Thus the observations are consistent with the conjecture that a typical absorption line system, encompassing one halo, has dust along the line of sight, corresponding to a local $E(B-V) \approx 0.05$. The simplest interpretation is that the dust-to-gas ratio in galaxy halos at intermediate redshifts is of the same order as in low-z conditions, and the dust causes selective extinction roughly as in our Galaxy. This agrees with the conclusion from the 2175 Å feature (Malhotra 1997), but not with the damped Lyman-$\alpha$ observations (e.g. Fall et al. 1989; Fall et al. 1996) in which the dust-to-gas ratio is smaller by a factor of ten, apparently because of an early evolutionary phase with less metals and worse conditions for dust.

In fact, reddening values obtained from (more or less) magnitude limited samples, are expected to be lower limits to the true average reddening (cf. Ostriker et al. 1990). It is quite possible that in Figs. 3-4 high reddenings are lacking for increasing $\Sigma _{\rm a}$, due to selection biases aided by an intrinsic spread in the value of e0. For example, a data point at ( $\Sigma_{\rm a}, \delta (B-V)) = (10, 0.60)$ would involve a high-redshift quasar obscured by about 2.5 mag. In Figs. 3-4 the quasars with the largest two values of $\Sigma _{\rm a}$ have z > 1.95.

  \begin{figure} \par\includegraphics[width=8cm,clip]{MS2258f3.eps} \end{figure} Figure 3: Colour residuals $\delta (B-V)$ vs. $\Sigma _{\rm a}$, for quasars with z>1. Dots: bright objects, $V \leq 18.0$; open circles: fainter objects, V > 18.0. The straight line has a slope of 0.045.
Open with DEXTER

6 Concluding remarks

The radio-loud quasars with narrow metal line absorption display a clear signal of reddening, roughly as expected: $E(B-V) \propto \sum (1+z_{\rm a})$. Typically, the rest frame e0 for one system is about 0.05 mag, which must be multiplied by about $4 \times \sum (1+z_{\rm a})$ to give the observed B-extinction. Thus the quasars with several absorption systems are seen obscured by dust of up to 1-2 B-mag.

  \begin{figure} \par\includegraphics[width=7.2cm,clip]{MS2258f4.eps} \end{figure} Figure 4: a) Residuals $\delta (B-V)$ vs. $\Sigma _{\rm a}$, for quasars with z>1, $V \leq 18.0$; diamonds: MgII objects, dots: CIV objects, circles: objects with at least one CIV system. b) $\delta (B-V)_{\rm cor}$, corrected for the diffuse reddening as in Schlegel et al. (1998), vs. $\Sigma _{\rm a}$.
Open with DEXTER

After Webster et al. (1995) suggested that a large scatter (up to 5 mag) in the $B_{\rm J} - K$ colours of Parkes radio quasars could be due to dust, there have been attempts to set an upper limit to the extinction towards radio quasars, including the host galaxy and intervening matter (Boyle & di Matteo 1995; Srianand & Kembhavi 1997; Benn et al. 2001). These studies have resulted in AB less than about 2 mag, consistent with our interpretation of the B-V vs. z diagram. Because here the reddenings are clearly correlated with intervening absorption, the scatter due to the extinction in the host galaxy is a minor factor.

The same may be said of the dust suggested to be in the medium giving rise to the Ly-$\alpha$ forest, which according to Ferrara et al. (1999) may cause observed extinction in the optical of no more than $\approx$0.05 up to z =5.

Acknowledgements
I thank A. Ferrara for useful referee's comments. The study was supported by the Academy of Finland ("Cosmology from the local to the deep galaxy universe'').

References

 

Copyright ESO 2002