A&A 386, 885-890 (2002)
DOI: 10.1051/0004-6361:20020317
Spherical planetary nebulae
N. Soker
Department of Physics, University of Haifa at Oranim,
Tivon 36006, Israel
Received 10 December 2001 / Accepted 19 February 2002
Abstract
By examining their mass loss history and their distribution
in the galaxy, I argue that spherical planetary nebulae (PNe)
form a special group among all planetary nebulae.
The smooth surface brightness of most spherical PNe suggests
that their progenitors did not go through a final intensive
wind (FIW, also termed superwind) phase.
While 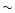 70% of the PNe of all other PNe groups are closer
to the galactic center than the sun is, only
70% of the PNe of all other PNe groups are closer
to the galactic center than the sun is, only 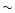 30% of
spherical PNe are;
30% of
spherical PNe are; 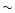 70% of them are farther away from the
galactic center.
These, plus the well-known high scale height above
the galactic plane of spherical PNe, suggest that the progenitors of
spherical PNe are low mass stars having low metallicity.
Although many stars have these properties, only
70% of them are farther away from the
galactic center.
These, plus the well-known high scale height above
the galactic plane of spherical PNe, suggest that the progenitors of
spherical PNe are low mass stars having low metallicity.
Although many stars have these properties, only 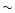 10%
of all PNe are spherical.
By comparing the galactic distribution of spherical PNe
to the metallicity evolution in the galaxy, I find that the
critical metallicity above which no spherical PNe are formed is
10%
of all PNe are spherical.
By comparing the galactic distribution of spherical PNe
to the metallicity evolution in the galaxy, I find that the
critical metallicity above which no spherical PNe are formed is
![${\rm [Fe/H]} \sim -0.4$](/articles/aa/full/2002/18/aa2180/img3.gif) .
I explain this as well as other properties of spherical PNe
in the context of the companion model for shaping PNe,
arguing that spherical PNe are formed from stars that have no
close companion, stellar or substellar, orbiting them.
I discuss the connection of the proposed scenario to the recent
finding of extrasolar planets and to the presence of
blue horizontal branch stars in globular clusters.
.
I explain this as well as other properties of spherical PNe
in the context of the companion model for shaping PNe,
arguing that spherical PNe are formed from stars that have no
close companion, stellar or substellar, orbiting them.
I discuss the connection of the proposed scenario to the recent
finding of extrasolar planets and to the presence of
blue horizontal branch stars in globular clusters.
Key words: planetary nebulae: general
- stars: AGB and post-AGB
- stars: mass loss
- stars: planetary systems
- stars: rotation
Most planetary nebulae (PNe) have a large-scale axisymmetrical
rather than spherical structure.
Axisymmetrical PNe can be classified into two main groups;
bipolar PNe, which are defined as PNe whose main structure contains
two lobes with an equatorial waist between them, and elliptical PNe,
which have a general elliptical shape, but no lobes, or only small ones.
In the present Paper I refer to PNe having a large and dense
concentration of mass in their equatorial plane, e.g., a ring,
but without lobes, as extreme elliptical PNe.
Whereas bipolar and elliptical PNe were the focus of many
studies in recent years, basic questions regarding spherical PNe
were not discussed much in the literature.
The only point mentioned in some papers is a large scale height
above (or below) the galactic plane of spherical PNe distribution,
which implies that they are formed from low mass stars (e.g.,
Manchado et al. 2000).
The question most often addressed is:
what is the mechanism for forming non-spherical, i.e., bipolar or
elliptical, structures?
In the present Paper I reverse the emphasis by asking:
what is required to form a spherical PN?
Presenting the question this way allows me to consider
a wider scope, e.g., the formation of blue horizontal
branch (HB) stars.
The two type of objects, I suggest, are connected in that both
spherical PNe and blue HB stars are formed from low mass stars,
but blue HB stars will not form PNe.
Therefore, the process behind the formation of blue HB stars
will prevent a star from forming a PN.
Manchado et al. (2000) argue that 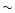 25% of the PNe in
their sample are round.
In the present Paper I use the term spherical PNe, assuming that
the PNe I classified as spherical are indeed spherical and not
pole-on elliptical or bipolar PNe.
I use my earlier classification of spherical PNe (Soker 1997,
hereafter S97), where more stringent criteria were used, and
where only 18 PNe are classified as spherical (Table 2 of S97).
These amount to 4% of the 458 PNe classified there,
but the estimate is that
25% of the PNe in
their sample are round.
In the present Paper I use the term spherical PNe, assuming that
the PNe I classified as spherical are indeed spherical and not
pole-on elliptical or bipolar PNe.
I use my earlier classification of spherical PNe (Soker 1997,
hereafter S97), where more stringent criteria were used, and
where only 18 PNe are classified as spherical (Table 2 of S97).
These amount to 4% of the 458 PNe classified there,
but the estimate is that 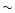 10% of all PNe are spherical.
Manchado et al. (1996) classify a PN as circular if its main
large scale outer nebula is circular, sometimes not referring to
the inner structure.
I consider the inner structure as well, hence many PNe classified as circular
by Manchado et al. (1996), are classified as elliptical in S97.
A few examples are given below.
Manchado et al. (1996) classify LSA 1
(PNG 029.8-07.8), K3-73 (PNG 084.0+09.5), and A 33
(PNG 238.0+34.8) as round PNe, but I can clearly see two arcs within
each of these PNe, which suggest that they are elliptical PNe.
On the other hand, K1-14 (PNG 045.6+24.3) and A71
(PNG 084.9+04.4), which are classified as round PNe by
Manchado et al. (1996), but not by S97,
may have been spherical PNe before distortion.
Another interesting case is A30 (PNG 208.5+33.2), which was
classified as round by Manchado et al., but not by S97.
The reason for the S97 classification of A30 as an elliptical PN is the
knots close to its central star, that show an axisymmetrical
structure. But beside these four knots the nebula shows
all the properties of a spherical PN.
In Sect. 2 some aspects of the distribution of these spherical
PNe in the galaxy and their mass loss history are studied.
In Sect. 3 these properties are related to the metallicity of
their progenitors.
The strong correlation between PNe morphology, including spherical
PNe, and metallicity holds for PNe in the Large Magellanic Cloud (LMC)
as well (Stanghellini et al. 2000).
In Sect. 3 I discuss also the formation of spherical PNe in
relation to blue HB stars and to the more than 70 known extrasolar
planets, arguing that the findings are compatible with the
planet-induced axisymmetrical mass loss model.
In this model low departure from spherical mass loss of some
stars on the upper AGB are attributed to planets
(Soker 2001a and references therein).
A summary of the main results, and some speculations and predictions, are
given in Sect. 4.
10% of all PNe are spherical.
Manchado et al. (1996) classify a PN as circular if its main
large scale outer nebula is circular, sometimes not referring to
the inner structure.
I consider the inner structure as well, hence many PNe classified as circular
by Manchado et al. (1996), are classified as elliptical in S97.
A few examples are given below.
Manchado et al. (1996) classify LSA 1
(PNG 029.8-07.8), K3-73 (PNG 084.0+09.5), and A 33
(PNG 238.0+34.8) as round PNe, but I can clearly see two arcs within
each of these PNe, which suggest that they are elliptical PNe.
On the other hand, K1-14 (PNG 045.6+24.3) and A71
(PNG 084.9+04.4), which are classified as round PNe by
Manchado et al. (1996), but not by S97,
may have been spherical PNe before distortion.
Another interesting case is A30 (PNG 208.5+33.2), which was
classified as round by Manchado et al., but not by S97.
The reason for the S97 classification of A30 as an elliptical PN is the
knots close to its central star, that show an axisymmetrical
structure. But beside these four knots the nebula shows
all the properties of a spherical PN.
In Sect. 2 some aspects of the distribution of these spherical
PNe in the galaxy and their mass loss history are studied.
In Sect. 3 these properties are related to the metallicity of
their progenitors.
The strong correlation between PNe morphology, including spherical
PNe, and metallicity holds for PNe in the Large Magellanic Cloud (LMC)
as well (Stanghellini et al. 2000).
In Sect. 3 I discuss also the formation of spherical PNe in
relation to blue HB stars and to the more than 70 known extrasolar
planets, arguing that the findings are compatible with the
planet-induced axisymmetrical mass loss model.
In this model low departure from spherical mass loss of some
stars on the upper AGB are attributed to planets
(Soker 2001a and references therein).
A summary of the main results, and some speculations and predictions, are
given in Sect. 4.
It is well known that spherical PNe have a larger average
galactic latitude b than that of the other PNe (e.g., Manchado
et al. 2000).
I now show that the class of spherical PNe, as classified by S97,
has also a larger galactic longitude than the other PNe.
The 458 PNe (of which 452 with good data are used here) that
were classified by S97 were all the PNe available (in the literature) at that
time that had good enough images to be classified according to their
morphology.
I use this list of PNe for the following reasons.
(1) I deal here with morphologies of PNe, and this is the only large list of
PNe where all PNe have well-resolved images.
(2) I examine the hypothesis that planets may play a role.
The classification of S97 takes the role of stellar companions,
as well as planets, into consideration (see below).
For example, considering a late interaction of a companion with the AGB
progenitor, a PN that has a large spherical halo but an inner elliptical
region is classified as an elliptical, rather than round PN.
(3) Due to large uncertainties in the distances to PNe,
and the fact that the PNe images are from very different telescopes
and researchers, it will be difficult to use any meaningful subsample.
(4) In any case, to have a large enough number of circular PNe,
all available circular PNe should be used.
In S97 I classified the PNe according to the type of binary
interaction that may have shaped them:
(i) Spherical PNe, which I assumed in S97 to be PNe whose
progenitors did not interact with any close companion, stellar or
substellar.
(ii) Bipolar PNe. Most, but not all, bipolar PNe
belong to this class. In S97 I assumed that these are PNe whose
progenitors interacted with close stellar companions
outside their envelopes.
(iii) Extreme-Elliptical PNe. This class includes some bipolar
PNe, but mainly extreme-elliptical PNe, e.g., having a ring but not
two lobes.
I assumed in S97 that the progenitors of most of these
PNe interacted with a stellar companion via a common envelope phase.
(iv) Elliptical PNe. By elliptical alone, I refer to moderate
elliptical PNe which show only small departure from sphericity.
In S97 the progenitors of these PNe were assumed to have interacted with
substellar objects, but not with a close stellar object.
In a later paper (Soker 2001b) I argue that many PNe that belong
to classes (iii) and (iv) can be formed from the influence of
a companion outside the progenitor's envelope, if the companion
is not too close and/or not too massive, but still accretes and blows
its own collimated fast wind (CFW).
In Table 1 I compare the galactic distribution of the
four classes listed by S97.
The quantities that are given for each class are as follows.
The total number of PNe in the class, 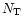 ,
the average galactic
longitude of all PNe in the class
,
the average galactic
longitude of all PNe in the class 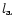 ,
and the number of PNe
toward the galactic center, i.e., having
,
and the number of PNe
toward the galactic center, i.e., having
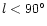 or
or
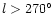 ,
,
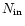 .
Also given are quantities just for PNe toward the
galactic center:
.
Also given are quantities just for PNe toward the
galactic center:
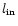 is the average value of the galactic
longitude,
is the average value of the galactic
longitude,
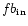 is the fraction of PNe having galactic
latitude of
is the fraction of PNe having galactic
latitude of
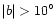 ,
and
,
and
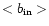 is the median value of
is the median value of
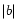 .
.
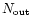 is the number of PNe away from the galactic center,
i.e., having
is the number of PNe away from the galactic center,
i.e., having
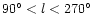 .
Other quantities with subscript "out'' have the same meaning
as those with subscript "in'', but only for PNe away from the
galactic center.
For statistics involving the galactic longitude I took the galactic
longitude of PNe with
.
Other quantities with subscript "out'' have the same meaning
as those with subscript "in'', but only for PNe away from the
galactic center.
For statistics involving the galactic longitude I took the galactic
longitude of PNe with
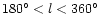 to be
to be
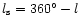 .
.
One well-known property and two new ones clearly emerge from
the table.
(1) As is well known (see, e.g., reviews by Corradi 2000 and
Manchado et al. 2000) bipolar PNe are concentrated toward the
galactic plane, elliptical ones have intermediate scale height, while
spherical PNe have the largest scale height.
The relevant quantities in the table that show this behavior
are
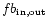 and
and
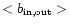 .
.
(2) The number of PNe towards and away from the galactic center
in each class,
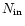 and
and
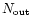 ,
and the average galactic
latitude
,
and the average galactic
latitude 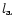 ,
reveal that spherical PNe tend to be concentrated
away from the galactic center.
While the differences in the fraction of PNe away from the
galactic center,
,
reveal that spherical PNe tend to be concentrated
away from the galactic center.
While the differences in the fraction of PNe away from the
galactic center,
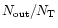 ,
between the three classes
of nonspherical PNe are within the statistical errors,
the value for spherical PNe is more than twice as large.
The selection effect due to galactic extinction is
unknown, and may affect the results.
,
between the three classes
of nonspherical PNe are within the statistical errors,
the value for spherical PNe is more than twice as large.
The selection effect due to galactic extinction is
unknown, and may affect the results.
(3) Another new property is the relatively very high average
galactic latitude of spherical PNe toward the galactic center.
This is seen from comparing the values of
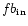 and
and
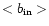 with
with
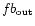 and
and
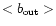 .
For the three classes of nonspherical PNe
.
For the three classes of nonspherical PNe
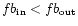 and
and
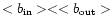 ,
while for spherical PNe opposite inequalities hold.
Another way to see this is by noticing that there is a smooth
increase in
,
while for spherical PNe opposite inequalities hold.
Another way to see this is by noticing that there is a smooth
increase in
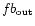 and
and
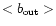 when moving from bipolar
to extreme-elliptical to elliptical and to spherical, while
in
when moving from bipolar
to extreme-elliptical to elliptical and to spherical, while
in
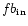 and
and
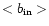 the smooth increase holds
only for the nonspherical PNe, with a sharp rise between
elliptical and spherical PNe.
Since spherical PNe in the sample used here tend to have low
surface brightness, this specific jump may be due to extinction in the
galactic plane. However, the general trend may be real.
This behavior is less certain also because of the poor statistics,
as there are only six spherical PNe toward the galactic center, and
because the relevant physical quantity is the galactic height,
for which the distance to each PN has to be known.
I use the galactic latitude in the statistical analysis in order
to avoid the large uncertainties in distances to PNe.
Despite these drawbacks, in the next section I suggest that this
behavior is real, and try to explain it.
the smooth increase holds
only for the nonspherical PNe, with a sharp rise between
elliptical and spherical PNe.
Since spherical PNe in the sample used here tend to have low
surface brightness, this specific jump may be due to extinction in the
galactic plane. However, the general trend may be real.
This behavior is less certain also because of the poor statistics,
as there are only six spherical PNe toward the galactic center, and
because the relevant physical quantity is the galactic height,
for which the distance to each PN has to be known.
I use the galactic latitude in the statistical analysis in order
to avoid the large uncertainties in distances to PNe.
Despite these drawbacks, in the next section I suggest that this
behavior is real, and try to explain it.
As discussed in the previous section, Manchado et al. (1996, 2000)
use a different classification for spherical PNe.
In their classification properties (2) and (3) listed above
are not found.
As also mention in the previous section, I disagree with Manchado
et al. (1996) in the classification of many PNe as spherical,
since these contain elliptical substructures within the main
circular shell.
Further studies, with larger samples, are clearly needed here.
Table 1:
Distribution of PNe in the galaxy.
| PNe Type |
Spherical |
Bipolar |
E-Elliptical |
Elliptical |
| Source (S97) |
Table 2 |
Table 3 |
Table 4 |
Table 5 |
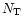 |
18 |
49 |
111 |
274 |
 |
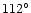 |
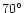 |
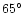 |
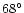 |
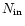 |
6 |
35 |
77 |
188 |
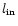 |
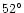 |
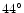 |
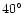 |
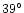 |
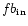 |
0.67 |
0.09 |
0.19 |
0.27 |
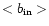 |
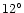 |
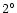 |
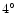 |
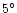 |
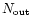 |
12 |
14 |
34 |
86 |
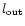 |
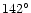 |
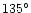 |
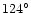 |
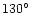 |
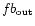 |
0.42 |
0.14 |
0.24 |
0.36 |
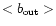 |
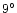 |
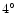 |
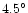 |
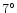 |
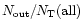 |
0.67(18) |
0.29(49) |
0.31(111) |
0.31(274) |
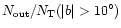 |
0.56(9) |
0.40(5) |
0.35(23) |
0.38 (81) |
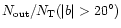 |
0.67(6) |
-(0) |
0.29(7) |
0.35 (31) |
The classification used is according to S97.
E-Elliptical means extreme-elliptical PNe, which S97 assumed to
be formed (in most cases) via interaction with a stellar
companion that went through a common envelope phase.
Bipolar were assumed by S97 to result from interaction with a
close stellar companion outside the AGB envelope, while elliptical
were assumed to result from interaction with substellar companions
or wide stellar companions.
The meaning of the symbols are:
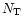
and
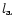
,
total number and average galactic longitude
of PNe in each class, respectively;
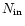
and
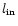
,
number of PNe toward the galactic center, i.e., having galactic
longitude of
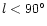
or
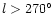
,
and their
average value of the galactic longitude
l;
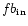
and
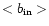
,
fraction of PNe having galactic
latitude of
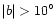
and the median value of
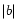
for PNe toward the galactic center.
Quantities with subscript "out'' have the same meaning but
for PNe away from the galactic center, i.e., having
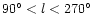
.
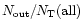
is the ratio of the number of all PNe
away from the galactic center to all PNe in each type of PNe, and
for all PNe in the type;
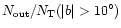
and
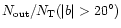
,
are the same ratio but only for PNe with
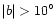
and
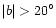
,
respectively.
The number in parenthesis follows that ratio is the number of PNe
in the denominator of each ratio.
For statistics involving the galactic longitude I took the galactic
longitude of PNe with
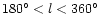
to be
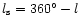
.
From the structures of most PNe, as well as other considerations,
we know that most stars terminate the AGB by blowing a superwind
(Renzini 1981), i.e., a final intensive wind (FIW), which is not
faster than the regular AGB wind but has a much higher mass loss rate.
In PNe this wind forms a dense shell.
In many cases, inward to this shell there is a bright rim formed
by the fast wind from the central star, and a fainter shell or
halo outside the shell (Frank et al. 1990).
Examining the images of the 18 spherical PNe (S97 Table 2),
I find that most do not show signatures of a FIW (Soker 2000).
I find dense shells only in Bd+30 3639 and IC 3568, both of
which were suspected as being elliptical seen pole-on
(marked PO by S97), H3-75, and possibly in A 15 and Lo 4.
As discussed in Soker (2000), where more details and references
can be found, the same correlation holds in many
elliptical PNe; their outer faint halo is spherical, or only
slightly elliptical, while the dense shell, which was formed from
the FIW (superwind), is highly nonspherical.
The positive correlation, albeit not perfect, between the onset
of a FIW and a more nonspherical mass loss geometry is discussed
by Soker (2000).
I propose the following explanation for the findings of the
previous section.
To form a spherical PNe the progenitor should have
a metallicity below a critical value.
This is supported by the correlation between metallicity and
morphology of PNe in the LMC, as presented in
Figs. 1-3 of Stanghellini et al. (2000).
For a given mass, the probability of forming a spherical PN
increases as metallicity decreases, starting from zero
probability at the critical metallicity
![${\rm [Fe/H]_c}$](/articles/aa/full/2002/18/aa2180/img49.gif) .
The star should also be above some lower mass limit.
For a given metallicity, the probability of forming a
spherical PN increases with the progenitor initial mass
.
The star should also be above some lower mass limit.
For a given metallicity, the probability of forming a
spherical PN increases with the progenitor initial mass 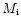 .
I further argue, as I have been doing for the last decade,
that this is expected if planets play a significant role in
spinning-up evolved stars (Soker 2001a and references therein).
To show that this is compatible with the galactic distribution
of spherical PNe, I consider the galactic-metallicity dependence
on age and the distance to the galactic center.
Hereafter the age t is expressed in Gyr (being positive with
t=0 at present), while the distance to the galactic center,
the Galactocentric radius, will be with respect to the distance
of the sun to the galactic center in units of kpc (r=0 at the
solar neighborhood, and r>0 moving away from the galactic center).
.
I further argue, as I have been doing for the last decade,
that this is expected if planets play a significant role in
spinning-up evolved stars (Soker 2001a and references therein).
To show that this is compatible with the galactic distribution
of spherical PNe, I consider the galactic-metallicity dependence
on age and the distance to the galactic center.
Hereafter the age t is expressed in Gyr (being positive with
t=0 at present), while the distance to the galactic center,
the Galactocentric radius, will be with respect to the distance
of the sun to the galactic center in units of kpc (r=0 at the
solar neighborhood, and r>0 moving away from the galactic center).
Lineweaver (2001) studies the relation between the metallicity of
sun-like stars and the presence of hot Jupiter-like planets orbiting them.
Lineweaver uses a galactic metallicity evolution in the solar
neighborhood which presently has
![${\rm [Fe/H]_s} = -0.2$](/articles/aa/full/2002/18/aa2180/img51.gif) ,
similar to the metallicity given by Allen et al. (1998)
in their PNe study, but lower than values given by others, e.g.,
Carraro et al. (1998) and Rocha-Pinto et al.
(2000; see reviews by Henry & Worthey 1999 and Shields 2002).
I take a metallicity evolution in the solar neighborhood
to be some average of these studies,
,
similar to the metallicity given by Allen et al. (1998)
in their PNe study, but lower than values given by others, e.g.,
Carraro et al. (1998) and Rocha-Pinto et al.
(2000; see reviews by Henry & Worthey 1999 and Shields 2002).
I take a metallicity evolution in the solar neighborhood
to be some average of these studies,
![$\displaystyle {\rm [Fe/H]_s}(t)$](/articles/aa/full/2002/18/aa2180/img52.gif) |
= |
-0.1-0.02t-a(t-5)4 |
|
| |
|
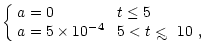 |
(1) |
where t is the age given in Gyr,
and subscript s refers to the solar neighborhood.
Allen et al. (1998) deduce from their PNe study that the
metallicity gradient, with respect to the distance from the galactic
center, was steeper in the past, while Carraro et al. (1998)
find a nonmonotonic evolution of the metallicity gradient that, they
argue, is compatible with a gradient that does not change with time.
Again, I take the gradient evolution to be the average between
these two studies,
![$\displaystyle \frac {{\rm d} {\rm [Fe/H]}}{{\rm d}r} =
-2\times 10^{-4} t^2 - 0.001 t -0.09 ~{\rm dex} ~\rm {kpc}^{-1},$](/articles/aa/full/2002/18/aa2180/img54.gif) |
|
|
(2) |
where r is the distance from the galactic center minus
the solar distance to the galactic center (in kpc).
The metallicity is therefore given by
![$\displaystyle {\rm [Fe/H]}(t,r)={\rm [Fe/H]}_{\rm s}+\frac {{\rm d} {\rm [Fe/H]}}{{\rm d}r}r.$](/articles/aa/full/2002/18/aa2180/img55.gif) |
|
|
(3) |
The contour map of
![${\rm [Fe/H]}(t,r)$](/articles/aa/full/2002/18/aa2180/img56.gif) is plotted in Fig. 1.
The contour levels have a constant spacing of
is plotted in Fig. 1.
The contour levels have a constant spacing of
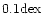 ,
with values marked near each contour line.
,
with values marked near each contour line.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{ms2180f1.eps}
\end{figure}](/articles/aa/full/2002/18/aa2180/Timg59.gif) |
Figure 1:
Metallicity contour map.
The value of [Fe/H] is written near each contour line,
r is the Galactocentric distance relative to the sun
(r=0 for the solar neighborhood, r>0 is away from the galactic
center) and t is the age (t=0 at present).
This contour map is used in the text together with the distribution
of spherical PNe in the galaxy (Table 1) to argue that the
progenitors of spherical PNe have
![$[{\rm Fe/H}] \protect\la -0.4$](/articles/aa/full/2002/18/aa2180/img58.gif) (marked by a thick line).
(marked by a thick line). |
| Open with DEXTER |
For present purposes the exact values of the metallicity are
not important, but only the general variation of metallicity with
r and t.
To demonstrate the proposed explanation for the spherical PNe
properties, I estimate the critical metallicity to be
![${\rm [Fe/H]_c} \simeq -0.4$](/articles/aa/full/2002/18/aa2180/img60.gif) ,
and mark this contour by a
thicker line.
If only stars with
,
and mark this contour by a
thicker line.
If only stars with
![${\rm [Fe/H]}<{\rm [Fe/H]_c} \simeq -0.4$](/articles/aa/full/2002/18/aa2180/img61.gif) can
form spherical PNe, it is clear from the figure that more
spherical PNe will be located at larger distances from the
galactic center, i.e., r>0, and they all will be descendants
of low mass progenitors.
These PNe occupy the upper left corner of Fig. 1, where the
large age means that these PNe are formed from low mass stars.
These low mass star progenitors imply that the galactic distribution
of the descendant PNe will have a large average galactic
latitude, as is indeed observed (Manchado et al. 2000).
Moreover, the spherical PNe closer to the galactic center, r<0,
with
can
form spherical PNe, it is clear from the figure that more
spherical PNe will be located at larger distances from the
galactic center, i.e., r>0, and they all will be descendants
of low mass progenitors.
These PNe occupy the upper left corner of Fig. 1, where the
large age means that these PNe are formed from low mass stars.
These low mass star progenitors imply that the galactic distribution
of the descendant PNe will have a large average galactic
latitude, as is indeed observed (Manchado et al. 2000).
Moreover, the spherical PNe closer to the galactic center, r<0,
with
![${\rm [Fe/H]} \ga -0.4$](/articles/aa/full/2002/18/aa2180/img62.gif) ,
are on average lighter (older) than those
farther away from the galactic center, r>0, meaning a larger
average galactic latitude.
This is compatible with the findings of Sect. 2 (compare
,
are on average lighter (older) than those
farther away from the galactic center, r>0, meaning a larger
average galactic latitude.
This is compatible with the findings of Sect. 2 (compare
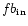 and
and
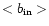 with
with
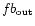 and
and
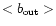 ,
all given in Table 1).
,
all given in Table 1).
To have  5-10% spherical PNe among all PNe, the probability for
forming a spherical PNe must increase substantially as metallicity
decreases by
5-10% spherical PNe among all PNe, the probability for
forming a spherical PNe must increase substantially as metallicity
decreases by 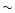 0.3-0.4 dex from the critical value.
In the case assumed here, it is from
0.3-0.4 dex from the critical value.
In the case assumed here, it is from
![${\rm [Fe/H]_c} \simeq -0.4$](/articles/aa/full/2002/18/aa2180/img60.gif) to
to
![${\rm [Fe/H]} \simeq -0.8$](/articles/aa/full/2002/18/aa2180/img63.gif) .
Two other relevant phenomena also change significantly when metallicity
is changed by
.
Two other relevant phenomena also change significantly when metallicity
is changed by 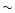 0.3-
0.3-
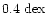 .
The first is the presence of hot-Jupiter stars around sun-like stars.
The several tens of extrasolar planets that have been found
tend to orbit metal-rich stars.
Lineweaver (2001) analyzes 32 hosts of Jupiter-like planets, and
argues that the probability of a sun-like star hosting a hot
Jupiter-like planet increases from
.
The first is the presence of hot-Jupiter stars around sun-like stars.
The several tens of extrasolar planets that have been found
tend to orbit metal-rich stars.
Lineweaver (2001) analyzes 32 hosts of Jupiter-like planets, and
argues that the probability of a sun-like star hosting a hot
Jupiter-like planet increases from 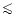 10% at
10% at
![${\rm [Fe/H]} = 0.1$](/articles/aa/full/2002/18/aa2180/img66.gif) to
to 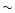
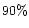 at
at
![${\rm [Fe/H]}=0.4$](/articles/aa/full/2002/18/aa2180/img68.gif) ,
and to almost
,
and to almost 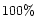 at
at
![${\rm [Fe/H]}=0.6$](/articles/aa/full/2002/18/aa2180/img70.gif) (see also Santos et al. 2001).
This is further strengthen by new detection of planets.
From 1200 stars discussed by Vogt et al. (2002; where more
details can be found) 44 planets and 4 brown dwarfs have been detected,
i.e.,
(see also Santos et al. 2001).
This is further strengthen by new detection of planets.
From 1200 stars discussed by Vogt et al. (2002; where more
details can be found) 44 planets and 4 brown dwarfs have been detected,
i.e., 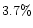 of surveyed stars were found to have planets.
For stars with metallicity above solar,
of surveyed stars were found to have planets.
For stars with metallicity above solar,
![$[{\rm Fe/H}]>0$](/articles/aa/full/2002/18/aa2180/img72.gif) ,
the detection fraction
is
,
the detection fraction
is 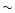 2.6 times that for the entire sample (Vogt et al. 2002).
Reid (2002) argues that at
2.6 times that for the entire sample (Vogt et al. 2002).
Reid (2002) argues that at
![$[{\rm Fe/H}]\ga 0.3$](/articles/aa/full/2002/18/aa2180/img73.gif) most sun-like
stars harbor planets around them.
most sun-like
stars harbor planets around them.
The second phenomenon is the distribution of HB
stars on the Hertzsprung-Russel diagram of globular clusters
(the HB morphology).
The distribution, e.g., the relative number of blue HB
stars, varies from one globular cluster to another.
It has long been known that metallicity is the main, but not sole,
factor which determines the HB morphology
(for a historical review see, e.g., Rood et al. 1997;
Fusi Pecci & Bellazzini 1997).
The other factor(s) which determine(s) the HB morphology
is termed the "second parameter'', and it is commonly thought that
it has to do with mass loss on the red giant branch (Rood 1973).
It is well known that the HB morphology
significantly changes its behavior in a relatively narrow
metallicity range of
![$-1.75 \la {\rm [Fe/H]} \la -1.3$](/articles/aa/full/2002/18/aa2180/img74.gif) (Soker & Hadar 2002 and references therein).
Therefore, it is not unlikely that the property which determines
the probability of forming a spherical PN significantly changes
over a narrow metallicity range, around
(Soker & Hadar 2002 and references therein).
Therefore, it is not unlikely that the property which determines
the probability of forming a spherical PN significantly changes
over a narrow metallicity range, around
![${\rm [Fe/H]} \sim -0.5$](/articles/aa/full/2002/18/aa2180/img75.gif) .
.
I now relate the metallicity dependence on time and Galactocentric
radius to the planet-induced axisymmetrical mass loss model.
In this model low departure from spherical mass loss of some
stars on the upper AGB is assumed to result from planets
or brown dwarfs, which spin-up the AGB stellar envelopes (Soker 2001a
and references therein).
In other stars the nonspherical mass loss is due to interaction with
stellar companions.
Therefore, it is assumed in the model that
if a massive enough and close enough planet is present
around a star, the stellar envelope will be spun-up by the
planet via tidal effects and common envelope evolution.
The maximum orbital separation for an interaction to take place
is 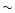
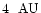 .
In a previous paper (Soker 2001a) I argue that even planets having
masses as small as
.
In a previous paper (Soker 2001a) I argue that even planets having
masses as small as
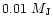 ,
where
,
where 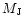 is Jupiter's mass, can lead to
a slightly nonspherical mass loss geometry.
Low mass stars hosting a close planet will engulf the planet already
on the first giant branch (RGB), prior to the HB.
The stars will be spun-up, their mass loss rate is likely to increase
(Soker & Hadar 2002), and they will retain very small mass in
their envelopes, forming blue HB stars.
Therefore, it is very likely that most known extrasolar systems
will not form PN at all, but rather the hosting stars will engulf the
orbiting planets during their RGB, lose most of their envelope on the
RGB, and turn into blue HB stars.
Blue HB stars are not likely to reach the upper AGB
and form PNe because of their very low envelope masses.
Even single low mass stars may lose too much
mass on the RGB, possibly due to fast rotation, and never form PNe.
For different reasons, Allen et al. (1998) argue that
less than half of all stars of initial mass
is Jupiter's mass, can lead to
a slightly nonspherical mass loss geometry.
Low mass stars hosting a close planet will engulf the planet already
on the first giant branch (RGB), prior to the HB.
The stars will be spun-up, their mass loss rate is likely to increase
(Soker & Hadar 2002), and they will retain very small mass in
their envelopes, forming blue HB stars.
Therefore, it is very likely that most known extrasolar systems
will not form PN at all, but rather the hosting stars will engulf the
orbiting planets during their RGB, lose most of their envelope on the
RGB, and turn into blue HB stars.
Blue HB stars are not likely to reach the upper AGB
and form PNe because of their very low envelope masses.
Even single low mass stars may lose too much
mass on the RGB, possibly due to fast rotation, and never form PNe.
For different reasons, Allen et al. (1998) argue that
less than half of all stars of initial mass
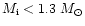 form PNe.
form PNe.
It seems therefore that stars hosting close planets with
mass 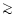
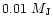 will either lose most of their envelope
on the RGB and never form PNe, or reach the AGB but form
nonspherical, i.e., elliptical, PNe.
To form a spherical PN a star should not have any
close planet with a mass
will either lose most of their envelope
on the RGB and never form PNe, or reach the AGB but form
nonspherical, i.e., elliptical, PNe.
To form a spherical PN a star should not have any
close planet with a mass 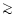
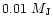 ,
and of course no close
stellar companion or brown dwarf either.
It is very likely, e.g., Lineweaver (2001), Santos et al. (2001),
and Reid (2002),
that the probability of forming a planet, and the planet's mass,
strongly depend on metallicity.
(In a recent paper Murray & Chaboyer 2002, on the other hand, argue that
accretion of 6 Earth masses of iron rich material can explain most
of the observations, with no need to assume a strong dependance of
planets formation on metallicity.)
Lineweaver (2001), for example, assumes that Earth-type planets are
formed only when
,
and of course no close
stellar companion or brown dwarf either.
It is very likely, e.g., Lineweaver (2001), Santos et al. (2001),
and Reid (2002),
that the probability of forming a planet, and the planet's mass,
strongly depend on metallicity.
(In a recent paper Murray & Chaboyer 2002, on the other hand, argue that
accretion of 6 Earth masses of iron rich material can explain most
of the observations, with no need to assume a strong dependance of
planets formation on metallicity.)
Lineweaver (2001), for example, assumes that Earth-type planets are
formed only when
![${\rm [Fe/H]} \ga -1$](/articles/aa/full/2002/18/aa2180/img81.gif) ,
with increasing probability
for increasing metallicity.
For planets to induce mass loss in globular clusters, low mass planets
should be formed already at
,
with increasing probability
for increasing metallicity.
For planets to induce mass loss in globular clusters, low mass planets
should be formed already at
![${\rm [Fe/H]} \sim -1.7$](/articles/aa/full/2002/18/aa2180/img82.gif) .
The initial mass of globular clusters stars now reaching the
HB is
.
The initial mass of globular clusters stars now reaching the
HB is 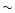 0.9, so Earth-like planets maybe enough in some cases
to enhance mass loss. More massive planets may be required to prevent
stars of
0.9, so Earth-like planets maybe enough in some cases
to enhance mass loss. More massive planets may be required to prevent
stars of
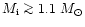 from reaching the AGB.
It is not unlikely that planets with mass of
from reaching the AGB.
It is not unlikely that planets with mass of 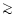
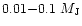 will be formed at high probability when
will be formed at high probability when
![${\rm [Fe/H]} \ga -0.4$](/articles/aa/full/2002/18/aa2180/img62.gif) ,
as I suggested in the previous subsection.
Such close planets will either cause their hosting star to form
an elliptical PN or cause the star to lose most of its envelope,
never forming a PN.
,
as I suggested in the previous subsection.
Such close planets will either cause their hosting star to form
an elliptical PN or cause the star to lose most of its envelope,
never forming a PN.
The main finding of the paper concerns the distribution of spherical
PNe in the galaxy.
I found that spherical PNe tend to be concentrated away from
the galactic center, and spherical PNe that are closer than the sun
to the galactic center have a relatively very high average
galactic latitude (Table 1).
These trends should be confirmed, or rejected, when larger
samples of well-resolved PNe become available, e.g., the
Edinburgh/AAO/Strasbourg Catalogue of Galactic PNe (Parker
et al. 2002; under construction).
I used this finding to argue that spherical PNe are formed from
low metallicity stellar progenitors (see Fig. 1).
This correlation is observed directly in the LMC (Stanghellini
et al. 2000).
A crude estimate suggests that spherical PNe are formed from stars
with
![${\rm [Fe/H]} \la -0.4$](/articles/aa/full/2002/18/aa2180/img85.gif) (and initial mass of
(and initial mass of
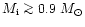 ), although only a minority of stars with these
properties do form spherical PNe.
), although only a minority of stars with these
properties do form spherical PNe.
I further argued that the dependence on metallicity may result from
the role played by planets in spinning-up the envelope of RGB and AGB
stars.
A planet will either spin-up the stellar envelope to blow
a non spherical wind, hence forming an elliptical PN, or, if the
spin-up occurs on the RGB of a low mass star, the relatively fast
rotating RGB star will lose most of its envelope and form a blue HB
star, but will never reach the upper AGB and form a PN.
Lineweaver (2001) finds the probability of forming Jupiter-like planets,
with masses of
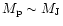 ,
to increase from
,
to increase from 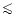 10%
at
10%
at
![${\rm [Fe/H]_l} = 0.1$](/articles/aa/full/2002/18/aa2180/img88.gif) to
to 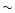 90% at
90% at
![${\rm [Fe/H]_u}=0.4$](/articles/aa/full/2002/18/aa2180/img89.gif) (see also Reid 2002).
The planet-induced axisymmetrical mass loss model to explain the
properties of spherical PNe requires that the probability of forming
planets of
(see also Reid 2002).
The planet-induced axisymmetrical mass loss model to explain the
properties of spherical PNe requires that the probability of forming
planets of
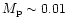 -
-
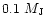 increase significantly from
increase significantly from
![${\rm [Fe/H]_l} \simeq -0.8$](/articles/aa/full/2002/18/aa2180/img92.gif) to
to
![${\rm [Fe/H]_u} \simeq -0.4$](/articles/aa/full/2002/18/aa2180/img93.gif) .
Of course, more massive planets can be formed as well.
For comparison, the planet second parameter model to explain some
HB morphologies of globular clusters (Soker & Hadar 2002) requires
that the probability of forming planets of
.
Of course, more massive planets can be formed as well.
For comparison, the planet second parameter model to explain some
HB morphologies of globular clusters (Soker & Hadar 2002) requires
that the probability of forming planets of
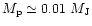 increases
significantly from
increases
significantly from
![${\rm [Fe/H]_l} \simeq -1.7$](/articles/aa/full/2002/18/aa2180/img95.gif) to
to
![${\rm [Fe/H]_u} \simeq -1.3$](/articles/aa/full/2002/18/aa2180/img96.gif) .
These three critical metallicity bands show a monotonic trend,
which, I claim, supports the conjecture that planets play a crucial
role in the mass loss history of evolved stars.
.
These three critical metallicity bands show a monotonic trend,
which, I claim, supports the conjecture that planets play a crucial
role in the mass loss history of evolved stars.
Acknowledgements
I thank the anonymous referee for clarifying comments.
This research was supported in part by a grant from the
US-Israel Binational Science Foundation.
- Allen, C., Carigi, L., & Peimbert, M. 1998, ApJ, 494, 247
In the text
NASA ADS
- Carraro, G., Ng, Y. K., & Portinari, L. 1998, MNRAS, 296, 1045
In the text
NASA ADS
- Corradi, R. L. M. 2000,
in Asymmetrical Planetary Nebulae II: From Origins
to Microstructures, ed. J. H. Kastner, N. Soker, &
S. Rappaport, ASP Conf. Ser., 199, 25
In the text
- Frank, A., Balick, B., & Riley, J. 1990, AJ, 100, 1903
In the text
NASA ADS
- Fusi Pecci, F., & Bellazzini, M. 1997,
in The Third Conference on Faint Blue Stars,
ed. A. G. D. Philip, J. Liebert, R. Saffer, & D. S. Hayes
(L. Davis Press), 255 [astro-ph/9701026]
In the text
- Henry, R. B. C., & Worthey, G. 1999, PASP, 111, 919
In the text
NASA ADS
- Lineweaver, C. H. 2001, Icarus, 151, 307 [astro-ph/0012399]
In the text
NASA ADS
- Manchado, A., Guerrero, M., Stanghellini, L.,
& Serra-Ricart, M. 1996, The IAC Morphological Catalog of Northern
Galactic Planetary Nebulae (Tenerife: IAC)
In the text
- Manchado, A., Villaver, E., Stanghellini, L.,
& Guerrero, M. A. 2000,
in Asymmetrical Planetary Nebulae II: From Origins
to Microstructures, ed. J. H. Kastner, N. Soker, &
S. Rappaport, ASP Conf. Ser., 199, 17
In the text
- Marcy, G. W., & Butler, R. P. 2000, PASP, 112, 137
NASA ADS
- Murray, N., & Chaboyer, B. 2002, preprint
[astro-ph/0106294]
In the text
- Parker, Q. A., et al.
2002, in Planetary Nebulae, IAU 209, in press
In the text
- Reid, I. N. 2002, PASP, in press [astro-ph/0112402]
In the text
- Renzini, A. 1981, in Effects of Mass Loss on Stellar
Evolution, ed. C. Chiosi, & R. Stalio (Dordrecht: Reidel), 319
In the text
- Rocha-Pinto, H. J., Maciel, W. J., Scalo, J., & Flynn, C.
2000, A&A, 358, 850
In the text
NASA ADS
- Rood, R. T. 1973, ApJ, 184, 815
In the text
NASA ADS
- Rood, R. T., Whitney, J., & D'Cruz, N. 1997,
in Advances in Stellar Evolution, ed. R. T. Rood, & A. Renzini
(Cambridge: Cambridge U. Press), 74
In the text
- Santos, N. C., Israelian, G., & Mayor, M. 2001,
A&A, 373, 1019
In the text
NASA ADS
- Shields, G. A. 2002, Rev. Mex. A & A, 12 (Serie de Conferencias),
Ionized Gaseous Nebulae, ed. W. Henney et al., 189
In the text
- Soker, N. 1997, ApJS, 112, 487 (S97)
In the text
NASA ADS
- Soker, N. 2000,
in Asymmetrical Planetary Nebulae II: From Origins to
Microstructures, ed. J. H. Kastner, N. Soker, & S. Rappaport, ASP
Conf. Ser., 199,
71 [astro-ph/9909258]
In the text
- Soker, N. 2001a, MNRAS, 324, 699 [astro-ph/0006362]
In the text
NASA ADS
- Soker, N. 2001b, ApJ, 558, 157
In the text
NASA ADS
- Soker, N., & Hadar, R. 2002, MNRAS, 331, 731
In the text
NASA ADS
- Stanghellini, L., Shaw, R. A., Balick, B., &
Blades, J. C. 2000, ApJ, 534, L167
In the text
NASA ADS
- Vogt, S. S., Butler, R. P., Marcy, G. W., et al. 2002, ApJ, 568, 352
In the text
NASA ADS
Copyright ESO 2002
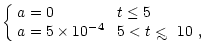
![$\displaystyle \frac {{\rm d} {\rm [Fe/H]}}{{\rm d}r} =
-2\times 10^{-4} t^2 - 0.001 t -0.09 ~{\rm dex} ~\rm {kpc}^{-1},$](/articles/aa/full/2002/18/aa2180/img54.gif)
![$\displaystyle {\rm [Fe/H]}(t,r)={\rm [Fe/H]}_{\rm s}+\frac {{\rm d} {\rm [Fe/H]}}{{\rm d}r}r.$](/articles/aa/full/2002/18/aa2180/img55.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{ms2180f1.eps}
\end{figure}](/articles/aa/full/2002/18/aa2180/Timg59.gif)