The standard TTI model cannot reproduce the very short supercycles
observed in ultra-low mass-ratio systems. Osaki (1995a)
reproduced RZ LMI's supercycle by ending prematurely the
superoutburst assuming
![]() instead of the
usual value of 0.35 a (note that in the TTI framework, one
assumes
instead of the
usual value of 0.35 a (note that in the TTI framework, one
assumes
![]() when modelling WZ Sge,
even though its mass ratio is presumably smaller than in most SU
UMa stars). In addition, the presence of superhumps after the end
of the superoutburst implies that the eccentricity stops much
later than the end of a superoutburst. The only ways for the disc
to remain eccentric after the end of a superoutburst are then: (i)
when modelling WZ Sge,
even though its mass ratio is presumably smaller than in most SU
UMa stars). In addition, the presence of superhumps after the end
of the superoutburst implies that the eccentricity stops much
later than the end of a superoutburst. The only ways for the disc
to remain eccentric after the end of a superoutburst are then: (i) ![]() is very long, or (ii) the accretion disc is always
eccentric in ER UMa systems.
is very long, or (ii) the accretion disc is always
eccentric in ER UMa systems.
In the first case, the transition time ![]() must be much
larger than the one used here. However, as shown in Fig. 3, the interval between a superoutburst and the next
normal outburst is far too long compared to observations. The
second solution implies that the tidal torque is no longer
responsible for superoutbursts, since
c(r) = c1 is a constant.
However, the presence of large outbursts is still possible, as the
(modified) DIM predicts the alternation of narrow and wide
outbursts (see Paper I) for large enough mass transfer rates. If
the mass transfer rate is constant, the light curve consists of
one or two small outbursts surrounded by large ones, but small
variations of the mass transfer rate can easily lead to ER UMa
type light curves, provided that these variations show some
regularity. Irradiation of the disc and of the secondary can also
account for the presence of long and short outbursts; Hameury et
al. (2000) have included these effects in the standard
disc instability model and produced light curves typical of
systems such as RZ LMi.
must be much
larger than the one used here. However, as shown in Fig. 3, the interval between a superoutburst and the next
normal outburst is far too long compared to observations. The
second solution implies that the tidal torque is no longer
responsible for superoutbursts, since
c(r) = c1 is a constant.
However, the presence of large outbursts is still possible, as the
(modified) DIM predicts the alternation of narrow and wide
outbursts (see Paper I) for large enough mass transfer rates. If
the mass transfer rate is constant, the light curve consists of
one or two small outbursts surrounded by large ones, but small
variations of the mass transfer rate can easily lead to ER UMa
type light curves, provided that these variations show some
regularity. Irradiation of the disc and of the secondary can also
account for the presence of long and short outbursts; Hameury et
al. (2000) have included these effects in the standard
disc instability model and produced light curves typical of
systems such as RZ LMi.
We therefore conclude that ER UMa stars should be dwarf novae with a permanently eccentric accretion disc, thereby accounting for superhumps, and where the illumination of the disc and the secondary star plays an important role. We thus predict that superhumps should exist at all phases of the supercycle of ER UMa stars; this apparently agrees with observations (Gao et al. 1999).
WZ Sge stars have very long supercycles and superoutbursts. In addition, no normal outbursts between two consecutive superoutbursts are observed. Some WZ Sge stars also show echo outbursts at the end of the superoutburst: several small outbursts, spaced every tens of days, during which superhumps are still present.
Smak (1993) deduces the mass transfer rate of WZ Sge from the luminosity of the hot spot. It is observed to increase at least by a factor 10 during superoutburst, and it decreases afterwards, remaining larger than the quiescent value during several tens of days. Such mass transfer rate fluctuation could result from irradiation of the secondary star by the white dwarf. Hameury et al. (2000) have shown that irradiation (including disc irradiation) could indeed account for some peculiarities of WZ Sge stars: for example, they reproduced the echo outbursts phenomenon without including the tidal instability in the DIM; however, they did not reproduce a full cycle with long recurrence times, and the echo outbursts they obtained were slightly too dim.
The long recurrence times can be due to low alpha value (Smak
1993; Osaki 1995b), possibly due to a decay of the MHD
turbulence that would lead to a time-dependant
![]() prescription (Osaki et al. 2001), thereby
explaining the echo outbursts. A low viscosity could result from
the secondary being a brown dwarf (Meyer & Meyer-Hofmeister
1999), but one would have to explain why the viscosity is
so much lower in these systems as compared to other SU UMa systems
which have comparable or even shorter orbital periods. Another
possibility (Lasota et al. 1995, 1999; Hameury et al. 1997) is that WZ Sge stars are in a stable low state
between superoutbursts, thus explaining the absence of normal
outbursts. This requires a hole in the central regions of the
disc, as a result of either a moderate magnetic field, or of
evaporation. The superoutbursts would then be triggered by an
externally imposed increase of the mass transfer rate, the long
duration of the outburst and the large mass accreted onto the
white dwarf being due to the irradiation of the secondary. They
did not include the tidal instability and, as in the case of ER
UMa stars, the presence of superhumps and late superhumps is
explained if the accretion disc is always eccentric. If one
combines these results with those of Hameury et al. (2000)
on the echo outburst, one should be able to reproduce a WZ Sge
star light curve with echo outbursts, which would however be
slightly different than the observed ones.
prescription (Osaki et al. 2001), thereby
explaining the echo outbursts. A low viscosity could result from
the secondary being a brown dwarf (Meyer & Meyer-Hofmeister
1999), but one would have to explain why the viscosity is
so much lower in these systems as compared to other SU UMa systems
which have comparable or even shorter orbital periods. Another
possibility (Lasota et al. 1995, 1999; Hameury et al. 1997) is that WZ Sge stars are in a stable low state
between superoutbursts, thus explaining the absence of normal
outbursts. This requires a hole in the central regions of the
disc, as a result of either a moderate magnetic field, or of
evaporation. The superoutbursts would then be triggered by an
externally imposed increase of the mass transfer rate, the long
duration of the outburst and the large mass accreted onto the
white dwarf being due to the irradiation of the secondary. They
did not include the tidal instability and, as in the case of ER
UMa stars, the presence of superhumps and late superhumps is
explained if the accretion disc is always eccentric. If one
combines these results with those of Hameury et al. (2000)
on the echo outburst, one should be able to reproduce a WZ Sge
star light curve with echo outbursts, which would however be
slightly different than the observed ones.
We have used our TTI model including irradiation and the presence
of an inner hole for the accretion disc as determined by Eq. (7) of Hameury et al. (2000). We use the parameters of
EG Cnc. The mass transfer rate from the secondary is
assumed to be affected by irradiation according to:
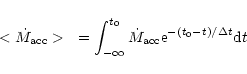 |
(5) |
This model predicts that the luminosity should increase just before the triggering of a superoutburst. The increase need not be large - one simply requires the mass transfer rate to exceed the critical rate for stability; this therefore does not contradict the observation of Ishioka et al. (2002) that no strong orbital hump due to a high mass transfer rate was detected during the early phase of WZ Sge 2001 outburst.
We obtain a light curve with a very long superoutburst followed by
3 normal outbursts that last ![]() 3 days and occur within two
months of the main outburst (Fig. 5). The disc radius
remains always larger than 0.35a, and is always in an eccentric
state; permanent superhumps are thus expected. However, the
interval between normal outbursts is twice longer than for EG Cnc
echo outbursts, which are brighter than observed. We did not
obtain a better fit with ER UMa light curves; in view of
the very crude assumptions made to derive the mass transfer rate
from the secondary under the influence of illumination, this is
not really a surprise.
3 days and occur within two
months of the main outburst (Fig. 5). The disc radius
remains always larger than 0.35a, and is always in an eccentric
state; permanent superhumps are thus expected. However, the
interval between normal outbursts is twice longer than for EG Cnc
echo outbursts, which are brighter than observed. We did not
obtain a better fit with ER UMa light curves; in view of
the very crude assumptions made to derive the mass transfer rate
from the secondary under the influence of illumination, this is
not really a surprise.
Copyright ESO 2002