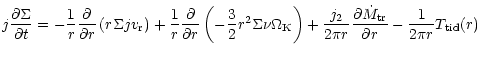 |
(1) |
The equation of angular momentum conservation in a disc is
(Hameury et al. 1998):
In the TTI model, c is no longer a constant, but depends on
whether the disc is eccentric or not. Ichikawa et al.
(1993) reproduced supercycles assuming that the disc
becomes eccentric when its radius reaches
![]() ;
c is then increased by a large factor. Afterward the disc starts
shrinking and can no longer maintain its eccentricity when its
radius becomes smaller than
;
c is then increased by a large factor. Afterward the disc starts
shrinking and can no longer maintain its eccentricity when its
radius becomes smaller than
![]() ,
at which
point c returns to its normal value. We choose to take a value
c0 when the disc is axisymmetric and a larger value c1 when
the disc is eccentric. This is our Prescription I for c, quite
similar to that of Ichikawa et al. (1993) who extended the
work of Osaki (1989) by taking into account a non zero tidal
torque during quiescence.
,
at which
point c returns to its normal value. We choose to take a value
c0 when the disc is axisymmetric and a larger value c1 when
the disc is eccentric. This is our Prescription I for c, quite
similar to that of Ichikawa et al. (1993) who extended the
work of Osaki (1989) by taking into account a non zero tidal
torque during quiescence.
We have included this variable tidal torque in the disc
instability model used in Paper I, which is a modified version of
the DIM described in Hameury et al. (1998) that includes
heating by the stream impact and the tidal torque (we have
corrected Eq. (1) of Paper I, in which the heating rate was
overestimated by a factor ![]() 2). In the following, we also
assume that
2). In the following, we also
assume that
![]() in quiescence and
in quiescence and
![]() in outburst. The inner radius is
fixed at
in outburst. The inner radius is
fixed at
![]() cm.
cm.
We obtain the cycle shown in Fig. 1. After a
superoutburst, the disc mass and radius are small. The disc mass
slowly increases, and several normal outbursts are triggered due
to the thermal instability. During each outburst, only a small
amount of mass is accreted by the white dwarf, so that the average
disc mass increases; a significant disc expansion occurs during
the rise to maximum, when the heat front reaches the outer edge of
the disc. The disk then shrinks when a cooling front brings the
disc back to a cool state, causing a significant reduction of the
outward angular momentum flow. After the end of an outburst, the
disc radius very slowly decreases as a result of mass addition and
viscous diffusion, but the net balance is an increase of the
radius from one outburst to the next one. Eventually,
![]() becomes larger than r3:1 during an outburst and the
tidal torque is increased, as well as the associated energy
dissipation. The disc is then maintained in the hot state until
most of the mass has been accreted. During this phase the radius
decreases until
becomes larger than r3:1 during an outburst and the
tidal torque is increased, as well as the associated energy
dissipation. The disc is then maintained in the hot state until
most of the mass has been accreted. During this phase the radius
decreases until
![]() .
The disc returns to a
circular shape, the anomalous tidal dissipation stops, and a
cooling wave starts from the disc outer edge, bringing the whole
disc in a cool state.
.
The disc returns to a
circular shape, the anomalous tidal dissipation stops, and a
cooling wave starts from the disc outer edge, bringing the whole
disc in a cool state.
![\begin{figure}
\par\resizebox{7.2cm}{!}{\includegraphics[angle=-90]{MS2065f1.eps}}
\end{figure}](/articles/aa/full/2002/18/aa2065/Timg31.gif) |
Figure 1:
Superoutburst cycle in the TTI model for SU UMa with
|
There is, however, no compelling reason to assume that the whole
disc is affected by the development of the tidal instability. We
therefore use another prescription for c (hereafter Prescription II). We assume that when the disc is circular, c = c0; when
eccentric,
c(r) = c1 for
![]() and c =
c0 for
and c =
c0 for
![]() .
A linear interpolation is
assumed between
.
A linear interpolation is
assumed between
![]() and
and
![]() .
We compare and discuss the results obtained using both
prescriptions in 3.1.
.
We compare and discuss the results obtained using both
prescriptions in 3.1.
Temporal variations of c(r) are not instantaneous. Observations
show that normal superhumps appear within a few of days after the
onset of a superoutburst, and that they develop within a day, so
that it does not take long for the disc to become eccentric
(Semeniuk 1980). However, it takes the disc at least a
dynamical time to change its geometrical shape; we assumed that,
when the tidal instability sets in, c increases linearly on a
timescale
![]() s. Note that in WZ Sge systems,
the early superhumps that first appear seem to be of a different
nature than the normal superhumps; Osaki & Meyer (2002)
suggested that they could be related to the 2:1 resonance.
s. Note that in WZ Sge systems,
the early superhumps that first appear seem to be of a different
nature than the normal superhumps; Osaki & Meyer (2002)
suggested that they could be related to the 2:1 resonance.
Similarly, the disc must dissipate its excess energy in order to return to a
circular shape. The relative energy difference between a circular and an
elliptic orbit with eccentricity e with the same angular momentum is
![]() .
As the dissipation at radius r is
.
As the dissipation at radius r is
![]() ,
the time needed for the disc to return to a normal state
is:
,
the time needed for the disc to return to a normal state
is:
We use three different sets of parameters that are representative
for SU UMa, a typical ER UMa star and a typical WZ Sge
star respectively, shown in Table 1.
![]() is
the circulation radius at which a particle leaving the Lagrangian
point would stay in circular orbit if there were no accretion disc
(see Paper I for details). One should note that
is
the circulation radius at which a particle leaving the Lagrangian
point would stay in circular orbit if there were no accretion disc
(see Paper I for details). One should note that
![]() is
calculated taking into account the gravitational potential of the
secondary, and therefore differs slightly from the Keplerian
value. In the following section, we will use the term ultra-low
mass-ratio (ULMR) stars when referring to simulations with
ER UMa parameters.
is
calculated taking into account the gravitational potential of the
secondary, and therefore differs slightly from the Keplerian
value. In the following section, we will use the term ultra-low
mass-ratio (ULMR) stars when referring to simulations with
ER UMa parameters.
| SU UMa | ULMR Stars | ||
| ER UMa type | WZ Sge type | ||
|
|
0.8 | 1.0 | 0.6 |
|
|
0.15 | 0.1 | 0.1 |
|
|
1.83 | 1.522 | 1.3752 |
| a / 1010 cm | 5.2 | 4.82 | 3.876 |
|
|
0.91 | 1.1 | 0.74 |
Copyright ESO 2002