![\begin{displaymath}\begin{tabular}{lcccc}
\hline\hline
Space Missions & \multico...
...t$ & & & DCT \\ [-1mm]
(1998) & & & & \\
\hline
\end{tabular}\end{displaymath}](/articles/aa/full/2002/18/aa1918/img5.gif)
|
A&A 386, 1143-1152 (2002)
DOI: 10.1051/0004-6361:20020225
L. Belmon1 - H. Benoit-Cattin2 - A. Baskurt3 - J.-L. Bougeret1
1 - Space Research Department of Paris Observatory (DESPA), Meudon, France
2 -
CREATIS, Research Unit associated to CNRS (# 5515) and affiliated to INSERM, Lyon, France
3 -
LIGIM, Computer Graphics, Image and Modelling Laboratory, Université Claude Bernard, Lyon, France
Received 28 July 2000 / Accepted 20 December 2001
Abstract
This paper presents a lossy coding scheme designed to be board on the Cassini
spacecraft which has been launched in 1997 to study Saturn planet. To deal with specific time-frequency data and numerous constraints, our coding algorithm is based on wavelet decomposition associated to an adaptive bit allocation procedure. The performances of our approach are validated by an adapted scientific evaluation.
Key words: techniques: image processing
The need for lossy compression in spacecraft data transmission has been growing in the last ten years consequently with the increasing number of space exploration missions. Table 1 gives some of the major spacecraft missions and the boarded compression approaches (Belmon 1998). One can see in this table that the boarded coding schemes are mainly based on Discrete Cosine Transform (DCT) or on Differential Pulse Code Modulation (DPCM) which can be found quite simple techniques compared to the last up to date techniques. That is justified by the need of robustness and by the severe hardware constraints imposed by spacecraft missions.
![\begin{displaymath}\begin{tabular}{lcccc}
\hline\hline
Space Missions & \multico...
...t$ & & & DCT \\ [-1mm]
(1998) & & & & \\
\hline
\end{tabular}\end{displaymath}](/articles/aa/full/2002/18/aa1918/img5.gif)
|
The Cassini mission (Gibbs 1996; Kellog et al. 2001) is a scientific spacecraft which has been launched on 15 October 1997, to study Saturn and Titan and in particular their ionised and magnetised environment and the related radio and plasma phenomena. It is made in collaboration with the European Space Agency (ESA), the National Aeronautics and Space Agency (NASA) and some European national agencies including the French Centre National d'Études Spatiales (CNES).
The Radio and Plasma Waves Science instrument (RPWS) is one of the major instrument (Kellogg et al. 2001) on board the Cassini Spacecraft. It has been built by a consortium of laboratories led by the university of Iowa, and including CNET/CRPE France, NASA Goddard Space Flight Center, space research department of Paris Observatory (DESPA). The DESPA takes in charge the high frequency radio receiver of the RPWS, named Kronos. The Kronos analysis covers range from 4 kHz up to 16 MHz with numerous modes, many of them producing 450 bps bitrates of data which are beyond the allowed limit of the project.
Lossless coding algorithms are implemented on the Kronos instrument (Belmon 1998; Rice 1991), for compression ratios less than 2:1. For other needs, such as telemetry problem, the Kronos Project required an answer concerning the lossy compression at a global bit-rate of 2 bpp. Our work on the coding algorithm began in 1994. The decision to develop, implement and assess a whole compression method based on the wavelet theory validated by the Antonini et al.'s works (1992) has been taken at this time. As a consequence, our approach is similar to the existing work at this period and quite different from the more recent works like the SPIHT (Said et al. 1996) and EBCOT (Taubman 1999) algorithms.
At the beginning of the work (1994), the acceptability of a lossy compression scheme in the Kronos context has to be proved. That is the reason why the qualitative and quantitative quality of the images obtained with our lossy compression algorithm were evaluated. Saturn's Electrostatic Discharges (SED) statistics were analysed in terms of details such as the event duration, the occurrence distribution and the energy distribution (see Sect. 4.2). The images were also visually evaluated by 7 experts in order to appreciate the pattern and texture recognition in the compressed images. These results allow us to conclude that the lossy compression with our coding scheme is acceptable for the Kronos Project.
This paper presents the coding algorithm, the assessment procedure and its results. In part 2, we present the Kronos data we deal with, and we introduce the link between the scientific need (in terms of time and frequency resolution) and the compression constraints. The part 3 concerns the compression scheme adapted to Kronos constraints. It is based on a wavelet decomposition associated with an adaptive bit allocation procedure. In part 4, our coder performances are evaluated for several types of data. The data set used for both learning and testing is issued from past experiments (such as WIND spacecraft, Bougeret et al. 1995) when available, or simulated. We compare our approach with the well-known JPEG (Pennebaker et al. 1993) image coding standard for both numerical tests and dedicated tests such as physical parameters extracted from decompressed data.
| |
Figure 1: Example of a dynamic spectrum with kilometric signals from Wind spacecraft (1995), in 64-256 kHz frequency range in Earth's neighborhood. |
| Open with DEXTER | |
DPU: Data Processing Unit;
bpp: bit per pixel;
bps: bit per second;
KWC: Kronos Wavelet Coder;
JPEG: Joint Photographic Picture Expert Group;
RPWS: Radio and Plasma Waves Science instrument;
SNR: Signal to Noise Ratio;
SKR: Saturn's Kilometric Radiation;
SED: Saturn's Electrostatic Discharges;
SSR: Solid State Recorder;
![]() holds for the hermitian scalar product of function A and B.
holds for the hermitian scalar product of function A and B.
The main scientific objectives of RPWS observations are the following:
Data concerning SED and SKR will be generally obtained as a function of time and frequency (i.e. spectral and temporal variations), under the form of "pseudo-images'' of the intensity and/or polarisation versus time and frequency. Figure 1 gives an example of such a dynamic spectrum.
The Kronos instrument has been designed to work in three major modes (Zarka et al. 1996) adapted to the different
post scientific analysis. The first one, so-called survey mode, allows the tracking of many events but is not
dedicated to any special analysis. The time and frequency resolution are medium in order to cover the largest
part of the spectrum. Frequency resolution is typically
![]() 10% in the 3.5-319 kHz frequency range,
10% in the 3.5-319 kHz frequency range,
![]() KHz up to 16 MHz. Time resolution, which is determined by integration time for the whole spectral range, is
about 10 s. Kronos survey mode bitrate is 509 bps. In this paper, the dynamic spectra in survey mode come from WIND spacecraft experiment (Bougeret et al. 1995).
KHz up to 16 MHz. Time resolution, which is determined by integration time for the whole spectral range, is
about 10 s. Kronos survey mode bitrate is 509 bps. In this paper, the dynamic spectra in survey mode come from WIND spacecraft experiment (Bougeret et al. 1995).
The second mode is dedicated to the lightning detection. The study of these phenomena requires from 1000 up to 2000 bps bitrate. For these wide band phenomena, only time resolution is crucial. For monitoring, fine structure study, and direction finding analysis, short sweep duration analysis (down to 0.3 s) are performed in the 100-16 KHz range. Frequency resolution is about 100-200 kHz. SED appear on dynamic spectra as short segments parallel to the frequency axis, because they are short lived broadband emissions, as detected by a swept-frequency analysis. A simple detection scheme based on subtraction of a boxcar average (on 3 pixels) and application of a threshold was applied successfully on Voyager observations of such events (Zarka et al. 1983). It can be used to detect a large number of events in the original and lossy compressed/decompressed dynamic spectrum, and to compare the properties of their statistical distributions. We simulate dynamic spectra (see Fig. 2) containing SED events (as well as interference) on the basis of the knowledge of SED properties (distribution of intensities, duration, and occurrences, and SED spectrum) derived from Voyager 1 and 2 observations (Zarka et al. 1983).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig2.eps}\end{figure}](/articles/aa/full/2002/18/aa1918/Timg11.gif) |
Figure 2: Simulated dynamic spectrum with SED. The blanck lines are constant electrostatic parasites (horizontal) or sudden parasite discharges. |
| Open with DEXTER | |
The third mode is adapted to SKR direction finding. Time and frequency resolution depend on scientific goals: polarisation study, source location. Needed bitrate for SKR DF mode is about 1000 bps. In order to retrieve the direction of arrival of the wave at the studied frequency, 7 measurements performed successively by 2 pairs of antennas (+X, Z) and (-X, Z), including auto and cross-correlation coefficients, can be combined. Within the exploration of the whole frequency range, the SKR source will be seen as a position slowly variable with frequency, as it is distributed at the gyrofrequency along aurora field lines. It is thus possible to generate simulated SKR data corresponding to a fixed distribution of source positions. Performing the direction-finding analysis before and after lossy compression gives a quantitative measure of the compression error, and allows the comparison of different coding schemes (cf. Sect. 4.2).
The compression of Kronos data is mainly required to maximise the duty cycle (from about 100 ms up to several seconds depending on chosen operating mode) of RPWS measurements such as the lightning monitoring or the following of the motions of instantaneous aurora radio sources. Lossy compression should also help to reduce the loss of capabilities of the instrument in case of a major failure. As an example, a failure on the high gain antenna of the Galileo spacecraft has reduced the data rate by a factor 1000.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig3.eps}\end{figure}](/articles/aa/full/2002/18/aa1918/Timg12.gif) |
Figure 3: Connections between the high frequency receiver Kronos (including the Digital Signal Processor) and the central Data Processing Unit (DPU) of the RPWS. On board storage is assumed by the Solid State Recorder (SSR). The storage capacity as well as the amount of data may vary in time. |
| Open with DEXTER | |
Spacecraft boarded coding scheme are generally strongly constrained. For the Kronos instrument, the constraints which take into account the specific data structure and the instrument context are the following:
| |
Figure 4: Kronos Wavelet Coder overview. The same statistical Laplacian model is used for allocation and coding. |
| Open with DEXTER | |
Figure 4 gives an overview of our coding scheme. It can be separated in 4 successive steps: the 2D discrete wavelet transform (DWT) which provides a subband decomposition of the original image, the bit allocation procedure which fixes a coding quality adapted to each subband, the scalar quantization and the entropy coder.
Wavelet theory has been investigated for a few decades in many signal processing applications (Rioul et al. 1991): series expansions, multiresolution analysis, singularities detection and subband coding for speech and images. A short overview on wavelet theory is given in Annex. On the other hand, coding techniques using filter banks to get a subband decomposition has been proposed for speech (Crochiere et al. 1976) and then for image coding (Woods et al. 1986). Different works (Daubechies 1988; Mallat 1989) have clearly establish the link between wavelet transform and subband decomposition. Indeed, wavelet transform can be easily implemented using filter banks (Vetterli et al. 1992) matching several constraints: Regularity, orthogonality, continuity, frequency selectivity, compact-support. Several families of wavelets filter banks satisfying these conditions can be found in the literature (Daubechies 1992; Antonini et al. 1992; Rioul et al. 1994).
| |
Figure 5: Two-dimensional dyadic successive approximations of a picture. a) The wavelet analysis is depicted as a tree decomposition with use of a low pass filter (G) and a high pass filter (H) and decimation operators (factor of 2). b) The wavelet coefficients organized in 7 sub-bands with different resoultions and directions. |
| Open with DEXTER | |
Wavelet based coder leads to interesting performances compared to standardised compression algorithms (Antonini et al. 1992; Said et al. 1996; Taubman 1999) and because of the good time and frequency localisation of the wavelet function, the wavelet transform is well suited for the non-stationnary signals such Kronos ones. Consequently, we decide to base our coder on the wavelet decomposition.
The filter bank used to implement the wavelet decomposition appears not to be so influent on the coder performances (Rioul 1993; Benoit-Cattin 1995). To implement the wavelet transform, regarding the small size of Kronos pictures, and to avoid border distortions, we use Daubechies' (Daubechies 1992) biorthogonal symmetric filters (tap length of 5 for low-pass filter and 3 for high-pass filter) with the symmetric signal extension (Brislawn 1996).
We apply an iterative 2D-dyadic decomposition on each picture with an analysis depth of 2. Then, we obtain 7 subbands (Fig. 5), 1 approximation (LL2) and 6 different horizontal (LH1, LH2), vertical (HL1, HL2) and diagonal (HH1, HH2) detail subbands. Each subband is quantized and coded respecting the bit allocation procedure.
The Laplacian probability density function (Eq. (1)) is used (Mallat 1989) to model the wavelet coefficients amplitude distribution in each subband.
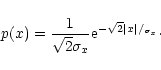 |
(1) |
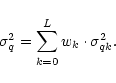 |
(2) |
For a given bit budget B, one can find the optimal bit allocation by minimising Eq. (2) using the
Lagrange multipliers method (Everett 1963):
| = | 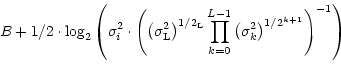 |
||
| = | (3) |
This bit allocation strategy may not be the optimal one, i.e. it is well known that wavelets coefficients are normally distributed only in the detail subbands. Moreover, we assume the high rate hypothesis which does not hold for our bitrates. Direct methods (Benoit-Cattin 1995; Ramchandran et al. 1993) lead to better bit allocation but they could not respect the current real-time context.
A residual correlation still exists between the approximation signal and the details signals. However in our approach, we propose to use "separate quantizers'' in order to have simplicity (independent quantizers) and flexibility (the possibility of using any kind of quantizer). In this implementation, we use the same uniform scalar quantizer.
As we do not deal with big pictures, we get some large magnitude coefficients that do not fit the statistical model. For these coefficients, the quantization step is larger.
Then, we use an Huffman coder (Huffman 1952) based on the Laplacian statistical model to code the coefficients
included in the dynamic range [![]() ,
+
,
+![]() ]. For coefficients out of this range, we use a code with a length proportional to their magnitude.
]. For coefficients out of this range, we use a code with a length proportional to their magnitude.
Finally, the compressed picture includes a header giving the 7 rounded subband variance values that we need for decoding, and the coded coefficients for each sub-band.
The compression performance is the ability of the coding scheme to reduce the amount of data with a minimum loss of information. What is crucial in this context is that the dynamic spectra information is not directly relevant, i.e. the useful scientific parameters are extracted from the pictures with post-processing computations.
However, we first study the numeric performance in term of SNR. Indeed, SNR is a the distortion measure used for the compression management since we cannot envisage in-flight scientific processing, and SNR is a standard image compression measure.
Secondly, we evaluate the consequence of compression on the scientific parameters extraction on SED data (peak detection) and SKR data (source spatial localisation). Tests with "human experts'' are also performed to assess the limits of recognition of patterns or structures in the survey dynamic spectra at various compression rates.
These results have been obtained with two types of data: Survey dynamic spectra from WIND spacecraft (1993) in earth neighbourhood and simulated data for the SED detection and the source localisation.
![\begin{figure}
\par\includegraphics[width=4.8cm,clip]{fig6a.eps}\hspace*{1.6cm}
...
...lip]{fig6b.eps} %\par\includegraphics[width=4.8cm,clip]{fig6c.eps}\end{figure}](/articles/aa/full/2002/18/aa1918/Timg27.gif) |
Figure 6: SNR performances for Kronos Wavelet Coder (KWC) and JPEG coder on 3 types of dynamic spectra form WIND TNR spacecraft. a) band A, mostly low frequency bursts, b) band C with noisy plasma ray, c) band E containing high dynamic range SKR. |
| Open with DEXTER | |
| KWC | JPEG | |
| Bit rate (bpp) | SNR (dB) | SNR (dB) |
| 1.0 | 45.7 | 42.8 |
| 1.5 | 48.9 | 45.0 |
| 2.0 | 51.6 | 46.7 |
| SED pixels | SED events | Missed SED | invented SED | invented SED | ||||||
| pixels/(ii) | pixels/(ii) | pixels/(i) | ||||||||
| Original spectrum (i) | 7838 | 5700 | - | - | - | |||||
| Noisy spectrum (ii) | 3137 | 2427 | - | - | 0% | |||||
| KWC/JPEG | 99% | 97% | 97% | 92% | 4.0% | 14.4% | 2.6% | 11.7% | 1.1% | 10.0% |
| 2.0 bpp | ||||||||||
| KWC/JPEG | 96% | 106% | 91% | 94% | 9.9% | 17.8% | 6.0% | 22.7% | 4.1% | 20.5% |
| 1.5 bpp | ||||||||||
| KWC/JPEG | 101% | 121% | 84% | 98% | 18.0% | 27.0% | 18.5% | 39.6% | 16.2% | 37.8% |
| 1.0 bpp | ||||||||||
For the survey dynamic spectra, Kronos Wavelet Coder (KWC) achieves better SNR results than JPEG for the planned average bitrate (2 bpp), especially on signals with large dynamic range (Figs. 6a and c). For low bitrates, the two methods are equivalent in term of SNR. Note that on a noisy band with poor information content (Fig. 6b), JPEG and KWC achieve the same performance at medium bitrate (2 bpp).
For the simulated SED spectra, KWC is much better than JPEG (Table 2). Indeed, when dealing with very sporadic events (1-3 pixels width), JPEG is not well suited to short-time variations characterisation because of the poor spatial localisation of the Discrete Cosine Transform (DCT). Consequently, the SED energy affects a large number of DCT coefficients and then the global quantization scheme used for JPEG produces lot of artefacts named "ringing'' effects around edges. At the opposite, the wavelet transform used in KWC packs peak energy in a very few coefficients and reduces this kind of distortion.
a) SED detection and characterisation
We use a simple SED detection based on a gradient algorithm (Zarka 1985). Then from the retained events, we derive statistics on the events duration, the occurrence distribution and energy distribution of the SED. We apply this analysis on 3 categories of spectrum:
At low bit rates, regarding only the SED events column, it seems that JPEG offers a better SED events numbering. But at the same bitrates, KWC gives less missed and invented SED pixels. In fact, JPEG induces false events numbering, which are detected by the missed and invented SED post-processing procedures which take into account the events localisation.
Finally, one notes that at high bitrates (2 bpp), wavelet compression performs a good denoising on the noisy spectrum. Indeed, only half of the invented pixels relative to (ii) does exist in the clean spectrum (i).
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{fig7a.eps}\hspace*{3mm}
\includegraphics[width=5.8cm,clip]{fig7b.eps}\end{figure}](/articles/aa/full/2002/18/aa1918/Timg28.gif) |
Figure 7: Occurrence distribution defined as the population for a given delay (expressed in terms of number of samples) between two SED occurrences, for simulated SED spectrum versus JPEG and KWC coded spectra at a) 2.0 bpp and b) 1.0 bpp. |
| Open with DEXTER | |
Regarding the SED pixels detection at low bitrates, it appears that JPEG compression tends to add SED pixels (up to 121%). This could be explained by the ringing effect artefacts generated by JPEG around SED pixels. Such artefacts are attenuated (101%) when using wavelet coding, because of good spatial localisation of wavelet analysis.
Figure 7 shows the occurrence distribution in terms of number of samples between 2 events (related to the time between 2 SED), for a noisy simulated spectrum versus JPEG and KWC compressed spectra. It appears that occurrence distribution slope is better preserved with KWC than with JPEG. If we look more precisely at the distribution slops, we can see that most of the distortion is concentrated in the short-time events (delay between 2 events less than 30 pixels) as a consequence of the ringing effect artefact. At 1 bpp (Fig. 7b), JPEG compression introduces so many isolated edges that distribution profile is lost.
| Kilometric signals | Small variations signal | Large variations signal | ||||||||||
| (Plasma ray) | (Low Frequency radio bursts) | |||||||||||
| JPEG | KWC | JPEG | KWC | JPEG | KWC | |||||||
| SNR | SNR | SNR | SNR | SNR | SNR | |||||||
| Bit rate | (dB) | (dB) | (dB) | (dB) | (dB) | (dB) | ||||||
| 1.0 bpp | 40.7 | 29% | 71% | 40.6 | 46.3 | 0% | 100% | 46.6 | 41.2 | 15% | 85% | 40.4 |
| 1.5 bpp | 43.1 | 43% | 57% | 42.6 | 48.4 | 50% | 50% | 48.2 | 43.6 | 43% | 57% | 43.4 |
| 2.0 bpp | 45.1 | 43% | 57% | 45.2 | 50.2 | 25% | 75% | 52.6 | 45.2 | 29% | 71% | 45.1 |
| 2.5 bpp | 46.6 | 57% | 43% | 48.0 | 51.9 | 25% | 75% | 54.1 | 46.7 | 71% | 29% | 47.3 |
| 3.0 bpp | 47.9 | 0% | 100% | 50.1 | 53.5 | 50% | 50% | 56.6 | 48.0 | 29% | 71% | 49.5 |
b) Human experts evaluation of survey dynamic spectra
We also study the consequence of lossy compression on visual appreciation from experts, that is, patterns and textures recognition, for both JPEG and KWC methods. For three categories of radio signal and for 30 dynamic spectra in each category, 7 experts choose the best picture from 2 proposed compressed ones (blind test). Table 4 gives the percentage of chosen images compressed with JPEG and with KWC for different bit rates.
We notice that SNR criteria doesn't fit so well average choice, especially for bit rates greater than 2 bpp. Globally, this table shows that KWC psychovisually overcomes JPEG on every kind of spectra. More precisely, as the bitrate decreases, experts choose massively KWC.
At low bit rate, fine structures in kilometric signal (at 1 bpp) and low frequency bursts (at 1 bpp) are affected by JPEG blocking effect as shown in Fig. 8b.
At high bit rate, excepted for kilometric signals, it seems that experts cannot choose between JPEG and KWC (See Fig. 9). Indeed for such bitrates, the image quality is so high that expert could note make real differences between the two compressed images and as a consequence, their choice tend to be randomised.
c) Direction Finding (DF)
From autocorrelation and inter-correlation spectra obtained from 2 pairs of antennae, one can know precisely the source localisation (defined by azimuth and longitude) and Stockes parameters (power and polarisation of the radio source) (Zarka 1985). The desired precision is above 1 degree for both angles. Dispersion of intercorrelation data is very large, so these spectra are much harder to compress than autocorrelation spectra. Consequently, high compression ratio can not be achieved for such data. Thus we address the correlation between angle measurement quality and lossy coding using KWC which offers the best SNR performances. Table 5 presents the error variance of angle recovery results due to lossy coding at high bitrate. Autocorrelation and intercorrelation spectra are compressed at 2 bpp and 4 bpp respectively. One can see that KWC affects angle computation, even for good SNR performances. It shows how much angle computation method (singular value decomposition) is sensitive to input data precision.
| |
Figure 8:
Example of survey dynamic spectra used for human expert evaluation. Original spectra a) and its coded version at low bit rate (1 bpp) using JPEG b) and KWC c) respectively. This spectrum is a small part (32 |
| Open with DEXTER | |
| |
Figure 9: Example of survey dynamic spectra used for human expert evaluation. Original spectra a) and its coded version at high bit rate (2 bpp) using JPEG b) and KWC c) respectively. |
| Open with DEXTER | |
| Data | Average bitrate | SNR | Longitude variance | Azimuth variance |
| (bpp) | (dB) |
|
|
|
| Autocorrelation | 2 | 42 | ||
| 8.9 |
13.7 |
|||
| Intercorrelation | 4 | 47 |
In this paper, we present a lossy coding algorithm designed for the coding of Kronos instrument data on board of the Cassini Spacecraft. It is based on wavelet decomposition associated to an adaptive bit allocation procedure and scalar quantization. We compare our coder with the JPEG standard using distortion criteria, automatic specific scientific data analysis as well as human expert analysis. Our wavelet coder suits very well the sporadicity of the expected radio signals and overcomes JPEG standard in most of the cases.
The results obtained show that on board lossy compression of scientific data is possible under limitations on specific data such as the dynamic spectra used for source localisation.
We briefly review the basis of wavelet analysis. Theory of wavelets and further developments may be found in (Mallat 1989; Daubechies 1990).
A wavelet function is an oscillating function of the form:
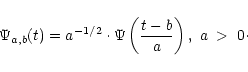 |
(4) |
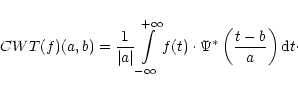 |
(5) |
| DWT (f)(j,k) | = | ||
| = | 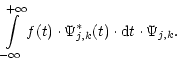 |
(6) |
From the point of view of signal processing, the notion of wavelet analysis has many connections with the multiresolution analysis (Mallat 1989). Such an analysis is characterized by a subset of enclosed subspaces Vj, ![]() ,
each subspace Vj being a basis of functions supported in
,
each subspace Vj being a basis of functions supported in
![]() .
There exists a function
.
There exists a function
![]() of V0 such that the family of functions
of V0 such that the family of functions
![]() is a basis of V0.
is a basis of V0.
| |
Figure 10:
Ideal dyadic partitioning of frequency space in approximation subspaces
|
| Open with DEXTER | |
Then, it has been shown (Meyer 1986) that there is a family of functions
![]() that forms an orthonormal basis of Vj. That is, with dilating and translating a single function
that forms an orthonormal basis of Vj. That is, with dilating and translating a single function ![]() called scaling function, one can define a set of orthonormal bases for the approximations subspaces Vj. The associated wavelet is then defined as:
called scaling function, one can define a set of orthonormal bases for the approximations subspaces Vj. The associated wavelet is then defined as:
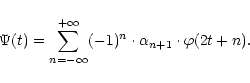 |
(7) |
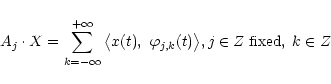 |
(8) |
Consequently, the operator
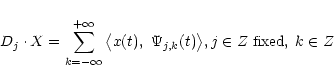 |
(9) |
One performs a m-DWT with these operators by retaining only the detail signal at different resolution (i=0...m), and the average signal at the maximum resolution ![]() .
For discrete-time signals, this can be implemented by using a dyadic decomposition tree and a pair of appropriated half-band lowpass and highpass filters (Mallat 1989).
.
For discrete-time signals, this can be implemented by using a dyadic decomposition tree and a pair of appropriated half-band lowpass and highpass filters (Mallat 1989).
For image analysis, 2D-DWT can be achieved with computing the detail and the average projections called subbands for the raws (horizontal analysis), then for the columns (vertical analysis) at each resolution (Fig. 5) shows the 2-dimensionnal (2D) wavelet analysis implementation, as used in our image compression scheme. Vertical and horizontal analysis are successively performed for each scale j. Then at each analysis scale j four different signal are derived from the input picture: