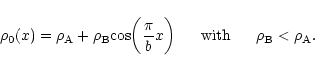A&A 386, 691-698 (2002)
DOI: 10.1051/0004-6361:20020204

Fast and Alfvén waves driven by azimuthal footpoint motions

II. Random driver

A. De Groof - M. Goossens

Centre for Plasma-Astrophysics, K.U. Leuven, Celestijnenlaan 200 B, 3001 Heverlee, Belgium

Received 12 November 2001 / Accepted 5 February 2002

Abstract
The excitation of Alfvén and fast magneto-acoustic waves in coronal loops driven by footpoint motions is studied in linear, ideal MHD. The analysis is restricted to azimuthally polarized footpoint motions so that only Alfvén waves are directly excited to couple to fast magneto-acoustic waves at later times. In the companion paper De Groof et al. (2002) (hereafter referred to as Paper I), the behaviour of the MHD waves is studied in case of a monochromatic driver. In the present study, the effects of a more realistic random driver are investigated.
First, we consider loops of equal length and width in order to limit the number of quasi-modes in the frequency range of the driver so that the influence of quasi-modes in the system can easily be detected. In contrast to the single resonant surface which was found in case of a periodic driver (see Paper I), a random pulse train excites a variety of resonant Alfvén waves and consequently the small length scales built up are spread over the whole width of the loop. The specific effects of the quasi-modes are not so easily recognized as for radial footpoint motions (De Groof & Goossens 2000) since the resonances corresponding to directly and indirectly excited Alfvén waves are mixed together. In the second part of the paper, longer loops are considered. Since more quasi-modes are involved, the resonant surfaces are more numerous and widely spread throughout the whole loop volume. On the other hand, it takes more time for the MHD waves to cross the loop and to form standing waves. Nevertheless this negative effect does not have too much impact since the simulations show that after a small time interval, resonant surfaces are created all over the loop, with length scales which are short enough for effective dissipation.

Key words: MHD - Sun: corona - Sun: magnetic fields - waves

1 Introduction

As explained in Paper I, resonant absorption of Alfvén waves in footpoint driven coronal loops could possibly play an important role in the heating of the solar corona. The footpoints of the magnetic field lines are driven by azimuthally and/or radially polarized motions, resonantly exciting Alfvén waves in respectively a direct or indirect way. Consequently, small length scales are generated which are necessary for the dissipation of the wave energy because of the high coronal Reynolds number. In order to get footpoint motions which are fast enough to generate MHD waves, the coronal loops are probably driven by reconnection events in shorter loops lying underneath or by explosive events in the neighbourhood of the loop. Roussev et al. carried out numerical simulations of explosive events where reconnection has indeed excited and driven fast magneto-acoustic and Alfvén waves.

Since earlier investigations have revealed that the coupling between magneto-acoustic waves and Alfvén waves is of major importance for the efficiency of resonant absorption (see references in Paper I), we choose to use a simple one-dimensional model in linear, ideal MHD, stratified only in the radial direction, in which we take into account all relevant wave modes, except for the slow waves which are absent in a pressureless plasma model. In this way, we focus on the intrinsic coupling between the waves and the role of the quasi-modes in the system with respect to the efficieny of resonant absorption.

In Paper I, the influence of the quasi-modes on the dissipation was found to be very important. For an harmonic driver, coupling to fast magneto-acoustic waves can have both a positive and negative effect on the growth of the Alfvén resonances. The efficiency depends on the frequency in a complicated way, with optimal efficiency for the quasi-mode frequencies and strongly reduced efficiency for frequencies far from any quasi-mode. However, for monochromatic drivers, in addition to the need for fine-tuning, only a few resonant layers can be formed which can never result in a globally heated coronal loop. Besides, the motions which are responsible for the oscillation of coronal field lines are obviously not restricted to one frequency. Therefore, in order to simulate coronal footpoint motions in a more realistic way, a broadband driver should be considered. Since for radial footpoint motions, the improvements found for a random driver as compared to a periodic driver were very promising (see De Groof & Goossens 2000), we have confidence that in the present model, the implementation of a broadband driver could remedy the problems we faced in Paper I.

The paper is organized as follows. In the next section we briefly discuss the physical model and the relevant equations. For the details and the description of the mathematical method used to derive the analytical solution describing the temporal behaviour of the excited MHD waves, we refer to Paper I and Tirry & Berghmans (1997). In Sect. 3, the meaning and importance of the "quasi-modes'' is clarified. Their influence on coronal heating is maximal after a broadband driver which excites them all together. Therefore, in Sect. 4, the influence of the random driver is shown in two parts. First, in Sect. 4.1, short loops are considered to keep the model as transparent as possible. In Sect. 4.2, this study is extended with the investigation of longer, more realistic loops. Finally in Sect. 5 we give a summary and discussion.

2 Physical model and mathematical model

Similarly as in Paper I, we model the coronal loop as a static, straight, gravitationless plasma slab with thickness b, obeying the standard set of ideal MHD equations (Fig. 1).

At z=0 we now impose random, azimuthally polarized footpoint motions so that a whole spectrum of resonant Alfvén waves, coupled to fast magneto-acoustic waves, will be generated in the loop. The continuously varying density inside the loop has the following form:

$$% \rho_0(x) = \rho_{\rm A} + \rho_{\rm B} \mbox{cos}\bigg(\fr... ...}{b}x\bigg) ~~~~~\mbox{with}~~~~~ \rho_{\rm B} < \rho_{\rm A}.$$ (1)

The coupled fast-Alfvén waves are described by a coupled system of partial differential equations in $\xi _x$ and $\xi _y$:

  

$$\bigg\{\frac{1}{v^2_{\rm A}}\frac{\partial^2}{\partial t^2} - \fr... ...{\partial^2}{\partial x^2}\bigg\}\xi_x = ik_y\frac{\partial \xi_y}{\partial x},$$ (2)

$$\bigg\{\frac{1}{v^2_{\rm A}}\frac{\partial^2}{\partial t^2} - \fr... ...{\partial z^2} + k^2_y\bigg\}\xi_y = ik_y\frac{\partial \xi_x}{\partial x}\cdot$$ (3)

Since the coupling parameter $k_y \neq 0$ is taken to be non-zero, the azimuthally polarized footpoint motions indirectly drive fast MHD waves which couple to Alfvén waves at the resonant surfaces where the ideal Alfvén wave resonance condition is satisfied (Mann & Wright 1995). Length, speed, magnetic field strength and density are non-dimensionalized with respect to b, $v_{\rm A}(0)$, B₀ and $\rho(0)$ respectively.

	Figure 1: Cartoon model of the coronal loop driven by azimuthally polarized footpoint motions.
Open with DEXTER

The mathematical method on which the results of this paper are based is identical to the one in Paper I. Inspired by Mann et al. (1995), Berghmans et al. (1996) and Tirry et al. (1997), the coupled Eqs. (2) and (3) are solved to get an analytical description of the temporal evolution of the excited linear MHD waves. We refer to Paper I for a description of the method and the analytical expression describing the temporal evolution of the waves.

3 Significance of the so-called quasi-modes

As explained before, "quasi-modes'' are modes associated with global fast magnetosonic waves whose frequency is lying inside the Alfvén continuum. Since we take all possible values of k_z into account, in contrast to many other related papers, an infinite number of Alfvén continua appears, each associated with a different value of $k_z=\frac{n\pi}{L}$ (see Eqs. (12) and (13) in Paper I).

	Figure 2: The eigenfrequencies of the first three fast eigenmodes (gray dots) together with the upper and lower bound of the Alfvén continuum (black lines) as function of kz for L=1 (top figure) and L=10 (bottom figure).
Open with DEXTER

Figure 2a shows the eigenfrequencies of the first three fast eigenmodes together with the upper and lower bound of the Alfvén continuous spectrum as function of k_z for a loop of length 1. For longer and more realistic loops, more eigenfrequencies ly in the same frequency range since k_z is inversely proportional to L. Figure 2b shows the resulting eigenspectrum for L=10.

Since, in the case of azimuthal footpoint motions, global fast modes can only be excited through coupling with Alfvén waves, the excited fast waves always have frequencies inside the Alfvén continuum and consequently only "body modes'', keeping the energy inside the loop, are present in the system. For $k_y \neq 0$ these body modes couple to localized Alfvén waves and form essentially quasi-modes (Tirry & Goossens 1996). Due to the resonant coupling, small length scales are generated around the resonant point which are necessary for dissipation and hence for the heating of the coronal plasma. As clear from Fig. 2, the longer the loop, the more quasi-modes are available in the system, given one particular k_z-interval.

4 Effects of a random driver on the behaviour of the excited MHD waves

As shown in several previous simulations, the implementation of a broadband driver at the footpoints of a coronal loop can drastically change the wave dissipation inside the loop (Ofman & Davila 1996; Ofman et al. 1996; Wright & Rickard 1995). Especially if all possible values of k_z are taken into account, several quasi-modes can be excited at once which results in more resonant layers, spread throughout the width of the loop (De Groof & Goossens 2000). From Paper I we know that for azimuthal footpoint motions, driving with quasi-mode frequencies is by far the most efficient way of building up small length scales. In fact, for periodic drivers with a frequency far from any quasi-mode, the coupling with fast magneto-acoustic waves has a negative effect of the growth of Alfvén resonances. Therefore, we expect the presence and excitation of several quasi-modes to have a positive influence on the wave dissipation as a whole.

In what follows, we drive the loop with a series of pulses with randomly distributed widths and with randomly distributed time intervals in between. The spatial dependence of the driver is constant (R(x)=1) so that waves are excited with a constant strength over the whole width of the loop. All individual pulses have the following form

$$\begin{eqnarray*}T(t)=1 - \cos(at) \end{eqnarray*}$$

with pulse widths varying between 0.4 and 2.1 ( 3 < a < 16). The time intervals in between the pulses are random and taken to be smaller than 1. Since the spectrum of each individual pulse is relatively broad and the pulses are separated by random time intervals, a broad range of frequencies drives the coronal loop.

4.1 Short loops

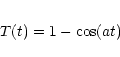
To keep the simulations as transparent as possible, we first consider an extremely short loop with a length equal to the (half) width of the loop (which is taken to be 1 in dimensionless time units). In that way, the number of quasi-modes present in the spectrum is limited (see Fig. 2a) so that their influence can easily be detected. Later we extend the analysis to longer and more realistic loops.

It immediately becomes clear that the implementation of the more realistic, random driver totally changes the wave dissipation in the loop. In contrast to the single resonant surface which was found after periodic driving (see Paper I), a random pulse train excites a variety of resonant Alfvén waves and consequently strong variations in $\xi _y$ take place on several surfaces spread over the total width of the loop. In Fig. 3, the x-dependence of the $\xi _y$ and $\xi _x$-component at half the loop length is shown for different Alfvén crossing times. The differences with the results found for the periodic driver are striking. A lot more Alfvén modes are excited, with different frequencies, so that multiple resonant surfaces appear at different locations in the loop. On the other hand, there is also an important (and expected) similarity with the results found in Paper I: the length scales of the $\xi _y$-component decrease in time while the amplitudes of the peaks increase. The overall amplitude of $\xi _y$ is significantly larger that the amplitude of the x-component since Alfvén waves are driven directly.

By comparing the $\xi _y$-component in Fig. 3 with the Alfvén mode energy calculated in the radially polarized driving case (Fig. 11 in De Groof & Goossens 2000), we notice that the quasi-mode surfaces which were easily recognized after a radially polarized random pulse train are not that clearly visible in the present case. Since Alfvén waves are now driven directly, resonances can occur all over the loop width through directly excited resonant Alfvén waves and as a consequence, the differences between pure Alfvén resonances and resonant absorption through quasi-mode coupling are not that clear for small times.

	Figure 3: x-dependence of $\xi _y$ and $\xi _x$ at z=0.5 (L=1) after a random pulse train at different times $t=20,\;30,\;40\;$and$\;50$ (ky =2).
Open with DEXTER

We will show however that the different types of resonances can be distinguished more easily through the analysis of the $\xi _x$-component. The graphs on the right hand side of Fig. 3 represent the sum of all fast magneto-acoustic waves excited through coupling with the resonant Alfvén waves. The characteristics of a generated fast wave totally depend on the frequency of the Alfvén wave involved in the coupling. Only fast waves characterized by a quasi-mode frequency lead to standing waves; hence only these will in their turn excite Alfvén waves and amplify the resonances established earlier. The amplitudes of $\xi _x$ seem to show little individual peaks on top of a larger and less peaked structure spread over the whole loop width. These signatures were earlier recognized in Paper I, in Figs. 7b and 8b, showing the $\xi _x$ component after a periodic driver with respectively $\omega _{\rm d}=3.5$ and $\omega _{\rm d}=5.52$, a quasi-mode frequency. These findings inspire us to believe that the over all structure recognized in Fig. 3 actually originates from the summed effect of small peaks corresponding to non-quasi-modes on top of the more global structure of the quasi-modes.

	Figure 4: 3D-plots showing the amplitude of $\xi _x$ after periodic drivers with $\omega _{\rm d}=3.5$ (left hand side) and $\omega _{\rm d}=5.52$, the first harmonic (right hand side), at 3 different times t=20, 30 and 40 (ky=1).
Open with DEXTER

To illustrate this effect, we plot in Fig. 4 the time evolution of $\xi _x$ after a periodic driver with respectively $\omega _{\rm d}=3.5$, pictured on the left, and $\omega _{\rm d}=5.52$, a quasi-mode frequency with n=1, depicted on the right hand side. As clear on the figures, the amplitude of the fast mode characterized by an ordinary frequency (left) shows one single bump moving up and down in time. A quasi-mode on the other hand, is a global, standing wave of the system, with in this particular case no nodes in the z-direction since n=1. The magnetic surface at which the coupling takes place ( $x \approx 0.75$) is clearly visible. These results give confidence that our earlier interpretation of the structure in $\xi _x$ is valuable.

In order to study the behaviour of the random generated waves over the whole loop length, we show in Figs. 5-6 3D and contour plots of the amplitude of $\xi _y$ at t=20 and t=50 respectively.

	Figure 5: 3D and contour plot of $\xi _y$ at t=20 after a random pulse train (ky =2).
Open with DEXTER

As expected, length scales are decreasing in time and amplitudes increasing over the whole length of the loop. From the contour plots we can conclude that small length scales and consequently dissipative layers are spread over the whole width of the loop. However most of the large gradients are still found in the interval 0.3<x<0.9. This behaviour is due to the density profile we used in the loop model. Especially for longer loops, the $\omega _{\rm A}$-profiles flatten out and the magnetic surfaces corresponding to the eigenfrequencies $\omega _{\rm A}$ move towards the outer layers of the loop (see De Groof & Goossens 2000, Fig. 16).

4.2 Longer loops

Up till now, we only considered very short loops with equal lengths and widths. In the solar corona however, a medium magnetic loop has a length/width proportion around 25 (Beaufumé et al. 1992). Therefore we extend the analysis presented above to longer loops. As mentioned in the previous chapter, longer loops lead to more quasi-modes ( $k_z=2\pi/L$). Consequently more waves play a prominent role in the heating mechanism and their effects will all mix together. On the other hand, since the loops are longer, it takes more time for the Alfvén waves to cross the total loop length in order to interfere with the new incoming waves or form standing waves. Therefore we have to go further in time in order to get snapshots which are comparable to the figures in the "short-loop case''. Recall that the dimensionless time unit t we use throughout the whole study is defined by the proportion of (half) the loop width to the Alfvén speed at the centre of the loop. (In the outer layers of the loop model, the Alfvén speed is more than twice the one in the centre so there it takes less time to cross the loop.) For reasons of clarity, we define a new time scale Twhich is related to the length of the coronal loop. In what follows we denote the dimensionless time scale corresponding to the time needed for an Alfvén wave in the loop centre ( $x\approx 0$) to cross the whole length of the loop by T, which implies that T=t/L.

	Figure 6: 3D and contour plot of $\xi _y$ at t=50 after a random pulse train (ky =2).
Open with DEXTER

At first we consider a loop of length 10. From Fig. 2 we know that in case of a long loop, the discrete quasi-mode frequencies ly closer to each other and consequently more resonant magnetic surfaces are available in the system. The presence and the location of the extra resonant surfaces can be illustrated by repeating parts of figures shown earlier in De Groof & Goossens (2000) (Figs. 14-15). Figure 7 shows the frequencies at which waves are excited by the random driver imposed at the footpoints of a loop of length 1 and 10 respectively. Figure 8 shows the same energy diagrams but now, the energy spikes are plotted as a function of x. The figures only have a qualitative value since the height of the depicted peaks only corresponds to the energy injected at one particular moment in time (t=40). But in this context it is important to notice that longer loops hold much more candidate resonant surfaces, filling up a substantial part of the loop width. Again it seems that the central layers of the long loop are not contributing to the heating of the plasma. As explained before, this behaviour is due to the density profile we use in our model.

From the results for L=20 which were also included in De Groof & Goossens (2000), we know that longer loops show a similar behaviour - except that even more quasi-modes can be excited - and thus do not bring in any more relevant or new information. Moreover, longer loops unnecessary complicate the 3D-figures. That is why, in what follows, we restrict ourselves to loops of length 10.

	Figure 7: Total energy in each eigenfrequency $\omega _{\rm A}$ at a particular time t=40. The loops of length L=1 (left) and L=10 (right) are driven by a random pulse train of 30 pulses.
Open with DEXTER

	Figure 8: Idem as Fig. 7 but here the total energy contributions are plotted as a function of the resonant surfaces $x_{\rm A}$ which correspond to $\omega _{\rm A}$.
Open with DEXTER

It is natural to expect that the presence of more quasi-modes influences the efficiency of the resonant absorption process. Besides, this effect is likely to support the ambition of a globally heated loop. Figure 9 shows the $\xi _x$ and $\xi _y$ component for t=50 at half the loop length. Since L=10, the loop length is crossed only 5 times at the centre (T=5) so in that context the figures are comparable with the (t=5)-case for a short loop.

At least two differences should be marked. First, the amplitude of the visible peaks is in general smaller than in Fig. 3. The reason is that the energy which is injected into the loop has to be distributed over a larger volume. Nevertheless, the amplitudes are still relatively large if one takes into account that the same input energy is spread over a volume that is 10 times as large. Second, we notice that the length scales are comparable to those for short loops and they are even smaller if you consider the number of crossing times that were needed to arrive at these narrow peaks.

	Figure 9: x-dependence of $\xi _y$ and $\xi _x$ at z=5, half the loop length L=10, after a random pulse train at T=5 (t=50) for ky =2.
Open with DEXTER

One of the reasons for this enhanced efficiency is probably the increased number of quasi-modes. In a long coronal loop, a lot more resonant peaks can grow due to a double process: on one hand the direct resonant excitation of the local Alfvén wave and on the other hand, the resonant coupling with global fast waves. As a consequence, small length scales are formed in a smaller time span $\Delta T$. A second reason might be that phase-mixing processes do not need that many crossing times to be efficient. Therefore, for small z, they operate on a time scale which is comparable to t.

	Figure 10: 3D plots of $\xi _y$ and $\xi _x$ at T=5 (t=50) after a random pulse train imposed at the footpoints of a loop with length L=10 (ky =2).
Open with DEXTER

	Figure 11:  Contour plot of $\xi _y$ at T=5 (t=50) after a random pulse train imposed at the footpoints of a loop with length L=10 (ky=2).
Open with DEXTER

In Fig. 10, $\xi _y$ and $\xi _x$ are plotted on a 3D-graph to show the overall picture in a longer loop. The $\xi _y$-component shows a lot of small length scales, spread over the whole width and length of the loop. In the structure of the $\xi _x$-component some standing waves can be recognized, mixed together with fast waves corresponding to a frequency different from any quasi-mode frequency. Since the Alfvén speed is x-dependent, the waves get sheared in time and a complex pattern appears.

The most important result we can derive from these figures is that after a small time interval, only 5 Alfvén crossing times, resonant surfaces are created all over the loop, with length scales which are small enough for effective dissipation. The contour plot in Fig. 11 confirms this conclusion.

5 Summary and discussion

From previous investigations we know that resonant absorption and phase-mixing are viable candidates to heat the corona. However, although both processes succeed in building small length scales, leading to effective heating at these surfaces, most investigations faced the problem of global heating. Especially for harmonic footpoint motions the resonant absorption process resulted in only one or two single resonant layers, corresponding to the first harmonics of the system's eigenspectrum. Even if a broadband driver was taken into account, like in Ofman & Davila (1996), the problem persisted. In order to investigate whether more realistic footpoint motions and the implementation of more significant waves modes in the model could enhance the efficiency, we chose to work in ideal MHD as a means to focus on the qualitative side of the problem.

In De Groof & Goossens (2000), we showed that it is crucial to take into account all possible values of k_z. In this way, all quasi-modes with frequencies lying in the driver's spectrum are excited and a variety of resonant layers are available, spread throughout the loop. For radial footpoint motions, the role of the quasi-modes and the importance of a broadband driver were significant (see De Groof & Goossens 2000). For loops driven by azimuthally polarized footpoint motions however, quasi-modes are not strictly necessary as energy carrier waves. Therefore we investigate in this paper the role of quasi-modes in case resonant Alfvén waves are driven directly by a random pulse train. The difference with a periodic driver is striking: in contrast to the single resonant surface, a random pulse train generates a variety of resonant Alfvén waves and excites indirectly a whole series of quasi-modes amplifying the original resonances through coupling with Alfvén waves. However, the distinction between the pure Alfvén resonances and the resonant peaks build up by resonant absorption of quasi-modes is not that clear as for a radial driver.

In case of longer loops, the generation of small length scales is even more efficient since more quasi-modes are involved and resonant peaks are formed all over the volume of the coronal loop, even after a time span as small as a few Alfvén crossing times.

These results give confidence that the combination of resonant absorption and phase-mixing may indeed play a key role in heating closed loops in the solar corona. In contrast to earlier findings, the heating is not restricted to one single shell but the whole coronal loop can be heated in a global way. We remark that, since dissipation is excluded from our model, the results found above do not give any quantitative view on the resulting heating but picture the efficiency of wave heating in a qualitative way. In order to compare the resulted heating with observations, dissipation has to be included in the model.

We remark that recent observations by TRACE, showing a concentration of heating at the footpoints of the loop, seem to be at first sight in contradiction with the results we presented above. However, as mentioned in the introduction, we are confident that the solar atmosphere is heated by a combination of different heating mechanisms, all working together. As explained before, in order to get fast footpoint motions, the coronal loops are probably driven by reconnection events in the chromosphere and transition region. These explosive events also release energy which is observed at the footpoints of the long coronal arcades (Sturrock et al. 1999; Falconer et al. 2000). Moreover, since the density is higher at the bottom of the atmosphere and mass flows propagating up and down coronal loops bounce back at the steep gradients with the photosphere, several mechanisms may contribute to the explanation why the footpoints of coronal loops seem brighter in observations.

References

 
• Beaufumé, P., Coppi, B., & Golub, L. 1992, ApJ, 393, 396 In the text NASA ADS  
• Berghmans, D., De Bruyne, P., & Goossens, M. 1996, ApJ, 472, 398 In the text NASA ADS  
• De Groof, A., & Goossens, M. 2000, A&A, 356, 724 In the text NASA ADS  
• De Groof, A., Paes, K., & Goossens, M. 2002, A&A, 386, 681 (Paper I)  
• Falconer, D. A., Gary, G. A., Moore, R. L., & Porter, J. G. 2000, ApJ, 528, 1004 In the text NASA ADS  
• Mann, I. R., Wright, A. N., & Cally, P. S. 1995, J. Geophys. Res., 100, 19441 In the text  
• Ofman, L., & Davila, J. M. 1996, ApJ, 456, L123 In the text NASA ADS  
• Ofman, L., Davila, J. M., & Shimizu, T. 1996, ApJ, 459, L39 In the text NASA ADS  
• Roussev, I., Galsgaard, K., Erdélyi, R., & Doyle, J. G. 2001, A&A, 370, 298 NASA ADS  
• Sturrock, P. A., Roald, C. B., & Wolfson, R. 1999, ApJ, 524, L75 In the text NASA ADS  
• Tirry, W. J., & Berghmans, D. 1997, A&A, 325, 329 In the text NASA ADS  
• Tirry, W. J., Berghmans, D., & Goossens, M. 1997, A&A, 322, 329 In the text NASA ADS  
• Tirry, W. J., & Goossens, M. 1996, ApJ, 471, 501 In the text NASA ADS  
• Wright, A. N., & Rickard, G. J. 1995, ApJ, 444, 458 In the text NASA ADS