A&A 386, 748-756 (2002)
DOI: 10.1051/0004-6361:20020250
GAIA accuracy on radial velocities assessed from a synthetic
spectra database
T. Zwitter
University of Ljubljana, Department of Physics, Jadranska 19, 1000 Ljubljana,
Slovenia
Received 29 October 2001 / Accepted 14 February 2002
Abstract
Spectrograph aboard the GAIA satellite operates in the near-IR, in
the 8490-8740 Å window accessible also from the ground.
The most important parameter yet to be determined is the spectral resolution.
Realistic estimates of the zodiacal light background are obtained and a total
of
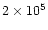 correlation runs are used to study the accuracy of
radial velocity measured by the spectrograph as a function of resolution,
magnitude of the target, its spectral type and luminosity class.
Accuracy better than 2 kms-1
is achievable for bright stars if a high enough dispersion is chosen.
Radial velocity error of 5 kms-1 is at V=17.5 for Cepheids and
at 17.7 for horizontal branch stars. Even for very
faint objects, with spectra dominated by background and readout noise,
the optimal dispersion is still in the 0.25/0.75 Å/pix range. This
is also true for complicated cases such as spectroscopic binaries or if
information other than radial velocity, i.e. abundances of individual
elements or stellar rotation velocity, is sought after.
The results can be scaled to assess performance of future ground based
instruments.
correlation runs are used to study the accuracy of
radial velocity measured by the spectrograph as a function of resolution,
magnitude of the target, its spectral type and luminosity class.
Accuracy better than 2 kms-1
is achievable for bright stars if a high enough dispersion is chosen.
Radial velocity error of 5 kms-1 is at V=17.5 for Cepheids and
at 17.7 for horizontal branch stars. Even for very
faint objects, with spectra dominated by background and readout noise,
the optimal dispersion is still in the 0.25/0.75 Å/pix range. This
is also true for complicated cases such as spectroscopic binaries or if
information other than radial velocity, i.e. abundances of individual
elements or stellar rotation velocity, is sought after.
The results can be scaled to assess performance of future ground based
instruments.
Key words: stars: kinematics - surveys - space vehicles: instruments
- techniques: radial velocities
GAIA is the approved ESA Cornerstone 6 mission designed to obtain
extremely precise astrometry (in the micro-arcsec regime), multi-band
photometry as well as spectroscopy for up to a billion stars in our Galaxy
and beyond. The goals are described in the mission
Concept and technology study report
(ESA-SCI (2000) 4, hereafter ESA 2000), and summarized by Perryman
et al. (2001). Astrometric
information will be used to derive star's position and distance. Proper
motion then yields the projection of the velocity vector on the sky plane.
The missing, sixth component in the position-velocity space, i.e.
the radial velocity of the target, is derived by spectroscopic observations
on board (Munari 1999). Apart from astrometry and spectroscopy a number
of photometric bands (15 are currently baselined) will collect broad-
and narrow-band photometric information useful for general
classification purposes (see Sect. 3.3). Spectroscopy can be used to obtain
additional astrophysical information that cannot be provided by other means.
This includes abundances of individual elements, stellar
rotational velocity (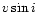 ), and information on line profiles
which is essential for derivation of orbital solutions of spectroscopic
binaries (Munari et al. 2001a) or for detection and classification of
peculiar stars (Munari et al. 2002). The spectrograph is described
in ESA 2000 and Munari (2001).
), and information on line profiles
which is essential for derivation of orbital solutions of spectroscopic
binaries (Munari et al. 2001a) or for detection and classification of
peculiar stars (Munari et al. 2002). The spectrograph is described
in ESA 2000 and Munari (2001).
![\begin{figure}
\par\includegraphics[width=9.6cm,height=16.8cm,angle=270,clip]{H3249fig1.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg6.gif) |
Figure 1:
a) Synthetic spectrum of a non-rotating G-type
metal-deficient giant at a 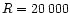 resolution. b)-f)
Spectral change if one of the spectral
parameters is modified. Each curve is the ratio of the given spectrum
divided by the top template. The values of the changing parameter are
indicated. All tracings share the scale of the top panel,
but are vertically offset for clarity.
resolution. b)-f)
Spectral change if one of the spectral
parameters is modified. Each curve is the ratio of the given spectrum
divided by the top template. The values of the changing parameter are
indicated. All tracings share the scale of the top panel,
but are vertically offset for clarity. |
| Open with DEXTER |
Performance of the spectrograph can be assessed by convolution of
spectra of real stars (Munari et al. 2001).
Here we resort to synthetic spectra that give more flexibility to simulate
parameters of the GAIA spectrograph. The goal of this paper is to assess
the accuracy of the radial velocities and to some extent other information
as a function of the chosen spectral dispersion. We upgrade the initial
assessment (ESA 2000) by a database of more realistic spectra, a better treatment
of the background, better correlation technique, updated spectrograph
parameters and extending results to significantly fainter magnitudes.
Most important, the initial assessment was done for only one
resolution (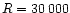 sampled at 0.75 Å/pixel, i.e. an undersampled case)
while here we explore a range of possible choices
(
sampled at 0.75 Å/pixel, i.e. an undersampled case)
while here we explore a range of possible choices
(
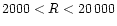 ,
always maintaining the usual criterion of 2 pixels per
resolution element). Given the fact that the spectral resolution
is the only spectrograph parameter yet to be decided and the possibility
to scale the results to any ground-based telescope observing in the
near-IR, the paper provides realistic error estimates for any future
campaigns in the near-IR domain.
,
always maintaining the usual criterion of 2 pixels per
resolution element). Given the fact that the spectral resolution
is the only spectrograph parameter yet to be decided and the possibility
to scale the results to any ground-based telescope observing in the
near-IR, the paper provides realistic error estimates for any future
campaigns in the near-IR domain.
We used Kurucz models to calculate a large database of
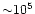 synthetic spectra that sample the grid in temperature, surface gravity,
metallicity, rotational velocity and spectral resolution. The grid
which will be described separately (Zwitter et al. 2002) upgrades the
initial calculations of Munari & Castelli (2000) and
Castelli & Munari (2001). Figure 1 illustrates the dependence of
spectral properties on basic model parameters. All tracings are ratios
to the template spectrum of a non-rotating metal-deficient giant of
spectral type G, which is shown in Fig. 1a. Plotting the ratio to the
chosen template instead of the spectrum itself permits a quick
evaluation of the signal to noise and resolution needed to determine
the value of a given parameter. Rise of effective temperature weakens
the Ca II lines while the Pashen lines get stronger (Fig. 1b).
Increase of gravity (Fig. 1c) also diminishes the width of the Ca II lines.
Stellar rotation (Fig. 1d) has a pronounced effect only for fast rotators
(
synthetic spectra that sample the grid in temperature, surface gravity,
metallicity, rotational velocity and spectral resolution. The grid
which will be described separately (Zwitter et al. 2002) upgrades the
initial calculations of Munari & Castelli (2000) and
Castelli & Munari (2001). Figure 1 illustrates the dependence of
spectral properties on basic model parameters. All tracings are ratios
to the template spectrum of a non-rotating metal-deficient giant of
spectral type G, which is shown in Fig. 1a. Plotting the ratio to the
chosen template instead of the spectrum itself permits a quick
evaluation of the signal to noise and resolution needed to determine
the value of a given parameter. Rise of effective temperature weakens
the Ca II lines while the Pashen lines get stronger (Fig. 1b).
Increase of gravity (Fig. 1c) also diminishes the width of the Ca II lines.
Stellar rotation (Fig. 1d) has a pronounced effect only for fast rotators
(
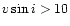 kms-1), but the smearing is different from that of
increase in gravity. The metallicity content (Fig. 1e) influences many lines,
but details are different from that of enrichment with the
kms-1), but the smearing is different from that of
increase in gravity. The metallicity content (Fig. 1e) influences many lines,
but details are different from that of enrichment with the  -elements
(Fig. 1f). These kind of dependencies are typical for relatively low
temperature stars that will be the most common GAIA targets.
-elements
(Fig. 1f). These kind of dependencies are typical for relatively low
temperature stars that will be the most common GAIA targets.
In the next section we use few of the calculated spectra to assess
the performance of the spectrograph for some representative targets.
Radial velocity spectrometer instrument aboard GAIA is a slitless
spectrograph operating in a time delay integration mode. The field of view is
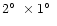 .
The telescope has a rectangular aperture of
.
The telescope has a rectangular aperture of
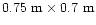 .
The focal plane is covered
with an array of CCDs. The total efficiency of the telescope +
spectrograph + CCD is baselined to 0.35. Each star drifts across the
plane in 60.4 s, with its signal read by two consecutive CCDs. The CCDs
have 20
.
The focal plane is covered
with an array of CCDs. The total efficiency of the telescope +
spectrograph + CCD is baselined to 0.35. Each star drifts across the
plane in 60.4 s, with its signal read by two consecutive CCDs. The CCDs
have 20 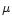 m pixels, corresponding to 1 arcsec on the sky. The
readout noise of each CCD is 3.0 e-. The dispersion direction is
perpendicular to the drift. Each star has all signal on one or two
pixels in the drift direction. It was suggested to study a
possibility of binning together the pixels
in the drift direction for faint objects and so avoid excessive RON.
The background is calculated from a suitable region displaced along
the direction of the drift scan. Altogether the number of pixels
sent to the Earth is
m pixels, corresponding to 1 arcsec on the sky. The
readout noise of each CCD is 3.0 e-. The dispersion direction is
perpendicular to the drift. Each star has all signal on one or two
pixels in the drift direction. It was suggested to study a
possibility of binning together the pixels
in the drift direction for faint objects and so avoid excessive RON.
The background is calculated from a suitable region displaced along
the direction of the drift scan. Altogether the number of pixels
sent to the Earth is
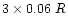 for bright stars, and
for bright stars, and
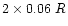 for faint stars binned across the spatial direction
(if the binning is used).
for faint stars binned across the spatial direction
(if the binning is used).
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{H3249fig2.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg16.gif) |
Figure 2:
Ecliptic latitude dependence of the zodiacal background for the 0.5 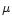 m
(filled symbols) and 1.43 m
(filled symbols) and 1.43 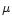 m (open symbols) bands. Adapted from
Matsumoto et al. (1996). The scale on the right gives the corresponding
number of electrons per pixel per observation detected by GAIA. m (open symbols) bands. Adapted from
Matsumoto et al. (1996). The scale on the right gives the corresponding
number of electrons per pixel per observation detected by GAIA. |
| Open with DEXTER |
For bright targets the results will be limited by Poisson noise, but at
the faint limit the read-out noise and noise of the background become more
important. GAIA will operate from the second Lagrangian point of the Sun-Earth
system. Save for the densest sky regions the dominant background signal
will be zodiacal light (ESA 2000, see also Sect. 5 below). Here we explore its spatial variation
in some detail.
The zodiacal background observed by GAIA will be much the same as seen
from Earth, as the cloud of scattering particles extends well beyond
the GAIA orbit (Kelsall et al. 1998; Gorkavyi et al. 2000). Observations
of the Infrared Telescope in Space (Matsumoto et al. 1996) show that sky
brightness at 0.5 and at 1.43 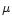 m has very similar
energy density and similar dependence on the viewing direction
(Fig. 2). This is consistent with earlier balloon observations
at 0.71
m has very similar
energy density and similar dependence on the viewing direction
(Fig. 2). This is consistent with earlier balloon observations
at 0.71 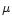 m and 0.82
m and 0.82 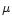 m (Frey et al. 1974). The angular
distribution of the zodiacal brightness is however remarkably un-uniform.
It depends on ecliptic coordinates of the viewing direction
(here we neglect minor asymmetries vs. ecliptic plane, see
James et al. 1997). Figure 3a shows the number of zodiacal
light photons (
m (Frey et al. 1974). The angular
distribution of the zodiacal brightness is however remarkably un-uniform.
It depends on ecliptic coordinates of the viewing direction
(here we neglect minor asymmetries vs. ecliptic plane, see
James et al. 1997). Figure 3a shows the number of zodiacal
light photons (
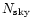 )
per pixel detected during a single 60.4 s transit.
The number is calculated from data in Levasseur-Regourd & Dumont (1980)
using the parameters of the spectrograph cited above and assuming that
a suitable filter blocks away any light outside the GAIA spectral window.
The numbers show that the zodiacal background noise (
)
per pixel detected during a single 60.4 s transit.
The number is calculated from data in Levasseur-Regourd & Dumont (1980)
using the parameters of the spectrograph cited above and assuming that
a suitable filter blocks away any light outside the GAIA spectral window.
The numbers show that the zodiacal background noise (
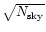 )
is
larger than the readout noise for two readouts (
)
is
larger than the readout noise for two readouts (
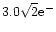 ),
except near the ecliptic poles where the two contributions are comparable.
),
except near the ecliptic poles where the two contributions are comparable.
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{H3249fig3CMYK.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg20.gif) |
Figure 3:
a) Number of electrons per pixel per transit due to zodiacal
light background. The data are shown in helioecliptic coordinates, where
the Sun stays at the center of the figure and equator coincides with the ecliptic.
b) Relative number of transits in the same coordinates. |
| Open with DEXTER |
GAIA spectroscope always points perpendicularly to the axis of the
satellite, which is aimed at the angle of
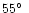 to the Sun. So the sky is
not sampled uniformly. Figure 3b shows that directions at the angle of
to the Sun. So the sky is
not sampled uniformly. Figure 3b shows that directions at the angle of
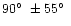 to the Sun are sampled more often than the ones in between.
As the telescope circles the Sun each star will have its helio-ecliptic
longitude drifting across the whole range, but its ecliptic latitude
remains constant.
to the Sun are sampled more often than the ones in between.
As the telescope circles the Sun each star will have its helio-ecliptic
longitude drifting across the whole range, but its ecliptic latitude
remains constant.
Note that the readout noise and the zodiacal background (per pixel) do not
depend on the chosen spectral resolution, while the stellar signal per pixel
is inversely proportional to the spectral resolution. So for faint targets
the background and read-out noise degrade the results more if the spectral
resolution is increased.
We ran
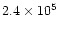 simulations to evaluate performance of the GAIA
spectrograph in measuring stellar radial velocities. Three cases were
considered: a relatively hot A8 type main sequence star, a cooler K1/2 main
sequence star and a G6 type supergiant. These choices are representative
of the most important GAIA targets: a hot relatively luminous star that
can be seen up to galactocentric distance, a cool dwarf of most common
type observed by GAIA and a luminous supergiant that can be seen even
in other galaxies.
simulations to evaluate performance of the GAIA
spectrograph in measuring stellar radial velocities. Three cases were
considered: a relatively hot A8 type main sequence star, a cooler K1/2 main
sequence star and a G6 type supergiant. These choices are representative
of the most important GAIA targets: a hot relatively luminous star that
can be seen up to galactocentric distance, a cool dwarf of most common
type observed by GAIA and a luminous supergiant that can be seen even
in other galaxies.
A spectrum of the object was degraded to a desired spectral resolution and
assigned the flux corresponding to its V magnitude. The spectrum was then
Doppler shifted to a randomly chosen velocity in the 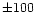 kms-1 range.
After addition of the zodiacal background the Poisson noise and the readout
noise (corresponding to two consecutive CCD readouts during a single transit)
were added. The radial velocity was recovered by correlation with a
synthetic spectrum (Tonry & Davis 1979). Correlations were done with the
xcsao task within the IRAF's rvsao package
(Kurtz et al. 1992). Degradation of
spectral resolution, rebinning, Doppler shifts etc. were performed with a
custom IRAF script.
kms-1 range.
After addition of the zodiacal background the Poisson noise and the readout
noise (corresponding to two consecutive CCD readouts during a single transit)
were added. The radial velocity was recovered by correlation with a
synthetic spectrum (Tonry & Davis 1979). Correlations were done with the
xcsao task within the IRAF's rvsao package
(Kurtz et al. 1992). Degradation of
spectral resolution, rebinning, Doppler shifts etc. were performed with a
custom IRAF script.
It would be unphysical to try to recover the radial velocity using the same
template as was used for initial input. GAIA photometric observations will
provide quite an accurate guess on the stellar parameters of the target,
but the match will never be perfect. Typical errors after the end of the
mission will be 125 K in temperature, 0.4 in
![$[{Z}/{Z}_\odot]$](/articles/aa/full/2002/17/aah3249/img25.gif) and 0.25 in
and 0.25 in 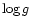 (ESA 2000).
To stay on the conservative side and to allow for
a limited ability to reproduce observed spectra by theoretical calculation
we used a larger mismatch: the spectrum used to recover the radial velocity
had a random mismatch of 250 K in temperature, 0.5 in
(ESA 2000).
To stay on the conservative side and to allow for
a limited ability to reproduce observed spectra by theoretical calculation
we used a larger mismatch: the spectrum used to recover the radial velocity
had a random mismatch of 250 K in temperature, 0.5 in
![$[{Z}/{Z}_\odot]$](/articles/aa/full/2002/17/aah3249/img25.gif) and 0.5 in
and 0.5 in 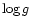 .
The rotational velocity
was also different: the initial input spectrum had
.
The rotational velocity
was also different: the initial input spectrum had
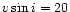 kms-1
(for A8 V and K1/2 V star), and 2 kms-1 (G6 I star), while the one used
as a correlation template had
kms-1
(for A8 V and K1/2 V star), and 2 kms-1 (G6 I star), while the one used
as a correlation template had
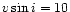 kms-1
(for A8 V and K1/2 V star), and 5 kms-1 (G6 I star).
kms-1
(for A8 V and K1/2 V star), and 5 kms-1 (G6 I star).
Table 1:
Radial velocity error (in km s-1) for a background of 74 e- per
wavelength bin, typical for an object in the ecliptic plane. Values are given for mission
averaged spectra (100 transits) while those in
brackets are for a single transit spectrum.
| Sp. Type |
Dispersion |
R |
Visual magnitude |
| |
Å/pix |
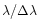 |
14.0 |
15.0 |
16.0 |
17.0 |
18.0 |
19.0 |
| A8 V |
0.25 |
17200 |
1.58 (5.43) |
1.90 (24.0) |
3.06 (>40) |
7.84 (>40) |
>40 (>40) |
>40 (>40) |
| |
0.50 |
8610 |
2.80 (6.31) |
3.01 (17.0) |
3.79 (>40) |
6.62 (>40) |
32.2 (>40) |
>40 (>40) |
| |
0.75 |
5740 |
4.66 (7.92) |
4.69 (17.7) |
5.15 (>40) |
7.72 (>40) |
26.0 (>40) |
>40 (>40) |
| |
1.00 |
4305 |
6.81 (10.9) |
6.87 (16.6) |
7.15 (>40) |
9.69 (>40) |
22.1 (>40) |
>40 (>40) |
| |
2.00 |
2160 |
13.2 (16.5) |
13.4 (24.5) |
13.9 (>40) |
15.9 (>40) |
25.6 (>40) |
>40 (>40) |
| K1 V |
0.25 |
17200 |
0.23 (1.84) |
0.40 (4.17) |
0.92 (14.9) |
2.30 (>40) |
5.59 (>40) |
>40 (>40) |
| |
0.50 |
8610 |
0.28 (2.10) |
0.44 (4.38) |
0.96 (9.97) |
2.10 (>40) |
5.24 (>40) |
19.4 (>40) |
| |
0.75 |
5740 |
0.29 (2.53) |
0.47 (5.06) |
1.08 (10.5) |
2.23 (>40) |
5.45 (>40) |
13.8 (>40) |
| |
1.00 |
4305 |
0.31 (3.00) |
0.56 (5.50) |
1.11 (12.5) |
2.54 (39.7) |
5.72 (>40) |
15.3 (>40) |
| |
2.00 |
2160 |
0.57 (5.20) |
0.93 (9.52) |
1.67 (17.3) |
3.35 (39.1) |
7.18 (>40) |
19.1 (>40) |
| G6 I |
0.25 |
17200 |
0.11 (1.09) |
0.20 (2.41) |
0.44 (5.92) |
1.09 (>40) |
2.86 (>40) |
25.9 (>40) |
| |
0.50 |
8610 |
0.17 (1.52) |
0.31 (3.37) |
0.65 (7.41) |
1.52 (32.7) |
3.48 (>40) |
12.4 (>40) |
| |
0.75 |
5740 |
0.48 (1.88) |
0.55 (3.60) |
0.82 (7.71) |
1.72 (27.2) |
4.11 (>40) |
11.9 (>40) |
| |
1.00 |
4305 |
0.67 (2.28) |
0.77 (4.25) |
1.07 (8.31) |
1.98 (23.7) |
4.54 (>40) |
11.4 (>40) |
| |
2.00 |
2160 |
0.63 (3.55) |
0.77 (6.45) |
1.25 (11.4) |
2.74 (28.2) |
5.69 (>40) |
13.5 (>40) |
| Cepheid |
0.25 |
17200 |
0.34 (2.60) |
0.59 (5.09) |
1.28 (22.3) |
3.14 (>40) |
7.48 (>40) |
>40 (>40) |
| |
0.50 |
8610 |
0.38 (2.86) |
0.60 (5.34) |
1.15 (13.4) |
2.70 (>40) |
6.52 (>40) |
24.6 (>40) |
| |
0.75 |
5740 |
0.63 (3.34) |
0.78 (5.64) |
1.32 (12.2) |
2.85 (>40) |
6.56 (>40) |
18.6 (>40) |
| |
1.00 |
4305 |
0.71 (3.32) |
0.87 (6.77) |
1.34 (13.2) |
2.98 (31.9) |
6.58 (>40) |
18.1 (>40) |
| |
2.00 |
2160 |
0.63 (5.24) |
0.97 (9.09) |
1.86 (17.0) |
3.54 (35.0) |
7.50 (>40) |
19.8 (>40) |
| HB |
0.25 |
17200 |
0.34 (2.19) |
0.52 (4.48) |
1.07 (20.8) |
2.51 (>40) |
7.30 (>40) |
>40 (>40) |
| |
0.50 |
8610 |
0.57 (2.51) |
0.72 (5.32) |
1.21 (16.4) |
2.64 (>40) |
6.00 (>40) |
33.8 (>40) |
| |
0.75 |
5740 |
0.90 (3.09) |
1.00 (5.95) |
1.47 (13.2) |
2.75 (>40) |
6.44 (>40) |
21.6 (>40) |
| |
1.00 |
4305 |
1.35 (3.98) |
1.45 (6.24) |
1.77 (14.0) |
2.95 (>40) |
6.66 (>40) |
23.8 (>40) |
| |
2.00 |
2160 |
2.32 (7.28) |
2.52 (10.2) |
2.93 (20.9) |
4.63 (>40) |
9.47 (>40) |
22.8 (>40) |
Table 2:
Radial velocity error (in km s-1) for a background of 20 e- per
wavelength bin, typical for an object at ecliptic latitude
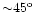 .
Values are given for mission averaged spectra (100 transits) while those in
brackets are for a single transit spectrum.
.
Values are given for mission averaged spectra (100 transits) while those in
brackets are for a single transit spectrum.
| Sp. Type |
Dispersion |
R |
Visual magnitude |
| |
Å/pix |
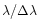 |
14.0 |
15.0 |
16.0 |
17.0 |
18.0 |
19.0 |
| A8 V |
0.25 |
17200 |
1.64 (4.63) |
1.67 (15.4) |
2.13 (>40) |
3.98 (>40) |
14.2 (>40) |
>40 (>40) |
| |
0.50 |
8610 |
2.82 (5.60) |
2.82 (11.0) |
3.21 (>40) |
4.16 (>40) |
8.98 (>40) |
>40 (>40) |
| |
0.75 |
5740 |
4.64 (7.54) |
4.65 (11.8) |
4.96 (35.8) |
5.73 (>40) |
9.57 (>40) |
>40 (>40) |
| |
1.00 |
4305 |
6.78 (10.1) |
6.76 (13.9) |
6.92 (32.7) |
7.73 (>40) |
12.4 (>40) |
31.2 (>40) |
| |
2.00 |
2160 |
13.2 (18.0) |
13.4 (22.9) |
13.6 (39.9) |
14.4 (>40) |
18.0 (>40) |
36.0 (>40) |
| K1 V |
0.25 |
17200 |
0.19 (1.52) |
0.28 (3.01) |
0.53 (6.82) |
1.19 (39.4) |
2.86 (>40) |
8.26 (>40) |
| |
0.50 |
8610 |
0.25 (1.83) |
0.36 (3.32) |
0.61 (7.10) |
1.24 (21.9) |
2.92 (>40) |
7.44 (>40) |
| |
0.75 |
5740 |
0.26 (2.32) |
0.42 (4.11) |
0.74 (7.58) |
1.32 (20.2) |
3.15 (>40) |
7.37 (>40) |
| |
1.00 |
4305 |
0.27 (2.98) |
0.45 (5.23) |
0.86 (8.81) |
1.66 (28.6) |
3.38 (>40) |
7.93 (>40) |
| |
2.00 |
2160 |
0.60 (4.85) |
0.80 (8.52) |
1.38 (13.5) |
2.42 (27.2) |
5.22 (>40) |
10.4 (>40) |
| G6 I |
0.25 |
17200 |
0.10 (0.98) |
0.14 (1.86) |
0.28 (4.05) |
0.59 (26.4) |
1.50 (>40) |
3.96 (>40) |
| |
0.50 |
8610 |
0.15 (1.38) |
0.24 (2.36) |
0.50 (4.78) |
0.95 (14.3) |
2.06 (>40) |
4.54 (>40) |
| |
0.75 |
5740 |
0.47 (1.70) |
0.52 (3.02) |
0.67 (5.79) |
1.07 (14.9) |
2.51 (>40) |
5.58 (>40) |
| |
1.00 |
4305 |
0.69 (2.11) |
0.71 (3.60) |
0.85 (6.77) |
1.36 (14.7) |
2.77 (>40) |
6.08 (>40) |
| |
2.00 |
2160 |
0.59 (3.79) |
0.75 (5.72) |
1.05 (10.1) |
1.76 (19.2) |
3.34 (>40) |
7.85 (>40) |
| Cepheid |
0.25 |
17200 |
0.31 (2.16) |
0.48 (4.09) |
0.90 (9.37) |
2.05 (>40) |
4.87 (>40) |
16.6 (>40) |
| |
0.50 |
8610 |
0.36 (2.47) |
0.48 (4.59) |
0.89 (8.79) |
1.80 (28.0) |
4.18 (>40) |
11.1 (>40) |
| |
0.75 |
5740 |
0.59 (2.72) |
0.72 (4.80) |
1.04 (10.1) |
1.94 (21.2) |
4.40 (>40) |
11.5 (>40) |
| |
1.00 |
4305 |
0.69 (3.55) |
0.81 (5.81) |
1.17 (9.89) |
2.00 (22.9) |
4.41 (>40) |
11.1 (>40) |
| |
2.00 |
2160 |
0.58 (5.49) |
0.95 (8.32) |
1.59 (13.9) |
2.85 (28.5) |
5.28 (>40) |
11.6 (>40) |
| HB |
0.25 |
17200 |
0.31 (1.75) |
0.44 (3.70) |
0.79 (8.97) |
1.68 (>40) |
4.06 (>40) |
23.0 (>40) |
| |
0.50 |
8610 |
0.52 (2.31) |
0.64 (4.22) |
0.92 (8.69) |
1.81 (37.5) |
4.27 (>40) |
12.1 (>40) |
| |
0.75 |
5740 |
0.88 (3.13) |
1.03 (4.79) |
1.22 (9.76) |
2.02 (36.0) |
4.67 (>40) |
11.1 (>40) |
| |
1.00 |
4305 |
1.38 (3.78) |
1.41 (6.16) |
1.65 (10.2) |
2.45 (28.2) |
4.81 (>40) |
11.6 (>40) |
| |
2.00 |
2160 |
2.37 (6.89) |
2.46 (10.1) |
2.92 (17.8) |
4.04 (37.7) |
7.08 (>40) |
15.9 (>40) |
![\begin{figure}
\par\includegraphics[width=17.5cm,height=15cm,angle=0]{H3249fig4CMYK.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg30.gif) |
Figure 4:
Average radial velocity determination error as a function
of stellar magnitude, spectral type and the used spectral dispersion.
Top labels at each graph quote a representative
distance if no interstellar absorption is present. Left column is
for single transit spectra, while the right one is for a mission-averaged
spectrum (100 transits). The assumed background is 74 e- per
wavelength bin. |
| Open with DEXTER |
Apart from a spectrum obtained during a single passage over the target
we also simulated mission-averaged spectra. On the average each target
will be observed 100 times during the 4-year mission. So we co-added
100 single mission spectra in order to simulate the ability of deriving
radial velocities for single non-varying stars. The conditions for such
summation will be met: each spectrum (and not only the correlation function)
will be sent to the Earth, and previewed accuracy of wavelength
calibration will permit their co-addition at the end of the mission.
Results of the achievable radial velocity accuracy are presented in
Fig. 4
and Tables 1 and 2. Each point presents a standard radial velocity error,
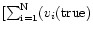 -
-
![$v_i ({\rm recovered}))^2 /N]^{0.5}$](/articles/aa/full/2002/17/aah3249/img32.gif) ,
as resulting from some N=400 tries using a given spectral
resolution for a star of a given spectral type and magnitude.
The distribution of errors of each point turns out to be Gaussian
within statistical errors also for the faintest stars and for all resolutions.
The xcsao correlation routine had no appreciable convergence problems
even for the faintest stars sampled at the lowest spectral resolution (the
convergence was always succesfull in >95% of the tries).
We used 5 different spectral dispersions, colour
coded in Fig. 4. The resolution element had always a size of two
pixels. The graphs are in three rows, each for a different type
of a star. The left column gives results for a single transit spectrum,
while the right one is for a mission-averaged spectrum. Top labels at
each graph quote a representative distance of the star, assuming no
interstellar absorption is present.
,
as resulting from some N=400 tries using a given spectral
resolution for a star of a given spectral type and magnitude.
The distribution of errors of each point turns out to be Gaussian
within statistical errors also for the faintest stars and for all resolutions.
The xcsao correlation routine had no appreciable convergence problems
even for the faintest stars sampled at the lowest spectral resolution (the
convergence was always succesfull in >95% of the tries).
We used 5 different spectral dispersions, colour
coded in Fig. 4. The resolution element had always a size of two
pixels. The graphs are in three rows, each for a different type
of a star. The left column gives results for a single transit spectrum,
while the right one is for a mission-averaged spectrum. Top labels at
each graph quote a representative distance of the star, assuming no
interstellar absorption is present.
Simulations presented in Fig. 4 assume the background of 74 e- per
wavelength bin. This is an average value of zodiacal light background
for an object on the ecliptic plane with the spectrum falling on a
single pixel row (Fig. 3a) and corresponds
to
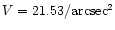 .
We also run an identical set of
simulations for a lower value of the sky background
(the adopted value of 20 e-
per wavelength bin is an average value for an object
.
We also run an identical set of
simulations for a lower value of the sky background
(the adopted value of 20 e-
per wavelength bin is an average value for an object
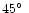 away from the
ecliptic).
away from the
ecliptic).
The results for the three types of stars are remarkably different. Spectrum
of a hot A8 V type star (T=7500 K,
![$[Z/Z_\odot]=0.0$](/articles/aa/full/2002/17/aah3249/img35.gif) ,
,
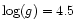 )
has relatively few lines, so its results are worse than those obtained for
cooler stars. It is dominated by weak and sharp Ca II lines
and the Paschen series lines. The relative intensity of the Ca II and
Paschen lines rapidly changes with temperature so a mismatch in the spectral
type of the star introduces a systematic error in the strength of both sets
of lines. The correlation routine tries to compensate for line intensity
mismatch by introducing an additional velocity shift that causes a systematic
offset in the recovered velocity. This error can be corrected by obtaining
spectra with better resolution: better sampling of line profiles means
more points carrying radial velocity information, so that the correlation
routine can avoid systematic errors in the recovered radial velocity.
This is well seen in top-right panel of Fig. 4, where the accuracy of
bright star (
)
has relatively few lines, so its results are worse than those obtained for
cooler stars. It is dominated by weak and sharp Ca II lines
and the Paschen series lines. The relative intensity of the Ca II and
Paschen lines rapidly changes with temperature so a mismatch in the spectral
type of the star introduces a systematic error in the strength of both sets
of lines. The correlation routine tries to compensate for line intensity
mismatch by introducing an additional velocity shift that causes a systematic
offset in the recovered velocity. This error can be corrected by obtaining
spectra with better resolution: better sampling of line profiles means
more points carrying radial velocity information, so that the correlation
routine can avoid systematic errors in the recovered radial velocity.
This is well seen in top-right panel of Fig. 4, where the accuracy of
bright star (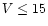 )
measurements depends only on spectral resolution
and not on the magnitude. The situation for
faint targets (
)
measurements depends only on spectral resolution
and not on the magnitude. The situation for
faint targets (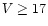 )
is different: the adopted relatively
high background starts to dominate the statistics for the highest resolutions,
so dispersions of 0.5 Å/pix or 0.75 Å/pix perform best for faint
hot targets. Note that the point of crossing, i.e. the limit where
choosing coarser dispersion starts to pay off, depends on the adopted value
of the background. For another set of simulations with assumed background
value of 20 e- (Table 2) the crossing occurs only at magnitude V=18.0.
)
is different: the adopted relatively
high background starts to dominate the statistics for the highest resolutions,
so dispersions of 0.5 Å/pix or 0.75 Å/pix perform best for faint
hot targets. Note that the point of crossing, i.e. the limit where
choosing coarser dispersion starts to pay off, depends on the adopted value
of the background. For another set of simulations with assumed background
value of 20 e- (Table 2) the crossing occurs only at magnitude V=18.0.
Cool dwarfs (K1/2 V: T=5000 K,
![$[Z/Z_\odot]=0.0$](/articles/aa/full/2002/17/aah3249/img35.gif) ,
,
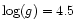 )
perform better. The reason are very strong,
core-saturated Ca II lines that dominate the spectrum. These lines enable
correlation at fainter magnitudes, so improving the accuracy. And because
Ca II lines are very broad and symmetrical the issue of resolution is
less important. Actually the radial velocity accuracy is very similar
for all dispersions except for the coarsest one (2 Å/pix) where
even the broad Ca II lines get undersampled. The crossing of the
0.25 Å/pix dispersion occurs at
)
perform better. The reason are very strong,
core-saturated Ca II lines that dominate the spectrum. These lines enable
correlation at fainter magnitudes, so improving the accuracy. And because
Ca II lines are very broad and symmetrical the issue of resolution is
less important. Actually the radial velocity accuracy is very similar
for all dispersions except for the coarsest one (2 Å/pix) where
even the broad Ca II lines get undersampled. The crossing of the
0.25 Å/pix dispersion occurs at
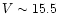 (spectrum from a single transit)
and
(spectrum from a single transit)
and 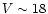 (mission average). If the background were lower
(20 e-, Table 2) the errors at the faint end would be 50% lower and the
crossing less pronounced. The results for a mission average
spectrum are very similar to those of
(mission average). If the background were lower
(20 e-, Table 2) the errors at the faint end would be 50% lower and the
crossing less pronounced. The results for a mission average
spectrum are very similar to those of 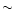 2.5 mag brighter stars
observed during a single transit. If the spectrum had no background and
readout noise limits, the gain would be a factor of 100 in flux or
a difference of 5 mag.
2.5 mag brighter stars
observed during a single transit. If the spectrum had no background and
readout noise limits, the gain would be a factor of 100 in flux or
a difference of 5 mag.
Cool supergiants (G6 I: T=4750 K,
![$[Z/Z_\odot]=0.0$](/articles/aa/full/2002/17/aah3249/img35.gif) ,
,
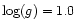 )
will be optimal targets for deriving accurate radial
velocities at extreme distances. Their spectra are much richer than
those of dwarfs of similar temperature, as the Paschen lines and many
lines of metals start to appear.
More lines mean more points that can constrain the position of the
peak of the correlation function. As a result the radial velocity
is derived with remarkable accuracy. The question of resolution is
important: better resolution allows for distinction of the Ca II and Pashen
lines, as well as deblending of close metallic lines. The crossing
of the 0.25 Å/pix dispersion occurs at
)
will be optimal targets for deriving accurate radial
velocities at extreme distances. Their spectra are much richer than
those of dwarfs of similar temperature, as the Paschen lines and many
lines of metals start to appear.
More lines mean more points that can constrain the position of the
peak of the correlation function. As a result the radial velocity
is derived with remarkable accuracy. The question of resolution is
important: better resolution allows for distinction of the Ca II and Pashen
lines, as well as deblending of close metallic lines. The crossing
of the 0.25 Å/pix dispersion occurs at
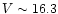 for single
transit spectra,
while the highest resolution still performs well even at magnitude V=18 for
a mission averaged spectrum. The reason is the richness of lines so that
co-addition of many well-sampled spectra is still advantageous. On the other
hand weak lines in faint stars get lost in the noise, so the question of a
chosen spectral resolution is less critical at the faint end than it is
for bright stars. In the case of low background (20 e-) the errors for
the faint stars are 50% lower.
for single
transit spectra,
while the highest resolution still performs well even at magnitude V=18 for
a mission averaged spectrum. The reason is the richness of lines so that
co-addition of many well-sampled spectra is still advantageous. On the other
hand weak lines in faint stars get lost in the noise, so the question of a
chosen spectral resolution is less critical at the faint end than it is
for bright stars. In the case of low background (20 e-) the errors for
the faint stars are 50% lower.
Figure 4 demonstrates that radial velocities with an accuracy of
2 kms-1 in A8 dwarfs are obtainable only for the case of the highest
spectral resolution (0.25 Å/pix). These stars can be observed up to
the distance of 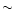 5 kpc. For cooler dwarfs (K1/2 V)
the same accuracy is achievable for fainter targets (
5 kpc. For cooler dwarfs (K1/2 V)
the same accuracy is achievable for fainter targets (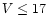 ),
corresponding to smaller distances (
),
corresponding to smaller distances (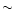 2 kpc). The issue of
spectral dispersion is less important than for hot dwarfs unless the worst
sampling (2 Å/pix) is chosen. Note that accuracy achievable from single
transit spectra is important: most spectroscopic binaries or intrinsically
variable (spot) stars will be cool dwarfs. Figure 4 shows that GAIA will
be able to measure their radial velocity down to V=15 with an error
of
2 kpc). The issue of
spectral dispersion is less important than for hot dwarfs unless the worst
sampling (2 Å/pix) is chosen. Note that accuracy achievable from single
transit spectra is important: most spectroscopic binaries or intrinsically
variable (spot) stars will be cool dwarfs. Figure 4 shows that GAIA will
be able to measure their radial velocity down to V=15 with an error
of 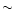 3 kms-1. But the superposition of various dispersions
can be misleading in this case: spectroscopic binaries or spotty stars
require a sufficient spectral resolution for any meaningful measurement
(Munari et al. 2001a, 2002). The cool supergiants can be used to measure
kinematics at the largest distances, reaching nearby galaxies.
3 kms-1. But the superposition of various dispersions
can be misleading in this case: spectroscopic binaries or spotty stars
require a sufficient spectral resolution for any meaningful measurement
(Munari et al. 2001a, 2002). The cool supergiants can be used to measure
kinematics at the largest distances, reaching nearby galaxies.
Tables 1 and 2 give detailed results for two levels of the background.
Relative uncertainties of the quoted standard velocity errors are
estimated at 3%, as can be seen from comparison of values for bright stars
in both tables.
We added results for classical Cepheids
(T=5500 K,
![$[Z/Z_\odot]=-0.2$](/articles/aa/full/2002/17/aah3249/img45.gif) ,
,
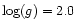 ,
,
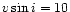 km s-1)
and horizontal branch stars
(T=5000 K,
km s-1)
and horizontal branch stars
(T=5000 K,
![$[Z/Z_\odot]=-0.5$](/articles/aa/full/2002/17/aah3249/img47.gif) ,
,
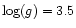 ,
,
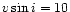 km s-1)
that are important kinematic tracers in
the Galaxy (ESA 2000).
Results can be readily scaled to any ground based
spectrograph with collecting area different from 0.53 m2as the single transit spectra have an effective exposure time
of 1 min and the mission averaged ones 100 min.
km s-1)
that are important kinematic tracers in
the Galaxy (ESA 2000).
Results can be readily scaled to any ground based
spectrograph with collecting area different from 0.53 m2as the single transit spectra have an effective exposure time
of 1 min and the mission averaged ones 100 min.
The results presented in Fig. 4 are compatible with initial performance
assessment of the GAIA radial velocity spectrometer (Katz 2000).
Recently Munari et al. (2001) published an extensive
series of cross-correlations using an observed set of Echelle spectra.
They limited themselves to stars brighter than those considered here.
But bright stars of identical spectral type are hard to find. So they had
to use a large spread of spectral types, and the actual mismatch
between spectra and templates was larger than will
be for the mission. Correspondingly they derived somewhat larger radial
velocity errors (within a factor of 2). But they came to the same basic
conclusion: a high-enough spectral dispersion is a critical factor
determining radial velocity accuracy for bright stars.
Here we extend this work to fainter magnitudes. We explore a range of
spectral types and include simulations of very faint stars having
a signal to noise ratio for a single transit S/N < 1. At such extreme
conditions a spectrum with the dispersion of 0.25 Å/pix is limited by
the sky background. And because this background is mostly zodiacal light
a somewhat lower dispersion (0.5 Å/pix) performs better for the faintest
(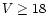 )
dwarfs. The resolution of 0.75 Å/pix is also acceptable
for the faintest stars.
)
dwarfs. The resolution of 0.75 Å/pix is also acceptable
for the faintest stars.
There are other reasons to collect high dispersion spectra. Figure 1 shows
that values of all spectral parameters can be accounted for by spectroscopy,
but note that a high spectral resolution is needed to make secure
distinctions. All tracings are plot for 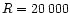 ;
halving the resolution
already mixes up gravity and rotation or metallicity and
;
halving the resolution
already mixes up gravity and rotation or metallicity and 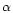 -element
enrichment. Additional set of simulations shows that
-element
enrichment. Additional set of simulations shows that 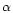 -element
enrichment of +0.4 can be detected down to V=14, and abundancies of
individual elements can be measured for bright stars. Abundance of a
particularly difficult one, Manganese (with the only useful line
in the GAIA spectral range at
-element
enrichment of +0.4 can be detected down to V=14, and abundancies of
individual elements can be measured for bright stars. Abundance of a
particularly difficult one, Manganese (with the only useful line
in the GAIA spectral range at
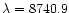 Å with
Å with
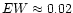 Å) can be determined within
a factor of 2 for V<8. Other elements, i.e. N, Si, Fe, Mg and Ti cause
much stronger lines and so can be studied down to
Å) can be determined within
a factor of 2 for V<8. Other elements, i.e. N, Si, Fe, Mg and Ti cause
much stronger lines and so can be studied down to
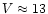 .
Stellar rotation is easy to determine for fast
rotators (Munari 1999), but cool dwarfs commonly observed
by GAIA rotate slowly. Stellar rotation with an error of 10 kms-1
of a T=5000 K dwarf can be
measured for V<9. All results quoted here are for the dispersion of
0.25 Å/pix and depend critically on the spectral resolution.
.
Stellar rotation is easy to determine for fast
rotators (Munari 1999), but cool dwarfs commonly observed
by GAIA rotate slowly. Stellar rotation with an error of 10 kms-1
of a T=5000 K dwarf can be
measured for V<9. All results quoted here are for the dispersion of
0.25 Å/pix and depend critically on the spectral resolution.
GAIA will observe many spectroscopic binaries. Munari et al. (2001a) showed
that good quality orbital solutions, including masses, can be derived.
But also this result critically depends on the resolution of the spectrum.
Single Angstrom corresponds to 35 kms-1 at the wavelengths of the GAIA
spectrograph. Velocity amplitudes of most spectroscopic binaries are
not much larger than this, so it is clear that a dispersion
of 0.25 or 0.5 Å/pix is needed for a proper deblending of lines from
both stars.
The Galaxy model (Torra et al. 1999) using Hakkila et al. (1997)
extinction law predicts an average surface density n of stars (Table 3).
This can be translated into an average stellar separation (n-0.5).
Two spectra are blended if their spectral tracings are separated
by less than the spatial extent s of a CCD pixel, i.e. 1 arcsec.
This happens if the length of the spectral tracing is larger than
the free length
l = (n s)-1. The length of the tracing depends on the
dispersion and equals 1000 arcsec for 0.25 Å/pix, 500 arcsec for
0.5 Å/pix and 333 arcsec for 0.75 Å/pix. So Table 3 demonstrates
that spectral superposition will be common close to the galactic plane,
but not away from it.
Light of contaminating stars
will be spread over many pixels, so the zodiacal light will usually remain
the dominant background signal. Stellar background features stellar lines
and this could influence the radial velocity accuracy. Still, extremely
accurate astrometry and photometry of contaminating stars will supply
enough information to handle the problem. In the worst cases the
situation will be similar to disentangling the two spectra in a spectroscopic
binary. But with an extra benefit that spectral overlap varies from
transit to transit. So, even if two spectra are badly superimposed,
the same two stars will be recorded separately during the next transit.
We studied performance of a slitless spectrograph observing in a
250 Å window centered at 8615 Å that will be used aboard GAIA.
The same spectral range is accessible also from the ground,
but cannot be much expanded, due to bracketing telluric absorptions.
So the results are relevant also for planning of ground based instruments.
The dominant parameter that can still be changed is the spectral resolution.
We used realistic estimates of zodiacal light background and spectrograph
parameters to derive expected accuracy of the radial velocity determination.
We showed that errors below 2 kms-1 are achievable for bright enough
stars if a high dispersion is chosen. This result could be still improved
with correlation methods that use software spectral masks
(Baranne et al. 1979; Queloz 1995).
The results show that it is worth to observe very faint targets, down to
magnitude 19 even though the expected radial velocity errors can be
well above 10 km s-1.
Such stars are numerous. One may expect a ratio of
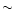 10:1 in the recorded number of targets between V=17 and 19 compared to
stars between V=14 and 16. For such stars the best results are obtained with
0.5 Å/pix or 0.75 Å/pix dispersion. But for brighter
stars a high dispersion (0.25 Å/pix) is always a preferred choice
and is critical in order to extract relevant information for non-trivial
cases, as spectroscopic binaries, variable stars and peculiar stars.
It remains to be determined if telemetry constraints permit
to use the dispersions of 0.25 or 0.5 Å/pix. Still
it is clear that such a choice has a strong support considering the
astrophysical information retrievable from the data.
10:1 in the recorded number of targets between V=17 and 19 compared to
stars between V=14 and 16. For such stars the best results are obtained with
0.5 Å/pix or 0.75 Å/pix dispersion. But for brighter
stars a high dispersion (0.25 Å/pix) is always a preferred choice
and is critical in order to extract relevant information for non-trivial
cases, as spectroscopic binaries, variable stars and peculiar stars.
It remains to be determined if telemetry constraints permit
to use the dispersions of 0.25 or 0.5 Å/pix. Still
it is clear that such a choice has a strong support considering the
astrophysical information retrievable from the data.
Acknowledgements
The author wishes to thank U. Munari for
initial motivation and many fruitful discussions and to F. Castelli for an
introduction to the art of Kurucz models. The referee, D. Katz, is
acknowledged for useful comments which improved the quality of the
paper. This work was supported by a grant from the Slovenian Ministry of
Education, Science and Sport.
- Baranne, A., Mayor, M., & Poncet, J. L.
1979, Vistas in Astronomy, 23, 279
In the text
NASA ADS
- Castelli, F., & Munari, U. 2001, A&A, 366, 1003
In the text
NASA ADS
- de Zeeuw, P. T., Gilmore, G., Perryman, M. A. C., et al. 2000,
GAIA - Composition, Formation and Evolution of the Galaxy,
ESA-SCI(2000)4, [ESA 2000]
- Frey, A., Hoffmann, W., Lemke, D., & Thum, C. 1974, A&A, 36, 447
In the text
NASA ADS
- Garcia, B. 1989, CDS Catalog, 3149
- Gorkavyi, N., Ozernoy, L., Mather, J., & Taidakova, T. 2000,
in Next Generation Space Telescope Science and Technology, ed. E. Smith, & K. Long, ASP Conf. Ser., 207, 462
In the text
- Hakkila, J., Myers, J. M., Stidham, B. J., & Hartmann, D. H. 1997,
AJ, 114, 2043
In the text
NASA ADS
- Katz, D. 2000, Ph.D. Thesis, Univ. Paris 7
In the text
- Kelsall, T., Weiland, J. L., Franz, B. A., et al.
1998, ApJ, 508, 44
In the text
NASA ADS
- James, F., Mukai, T., Watanabe, T., Ishiguro, M., & Nakamura, R.
1997, MNRAS, 288, 1022
In the text
NASA ADS
- Levasseur-Regourd, A. C., & Dumont, R. 1980, A&A, 84, 277
In the text
NASA ADS
- Kurtz, M. J., Mink, D. J., Wyatt, W. F., et al. 1992,
in Astronomical data analysis software and systems, ed. D. M. Worrall,
C. Biemesderfer, & J. Barneseds, ASP Conf. Ser., 25, 432
In the text
- Matsumoto, T., Kawada, M., Murakami, H., et al. 1996, PASJ, 48, L47
In the text
NASA ADS
- Munari, U. 1999, in Proceedings of the ESA Leiden Workshop on
GAIA, 23-27 Nov. 1998, Baltic Astronomy, 8, 73
In the text
NASA ADS
- Munari, U., & Tomasella, L. 1999, A&AS, 137, 521
NASA ADS
- Munari, U., & Castelli, F. 2000, A&AS, 141, 141
In the text
NASA ADS
- Munari, U. 2001, in GAIA, an European Space Project,
Proc. of Les Houches 2001 summer sch., EDP Sciences,
in press [astro-ph/0109057]
In the text
- Munari, U., Agnolin, P., & Tomasella, L. 2001, Baltic Astronomy,
10, 613
NASA ADS
- Munari, U., Tomov, T., Zwitter, T., et al. 2001a, A&A, 378, 477
In the text
NASA ADS
- Munari, U., Tomasella, L., Marrese, P. M., et al. 2002, A&A, submitted
In the text
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339
In the text
NASA ADS
- Queloz, D. 1995, in New developments in array technology and
applications, IAU Symp., 167 (Kluwer), 221
In the text
- Tonry, J., & Davis, M. 1979, AJ, 84, 1511
In the text
NASA ADS
- Torra, J., Chen, B., Figuera, F., Jordi, C., & Luri, X. 1999,
in Proceedings of the ESA Leiden Workshop on GAIA, 23-27 Nov. 1998,
Baltic Astronomy, 8, 171
In the text
NASA ADS
- Zwitter, T., Munari, U., & Castelli, F. 2002, A&A, submitted
In the text
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=9.6cm,height=16.8cm,angle=270,clip]{H3249fig1.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg6.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{H3249fig2.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{H3249fig3CMYK.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg20.gif)
![\begin{figure}
\par\includegraphics[width=17.5cm,height=15cm,angle=0]{H3249fig4CMYK.eps}\end{figure}](/articles/aa/full/2002/17/aah3249/Timg30.gif)