The measurements of the lines of the short-period RS CVn systems
are difficult for several reasons. First, the lines arising
from each component are rotationally broadened and blended with
the surrounding metal lines of itself and the companion star.
Second, the profiles are distorted by the presence of emission
features.
The absorption H![]() and FeI 6678 lines show double
profiles outside the eclipses. Although the FeI 6678
line is significantly weaker than H
and FeI 6678 lines show double
profiles outside the eclipses. Although the FeI 6678
line is significantly weaker than H![]() its doubling is
better pronounced.
its doubling is
better pronounced.
| Phase | RV1(H |
|
RV2(H |
|
RV1(FeI) |
|
RV2(FeI) |
|
0.105 |
-60.4 | 7.60 | -69.6 | 24.78 | 121.3 | 11.70 | ||
| 0.130 | -74.0 | 10.60 | -73.0 | 19.13 | 134.0 | 15.20 | ||
| 0.153 | -90.0 | 3.42 | -96.6 | 23.04 | 164.0 | 28.00 | ||
| 0.177 | -94.6 | 6.09 | -105.6 | 20.86 | 191.0 | 28.00 | ||
| 0.200 | -96.9 | 6.66 | -114.5 | 20.86 | 195.0 | 25.80 | ||
| 0.225 | -99.2 | 8.53 | -116.8 | 26.95 | ||||
| 0.250 | -101.5 | 11.26 | 205.0 | 27.50 | -119.0 | 28.69 | 218.0 | 50.40 |
| 0.270 | -106.0 | 10.66 | -123.5 | 23.04 | 195.4 | 21.06 | ||
| 0.295 | -103.7 | 9.13 | 200.0 | 25.00 | -105.6 | 19.13 | 183.0 | 18.66 |
| 0.320 | -101.5 | 7.93 | 195.0 | 27.40 | -105.6 | 30.43 | 173.0 | 33.60 |
| 0.590 | 81.4 | 10.93 | 62.9 | 26.52 | -123.0 | 30.13 | ||
| 0.613 | 92.8 | 8.00 | 78.6 | 24.78 | -132.5 | 26.66 | ||
| 0.637 | 104.2 | 6.06 | 96.5 | 11.73 | ||||
| 0.660 | 111.1 | 5.80 | 110.0 | 22.60 | ||||
| 0.668 | 118.0 | 4.93 | -193.0 | 22.00 | 119.0 | 27.40 | ||
| 0.700 | 122.5 | 4.80 | -199.7 | 17.80 | 128.0 | 28.20 | -195.4 | 49.06 |
| 0.720 | 145.3 | 4.92 | 134.7 | 20.80 | ||||
| 0.740 | 151.0 | 6.26 | 137.0 | 27.39 | -213.9 | 49.06 | ||
| 0.766 | 145.3 | 6.27 | -201.0 | 20.30 | 130.0 | 23.40 | -213.0 | 41.86 |
| 0.790 | 140.3 | 6.26 | -197.0 | 21.65 | 123.0 | 23.47 | -204.0 | 45.33 |
| 0.814 | 137.0 | 5.93 | -193.0 | 24.20 | 114.0 | 27.40 | -198.0 | 30.93 |
| 0.840 | 105.0 | 29.13 | ||||||
| 0.860 | 96.5 | 21.30 | -186.0 | 19.20 |
Our ![]() value is almost the same as that determined by
Rainger et al. (1991)
(122.3 kms-1) and that of Hiltner (1953)
(123 kms-1) but it is slightly bigger than that of Hempelmann et al.
(1997) (117 kms-1) and that of Pojmanski (1998) (118.3 kms-1). Our
value of
value is almost the same as that determined by
Rainger et al. (1991)
(122.3 kms-1) and that of Hiltner (1953)
(123 kms-1) but it is slightly bigger than that of Hempelmann et al.
(1997) (117 kms-1) and that of Pojmanski (1998) (118.3 kms-1). Our
value of ![]() is close to the only value known so far,
published by Pojmanski (211.5 kms-1) and obtained from the
analysis of near IR CaII spectral lines.
is close to the only value known so far,
published by Pojmanski (211.5 kms-1) and obtained from the
analysis of near IR CaII spectral lines.
Assuming the photometrically determined value of
![]() (Hilditch
et al. 1979; Kjurkchieva et al. 2000a)
and using our values for
(Hilditch
et al. 1979; Kjurkchieva et al. 2000a)
and using our values for ![]() and
and ![]() the resulting
values of the mass ratio and masses of the components are
the resulting
values of the mass ratio and masses of the components are
![]() ,
,
![]() and
and
![]() .
.
On the basis of our radial velocity solution and photometrically
obtained fractional radii
![]() and
and
![]() (Paper I),
we determined the absolute star's radii
(Paper I),
we determined the absolute star's radii
![]() and
and
![]() .
It should be noted that the values of
.
It should be noted that the values of ![]() and
and ![]() determined by
different authors lie in the ranges 0.32-0.4 and 0.19-0.25 (Budding
determined by
different authors lie in the ranges 0.32-0.4 and 0.19-0.25 (Budding
![]() Zeilik 1987; Zeilik et al. 1988; Patkos
Zeilik 1987; Zeilik et al. 1988; Patkos ![]() Hempelmann 1994;
Djurasevic 1998; Heckert et al. 1998).
The radii of the components of SV Cam corresponding to their masses calculated
from the mass-radius relation for MS stars are
Hempelmann 1994;
Djurasevic 1998; Heckert et al. 1998).
The radii of the components of SV Cam corresponding to their masses calculated
from the mass-radius relation for MS stars are
![]() and
and
![]() for the primary and secondary, respectively.
This means that the masses and the radii of the two components almost obey
the mass-radius relation for MS stars in spite of their gravity
distortions.
for the primary and secondary, respectively.
This means that the masses and the radii of the two components almost obey
the mass-radius relation for MS stars in spite of their gravity
distortions.
We determined the rotational broadenings of the two profiles of
the investigated lines by measurements of the widths at the continuum
level of the 6th order polynomial fit (Fig. 1).
The mean values of the full width of the broadened profiles
are almost the same for the H![]() and
FeI 6678 lines:
and
FeI 6678 lines:
![]() Å for the primary
profiles and
Å for the primary
profiles and
![]() Å for the secondary
ones. The corresponding equatorial velocities to these rotational
broadenings (
Å for the secondary
ones. The corresponding equatorial velocities to these rotational
broadenings (
![]() )
are
)
are
![]() kms-1 and
kms-1 and
![]() kms-1. For comparison, assuming synchroneous rotation of the
components and the obtained stars' radii the calculated equatorial
velocities of the stars (
kms-1. For comparison, assuming synchroneous rotation of the
components and the obtained stars' radii the calculated equatorial
velocities of the stars (
![]() )
are
)
are
![]() kms-1 and
kms-1 and
![]() kms-1. Hence, in spite of the fact that the spectral lines
are distorted by different
effects their widths agree with the expected rotational broadenings.
kms-1. Hence, in spite of the fact that the spectral lines
are distorted by different
effects their widths agree with the expected rotational broadenings.
The normalized H![]() and FeI 6678 profiles are shown in
Figs. 3-12 together with the corresponding orbital phases.
We established the following pecularities in the phase behavior of
the H
and FeI 6678 profiles are shown in
Figs. 3-12 together with the corresponding orbital phases.
We established the following pecularities in the phase behavior of
the H![]() profile of the primary star:
profile of the primary star:
(1) The profile has a central pseudo-emission bump in the middle of the primary eclipse. We attribute this distortion to the obscuration of the primary star by the cooler secondary that causes masking of a part of the primary's absorption line. The width of the central bump is 3.4 Å and corresponds precisely to the secondary star's radius (see the previous section).
(2) The profile is deeper around the second quadrature than
around the first one. The shape of the H![]() profile is
symmetrical at the second quadrature and distorted at the
first quadrature.
profile is
symmetrical at the second quadrature and distorted at the
first quadrature.
(3) Some emission feature at the end of the left wing of the profile appears at phase range 0.95-0.98 that repeats on two dates (Figs. 3 and 5). One can also note a similar, weaker emission feature almost half orbital cycle later (in the phase range 0.54-0.56) at the end of the right wing. This feature may be due to the emission from circumstellar matter, perhaps ejected from the component(s) whose contribution is most apparent in the spectra around the eclipses. The presence of circumstellar matter in SV Cam was suspected a long time ago on the basis of its optical light curves (Patkos 1982a,b) and the X-ray data (Hempelmann et al. 1997). Another reason for the emission feature can be the increased contribution of the trailing and leading part of the secondary star chromosphere in the corresponding phase ranges.
(4) The profile has a nearly flat core at phases 0.86, 0.105
and 0.79. The first two phases are almost symmetric relative to
the primary eclipse. We found the same behavior in the
H![]() line of the primary star in the short-period RS
CVn-type star RT And (Kjurkchieva et al. 2001).
line of the primary star in the short-period RS
CVn-type star RT And (Kjurkchieva et al. 2001).
(5) The profile is distorted and filled-in in the phase ranges
0.2-0.34 and 0.84-0.91. The distortions of the profile are
variable and seem to be caused by features that moves through the
stellar disk during the above phases (see Figs. 4 and 6). They could
be attributed, at least partially, to the effects of cool spots.
The phases 0.27 and 0.86 of the biggest distortions (flat cores)
of the H![]() profile almost coincide with phases of the
maximum spot visibility determined by modeling of the SV Cam light
curves (Paper I). It should be stressed out that the strong
decrease of the profiles depths at the phase range 0.225-0.295 is
difficult to explain only by spots with a reasonable size.
profile almost coincide with phases of the
maximum spot visibility determined by modeling of the SV Cam light
curves (Paper I). It should be stressed out that the strong
decrease of the profiles depths at the phase range 0.225-0.295 is
difficult to explain only by spots with a reasonable size.
We established the following similarities in the phase behavior of
the FeI 6678 and H![]() profiles of the primary star: (i)
the depth of the FeI 6678 line is also greater around the second
quadrature than around the first one but the difference between
them is smaller for FeI 6678; (ii) there is also an emission
feature at the end of the left wing of the profile at the phases
0.95-0.98; (iii) in the middle of the primary eclipse, the FeI 6678
profile also has a central pseudo-emission bump with the same
width (about 3.4 Å), but its relative height is somewhat
less than in H
profiles of the primary star: (i)
the depth of the FeI 6678 line is also greater around the second
quadrature than around the first one but the difference between
them is smaller for FeI 6678; (ii) there is also an emission
feature at the end of the left wing of the profile at the phases
0.95-0.98; (iii) in the middle of the primary eclipse, the FeI 6678
profile also has a central pseudo-emission bump with the same
width (about 3.4 Å), but its relative height is somewhat
less than in H![]() .
.
We found additional peculiarities of the FeI 6678 profile of the primary star:
(1) Apparent central emission features are visible at phases 0.25,
0.84 and 0.564. The first two of them almost coincide with the
phases of maximum visibility of the two spots on the primary star
reproducing the distortion light curve of SV Cam from 1997 (Paper I). We may calculate the angular size
![]() of the spots
from the equation (Kjurkchieva 1995):
of the spots
from the equation (Kjurkchieva 1995):
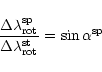 |
(2) |
(2) A strong increase of the depth of the profile is seen at phase 0.98 that repeats on two dates.
Consequently, the phase behavior of the H![]() and FeI 6678
profiles show the presence of two cool spots on the primary star
of SV Cam. The Doppler image of SV Cam obtained by Hempelmann et al. (1997) also shows a distinct spot on the primary star whose
location coincides with the spot found by modeling of the optical
light curve.
and FeI 6678
profiles show the presence of two cool spots on the primary star
of SV Cam. The Doppler image of SV Cam obtained by Hempelmann et al. (1997) also shows a distinct spot on the primary star whose
location coincides with the spot found by modeling of the optical
light curve.
Our observations out of the eclipses show a weak H![]() absorption profile from the secondary star that is deeper around
the second quadrature than around the first one similarly to the
behavior of the H
absorption profile from the secondary star that is deeper around
the second quadrature than around the first one similarly to the
behavior of the H![]() line of the primary star. For
comparison, the H
line of the primary star. For
comparison, the H![]() profiles obtained by Hempelmann et al. (1997) revealed no features that could be attributed to the
secondary star at the out-of-eclipse phases and they determined
the contribution of the secondary star by an analysis of the single
H
profiles obtained by Hempelmann et al. (1997) revealed no features that could be attributed to the
secondary star at the out-of-eclipse phases and they determined
the contribution of the secondary star by an analysis of the single
H![]() profile during both eclipses.
Our observations of the FeI 6678 line outside the eclipses show
also an absorption line from the secondary star. This line is
shallower at quadratures than in the phases around them.
profile during both eclipses.
Our observations of the FeI 6678 line outside the eclipses show
also an absorption line from the secondary star. This line is
shallower at quadratures than in the phases around them.
The central intensities (
![]() )
of the primary's and secondary's
H
)
of the primary's and secondary's
H![]() profiles change during the orbital cycle in the
ranges 0.2-0.38 and 0.02-0.07 while intensities for the
FeI 6678 line vary in the ranges 0.015-0.04 and 0.005-0.01.
profiles change during the orbital cycle in the
ranges 0.2-0.38 and 0.02-0.07 while intensities for the
FeI 6678 line vary in the ranges 0.015-0.04 and 0.005-0.01.
Because we have no observations of standard, non-active stars we
cannot apply the widespread method of substraction of comparison
spectrum from that of the active star (Strassmeier et al. 1990;
Frasca ![]() Catalano 1994; Pojmanski 1998;
Frasca et al. 2000, etc.).
However, in order to obtain some information about the emission
from the stellar components of SV Cam we analyzed the
profiles at the primary eclipse. The line profile in the middle of
this eclipse (adopting
Catalano 1994; Pojmanski 1998;
Frasca et al. 2000, etc.).
However, in order to obtain some information about the emission
from the stellar components of SV Cam we analyzed the
profiles at the primary eclipse. The line profile in the middle of
this eclipse (adopting
![]() )
is described roughly by
the expressions:
)
is described roughly by
the expressions:
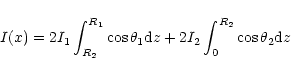 |
(3) |
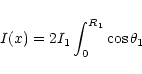 |
(4) |
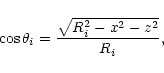 |
(5) |
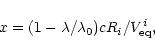 |
(6) |
The expressions (3) and (4) describe the line profile with two-wave or W-like shape, i.e. a line profile with a central bump. The main parameters of this profile are:
(a) width of the bump
![]() ;
;
(b) width of the whole profile
![]() ;
;
(c) depth of the center of the bump
(d) depths of the ends of the bump
| Line | ||||
| H |
0.380 | 0.060 | 0.120 | 0.175 |
| FeI 6678 | 0.085 | 0.012 | 0.034 | 0.048 |
For the H![]() profile the measured and calculated values of
profile the measured and calculated values of
![]() are respectively 0.316 and 0.38,
i.e. the calculated value is about
are respectively 0.316 and 0.38,
i.e. the calculated value is about ![]() bigger than the
observed one. The measured and calculated values of
bigger than the
observed one. The measured and calculated values of ![]() (e)/
(e)/
![]() are respectively 0.46 and 0.55, i.e. the
calculated value is also about
are respectively 0.46 and 0.55, i.e. the
calculated value is also about ![]() bigger than the observed
one. Consequently, the observed bump of the H
bigger than the observed
one. Consequently, the observed bump of the H![]() profile
in the middle of the primary eclipse is higher than one
would expect. We attribute this to the H
profile
in the middle of the primary eclipse is higher than one
would expect. We attribute this to the H![]() emission from
the secondary star.
For the FeI 6678
line, the measured and calculated values of
emission from
the secondary star.
For the FeI 6678
line, the measured and calculated values of
![]() (0) are 0.4 and 0.36, respectively. Therefore, the calculated value
for this parameter is smaller than the measured one. The
measured and calculated values of
(0) are 0.4 and 0.36, respectively. Therefore, the calculated value
for this parameter is smaller than the measured one. The
measured and calculated values of ![]() (e)/
(e)/![]() (0),
0.55 and 0.56, respectively agree very well. Thus the calculated
profile of FeI 6678 in the middle of the primary eclipse is
slightly above the observed one.
In this way, our spectral observations show an enhanced
emission of the secondary star of SV Cam in the
H
(0),
0.55 and 0.56, respectively agree very well. Thus the calculated
profile of FeI 6678 in the middle of the primary eclipse is
slightly above the observed one.
In this way, our spectral observations show an enhanced
emission of the secondary star of SV Cam in the
H![]() line but not in the FeI 6678 line. The result of
our analysis supports the conclusion of Ozeren et al. (2001)
about the H
line but not in the FeI 6678 line. The result of
our analysis supports the conclusion of Ozeren et al. (2001)
about the H![]() emission excess from the secondary star of
SV Cam obtained by spectral substraction technique as well as the more
general conclusion of Frasca
emission excess from the secondary star of
SV Cam obtained by spectral substraction technique as well as the more
general conclusion of Frasca ![]() Catalano (1994) about the H
Catalano (1994) about the H![]() emission in late-type active binaries.
emission in late-type active binaries.
Copyright ESO 2002