A&A 386, 446-455 (2002)
DOI: 10.1051/0004-6361:20020259
Photometric redshifts from evolutionary synthesis with PÉGASE: The code Z-PEG and the z=0 age constraint
D. Le Borgne1 - B. Rocca-Volmerange1,2
1 - Institut d'Astrophysique de Paris, 98bis,
boulevard Arago, 75014 Paris, France
2 -
Institut d'Astrophysique Spatiale, Bât. 121, Université Paris XI,
91405 Orsay, France
Received 19 November 2001 / Accepted 8 February 2002
Abstract
Photometric redshifts are estimated on the basis of
template scenarios with the help of the code Z-PEG, an extension of the
galaxy evolution model PÉGASE.2 and available on
the PÉGASE web site. The spectral energy distribution (SED) templates are
computed for nine spectral types including starburst, irregular,
spiral and elliptical. Dust, extinction and metal effects
are coherently taken into account, depending on evolution scenarios.
The sensitivity of results to adding
near-infrared colors and IGM absorption is analyzed. A comparison
with results of other models without evolution measures the evolution factor which
systematically increases the estimated photometric redshift values by
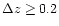 for z > 1.5. Moreover we systematically check that
the evolution scenarios match observational standard templates
of nearby galaxies, implying an age constraint of the stellar
population at z=0 for each type. The respect of this
constraint makes it possible to significantly improve the accuracy of photometric
redshifts by decreasing the well-known degeneracy problem. The
method is applied to the HDF-N sample (see in Fernández-Soto et al.
1999). From fits on SED templates by a
for z > 1.5. Moreover we systematically check that
the evolution scenarios match observational standard templates
of nearby galaxies, implying an age constraint of the stellar
population at z=0 for each type. The respect of this
constraint makes it possible to significantly improve the accuracy of photometric
redshifts by decreasing the well-known degeneracy problem. The
method is applied to the HDF-N sample (see in Fernández-Soto et al.
1999). From fits on SED templates by a  -minimization procedure, not
only is the photometric redshift derived but also the corresponding
spectral type and the formation redshift
-minimization procedure, not
only is the photometric redshift derived but also the corresponding
spectral type and the formation redshift
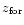 when stars first formed.
Early epochs
of galaxy formation
when stars first formed.
Early epochs
of galaxy formation
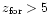 are found from this new method and results
are compared to faint galaxy count interpretations. The new tool is
available at: http://www.iap.fr/pegase
are found from this new method and results
are compared to faint galaxy count interpretations. The new tool is
available at: http://www.iap.fr/pegase
Key words: galaxies:
distances and redshifts, evolution - methods: data analysis -
techniques: photometric
The determination of galaxy distances is so crucial for clues on
galaxy evolution and cosmic structures that a large variety of methods
is currently being explored. Spectroscopic determinations are the most
precise but they consume excessive observing time for deeper and deeper
large galaxy samples. For instance, the redshift surveys
such as CFRS (Le Fèvre 1995), 2dF (Folkes et al. 1999), Hawaii (Cowie et al. 1994) and more
recently the SLOAN, with millions of targets with various spectral types,
are complete to
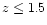 .
At higher redshifts z > 1.5, the
galaxy populations observed at faint magnitudes in deep surveys cover
a large range of redshifts which will be easily accessible from
photometry. However many problems of degeneracy, number and
width of filters and extinction first have to be clarified.
Typical SED
features like the 4000 Å discontinuity or the Lyman break are known to
be fruitful signatures for evaluation of redshifts when compared with
template SEDs. Steidel et al. (1999) proposed an empirical method based on
these discontinuities to detect
.
At higher redshifts z > 1.5, the
galaxy populations observed at faint magnitudes in deep surveys cover
a large range of redshifts which will be easily accessible from
photometry. However many problems of degeneracy, number and
width of filters and extinction first have to be clarified.
Typical SED
features like the 4000 Å discontinuity or the Lyman break are known to
be fruitful signatures for evaluation of redshifts when compared with
template SEDs. Steidel et al. (1999) proposed an empirical method based on
these discontinuities to detect 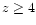 galaxies. Successful in
discovering distant sources, the method is however imprecise and
prone to degeneracies. The comparison of observed SEDs with calibrated
templates on an extended wavelength range is the best way to rapidly
determine redshifts of a large number of faint galaxies, on a
continuous range
galaxies. Successful in
discovering distant sources, the method is however imprecise and
prone to degeneracies. The comparison of observed SEDs with calibrated
templates on an extended wavelength range is the best way to rapidly
determine redshifts of a large number of faint galaxies, on a
continuous range
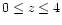 . Such comparisons were proposed
with templates from no-evolution models by Baum (1962), Koo (1985),
Loh & Spillar (1986) and more recently Fernández-Soto et al. (1999) (hereafter
FSLY); others proposed evolutionary SED methods such as Bolzonella et al. (2000) and
Massarotti et al. (2001a) using templates derived from a variety of evolutionary
codes. However the evolutionary codes and their applications may
differ. If results are roughly similar at low redshifts
(see Leitherer et al. 1996), they may actually strongly differ from each other at
high redshifts, depending on adopted star formation laws and the
corresponding age constraints, initial mass function, dust and metal
effects as well as interpolation algorithms.
. Such comparisons were proposed
with templates from no-evolution models by Baum (1962), Koo (1985),
Loh & Spillar (1986) and more recently Fernández-Soto et al. (1999) (hereafter
FSLY); others proposed evolutionary SED methods such as Bolzonella et al. (2000) and
Massarotti et al. (2001a) using templates derived from a variety of evolutionary
codes. However the evolutionary codes and their applications may
differ. If results are roughly similar at low redshifts
(see Leitherer et al. 1996), they may actually strongly differ from each other at
high redshifts, depending on adopted star formation laws and the
corresponding age constraints, initial mass function, dust and metal
effects as well as interpolation algorithms.
An essential property of most codes is the large wavelength coverage
from the far-UV to the near-infrared needed to compute SEDs that are highly
redshifted. Moreover our code PÉGASE.2, Fioc & Rocca-Volmerange (1997), in
its current version (see next footnote) is able to take into
account metallicity effects in its stellar library and isochrones.
Evolution scenarios of nine spectral types, defined by star formation
parameters, have been selected to reproduce the observed statistical
SEDs of z=0 galaxy templates, Fioc & Rocca-Volmerange (1999b). Then two correction
factors (cosmological k-correction and evolutionary e-correction) are
computed with the model to predict redshifted SEDs, in order to be used as
comparison templates to observations. Other PEGASE.2 scenarios based on
different prescriptions of dust properties or star formation parameters might be
computed and used as templates only if they respect fits of
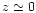 galaxy properties. This is beyond the objectives of this paper.
Another method of photometric
redshift determination supposes that the evolution effect is dominated by
shot noise, Connolly et al. (1995).
galaxy properties. This is beyond the objectives of this paper.
Another method of photometric
redshift determination supposes that the evolution effect is dominated by
shot noise, Connolly et al. (1995).
We present in Sect. 2 a new tool, Z-PEG, to estimate
photometric redshifts on a continuous redshift range
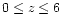 or more. Observed colors or spectra are statistically compared to
the PÉGASE.2 atlas for 9 spectral types (starburst: SB, irregular:
Im, spiral: Sd, Sc, Sbc, Sb, Sa, SO and elliptical: E galaxies).
Section 3 presents the results for the well-known Hubble Deep Field North
and the comparison with spectroscopic redshifts allows us to derive average
values of evolution factors. Section 4 shows the sensitivity to various
parameters such as the NIR colors and IGM absorption. Interesting
consequences for the redshifts of formation of the sample are
derived in Sect. 5. Discussion and conclusions are proposed
in Sects. 6 and 7 respectively.
or more. Observed colors or spectra are statistically compared to
the PÉGASE.2 atlas for 9 spectral types (starburst: SB, irregular:
Im, spiral: Sd, Sc, Sbc, Sb, Sa, SO and elliptical: E galaxies).
Section 3 presents the results for the well-known Hubble Deep Field North
and the comparison with spectroscopic redshifts allows us to derive average
values of evolution factors. Section 4 shows the sensitivity to various
parameters such as the NIR colors and IGM absorption. Interesting
consequences for the redshifts of formation of the sample are
derived in Sect. 5. Discussion and conclusions are proposed
in Sects. 6 and 7 respectively.
The atlas of synthetic galaxies used as templates is computed with
PÉGASE.2 on the basis of evolution scenarios of star formation. The
synthesis method assumes that distant galaxies are similar to nearby
galaxies, but look younger at high z since they are seen at
more remote epochs. Respecting this constraint will make our
redshift determinations more robust. In an earlier paper (Fioc & Rocca-Volmerange 1997), we
investigated the selection of star formation rates able to reproduce
the multi spectral stellar energy distributions of nearby
galaxies. Another article by Fioc & Rocca-Volmerange (1999b) computed the
statistical SEDs of about 800 nearby galaxies observed from the
optical and the near-infrared for eight spectral types of galaxies
and used to fit scenarios at z=0. Star formation rates (SFRs) are
proportional to the gas density (with one exception, see Table
1), the astration rate 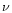 increasing from
irregular Im to elliptical E galaxies. The
star formation rate of starburst SB scenario is instantaneous. Infall
and galactic winds are typical gaseous exchanges with the
interstellar medium. They aim to simulate the mass
growth and to subtract the gas fraction
(preventing any further star formation) respectively.
Unlike other studies (Fernández-Soto et al. 2001a; Massarotti et al. 2001b), our scenarios
do not need to add any starburst component to be consistent with
increasing from
irregular Im to elliptical E galaxies. The
star formation rate of starburst SB scenario is instantaneous. Infall
and galactic winds are typical gaseous exchanges with the
interstellar medium. They aim to simulate the mass
growth and to subtract the gas fraction
(preventing any further star formation) respectively.
Unlike other studies (Fernández-Soto et al. 2001a; Massarotti et al. 2001b), our scenarios
do not need to add any starburst component to be consistent with
 observations.
observations.
Table 1:
PEGASE.2 scenarios used as template parameters. SFR=
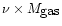 ,
except for starbursts and irregular galaxies.
,
except for starbursts and irregular galaxies. 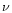 is in units of
Gyr-1 and M
gasis the gas density. Infall time-scales are in Myrs.
The dust distribution is fitted on a King profile for E and S0,
while an inclinaison-averaged disk distribution is applied to spiral and irregular galaxies
(see text for details).
Starburst galaxies have no extinction correction. For all the scenarios, the age of the universe is an upper limit on the age.
is in units of
Gyr-1 and M
gasis the gas density. Infall time-scales are in Myrs.
The dust distribution is fitted on a King profile for E and S0,
while an inclinaison-averaged disk distribution is applied to spiral and irregular galaxies
(see text for details).
Starburst galaxies have no extinction correction. For all the scenarios, the age of the universe is an upper limit on the age.
| Type |
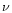 |
infall |
gal. winds |
age at z=0 |
| SB |
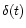 |
|
|
1 Myr to 2 Gyr |
| E |
3.33 |
300 |
1 Gyr |
>13 Gyr |
| S0 |
2 |
100 |
5 Gyr |
>13 Gyr |
| Sa |
0.71 |
2800 |
|
>13 Gyr |
| Sb |
0.4 |
3500 |
|
>13 Gyr |
| Sbc |
0.175 |
6000 |
|
>13 Gyr |
| Sc |
0.1 |
8000 |
|
>13 Gyr |
| Sd |
0.07 |
8000 |
|
>13 Gyr |
| Im |
0.065a |
8000 |
|
>9 Gyr |
a For this scenario only, we have
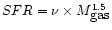
.
The initial mass function (IMF) (Rana & Basu 1992), is used in our evolution
scenarios. However Giallongo et al. (1998) showed that the choice of the IMF
does not influence much the photometric redshift estimates of high-z
candidates (z>2.5).
PÉGASE.2 is the most
recent version of PÉGASE, available by ftp and on a web
site![[*]](/icons/foot_motif.gif) .
Non-solar metallicities are implemented in stellar tracks and spectra
but also a far-UV spectral library for
hot stars (Clegg & Middlemass 1987) complements the Lejeune et al. (1997, 1998)
library. The metal enrichment is followed through
the successive generations of stars and is taken into account for spectra
of the stellar library as well as for isochrones.
In PÉGASE.2, a consistent treatment of the
internal extinction is proposed by fitting the dust amount
on metal abundances. The extinction factor depends on the
respective spatial distribution of dust and stars as well as on its
composition. Two patterns are modeled with either the geometry of bulges
for elliptical galaxies or disks for spiral galaxies. In elliptical galaxies, the
dust distribution follows a King's profile. The density of dust is described
as a power of the density of stars (see Fioc & Rocca-Volmerange 1997 for details). Through
such a geometry, light scattering by dust is computed using a transfer
model, outputs of which are tabulated in one input-data file of the model
PÉGASE. For spirals and irregulars, dust is distributed along a
uniform plane-parallel slab and mixed with gas. As a direct consequence,
the synthetic templates used to
determine photometric redshifts at any z, as well as to fit the
observational standards at z=0, are systematically reddened.
We also add the IGM
absorption following Madau (1995) on the hypothesis of
Ly
.
Non-solar metallicities are implemented in stellar tracks and spectra
but also a far-UV spectral library for
hot stars (Clegg & Middlemass 1987) complements the Lejeune et al. (1997, 1998)
library. The metal enrichment is followed through
the successive generations of stars and is taken into account for spectra
of the stellar library as well as for isochrones.
In PÉGASE.2, a consistent treatment of the
internal extinction is proposed by fitting the dust amount
on metal abundances. The extinction factor depends on the
respective spatial distribution of dust and stars as well as on its
composition. Two patterns are modeled with either the geometry of bulges
for elliptical galaxies or disks for spiral galaxies. In elliptical galaxies, the
dust distribution follows a King's profile. The density of dust is described
as a power of the density of stars (see Fioc & Rocca-Volmerange 1997 for details). Through
such a geometry, light scattering by dust is computed using a transfer
model, outputs of which are tabulated in one input-data file of the model
PÉGASE. For spirals and irregulars, dust is distributed along a
uniform plane-parallel slab and mixed with gas. As a direct consequence,
the synthetic templates used to
determine photometric redshifts at any z, as well as to fit the
observational standards at z=0, are systematically reddened.
We also add the IGM
absorption following Madau (1995) on the hypothesis of
Ly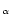 ,
Ly
,
Ly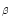 ,
Ly
,
Ly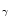 and Ly
and Ly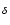 line
blanketing induced by Hi clouds,
Poisson-distributed along the line of sight.
This line blanketing can be expressed for each order of the Lyman series by
an effective optical depth
line
blanketing induced by Hi clouds,
Poisson-distributed along the line of sight.
This line blanketing can be expressed for each order of the Lyman series by
an effective optical depth
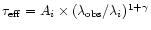 ,
with
,
with
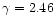 and
and
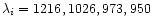 Å for Ly
Å for Ly ,
Ly
,
Ly ,
Ly
,
Ly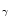 and Ly
and Ly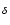 respectively.
The values of Ai are taken from Madau et al. (1996), in agreement
with the Press et al. (1993) analysis on a sample of 29 quasars at z>3.
We shall see below that the IGM absorption alters the visible and
IR colors more than about 0.1 mag as soon as z >2, leading to
a more accurate determination of photometric redshifts at these
distances.
respectively.
The values of Ai are taken from Madau et al. (1996), in agreement
with the Press et al. (1993) analysis on a sample of 29 quasars at z>3.
We shall see below that the IGM absorption alters the visible and
IR colors more than about 0.1 mag as soon as z >2, leading to
a more accurate determination of photometric redshifts at these
distances.
For each spectral
type, a typical age of the stellar population is derived. Time
scales, characteristics and ages of the scenarios are listed in Table
1.
2.2 The  minimization procedure
minimization procedure
A 3D-subspace of parameters (age, redshift, type) is defined by the
template sets. It is used to automatically fit observational data. This
subspace in the age-redshift plane is limited by the cosmology in
order to avoid inconsistencies: a 10 Gyr old galaxy at z=2 cannot
exist in the standard cosmology![[*]](/icons/foot_motif.gif) because at this
redshift, the age of the universe is about 5 Gyr. Moreover the subspace
is also
limited by the age (redshift corrected) imposed by the adopted
scenario of spectral type evolution. As an example, if elliptical and
spiral galaxies must be at least 13 Gyr old at z=0, it means at
least 5 Gyr at z=1 and so on.
because at this
redshift, the age of the universe is about 5 Gyr. Moreover the subspace
is also
limited by the age (redshift corrected) imposed by the adopted
scenario of spectral type evolution. As an example, if elliptical and
spiral galaxies must be at least 13 Gyr old at z=0, it means at
least 5 Gyr at z=1 and so on.
Each point is granted a synthetic
spectrum; its flux through the filter i is called
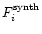 .
For each point of this 3D-subspace, the
fourth parameter
.
For each point of this 3D-subspace, the
fourth parameter 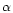 is computed with a
is computed with a  minimization to
fit as well as possible the observed fluxes in filters:
minimization to
fit as well as possible the observed fluxes in filters:
![\begin{displaymath}\chi^2= \sum_{i=1}^{\it N}\left[\frac{F^{\rm obs}_i-\alpha \times F^{\rm synth}_i}{\sigma_i}\right]^2\cdot
\end{displaymath}](/articles/aa/full/2002/17/aa2109/img44.gif) |
(1) |
N is the number of filters,
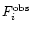 and
and 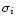 are
the observed flux and its error bar through the filter
i respectively. In the case of an observed spectrum without redshift signatures, the sum can also be computed from wavelength bins.
Then, each point of the 3D-subspace of parameters has a
are
the observed flux and its error bar through the filter
i respectively. In the case of an observed spectrum without redshift signatures, the sum can also be computed from wavelength bins.
Then, each point of the 3D-subspace of parameters has a  value. A projection of this 3D-
value. A projection of this 3D- array on the redshift
dimension gives the photometric redshift value
array on the redshift
dimension gives the photometric redshift value
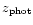 .
.
The values of
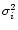 can be evaluated by the quadratic sum
of the systematic errors and of the statistical errors. The extremely low
values of observational errors, adopted as statistical, may result in
anomalously high reduced
can be evaluated by the quadratic sum
of the systematic errors and of the statistical errors. The extremely low
values of observational errors, adopted as statistical, may result in
anomalously high reduced  minima.
In this study we consider as negligible systematic errors,
keeping in mind that it maximizes the
minima.
In this study we consider as negligible systematic errors,
keeping in mind that it maximizes the  minimum value
(possibly up to 100).
In such a case, statistical rules
claim that the result (the photometric redshift) is not reliable and
has to be excluded. Yet, with such prescriptions, most of the results
would be excluded, because the photometric errors of the
observations are very low. This is why all the primary
solutions are often kept, including cases of very high reduced
minimum value
(possibly up to 100).
In such a case, statistical rules
claim that the result (the photometric redshift) is not reliable and
has to be excluded. Yet, with such prescriptions, most of the results
would be excluded, because the photometric errors of the
observations are very low. This is why all the primary
solutions are often kept, including cases of very high reduced  minima. In
the following, we will also adopt this philosophy. However, our error bars
might appear larger than in the previous studies, that limit
their results to one unique but less robust solution. Indeed,
the estimation of the error bar of a photometric redshift is often
estimated by the redshifts for which
minima. In
the following, we will also adopt this philosophy. However, our error bars
might appear larger than in the previous studies, that limit
their results to one unique but less robust solution. Indeed,
the estimation of the error bar of a photometric redshift is often
estimated by the redshifts for which
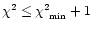 .
This method is only valid when the minimum reduced
.
This method is only valid when the minimum reduced
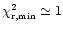 (otherwise the error bar is
very underestimated).
(otherwise the error bar is
very underestimated).
We choose to estimate the error bar by the
redshift values for which
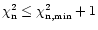 ,
where
,
where
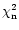 is the
is the  "normalized'' with
"normalized'' with
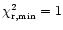 . The error bar is then much larger
and may lead to secondary solutions. Fernández-Soto et al. (2001b) use another accurate estimation
of the error bars which also gives secondary solutions, for the
. The error bar is then much larger
and may lead to secondary solutions. Fernández-Soto et al. (2001b) use another accurate estimation
of the error bars which also gives secondary solutions, for the
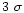 level for instance. This is the case when the Lyman and Balmer breaks are hardly
distinguished, as an example.
level for instance. This is the case when the Lyman and Balmer breaks are hardly
distinguished, as an example.
Z-PEG is an interface available on the PÉGASE web site (see footnote on page 2).
Inputs are fluxes or colors of the observed galaxies and their error bars. Sets
of classical
filters defined in a variety of photometric systems are proposed. It is
possible to use a user-defined filter, with its passband and
calibration. In the general case, for which no information on
the galaxy spectral type is a priori known, the minimization
procedure is tested on all the template types. It is also possible to
restrain the template galaxies to a given type. Types are then chosen among the
9 pre-computed synthetic spectra. The default redshift sampling is
0.25 and may be reduced on a narrower redshift range. The age and
redshift axes are respectively defined
by step, lower and upper limits.
The user will choose the cosmological parameters (H0, 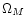 ,
,
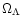 ), on which the time-redshift relation depends. The
default values of cosmological parameters are those adopted in this
article.
), on which the time-redshift relation depends. The
default values of cosmological parameters are those adopted in this
article.
Outputs are the estimated photometric redshift
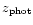 and its
error bar, the age and the spectral type of the best fitted synthetic galaxy.
A
and its
error bar, the age and the spectral type of the best fitted synthetic galaxy.
A  projection map in the age-redshift plane and
its projection on the redshift and age axes (see Fig. 1) are also presented.
projection map in the age-redshift plane and
its projection on the redshift and age axes (see Fig. 1) are also presented.
The relevance of the fit procedure is checked on a synthetic galaxy of the atlas
with a known z.
As an example, input data are the colors computed from the SED of the Sbc galaxy
at age 5 Gyr and redshift z=0.989. The output value is,
as expected, z=0.99, identical to the input galaxy redshift (z=0.989)
with a precision of
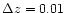 (no photometric error).
Figure 1 shows the resulting projected
(no photometric error).
Figure 1 shows the resulting projected  map on the
age vs redshift plane for this test.
map on the
age vs redshift plane for this test.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2109f1.eps}\vspace*{1mm}
\includegraphics[width=8.8cm,clip]{MS2109f2.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg58.gif) |
Figure 1:
The test of coherency on the z=0.989 and 5 Gyr old galaxy:
darker grey zones correspond to lower  values in the age - z plane.
The minimum
values in the age - z plane.
The minimum  location is the cross center of the two solid lines.
The plot log
location is the cross center of the two solid lines.
The plot log
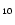 ( ( )
versus redshift estimates the accuracy of the minimum
and shows possible secondary minima. )
versus redshift estimates the accuracy of the minimum
and shows possible secondary minima. |
| Open with DEXTER |
The Hubble Deep Field North (HDF-N) catalog (Williams et al. 1996)
was chosen to test the evolution factor. Spectroscopic redshifts
were measured carefully by Cohen et al. (2000), with some additions and
corrections in Cohen (2001). FSLY give photometric
data for the HDF-N objects and Fernández-Soto et al. (2001a) give a
correspondence between their objects and the objects in Cohen et al. (2000).
We exclude from the sample galaxies with negative fluxes.
The remaining selected sub-sample contains 136 galaxies
with redshifts distributed from 0 to 5.6.
The HDF-N sample presents a series of advantages
to explore the accuracy of our method and to compare it
to others. With a large redshift range
(
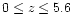 ), the sample data acquired with
the WFPC2/HST camera is one
of the deepest (down to B=29) with an extent
over the wavelength range from about 3000 Å to 8000 Å
with the filters F300W, F450W, F606W, and F814W (hereafter called
U, B, V, I).
Moreover the near-infrared standard Johnson-Cousins J, H and
), the sample data acquired with
the WFPC2/HST camera is one
of the deepest (down to B=29) with an extent
over the wavelength range from about 3000 Å to 8000 Å
with the filters F300W, F450W, F606W, and F814W (hereafter called
U, B, V, I).
Moreover the near-infrared standard Johnson-Cousins J, H and 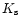 (hereafter K)
colors listed in FSLY from Dickinson (1998) were observed at the KPNO/4 m telescope.
The calibration used is AB magnitudes.
(hereafter K)
colors listed in FSLY from Dickinson (1998) were observed at the KPNO/4 m telescope.
The calibration used is AB magnitudes.
with 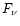 in ergs-1cm
in ergs-1cm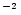 Hz-1.
Hz-1.
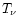 is the transmission of the filter.
is the transmission of the filter.
A further advantage is the benefit of spectroscopic redshifts of the
selected sub-sample,
as given by Cohen (2001). This allows a statistical comparison with our
photometric redshifts and an estimation of the dispersion.
Another advantage of this sample is the possibility
of measuring the type-dependent evolution factor
by comparing our results with
the FSLY's results, since the latter authors propose photometric redshift
determinations based on a maximum
likelihood analysis and 4 spectral types without any evolution effect.
Figure 2 presents the plane
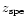 -
-
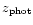 resulting
from our fit of the HDF-N sample with PÉGASE templates.
resulting
from our fit of the HDF-N sample with PÉGASE templates.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f3.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg66.gif) |
Figure 2:
Comparison of photometric redshifts (points with error bars)
predicted by the model Z-PEG.1 to
spectroscopic redshifts of the selected HDF-N sample. The solid line of slope = 1 shows
the case of equality
for comparison. The dotted line is the linear regression of our photometric redshifts
if we exclude the points with
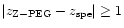 .
Predictions are computed
with IGM absorption from Madau et al. (1996) and ISM
reddening according to PÉGASE algorithms.
When two solutions or more are found (degeneracy), the error bars
are linked by a dotted line. The squares are objects with discordant
redshifts also pointed out by Fernández-Soto et al. (2001a). .
Predictions are computed
with IGM absorption from Madau et al. (1996) and ISM
reddening according to PÉGASE algorithms.
When two solutions or more are found (degeneracy), the error bars
are linked by a dotted line. The squares are objects with discordant
redshifts also pointed out by Fernández-Soto et al. (2001a). |
| Open with DEXTER |
We compare our best results
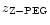 ,
from the evolutionary model Z-PEG.1 (selected from the variety
of models in Table 2) to photometric redshifts
,
from the evolutionary model Z-PEG.1 (selected from the variety
of models in Table 2) to photometric redshifts
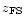 estimated
by FSLY. These authors only took into account
k-corrections of the galaxy spectral distributions from Coleman et al. (1980) while
we simultaneously compute the k- and e- correction factors at any z.
Figure 3 shows the difference for each galaxy of the sample.
Lines trace the median values of the difference of
estimated
by FSLY. These authors only took into account
k-corrections of the galaxy spectral distributions from Coleman et al. (1980) while
we simultaneously compute the k- and e- correction factors at any z.
Figure 3 shows the difference for each galaxy of the sample.
Lines trace the median values of the difference of
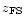 with
Z-PEG.1, and
with
Z-PEG.1, and
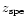 values respectively. The zero value
(difference to
values respectively. The zero value
(difference to
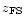 )
is plotted for comparison.
A systematic effect is observed for
)
is plotted for comparison.
A systematic effect is observed for
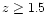 .
The evolution effect is
measured around
.
The evolution effect is
measured around
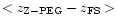 = 0.2, independent of type.
The median
= 0.2, independent of type.
The median![[*]](/icons/foot_motif.gif) value
value
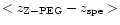 = - 0. 03is measured and remains inside the error bars.
Evolution effects are more important for
distant galaxies and an appropriate evolutionary code is required for such estimates.
= - 0. 03is measured and remains inside the error bars.
Evolution effects are more important for
distant galaxies and an appropriate evolutionary code is required for such estimates.
![\begin{figure}
\par\includegraphics[clip,width=8.3cm,clip]{MS2109f4.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg73.gif) |
Figure 3:
Crosses are differences
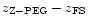 .
For .
For
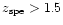 ,
the evolution factor is measured by the distance between the
dotted and full lines,
respectively the median value ,
the evolution factor is measured by the distance between the
dotted and full lines,
respectively the median value
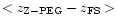 and 0. and 0.
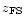 are the FSLY's
determinations. The dashed line is the median value
are the FSLY's
determinations. The dashed line is the median value
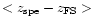 .
For .
For
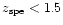 ,
the evolution factor has the same magnitude as the error bars. ,
the evolution factor has the same magnitude as the error bars. |
| Open with DEXTER |
Our best fit gives a minimal  for a triplet (age, redshift, type),
so that we can deduce the spectral type of the observed galaxies by comparing to the
SEDs of 9 different types.
The comparison of types derived by Z-PEG.1 and by FSLY is
shown in Fig. 4. In most cases, "earlier type'' galaxies
are found with Z-PEG.1, particularly
at high redshifts. This effect is expected from evolution scenarios
because, when considering only the k-correction, FSLY would
find an evolved spiral galaxy when Z-PEG.1 finds a
young elliptical galaxy. A better definition of
the morphological properties of galaxies in the near future will help us to
arrive at a conclusion.
for a triplet (age, redshift, type),
so that we can deduce the spectral type of the observed galaxies by comparing to the
SEDs of 9 different types.
The comparison of types derived by Z-PEG.1 and by FSLY is
shown in Fig. 4. In most cases, "earlier type'' galaxies
are found with Z-PEG.1, particularly
at high redshifts. This effect is expected from evolution scenarios
because, when considering only the k-correction, FSLY would
find an evolved spiral galaxy when Z-PEG.1 finds a
young elliptical galaxy. A better definition of
the morphological properties of galaxies in the near future will help us to
arrive at a conclusion.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f5.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg75.gif) |
Figure 4:
Comparison of our spectral type estimates to FSLY's. The values are
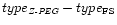 assuming the following values for the spectral types (type 0: starburst,
1: elliptical, 2: S0, 3: Sa, 4: Sb, 5: Sbc, 6: Sc, 7: Sd, 8: Im).
assuming the following values for the spectral types (type 0: starburst,
1: elliptical, 2: S0, 3: Sa, 4: Sb, 5: Sbc, 6: Sc, 7: Sd, 8: Im). |
| Open with DEXTER |
4 Sensitivity to parameters
Table 2 summarizes the comparison
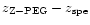 and the corresponding dispersion, given by a series of various Z-PEG models
computed by changing only one parameter. The considered parameters are age, absorption
by the IGM and the addition of NIR colors (JHK).
We evaluate the offset and the dispersion of the
and the corresponding dispersion, given by a series of various Z-PEG models
computed by changing only one parameter. The considered parameters are age, absorption
by the IGM and the addition of NIR colors (JHK).
We evaluate the offset and the dispersion of the
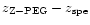 distribution with
distribution with
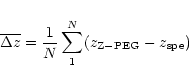 |
(2) |
![\begin{displaymath}\sigma^2_z=\frac{1}{N-1} \sum _1^N \left[ (z_{{\rm Z-PEG}}-z_{{\rm spe}})-\overline{\Delta z}~\right]^2
\end{displaymath}](/articles/aa/full/2002/17/aa2109/img84.gif) |
(3) |
where N is the number of solutions. Most teams only limit their
results and corresponding error bars to primary solutions for
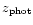 .
In such cases, N is the number of galaxies in the sample.
Yet, as the uncertainties on
.
In such cases, N is the number of galaxies in the sample.
Yet, as the uncertainties on
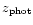 are often underestimated (see Sect. 2.2),
we choose to use
are often underestimated (see Sect. 2.2),
we choose to use
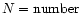 of primary solutions + number of secondary solutions.
Thus, the estimation of the dispersion is made with more points than the number of galaxies.
As a consequence, the value of the dispersion differs from the dispersion computed using
only primary solutions: the latter value might, by chance, be sometimes smaller.
This is the case when the number of galaxies for which the primary solution
is in agreement with the real redshift, dominates.
of primary solutions + number of secondary solutions.
Thus, the estimation of the dispersion is made with more points than the number of galaxies.
As a consequence, the value of the dispersion differs from the dispersion computed using
only primary solutions: the latter value might, by chance, be sometimes smaller.
This is the case when the number of galaxies for which the primary solution
is in agreement with the real redshift, dominates.
The basic procedure of the spectral synthesis of distant galaxies
requires one to respect the observed SEDs of standard nearby galaxies.
The correction factors (k-correction for expansion and e-correction for
evolution) are computed from the z=0 templates, fitting at best
observational data.
As a consequence, a z=0 age of the
stellar population is imposed by the synthetic SED template.
When the so-called z=0 age constraint is
taken into account, the dispersion
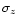 is reduced by 15% for z<1.5 (
is reduced by 15% for z<1.5 (
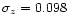 with model Z-PEG.1, Fig. 2,
compared to
with model Z-PEG.1, Fig. 2,
compared to
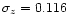 with model Z-PEG.2, Fig. 5).
For 0<z<5, the improvement factor is 8%.
As discussed above, computations with evolution require the age
constraint in order to make synthetic redshifted templates compatible
with z=0 observed templates. As discussed below, a similar constraint is used
in the interpretation models of faint galaxy counts
(see Fioc & Rocca-Volmerange 1999a). The remark is all the more important as
most photometric redshift models, even with evolution corrections, compute redshifts
without the age constraint, finding fits with synthetic templates
sometimes unable to reproduce z=0 galaxies.
Yet, we demonstrate here that our strong age constraint and the use of
appropriate scenarios of evolution give better results than the often-used
"no age constraint'' method.
with model Z-PEG.2, Fig. 5).
For 0<z<5, the improvement factor is 8%.
As discussed above, computations with evolution require the age
constraint in order to make synthetic redshifted templates compatible
with z=0 observed templates. As discussed below, a similar constraint is used
in the interpretation models of faint galaxy counts
(see Fioc & Rocca-Volmerange 1999a). The remark is all the more important as
most photometric redshift models, even with evolution corrections, compute redshifts
without the age constraint, finding fits with synthetic templates
sometimes unable to reproduce z=0 galaxies.
Yet, we demonstrate here that our strong age constraint and the use of
appropriate scenarios of evolution give better results than the often-used
"no age constraint'' method.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f6.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg88.gif) |
Figure 5:
Photometric redshift estimations like in Fig. 2
when our computations are free of any age constraint (model Z-PEG.2).
The dotted diagonal line is the linear regression of points
with
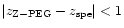 .
The dashed line
is the linear regression without the IGM absorption (model Z-PEG.3). .
The dashed line
is the linear regression without the IGM absorption (model Z-PEG.3). |
| Open with DEXTER |
Moreover, not constraining the z=0 ages of galaxies (models Z-PEG.2 and beyond)
increases the age-redshift-type degeneracy (see Fig. 6,
left hand side): at a given redshift, a young (<1 Gyr) elliptical
galaxy would be an acceptable
solution, with almost the same optical colors as an old irregular one.
But using the model Z-PEG.1
that takes care of ages, we restrain the acceptable range
in the age-redshift-type space and raise partially a degeneracy.
Figure 6 clearly shows this effect on galaxy number 319 of
the FSLY sample.
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{MS2109f7.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg89.gif) |
Figure 6:
Fit of galaxy 319 (number from FSLY).
On the left hand side, the fit is made with model Z-PEG.2
(without age constraint) and on the right hand side we use model Z-PEG.1
(with age constraint): a) observed colors with ten times magnified error bars (for plotting only) and best-fitting synthetic SED,
b)  map on the age-z plane (black corresponds to low
map on the age-z plane (black corresponds to low  ),
c) ),
c)  projection on the age axis, d)
projection on the age axis, d)  projection on the redshift axis,
and e) Type maps on the age-z plane; the age-z solutions found in b) are also plotted.
The model Z-PEG.2 (left) shows several minimum redshifts around 1 whereas model
Z-PEG.1 (right) only shows one minimum close to the spectroscopic redshift
(
zspe=0.961).
projection on the redshift axis,
and e) Type maps on the age-z plane; the age-z solutions found in b) are also plotted.
The model Z-PEG.2 (left) shows several minimum redshifts around 1 whereas model
Z-PEG.1 (right) only shows one minimum close to the spectroscopic redshift
(
zspe=0.961). |
| Open with DEXTER |
Since the strong discontinuities (4000 Å, Lyman break) are the most
constraining features for redshift determinations, several consequences
are implied (see also discussions in Bolzonella et al. 2000 and Massarotti et al. 2001a).
The observations of colors in the near infrared is the only way to follow
the discontinuities at the highest redshifts (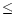 4.5 for the 4000 Å discontinuity
and
4.5 for the 4000 Å discontinuity
and 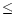 23 for the Lyman break in the K band). Moreover SED continua also contribute
to the best fits, so that in most cases, minimizing the
23 for the Lyman break in the K band). Moreover SED continua also contribute
to the best fits, so that in most cases, minimizing the  on the largest
wavelength coverage will decrease the degeneracy. Figure 7
and Table 2 show that without J, H and K bands, the photometric
redshift determination is poor (
on the largest
wavelength coverage will decrease the degeneracy. Figure 7
and Table 2 show that without J, H and K bands, the photometric
redshift determination is poor (
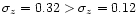 for
for
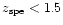 ).
Moreover, we do not use any filter between 8500 and
).
Moreover, we do not use any filter between 8500 and 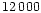 Å to fit the data,
because on the one hand we do not have the corresponding observations and on the other hand
only very few galaxies in our sample are at 1<z<2.
To analyze galaxies in the redshift range 1<z<2 , a Z filter
(or equivalent) would be necessary for observations as well as modeling.
Å to fit the data,
because on the one hand we do not have the corresponding observations and on the other hand
only very few galaxies in our sample are at 1<z<2.
To analyze galaxies in the redshift range 1<z<2 , a Z filter
(or equivalent) would be necessary for observations as well as modeling.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f8.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg93.gif) |
Figure 7:
Comparison of the photometric redshifts from Z-PEG (model Z-PEG.4) with the HDF-N measured spectroscopic redshifts without J, H, K bands, and without any particular age constraint. These results have to be compared to Fig. 5 for which there is no age constraint either. The dotted line is the linear regression of our photometric redshifts
if we exclude the points with
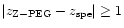 . . |
| Open with DEXTER |
When comparing results with and without IGM absorption (Fig. 5),
an important deviation to the spectroscopic redshifts is observed
at high redshifts if we do not take the IGM into account: a linear regression
on fits without the IGM shows a systematic deviation towards high photometric redshifts. This was already noted by
Massarotti et al. (2001a, 2001b), and can be understood quite easily:
not including IGM absorption in models, one can mistake the Lyman forest
absorption by intergalactic Hi (below
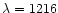 Å) for
the real Lyman break (
Å) for
the real Lyman break (
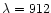 Å in the rest frame).
In such a case, we overestimate the redshift.
Å in the rest frame).
In such a case, we overestimate the redshift.
Given the photometric redshift and age found with Z-PEG for any observed galaxy, a
corresponding formation redshift
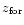 , defined as the epoch of the first stars generation, may be
derived. The result, constrained by the age of the universe (age
, defined as the epoch of the first stars generation, may be
derived. The result, constrained by the age of the universe (age
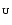 ),
depends on cosmology; as previously mentioned, standard cosmological parameters
are hereafter adopted.
Figure 8 shows iso-
),
depends on cosmology; as previously mentioned, standard cosmological parameters
are hereafter adopted.
Figure 8 shows iso-
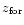 curves. The galaxy sample
is also plotted and compared to curves.
For
curves. The galaxy sample
is also plotted and compared to curves.
For
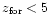 ,
our formation redshift
determination is reliable, if we keep in mind that we constrained the ages
of galaxies and thus the formation redshift. Unfortunately, the precision of redshift determination from photometry is quite
poor (about 0.1 for z < 1.5 with our sample). Above
,
our formation redshift
determination is reliable, if we keep in mind that we constrained the ages
of galaxies and thus the formation redshift. Unfortunately, the precision of redshift determination from photometry is quite
poor (about 0.1 for z < 1.5 with our sample). Above
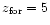 ,
the iso-
,
the iso-
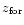 lines are so close to each other that we cannot rely on this formation redshift
determination.
lines are so close to each other that we cannot rely on this formation redshift
determination.
The histogram of the formation redshifts is shown in Fig. 9.
Note that this histogram is in agreement with
Lanzetta et al. (2001) figures of the star formation rate as a function of redshift, deduced from
FSLY's photometry, and taking into account the effects of cosmological surface brightness.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f9.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg98.gif) |
Figure 8:
Galaxies of the HDF-N sample in the redshift-age diagram, after
Z-PEG fits. The dotted lines show the z-age relations for various
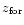 (iso- (iso-
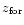 lines) and the standard cosmology, previously defined. For example, the
dotted line crossing the y-axis (
lines) and the standard cosmology, previously defined. For example, the
dotted line crossing the y-axis (
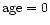 )
at z=2 corresponds to )
at z=2 corresponds to
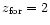 .
The solid line
shows the age of the universe at a given redshift (formally, this line is equivalent to .
The solid line
shows the age of the universe at a given redshift (formally, this line is equivalent to
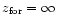 ). As a result,
most galaxies form at z>3 (we can also check this result in Fig. 9). ). As a result,
most galaxies form at z>3 (we can also check this result in Fig. 9). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{MS2109f10.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg99.gif) |
Figure 9:
Histogram of
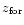 from our sample. For
from our sample. For
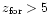 ,
due to
the lack of precision on the determination of (age, ,
due to
the lack of precision on the determination of (age,
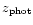 ), we cannot conclude on ), we cannot conclude on
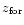 real values.
real values.
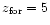 is then a lower value.
is then a lower value. |
| Open with DEXTER |
The determination of photometric redshifts significantly depends on
the adopted evolution scenarios. The basic principle is that distant galaxies
evolve according to the same basic principles as our nearby galaxies, only observed
at earlier epochs. As a direct consequence, evolution scenarios must
reproduce the SEDs of galaxy templates observed at z=0. This constraint
requires meaningful statistical templates. The literature appears
poor in this domain. From a large series of catalogs, we built statistical
samples corrected for various effects: aperture, inclination, reddening, etc.
(see Fioc & Rocca-Volmerange 1999b) in order to
focus specifically on visible to near-infrared colors of eight
spectral types of galaxies. All our redshifted templates are
compatible with these statistical colors at z=0.
The evolution principles are linked to the time-dependent star formation
rates. Corresponding to so-called "monolithic'' scenarios, each type
evolves with a star formation rate proportional to the gas content
and typical astration rates. The time-scale of star
formation increases from ellipticals (half Gyr) to Irregulars
(more than 10 Gyr). A test of the reliability of the adopted scenarios
is given with the interpretation of the deepest multi-spectral
faint galaxy counts on the largest multi-spectral coverage.
Figure 5 of Fioc & Rocca-Volmerange (1999a)
shows the best simultaneous fits of the deepest surveys, including the
HDF-N sample, from the far-UV to the K band.
The most constraining data are the reddest and deepest counts, only fitted by scenarios of old
elliptical galaxy models. The evolution
scenarios are from PÉGASE and similar to those used in the code Z-PEG.
These considerations make the
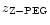 results
more robust and the evolution scenarios of elliptical galaxies
compatible with a rapid evolution at the earliest
epochs. The high values of
results
more robust and the evolution scenarios of elliptical galaxies
compatible with a rapid evolution at the earliest
epochs. The high values of
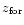 found from the present analysis
favor this result.
The star formation rate continuously follows the gas density, so that
the current SFR depends on the past star formation history.
An interesting interpretation, though tentative given the small incomplete
samples, would arise if the apparent continuous law is considered as the envelop
of small bursts. The intensity of these bursts decreases over time,
as the gas is depleted by star formation.
found from the present analysis
favor this result.
The star formation rate continuously follows the gas density, so that
the current SFR depends on the past star formation history.
An interesting interpretation, though tentative given the small incomplete
samples, would arise if the apparent continuous law is considered as the envelop
of small bursts. The intensity of these bursts decreases over time,
as the gas is depleted by star formation.
If the photometric redshifts
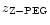 are faintly dependent
on the adopted cosmology, the results of
are faintly dependent
on the adopted cosmology, the results of
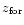 are more sensitive to
the choice of the cosmological parameters through
the age-redshift relation.
are more sensitive to
the choice of the cosmological parameters through
the age-redshift relation.
Finally the discussion of the dispersion and the degeneracy
of solutions has been detailed at each step of the
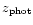 determination. In this analysis, like the age constraint,
the extension of the wavelength coverage, increasing with the number of filters,
limits the degeneracy. Conversely, if galaxies are observed
through only a few filters, the degeneracy may be high and results
have to be used with caution.
determination. In this analysis, like the age constraint,
the extension of the wavelength coverage, increasing with the number of filters,
limits the degeneracy. Conversely, if galaxies are observed
through only a few filters, the degeneracy may be high and results
have to be used with caution.
A new code Z-PEG is proposed for public use, available on the web,
to predict photometric redshifts from a data set of classical broad-band
colors or spectra. The code is derived from the model PÉGASE, also available
on the same web site, frequently downloaded for evolution
spectrophotometric analyses and quoted in many articles.
The particularity of the analysis presented here is to underline the
hypotheses implicitly (or explicitly) accepted when computing
photometric redshifts with evolution.
The comparison with a spectrophotometric redshift sample makes the predictions
robust. In its recent version PÉGASE.2, the model
constrains typical evolution scenarios to fit nearby galaxies.
Type-dependent extinction, IMF
and metal effects are taken into account, although we assumed
their modeling is not essential in our conclusions.
The most constraining parameter is the
z=0 galaxy age, typical of the nearby stellar population of
each spectral type. This constraint makes it possible to
eliminate implausible secondary solutions, the degeneracy being
the largest cause
of uncertainties on photometric redshifts. The dispersion for z <1.5reaches its minimum value 0.0980 with the age constraint, compared to other
dispersion values whatever the other
parameter values (IGM absorption or NIR colors).
The improvement in photometric redshift accuracy brought by near-infrared colors is
also measured by comparing models Z-PEG.4 and Z-PEG.2. The dispersion decreases from
0.32 to 0.12 for z < 1.5 and is more important for high redshifts when the 4000 Å discontinuity
enters in the NIR domain and the Lyman break does not yet reach the ultraviolet bands.
Finally Z-PEG is proposed to the community with PÉGASE.2. The site will be
updated and improved, so that Z-PEG will also follow improvements in the spectrophotometric
evolution modeling, in particular with the series of flux-calibrated samples allowing better
fits of highly redshifted templates. A possible extension of Z-PEG will involve the adaptation
of any photometric system, including narrow bands around emission lines,
with the help of the coupled code PÉGASE+CLOUDY (Ferland 1996),
predicting stellar and photoionised gas emissions (Moy et al. 2001).
Acknowledgements
We would like to thank Emmanuel Moy, Michel Fioc and Jérémy Blaizot for the fruitful discussions we had with them.
We are also grateful to the referee for his/her useful comments.
-
Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540
NASA ADS
-
Baum, W. A. 1962, Problems of Extra-Galactic Research, IAU Symp. 15, 390
In the text
-
Benítez, N. 2000, ApJ, 536, 571
NASA ADS
-
Bolzonella, M., Miralles, J., & Pelló, R. 2000, A&A, 363, 476
In the text
NASA ADS
-
Budavari, T. 2001, Publications of the Astronomy Deparment of the Eotvos Lorand University, 11, 41
NASA ADS
-
Budavari, T., Csabai, I., Szalay, A.S., et al. 2001, AJ, 122, 1163
NASA ADS
-
Clegg, R. E. S., & Middlemass, D. 1987, MNRAS, 228, 759
In the text
NASA ADS
-
Cohen, J. G., Hogg, D. W., Blandford, et al. 2000, ApJ, 538, 29
In the text
NASA ADS
-
Cohen, J. G. 2001, AJ, 121, 2895
In the text
NASA ADS
-
Coleman, G. D., Wu, C. C., & Weedman, D. W. 1980, Astrophys. J. Sup. Ser., 43, 393
In the text
-
Connolly, A. J., Csabai, I., Szalay, A. S., et al. 1995, AJ, 110, 2655
In the text
NASA ADS
-
Cowie, L. L., Gardner, J. P., Hu, E. M., et al. 1994, ApJ, 434, 114
In the text
NASA ADS
-
Cowie , L. L., Songaila, A., Hu, E. M., et al. 1996, AJ, 112, 839
NASA ADS
-
Dickinson, M. 1998, in The Hubble Deep Field,
ed. M. Livio, S. M. Fall, & P. Madau (Cambridge University Press),
219
In the text
-
Dressler, A. 1980, AJ, 236, 351
-
Ferland, G. J., 1996, HAZY, a brief introduction to Cloudy, University of Kentucky, Department of Physics and Astronomy Internal Report
In the text
-
Fernández-Soto, A., Lanzetta, K. M., & Yahil, A. 1999, ApJ, 513, 34
(FSLY)
In the text
NASA ADS
-
Fernández-Soto, A., Lanzetta, K. M., Chen, H.-W., et al. 2001a, ApJS, 135, 41
In the text
NASA ADS
-
Fernández-Soto, A., Lanzetta, K. M., Chen, H.-W., et al. 2001b [astro-ph/0111227]
In the text
-
Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950
In the text
NASA ADS
-
Fioc, M., & Rocca-Volmerange, B. 1999a, A&A, 344, 393
In the text
NASA ADS
-
Fioc, M., & Rocca-Volmerange, B. 1999b, A&A, 351, 869
In the text
NASA ADS
-
Folkes, S., Ronen, S., Price, I., et al. 1999, MNRAS, 308, 459
In the text
NASA ADS
-
Fontana, A., D'Odorico, S., Poli, F., et al. 2000, AJ, 120, 2206
NASA ADS
-
Giallongo, E., D'Odorico, S., Fontana, A., et al. 1998, AJ, 115, 2169
In the text
NASA ADS
-
Koo, D. C. 1985, AJ, 90, 418
In the text
NASA ADS
-
Lanzetta, K., Yahata, N., Pascarelle, S., et al. 2001 [astro-ph/0111129]
In the text
-
Le Fèvre, O., Crampton, D., Hammer, F., & Tresse L. 1995, ApJ, 455, 60
In the text
NASA ADS
-
Leitherer, C., Fritze-von Alvensleben, U., & Huchra, J. (eds.) 1996,
in Proceedings of From Stars to Galaxies: The Impact of Stellar
Physics on Galaxy Evolution, Crete, ASP Conf. Ser., 98
In the text
-
Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229
NASA ADS
-
Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65
In the text
NASA ADS
-
Loh, E. D., & Spillar, E. J. 1986, ApJ, 303, 154
In the text
NASA ADS
-
Madau, P. 1995, ApJ, 441, 18
In the text
NASA ADS
-
Madau, P., Ferguson, H. C., Dickinson, M., et al. 1996, MNRAS, 283, 1388
In the text
NASA ADS
-
Massarotti, M., Iovino, A., & Buzzoni, A. 2001a, A&A, 368, 74
In the text
NASA ADS
-
Massarotti, M., Iovino, A., Buzzoni, A., et al. 2001b, A&A, 380, 425
In the text
NASA ADS
-
Moy, E., Rocca-Volmerange, B., & Fioc, M. 2001, A&A, 365, 347
In the text
NASA ADS
-
Press, W. H., Rybicki, G. B., & Schneider, D. P. 1993, ApJ, 414, 64
In the text
NASA ADS
-
Rana, N. C., & Basu, S. 1992, A&A, 265, 499
In the text
NASA ADS
-
Rocca-Volmerange, B. 2000, in Galaxy Disks and disk galaxies, ed.
Funés, & Corsini, PASP Ser., 230, 597
-
Steidel, C. C., Adelberger, K. L., Giavalisco, M., et al. 1999, ApJ, 519, 1
In the text
NASA ADS
-
Williams, R. E., Blacker, B., Dickinson, M., et al. 1996, AJ, 112, 1335
In the text
NASA ADS
-
Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181
NASA ADS
Copyright ESO 2002
![\begin{displaymath}\chi^2= \sum_{i=1}^{\it N}\left[\frac{F^{\rm obs}_i-\alpha \times F^{\rm synth}_i}{\sigma_i}\right]^2\cdot
\end{displaymath}](/articles/aa/full/2002/17/aa2109/img44.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2109f1.eps}\vspace*{1mm}
\includegraphics[width=8.8cm,clip]{MS2109f2.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg58.gif)
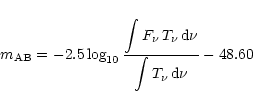
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f3.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg66.gif)
![\begin{figure}
\par\includegraphics[clip,width=8.3cm,clip]{MS2109f4.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f5.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg75.gif)
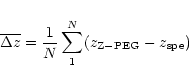
![\begin{displaymath}\sigma^2_z=\frac{1}{N-1} \sum _1^N \left[ (z_{{\rm Z-PEG}}-z_{{\rm spe}})-\overline{\Delta z}~\right]^2
\end{displaymath}](/articles/aa/full/2002/17/aa2109/img84.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f6.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{MS2109f7.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f8.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f9.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg98.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{MS2109f10.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg99.gif)