A&A 386, 517-530 (2002)
DOI: 10.1051/0004-6361:20020247
Jg. Fischera - R. J. Tuffs - H. J. Völk
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69115 Heidelberg, Germany
Received 17 August 2001 / Accepted 8 February 2002
Abstract
We present measurements of the mid-infrared (MIR) emission from SN 1987A,
made using the Infrared Space Observatory (ISO) 11 years
after outburst. They are the only late epoch detections
of this source in the thermal IR regime.
The position of the source, determined from an offset to an IR-emitting star,
suggests that the emission is associated with SN 1987A or its
extended supernova remnant (SNR).
A predominantly circumstellar origin is however suggested by
the size and orientation of the IR-emitting region, which is
comparable with the extension of the inner ring seen with the
Hubble Space Telescope (HST). The emission is most probably from
collisionally-heated circumstellar grains embedded in
shocked gas downstream of the blast wave. The MIR extent is consistent with
the hypothesis that the blast wave was propagating into material of
moderate density interior to the thick inner ring at the epoch of the ISOCAM observations.
Key words: stars: supernovae: individual: SN 1987A - ISM: dust - infrared: ISM - supernova remnants
Supernovae are thought to play an important role in the life cycle of interstellar dust grains. On the one hand, shocks driven by supernovae into the interstellar medium (ISM) are considered to be responsible for the destruction of interstellar grains (see e.g. Shull 1977; Draine & Salpeter 1979; Tielens et al. 1994; Jones et al. 1994). On the other hand, supernovae have also been proposed as sources of interstellar dust (e.g. Hoyle & Wickramasinghe 1970; Dwek & Scalo 1980).
SN 1987A in the Large Magellanic Cloud (LMC) was the first supernova in which the condensation of dust in the central metal-rich part of the expanding ejecta has been observed. The appearance of a continuum emission in the IR in the spectrum of SN 1987A 614 days after outburst is attributed to grains formed after at least 500 days (e.g. Wooden 1997). The infrared emission from the condensates was (maybe except at the onset of dust formation; Roche et al. 1993) optically thick at the early epochs when the IR-emission was still bright enough to be observable from ground. Therefore, it was not possible to get clear information about their properties and in particular their mass.
Observations with the HST have revealed a bipolar ring structure
consisting of a thick inner ring centred at the position
of the supernova, and two thin outer rings of
larger radius at each side (Burrows et al. 1995).
Radio and X-ray observations suggest that, after an initial period
of free expansion, the blast wave started to propagate through
a region of moderate density with
![]() interior to the thick inner ring
(Chevalier & Dwarkadas 1995).
Chevalier & Dwarkadas suggested this region to be an HII region, illuminated by
the blue supergiant supernova progenitor and composed of
wind material ejected during the prior red supergiant phase.
interior to the thick inner ring
(Chevalier & Dwarkadas 1995).
Chevalier & Dwarkadas suggested this region to be an HII region, illuminated by
the blue supergiant supernova progenitor and composed of
wind material ejected during the prior red supergiant phase.
If the HII region contains dust,
extended thermal emission
from collisionally heated grains embedded in the shocked gas
downstream of the blast wave is to be expected.
The presence of circumstellar grains was already invoked at early epochs
to account for observations of a prompt echo effect in the mid-infrared
(Rank et al. 1988; Chalabaev et al. 1989).
It has also been suggested that circumstellar grains can account for observations after 580 days
showing an extension of
![]() at
at
![]() (Roche et al. 1993). Light echos in the optical have
further been used to reconstruct a three dimensional model of the larger
scale structures around SN 1987A (Crotts et al. 1995).
(Roche et al. 1993). Light echos in the optical have
further been used to reconstruct a three dimensional model of the larger
scale structures around SN 1987A (Crotts et al. 1995).
The ISO mission (Kessler et al. 1996) gave a unique opportunity to probe the early evolution of SN 1987A in the IR prior to the envelopment of the thick inner ring by the blast wave. In this paper we present sensitive measurements made with the ISOCAM instrument (Cesarsky et al. 1996) on board ISO 11 years after outburst. Thus far, these measurements constitute the only late epoch detection of the source in the IR regime. Preliminary results were presented by Tuffs et al. (1998). Here we demonstrate that the detected IR emission is most probably of circumstellar origin.
The paper is structured as follows: in Sect. 2 we present the ISOCAM measurements and describe the reduction and calibration of the data. In Sect. 3 we derive the flux density, position, orientation and size of the mid-infrared (MIR) source, showing that the IR emission from the remnant is resolved, with an extent comparable to that of the thick inner ring. These results are discussed in Sect. 4. A summary of the paper is given in Sect. 5.
Throughout the paper we adopt a distance of 51 kpc to the supernova
as was used to analyse the X-ray observations
by Hasinger et al. (1996). This is close to the distance of
![]() kpc
derived by Panagia et al. (1991) but slightly larger than the
values given in later publications
(Gould 1995; Sonneborn et al. 1997; Gould & Uza 1998).
kpc
derived by Panagia et al. (1991) but slightly larger than the
values given in later publications
(Gould 1995; Sonneborn et al. 1997; Gould & Uza 1998).
The measurements in LW10 and LW3 were optimized for obtaining
sensitive photometry and structural information of a faint compact target.
A pixel field of view (PFOV)
of
![]() was chosen as for the anticipated backgrounds
it gave the best trade off between angular resolution and
detector illumination. We used a
was chosen as for the anticipated backgrounds
it gave the best trade off between angular resolution and
detector illumination. We used a ![]() raster with raster interval
raster with raster interval
![]() to sample the sky at intervals of
to sample the sky at intervals of
![]() .
This comfortably oversampled the point spread function (psf), which has a
FWHM of
.
This comfortably oversampled the point spread function (psf), which has a
FWHM of ![]() 4
4
![]() at
at
![]() for the
for the
![]() PFOV.
PFOV.
The raster interval of
![]() was the minimum
interval that provides a sky sampling for
which each view of the target in a given pixel
is immediately preceded or followed by a
view of the underlying background.
This optimized the knowledge of the relative
response of the detector between source and background,
which in turn could be used to minimize the effect of residual
uncertainties in the flat-field response of the
was the minimum
interval that provides a sky sampling for
which each view of the target in a given pixel
is immediately preceded or followed by a
view of the underlying background.
This optimized the knowledge of the relative
response of the detector between source and background,
which in turn could be used to minimize the effect of residual
uncertainties in the flat-field response of the
![]() pixel detector
on the determination of source structure.
The observations were separated in epoch over the period September 1997 to
February 1998. The measurement in the
pixel detector
on the determination of source structure.
The observations were separated in epoch over the period September 1997 to
February 1998. The measurement in the
![]() band
was a follow up observation to the detection in the
band
was a follow up observation to the detection in the
![]() ,
while the measurement in the
,
while the measurement in the
![]() band was part of an independent
program of large-scale mapping of the LMC led by L. Vigroux.
band was part of an independent
program of large-scale mapping of the LMC led by L. Vigroux.
| Filter | LW2 | LW10 | LW3 |
| TDT | 667017 | 811022 | 750019 |
| observer | L. Vigroux | R.J. Tuffs | R.J. Tuffs |
|
|
6.75 | 12. | 14.3 |
| filter range
|
5.00-8.50 | 8.00-15.00 | 12.0-18. |
| observation date | 13.9.97 | 5.12.97 | 3.2.98 |
| day after outbursta | 3855.2 | 3998.7 | 3937.7 |
| raster | |||
| pixel size |
|
|
|
| step size |
|
|
|
| read out interval
|
2.10 s | 5.04 s | 5.04 s |
| reads per pointing |
31 | 19 | 19 |
aThe time of the outburst is taken to be February 23.316, 1987 (Arnett et al. 1989).
The data were first corrected for dark current using the model of the Cam Interactive Analysis (CIA) package (Ott et al. 1998; version April 2000). This was followed by glitch removal using the Multi resolution Median Transform, also provided by CIA. The data were then inspected and residual events and strong longer-lived glitch-induced distortions were removed manually. To allow an accurate determination of the illumination seen by each single pixel during the raster, the data were then corrected for the transient response behavior of the detector. To this end we developed and implemented a routine based on the drift model of the ISOPHOT-S detector on board ISO (Schubert 1995). The routine derived the time constants and jump factors determining the drift behaviour of the individual detector pixels from the measured data.
![\begin{figure}
\par\includegraphics[width=8.5cm]{ms1827f1.epsi}\hspace*{4mm}
\includegraphics[width=8.5cm]{ms1827f2.epsi}
\end{figure}](/articles/aa/full/2002/17/aa1827/Timg52.gif) |
Figure 1:
Region around the SN 1987A in the MIR, as seen at
|
| Open with DEXTER | |
To create a map showing the background structure underlying the sources
we applied a flat-field correction, which was optimized for the smooth
variation of the background. The flat-field was derived from a map, which had already been corrected
using a library flat provided by CIA and which had been spatially filtered to reduce the noise.
The flat-field-corrected data were then binned (without interpolation)
on a grid with a sampling of
![]() .
For visualization the data were further filtered by setting pixel values differing more than one sigma
from their surroundings to the average value of the surrounding pixels (the filter was not
applied for obvious discrete sources).
Then map pixels without any data were set to the average values of the neighbouring pixels.
Finally, we convolved the image with a Gauss function with a variance of
.
For visualization the data were further filtered by setting pixel values differing more than one sigma
from their surroundings to the average value of the surrounding pixels (the filter was not
applied for obvious discrete sources).
Then map pixels without any data were set to the average values of the neighbouring pixels.
Finally, we convolved the image with a Gauss function with a variance of
![]() .
The resulting maps are shown in Fig. 1.
.
The resulting maps are shown in Fig. 1.
The quantitative analysis of
the individual compact sources seen in the ISOCAM maps
was done directly from the observed brightnesses
as a function of sky position, without use of maps, as
described in Sect. 3. This required a
different calibration procedure compared to that for the maps.
For the observations at 12 and
![]() we made use of the
almost flat emission around
the two sources and normalized all pixel values at individual raster
positions
with the corresponding values of the
background. This was done by making a linear fit to the variation
of (responsivity drift-corrected) illumination in each given detector
pixel with spacecraft raster position, leaving out raster positions
where the pixel was viewing the source.
In the case of the measurement at
we made use of the
almost flat emission around
the two sources and normalized all pixel values at individual raster
positions
with the corresponding values of the
background. This was done by making a linear fit to the variation
of (responsivity drift-corrected) illumination in each given detector
pixel with spacecraft raster position, leaving out raster positions
where the pixel was viewing the source.
In the case of the measurement at
![]() ,
we used the library flat
provided in CIA, as the raster pattern was not suitable for this method.
For the measurement at 12 and at
,
we used the library flat
provided in CIA, as the raster pattern was not suitable for this method.
For the measurement at 12 and at
![]() the sky coordinates of each detector pixel at each raster pointing were
evaluated from the actual (post posteri) pointing position of the satellite
using the median of all the data used.
To derive the pixel coordinates of the observation at
the sky coordinates of each detector pixel at each raster pointing were
evaluated from the actual (post posteri) pointing position of the satellite
using the median of all the data used.
To derive the pixel coordinates of the observation at
![]() we
made use of the astronomical information provided by the CIA-program.
Corrections were applied
for the astrometrical distortions in the ISOCAM field
(Aussel 1998) induced by the field lens using the polynomial
correction coefficients for the different filters as given in CIA.
we
made use of the astronomical information provided by the CIA-program.
Corrections were applied
for the astrometrical distortions in the ISOCAM field
(Aussel 1998) induced by the field lens using the polynomial
correction coefficients for the different filters as given in CIA.
The final images show two clear individual sources. The source close to the middle corresponds to emission from the remnant of SN 1987A, whereas the source near the edge is an IR-emitting star. The two sources show different colours, indicating a higher temperature for the star. The serendipitous detection of the star provided a unique possibility to determine an accurate position for the central MIR source near SN 1987A (see Sect. 3.3). The bright ridge of emission to the NNW of SN 1987A is an arm of the 30 Doradus nebula. Although backgrounds are dominated by smooth emission from zodiacal light, there is some evidence for faint cirrus structure at the 1% level in the southern part of the field. At both wavelengths the IR emission near the map centre is offset several arcsec from the nominal position of SN 1987A. These offsets are partly due to the inaccuracy of the position of the satellite but are mainly attributable to a displacement of the field lens of the camera (Blommaert & Cesarsky 1998).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{ms1827f3.epsi}\hspace*{0.4cm}
\includegraphics[width=8.7cm,clip]{ms1827f4.epsi}
\end{figure}](/articles/aa/full/2002/17/aa1827/Timg56.gif) |
Figure 2:
Best fits of the theoretical image (solid line) to the measured brightnesses (diamonds)
of the remnant of SN 1987A
at
|
| Open with DEXTER | |
Various parameters of the discrete sources, expressed as the vector ![]() ,
were derived
using a non-linear
,
were derived
using a non-linear ![]() -fit, where we compared the measured data
-fit, where we compared the measured data
![]() and uncertainties
and uncertainties
![]() at the sky positions
at the sky positions
![]() around the individual sources
with a model image
around the individual sources
with a model image
![]() :
:
To achieve a higher accuracy, in
particular for the determination of the size of the emitting region,
we took into account the dependence of beam profile
on source colour. This was done by
averaging simulated beam shapes obtained at a series of
wavelengths across the broad filter pass bands,
weighted according to a power law
source spectrum
![]() with a spectral index k (see Appendix A).
For the star the spectral index was always taken
to be k=4 appropriate to a Rayleigh-Jeans spectrum.
For the source associated with the supernova k was estimated from the finally determined
colour corrected (see e.g. Blommaert 1998) flux densities to be
with a spectral index k (see Appendix A).
For the star the spectral index was always taken
to be k=4 appropriate to a Rayleigh-Jeans spectrum.
For the source associated with the supernova k was estimated from the finally determined
colour corrected (see e.g. Blommaert 1998) flux densities to be
![]() .
The model image was calculated on a grid
with a resolution of
.
The model image was calculated on a grid
with a resolution of
![]() .
In the fitting procedure
the predicted fluxes at the observed positions
were found using linear interpolation.
.
In the fitting procedure
the predicted fluxes at the observed positions
were found using linear interpolation.
The true uncertainties
![]() in each individual measurement for a detector pixel at a given
spacecraft raster pointing direction are
difficult to estimate and may be partly
affected by systematic uncertainties.
This particularly applies to measurements viewing
the discrete sources, where
the illumination and detector response function may vary with position
over the field of view of the individual detector pixels.
We therefore assumed in nearly all model calculations
that the uncertainties of all measurements are equal.
This is justified by the fact that the distribution of the residuals was
found to be normal.
The only exception to this was made for the
measurement of the star at
in each individual measurement for a detector pixel at a given
spacecraft raster pointing direction are
difficult to estimate and may be partly
affected by systematic uncertainties.
This particularly applies to measurements viewing
the discrete sources, where
the illumination and detector response function may vary with position
over the field of view of the individual detector pixels.
We therefore assumed in nearly all model calculations
that the uncertainties of all measurements are equal.
This is justified by the fact that the distribution of the residuals was
found to be normal.
The only exception to this was made for the
measurement of the star at
![]() ,
where the uncertainties of
the high source fluxes were mainly attributed to a
particularly strong transient behaviour.
,
where the uncertainties of
the high source fluxes were mainly attributed to a
particularly strong transient behaviour.
The absolute uncertainties
![]() of the measured data
were chosen such that the value of the minimum
of the measured data
were chosen such that the value of the minimum ![]() (Eq. (1))
corresponds to a confidence level of 90%.
In the case of the
measurements at 12 and at
(Eq. (1))
corresponds to a confidence level of 90%.
In the case of the
measurements at 12 and at
![]() we made a special fit letting
we made a special fit letting
![]() ,
,
![]() ,
,
![]() and k as free variables.
The joint uncertainties of
and k as free variables.
The joint uncertainties of ![]() parameters were estimated
by finding the range within which the function
parameters were estimated
by finding the range within which the function
![]() did not exceed the value corresponding to a confidence level of one sigma,
letting all other parameters as free variables.
Thus, apart from the jointly determined uncertainties in the coordinates, which were estimated from
did not exceed the value corresponding to a confidence level of one sigma,
letting all other parameters as free variables.
Thus, apart from the jointly determined uncertainties in the coordinates, which were estimated from
![]() ,
the uncertainties in individual parameters correspond to
,
the uncertainties in individual parameters correspond to
![]() (see e.g. Press et al. 1992).
(see e.g. Press et al. 1992).
In the case of the measurement at
![]() the parameters varied were
the parameters varied were
![]() ,
the coordinates
,
the coordinates ![]() and the background brightness
and the background brightness ![]() .
We used a model image corresponding
to an ideal point source (
.
We used a model image corresponding
to an ideal point source (
![]() )
assuming a spectrum with k=1 for
the IR emission from the supernova remnant.
)
assuming a spectrum with k=1 for
the IR emission from the supernova remnant.
At 12 and at
![]() the flux density and the coordinates were optimized together
with the extension of the source. The variables varied were therefore
the flux density and the coordinates were optimized together
with the extension of the source. The variables varied were therefore
![]() ,
,
![]() and
and
![]() .
Because of the normalization of the pixel data to the background we held
.
Because of the normalization of the pixel data to the background we held ![]() fixed.
The uncertainties in
fixed.
The uncertainties in ![]() and
and ![]() were estimated for a fixed (most probable) source size.
The best fits to the measured data with LW10 and LW3 are shown in Fig. 2.
were estimated for a fixed (most probable) source size.
The best fits to the measured data with LW10 and LW3 are shown in Fig. 2.
| SN 1987A | reference star | |||||
| Filter | LW2 | LW10 | LW3 | LW2 | LW10 | LW3 |
|
|
6.75 | 12. | 14.3 | 6.75 | 12. | 14.3 |
| ADUa /(mJy/pixel)b |
|
|
|
|
|
|
| beam size (FWHM
|
|
|
|
|
|
|
| spectral index kd | 1. | 1.08 | 1.08 | 4 | 4 | 4 |
| derived source size (FWHM
|
- | 1.50-0.24+0.21 | <2.3(3 |
- | 2.26-0.30+0.27 | <2.4(3 |
|
|
0.76 (51) | 0.82 (94) | 0.83 (127) | 0.77 (60) | 0.69 (41) | 0.78 (75) |
| Uncertainty of pixel values
|
3.6% | 1.9% | 1.7% | 12.%f | 2.5% | 1.5% |
|
|
|
|
|
|
|
|
| background
|
|
|
|
|
|
|
| source flux density
|
|
|
|
|
|
|
| source flux density
|
|
|
|
|
|
|
|
aAnalog to Digital Units.
bBlommaert et al. (1999). cAverage FWHM of cuts in Z and Y through the maximum of the theoretical psf. Uncertainties correspond to the difference of these two values. dSpectral index assumed in calculating the theoretical psf (see text). eFWHM of the symmetrical Gaussian model assumed for the source. Uncertainties are given as 1 fMedian of the uncertainties. gFlux density without colour correction. hColour-corrected according to a spectrum |
The surface brightness of the background at these
two wavelengths was estimated from the images calculated as described in
Sect. 2.1, but without filtering and convolution.
To derive the surface brightness ![]() at the position
of the supernova from the maps we took the average
value within two circular areas of radius of
at the position
of the supernova from the maps we took the average
value within two circular areas of radius of
![]() offset
offset
![]() to the east and to the west of SN 1987A.
At both
12 and
to the east and to the west of SN 1987A.
At both
12 and
![]() the difference between the two values is less than
the difference between the two values is less than ![]() .
For the background brightnesses at the position of the
star we took the average of a number of single
measurements around the star; here the estimated uncertainties
in the background are
.
For the background brightnesses at the position of the
star we took the average of a number of single
measurements around the star; here the estimated uncertainties
in the background are ![]() (LW10) and
(LW10) and ![]() (LW3).
(LW3).
The derived values for the source flux and size,
and the background brightnesses, are summarized
in Table 2, together with the assumed value for
the spectral index k used in the determination of source size.
The table also gives the source flux densities
normalized to the surface brightness of the background.
The uncertainties quoted for the normalized flux densities
at 12 and
![]() are statistical uncertainties
derived from the
are statistical uncertainties
derived from the ![]() -fit.
-fit.
The IR spectrum of the supernova remnant can be approximated
by a simple black body spectrum with
![]() K (
K (
![]() )
or a modified black body spectrum
)
or a modified black body spectrum
![]() with
with
![]() where a good
fit is achieved (
where a good
fit is achieved (
![]() ).
Assuming the same modified spectrum for the star we get a temperature of
).
Assuming the same modified spectrum for the star we get a temperature of
![]() .
The fit is
again very good
(
.
The fit is
again very good
(
![]() ). A simple black body for the star seems to be unlikely (
). A simple black body for the star seems to be unlikely (
![]() ).
).
The probability distributions for the extension of the IR-emitting regions
associated with SN 1987A were derived
at 12 and at
![]() from a
from a ![]() -fit using
a symmetrical Gaussian as source function
(see Appendix B). These are shown in Fig.
3.
The different probability distributions correspond to different colour
indices used in the calculation of the theoretical psf.
The distributions plotted with thick solid lines have been derived for the most
probable colour of the source, a power law with k=1.08.
As can be seen in the figure, the
probability distributions are only slightly affected by the uncertainty in the spectral index kfor the MIR emission associated with the supernova. The probability distributions corresponding
to the upper and lower limits for k (0.56 and 1.59, respectively, at 90% confidence level)
are plotted as thin solid lines.
The dashed and dotted curves peaking near
-fit using
a symmetrical Gaussian as source function
(see Appendix B). These are shown in Fig.
3.
The different probability distributions correspond to different colour
indices used in the calculation of the theoretical psf.
The distributions plotted with thick solid lines have been derived for the most
probable colour of the source, a power law with k=1.08.
As can be seen in the figure, the
probability distributions are only slightly affected by the uncertainty in the spectral index kfor the MIR emission associated with the supernova. The probability distributions corresponding
to the upper and lower limits for k (0.56 and 1.59, respectively, at 90% confidence level)
are plotted as thin solid lines.
The dashed and dotted curves peaking near
![]() are probability distributions for the
measurements at
are probability distributions for the
measurements at
![]() using as psf the image of a calibration star and the theoretical
psf for a spectral index k=4, respectively. Since the spectrum of the star should be
a power law with k=4, the similarity of these two curves demonstrates that the effect of interchanging
the theoretical psf with the measured psf is small.
The larger apparent source sizes
calculated from the psfs with k=4
arise from the decrease in FWHM of the psf with increasing k compared with the true value
using as psf the image of a calibration star and the theoretical
psf for a spectral index k=4, respectively. Since the spectrum of the star should be
a power law with k=4, the similarity of these two curves demonstrates that the effect of interchanging
the theoretical psf with the measured psf is small.
The larger apparent source sizes
calculated from the psfs with k=4
arise from the decrease in FWHM of the psf with increasing k compared with the true value
![]() for the MIR emission associated with SN 1987A.
for the MIR emission associated with SN 1987A.
For the LW10 observation we obtained
a FWHM of
1.50-0.24+0.21 arcsec
for the extension of the source. This
size is in agreement with the extensions of the projected inner ring,
seen in the HST picture. The distribution we derived from the LW3 observation is broader, and
also has a higher probability for small extensions.
This might be due to the strong glitches causing long time distortions of the detector response
of the observation (see also Sect. 3.2). From this observation we were only able to
obtain an upper limit for the source size of
![]() at
at ![]() level.
Table 3 gives
the maximum and minimum sizes of the IR-emitting region for
certain confidence levels derived from the probability distributions for k=1.08.
As shown in Appendix B.2 the theoretical psf for the LW10 filter
is a sufficiently accurate representation of the
real psf to resolve sources with a FWHM greater than
level.
Table 3 gives
the maximum and minimum sizes of the IR-emitting region for
certain confidence levels derived from the probability distributions for k=1.08.
As shown in Appendix B.2 the theoretical psf for the LW10 filter
is a sufficiently accurate representation of the
real psf to resolve sources with a FWHM greater than ![]() 0
0
![]() .
If we take the measurement at
.
If we take the measurement at
![]() the source is extended with a certainty
of more than 99%.
the source is extended with a certainty
of more than 99%.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1827f5.epsi}\end{figure}](/articles/aa/full/2002/17/aa1827/Timg140.gif) |
Figure 3:
Derived probability distributions of the size s of the theoretical image
(see Eq. (B.1)) as a function
of the FWHM of the IR source for the two filter measurements LW10 (
|
| Open with DEXTER | |
| conf. level | 68% | 90% | 95% | 99% | 99.9% |
| Maximum size of the source (FWHM) | |||||
| LW3 |
|
|
|
|
|
| LW10 |
|
|
|
|
|
| Minimum size of the source (FWHM) | |||||
| LW3 |
|
|
|
|
|
| LW10 |
|
|
|
|
|
Some evidence was found for extended emission associated with the
star at
![]() (Table 2).
This may in part be due to the strong
edge position and the course sampling of the star. But it cannot be excluded from the IR observations
that the star itself is extended.
(Table 2).
This may in part be due to the strong
edge position and the course sampling of the star. But it cannot be excluded from the IR observations
that the star itself is extended.
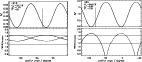 |
Figure 4:
The top panel shows the variation of
|
| Open with DEXTER | |
In addition to the extension we also examined the orientation angle of the IR-source.
Herefore we described the source through a two dimensional elliptical Gauss function with
variances
![]() and
and
![]() and a rotation angle
and a rotation angle
![]() ,
which was taken to be the angle between the negative Z-axis in the satellite coordinate system
and the
,
which was taken to be the angle between the negative Z-axis in the satellite coordinate system
and the ![]() -axis of the rotated Gaussian, measured counter clockwise.
-axis of the rotated Gaussian, measured counter clockwise.
![]() is then
is then
![]() and the model image given by:
and the model image given by:
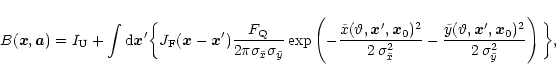 |
(3) |
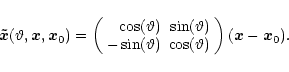 |
(4) |
The variation in
![]() is low in the case of the measurement with LW10. But
the coincidence of the derived parameters of the extensions and the rotation angle of the
two dimensional Gauss function with the parameters of the inner ring are remarkable.
The derived region of the IR source at
is low in the case of the measurement with LW10. But
the coincidence of the derived parameters of the extensions and the rotation angle of the
two dimensional Gauss function with the parameters of the inner ring are remarkable.
The derived region of the IR source at
![]() on the other hand
seems to have an extension with the dimension of the inner ring only in one
direction. In the other direction, the shown extension is the minimum we allowed to
avoid inaccuracies in the modeling. We think that this strong asymmetry is artificial and an
effect due to strong glitches at the beginning of the LW3 observation.
on the other hand
seems to have an extension with the dimension of the inner ring only in one
direction. In the other direction, the shown extension is the minimum we allowed to
avoid inaccuracies in the modeling. We think that this strong asymmetry is artificial and an
effect due to strong glitches at the beginning of the LW3 observation.
![\begin{figure}
\par\mbox{\subfigure[Derived positions of the IR emission]{
\incl...
...ng region]{
\includegraphics[width=8.75cm,clip]{ms1827f9.epsi} }}
\end{figure}](/articles/aa/full/2002/17/aa1827/Timg174.gif) |
Figure 5:
Derived absolute coordinates and sizes of the IR-emitting region
of the measurements at
|
| Open with DEXTER | |
As an independent property of the IR emission from the remnant of SN 1987A
we derived the absolute coordinates relative to the position of the IR-emitting star
visible in the two mosaics at 12 and at
![]() (Fig. 1).
The position of the IR-emitting star itself was not known so that we first had to determine
the absolute coordinates of this star (see Appendix C).
(Fig. 1).
The position of the IR-emitting star itself was not known so that we first had to determine
the absolute coordinates of this star (see Appendix C).
We derived the following offset positions of the IR emission from the position of the supernova,
where we have taken the coordinates given by Reynolds et al. (1995):
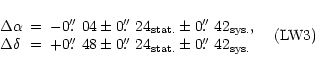 |
(5) |
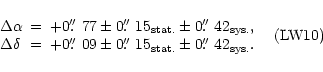 |
(6) |
The absolute coordinates of the IR-emission from the remnant of SN 1987A at 12 and
![]() with the corresponding uncertainties are shown in Fig. 5a in relation
to the WFPC2-image. Figure 5b shows a visualization of the fits to the
size of the emitting region.
As seen in Fig. 5a the
IR emission measured with ISOCAM should be from the remnant of SN 1987A.
Taking the joint probability
distribution of both measurements, the most probable location for the IR counterpart
is to the north east
of the supernova, which is also the position of the maxima in the
X-ray and radio surface brightness distributions (Burrows et al. 2000).
But it is also possible that the centre of the IR emission lies
at the position of the supernova so that the outer boundary of the emitting region could indeed
coincide with the inner ring as seen in Fig. 5b.
Therefore there is no firm evidence of asymmetry in the MIR emission comparable with that seen in radio
and X-ray wavelengths.
with the corresponding uncertainties are shown in Fig. 5a in relation
to the WFPC2-image. Figure 5b shows a visualization of the fits to the
size of the emitting region.
As seen in Fig. 5a the
IR emission measured with ISOCAM should be from the remnant of SN 1987A.
Taking the joint probability
distribution of both measurements, the most probable location for the IR counterpart
is to the north east
of the supernova, which is also the position of the maxima in the
X-ray and radio surface brightness distributions (Burrows et al. 2000).
But it is also possible that the centre of the IR emission lies
at the position of the supernova so that the outer boundary of the emitting region could indeed
coincide with the inner ring as seen in Fig. 5b.
Therefore there is no firm evidence of asymmetry in the MIR emission comparable with that seen in radio
and X-ray wavelengths.
The contribution of synchrotron radiation can be estimated
by extrapolating the radio spectrum given by Gaensler et al. (1997) to
![]() .
Taking into account the linear increase of radio emission with time,
this yields the value
.
Taking into account the linear increase of radio emission with time,
this yields the value ![]() 5.1
5.1
![]() ,
two orders of magnitude less than the flux densities measured by ISOCAM.
,
two orders of magnitude less than the flux densities measured by ISOCAM.
We can also exclude free-free emission from the debris or the thick inner ring as a substantial contributor to the observed MIR flux densities. We have estimated the MIR free-free continuum from optical recombination line measurements using published emissivities and recombination coefficients for case B of Martin (1988).
For the free-free emission from the ejected material
we adopted the
![]() flux 2873 days after outburst
(Chugai et al. 1997) assuming a temperature of 103 K, which is consistent with
the measured balmer decrement of 3.8.
The predicted flux density at
flux 2873 days after outburst
(Chugai et al. 1997) assuming a temperature of 103 K, which is consistent with
the measured balmer decrement of 3.8.
The predicted flux density at
![]() is roughly
three orders of magnitudes lower (
is roughly
three orders of magnitudes lower (![]() 3.2
3.2
![]() ).
Even in the case of a higher temperature of 104 K the free-free
emission from the supernova debris in the IR is negligible (
).
Even in the case of a higher temperature of 104 K the free-free
emission from the supernova debris in the IR is negligible (![]() 0.027
0.027
![]() ).
).
The predicted free-free emission from
the thick inner ring is brighter, but still insufficient to account for the ISOCAM detections.
To estimate its contribution to the IR the temperature of the whole inner ring was taken to be
104 K as was derived from analysis of emission spectra,
made with the HST at different epochs from a bright part of the inner ring
(Lundqvist & Sonneborn 1997).
We used the flux of the inner ring in R-band, measured with the WFPC2 of the HST 3268 days after outburst
(Soderberg et al. 1999). Further, we assumed that 19% of the flux is due to the
![]() -line
and the rest to the neighbouring NII lines at 6548 and 6583 Å,
which is roughly consistent with the line ratios
in the line spectrum of a luminous part of the ring presented by Panagia et al. (1996).
For the flux density of the free-free emission at
-line
and the rest to the neighbouring NII lines at 6548 and 6583 Å,
which is roughly consistent with the line ratios
in the line spectrum of a luminous part of the ring presented by Panagia et al. (1996).
For the flux density of the free-free emission at
![]() from the inner thick ring
we derived an upper limit of
from the inner thick ring
we derived an upper limit of ![]() 0.053
0.053 ![]() .
.
The contribution of the synchrotron radiation, the free-free emission of the ring and the debris to the IR is shown in Fig. 6, which summarizes the spectral energy distribution of the SN 1987A at late times.
No sensitive observations of the MIR cooling lines at late epochs are available. However, according to the theoretical predictions for the evolution of the emission from various fine structure lines of the supernova debris (Kozma & Fransson 1998a) their contribution should be negligible. We conclude that the measured IR emission is most probably thermal emission from dust. This emission could either be due to grains in the shocked gas in the circumstellar environment or originate in condensates heated mainly by the energy of the radioactive decay of the nucleosynthesis products.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{ms1827f10.epsi}
\end{figure}](/articles/aa/full/2002/17/aa1827/Timg189.gif) |
Figure 6:
Spectral energy distribution of the SN 1987A at late times.
The measured ISOCAM fluxes are shown as open diamonds. They are colour-corrected according to the
modified black body spectrum
|
| Open with DEXTER | |
To derive dust masses knowledge of the optical properties of the grains is needed.
The grain emissivity can depend quite strongly on grain composition and in particular in the ISOCAM range
on wavelength (see e.g. Draine & Lee 1984). Nevertheless,
for a first interpretation the dust spectrum may be approximated by a modified blackbody function
of the form already used for the colour correction in Sect. 3.1.
The flux density of N(a) dust grains with radius a at
a distance D radiating at a certain temperature T is then given by
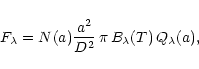 |
(7) |
| L | = | (8) | |
| = | 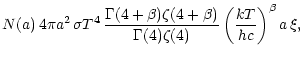 |
(9) |
The luminosity can be compared with
the rate of deposition of energy from the decay of radioactive decay products.
Assuming the ejecta after 11 years to be optically thin to gamma rays
and taking an initial mass of
![]() of
of
![]() which is mainly responsible
for the heating at late epochs
then the luminosity emitted by dust grains in the MIR is at least
which is mainly responsible
for the heating at late epochs
then the luminosity emitted by dust grains in the MIR is at least ![]() 20% of the
deposited energy rate
20% of the
deposited energy rate
![]() (Fischera 2000).
(Fischera 2000).
The dust mass was estimated from the equation
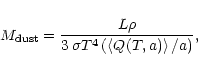 |
(10) |
These values indicate a dust mass which is much
lower than the minimum dust mass of ![]() 10
10
![]() derived for the newly formed
dust in the metal rich part of supernova ejecta (Wooden 1997). It is probable that the bulk
of the condensates are currently emitting in the FIR/submm and were too cold to be visible
to ISOCAM.
A temperature of at least
derived for the newly formed
dust in the metal rich part of supernova ejecta (Wooden 1997). It is probable that the bulk
of the condensates are currently emitting in the FIR/submm and were too cold to be visible
to ISOCAM.
A temperature of at least ![]() 200 K is needed to explain
the colours of the ISOCAM measurement. By contrast,
even as soon as
200 K is needed to explain
the colours of the ISOCAM measurement. By contrast,
even as soon as ![]() 1300 days after outburst, the inferred temperature of condensates was only
1300 days after outburst, the inferred temperature of condensates was only
![]() 140 K (Bouchet et al. 1991; Biermann et al. 1992). The condensate
temperature should,
due to the expansion of the ejecta and weaker heating, have been even lower during the
ISOCAM observation
140 K (Bouchet et al. 1991; Biermann et al. 1992). The condensate
temperature should,
due to the expansion of the ejecta and weaker heating, have been even lower during the
ISOCAM observation ![]() 4000 days after outburst. The bulk of the condensates should therefore
mainly emit in the FIR. Energetically, it is feasible that
the observed MIR emission could nevertheless be attributed to a small fraction of
condensates residing in clumpy regions rich in
radioactive nucleosynthesis products where the local heating would be stronger.
However, detailed modeling of this case shows that the MIR spectral shape would only be reproduced
for a small range of filling factors, composition and sizes
(Fischera 2000).
4000 days after outburst. The bulk of the condensates should therefore
mainly emit in the FIR. Energetically, it is feasible that
the observed MIR emission could nevertheless be attributed to a small fraction of
condensates residing in clumpy regions rich in
radioactive nucleosynthesis products where the local heating would be stronger.
However, detailed modeling of this case shows that the MIR spectral shape would only be reproduced
for a small range of filling factors, composition and sizes
(Fischera 2000).
The fact that the MIR-emission was resolved by ISOCAM strongly suggests that the bulk of the
detected emission does not arise from condensates.
The condensates are thought to be restricted to the central metal
rich core of the ejecta (see e.g. Wooden 1997),
that is expanding with a velocity of
![]() (Kozma & Fransson 1998b).
At the time of the ISOCAM observations
(Kozma & Fransson 1998b).
At the time of the ISOCAM observations ![]() 4000 days after outburst the condensates did not
cover a region larger than
4000 days after outburst the condensates did not
cover a region larger than ![]() 0
0
![]() .
.
The derived size of 1.50-0.24+0.21 arcsec and the orientation of the emitting region, with an extension consistent with the elliptical projection of the thick inner ring (Sect. 3.2), both point to a predominantly circumstellar origin for the dust emission. The MIR extent is furthermore consistent with the extensions of the radio (Gaensler et al. 1997) and X-ray (Burrows et al. 2000) emitting regions. The presence of dust in the circumstellar environment has also been concluded from observations of scattered light correlated with the thick inner ring and the associated nebula (Wampler et al. 1990; Crotts et al. 1995).
Due to the fact that both the radio and the X-ray emission are thought to be associated with the blast wave as it propagated
into an HII-region of moderate density interior of the thick inner ring (Chevalier & Dwarkadas 1995),
it is likely that the emission in the MIR arises from circumstellar dust heated by shocked gas.
The observed dust temperature of ![]() 200 K is consistent with the predictions for collisionally heated grains
in equilibrium with a surrounding hot gas with a density of several
200 K is consistent with the predictions for collisionally heated grains
in equilibrium with a surrounding hot gas with a density of several
![]() (Fig. 7 in Dwek 1987).
Gas density of this order is indeed inferred from the observed X-ray emission in the shocked circumstellar medium of
SN 1987A (Borkowski et al. 1997). It is therefore to be expected that
the MIR emission should have a detailed morphology similar to the ring-like structure as seen in X-rays
(Burrows et al. 2000) with the centre close to the position of the supernova.
The derived luminosity in the MIR is higher than in X-rays (Hasinger et al. 1996)
by a factor of
(Fig. 7 in Dwek 1987).
Gas density of this order is indeed inferred from the observed X-ray emission in the shocked circumstellar medium of
SN 1987A (Borkowski et al. 1997). It is therefore to be expected that
the MIR emission should have a detailed morphology similar to the ring-like structure as seen in X-rays
(Burrows et al. 2000) with the centre close to the position of the supernova.
The derived luminosity in the MIR is higher than in X-rays (Hasinger et al. 1996)
by a factor of ![]() 10 as seen also in Fig. 6.
This is in agreement with values typically observed in galactic SNRs (Fig. 6 in Dwek 1988).
10 as seen also in Fig. 6.
This is in agreement with values typically observed in galactic SNRs (Fig. 6 in Dwek 1988).
The presence of dust in the circumstellar environment is consistent with a red supergiant phase in the time evolution of the supernova progenitor (Woosley 1988). In particular, our interpretation of the IR emission is qualitatively in agreement with the hypothesis that the HII-region is wind material from this red supergiant phase as suggested by Chevalier & Dwarkadas (1995).
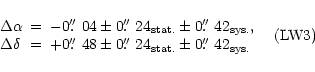 |
(11) |
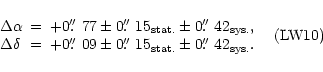 |
(12) |
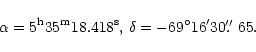
Acknowledgements
The work was supported by Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR) through the projects "50 OR 9702'' and "50 OR 99140''. The ISOCAM data presented in this paper were analysed using "CIA'', a joint development by the ESA Astrophysics Division and the ISOCAM Consortium. The ISOCAM Consortium is led by the ISOCAM PI, C. Cesarsky. The paper is based on observations made with ESO Telescopes at the La Silla or Paranal Observatories under program ID 000.0-0000 (observation day: 10/01/95, observer: S. Benetti). It is further based on observations made with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Institute. STScI is operated by the association of Universities for Research in Astronomy, Inc. under the NASA contract NAS 5-26555. We thank René Gastaud, Stephan Ott, Leo Metcalf and Ralf Siebenmorgen for discussions and information relevant to the analysis of the ISOCAM data. We thank the referees for their helpful suggestions.
To estimate the flux, size and coordinates of the IR-source we made use of a theoretical
point spread function (psf) for the ISO-satellite kindly made available to us by Dr. Ralph Siebenmorgen.
Images of point sources observed
in narrow band LW-filters of ISOCAM have been shown to be (except for LW1) in good agreement with this
function, which we will refer to as the monochromatic psf (Okumura 1998).
For the broad-band filters the psf
depends however on the source spectrum.
Therefore to achieve a high accuracy
in the determination of the source extension
we used a theoretical broad-band psf,
given by:
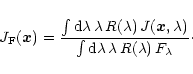 |
(A.1) |
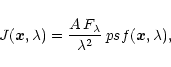 |
(A.2) |
Finally, we convolved the obtained function
![]() with the used pixel size and
the probability distribution of the actual pointing position of the satellite
during the observation (jitter).
with the used pixel size and
the probability distribution of the actual pointing position of the satellite
during the observation (jitter).
| Filter | LW10 | LW3 |
| FWHM of cuts through the maximum | ||
|
|
|
|
|
|
|
|
|
|
|
|
| relation meas./theor.d |
|
|
| FWHM of a Gaussian approximation | ||
|
|
4.071 | 4.896 |
|
|
4.035 | 4.866 |
| relation meas./theor. | 1.009 | 1.006 |
|
a Values taken from Okumura (1998).
b The given uncertainties correspond to the difference in the two values derived in Y and Z direction. c Derived from observations of HIC 78527 (LW10) and HIC 80331 (LW3). d Due to values from Okumura.6 |
An uncertainty of less than ![]() is smaller than the effect of varying
the spectral shape in the calculation in the psf. For Gaussian approximations to the
theoretical psf we found that the dependence of the FWHM
on the spectral index for the LW3 and LW10 filters
is close to linear. In a broad range from
is smaller than the effect of varying
the spectral shape in the calculation in the psf. For Gaussian approximations to the
theoretical psf we found that the dependence of the FWHM
on the spectral index for the LW3 and LW10 filters
is close to linear. In a broad range from
![]() to
to ![]() the FWHM is approximately given by
(Fischera 2000):
the FWHM is approximately given by
(Fischera 2000):
To derive the probability distributions shown in Fig. 3 we measured the variation
of
![]() as function of the variance
as function of the variance
![]() of the symmetrical Gauss function
assumed for the source. We also left flux density (
of the symmetrical Gauss function
assumed for the source. We also left flux density (![]() )
and coordinates (
)
and coordinates (![]() )
as free variables.
Because the source is smaller than the resolution of the
telescope, we had to convolve the source function with the theoretical psfdescribed in the previous section. To transform the variation of
)
as free variables.
Because the source is smaller than the resolution of the
telescope, we had to convolve the source function with the theoretical psfdescribed in the previous section. To transform the variation of ![]() into a probability
distribution we approximated the psf itself through a two dimensional
symmetrical Gaussian function with variance
into a probability
distribution we approximated the psf itself through a two dimensional
symmetrical Gaussian function with variance
![]() .
The value of
.
The value of
![]() was found through
a simple
was found through
a simple ![]() -fit between the psf and the Gaussian.
Measuring the most probable size
-fit between the psf and the Gaussian.
Measuring the most probable size
![]() of the source is then equivalent to measuring the
size of the image with the variance
of the source is then equivalent to measuring the
size of the image with the variance
![]() .
In the case
of normal distributed errors
the probability distribution of s with
.
In the case
of normal distributed errors
the probability distribution of s with
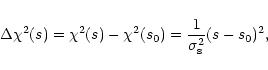 |
(B.3) |
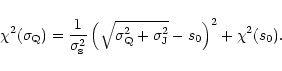 |
(B.4) |
To get the probability distribution over the physical sizes of the source we
normalized the distribution with:
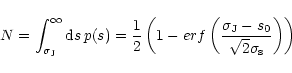 |
(B.5) |
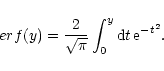 |
(B.6) |
The accuracy of the used method to derive the extension of the emitting region can be estimated
by assuming that IR source and psf are given by
Gauss functions with variances
![]() and
and
![]() .
An uncertainty
.
An uncertainty
![]() in the variance of the psflimits a measurement of the extension,
neglecting uncertainties in the data, to sources that are larger than
in the variance of the psflimits a measurement of the extension,
neglecting uncertainties in the data, to sources that are larger than
![]() .
The uncertainties in the FWHM of the theoretical psf as stated in Table A.1
gives a resolution limit of
.
The uncertainties in the FWHM of the theoretical psf as stated in Table A.1
gives a resolution limit of ![]() 0
0
![]() (FWHM) for both filters as will be verified in the next section.
(FWHM) for both filters as will be verified in the next section.
To verify the method for measuring the angular size of the MIR emission associated with SN 1987A we did two independent tests.
Firstly, we made a control experiment by applying the same method to observations of point-like source
calibration stars (Sect. B.2.1). Secondly, we repeated the procedure on the supernova data, but using the image
of a calibration star as the psf in place of the theoretical psf (see Sect. B.2.2).
The results both show that the model of the theoretical psf allows a measurement of the size of a
Gaussian source with a precision which corresponds to an inaccuracy of less than ![]() 1% in the FWHM. For the
two filters we derived a resolution limit of about
1% in the FWHM. For the
two filters we derived a resolution limit of about
![]() at 95% confidence level.
at 95% confidence level.
As measurements of point-like sources we have chosen for LW3 and LW10 filters observations of HIC 78527 and of HIC 80331, respectively.
As in the case of SN 1987A the observation provides a sampling of the source with an angular resolution of
![]() with a pixel size of
with a pixel size of
![]() (Table. B.1).
The data were calibrated in an almost identical way as the observation of SN 1987A
with the LW2 filter. The only difference was that
the deglitching for the calibration star data could be done fully automatically using standard procedures due
to the benign radiation environment encountered for these observations.
From the data we first derived four images with a sampling of
(Table. B.1).
The data were calibrated in an almost identical way as the observation of SN 1987A
with the LW2 filter. The only difference was that
the deglitching for the calibration star data could be done fully automatically using standard procedures due
to the benign radiation environment encountered for these observations.
From the data we first derived four images with a sampling of
![]() and calculated the final one as a weighted
average.
and calculated the final one as a weighted
average.
| Filter | LW10 | LW3 |
| target | HIC 78527 | HIC 80331 |
| TDT | 189007 | 119036 |
| observer | CAM CAL | CAM CAL |
| observation date | 15.3.1996 | 24.5.1996 |
| raster | ||
| pixel size |
|
|
| step size |
|
|
| read out interval | 0.28 s | 0.28 s |
| time between pointings | 60 s | 60 s |
The probability distributions in source size of the calibration stars were
derived from background-subtracted images using
theoretical psfs for a
spectral index of k=4 appropriate for the Rayleigh-Jeans part of the spectrum.
For the calculation we used a subimage of
![]() pixels centred on the source.
pixels centred on the source.
The result
is shown in Fig. B.1.
As for the supernova data we have taken the uncertainties of the pixel values to be equal and
assigned a value such that the minimum ![]() corresponds to a confidence level of 90%.
The most probable sizes are found to be much smaller than the FWHM of the psf.
For both filters we found that the source is smaller than
corresponds to a confidence level of 90%.
The most probable sizes are found to be much smaller than the FWHM of the psf.
For both filters we found that the source is smaller than ![]() 0
0
![]() with a confidence level of
with a confidence level of ![]() .
This is consistent with
the rough estimate of
.
This is consistent with
the rough estimate of
![]() given in Sect. B.1.
given in Sect. B.1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1827f11.epsi}\hspace*{4mm}
\includegraphics[width=8.8cm,clip]{ms1827f12.epsi}
\end{figure}](/articles/aa/full/2002/17/aa1827/Timg271.gif) |
Figure B.1: Result of the size measurement for the point-like sources HIC 80331 (LW3-filter) and HIC 78527 (LW10-filter). The derived probability distributions of the size s (see Eq. (B.1)) of the theoretical image B (Eq. (2)) as a function of the FWHM of the Gaussian source is shown in the left panel. The right panel gives the corresponding confidence levels for upper limits on source size derived using Eq. (B.7). |
No point-like calibration source with the same spectrum of the source associated with SN 1987A was observed
with ISOCAM. However, the effect of interchanging the theoretical psf with the observed psfcould still be evaluated. This was done by comparing calculations for the size probability distributions
at
![]() ,
respectively
using as psf the observed image of a star and a theoretical psf for a spectral index k=4.
To achieve
for the image of the calibration star the same sampling of
,
respectively
using as psf the observed image of a star and a theoretical psf for a spectral index k=4.
To achieve
for the image of the calibration star the same sampling of
![]() as for the theoretical psfwe used a cubic interpolation applied to the logarithm of the pixel values.
It can be seen from Fig. 3 that a most probable size of
as for the theoretical psfwe used a cubic interpolation applied to the logarithm of the pixel values.
It can be seen from Fig. 3 that a most probable size of
![]() is derived both for the measured
and the theoretical psf.
The larger size derived by using the measured image of a calibration star instead
of the theoretical psf appropriate for the supernova is caused by
the steeper spectrum.
is derived both for the measured
and the theoretical psf.
The larger size derived by using the measured image of a calibration star instead
of the theoretical psf appropriate for the supernova is caused by
the steeper spectrum.
To determine the position of the IR-emitting star we used archival observations with the WFPC2 of the HST,
made in V-band in February 1996
and three observations (two in R one in V-band) made in 1995 of the supernova with the SUSI-instrument
(SUperb-Seeing Imager) of the NTT (New Technology Telescope).
The V-band filter was also used to determine the correction
of the distortion on the
WFPC2-fields (Holtzman et al. 1995).
The measurement with the NTT
was necessary due to the fact that the supernova and the IR-emitting star were on different CCDs
of the observation with the WFPC2, which can give an additional error in the astrometry. The astrometry
on one single CCD of the WFPC2 is accurate to
![]() .
The only object, whose coordinates are determined with high accuracy is the SN 1987A itself.
To remove the offset in the astrometry
of the WFPC2 data,
we have taken the position
.
The only object, whose coordinates are determined with high accuracy is the SN 1987A itself.
To remove the offset in the astrometry
of the WFPC2 data,
we have taken the position
![]() (J2000)
from Reynolds et al. (1995),
which is accurate to
(J2000)
from Reynolds et al. (1995),
which is accurate to ![]()
![]() 10-3 arcsec.
We removed the distortion on the WFPC2-field using the
polynomial correction given by Holtzman et al. (1995).
10-3 arcsec.
We removed the distortion on the WFPC2-field using the
polynomial correction given by Holtzman et al. (1995).
To derive the astrometry of the observations made with the SUSI instrument, we projected
all possible star positions, seen on a single CCD of the WFPC2, with a tangential projection on the
SUSI field and compared these coordinates (xi,yi) with the star positions
![]() on the SUSI field with a non linear
on the SUSI field with a non linear ![]() -fit:
-fit:
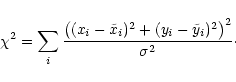 |
(C.1) |
We found no indication of a distortion on the SUSI field.
The final derivations of the star positions in the observations with the SUSI instrument and the
WFPC2 were accurate by
![]() in the case
of the PC-field of the WFPC2 and by
in the case
of the PC-field of the WFPC2 and by
![]() in the case of the CCD with
the star (WF3). This is consistent with the accuracy given for the single CCDs of the WFPC2 after
correcting for distortion (
in the case of the CCD with
the star (WF3). This is consistent with the accuracy given for the single CCDs of the WFPC2 after
correcting for distortion (
![]() ,
Holtzman et al. 1995).
The single CCDs indeed show a small offset of up to
,
Holtzman et al. 1995).
The single CCDs indeed show a small offset of up to ![]() 0
0
![]() .
On the other hand we found
no measurable offset for the two CCDs with the supernova and the single IR-emitting star.
The absolute coordinates of the single IR-emitting star in the SUSI field are found to be
.
On the other hand we found
no measurable offset for the two CCDs with the supernova and the single IR-emitting star.
The absolute coordinates of the single IR-emitting star in the SUSI field are found to be
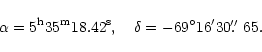 |
(C.2) |