A&A 386, 721-731 (2002)
DOI: 10.1051/0004-6361:20020113
1 - Institut d'Astrophysique Spatiale, Université Paris XI, 91405 Orsay, France
2 -
Département Atomes et Molécules en Astrophysique, Observatoire de Paris-Meudon, 92195 Meudon, France
Received 17 July 2001 / Accepted 14 December 2001
Abstract
The aim of the present work is to present theoretical results on the Stokes parameters of a resonance spectral line, scattered by moving atoms (or ions) in the presence of a local magnetic field. We assume that the scattered line is sensitive to the Hanle effect due to the magnetic field and also to Doppler redistribution due to the atomic motions. The present theory is developed for a two-level atom, in the framework of the density matrix formalism Blum (1981). Analogous results given in Sahal-Bréchot et al. (1986) for the magnetic-field effect alone, and in Sahal-Bréchot et al. (1998) for the velocity-field effect alone, can be obtained from our theory by cancelling in the equations, respectively, the velocity field or the magnetic field. The results of our theory are general and can be used for astrophysical studies concerning the Hanle effect and the Doppler redistribution effect on the linear polarization parameters of the scattered radiation. They can be used particularly to interpret linear polarization of coronal spectral lines to get a complete determination of vectorial quantities such as the coronal magnetic field and the solar wind velocity field vectors. As an application, the atomic velocity field distribution is supposed to be Maxwellian with a drift velocity field vector. This latter describes the macroscopic motion of the scattering atoms. In the solar corona, it can be assimilated into the solar wind velocity field vector.
Key words: atomic processes - polarization - scattering - Sun: corona - Sun: magnetic fields - Sun: solar wind
Processes in the solar atmosphere such as coronal heating and solar wind acceleration have been studied (observationally and theoretically) for a long time. But until now, due to our very limited knowledge of their sources and nature, they still remain among the great challenges of solar physics. The interpretation of these phenomena arises from magnetohydrodynamic theoretical developments, which require the knowledge of vectorial quantities such as the coronal magnetic field and the solar wind velocity field vectors.
In astrophysics, the complete determination of vectorial quantities is more difficult than the determination of thermodynamic scalar quantities (temperature, density, pressure etc.). These in fact can be determined by using spectroscopic methods based on the interpretation of the intensity profile of spectral lines. Common spectropolarimetric methods can only give a partial determination of the vectorial quantities (here, we limit ourselves to resonant scattering): the longitudinal component of the magnetic field via the Zeeman effect, or the line-of-sight component of the scattering atoms velocity field via Doppler shifts of the emitted spectral lines... However, spectropolarimetric methods have the potential to provide a complete determination of vectorial quantities. These methods are based on the interpretation of the Stokes parameters of spectral lines sensitive to the Hanle effect (for the magnetic field) and to the Doppler redistribution (for the velocity field vector). In fact, the Stokes parameters of well selected spectral lines sensitive to the Hanle effect depend on the three components of the magnetic field. Thus, they contain all the information on this vector (strength and direction) as shown by Sahal-Bréchot et al. (1977). Similarly, the Stokes parameters of spectral lines sensitive to the Doppler redistribution of an incident anisotropic and frequency dependent radiation field depend on the strength and direction of the macroscopic velocity-field vector of the scattering atom (Sahal-Bréchot et al. 1998). Consequently, the presence of a magnetic field (velocity field) modifies the polarization of the scattered line which is sensitive to the Hanle effect (Doppler redistribution). Inversely, by measuring the frequency-integrated linear-polarization![]() parameters (degree and direction of linear polarization) of a spectral line sensitive to the magnetic or to the velocity field and another spectral quantity, we can get complete information on the field vector. To determine completely a vector, we need in fact three independent measurements. This is why we need an additional measurement other than the degree and direction of linear polarization. The third quantity may be the electronic density, the Doppler shift, etc.
parameters (degree and direction of linear polarization) of a spectral line sensitive to the magnetic or to the velocity field and another spectral quantity, we can get complete information on the field vector. To determine completely a vector, we need in fact three independent measurements. This is why we need an additional measurement other than the degree and direction of linear polarization. The third quantity may be the electronic density, the Doppler shift, etc.
In the solar corona, the emitted resonance lines from lithium-like ion (O VI, N V, C IV, ...) are excited by isotropic electronic collisions (that do not create polarization in the Zeeman sublevels) and by photoexcitation by the unpolarized and anisotropic radiation coming from the underlying chromosphere-corona transition region. The de-excitation in these lines is by spontaneous emission. The partial anisotropy of the incident radiation from the transition region is at the origin of the atomic alignment in the upper levels. These scattered lines are, consequently, linearly and partially polarized. In addition, they are among the strongest lines emitted in the corona up to large heights above the solar limb (Vial et al. 1980; Kohl et al. 1998; Xing Li et al. 1998; and other papers related to UVCS (UltraViolet Coronagraph Spectrometer, Kohl et al. 1995) aboard the SoHO (the Solar and Heliospheric Observatory, Domingo et al. 1995)).
At low latitudes in the solar corona, these lines have typical widths of a few 10 km s-1, and they are affected by the Doppler dimming effect due the outflow velocity field of the coronal material (which is also of the order of few 10 km s-1). The moving atoms (or ions) absorb the incident radiation somewhere in the wings of the incident line profile, at some distance from the zero velocity line center. This means that the absorption takes place away from the maximum of the incident radiation line profile. Consequently, the reemitted line is not only shifted and has its intensity dimmed compared to the incident one, but also its linear polarization parameters (degree and direction of linear polarization) are modified due to the Doppler redistribution effect (Sahal-Bréchot et al. 1998). The linear polarization parameters of the scattered radiation depend on the strength and direction of the macroscopic velocity field vector of the scattering ions, so they carry complete information on the solar wind velocity field vector. Therefore, the measurement of the polarization parameters of such lines (especially the O VI
![]() line, hereafter O VI D2) permits one to determine completely the solar wind velocity field vector. Moreover, the upper levels of the corresponding transitions have short lifetimes. Owing to the smallness of the coronal magnetic field strength, some of these lines are expected to be sensitive to the Hanle effect. The linear polarization profiles of these lines are also expected to contain the complete information on the three components of the coronal magnetic field vector. This makes the measurement of the linear polarization of these coronal lines very important and may be the best method to get information on the solar wind velocity field vector and on the coronal magnetic field vector.
line, hereafter O VI D2) permits one to determine completely the solar wind velocity field vector. Moreover, the upper levels of the corresponding transitions have short lifetimes. Owing to the smallness of the coronal magnetic field strength, some of these lines are expected to be sensitive to the Hanle effect. The linear polarization profiles of these lines are also expected to contain the complete information on the three components of the coronal magnetic field vector. This makes the measurement of the linear polarization of these coronal lines very important and may be the best method to get information on the solar wind velocity field vector and on the coronal magnetic field vector.
In the second section, we will review briefly the magnetic-field effect (Hanle effect) and the Doppler redistribution effect on the linear polarization parameters of a resonance scattered line. The third section is devoted to the presentation of the physical and astrophysical context of the present work and to the description of the physical system considered to compute the linear polarization of a spectral line due to the resonance scattering of the incident chromosphere-corona transition region radiation by the coronal ions. In our model, we will limit ourself to an elementary scattering medium in a limited volume located on the solar vertical (theoretically, one scattering point). In the fourth section, we will derive the density matrix elements of the unpolarized incident radiation coming from the underlying chromosphere-corona transition region. The fifth section is devoted to the computation of the atomic density matrix elements interacting with the incident radiation and the isotropic electrons of the surrounding medium, in the presence of a local magnetic field. In the computations, we will take into account the effect of the atomic velocity field distribution and the effect of the local magnetic field. The sixth section is devoted to the computation of the density matrix elements of the scattered radiation along the line of sight. In Sect. 7, we use the precedent results to derive the Stokes parameters of a spectral line sensitive to the Hanle effect and to the effect of the drift velocity field of the scattering medium. In the following section, we apply the results of the theory to the case of the O VI D2 coronal line. We limit ourself for this application to a Maxwellian velocity distribution with a drift velocity field describing the macroscopic motion of the scattering ion. The last section is devoted to the conclusions and the prospects relative to the present work.
![\begin{figure}
\includegraphics[width=10cm,clip]{1681_f1.eps}\end{figure}](/articles/aa/full/2002/17/aa1681/Timg16.gif) |
Figure 1:
Case of resonance scattering of a purely directive and unpolarized incident radiation in the direction (Pz) by moving atoms with a velocity
|
| Open with DEXTER | |
The Hanle effect results in the modification of the linear polarization
parameters (degree and direction of linear polarization) of a
spectral line by a local magnetic field vector. From a classical
point of view, the excited atom (or ion) acts as a dipole, so the
corresponding dipolar electric field is submitted to a precession motion
around the magnetic field vector at the Larmor frequency, ![]() ,
which is
directly related to the magnetic field strength (
,
which is
directly related to the magnetic field strength (
![]() ,
,
![]() is the Bohr magneton and B is the magnetic field strength). In addition, the dipolar electric field strength is damped by the finite lifetime of the upper level of the atomic transition considered. In the case where the magnetic field is strong, the precession motion dominates the damping and, consequently, the electric field vector follows a completely symmetric path, and the re-emitted radiation is depolarized (see cf., Landi Degl'Innocenti 1992: Fig. 8). However, if the damping time and the precession period are approximately of the same order of magnitude, the emitted radiation is linearly polarized with a degree lower than in the case of zero magnetic field. The polarization direction also makes an angle with that for zero magnetic field (for more details, see Mitchell & Zemansky 1934). The modification of the polarization parameters depends on the strength and direction of the magnetic field vector. We should notice that this classical description can explain only the case of the normal Zeeman triplet (i.e., two-level atom
is the Bohr magneton and B is the magnetic field strength). In addition, the dipolar electric field strength is damped by the finite lifetime of the upper level of the atomic transition considered. In the case where the magnetic field is strong, the precession motion dominates the damping and, consequently, the electric field vector follows a completely symmetric path, and the re-emitted radiation is depolarized (see cf., Landi Degl'Innocenti 1992: Fig. 8). However, if the damping time and the precession period are approximately of the same order of magnitude, the emitted radiation is linearly polarized with a degree lower than in the case of zero magnetic field. The polarization direction also makes an angle with that for zero magnetic field (for more details, see Mitchell & Zemansky 1934). The modification of the polarization parameters depends on the strength and direction of the magnetic field vector. We should notice that this classical description can explain only the case of the normal Zeeman triplet (i.e., two-level atom
![]() ). For more complicated atomic transitions, one must use quantum theory.
). For more complicated atomic transitions, one must use quantum theory.
The Hanle effect was used successfully to study the magnetic field vector in solar prominences (Leroy 1977; Sahal-Bréchot et al. 1977; Bommier & Sahal-Bréchot 1978; Leroy 1978; Bommier et al. 1981; Sahal-Bréchot 1981; Landi Degl'Innocenti 1982; Athay et al. 1983; Leroy et al. 1983; Leroy et al. 1984; Querfeld et al. 1985; Bommier et al. 1986a,b; Bommier et al. 1994). Bommier & Sahal-Bréchot (1978 & 1982) showed that the sensitivity of a given spectral line to the Hanle effect occurs within the range
| (1) |
![\begin{figure}
\includegraphics[width=6.1cm,clip]{1681_f2.eps}\includegraphics[width=6.1cm]{1681_f3.eps}\end{figure}](/articles/aa/full/2002/17/aa1681/Timg25.gif) |
Figure 2: Effect of the velocity field of the scattering atoms on the linear polarization parameters of the reemitted radiation. To obtain the modification of the polarization parameters, we need a partially anisotropic incident radiation field. This is the case of the chromosphere-corona transition region radiation field scattered by the coronal ions. The polarization parameters of the reemitted photons carry with them important information on the macroscopic velocity field vector of the coronal ions which can be assimilated to the solar wind velocity field vector. In the present figure, we consider the case of right scattering, the line of sight (PZ) is parallel to the axis (Py). |
| Open with DEXTER | |
In the present section, we consider the case of unpolarized radiation beam propagating in the direction
![]() (Fig. 1) and which is scattered by moving atoms or ions at P. We observe the scattered photons in the direction of the line of sight
(Fig. 1) and which is scattered by moving atoms or ions at P. We observe the scattered photons in the direction of the line of sight
![]() .
We assume that the incident line profile is a Gaussian centered at the frequency
.
We assume that the incident line profile is a Gaussian centered at the frequency
![]() of the corresponding atomic transition. In the atomic frame, an atom (or ion) absorbs the incident radiation and reemits photons at the frequency
of the corresponding atomic transition. In the atomic frame, an atom (or ion) absorbs the incident radiation and reemits photons at the frequency
![]() .
This assumes that the atomic sublevels are infinitely sharp and that the absorption profile can be assimilated to a
.
This assumes that the atomic sublevels are infinitely sharp and that the absorption profile can be assimilated to a ![]() -function. Since the natural width of the transition is several orders of magnitude smaller than the (Doppler) width of the incident radiation, this is indeed a very good approximation. In the laboratory frame, the moving atom with a velocity
-function. Since the natural width of the transition is several orders of magnitude smaller than the (Doppler) width of the incident radiation, this is indeed a very good approximation. In the laboratory frame, the moving atom with a velocity
![]() absorbs incident photons at the shifted frequency
absorbs incident photons at the shifted frequency
![]() .
Thus, the absorption takes place somewhere in the wings of the incident line profile, which means that the absorbed intensity is lower than that of the central zero velocity field frequency of the incident line profile. Consequently, the scattered line is not only shifted (by
.
Thus, the absorption takes place somewhere in the wings of the incident line profile, which means that the absorbed intensity is lower than that of the central zero velocity field frequency of the incident line profile. Consequently, the scattered line is not only shifted (by
![]() ,
where
,
where
![]() is the component of the atomic velocity field along the line of sight), but has also its intensity dimmed compared to the incident one (Fig. 1). In this case (perfectly directive incident radiation, i.e., maximum anisotropy), it is found that the atomic velocity field affects only the scattered line intensity but has no effect on
its linear polarization parameters, which are the same as those of photons scattered by atoms at rest (here we take into account only radiative excitation). The corresponding formulae are given by Sahal-Bréchot et al. (1998) (formulae 51-55). To get the effect of the velocity field on the linear polarization parameters of the scattered radiation, we need partial anisotropy of the incident radiation.
is the component of the atomic velocity field along the line of sight), but has also its intensity dimmed compared to the incident one (Fig. 1). In this case (perfectly directive incident radiation, i.e., maximum anisotropy), it is found that the atomic velocity field affects only the scattered line intensity but has no effect on
its linear polarization parameters, which are the same as those of photons scattered by atoms at rest (here we take into account only radiative excitation). The corresponding formulae are given by Sahal-Bréchot et al. (1998) (formulae 51-55). To get the effect of the velocity field on the linear polarization parameters of the scattered radiation, we need partial anisotropy of the incident radiation.
To explain qualitatively the velocity-field effect on the polarization parameters of the scattered radiation, we consider the case of the coronal ions which scatter the unpolarized and partially anisotropic radiation coming from the underlying chromosphere-corona transition region. In the laboratory frame, the frequency absorption of the incident radiation by the moving ion depends on the incidence direction of the photons, which makes different angles with the ion velocity field as it varies within the radiation cone. Radiation coming from a given direction is more or less dimmed than others as shown by Fig. 2. The angular dependence of the dimming due to the scattering ion motion leads to a modification of the linear polarization parameters of the scattered line. The rotation angle of the direction of linear polarization and the decrease of the polarization degree of the scattered radiation depend on the three components of the velocity vector of the scattering ion. The quantum theory of this phenomenon and the resulting analytical formulae are developed in Sahal-Bréchot et al. (1998).
The aim of the present work is to determine the equations giving the Stokes parameters of a resonance scattered spectral line by moving atoms in the presence of a local magnetic field. The scattered line is supposed to be sensitive simultaneously to the Hanle effect due the local magnetic field and to the Doppler redistribution effect due the macroscopic velocity field of the scattering atoms. These atoms are supposed to be excited by isotropic collisions and by a partially anisotropic radiation field. Owing to this partial anisotropy, the scattered photons are linearly and partially polarized. This is the case of the coronal ions which scatter the partially anisotropic radiation coming from the underlying chromosphere-corona transition region.
The physical system considered is composed of moving atoms in an elementary volume located at P (theoretically, one point: Fig. 3). The scattering volume is located at a given distance above the limb. The incident unpolarized photons come from a spherical cap on the Sun, limited by the cone tangent to the Sun and with vertex at the point P. The atoms interact with the local magnetic field embedded in the surrounding medium. This is the case of the coronal ions, such as O VI, which absorb and reemit by resonance scattering the unpolarized radiation coming from the underlying transition region. The scattered photons are observed in the direction of the line of sight which makes an angle ![]() (scattering angle) with the vertical to the Sun which is the symmetry axis of the incident radiation cone.
(scattering angle) with the vertical to the Sun which is the symmetry axis of the incident radiation cone.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1681_f4.eps}\end{figure}](/articles/aa/full/2002/17/aa1681/Timg34.gif) |
Figure 3:
The physical system considered is composed of atoms or ions located around the point P. The atoms (ions) interact independently with the partially anisotropic incident radiation coming from the spherical cap limited by the tangents to the sphere with center O and radius
|
| Open with DEXTER | |
Hereafter, we adopt the model of the two-level atom which is valid for the description of the scattered radiation by the coronal ions in the EUV wavelength domain. We assume that the lower level of the atomic transition considered is not polarizable (which is the case of the lower level of the
![]() transition of the O VI D2 coronal line). The electrons velocity field distribution is an isotropic Maxwellian, so the electronic collisions do not create atomic polarization (i.e., population imbalance) in the upper level of the atomic transition.
transition of the O VI D2 coronal line). The electrons velocity field distribution is an isotropic Maxwellian, so the electronic collisions do not create atomic polarization (i.e., population imbalance) in the upper level of the atomic transition.
Atoms interact with photons and colliding particles (electrons) independently. Studying the interaction of one atom with the local medium leads to the statistical equilibrium equations where the solutions are the populations and coherences between the Zeeman sublevels which are related to the Stokes parameters of the scattered photons. To obtain solutions (Stokes parameters) of the whole system at a given frequency, we then can sum the obtained solutions for one atom over all the atoms of the system, having the same velocity field along the line of sight. Hereafter we will consider only one scattering atom for the computations of the Stokes parameters of the scattered photons as a function of the magnetic field and the atoms macroscopic velocity field vectors. At the end, we will sum the final results over the atoms of the whole system (for more details, see Sahal-Bréchot et al. 1998).
The total system (scattering atom, colliding particles, radiation and magnetic field) is isolated and reversible. So, it can be described by its density matrix, ![]() ,
solution of the Schrödinger equation
,
solution of the Schrödinger equation
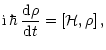 |
(2) |
For the calculations of the Stokes parameters of the scattered line, the magnetic field vector is defined by its strength B, by the polar angle ![]() with the polar axis, and by the azimuthal angle
with the polar axis, and by the azimuthal angle ![]() between the solar limb tangent (Px) and the projection of the magnetic field vector on the plane (xPy) tangent to the solar limb.
between the solar limb tangent (Px) and the projection of the magnetic field vector on the plane (xPy) tangent to the solar limb.
In the comoving frame, the atom absorbs the incident radiation at the transition frequency
![]() (we assume that the absorption profile is a
(we assume that the absorption profile is a ![]() -function). However in the laboratory frame, the moving atom, with a velocity vector
-function). However in the laboratory frame, the moving atom, with a velocity vector
![]() ,
absorbs the incident radiation coming from a given elementary area around a point M on the spherical cap at the shifted frequency
,
absorbs the incident radiation coming from a given elementary area around a point M on the spherical cap at the shifted frequency
![]() .
.
![]() is the unitary vector of the direction
is the unitary vector of the direction
![]() of angular coordinates
of angular coordinates
![]() in the solar frame (Pxyz).
We note by
in the solar frame (Pxyz).
We note by
![]() the angular distribution of the local intensity at the scattering point P for the radiation coming from the direction
the angular distribution of the local intensity at the scattering point P for the radiation coming from the direction
![]() at the frequency
at the frequency ![]() (given in erg cm-2 s-1 sr-1 Hz-1).
(given in erg cm-2 s-1 sr-1 Hz-1).
We denote the polarization matrix of the incident photons at the frequency ![]() by
by
![]() ,
which depends on the frequency because of the scattering atom motion. This matrix is obtained by averaging the incident radiation on all the directions (Sahal-Bréchot et al. 1998). It should be normalized to the mean local intensity of the incident radiation
,
which depends on the frequency because of the scattering atom motion. This matrix is obtained by averaging the incident radiation on all the directions (Sahal-Bréchot et al. 1998). It should be normalized to the mean local intensity of the incident radiation
Equation (3) implies that the polarization matrix of the incident radiation can be written as the angular average
![]() multiplied by a unitary matrix
multiplied by a unitary matrix
![]() ,
which describes the angular behavior of the incident radiation coming in the direction
,
which describes the angular behavior of the incident radiation coming in the direction
![]() (for more details see Sahal-Bréchot et al. 1998). The elements of the polarization matrix expanded on the irreducible tensor basis
(for more details see Sahal-Bréchot et al. 1998). The elements of the polarization matrix expanded on the irreducible tensor basis
![]() are obtained by expanding the matrix
are obtained by expanding the matrix
![]() in multipole terms on the same basis in the solar frame (Pxyz) ((Pz) is the quantization axis), thus
in multipole terms on the same basis in the solar frame (Pxyz) ((Pz) is the quantization axis), thus
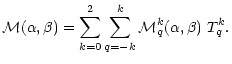 |
(4) |
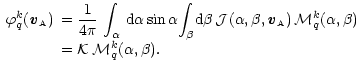 |
(5) |
The density matrix of an atom in interaction with its surrounding medium (incident photons and colliding particles) depends on the local magnetic field and eventually on the atomic velocity field. It is more practical to write the equations describing this interaction in the frame where the magnetic field vector is parallel to the quantization axis. This permits to keep the magnetic quantum number as a good quantum number. In addition, the density matrix elements of the reemitted photons are easily obtained in this frame.
We note by
![]() the magnetic frame, the quantization axis
the magnetic frame, the quantization axis
![]() is parallel to the magnetic field vector. It is, so, necessary to rewrite the density matrix elements of the incident photons in the frame
is parallel to the magnetic field vector. It is, so, necessary to rewrite the density matrix elements of the incident photons in the frame
![]() which is obtained from the solar one (Pxyz) by a rotation with the Euler angle
which is obtained from the solar one (Pxyz) by a rotation with the Euler angle
![]() (
(![]() and
and ![]() are respectively the azimuth and the polar angle of the magnetic field vector in the frame (Pxyz)).
are respectively the azimuth and the polar angle of the magnetic field vector in the frame (Pxyz)).
The formula giving the density matrix elements
![]() (relative to a frame
(relative to a frame
![]() )
obtained from the elements
)
obtained from the elements
![]() (relative to a frame
(relative to a frame ![]() )
through a rotation from
)
through a rotation from ![]() to
to
![]() of angles
of angles
![]() is given by (Bommier 1977)
is given by (Bommier 1977)
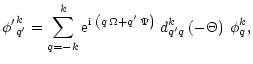 |
(6) |
We note by
![]() the incident photons density matrix in
the incident photons density matrix in
![]() .
The matrix elements of
.
The matrix elements of
![]() are obtained from those of
are obtained from those of
![]() by using the equation of the density matrix element transformation by an Euler rotation given by
by using the equation of the density matrix element transformation by an Euler rotation given by
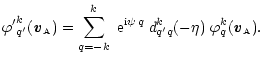 |
(7) |
![\begin{eqnarray*}\begin{array}{l}
{\varphi^\prime}^0_0({\textbf{\textit{v}}}_{\s...
...f{\textit{v}}}_{\scriptscriptstyle{\rm {A}}})\right]
\end{array}\end{eqnarray*}](/articles/aa/full/2002/17/aa1681/img72.gif)
![$\displaystyle \begin{array}{l}
{\varphi^\prime}^2_1({\textbf{\textit{v}}}_{\scr...
...phi^2_2({\textbf{\textit{v}}}_{\scriptscriptstyle{\rm {A}}})\right]
\end{array}$](/articles/aa/full/2002/17/aa1681/img73.gif) |
(8) |
![\begin{eqnarray*}\begin{array}{l}
{\varphi^\prime}^2_2({\textbf{\textit{v}}}_{\s...
...f{\textit{v}}}_{\scriptscriptstyle{\rm {A}}})\right].
\end{array}\end{eqnarray*}](/articles/aa/full/2002/17/aa1681/img74.gif)
| (9) |
As mentioned in Sahal-Bréchot et al. (1998), the expressions obtained for the polarization matrix elements of the incident radiation are general and no restricting assumptions are made to this part. In order to get the density matrix of the reemitted photons which lead to the Stokes parameters of the scattered radiation, we should write and solve the statistical equilibrium equations describing the interaction of the moving atom with the incident radiation.
We denote with
![]() the density matrix of an atom having the velocity vector
the density matrix of an atom having the velocity vector
![]() .
We have
.
We have
| (10) |
In order to obtain, in the laboratory frame, the master equation for
![]() ,
which describes the evolution of the atomic subsystem coupled with its surrounding medium (photons and colliding particles (electrons)) (Bommier & Sahal-Bréchot 1978; Cohen-Tannoudji 1962 & 1977; Fano 1957), we assume few approximations. The impact approximation (Bommier & Sahal-Bréchot 1991) supposes that the mean duration of the atom interaction with a photon or an electron is much shorter than the mean duration separating two successive interactions; the "no-back reaction'' approximation (Bommier & Sahal-Bréchot 1991; Cohen-Tannoudji 1977; Cohen-Tannoudji et al. 1988; Fano 1957), also supposes that the atom surrounding medium has enough degrees of freedom to dissipate rapidly the atom interaction effects in the way that they will not have any back effect on this atom; the Markovian evolution of
,
which describes the evolution of the atomic subsystem coupled with its surrounding medium (photons and colliding particles (electrons)) (Bommier & Sahal-Bréchot 1978; Cohen-Tannoudji 1962 & 1977; Fano 1957), we assume few approximations. The impact approximation (Bommier & Sahal-Bréchot 1991) supposes that the mean duration of the atom interaction with a photon or an electron is much shorter than the mean duration separating two successive interactions; the "no-back reaction'' approximation (Bommier & Sahal-Bréchot 1991; Cohen-Tannoudji 1977; Cohen-Tannoudji et al. 1988; Fano 1957), also supposes that the atom surrounding medium has enough degrees of freedom to dissipate rapidly the atom interaction effects in the way that they will not have any back effect on this atom; the Markovian evolution of
![]() supposes that this evolution depends only on the present time. We neglect also the atom recul during the interaction with the electrons, this is because of the atom-electron mass ratio. It is also the case for the atom-photon interaction.
supposes that this evolution depends only on the present time. We neglect also the atom recul during the interaction with the electrons, this is because of the atom-electron mass ratio. It is also the case for the atom-photon interaction.
The complete equation for the atomic density matrix evolution is given by Eq. (36) in Bommier & Sahal-Bréchot (1978). By taking into account the approximations cited previously, the master equation of the atomic subsystem density matrix takes the following form
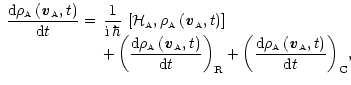 |
(11) |
Writing the coupling terms of the master equation as a function of the corresponding S matrixes (scattering matrixes) (see Bommier & Sahal-Bréchot 1991) permits us to compute them easily. The atom interaction with the electrons with a isotropic distribution affects only the Zeeman sub-level populations. The atom motion appears only in the coupling terms with the incident photons, whose density matrix elements were computed previously.
In the case of a two-level atom (e.g. the case of the O VI D2 coronal line), we obtain the statistical equilibrium equations between the upper level u and the lower level l of the atomic transition considered. In the irreducible tensor basis, by taking into account of the magnetic-field effect and of the atom velocity-field effect (the quantization axis is parallel to the magnetic field vector), we obtain in the frame
![]()
![\begin{displaymath}\begin{array}{l}
{\displaystyle
^{J_{\rm u}J_{\rm u}}{\rho_{\...
...J_{\rm u} & J_{\rm l}
\end{array}\right\} \Bigg] },
\end{array}\end{displaymath}](/articles/aa/full/2002/17/aa1681/img84.gif) |
(12) |
The polarization matrix elements of the reemitted photons can be obtained from the previous equation describing the evolution of the atomic subsystem in interaction with the incident photons and the colliding particles in the presence of a magnetic field. We denote by
![]() this matrix in the magnetic field frame
this matrix in the magnetic field frame
![]() where the quantization axis
where the quantization axis
![]() is parallel to the magnetic field vector. The polarization matrix elements
is parallel to the magnetic field vector. The polarization matrix elements
![]() of the reemitted photons are given (as number of re-emitted photons per unit time, per unit volume and per unit velocity distribution) by
of the reemitted photons are given (as number of re-emitted photons per unit time, per unit volume and per unit velocity distribution) by
![\begin{displaymath}\begin{array}{l}
{\displaystyle
\phi_{q}^{k}
\left({\textbf{...
...riptscriptstyle{\rm {A}}}\right) }
\; c(k) \Bigg],
\end{array}\end{displaymath}](/articles/aa/full/2002/17/aa1681/img93.gif) |
(13) |
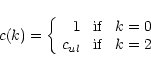 |
(14) |
Then, the polarization matrix elements of the reemitted photons written in the frame of the magnetic field are given by
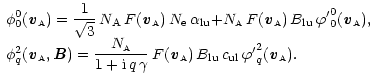 |
(15) |
| (16) |
It is more useful to rewrite these polarization matrix elements of the reemitted radiation first in the solar frame (Pxyz) and then in the frame of the line of sight (PXYZ). This is to reduce the number of rotation angles in the final expressions. The atomic frame (Pxyz) is obtained from the magnetic frame
![]() by a rotation with angles
by a rotation with angles
![]() .
We note with
.
We note with
![]() and
and
![]() ,
respectively, the polarization matrix elements of the scattered photons (developed on the irreducible tensor basis) in the solar frame (Pxyz) and in the frame of the line of sight (PXYZ).
,
respectively, the polarization matrix elements of the scattered photons (developed on the irreducible tensor basis) in the solar frame (Pxyz) and in the frame of the line of sight (PXYZ).
The polarization matrix elements of the reemitted photons
![]() written in (Pxyz) are given by
written in (Pxyz) are given by
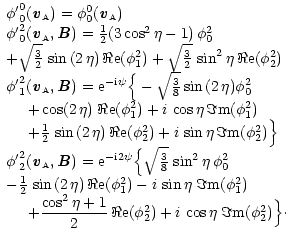 |
(17) |
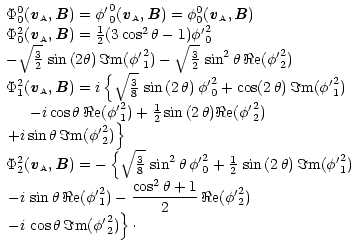 |
(18) |
The Stokes parameters of the re-emitted radiation by moving atom with a velocity field
![]() are given as a function of the density matrix elements of the reemitted photons written in the frame of the line of sight (in number of reemitted photons per unit of time, per unit of volume and per unit of velocity distribution)
by the following relations (Sahal-Bréchot et al. 1998, 1986)
are given as a function of the density matrix elements of the reemitted photons written in the frame of the line of sight (in number of reemitted photons per unit of time, per unit of volume and per unit of velocity distribution)
by the following relations (Sahal-Bréchot et al. 1998, 1986)
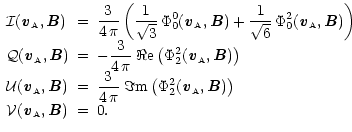 |
(19) |
The general form of the reemitted radiation Stokes parameters (here we take into account only of the linear polarization) is given by
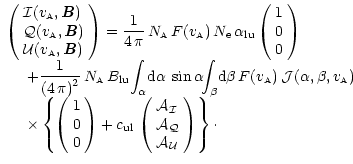 |
(20) |
From the forms of the equations giving the Stokes parameters as a function of the magnetic field and the velocity field, it is clear that the Hanle effect and the Doppler redistribution effect are completely decoupled. Particularly, by cancelling the magnetic field in the terms
![]() ,
,
![]() and
and
![]() ,
we obtain the results of Sahal-Bréchot et al. (1998) which give only the velocity-field effect. To obtain the Stokes parameters as a function of the magnetic field alone, we can just cancel the velocity field vector in the dimming term.
,
we obtain the results of Sahal-Bréchot et al. (1998) which give only the velocity-field effect. To obtain the Stokes parameters as a function of the magnetic field alone, we can just cancel the velocity field vector in the dimming term.
We note that we have assumed only the two-level atom approximation and there is no approximation on the incident and the reemitted line profiles. There is also no approximation on the velocity distribution
![]() of the scattering atoms. It can be isotropic as in the inner corona (although this point is not really clear) or anisotropic as observed by UVCS/SoHO in the high solar corona.
of the scattering atoms. It can be isotropic as in the inner corona (although this point is not really clear) or anisotropic as observed by UVCS/SoHO in the high solar corona.
Following Sahal-Bréchot et al. (1998), to get the distribution in frequency and intensity of the polarization of the scattered radiation, it is necessary to sum the contribution of all the
atoms having the velocity
![]() along
the line of sight. This can be performed by an integration
over the velocity field distributions
along
the line of sight. This can be performed by an integration
over the velocity field distributions
![]() and
and
![]() in the plane perpendicular to the line of sight.
in the plane perpendicular to the line of sight.
The Stokes parameters as a function of the scattered radiation frequency ![]() are given (in number of photons per unit of time, per unit of volume, per unit of frequency and per unit of solid angle) by
are given (in number of photons per unit of time, per unit of volume, per unit of frequency and per unit of solid angle) by
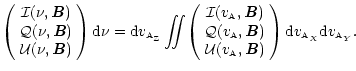 |
(21) |
We consider the case of the O VI D2 coronal line formed in the solar corona by the resonant scattering of the unpolarized and partially anisotropic radiation coming from the underlying transition region. We assume that the incident and reemitted line profiles are both Gaussian with respective linewidths
![]() and
and
![]() .
We obtain a corresponding equation for the incident photons polarization matrix element by replacing, in the Eq. (47) in Sahal-Bréchot et al. (1998), the limb-brightening function
.
We obtain a corresponding equation for the incident photons polarization matrix element by replacing, in the Eq. (47) in Sahal-Bréchot et al. (1998), the limb-brightening function ![]() by a function
by a function
![]() ,
for the more general case when the incident radiation field is not cylindrically symmetric around the solar vertical (Pz), which is the case when one observes in the coronal polar holes. The polarization matrix of the incident photons is given by
,
for the more general case when the incident radiation field is not cylindrically symmetric around the solar vertical (Pz), which is the case when one observes in the coronal polar holes. The polarization matrix of the incident photons is given by
![$\displaystyle \begin{array}{l}
{\displaystyle
\varphi\left({\textbf{\textit{v}}...
...iptstyle{\rm {D_i}}}}}\right)^2\right] \,
{\cal{M}}(\alpha,\beta)}.
\end{array}$](/articles/aa/full/2002/17/aa1681/img120.gif) |
(22) |
![\begin{displaymath}{\displaystyle
F({\vec{v}}_{\scriptscriptstyle{\rm {A}}}) =
\...
...criptstyle{\rm D}_{\rm s}}}\right)^{\scriptstyle{2}}\right]}.
\end{displaymath}](/articles/aa/full/2002/17/aa1681/img121.gif) |
(23) |
The equations giving the Stokes parameters for this case are a generalization of those given in the Appendix A in Sahal-Bréchot et al. (1998) (Eq. (A1) for the frequency dependent Stokes parameters, and Eq. (A8) for the integrated Stokes parameters on the line profile). They can be written in the general form
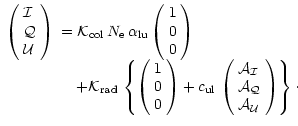 |
(24) |
![$\displaystyle \begin{array}{l}
{\displaystyle
{\cal{K}}_{\rm rad}\propto\frac{1...
...{D_i}}}+
\Delta\nu^2_{\scriptscriptstyle{\rm {D_s}}}}
\right]}\cdot
\end{array}$](/articles/aa/full/2002/17/aa1681/img126.gif) |
(25) |
We have developed, in the frame of the density matrix formalism, the theory giving the Stokes parameters of a linearly polarized spectral line sensitive simultaneously to the Hanle effect due to a local magnetic field and to the Doppler redistribution due to the macroscopic velocity field of the scattering atoms. In the obtained equations, there is no assumption on the geometry of the magnetic field and velocity field vectors. There is no hypothesis also on the line profiles nor on the velocity distribution of the scattering atoms. The obtained results are general and can be applied to physical problems implicating the magnetic field and/or the velocity field. From the final results, it is possible to obtain the Stokes parameters of a spectral line sensitive only to the Hanle effect or only to the velocity-field effect. This is done by cancelling one or other of these quantities in the final equations. In particular, we get the results obtained by Sahal-Bréchot et al. (1998), by cancelling the Larmor frequency (the magnetic field) in the angular terms
![]() ,
,
![]() ,
,
![]() .
We obtain the Hanle effect alone by cancelling the velocity field in the dimming term.
.
We obtain the Hanle effect alone by cancelling the velocity field in the dimming term.
As an application to the coronal case, we have used a Maxwellian velocity field distribution with a macroscopic velocity field vector for the coronal ions. In future work, we will take into account, in the calculations, the velocity distribution anisotropy observed by UVCS/SoHO (the ion cyclotron effect). The integration along the line of sight will be the subject of a more complete future work.
We will use these results in a further paper to interpret the linear polarization parameters of the O VI D2 coronal line measured by using observations performed by the SUMER (Solar Ultraviolet Measurements of Emitted Radiation) spectrometer (Wilhelm et al. 1995; Wilhelm et al. 1997; Hassler et al. 1997) on board of SoHO on March 19, 1996 (Raouafi et al. 1999a,b,c,d; Raouafi 2000).
Acknowledgements
The author gratefully acknowledges helpful discussion with S. Sahal-Bréchot and P. Lemaire. The author is also indebted to Roberto Casini for deep reading of the manuscript and for critical and helpful comments.
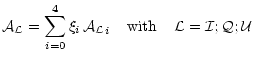 |
(A.1) |
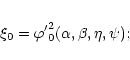 | |||
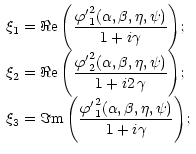 |
(A.2) |
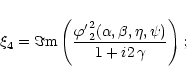
\sin(2\psi) ;
\end{array}$](/articles/aa/full/2002/17/aa1681/img133.gif) |
(A.3) |
\big[d^2_{22}-d^2_{2-2}\big](\eta)\sin(2\psi) ;
\end{array}$](/articles/aa/full/2002/17/aa1681/img134.gif) |
(A.4) |
\big[d^2_{22}-d^2_{2-2}\big](\eta)\cos(2\psi) .
\end{array}$](/articles/aa/full/2002/17/aa1681/img135.gif) |
(A.5) |