A&A 386, 399-414 (2002)
DOI: 10.1051/0004-6361:20020245
The signature of high-velocity gas in the spectra of NGC 4151
M. Contini1,2 -
S. M. Viegas2 - M. A. Prieto3
1 - School of Physics & Astronomy, Tel Aviv University,
69978 Tel Aviv, Israel
2 -
Instituto Astronômico e Geofísico, USP, Av. Miguel Stefano
4200, 04301-904 São Paulo, Brazil
3 -
European Southern Observatory, 85748 Garching, Germany
Received 5 July 2001 / Accepted 5 February 2002
Abstract
The multiwavelength emission spectrum and associated velocity field
of the Seyfert prototype NGC 4151 is modeled.
Since the thirties NGC 4151 has been the subject of extensive modeling,
nuclear photoionization being the basic approach considered by all
authors.
HST data has impressively revealed the
existence of a large range of velocities (100-1500
 )
dominating the emitting clouds in the
extended emission line region of the galaxy. Following this
observational result, a revision of the photoionization modeling
approach
applied to NGC 4151 is presented.
It is concluded that a mixture of radiation-dominated clouds and shock-dominated
clouds are required to explain the multiwavelength
line and continuum spectra of the galaxy.
The relative contribution of shock excitation versus photoionization
is consistently modeled along the nebulae
taking into account the spatial variation of both flux and velocity of
main
optical and UV lines.
The multiwavelength continuum spectrum of NGC 4151 is then nicely
accounted for
by a combination of nuclear emission at high energy, gas Bremsstrahlung,
and dust emission. The last two phenomena are
directly linked to the composite shock and photoionization
excitation of the gas.
The radio SED however is found dominated by
synchrotron emission created by the Fermi mechanism at the shock front.
In addition, a
)
dominating the emitting clouds in the
extended emission line region of the galaxy. Following this
observational result, a revision of the photoionization modeling
approach
applied to NGC 4151 is presented.
It is concluded that a mixture of radiation-dominated clouds and shock-dominated
clouds are required to explain the multiwavelength
line and continuum spectra of the galaxy.
The relative contribution of shock excitation versus photoionization
is consistently modeled along the nebulae
taking into account the spatial variation of both flux and velocity of
main
optical and UV lines.
The multiwavelength continuum spectrum of NGC 4151 is then nicely
accounted for
by a combination of nuclear emission at high energy, gas Bremsstrahlung,
and dust emission. The last two phenomena are
directly linked to the composite shock and photoionization
excitation of the gas.
The radio SED however is found dominated by
synchrotron emission created by the Fermi mechanism at the shock front.
In addition, a
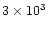 K black body component
accounts for the host galaxy contribution.
As a result of the modeling,
silicon is found depleted by a
high factor and included in dust
grains, while the N/C abundance ratio is found compatible with cosmic
values.
K black body component
accounts for the host galaxy contribution.
As a result of the modeling,
silicon is found depleted by a
high factor and included in dust
grains, while the N/C abundance ratio is found compatible with cosmic
values.
Key words: galaxies: nuclei - galaxies: Seyfert - shock waves -
galaxies: individual: NGC 4151 - X-ray: galaxies
Detailed imaging of the narrow-line region (NLR) of Seyfert galaxies
with the Hubble Space Telescope (HST) has revealed its complex
morphology
and velocity field. Recently, observations of NGC 4151
indicated the presence of emitting clouds with velocities ranging
from +846 to -1716
 (Winge et al. 1997; Kaiser et al. 1999).
(Winge et al. 1997; Kaiser et al. 1999).
NGC 4151 is a nearby barred galaxy, usually classified as a Seyfert
type 1, although it has already been considered as a Seyfert 1.5
(Osterbrock & Koski 1976) and has also shown the
characteristics of a Seyfert 2 galaxy (Penston & Pérez 1984). NGC 4151
is one of the most observed active galactic nuclei (AGN), from radio to
X-rays. The recent HST longslit emission-line data (Nelson et al.
2000), coupled to ISO data (Alexander et al. 1999),
offer an excelent opportunity to improve our understanding of the
NLR physical conditions with the added effect of the velocity
field.
The kinematics derived from the long slit observations (Nelson et al.
2000; Crenshaw et al. 2000) show evidence of three components: a low
velocity system,
consistent with normal
disk rotation, a high velocity system in radial outflow at a few hundred
 and an additional high velocity system with velocities up to
1400
and an additional high velocity system with velocities up to
1400
 ,
as previously found from STIS slitless spectroscopy
(Hutchings
et al. 1998, 1999; Kaiser et al. 1999). The authors see the signature of
a radial outflow, with no interaction with the radio jet. However,
high velocity components, shifted up to about 1500
,
as previously found from STIS slitless spectroscopy
(Hutchings
et al. 1998, 1999; Kaiser et al. 1999). The authors see the signature of
a radial outflow, with no interaction with the radio jet. However,
high velocity components, shifted up to about 1500
 from the
systemic velocity, are also seen
by Winge et al. (1997) associated with individual clouds
located preferentially along the edges of the radio knots. Such
association suggests a cloud-jet interaction, which definitively may
influence the morphology
and the physical conditions of the NLR.
from the
systemic velocity, are also seen
by Winge et al. (1997) associated with individual clouds
located preferentially along the edges of the radio knots. Such
association suggests a cloud-jet interaction, which definitively may
influence the morphology
and the physical conditions of the NLR.
The high spatial resolution permits us to see that the emission
line ratios vary substantially on scales
of a few tenth of an arcsecond, indicating that the density and
ionization
state of the emitting gas are strongly influenced by the local
conditions, hence
suggesting that shock fronts may be at work.
The presence of high-velocity clouds in the NLR of active galaxies
has been predicted from the modeling
of the emission-line and continuum spectra of the Seyfert 2 objects
NGC 5252 and Circinus (Contini et al. 1998a, 1998b), as
well as suggested from the more general
analysis of the optical-ultraviolet
continuum of a relatively large sample of Seyfert 2 galaxies (Contini
& Viegas 2000). High velocity clouds are also
invoked in an alternative model
based on a multiwavelength analysis of
the emission-line and continuum spectra of the source
(Contini & Viegas 1999), which explains the soft X-ray excess
in NGC 4051.
In all of these models the physical
conditions of the high velocity clouds are usually shock-dominated.
The shocks contribute to the high ionization emission-lines and to the
continuum emission, mainly by providing efficient heating of dust,
contributing to reproduce the observed middle-infrared emission, and
to the observed soft X-ray spectrum which originates in the high
temperature post-shock zone.
Yet, the interpretation of the NGC 4151 emission-line and continuum
spectra
so far rests exclusively on photoionization models.
All the authors agree that, given the simplicity of the models,
the observed line ratios can be reproduced.
In NGC 4151 the high velocity clouds are directly observed.
Velocities of  1500
1500
 could be theoretically explained
extrapolating to the NLR the arguments about high velocity clouds
raised by Weymann et al. (1997).
Here, however, in order to obtain a large range of velocities,
collisions
are invoked.
could be theoretically explained
extrapolating to the NLR the arguments about high velocity clouds
raised by Weymann et al. (1997).
Here, however, in order to obtain a large range of velocities,
collisions
are invoked.
Although
photoionization models reproduce within better than a factor of 2 the
most
important line ratios (Schulz 1988, 1990;
Kraemer et al. 2000; Alexander et al. 1999),
some questions remain still open, as for example
the mere fact of the influence of the velocity field in the cloud
spectrum.
Thus, in this paper we
will look for the signature of the high velocity gas in the
emission-line spectrum, as well as in the
radio to X-ray continuum spectral energy distribution (SED).
We present a new type of single-cloud modeling based on the spatial
distribution of the observational data in the optical range;
then, a multi-cloud model is proposed to explain the emission lines in
the IR.
As was done previously in modeling other objects (NGC 5252, Circinus),
the multi-cloud model issued from the analysis of the emission lines
is then constrained by fitting
the continuum SED in a large frequency range.
This is possible only with composite models (shock + photoionization),
because
the gas heated only by the radiation from the active center cannot
reach temperatures high enough to fit the Bremsstrahlung emission
and dust reradiation in the large range of the observed frequencies.
A review focused in the successes and problems of photoionization
models is
presented in Sect. 2. The composite models, coupling photoionization
and shocks, are described in Sect. 3. The optical emission-line
spectrum is
discussed in Sect. 4, while the infrared lines are presented
in Sect. 5, and the results for the ultraviolet lines
appear in Sect. 6. The observed and calculated SED are compared
in Sect. 7, and the conclusions appear in Sect. 8.
Most recently, photoionization models for the NLR of NGC 4151 have
been proposed by Alexander et al. (1999) and Kraemer et al. (2000).
In both cases, the observed emission-line
ratios are reproduced within a factor of 2.
Both set of authors use, however, different modeling approach:
the matter distribution adopted
is different. In Alexander's et al. (1999) models (hereinfter
called type A), the best fit is found with a
single cloud component with a
filling factor less than unity; in Kraemer's et al. (2000) models
(type B), a multi-cloud is used, namely a less dense
matter-bound component is added to a dense
radiation-bounded component. We note that Alexander et al. discarded
this latter solution arguing that a matter-bounded component implies
three free additional parameters, whereas the introduction of a
filling factor - their case - implies only one.
Nevertheless, let us recall
that a matter-bounded component favors the high ionization lines,
while (radiation-bounded) models with filling-factor less than unity
mimic a lower average density, leading to a larger ionized zone and
favoring the low-ionization lines. Thus, models assuming a filling
factor less than unity are not a good
physical representation of a clumpy zone; yet, the spatial
distribution of [SII] ratios across NGC 4151 extended emission
line region reveals instead a
rather clumpy region with regions of higher and lower density at
different points along the HST slit (Nelson et al. 2000).
Regarding both type A and type B models, the authors
agree that "the fit of the line
ratios is good taking into account the simplicity of the models''.
Simplicity has always been a strong argument in favor of
photoionization models applied to nebular regions in AGNs, in addition
to the
undisputable presence of
a strong central radiation source. However, in Science
it is usually from the
attempt to explain the "imperfections'' of a model, (those data not
explained by it), that a more realistic scenario can be drawn.
With that in mind we list below the discrepancies
between the above proposed photoionization models and
the observational data of NGC 4151.
Due to the various difficulties to have a self-consistent data
set (data from different epoch, different resolutions and apertures),
Alexander et al. (1999) use several criteria to select the
set of emission-lines to be reproduced by type A models.
One of the criteria excludes lines emitted by ions that
"can be easily ionized by other processes''. The set of
emission-lines excluded
includes some usually used in the diagnostic diagrams of nebular gas:
He II 4686, [O III] 4363, [O I] 6300, [N II] 6548+6584 and the
density indicator [SII] 6716, 6731 doublet,
in addition to the high-ionization Fe lines: [Fe X] 6734 and
[Fe XI] 7892. The final set of lines used for modeling, that includes
UV, optical, and IR lines, is reproduced within a factor of 2 by their
best fit models.
Discrepancies larger than two are derived for [Fe VII] 5721, [Fe VII]
6086,
[Ne II] 12.8 and [Ne III] 36.0 which are underpredicted, and for
[S III] 9069, [Ne V] 14.3, [S III] 18.7,
[Ne V] 24.3, and [S III] 33.5 that are overpredicted.
Regarding the SED implied by models,
the presence of a big blue bump
in the ionizing radiation spectrum, peaking at 50 eV, is excluded
by their best-fit model because its effect would be to overproduce
the low-ionization lines and underproduce the high-ionization
lines. However, this is the net effect produced by imposing a
filling factor less than unity, as adopted in their best-fit model.
Kraemer et al. models (type B) use HST/STIS low-dispersion long-slit
data at position angle PA = 221 .
Thus, their data
set includes UV and optical lines, but no infrared lines that are
the basis of type A models by Alexander et al. (1999).
Their model results are compared with observed emission-line ratios
derived at different positions along the slit. The
large majority of the lines are reproduced within a factor of
2. Divergencies larger than 2 are often found for the high ionization
lines:
[Fe VII] lines, and the UV lines
N V 1240, [Ne IV] 2423, and NIV] 1486, although in the latter case
the signal-to-noise is very low. At some locations of the emitting
nebulae, the calculated C III] 1909, C II] 2326, [O III] 4363,
and the [S III] lines, also largely diverge from the data.
Notice, however, that C III] and C II] are blended and that,
in the case of the [S III] lines, the discrepancy may be
due to an instrumental effect, as pointed out by Kraemer et al. (2000).
.
Thus, their data
set includes UV and optical lines, but no infrared lines that are
the basis of type A models by Alexander et al. (1999).
Their model results are compared with observed emission-line ratios
derived at different positions along the slit. The
large majority of the lines are reproduced within a factor of
2. Divergencies larger than 2 are often found for the high ionization
lines:
[Fe VII] lines, and the UV lines
N V 1240, [Ne IV] 2423, and NIV] 1486, although in the latter case
the signal-to-noise is very low. At some locations of the emitting
nebulae, the calculated C III] 1909, C II] 2326, [O III] 4363,
and the [S III] lines, also largely diverge from the data.
Notice, however, that C III] and C II] are blended and that,
in the case of the [S III] lines, the discrepancy may be
due to an instrumental effect, as pointed out by Kraemer et al. (2000).
Several interpretations for the above discrepancies are discussed by
Kraemer et al. (2000). Our assumption is that those discrepancies may
be
revealing the presence of an additional ionizing mechanism, which is
not the dominant process, but that shows its signature through
particular observational features. This point of view is adopted
here assuming that the additional mechanism is due to the presence
of shocks.
Faint high velocity emission regions intermingled with brighter
emission clouds are shown in NGC 4151 imaging (Hutchings et al.
1999). We consider this observational fact as an indication
that the extended NLR of NGC 4151
is a mixture of low velocity radiation-dominated
clouds and high velocity shock-dominated clouds, all
contributing to the emission-line spectrum. Accordingly,
composite models accounting
for the coupled effect of the central ionizing radiation
and shock excitation due to cloud motions are assumed.
Numerical simulations for single clouds are obtained with
the SUMA code (see, for instance, Viegas & Contini 1994). Notice that
the simulations apply whether the shocks originate from an interaction
of the emitting clouds with the radio jet or from a radial
outflow of the clouds.
The input parameters are the shock velocity,  ,
the preshock density,
0, the preshock magnetic field, 0,
the ionizing radiation spectrum,
the chemical abundances,
the dust-to-gas ratio by number, d/g,
and the geometrical thickness of the clouds, D. A power-law,
characterized by the power index
,
the preshock density,
0, the preshock magnetic field, 0,
the ionizing radiation spectrum,
the chemical abundances,
the dust-to-gas ratio by number, d/g,
and the geometrical thickness of the clouds, D. A power-law,
characterized by the power index 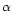 and the
flux,
and the
flux, 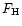 ,
at the Lyman limit, reaching the cloud (in units of
cm-2 s-1 eV-1)
is generally adopted.
For all the models, 0 = 10-4 Gauss,
,
at the Lyman limit, reaching the cloud (in units of
cm-2 s-1 eV-1)
is generally adopted.
For all the models, 0 = 10-4 Gauss,
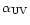 = 1.5,
and
= 1.5,
and
 ,
and cosmic abundances (Allen 1973) are adopted.
The basic models are calculated with
d/g = 10-15, however,
this value is changed a posteriori to better fit the continuum SED.
,
and cosmic abundances (Allen 1973) are adopted.
The basic models are calculated with
d/g = 10-15, however,
this value is changed a posteriori to better fit the continuum SED.
Shock dominated models (SD) are calculated
assuming that the effects of the shock prevail on radiation (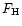 =0.).
Radiation dominated models (RD),
however, are composite, i.e. they account both for photoionization
and shocks up to
=0.).
Radiation dominated models (RD),
however, are composite, i.e. they account both for photoionization
and shocks up to  =500
=500
 ,
but photoionization
dominates the physical conditions of the emitting gas.
,
but photoionization
dominates the physical conditions of the emitting gas.
The grid of models which are actually used for modeling is
presented in an accompanying paper by Contini & Viegas (2001,
hereafter referred to as CV01).
In the following, calculated emission-line ratios from a selected
number of models in the grid
are compared to the HST log-slit optical
data at PA=221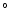 (Nelson et al. 2000; Kraemer et al.
2000) and to the ISO
integrated aperture SWS data by Sturm et al. (1999).
Models are selected on the basis of the physical conditions of the
emitting gas dictated by the observations, e.g. the
FWHM of the line profiles
for
(Nelson et al. 2000; Kraemer et al.
2000) and to the ISO
integrated aperture SWS data by Sturm et al. (1999).
Models are selected on the basis of the physical conditions of the
emitting gas dictated by the observations, e.g. the
FWHM of the line profiles
for  .
.
In models which account for shock effects, the density downstream
is determined by compression, which depends on the shock velocity,
and changes considerably with
distance from the shock front (CV01, Figs. 5a, 6a, and 7a).
Therefore, the preshock density and the shock velocity chosen
define a distribution of the density across the cloud, which
must be adequate to provide a good fit to the density sensitive
lines, e.g., [O II] 3727, [N I] 5200, [N II] 6548 ([S II] 6716+
is not very significant because S can be locked in dust grains).
Moreover, in the NLR, the density of the clouds
follows the gradient of the cloud velocity, decreasing
with the distance to the center. For each cloud,
the observed [S II] 6717/6730 line ratio (which does not depend on S/H)
is used as a first test for the choice of 0 and  .
Then, the intensity of the ionizing radiation, the physical conditions
calculated by the model, and the geometrical thickness of the cloud
are deduced from the line spectrum, as a whole.
The [O III]/H
.
Then, the intensity of the ionizing radiation, the physical conditions
calculated by the model, and the geometrical thickness of the cloud
are deduced from the line spectrum, as a whole.
The [O III]/H line ratio is an indicator for
line ratio is an indicator for 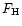 .
On the other hand,
wide clouds are optically thick, leading to stronger
low ionization level lines, while narrow clouds
are matter-bounded, with fainter low-ionization lines.
Thus the choice of D is then constrained by the best fit of
a large number of line ratios, particularly,
the ratio of the low ionization lines to H
.
On the other hand,
wide clouds are optically thick, leading to stronger
low ionization level lines, while narrow clouds
are matter-bounded, with fainter low-ionization lines.
Thus the choice of D is then constrained by the best fit of
a large number of line ratios, particularly,
the ratio of the low ionization lines to H .
.
Modeling the spatial distribution
Because of the availability of spatially resolved emission-line spectra
in different regions of NGC 4151, a new modeling approach is followed in
this work.
The most significant optical emission lines are modeled
accounting for their spatial distribution across the NLR.
In each position we
check the consistency of the prevailing models explaining several
line ratios, including those that are poorly reproduced by the
photoionization models.
The observed and calculated emission-line intensities relative
to H are presented in a series of figures (Figs. 1-4), where
the emission-line ratios
are shown as a function of the projected nuclear distance, including
both the SW data (on the left) and the NE data (on the right) at PA=221
are presented in a series of figures (Figs. 1-4), where
the emission-line ratios
are shown as a function of the projected nuclear distance, including
both the SW data (on the left) and the NE data (on the right) at PA=221 .
.
In order to determine the intensity of the power-law
radiation flux in the NLR edge closer to the nucleus
a preliminary estimate is made by comparing model results with
the observed line ratios as presented in Fig. 1.
Filled squares refer to Nelson et al. (2000) (not reddening corrected)
and filled triangles to
Kraemer et al. (2000) (reddening corrected) data, respectively.
The scales for log 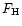 are indicated upon the upper horizontal axis.
Each curve represents RD models calculated with different
are indicated upon the upper horizontal axis.
Each curve represents RD models calculated with different 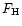 but
corresponding to
the same
but
corresponding to
the same  - 0:
- 0:
 =100
=100
 and 0=100 3 (dotted lines),
and 0=100 3 (dotted lines),
 =200
=200
 and 0=200 3 (dash-dotted lines),
and 0=200 3 (dash-dotted lines),
 =300
=300
 and 0=300 3 (short-dash lines),
and 0=300 3 (short-dash lines),  =500 and 0=300 3, (long-dash lines). Thin lines refer to a narrow cloud
(
D=1017-18 cm)
and thick lines to wider clouds (
D = 1019 cm).
=500 and 0=300 3, (long-dash lines). Thin lines refer to a narrow cloud
(
D=1017-18 cm)
and thick lines to wider clouds (
D = 1019 cm).
A sequence of three different cases (log
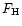 =13,
12, and 11.3) is shown in the top, middle, and bottom diagrams,
respectively.
We have chosen the [OIII]/H
=13,
12, and 11.3) is shown in the top, middle, and bottom diagrams,
respectively.
We have chosen the [OIII]/H and [OII]/H
and [OII]/H line ratios, because
are the most significant.
The fit of both [OIII]/H
line ratios, because
are the most significant.
The fit of both [OIII]/H and [OII]/H
and [OII]/H data is acceptable only
in the bottom
diagrams (notice that in these diagrams the flux is not fully symmetric,
indicating that
the SW and NE regions are slightly different). So, for consistency we
chose the bottom
case to model also the other line ratios.
data is acceptable only
in the bottom
diagrams (notice that in these diagrams the flux is not fully symmetric,
indicating that
the SW and NE regions are slightly different). So, for consistency we
chose the bottom
case to model also the other line ratios.
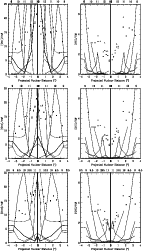 |
Figure 1:
The [O III] 5007+4959/H (left diagrams) and the [O II] 3727/H (left diagrams) and the [O II] 3727/H (right diagrams) emission-line ratios
are shown as a function of the projected nuclear distance. (right diagrams) emission-line ratios
are shown as a function of the projected nuclear distance. |
| Open with DEXTER |
Since we are investigating the intensity of ionizing radiation
from the active center (AC)
and the velocity distribution in the central region of NGC 4151, both
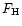 and
and  are shown in Figs. 2-4 diagrams.
In this way, the relative importance of the velocity field and the AC
radiation field can be recognized.
The scales for log
are shown in Figs. 2-4 diagrams.
In this way, the relative importance of the velocity field and the AC
radiation field can be recognized.
The scales for log 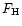 and
and  (in
(in
 )
are indicated upon the horizontal upper axis of the
top and middle and bottom diagrams, respectively.
)
are indicated upon the horizontal upper axis of the
top and middle and bottom diagrams, respectively.
In the top diagrams of Figs. 2-4 (panels a and d) each line corresponds to RD model
results as in Fig. 1.
Panels b and e show
the
solid lines corresponding to SD models (CV01, Tables 1-10)
for which the maximum value of the velocity distribution is
 =700
=700
 in the central region, while diagrams c and f correspond
to the
results with a maximum velocity of
in the central region, while diagrams c and f correspond
to the
results with a maximum velocity of  =1400
=1400
 .
.
Because shock dominated models for
narrow and wide clouds give very similar results,
these models are represented by one line (model results overlap),
corresponding to one serie of results.
We draw attention to the thin and thick lines in the two bottom
diagrams
which refer to reduced and full intensity line ratios,
respectively, and not to models calculated by small and large D, as
shown
in the top diagrams.
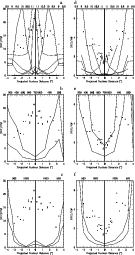 |
Figure 2:
The [O III] 5007+4959/H (left) and the [O II] 3727/H (left) and the [O II] 3727/H (right)
emission-line ratios
are shown as a function of the projected nuclear distance. Same notation
as in Fig. 1. (right)
emission-line ratios
are shown as a function of the projected nuclear distance. Same notation
as in Fig. 1. |
| Open with DEXTER |
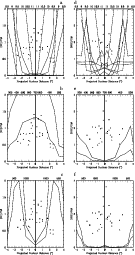 |
Figure 3:
The [O I] 6300+6360/H (left) and
the [S III] 9069/H (left) and
the [S III] 9069/H (right) emission-line ratios as a function of the
projected nuclear distance. Same notation as in Fig. 1. (right) emission-line ratios as a function of the
projected nuclear distance. Same notation as in Fig. 1. |
| Open with DEXTER |
 |
Figure 4:
The [S II] 6713+6731/H (left) and
the [Fe VII]6086/H (left) and
the [Fe VII]6086/H (right) emission-line ratios as a function of the
projected
nuclear distance. Same notation as in Fig. 1. (right) emission-line ratios as a function of the
projected
nuclear distance. Same notation as in Fig. 1. |
| Open with DEXTER |
The model results shown in Figs. 2-4 cover most of the data consistently
for the [O III] 5007+4959/H ,
[O II] 3727/H
,
[O II] 3727/H ,
[O I] 6300+6363/H
,
[O I] 6300+6363/H ,
[S III] 9069/H
,
[S III] 9069/H ,
[S II] 6713+6731/H
,
[S II] 6713+6731/H ,
and [Fe VII] 6086/H
,
and [Fe VII] 6086/H line ratios. The first three ratios are related to
the
ionization state of the gas, while the other three are chosen because
they are not well reproduced by pure photoionization models.
line ratios. The first three ratios are related to
the
ionization state of the gas, while the other three are chosen because
they are not well reproduced by pure photoionization models.
The ranges and the spatial distributions of  were chosen
phenomenologically
by the fit, particularly, of the [O III]/H
were chosen
phenomenologically
by the fit, particularly, of the [O III]/H and [S III]/H
and [S III]/H ratios,
while the ranges
and the distributions of
ratios,
while the ranges
and the distributions of  were chosen by fitting the low
ionization
([O II]/H
were chosen by fitting the low
ionization
([O II]/H ,
[S II]/H
,
[S II]/H )
and neutral ([O I]/H
)
and neutral ([O I]/H )
line ratios. The data
corresponding
to the high ionization line ratio [Fe VII]/H
)
line ratios. The data
corresponding
to the high ionization line ratio [Fe VII]/H are not enough to
constrain the models.
are not enough to
constrain the models.
We adopt a velocity field decreasing from the center of the galaxy
outwards.
The observed velocity field is, however, complex, so, two different
shock velocity distributions are shown,
one with a maximum 
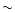 700
700
 in the central region
(middle diagrams), and another with
a higher maximum
in the central region
(middle diagrams), and another with
a higher maximum  ,
up to 1400
,
up to 1400
 (bottom diagrams).
(bottom diagrams).
Two different lines represent the SD models
in both middle and bottom diagrams.
The thick one corresponds to the calculated models, the thin one to the
models downwards shifted by a factor of 3 (middle diagrams) and of 2
(bottom
diagrams). The shift in the middle diagram is dictated by the
fit of the [O I]/H ratios (see Sect. 4.1) and in the bottom diagram by
the [Fe VII]/H
ratios (see Sect. 4.1) and in the bottom diagram by
the [Fe VII]/H ratios (see Sect. 4.3).
These shifts do not represent lower abundances
of the elements relative to H, but they indicate that in a multi-cloud
model corresponding to the weighted sum of single-cloud models,
the weights of the SD high velocity (>300
ratios (see Sect. 4.3).
These shifts do not represent lower abundances
of the elements relative to H, but they indicate that in a multi-cloud
model corresponding to the weighted sum of single-cloud models,
the weights of the SD high velocity (>300
 )
clouds is reduced
(see Sect. 5).
Indeed, by modeling the data on a large scale, this solution may look
arbitrary, particularly
considering faint lines (e.g. [O I]),
and lines affected by the presence of dust (e.g. [S III], [S II], etc.).
If reducing the weights of the SD models, the fit of all the
emission-lines
is consistently improved, we can conclude that
this reduction is sound and SD models corresponding
to high velocities in the nuclear region have lower weights.
The relative weight accounts for
the relative number of clouds in the conditions determined by the
model, for the dilution factor (i.e., the square
ratio between the distance of the cloud from the galaxy center) and the
distance
of the galaxy from Earth.
Notice that the middle and bottom diagrams in Figs. 2-4
refer to "high velocities'' in the nuclear region of the galaxy
(between 1500-700
)
clouds is reduced
(see Sect. 5).
Indeed, by modeling the data on a large scale, this solution may look
arbitrary, particularly
considering faint lines (e.g. [O I]),
and lines affected by the presence of dust (e.g. [S III], [S II], etc.).
If reducing the weights of the SD models, the fit of all the
emission-lines
is consistently improved, we can conclude that
this reduction is sound and SD models corresponding
to high velocities in the nuclear region have lower weights.
The relative weight accounts for
the relative number of clouds in the conditions determined by the
model, for the dilution factor (i.e., the square
ratio between the distance of the cloud from the galaxy center) and the
distance
of the galaxy from Earth.
Notice that the middle and bottom diagrams in Figs. 2-4
refer to "high velocities'' in the nuclear region of the galaxy
(between 1500-700
 and about 300
and about 300
 ).
Indeed, Nelson et al. (2000, Fig. 5) show that the bulk of cloud
velocities
is within 300
).
Indeed, Nelson et al. (2000, Fig. 5) show that the bulk of cloud
velocities
is within 300
 .
So, the reduction of the weights in the SD diagrams
indicates that the number of high velocity SD clouds is small.
.
So, the reduction of the weights in the SD diagrams
indicates that the number of high velocity SD clouds is small.
Recall that observational data result from the integration along the
line of sight, which may include different clouds. Thus, a more
realistic fit
should be obtained by a multi-cloud average (see Sect. 5).
A compromise between a consistent picture over a large spatial
distribution
of several emission lines and the precision of the fit must be achieved.
Observed features
In several cases there are two or more emission
lines within the passband, so
that different velocities are sampled for the different lines
(Hutchings et al. 1999).
These are the [O II] 3727 and [S II] doublets, as well as [N II] lines
plus
H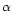 at about 6548 Å.
The [O III] image covers velocities between -1200 and -860
at about 6548 Å.
The [O III] image covers velocities between -1200 and -860
 .
High velocity material in this velocity range is much fainter than the
main bright clouds showing low velocities.
It is seen on both sides of the nucleus and outside
the main biconical emission regions.
The high velocity gas is weak in H
.
High velocity material in this velocity range is much fainter than the
main bright clouds showing low velocities.
It is seen on both sides of the nucleus and outside
the main biconical emission regions.
The high velocity gas is weak in H and [O II] lines and seems to
be associated with highly ionized material.
Ionization of oxygen is higher along radial locations on both
sides of the nucleus. Generally, there is an association
of high velocity clouds with high ionization gas, however, there are
regions
of high ionization (mainly to the E side) with no known high
velocity gas.
Nelson et al. (2000) claim that the high velocity components
generally account for a small
fraction of the total flux in the [O III] emission lines.
In several cases they find clouds with multiple velocity
components.
and [O II] lines and seems to
be associated with highly ionized material.
Ionization of oxygen is higher along radial locations on both
sides of the nucleus. Generally, there is an association
of high velocity clouds with high ionization gas, however, there are
regions
of high ionization (mainly to the E side) with no known high
velocity gas.
Nelson et al. (2000) claim that the high velocity components
generally account for a small
fraction of the total flux in the [O III] emission lines.
In several cases they find clouds with multiple velocity
components.
The results for [O III]/H and [O II]/H
and [O II]/H are shown in Fig. 2.
Different models are selected to fit the data as expected from the
multiple structure of the observed lines (Kaiser et al. 2000). As shown
in
Fig. 2a, the data are well reproduced by composite RD models,
with the intensity of the ionizing radiation
are shown in Fig. 2.
Different models are selected to fit the data as expected from the
multiple structure of the observed lines (Kaiser et al. 2000). As shown
in
Fig. 2a, the data are well reproduced by composite RD models,
with the intensity of the ionizing radiation 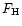 decreasing
by more than two orders of magnitude from the center
towards the outskirts of the nuclear region.
decreasing
by more than two orders of magnitude from the center
towards the outskirts of the nuclear region.
Focusing on [O III]/H ,
RD clouds (Fig. 2a) with velocities of 200-300
,
RD clouds (Fig. 2a) with velocities of 200-300
 contribute preferentially in the inner 1 arcsec region, while those
with
velocities of 100
contribute preferentially in the inner 1 arcsec region, while those
with
velocities of 100
 appear at larger distances from the center, in
agreement with Winge et al. (1999).
The contribution to [O III]/H
appear at larger distances from the center, in
agreement with Winge et al. (1999).
The contribution to [O III]/H line ratios from RD clouds with
line ratios from RD clouds with 
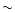 500
500
 is small.
is small.
Regarding the SD clouds (Figs. 2b and c), the high velocity ones ( >500
>500
 )
are responsible
for only a few percent of the central region emission, while a larger
contribution
at 3'' from the center comes from the low velocity clouds (
)
are responsible
for only a few percent of the central region emission, while a larger
contribution
at 3'' from the center comes from the low velocity clouds ( <500
<500
 ).
).
The situation is markedly different regarding [O II]/H (Figs. 2d, e,
and f)
as it appears dominated by SD models. The trend of [O II]/H
(Figs. 2d, e,
and f)
as it appears dominated by SD models. The trend of [O II]/H is nicely explained by SD models with
is nicely explained by SD models with
 between
between  400 and 700
400 and 700
 (thick line).
(thick line).
Recall that the contribution of high velocity clouds to the [O II]/H line ratio is due to the diffuse radiation generated at the high
temperature
post-shock zone reaching the low ionization zone.
In order to illustrate this, the distribution
of the temperature as well as the fractional abundance of oxygen ions
downstream are plotted in Fig. 5 for an SD model with
line ratio is due to the diffuse radiation generated at the high
temperature
post-shock zone reaching the low ionization zone.
In order to illustrate this, the distribution
of the temperature as well as the fractional abundance of oxygen ions
downstream are plotted in Fig. 5 for an SD model with  =700
=700
 .
.
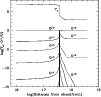 |
Figure 5:
The distribution of the electron temperature and of the
ionic fractional abundance of oxygen downstream for a shock-dominated
model (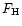 =0) with =0) with  =700 =700
 and 0=700 3.
The shock front is on the left.
and 0=700 3.
The shock front is on the left. |
| Open with DEXTER |
Notice, however, that
explaining the [O II]/H line ratio only with SD clouds may
not be acceptable in a global picture for the NLR, since RD
clouds must be present and contributing to other emission lines.
Indeed, the reduction by a factor of 3 is not only dictated by the fit
of the [O I]/H
line ratio only with SD clouds may
not be acceptable in a global picture for the NLR, since RD
clouds must be present and contributing to other emission lines.
Indeed, the reduction by a factor of 3 is not only dictated by the fit
of the [O I]/H data (Fig. 3b), but is consistent with a general scenario.
data (Fig. 3b), but is consistent with a general scenario.
Regarding the [OI]/H line ratio,
notice that SD models overpredict the observed
[O I]/H
line ratio,
notice that SD models overpredict the observed
[O I]/H data
by a factor of
data
by a factor of  3. This indicates that SD models with
3. This indicates that SD models with

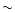 700
700
 in the central region must be taken with a lower
weight
in an eventual averaged model.
The shift of the SD models dictated by the [O I]/H
in the central region must be taken with a lower
weight
in an eventual averaged model.
The shift of the SD models dictated by the [O I]/H ratios is
consistent with all the other lines.
ratios is
consistent with all the other lines.
To further investigate NGC 4151 line emission we address a problem
raised by
Kraemer et al. (2000), namely, the overprediction of the
[S III] 9069+9532
/H line ratio by photoionization models.
This ratio is shown in Fig. 3.
line ratio by photoionization models.
This ratio is shown in Fig. 3.
Different clouds with different
 coexist in the center. The larger values can be fitted by
RD models with
coexist in the center. The larger values can be fitted by
RD models with 
 500
500
 .
Notice, however, that RD models with
.
Notice, however, that RD models with  =500
=500
 and log
and log 
 10.5 overpredict the data in the
region beyond 1'' at both sides of the center. Therefore, for
consistency, they were taken out from all figures.
10.5 overpredict the data in the
region beyond 1'' at both sides of the center. Therefore, for
consistency, they were taken out from all figures.
There is no contribution from SD clouds to the [S III]/H ratio
in the central region (Fig. 3e,
ratio
in the central region (Fig. 3e, f).
On the other hand, a strong contribution
to the [S II]/H
f).
On the other hand, a strong contribution
to the [S II]/H line ratios comes from the
SD clouds with rather high velocities (700
line ratios comes from the
SD clouds with rather high velocities (700
 )
in the central region,
and a not negligible contribution of SD clouds with
)
in the central region,
and a not negligible contribution of SD clouds with  =1000
=1000
 (Fig. 4c), as for the case of [O II]/H
(Fig. 4c), as for the case of [O II]/H .
Here too the signature of the diffuse radiation generated at
the high temperature post-shock zone is seen.
.
Here too the signature of the diffuse radiation generated at
the high temperature post-shock zone is seen.
From the [S II]6717/6731 diagrams of Nelson et al. (2000, Fig. 10), the
gas is rather
clumpy and also indicates a decrease in density with distance.
The data in the outer region (>2'') are well explained by RD models
with  =100
=100
 and 0=100 3, leading to [S II] 6716/[S II]
and 0=100 3, leading to [S II] 6716/[S II]
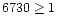 .
Density downstream decreases for lower shock velocities and lower
preshock
densities (see Contini & Aldrovandi 1986), therefore,
[S II] 6716/[S II]
.
Density downstream decreases for lower shock velocities and lower
preshock
densities (see Contini & Aldrovandi 1986), therefore,
[S II] 6716/[S II]
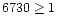 is expected in the regions farther from
the center.
In fact, we have found that velocities generally decrease with distance
from the
center. However, some ratios of about 0.5 are given by Nelson et al.
They are supported by the fact
that some models with
is expected in the regions farther from
the center.
In fact, we have found that velocities generally decrease with distance
from the
center. However, some ratios of about 0.5 are given by Nelson et al.
They are supported by the fact
that some models with  of about 500
of about 500
 also fit the data
beyond 1'' (Figs. 4b and c).
also fit the data
beyond 1'' (Figs. 4b and c).
Fe coronal lines are usually underpredicted by pure photoionization
models. In the case of NGC 4151, [Fe VII]/H is underpredicted by a
factor of
is underpredicted by a
factor of 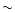 3 by Kraemer et al. (2000) and by Alexander et al.
(1999). To explain the discrepancy, an overabundance of Fe is often suggested,
which is somewhat surprising since a fraction of Fe may
be locked in grains, although sputtering is strong
for small grains and high velocity shocks.
3 by Kraemer et al. (2000) and by Alexander et al.
(1999). To explain the discrepancy, an overabundance of Fe is often suggested,
which is somewhat surprising since a fraction of Fe may
be locked in grains, although sputtering is strong
for small grains and high velocity shocks.
[Fe VII]/H values for PA=221
values for PA=221 are shown in Figs. 4d,
are shown in Figs. 4d, e, and f.
The available
data are scarce, hence further constraints to the models are really not
possible. The models used to fit the other lines are compared with
the available data. As seen in Fig. 4f high velocity models
overpredict the [Fe VII]/H
e, and f.
The available
data are scarce, hence further constraints to the models are really not
possible. The models used to fit the other lines are compared with
the available data. As seen in Fig. 4f high velocity models
overpredict the [Fe VII]/H line ratio.
A better fit is obtained reducing the weight of the high velocity
models by a factor of 2. This reduction does not change our
discussion above concerning the other lines,
because models with
line ratio.
A better fit is obtained reducing the weight of the high velocity
models by a factor of 2. This reduction does not change our
discussion above concerning the other lines,
because models with  =1400
=1400
 contribute by
no more than 20% to [O II]/H
contribute by
no more than 20% to [O II]/H and [S II]/H
and [S II]/H line ratios.
As we will see over the next sections, a low contribution from high
velocity clouds is also needed to explain the IR lines (Sect. 6)
and the continuum SED (Sect. 7).
Notice that the [Ne V] 3426 lines, also coming from the
high ionization zone in the clouds, are overestimated by high
velocity models (see Sect. 5).
line ratios.
As we will see over the next sections, a low contribution from high
velocity clouds is also needed to explain the IR lines (Sect. 6)
and the continuum SED (Sect. 7).
Notice that the [Ne V] 3426 lines, also coming from the
high ionization zone in the clouds, are overestimated by high
velocity models (see Sect. 5).
The ISO coronal line data reported by Sturm et al.
(1999) are used to further constrain the models.
Since the ISO aperture are of the order of several
arcminutes, only the coronal lines are used.
Lines from lower ionization stages may include the contribution from
star
forming regions in the galaxy. Nevertheless, they are included in the
discussion in order to complete the data set with information from
different ionization stages.
Two Ne coronal lines are observed: [Ne VI] 7.6 and [Ne V] 14.3 in
addition to
two other strong lines, [Ne III] 15.5, and [Ne II] 12.8.
Regarding Si, [Si IX] 3.94, [Si VII] 2.48, and [Si II] 34.8 are detected.
From all the models plotted in Figs. 2 to 4, we select those
which could better reproduce the IR line ratios. The corresponding input
parameters are listed in Table 1, as well as the weights (W(Ne))
adopted for the best average model (AV). The weights are relative to
that of model 2.
The weights adopted for the Si lines (W(Si)) are, however, different
because they
account for Si depletion from the gas phase (and included in grains),
which is different in each model.
To account for the Si coronal line emission, Si/H has to be depleted
by a factor of about 15.
Moreover, the different depletion of Si
in the different clouds may be indicating that
the dust is not homogeneously distributed in the emitting clouds
(see Kraemer et al. 2000).
Notice that the weights are very different for different models because
they must
compensate the difference by many orders of magnitude of the line
intensity fluxes, in order to obtain similar contribution to the
emission
lines from different models (CV01).
SD and RD clouds correspond respectively to
models 2, 3, 4, 6, and models 1 and 5.
Table 1:
The models for the infrared lines.
| model |
1 |
2 |
3 |
4 |
5 |
6 |
 ( (
 ) ) |
100 |
300 |
500 |
500 |
500 |
1500 |
| 0 (3) |
100 |
300 |
300 |
300 |
300 |
300 |
log 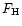 |
11 |
- |
- |
- |
12.7 |
- |
| D (1017 cm) |
100 |
100 |
10 |
100 |
100 |
1 |
| W(Ne) |
5.(-4) |
1. |
6.5(-4) |
7.9(-4) |
2.(-6) |
2.9(-8) |
| W(Si) |
0.114 |
1. |
1.4(-3) |
1.43(-3) |
1.4(-4) |
1.6(-6) |
The observed IR emission-line flux as well as the ratios of the
calculated to observed
lines are listed in Table 2.
This table is organized as follows:
(a) line fluxes (row 1);
(b) the results corresponding to the best fit model of
Alexander et al. (1999) (row 2);
(c) single-cloud results (rows 3 to 8);
(d) the weighted average model AV (row 9);
(e) the contribution to the IR emission lines from each single-cloud
model (rows 10 to 15).
Actually, the line and continuum spectra must be modeled consistently,
so, the results
of the AV model in Table 2 are cross-checked by the results of the
continuum SED in Sect. 7,
until the best tuning for both is achieved.
Because the theoretical fluxes are calculated at the nebula and
the observed fluxes are measured at Earth, the ratio of the
square distance of the galaxy to Earth (d2)
to the square distance of the nebula to the galaxy center (R2)
is given in the last column of Table 2.
From Table 2, one sees that model 2 (SD,  =300
=300
 )
strongly contributes to all the lines.
Gas is heated to temperatures between
)
strongly contributes to all the lines.
Gas is heated to temperatures between
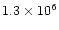 K and
K and
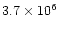 K
for SD clouds with
K
for SD clouds with  of 300
of 300
 and 500
and 500
 ,
respectively.
Radiation dominated model 1 contributes mainly
to [Ne V] and [Si II] and model 5 to [Ne III] and [Si VII].
Model 5 is associated with a very high ionizing flux:
,
respectively.
Radiation dominated model 1 contributes mainly
to [Ne V] and [Si II] and model 5 to [Ne III] and [Si VII].
Model 5 is associated with a very high ionizing flux:
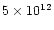 (cm-2 s-1 eV-1 at the Lyman limit).
(cm-2 s-1 eV-1 at the Lyman limit).
The high velocity clouds (model 6,  =1500
=1500
 )
do have a low contribution. This contribution must remain low as to
prevent the increase of [Si IX] flux far beyond its observational value.
)
do have a low contribution. This contribution must remain low as to
prevent the increase of [Si IX] flux far beyond its observational value.
Ultraviolet lines may provide important information about their
origin in a gas either heated by shocks or ionized by a
strong radiation.
The most significant lines are N V 1240, C IV 1550, and He II 1640.
Other strong UV lines are generally blended (O IV, Si IV 1402,
C III], Si III] 1909, etc.), and have not been used in the modeling.
Because the reddening correction in the UV is important, we use
the N V/C IV and He II/C IV line ratios instead of intensities
relative to H .
.
The UV data correspond to PA=221 observations.
Model results are presented in
Fig. 6 where South-West (SW) data
(filled triangles) are separated from those form the North-East (NE)
region
(open triangles).
observations.
Model results are presented in
Fig. 6 where South-West (SW) data
(filled triangles) are separated from those form the North-East (NE)
region
(open triangles).
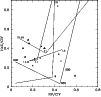 |
Figure 6:
He II 1640/C IV 1550 versus N V 1240/C IV 1550.
SW UV data and NE UV data correspond, repectively, filled and empty
triangles.
The RD results for  =100 =100
 and 0=100 3 (dotted line),
and
and 0=100 3 (dotted line),
and  =200 =200
 and 0=200 3 (dash-dotted line) are labelled
by the values of log(
and 0=200 3 (dash-dotted line) are labelled
by the values of log(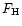 ), and the SD results (solid line) by ), and the SD results (solid line) by  in in
 . . |
| Open with DEXTER |
The theoretical results indicate that the NE UV data
can be explained by low velocity RD clouds (<300
 )
reached
by an ionizing flux
)
reached
by an ionizing flux 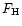 < 1011 units, while the SW UV data
come from the RD clouds reached by a stronger radiation field,
with some contribution from SD clouds with
< 1011 units, while the SW UV data
come from the RD clouds reached by a stronger radiation field,
with some contribution from SD clouds with  > 500
> 500
 .
However,
these
results are only indicative
(see the discussion by Kraemer et al. 2000).
It is well known that the He II 1640 line is
strongly dependent on the spectral index of the ionizing radiation,
and the N V/C IV ratio depends on the adopted N/C abundance ratio.
Regarding the He II lines, if
.
However,
these
results are only indicative
(see the discussion by Kraemer et al. 2000).
It is well known that the He II 1640 line is
strongly dependent on the spectral index of the ionizing radiation,
and the N V/C IV ratio depends on the adopted N/C abundance ratio.
Regarding the He II lines, if
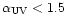 the theoretical results
may
vertically shift to the upper part of the diagram, and the derived
velocities would be larger.
Regarding the N/C abundance ratio, the cosmic values is adopted.
the theoretical results
may
vertically shift to the upper part of the diagram, and the derived
velocities would be larger.
Regarding the N/C abundance ratio, the cosmic values is adopted.
For consistency, we present in Table 3 the observed/calculated
UV-optical
line ratios obtained with the same AV model as for the IR lines
(see Table 2).
To avoid the uncertainty of the dilution factor the ratios of the
AV model are calculated between the line ratios to H .
.
The fit is within 1.6 and the trend is always to overestimate the
values.
This is consistent with reduction of the SD models which was adopted in
Figs. 2-4b, c, and e, f.
To further constrain our model for NGC 4151, the continuum SED
is analysed and modeled using the
composite model derived from the Ne and Si lines in Sect. 5.
Gamma-rays to the optical continuum emission
is taken from
the 1993 December multiwavelength
monitoring campaign of NGC 4151 (Edelson et al. 1996).
The source was near its peak historical
brightness during this campaign and showed the strongest variations of
its
continuum emission at
medium energy X-rays (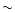 1.5 keV) with amplitude variations of
1.5 keV) with amplitude variations of
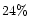 ,
weaker variations (6
,
weaker variations (6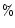 )
at the gamma-ray energies, decreasing
variation from ultraviolet (9
)
at the gamma-ray energies, decreasing
variation from ultraviolet (9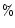 )
to optical (1
)
to optical (1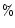 )
and finally, not
significant variation at the soft X-rays (0.1-1 keV).
)
and finally, not
significant variation at the soft X-rays (0.1-1 keV).
Assuming that the continuum emission variations are within a few
percent level beyond optical wavelengths, the 1993 data are
combined with
IR data taken at different epochs. Since the optical aperture used by
Edelson et al. (1996) is 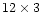 arcsec, near-IR fluxes from an aperture size of 10 arcsec
is adopted when possible. Sources are as follows:
arcsec, near-IR fluxes from an aperture size of 10 arcsec
is adopted when possible. Sources are as follows:
The data for the near-IR come from the NASA Extragalactic Data
(NED), J, H and K data are taken from Balzano &
Weedman (1981) and L and M data from McAlary et al (1979).
The 10 microns emission is from Lebofsky & Rieke (1979) and
corresponds to an aperture size of 6 arcsecs.
In addition, to trace the non-stellar contribution at the
near-IR, Kotilanien's et al. (1992) data within a 3 arcsec aperture
are also considered for comparative purposes.
For the far-IR region between 16 and 200 microns, ISOPHOT data from
Perez-Garcia et al. (1998) are taken. Due to the large aperture
size used in ISOPHOT, those data are integrated over the complete
galaxy.
For the radio data, values at 1.4 GHz, 4.85 GHz, and 408 MHz were at the NED, and come from Becker
et al. (1995), Becker et al. (1991), and Ficarra et al. (1985), respectively, while data at 8.4 and 5 GHz
are taken from Pedlar et al. (1993).
Compared with other Seyfert galaxies, NGC 4151 is relatively weak in
X-rays
with L(2-10 keV)
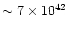 erg s-1 (Weaver et al. 1994).
The soft X-ray emission is extended (Morse et al. 1995).
Recent Chandra data resolve
up to
erg s-1 (Weaver et al. 1994).
The soft X-ray emission is extended (Morse et al. 1995).
Recent Chandra data resolve
up to  70
70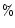 of the 0.4-2.5 keV emission (Ogle et al. 2000).
This emission appears to be associated with
the optical narrow line gas (NLR) extending asymmetrically
to the South-West of the nucleus.
of the 0.4-2.5 keV emission (Ogle et al. 2000).
This emission appears to be associated with
the optical narrow line gas (NLR) extending asymmetrically
to the South-West of the nucleus.
Both, Weaver et al. (1994) and Ogle
et al. (2000) provide similar estimates for the
plasma pressure of the hot
gas of about
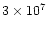 cm-3 K. This is one
order of magnitude larger than the pressure derived from the cold NLR
gas (Penston et al. 1990). The difference strongly argues against the
soft
X-ray emission being associated with the NLR confining medium (Weaver
et al. 1994; Ogle et al. 2000).
cm-3 K. This is one
order of magnitude larger than the pressure derived from the cold NLR
gas (Penston et al. 1990). The difference strongly argues against the
soft
X-ray emission being associated with the NLR confining medium (Weaver
et al. 1994; Ogle et al. 2000).
Weaver et al. (1994) also found that the Fe K edge
energy in their 0.4-11 keV data (from the BBXRT mission) is
inconsistent with an origin in a gas
with the same ionization parameter as the low-energy absorber.
This allows the authors to rule out a line-of-sight ionized absorber
as the sole source of the soft X-ray excess in NGC 4151
(see also Contini & Viegas 1999 for the case of NGC 4051).
George et al. (1998) propose a model for the 0.2-10 keV
spectrum where the underlying power law nuclear component is
partially absorbed by an ionized absorber and partially
scattered. However, it requires an additional
component due to Bremsstrahlung thermal
emission from an extended photoionized gas at
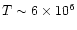 K.
K.
Recent Chandra data provide direct evidence of X-ray line emission gas
at
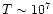 K. The strength and ionization potential of the
X-ray narrow emission lines indicate a composite spectrum in which
both photoionization and shocks are at work (Ogle et al. 2000).
The fair spatial association between
the central NLR optical region and the soft X-ray emission indicated
that both mechanisms are contributing to the multi-wavelength SED
and to the line spectrum of NGC 4151 (cf. Komossa 2001).
Taking into account these observational constraints, the
origin of this soft X-ray excess is evaluated in the next section
assuming high velocity models dominated by shocks.
K. The strength and ionization potential of the
X-ray narrow emission lines indicate a composite spectrum in which
both photoionization and shocks are at work (Ogle et al. 2000).
The fair spatial association between
the central NLR optical region and the soft X-ray emission indicated
that both mechanisms are contributing to the multi-wavelength SED
and to the line spectrum of NGC 4151 (cf. Komossa 2001).
Taking into account these observational constraints, the
origin of this soft X-ray excess is evaluated in the next section
assuming high velocity models dominated by shocks.
NGC 4151 shows the characteristics of Seyfert galaxies rather than
starbursts. Therefore, we consider that the continuum
SED is Bremsstrahlung radiation from clouds ionized and heated
by the radiation from the AC and by shocks.
We refer to previous studies (e.g. Contini & Viegas-Aldrovandi 1990;
Contini & Viegas 1991; Viegas & Contini 1994; Contini & Viegas 2000,
etc.)
on this subject which could lead to a better understanding of the
results.
Particularly, dust and gas are coupled entering the shock front and
mutually heat each other. The grains are collisionally heated to
the highest temperatures (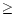 300 K) leading to emission in the
near-IR.
On the other hand, heating by the central radiation is not efficient
enough, so dust in the radiation dominated zone does not reach such high
temperatures.
300 K) leading to emission in the
near-IR.
On the other hand, heating by the central radiation is not efficient
enough, so dust in the radiation dominated zone does not reach such high
temperatures.
Before discussing model results, let us notice that below the Lyman
limit, up to say 0.2 keV, we have very little observational information:
this is the "unknown window'' where observations are difficult because
of the heavy absorption by our Galaxy. However, in the 0.2 to 2 keV
region, NGC 4151 shows extended emission, spatially
correlated with the optical NLR gas. If due to Bremsstrahlung,
the tail of this X-ray emission should somehow show up in the far UV.
However, no detected extended emission appears in the UV HST images
of NGC 4151 (Boksenberg et al. 1995). Therefore, the emission from the
NLR gas should be lower than that of the UV nucleus of NGC 4151. We
will use this observational fact as a constraint in the proposed
modeling in the sense that the observed
nuclear UV emission can only be
associated with model emission within a nuclear region of outmost 3 pc
size.
Observational data and model results are plotted in Figs. 7 and 8,
which refer to models and relative weights adopted to fit the Ne
infrared
lines (Table 1, row 5). Notice that Bremsstrahlung peaks at high
frequencies depending on  (see Viegas & Contini 1994).
(see Viegas & Contini 1994).
The large geometrical thickness of the emitting clouds and the high
densities downstream due to compression (n/0 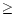 10, depending on
10, depending on
 ,
0, and 0) lead to high optical thickness of the emitting gas
with column densities of the order of 1021-1024 cm-2.
This is within the range of column densities estimated from
the X-ray data,
,
0, and 0) lead to high optical thickness of the emitting gas
with column densities of the order of 1021-1024 cm-2.
This is within the range of column densities estimated from
the X-ray data, 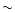
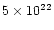 cm-2 (Weaver
et al. 1994; George et al. 1998; Ogle et al. 2000).
Accordingly, the emitted radiation gets absorbed in the cloud itself
between
cm-2 (Weaver
et al. 1994; George et al. 1998; Ogle et al. 2000).
Accordingly, the emitted radiation gets absorbed in the cloud itself
between  13.6 eV and 500 eV, hence the emission gap in this
region shows up in Figs. 7 and 8. The high velocity model 6
has however a lower column density (<1021 cm-2)
because is radiation-bounded.
In fact, due to strong compression, the temperature rapidly
decreases downstream at a distance <1016 cm from the shock
front. Thus, the contribution of model 6 to the SED extends
into the far UV range (Fig. 7 long-dashed line). However, the
X-ray data in the frequency range 1015 and 1017 Hz impose
a limit on the relative constribution of this model 6 (see below).
All together, the fit of the continuum at the UV range is
obtained with model 2.
The dust-to-gas ratio that characterizes this model is
d/g = 10-14. The other models (models 3, 4, 5, and 6) underpredict
the data.
13.6 eV and 500 eV, hence the emission gap in this
region shows up in Figs. 7 and 8. The high velocity model 6
has however a lower column density (<1021 cm-2)
because is radiation-bounded.
In fact, due to strong compression, the temperature rapidly
decreases downstream at a distance <1016 cm from the shock
front. Thus, the contribution of model 6 to the SED extends
into the far UV range (Fig. 7 long-dashed line). However, the
X-ray data in the frequency range 1015 and 1017 Hz impose
a limit on the relative constribution of this model 6 (see below).
All together, the fit of the continuum at the UV range is
obtained with model 2.
The dust-to-gas ratio that characterizes this model is
d/g = 10-14. The other models (models 3, 4, 5, and 6) underpredict
the data.
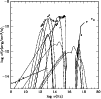 |
Figure 7:
Different components contributing to the SED of the
continuum of NGC 4151,
corresponding to the results of several models, scaled following the
weights used to fit
the IR lines. The models are the following:
1 (dash-dotted line), 2 (dotted
line),
3 (short dash-dotted line), 4 (short-dashed line), 5 (solid line), 6
(long dashed line).
The flux from the AC in the far X-rays, which is seen through the
clouds,
is represented by a thick dotted line, while the continuum from the old
stellar
population is indicated by a thick long dash-dotted line.
The theoretical results are compared to observational data taken from
the NED
(filled squares) and from other sources described in Sect. 7 (open
squares). |
| Open with DEXTER |
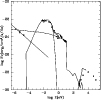 |
Figure 8:
The continuum spectrum of NGC 4151. The thin solid lines
correspond to the
summed theoretical contributions from dust emission, gas Bremsstrahlung
and radio emission as shown in Fig. 7. The thick solid line
corresponds to
the summed contributions from dust emission, gas Bremsstrahlung and the
old
stellar population continuum, while the dotted line corresponds to the AC
continuum seen
through the clouds. The observational data are taken from the NED
(filled squares) and from other sources described in Sect. 7 (open
squares). |
| Open with DEXTER |
The summed SED which better explains the observations is shown in
Fig. 8.
The main components are summed separately: radio emission, reradiation
by dust in the IR, gas Bremsstrahlung, and the flux from the active
source. Moreover, as was found for many Seyfert galaxies (see Contini
& Viegas 2000)
a black-body with temperature of 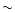 3000 K is used to roughly represent the optical continuum due to the
stellar population (thick solid line).
3000 K is used to roughly represent the optical continuum due to the
stellar population (thick solid line).
Notice that we are interested in the bulk contribution of the stars
rather than
the detailed shape of their continuum emission. Thus, although we could
use
the spectrum of an early-type galaxy or the spectrum of the central
region of
a Sa galaxy to get a more realistic fit of the stellar contribution,
it would not change our conclusions.
For instance, Malkan & Filippenko (1983) find that about 1/10 of the
emission at 5500 Å and 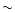 1/3 at 9000 Å are due to stars (in aperture of 10'',
just the same aperture of the optical and IR data used in this paper),
namely they estimated the stellar emission to be 14 mJy at 5500 Å.
We have added the corresponding value to
Fig. 7 (star). Accounting for the errors in the observations
and models, notice the good agreement
(within 30%) with the black body emission curve.
1/3 at 9000 Å are due to stars (in aperture of 10'',
just the same aperture of the optical and IR data used in this paper),
namely they estimated the stellar emission to be 14 mJy at 5500 Å.
We have added the corresponding value to
Fig. 7 (star). Accounting for the errors in the observations
and models, notice the good agreement
(within 30%) with the black body emission curve.
The bump in the IR is rather wide, representing the
sum of contributions from different models. In previous papers
(e.g. Contini et al. 1999b, Appendix A) it was explained that the bump
in the IR due to each model depends on the shock velocity.
Particularly, the high velocity model (model 6) has its maximum at the
near-IR. To fit the near-IR data, a high d/g (
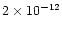 )
is
assumed in model 6,
indicating that high velocity material is rather dusty.
A shock velocity of 1500
)
is
assumed in model 6,
indicating that high velocity material is rather dusty.
A shock velocity of 1500
 produces a post shock region at a
temperature of
produces a post shock region at a
temperature of
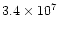 K, in agreement with the hot plasma
temperatures derived from the X-ray data.
indicating that high velocity material is rather dusty.
K, in agreement with the hot plasma
temperatures derived from the X-ray data.
indicating that high velocity material is rather dusty.
Shocked clouds with 
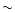 700
700
 produce lower temperatures,
produce lower temperatures,
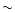 106 K, which are still within the range of values estimated
from X-ray data (e.g. George et al. 1998).
These velocities are also revealed by optical lines (Sect. 4).
106 K, which are still within the range of values estimated
from X-ray data (e.g. George et al. 1998).
These velocities are also revealed by optical lines (Sect. 4).
Yet, the contribution of a model with  =1500
=1500
 in the SED
should be taken with a relative small weight (
in the SED
should be taken with a relative small weight (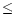
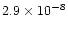 ),
because the
data in the soft X-ray range constrain the model. As a consequence,
the contribution of this model to the IR lines is very low. Thus,
a signature of these high velocity clouds is not expected to
be seen in the infrared emission-line spectrum.
),
because the
data in the soft X-ray range constrain the model. As a consequence,
the contribution of this model to the IR lines is very low. Thus,
a signature of these high velocity clouds is not expected to
be seen in the infrared emission-line spectrum.
In the radio range, Pedlar et al. (1993) derive an average spectral
index for the entire source of
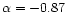 from their 8.4 and 5 GHz
data. They interpreted the emission as due to thermal free-free
emission from the NLR. In the present modeling, the radio data are instead
well explained by synchrotron radiation with spectral index -0.75, generated by
Fermi mechanism at the shock front (Bell 1978).
Notice that self-absorption of the Bremsstrahlung
emission at these radio wavelengths may be important, hence its
contribution
is negligeble (see, for instance Contini et al. 1998b).
from their 8.4 and 5 GHz
data. They interpreted the emission as due to thermal free-free
emission from the NLR. In the present modeling, the radio data are instead
well explained by synchrotron radiation with spectral index -0.75, generated by
Fermi mechanism at the shock front (Bell 1978).
Notice that self-absorption of the Bremsstrahlung
emission at these radio wavelengths may be important, hence its
contribution
is negligeble (see, for instance Contini et al. 1998b).
In this paper we have modeled the narrow emission-line
and continuum spectra of NGC 4151 with particular attention to the
large range of velocities indicated by the line profiles.
The analysis of the line profiles is complex and
clouds in many different conditions can contribute to each line.
By modeling the NLR to analyse the high spatial resolution data
(Nelson et al. 2000; Kraemer et al. 2000), it is found that the
contribution of each cloud to a given line may show a large variation from line to line.
In the central region high velocity clouds revealed by the observations
(Hutchings et al. 1999; Winge et al. 1997, etc.) are shock dominated
(SD). There is a strong contribution of SD clouds with shock velocity 
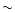 700
700
 to [OII] 3727/H
to [OII] 3727/H ,
and [OI] 6300/H
,
and [OI] 6300/H .
Radiation dominated (RD) clouds with
.
Radiation dominated (RD) clouds with 
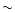 500
500
 are necessary
to explain [SIII]/H
are necessary
to explain [SIII]/H and [OI]/H
and [OI]/H ,
while clouds
with low
,
while clouds
with low  (100-200
(100-200
 )
and reached by a relatively
strong ionizing radiation (log
)
and reached by a relatively
strong ionizing radiation (log 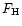
 11)
contribute to the [OIII]/H
11)
contribute to the [OIII]/H ,
[OII]/H
,
[OII]/H ,
and [SII]/H
,
and [SII]/H line ratios.
line ratios.
Beyond 2'' from the center, RD clouds, photoionized by a weaker
radiation flux are responsible for the observed line emission.
Quantitative modeling of the Ne and Si infrared lines
from different ionization levels leads to more results.
Notice, however, that the observations give the integrated flux
from all the galaxy, so that it is not possible to understand
which type of clouds prevail in different regions.
SD clouds with  =300
=300
 strongly contribute to all Ne lines
corresponding
to different ionization levels (Table 2), while
RD clouds with velocities of 500
strongly contribute to all Ne lines
corresponding
to different ionization levels (Table 2), while
RD clouds with velocities of 500
 and reached by a strong radiation
flux
(log
and reached by a strong radiation
flux
(log 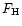 =12.7)
contribute particularly to the [NeIII] and [SiVII] IR lines.
Due to the high postshock temperature, high velocity clouds
(
=12.7)
contribute particularly to the [NeIII] and [SiVII] IR lines.
Due to the high postshock temperature, high velocity clouds
( =1500
=1500
 )
would overpredict the [SiIX] 3.94 line.
Therefore, the contribution of these clouds is low.
A large contribution to [NeV] and [SiII] lines
come from low velocity (100
)
would overpredict the [SiIX] 3.94 line.
Therefore, the contribution of these clouds is low.
A large contribution to [NeV] and [SiII] lines
come from low velocity (100
 )
clouds reached by an
ionizing radiation characterized by log
)
clouds reached by an
ionizing radiation characterized by log 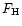 =11.
=11.
Modeling of the IR lines also shows that
silicon is depleted by a factor of 15
because included in dust grains, while N/C abundance ratio is found
compatible with cosmic values from the modeling of the UV lines.
Comparing the results of the present work with those of other authors,
notice that our results are slightly better. Indeed, better fits
could be obtained with a different choice of weights. However, the
results presented in Tables 2 and 3 are consistent with the fit of the
continuum SED (Sect. 7) and were chosen accordingly. More particularly, it
seems that the three Ne emission lines are higher than observed by
factors of 1.3-1.5. This may be an indication that the Ne abundance
we have used is a factor of 1.3-1.5 too high.
So, decreasing the Ne/H abundance by
1.3, we get a better agreement. The He II 4686 line is slightly higher,
but this is mainly due to the power law above 54.4 eV, which we (and the
others) could have taken somehow too flat. The only problem is the
[O III]4363 line. Because oxygen is a coolant, changing the O abundance
may not solve the problem. However, a factor of 1.6 higher is still
within the limit of a factor of 2 proposed by Alexander et al., who do
not give their results for [O III] 4363.
Notice that we based our models on IR lines and we compared with
Alexander et al. (1999). So, we should refer only to them. The results
of Kraemer et al in row 2 of Table 3 are better than ours only for [O III]
4363 and [Ne III]. Actually, they come from observations in the region
between 0.1'' and 0.3'' SW, whereas we average on all the regions.
The analysis of the continuum SED leads to the following results:
The high velocity material is very dusty
(
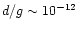 ).
The radio emission is synchrotron created by Fermi mechanism
at the shock front.
Moreover, shocks are important to explain the soft X-rays:
shocks with velocities of 1500
).
The radio emission is synchrotron created by Fermi mechanism
at the shock front.
Moreover, shocks are important to explain the soft X-rays:
shocks with velocities of 1500
 produce a post shock region at a
temperature of
produce a post shock region at a
temperature of
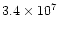 K.
This value is in agreement with the temperature found by Weaver et al.
(1994) and Ogle et al. (2000) for a non-equilibrium plasma from
X-ray observations, while
clouds with
K.
This value is in agreement with the temperature found by Weaver et al.
(1994) and Ogle et al. (2000) for a non-equilibrium plasma from
X-ray observations, while
clouds with 
 750
750
 produce temperatures of
produce temperatures of
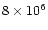 K (George et al. 1998).
K (George et al. 1998).
An estimate of several physical quantities applying to the central
AGN region can be derived from the proposed modeling.
If d is the distance from Earth (19.8 Mpc) and
d2/R2 = 109(see Table 2),
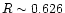 kpc is the average distance of
the emitting nebula to the AC.
Adopting an average downstream density n=105 3, and
D=1018 -
1019 cm,
the calculated mass is
kpc is the average distance of
the emitting nebula to the AC.
Adopting an average downstream density n=105 3, and
D=1018 -
1019 cm,
the calculated mass is
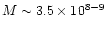 ff
ff  ,
where ff is the filling factor which is likely to be less than unity.
In this case our estimation of the NLR mass is lower than the values
quoted
by Ulrich (2000) for an emitting region closer to the center, i.e.
109
,
where ff is the filling factor which is likely to be less than unity.
In this case our estimation of the NLR mass is lower than the values
quoted
by Ulrich (2000) for an emitting region closer to the center, i.e.
109  within 40 pc and
within 40 pc and
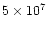
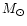 within 12 pc (0.15'').
The corresponding calculated central source luminosity is about
within 12 pc (0.15'').
The corresponding calculated central source luminosity is about
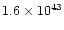 erg s-1.
The average kinetic energy of the NLR is about
erg s-1.
The average kinetic energy of the NLR is about
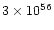 ff ergs,
assuming an average velocity of the NLR clouds of 300
ff ergs,
assuming an average velocity of the NLR clouds of 300
 .
This would imply that the time scale for the AGN phase in NGC 4151
should be
larger than
.
This would imply that the time scale for the AGN phase in NGC 4151
should be
larger than
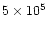 years.
years.
Summarizing, we provide a self-consistent modeling of the
multiwavelength line spectrum and SED of the nuclear region of NGC 4151.
The modeling is based on the coupled effect of shocks and
photoionization operating in the narrow emission line gas. As such, it
implies the existence of emitting clouds with
velocities and densities in a large range. An emitting-cloud
distribution in the
velocity/density space is precisely what is revealed by the HST
observations of this galaxy. This together with the fair
fitting of the line and continuum spectra obtained in this work
reinforces
our hypothesis that shocks and photoionization are effectively coupled
in
the NLR of AGN.
Acknowledgements
We are grateful to the referee for many helpful comments.
This paper is partially supported by the Brazilian agencies:
CNPq (304077/77-1),
PRONEX/Finep (41.96.0908.00), and FAPESP (00/06695-0).
-
Alexander, T., Sturm, E., Lutz, D.,
Sternberg, A., Netzer, H., &
Genzel, R. 1999, ApJ, 512, 204
In the text
NASA ADS
-
Balzano, V. A., & Weedman,
D. W. 1981, ApJ, 243, 756
In the text
NASA ADS
-
Becker, R., White, R., & Helfand,
D. 1995, ApJ, 450, 559
In the text
NASA ADS
-
Becker, R., White, R., & Edwards, A. 1991, ApJS, 75, 1
In the text
NASA ADS
-
Bell, A. R. 1978, MNRAS, 182, 443
In the text
NASA ADS
-
Boksenberg, A., Catchpole, R. M.,
Macchetto, F., et al. 1995, ApJ, 440, 151
In the text
NASA ADS
-
Contini, M., & Aldrovandi, S. M. V. 1986, A&A, 168, 41
In the text
NASA ADS
-
Contini, M., & Viegas-Aldrovandi, S. M. 1990, ApJ, 350, 125
In the text
NASA ADS
-
Contini, M., & Viegas, S. M. 1991, ApJ, 373, 405
In the text
NASA ADS
-
Contini, M., & Viegas, S. M. 1999, ApJ, 523, 114
In the text
NASA ADS
-
Contini, M., & Viegas, S. M. 2000, ApJ, 535, 721
In the text
NASA ADS
-
Contini, M., & Viegas, S. M. 2001, ApJS, 132, 211 (CV01)
In the text
NASA ADS
-
Contini, M., Prieto, M. A., & Viegas, S. M. 1999a, ApJ, 492, 511
NASA ADS
-
Contini, M., Prieto, M. A., & Viegas, S. M. 1999b, ApJ, 505, 621
In the text
NASA ADS
-
Crenshaw, D. M., Kraemer, S. B.,
Hutchings, J. B., et al. 2000, AJ, 120, 1731
In the text
NASA ADS
-
Ficarra, A., Grueff, G., & Tommasetti, G. 1985, A&AS, 59, 255
In the text
NASA ADS
-
George, I. M., Turner, T. J., Netzer, H., et al. 1998, ApJS, 114, 73
In the text
NASA ADS
-
Hutchings, J. B., Crenshaw, D. M., Kaiser, M. E., et al. 1998, ApJ, 492, L115
In the text
NASA ADS
-
Hutchings, J. B., Crenshaw, D. M., Dank, A. C., et al. 1999, AJ, 118, 210
In the text
-
Kaiser, M. E., Bradley, L. D., II, Hutchings, J. B., et al. 2000, ApJ, 528, 260
In the text
NASA ADS
-
Komossa, S. 2001, A&A, 371, 507
In the text
NASA ADS
-
Kotilanien, J. K., Ward, M., Boisson, C., Depoy, D. L., & Smith, M. G. 1992,
MNRAS, 256, 149
In the text
NASA ADS
-
Kraemer, S. B., Crenshaw, D. M.,
Hutchings, J. B., et al. 2000, ApJ, 531, 278
In the text
NASA ADS
-
Lebofsky, M. J., & Rieke, G. H. 1979, ApJ, 229, 111
In the text
NASA ADS
-
Malkan, M. A., & Filippenko, A. V. 1983, ApJ, 275, 477
In the text
NASA ADS
-
McAlary, C. W., McLaren, R. A., & Crabtree, D. R.
1979, ApJ, 234, 471
In the text
NASA ADS
-
Morse, J., Wilson, A., Martin, E., & Weaver, K. 1995, ApJ, 439, 121
In the text
NASA ADS
-
Nelson, C. H., Weistrop, D., Hutchings, J. B.,
et al. 2000, ApJ, 531, 257
In the text
NASA ADS
-
Ogle, P., Marshall, H. L., Lee, J. C., & Canizares, C. 2000,
ApJ, 545, L810
In the text
-
Osterbrock, D., & Koski, A. 1976, MNRAS, 176, P61
In the text
NASA ADS
-
Pedlar, A., Kukula, M. J., Longley, D. P. T., et al. 1993, MNRAS, 263, 471
In the text
NASA ADS
-
Penston, M. V., & Pérez, E. 1984, MNRAS, 211, 33p
In the text
NASA ADS
-
Perez-Garcia, A. M., Rodriguez Espinoza, J. M., & Santolaya Rey, A. E. 1998,
ApJ, 500, 685
In the text
NASA ADS
-
Rieke, G. H., & Low, F. J. 1972, ApJ, 176, L95
NASA ADS
-
Schulz, H. R. 1988, A&A, 203, 233
In the text
NASA ADS
-
Schulz, H. R. 1990, AJ, 99, 1442
In the text
NASA ADS
-
Sturm, E., Alexander, T., Lutz, D., et al. 1999, ApJ, 512, 197
In the text
NASA ADS
-
Ulrich, M. H. 2000, A&AR, 10, 135
In the text
-
Viegas, S. M., & Contini, M. 1994, ApJ, 428, 113
In the text
NASA ADS
-
Weaver, K. A., Mushotzky, R. F., Arnaud, K. A., et al. 1994, ApJ, 423, 621
In the text
NASA ADS
-
Weyman, R. J., Morris, S. L., Gray, M. E., & Hutchings, J. B. 1997, 483, 717
In the text
-
Winge, C., Axon, D. J., Macchetto, F. D., & Capetti, A. 1997, ApJ, 487,
In the text
-
Winge, C., Axon, D. J., Macchetto, F. D., Capetti, A., & Marconi, A.
1999, ApJ, 519, 324
In the text
NASA ADS
Copyright ESO 2002







