A&A 386, L9-L12 (2002)
DOI: 10.1051/0004-6361:20020315

HD 304373, the second case of 1O/2O double-mode Cepheid in the Galaxy

M. Beltrame1 - E. Poretti1


1 - Università degli Studi, Dipartimento di Fisica, Milano, Italy
2 - Osservatorio Astronomico di Brera, Via Bianchi 46, 23807 Merate, Italy

Received 28 January 2002 / Accepted 1 March 2002

Abstract
We report on the discovery of the second case of a galactic Cepheid, ASAS 112843 -5925.7$\equiv$HD 304373, pulsating in the the first (1O) and second (2O) radial overtones. The ratio between the periods (0.8058), the short value of the 1O period (0.922405 d) and the shape of the 1O light curve makes HD 304373 very similar to the 1O/2O Cepheids in the Magellanic Clouds. The implications of a so close similarity between a galactic 1O/2O pulsator and LMC ones are discussed in terms of importance of the metallicity effects.

Key words: methods: data analysis - stars: oscillations - Cepheids - techniques: photometric -
stars: individual: HD 304373


1 Introduction

The All Sky Automated Survey (ASAS) is a project started at the beginning of 1996; its ultimate goal is to detect any kind of photometric variability present on a large area of the sky (Pojmansky 1997). The aim has been pursued by means of an automated mount equipped with a $716\times512$ pixel MEADE CCD camera, a 135-mm f/1.8 lens and an I-band filter. The instrument is located at Las Campanas Observatory in Chile and in the first three years it surveyed fifty $2\times3$ deg2 fields. Detailed descriptions of the project, the instrument, the data reduction and analysis can be found in three dedicated papers (Pojmansky 1997, 1998 and 2000).

In 2001 we started a careful re-examination of the pulsating stars included in the ASAS catalogue, to find further confirmations of the characteristics of Cepheids with $P<\ 8$ d, RR Lyr stars and High Amplitude Delta Scuti stars. Such a re-examination can be useful to detect new double-mode radial pulsators, which are among the most elusive variable stars. Their discovery constitutes a continuous observational challenge in the study of stellar oscillations, especially in the Galaxy, where selection effects are very important. From a physical point of view, the period ratio directly allows us to identify the pulsation modes. In turn, the matching of the observed period ratios constitutes a powerful and practical tool to model the interior of stars. Pardo & Poretti (1997) provide a systematic frequency analysis of the available photometry of the galactic double-mode Cepheids. Thirteen stars show the fundamental (F) period (P0) and the first overtone (1O, P1) periods, (P1/P0 between 0.7127 and 0.6968), only one shows the 1O and second (2O, P2) overtone periods (CO Aur, P2/P1=0.8008). Therefore, after the detection of a large number of double-mode Cepheids in the Magellanic Clouds, it is quite evident that the discovery of new double-mode Cepheids, and in particular new 1O/2O cases, can help to compare Cepheids of our Galaxy with those in other ones.

ASAS 112843 -5925.7 has been classified as a RR Lyr variable with P=0.9220 d (Pojmanski 2000). The light curve has an amplitude of 0.22 mag in I-band. It looks scattered, but no second periodicity has been suspected during the automatic period search, performed by analysis of variance method (Pojmanski 1998). The SIMBAD database identifies ASAS 112843 -5925.7 as HD 304373$\equiv$TYC 8629-00990-1 (spectral type F8). TYCHO photometry yields $B_T=11.22\pm0.06$ and $V_{\rm {T}}=10.57\pm0.05$ (H$\o$g et al. 2000).

2 Data analysis

The original dataset consists of 544 measurements in the I-band. They span about 1000 d, from 1997 April to 2000 January. The first 209 measurements were collected in 40 days in April and May 1997. Later, the survey started again in October 1998 and lasted until January 2000, only stopped for the heliacal conjunction (a gap of 70 day from August to October 1999). Thanks to this extensive coverage, the spectral window shows the 1 cy-1 peak reduced at only 53% of the power. In many occasions HD 304373 was measured several times during every night and therefore the alias at 1 cd-1 is also reduced (55% of the power). Hence, the dataset on HD 304373 appears very appropriate for an accurate frequency analysis. In order to detect the frequency content of HD 304373 we applied the same technique used by Pardo & Poretti (1997). The least-squares power spectrum method (Vanicek 1971) allowed us to detect one by one the constituent of the light curve. After each detection, we refined the frequency values by applying the MTRAP code (Carpino et al. 1987), particularly suitable for the double-mode pulsation as it keeps the relationships between the detected terms (i.e., 2f1, f1+f2, ...) locked.

A quick glance to the original dataset was enough to discover the double-mode nature of HD 304373: two terms at f1=1.084 cd-1 and f2=1.345 cd-1 clearly stand out, but a very high peak appeared at a very low frequency in the subsequent power spectrum. Therefore, we repeated the analysis by subdividing the original datasets into subsets (Table 1) as the low-frequency peak suggested the presence of systematic errors. In the first subset we detected not only the f1 and $.\!\!^{\rm d}$ term, but also 2f1 and, more hidden in the noise, f1+ $.\!\!^{\rm d}$. In the second dataset we detected again the f1, 2f1 and $.\!\!^{\rm d}$ terms, but also the f1+ $.\!\!^{\rm d}$ and 3f1 ones, which are clearly over the noise. In the third dataset we only detected the f1, 2f1 and $.\!\!^{\rm d}$ terms. The second and third subsets had the same mean magnitude, while the first one showed a remarkable systematic shift (Table 1). Therefore, we built up a homogenous dataset by shifting all the magnitudes of the first subset by -0.029 mag.

The results of the frequency analysis of such a dataset is shown in Fig. 1. The first power spectrum is dominated by the f1=1.0842 cd-1 term and its alias structure. This frequency is coincident with that reported in the ASAS database. The low peak at f2=1.3454 cd-1 becomes the highest in the second spectrum. The double-mode nature of HD 304373 is clearly established looking at these two panels. The subsequent analysis detected the 2f1 term (left panel in the middle row) and the coupling term f1+ $.\!\!^{\rm d}$ (right panel in the middle row). The presence of the coupling term ruled out the possibility of a binary system composed of two pulsating stars. In the bottom row the signal detection is more complicated. If the 3f1 term can be recognized in the fifth panel, the sixth one looks characterized by a bunch of frequencies around integer values of cd-1. One peak structure is at the sinodical month (f=0.034 cd-1) and its aliases, reflecting the Full-Moon interference: this spurious peak is quoted by Pojmanski (1998) as a common result in his period search in the ASAS database. Another one is close to the f1 value, just at the limit of the frequency resolution. Its presence can be explained pointing out that the amplitude of the f1 term results smaller in the third dataset ( $0.067\pm0.003$ mag) than in the other two ( $0.089\pm0.002$, $0.090\pm0.002$ mag). This term disappears analyzing only the first two datasets combined together. We also modified the last 90 measurements by amplifying the contribution of the first frequency, increasing its amplitude by a factor 1.33. In such a way, we obtained a dataset in which the A1 term is constant. The frequency analysis detected the f1, f2, 2f1, f1+f2, 3f1 and f=0.034 cd-1  terms, but no peak close to f1. Therefore, it is definitely established that the smaller A1 amplitude in the third dataset is responsible for the observed doublet.

  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{Ea281_f1.eps}}\end{figure} Figure 1: Power spectra of all the ASAS measurements of HD 304373. Each panel shows the spectrum obtained by introducing all the previous identified frequencies as known constituents; this means that the frequency values are considered already determined, but their amplitude and phase values are worked out for each new trial frequency.
Open with DEXTER

3 Least-squares fits and Fourier decomposition

Table 1 reports the parameters of the least-squares fits obtained by means of the formula

\begin{displaymath}I(t)= I_{\rm {o}} + \sum_z {A_z \cos [2\pi f_z (t-T_{\rm {o}}) +\phi_z ]} \end{displaymath} (1)

where fz is the generic frequency, which can be an independent frequency (f1 and $.\!\!^{\rm d}$), a harmonic (2f1 and 3f1) or the cross coupling term f1+ $.\!\!^{\rm d}$. The fits of the three subsets are reported for comparison purposes; the procedure to identify the terms present in the light curve of HD 304373 is the same used by Pardo & Poretti (1997, see their Table 3), but here we failed to build a homogenous dataset owing to the differences in amplitudes. Indeed, the amplitude variation of f1 looks big; its instrumental origin is not confirmed by the values of the $.\!\!^{\rm d}$ term, which remains constant among the three subsets. Moreover, the amplitude ratio R21 ( $0.18\,\pm\,0.02$, $0.22\,\pm\,0.02$ and $0.18\,\pm\,0.04$) and the phase difference $\phi_{21}$ ( $3.89\,\pm\,0.20$, $3.78\,\pm\,0.18$, $3.62\,\pm\,0.33$ rad) of the f1 term remain constant. That does not support a beating modulation between two close frequencies as in this case the shape of the f1 light curve should vary following the beat phase. Our analysis clearly indicates a sudden decrease of the f1 amplitude, but it is not able to point out the reason precisely. Therefore, we considered the 454 measurements between JD 2450546 and 2451402 as the final dataset, adjusted for the systematic differences.

In order to fit the f1 curve three harmonics are necessary, while the $.\!\!^{\rm d}$ curve does not require any harmonics. Therefore it is possible to calculate the Fourier parameters only in the former case. The values obtained from the final dataset are $\phi_{21}=3.80\pm0.11$ rad, $\phi_{31}=1.75\pm0.23$ rad and $R_{21}=0.21\pm0.02$. Figure 2 shows the light curves of the two periods of HD 304373: the upper curve was obtained by subtracting the $.\!\!^{\rm d}$ and f1+ $.\!\!^{\rm d}$ terms from the measurements, the lower one by subtracting f1, 2f1, 3f1, f1+ $.\!\!^{\rm d}$. Note also that the spurious term at f=0.034 cd-1 was not removed from the data. When considering it, the least-squares parameters don't change in a significant way and the residual rms decreases just a little, to 0.019 mag.

   
Table 1: Parameters of the least-squares fits of the ASAS measurements on HD 304373. They are divided into two subsets owing to the different mean magnitudes and to the change in the amplitude of the f1 term. $T_0=\,$HJD 2451026.2671.
        JD 2450546-2450584   JD 2451109-2451402   JD 2451469-2451583   JD 2450546-2451402
Term   Freq.   Ampl. Phase   Ampl. Phase   Ampl. Phase   Ampl. Phase
    [cd-1]   [mag] [rad]   [mag] [rad]   [mag] [rad]   [mag] [rad]
f1   1.084123   0.089 5.82   0.090 5.84   0.067 5.73   0.089 5.83
    $\pm$.000007   $\pm$.002 $\pm$.03   $\pm$.002 $\pm$.02   $\pm$.003 $\pm$.05   $\pm$.002 $\pm$.02
f2   1.345458   0.028 2.11   0.027 2.06   0.029 2.11   0.028 2.08
    $\pm$.000021   $\pm$.002 $\pm$.08   $\pm$.002 $\pm$.06   $\pm$.003 $\pm$.10   $\pm$.002 $\pm$.05
2f1       0.016 2.97   0.020 2.90   0.012 2.52   0.019 2.90
        $\pm$.002 $\pm$.14   $\pm$.002 $\pm$.08   $\pm$.003 $\pm$.23   $\pm$.002 $\pm$.07
f1+f2       0.010 6.12   0.011 6.10   - -   0.010 6.09
        $\pm$.002 $\pm$.23   $\pm$0.002 $\pm$.16         $\pm$.002 $\pm$.13
3f1       - -   0.019 0.75   - -   0.008 0.40
              $\pm$0.002 $\pm$.18         $\pm$.002 $\pm$.17

Mean I magnitude

   $9.734\pm.002$   $9.705\pm.001$   $9.704\pm.002$   $9.705\pm.002$
Residual rms [mag]   0.022   0.019   0.019   0.020
N   209   245   90   454


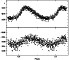  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{Ea281_f2.eps}}\end{figure} Figure 2: Light curves of the two independent frequencies f1=1.084123 cd-1 (upper panel) and f2=2.345458 cd-1 (lower panel) as obtained from the measurements of HD 304373 between JD 2450546 and 2451402.
Open with DEXTER

4 The double-mode pulsation

Our analysis detected the simultaneous excitation of two modes in the light curve of HD 304373: P1=0.922405 d and P2=0.743241 d. The resulting ratio, P2/P1=0.8058, is that expected for Cepheids pulsating in the 1O and 2O radial modes. In the Galaxy there was only one similar star so far, i.e., CO Aur ( P1=1.78303 d, P2=1.42778 d, P2/P1=0.8008; Mantegazza 1983).

Figure 3 shows the P2/P1 ratio as a function of $\log~P_1$ period (Petersen diagram) for 1O/2O pulsators in the Large (Alcock et al. 1999; Soszynski et al. 2000) and in the Small (Udalski et al. 1999) Magellanic Clouds. The parabolic fit of the LMC stars shown in Fig. 3 is after Soszynski et al. (2000), while the linear fit of the SMC stars has been worked out again. Figure 3 gives evidence that the P2/P1 values are not well separated in the Magellanic Clouds. It implies that the P2/P1 ratio is less sensitive than the P1/P0 ratio to the difference in metallicity between the Magellanic Clouds. Indeed, the P1/P0 ratio for each galaxy defines three well separated lines in the Petersen diagram (see Fig. 1 in Soszynski et al. 2000).

The P2/P1 value related to HD 304373 is quite normal for both samples and very similar to that of MACHO*05:30:11.7 -69:52:02, a star belonging to the LMC (Fig. 3). Moreover, this ratio cannot be matched by the galactic composition models proposed by Morgan & Welch (1997), while it can be by the SMC and LMC ones. If HD 304373 is a normal Pop. I star, its P2/P1 value suggests a small dependence on metallicity, as it does not change in a environment as the Milky Way, which is more metallic than the Clouds.

We obtain $<I>\,=16.51$ (standard deviation $\pm$0.12 mag) considering the eleven 1O/2O Cepheids with 0.80<P1<1.00 d in the LMC (see Table 2 in Soszynski et al. 2000). Assuming m-M=18.5 for LMC stars, we get $<M_I>\,=-2.0$ for 1O/2O Cepheids. Therefore, I=9.70 locates HD 304373 at 2.2 kpc from the Sun. Taking into account the galactic coordinates ( $l=293^{\circ}$, $b=2^{\circ}$), HD 304373 is 77 pc away from the galactic plane. These considerations support the hypothesis that HD 304373 is a disk Pop. I star. Christensen-Dalsgaard & Petersen (1995) pointed out that the matching between the F/1O ratios for galactic pulsators and the theoretical models occurs for metallicities smaller than the solar value of 0.017-0.020; if that applies for the 1O/2O pulsators too, a metallicity close to 0.010 allows the P2/P1=0.8058and P1=0.922405 d values to reasonably fit the theoretical models (Christensen-Dalsgaard & Petersen 1995; Morgan & Welch 1997).

Moreover, we notice that the scatter of the P2/P1 values observed in both Clouds is intrinsic, i.e., originated from slightly different physical conditions inside the stars (it is much larger than the error bars on the period ratios, typically a few units of 10-5, since the periods are known with high accuracy). Therefore, the weak effect of the metallicity can be masked by other reasons (see also Fig. 4 in Christensen-Dalsgaard & Petersen 1995).

As in the case of CO Aur, there is no significant contribution of the 2 $.\!\!^{\rm d}$ harmonic in the light curve of HD 304373, i.e., it is perfectly sine-shaped within error bars. This is quite common among the 1O/2O pulsators. On the other hand, the $\phi_{21}$, $\phi_{31}$ and R21 values found for the 1O light curve of HD 304373 are in excellent agreement with the values observed in the 1O light curves of 1O/2O pulsators in the Magellanic Clouds.

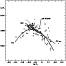  \begin{figure} \resizebox{\hsize}{!}{\includegraphics{Ea281_f3.eps}}\end{figure} Figure 3: Period ratios among the 1O/2O pulsators in the Small (crosses) and Large (circles) Magellanic Clouds. Fits are also shown. The filled circles indicate the value observed for the galactic 1O/2O pulsators, HD 304373 and CO Aur.
Open with DEXTER

5 Conclusions

In each class (HADS, RR Lyr and Cepheids) the shortest period stars are typical of metal-poor environments. The more evident cases are the very-short period SX Phe stars observed in globular clusters. HD 304373 has a very short fundamental period for a classical Cepheid: assuming P1/P0=0.70, we obtain P0=1.32 d. This result supports the previous discussion, suggesting a low metallicity for HD 304373 and explaining why its P2/P1 value is so similar to that of 1O/2O pulsators in the Magellanic Clouds.

From a methodological point of view, we identified the presence of a peak close to f1 as the result of a smaller amplitude in the last observing season. No reasonable physical explanation has been found and its instrumental origin is likely. We also detected the influence of a non perfect sky subtraction or flat-fielding in presence of the Full Moon. It is interesting to note that this instrumental effect makes HD 304373 brighter at the New Moon and fainter at the Full Moon. We stress the importance of checking the homogeinity of the time-series on pulsating stars before processing them.

Acknowledgements
The research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. The authors wish to thank L. E. Pasinetti for help and encouragement in this work, E. Antonello, L. Mantegazza, S. M. Morgan, J. O. Petersen, L. Szabados and the referee, P. Moskalik, for useful comments on a first draft of the manuscript.

References

 
Copyright ESO 2002