A&A 386, 286-295 (2002)
DOI: 10.1051/0004-6361:20020217

Spectral line ratios as ${\vec T}_{\bf\sf eff}$ indicators in solar-like stars

B. Caccin 1,2 - V. Penza 1 - M. T. Gomez 3


1 - Dipartimento di Fisica, Università di Roma "Tor Vergata'', via della Ricerca Scientifica 1, 00133 Roma, Italia
2 - Consorzio Interuniversitario per la Fisica Spaziale (CIFS)
3 - Osservatorio astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italia

Received 22 November 2001 / Accepted 5 February 2002

Abstract
The ratios of spectral line depths are often used as indicators of the stellar effective temperature $T_{\rm eff}$. In particular, Gray & Livingston (1997a) calibrated the temperature sensitivity of the ratios between the central depths of the line C I 538.032 nm and either the Fe I 537.958 or the Ti II 538.103, making use of observed spectra of several solar-like stars. The ultimate reason for choosing these lines was the subsequent application of their calibration to a long series of solar data, collected at Kitt Peak (in disk-integrated light) from 1978 to 1992, in order to get the $T_{\rm eff}$ variation of the Sun during its 11-yr magnetic cycle (Gray & Livingston 1997b). We propose a theoretical calibration that includes a careful treatment of convective transport and fits the stellar data very well , showing, at the same time, that the empirical calibration of Gray and Livingston incorporates in the $T_{\rm eff}$ sensitivity an undesired dependence of line ratios on the surface gravities of the individual stars they used. A possible dependence of the calibration upon stellar rotation is also explored.

Key words: stars: late-type - stars: atmosphere - stars: fundamental parameters - Sun: activity - convection


1 Introduction

The determination of the global parameters of a star is a key point in stellar physics. In particular, that of $T_{\rm eff}$ has a very long history, so that several different methods, based either on photometric or on spectroscopic data, are available. Each has its advantages and limitations, but errors of a few hundred degrees on $T_{\rm eff}$ are often encountered. Among them, those using spectral lines have always played an important role since the early times of stellar classification. With high-resolution spectra, differences of about $\pm 10$K can be detected, although the $T_{\rm eff}$ scale is uncertain by at least ten times that amount, thus allowing to rank stars by $T_{\rm eff}$ and trace cyclic temperature changes (Gray & Johanson 1991). Usually, instead of looking at single line strengths, the central depth ratios $r_{\rm D}$ or the equivalent width ratios $r_{\rm W}$ of lines having different sensitivity to temperature variations are employed, as line ratios are less subject to instrumental and other systematic errors (e.g. Gray & Johanson 1991; Gray 1992b, 1994; Strassmeier & Schordan 2000; Kovtyukh & Gorlova 2000). Of course, different spectral lines and calibrations must be used for different temperature ranges and luminosity classes. The fundamental limits are likely set by intrinsic variations arising from surface features and rotational modulation, from variations during stellar magnetic cycles and other subtle effects that may occur in the atmospheres of the stars (Gray 1995). In a few favourable cases, errors of $\approx$1K on relative temperatures have been estimated, with inconsistencies of $\approx$50K between temperatures derived from colour indices and from spectral lines (Gray 1994).

Gray & Livingston (1997a, henceforth G&La) calibrated the temperature sensitivity C0, defined through the following approximate linear relation

 \begin{displaymath}\delta T_{\rm eff} = C_{0} \frac{\delta r_{\rm D}}{r_{\rm D}} \end{displaymath} (1)

of the ratio $r_{\rm D}$ between the central depth of C I 538.032 nm and either the Fe I 537.958 or the Ti II 538.103 line, making use of observed spectra of several solar-like stars. The final goal of their work, which ultimately motivated the choice of these lines, was that of evaluating possible $T_{\rm eff}$ variations of the Sun along the 11-yr magnetic cycle by applying the result of their empirical calibration to the solar data collected at Kitt Peak (in disk-integrated light) over the years 1978-1992 (Gray & Livingston 1997b, henceforth G&Lb). They obtained as a result $\delta T_{\rm eff}$ = 1.5 K, corresponding to the whole amplitude of irradiance variation measured by active cavity bolometers (Fröhlich 2000).
The result is less exciting than it may seem at first sight, because it leaves no room for the effects due to the balance of bright and dark magnetic features (spots, faculae and, possibly, network), the contribution of which to irradiance variations, on the contrary, has been well proven (Oster et al. 1982; Foukal & Lean 1988; Foukal et al. 1991). Moreover (Caccin & Staro 1998; Caccin & Penza 2001) G&La experimental calibration could not be reproduced theoretically by using a series of one-dimensional models with different $T_{\rm eff}$ and constant gravity ( $\log g = 4.5$), nor with a gravity varying with $T_{\rm eff}$ as it does, on average, along the main sequence according to Gray (1992a). Here we will show that the G&La data can instead be satisfactorily reproduced by one-dimensional models, provided that the proper values of $\log g$ for individual stars are used. As a consequence, the value of C0 obtained by G&La cannot be directly applied to evaluate $T_{\rm eff}$ variations with the solar cycle as it was done in G&Lb. A theoretical calibration, consistent with the stellar data, would instead be possible, on the basis of model calculations, but other effects concur to make the scenario more complicated.

2 Atmospheric models

Suitable grids of theoretical photospheric models are currently available in the literature; in this work we used and modified a subset of Kurucz's models obtainable at http://cfaku5.harvard.edu/grids.html, that cover a wide range of the free parameters (effective temperature $T_{\rm eff}$, surface gravity g, abundance [Fe/H] and microturbulence $\xi $). In all of the grid models, convective transport is treated according to the mixing-length theory (MLT), with a unique mixing-length ratio $\alpha \equiv \ell/H_{\rm P}=1.25$ (where $H_{\rm P}$ is the pressure scale height). However, two different series of models are available: the first (Kurucz 1994, henceforth Ku94) include the effects of overshooting, while in the second (Castelli et al. 1997, henceforth Ca97) the convection is treated, on the contrary, in the purely classical way (without overshooting). Actually (Kurucz 1992; Castelli et al. 1997), the introduction of overshooting in these models is not made by means of a really physical treatment of its effects, but only by computing the convective flux in the standard way and then smoothing it over a bubble diameter.

In order to explore the effects of changing the value of $\alpha $ without recomputing a whole set of models every time, we have simply extended the radiative equilibrium part of Ca97 models, starting from the point where the convective instability begins ( $\nabla=\nabla_{\rm A}=(\gamma-1)/\gamma$), with a gradient recalculated by us according to the MLT. In the same way we studied also the effects of using an alternative treatment of convection, extending the models with the Canuto-Mazzitelli theory (Canuto & Mazzitelli 1991, henceforth CMT). Here we describe very briefly the calculations we made in the two cases, with the same notations used by Canuto & Mazzitelli (1991).

In MLT the gradient throughout the convective zone is given by the solution of a cubic equation for the convective efficiency $\Gamma$, defined as:

 \begin{displaymath}\Gamma = \frac{(1 + \Sigma)^{1/2} - 1}{2} \end{displaymath} (2)

where $\Sigma$ is a quantity proportional to the difference between the true and the adiabatic gradient:

 \begin{displaymath}\Sigma = 4 A^{2} (\nabla - \nabla_{A}) \end{displaymath} (3)

and A, with standard notation, is given by

 \begin{displaymath}A = \frac{c_{\rm P} \rho^2 k_{\rm R} \ell^2}{12 a c T^3} \sqrt{\frac{g}{2 H_{\rm P}}}\cdot \end{displaymath} (4)

The cubic equation is then

 \begin{displaymath}a_{0} \Gamma^{3}+ \Gamma^{2} + \Gamma - \delta = 0 \end{displaymath} (5)

where a0=9/4 and, defining the radiative gradient as $\nabla_{\rm R}$, we have

 \begin{displaymath}\delta = A^{2}(\nabla_{\rm R} - \nabla_{A}). \end{displaymath} (6)

We adopted for the equation of state $\rho(P,T)$ that of a perfect gas, with constant molecular weight, while for $k_{\rm R}(P,T)$ we used a grid extracted from the tables of the Rosseland opacity calculated by Kurucz (1994). Knowing $\nabla(P,T)$, we got the temperature structure T(P) from the numerical solution of the differential equation $\nabla={\rm d}(\ln T)/{\rm d}(\ln P)$. The passage from T(P) to $T(\tau )$ is then obtained by solving the hydrostatic equilibrium equation

 \begin{displaymath}\frac{{\rm d}P}{{\rm d}\tau_{\rm R}} = \frac{g}{k_{\rm R}(P,T(P))}\cdot \end{displaymath} (7)

We verified that, when $\alpha =1.25$, we could reproduce very well the Ca97 models in the region of temperature and surface gravity in which we were interested, in spite of the additional approximations we made with respect to the original calculations.
  \begin{figure} \includegraphics[width=14.8cm,clip]{figgrad.eps} \end{figure} Figure 1: Comparison between a Ca97 model ( $T_{\rm eff}$ = 5750K, $\lg g =$ 4.5) and that recalculated by us with CMT (both values of $\alpha $ are "canonical''). On the left we reported the gradients $\nabla ={\rm d}({\rm ln}T)/{\rm d}({\rm ln}P)$ and on the right the temperature structures T($\tau $).
Open with DEXTER

In the CMT theory the approach to convection is rather different, since the whole energy spectrum of turbulence is taken into account. However there is a new relation that replaces Eq. (5), namely

 \begin{displaymath}a_{0}\, \Omega (\Gamma)\,\Gamma^{3}+ \Gamma^{2} + \Gamma^{2} - \delta = 0. \end{displaymath} (8)

The MLT corresponds to $\Omega(\Gamma)=1$; in practice $\Omega$ is determined by the ratio between the "new'' convective flux and that calculated with MLT: more precisely, it is equal to $\Phi / \Phi_{\rm MLT}$, where $\Phi$ is a dimensionless function, that in MLT corresponds to

 \begin{displaymath}\Phi_{\rm MLT} = \frac{a_{0}}{2 \Sigma} (\sqrt{1 + \Sigma} - 1)^{3} \end{displaymath} (9)

and in CMT is given by

 \begin{displaymath}\Phi = a_{1} \Sigma^{m} ((1 + a_{2} 2 \Sigma)^{n} - 1)^{p} \end{displaymath} (10)

where the coefficients are a1 = 24.868, $a_{2}=9.7666\times 10^{-2}$, m=0.14792, n=0.18931 and p = 1.8503. By solving Eq. (8), we obtain the new gradient $\nabla$, with which we extend the radiative part of Ca97 models in the same way as we did for MLT.

For both classes of convective models, $\ell$ is given through the parameter $\alpha $. It's now commonly accepted that it is not correct to maintain constant the value of $\alpha $ along the main sequence, so we decided to consider in CMT a dependence of $\alpha $ on $T_{\rm eff}$ and g, as suggested by Ludwig et al. (1999):

 \begin{displaymath}\alpha= A_{0} + (A_{1} + (A_{3} + A_{5}\tilde{T} + A_{6}\tilde {g})\tilde{T} + A_{4}\tilde{g})\tilde{T} + A_{2}\tilde{g} \end{displaymath} (11)

with A0 = 0.414, A1 = -0.1, A2 = -0.026, A3 = -0.065, $A_{4}=\,-0.092$, A5 = 0.193 and A6 = 0.125, while

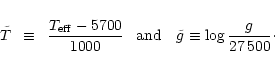
\begin{eqnarray*}\tilde{T}\,\,\, \equiv \,\,\,\frac{T_{\rm eff} - 5700}{1000}\,\... ...m and} \,\,\,\,\,\, \tilde{g} \equiv \log \frac{g}{27\,500}\cdot \end{eqnarray*}


This expression is obtained by studying the results of 2D radiation hydrodynamic numerical calculations of time-dependent compressibile convection, that provide information about the convective efficiency and the entropy at the top of the convective envelope. This information is then translated into an effective parameter $\alpha $ both for MLT and CMT. The results of the simulations are in agreement, at least in the close neighbourhood of the Sun, with those of other approaches, like the numerical experiments by Chan & Sofia (1989).

The use of such a relation for $\alpha $ makes the models physically more consistent, however Eq. (11) was not intended to reproduce necessarily the temperature profile of the superadiabatic layers, therefore it may be not suitable, as noted by the authors themselves, to providing the optimum $\alpha $ value for convective stellar atmospheres. In any way, we will presently see that the effect on $r_{\rm D}$ of using either the MLT with constant $\alpha $ or CMT with variable $\alpha $ is rather small.

In Fig. 1 we show the effect of changing the convective theory (from MLT to CMT with "canonical'' values of $\alpha $) on the temperature structure and on its gradient. As expected (Kiefer et al. 2000), in CMT the temperature gradient is steeper than in MLT (which in turn is steeper than that calculated in MLT by introducing the overshooting effects), but the two models begin to differ from each other only at $\log\tau \geq 0.6$, so that the effects cannot be too large.

3 Theoretical calibrations

3.1 UBV colours

In the following we will apply different kinds of models to a given set of stars, with given observed colours. Because the models that we have modified, in spite of their simplified treatment of convection (MLT), well reproduce the observed colours, we have checked, first of all, whether our passing to CMT alters very much the colours computed with given values of $T_{\rm eff}$ and g. To do that, we recalculated the UBV colours by means of available Kurucz's programs and adopting, as input data, the flux values corresponding to 1221 fixed wavelengths, calculated by ATLAS9 code (Kurucz 1993) running with our CMT models.


  \begin{figure} \par\includegraphics[width=14.8cm,clip]{color2.eps} \end{figure} Figure 2: Colour differences obtained by changing the convective theory (from MLT with $\alpha =1.25$ to CMT with $\alpha =0.4$) in the Ca97 models are plotted vs. $T_{\rm eff}$ for two values of g. The differences are never large, but are greater for cooler stars.
Open with DEXTER

In Fig. 2 we plot vs. $T_{\rm eff}$ the differences between the "new'' colours and those reported in Ca97 tables, for two values of $\log g$. Note that, although the differences are never very large, they are greater for cooler stars. The reason of that becomes clear if we look at Fig. 3, in which we plotted (on arbitrary scale) the difference between the temperature structure $T(\tau )$ in MLT and in CMT models for $T_{\rm eff}=$ 5250 K and for $T_{\rm eff}$ = 5750 K, superimposed to the temperature response function (Caccin et al. 1977) of the B-V colour, locating the layers where the temperature perturbation has the largest effect on the colour.
The expression of the response function of the emergent intensity is

 \begin{displaymath}RF = (\chi^{\prime} (1 - I/S) + S^{\prime}) {\rm e}^{-\tau} \end{displaymath} (12)

where, for a given $\lambda$, $\chi^{\prime}$ and $S^{\prime}$ are the partial derivatives of the opacity ( $\chi=k \rho$) and of the source function respectively with respect to the perturbed quantity (in our case T, at constant P), while I is the outward intensity at current z. The effect on the emergent intensity, then, is given by

 \begin{displaymath}\delta I(\lambda) = \int_{-\infty}^{+\infty} \delta T(z)\,\, RF (\lambda,z) \,\, {\rm d}z. \end{displaymath} (13)

In order to get a quick estimate of the (B-V) response function, we have approximated the values of the B and V fluxes with those of the monochromatic intensities at $\lambda_B$ = 420 nm and $\lambda_V$ = 540 nm and written

 \begin{displaymath}\delta (B-V) \,\approx\, \frac{\delta I_V}{I_V} - \frac{\delta I_B}{I_B}\cdot \end{displaymath} (14)

The response function of (B-V), then, is given simply by the difference between those of IV and IB.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figRF.eps} \end{figure} Figure 3: Response function of (B-V) to a temperature perturbation at constant pressure (solid line), together with the difference (on arbitrary scale) between the temperature structure $T(\tau )$ in Ca97 and in CMT models for $T_{\rm eff}$ = 5250K (dotted line) and for $T_{\rm eff}$ = 5750K (dashed line).
Open with DEXTER

The interpretation of Fig. 3 is immediate: where temperature perturbations have the largest effect on the emergent intensity (i.e. where RF is largest), the difference between the temperature structure in MLT and that in CMT models ( $\delta T=T_{\rm CMT}\,-\,T_{\rm MLT}$) is larger for $T_{\rm eff}$ = 5250 K than for $T_{\rm eff}$ = 5750 K, so the effects on colours determination are more evident for the former. Notice also that the "effective'' sign of $\delta T$ is different in the two cases and this changes the sign of $\delta (B-V)$.

However, the maximum error is $\approx$0.01 mag, which corresponds, according to Gray (1992a) calibration, to an uncertainty on $T_{\rm eff}$ of about 0.5% and cannot influence too much our choices of $T_{\rm eff}$ and g for the different stars.

In the same way, we don't expect a large effect on the colours calculation (hence on the $T_{\rm eff}$ determination) if we switch between models with or without overshooting: Castelli et al. (1997) found indeed that the largest effect of this change on the model structure occurs for $T_{\rm eff}\geq$ 6500 K, that is hotter than any star we used (e.g. for $T_{\rm eff} = 6000$ K the difference between the B-V colours obtained with the two models corresponds to a difference in temperature of about 20 K). Moreover, in a subsequent paper (Castelli 1999) further comparisons with different synthetic grids of colors show again differences lower than 100 K.

3.2 Line depth ratios

G&La calibrated the relation between line-depth ratios and $T_{\rm eff}$ variations, which we repeat below:

 \begin{displaymath}\delta T_{\rm eff} = C_{0} \frac{\delta r_{\rm D}}{r_{\rm D}} \end{displaymath} (15)

using the stars listed in Table 1, where we give also
 

 
Table 1: Atmospheric parameters adopted for each star and, for comparison, the temperature values ( $T_{\rm eff}^{\,\,{\rm G}})$ used by G&La. The references for $T_{\rm eff}$, g and [Fe/H] are denoted by their number in Table 2, while those for U-B and B-V are the following: (a) Oja (1994), (b) Clements & Neff (1979), (c) Tüg & Schmidt-Kaler (1982), (d) Jennens & Helfer (1975).
STAR $T_{\rm eff}^{\rm\,\, G}$ $T_{\rm eff}$ log g B-V U-B [F/H]
$\sigma $Dra 5432 5253 (1) 4.50(1) 0.79(a) 0.38(a) -0.21(6)
$\tau $Cet 5441 5250 (2) 4.50(2) 0.72(a) 0.21(a) -0.50(7)
51 Peg 5831 5880 (3) 4.37(3) 0.67(b) 0.20(b) +0.21(8)
SUN 5791 5777 4.44 0.64(c) 0.18(c) +0.00
$\iota$Per 5970 5890 (4) 4.19(4) 0.59(d) 0.12(d) +0.05(9)
$\upsilon$And 6081 6205 (5) 4.00(5) 0.54(b) 0.06(b) +0.00(10)


the values of $T_{\rm eff}$ and g that we chose among the numerous scattered data avalaible in the literature. The values adopted are those best reproducing, in Kurucz's tables (1994), the observed values of (B-V) and (U-B) colours (which do not present significant differences for any star). With "best reproduction'' we mean the minimum of $\delta(B-V)^2 + \delta(U-B)^2$, where $\delta$ indicates the difference between the observed value and that obtained from Kurucz's table by using for the calculation the given values of $T_{\rm eff}$ and g.
  \begin{figure} \par\includegraphics[width=8.5cm,clip]{stars2.eps} \end{figure} Figure 4: Representative points of the stars in the ( $T_{\rm eff}$, $\log g$) plane found in the literature. The bolded circles mark the values we used. The solid line represent the average relation between $T_{\rm eff}$ and g along the main sequence (Gray 1992a).
Open with DEXTER

To give an idea of the dispersion in the literature data, we plot in Fig. 4 all the couples ( $T_{\rm eff}$, $\log g$) that we could find for the five stars; the average relation between $T_{\rm eff}$ and g along the main sequence (Gray 1992a) is also shown. All references concerning this plot are listed in Table 2.
 

 
Table 2: References used for the plot in Fig. 4; the numbers mark those actually used for model calculations.
STAR $T_{\rm eff}$ log g References
$\sigma $Dra 5140 4.50 Cayrel de Strobel & Bentolila (1983)
  5310 4.60 Clegg et al. (1981)(6)
  5227 4.50 Alonso et al. (1996)
  5200 4.60 Perrin et al. (1977)
  5227 4.52 Prieto & Lambert (2000)
  5253 4.50 Bell & Gustafsson (1989)(1)
$\tau $Cet 5358 4.59 Cayrel de Strobel & Bentolila (1983)
  5358 4.49 Perrin et al. (1977)
  5316 4.3 Blackwell & Lynes-Gray (1994)
  5250 4.7 Arribas & Martínez-Roger (1988)
  5300 4.4 Flynn & Morell (1997)(7)
  5250 4.5 Borges & Idiart (1995)(2)
  5330 4.30 Tomkin & Lambert (1999)
51 Peg 5728 4.27 Cayrel de Strobel & Bentolila (1983)
  5793 4.33 Fuhrmann et al. (1997)
  5755 4.18 Tomkin et al. (1995)
  5880 4.37 Gray R.O. et al. (2001)(3)
  5500 4.25 Sadakane et al. (1999)
  5755 4.18 Cayrel de Strobel (1996)
  5730 4.27 Kobi & North (1990)
  5795 4.41 Gonzales et al. (2001)(8)
  5750 4.40 Ford & Rasio (1999)
  5669 4.27 Prieto et al. (1999)
  5740 3.76 McWilliam (1990)
$\iota$Per 5929 4.10 Cayrel de Strobel & Bentolila (1983)(9)
  5890 4.19 Nissen (1981)
  5950 4.11 Gray R.O. et al. (2001)
  6000 4.0 Borges & Idiart (1995)
  5970 4.06 Cayrel de Strobel (1996)
  5930 4.09 Kobi & North (1990)
  5996 4.00 Alonso et al. (1996)
  5890 4.19 Bell et al. (1994)(4)
  6088 4.5 Castelli et al. (1997)
  5929 4.09 Perrin et al. (1977)
$\upsilon$And 6067 4.10 Cayrel de Strobel & Bentolila (1983)
  6250 4.30 Ford & Rasio (1999)
  6155 4.00 Alonso et al. (1999)
  5998 4.00 Perrin et al. (1977)
  6205 4.0 Blackwell & Lynes-Gray (1994)(5)
  6140 4.22 Bell et al. (1994)(10)
  6212 4.17 Tomkin et al. (1995)
  6128 4.22 Balachandran (1990)
  6210 4.06 Gray R.O. et al. (2001)
  6125 3.98 Prieto et al. (1999)


It appears that these stars are not "typical'' stars; specifically, in spite of the limited $T_{\rm eff}$ range, the values of g are significantly spread, and differences with the average relation are systematic. We note, by passing, that the values of $T_{\rm eff}$ obtained are different from those used by G&La, which were taken from Gray (1994); moreover all of the adopted g values, but that of 51Peg, happen to be spectroscopic rather than photometric or trigonometric determinations.

Through their empirical calibration G&La obtained, for the two central-depth ratios C/Fe and C/Ti, the values C0=346 and C0=468 respectively.

  \begin{figure} \par\includegraphics[width=8.6cm,clip]{Fe2.eps} \end{figure} Figure 5: Experimental values of C/Fe line-depth ratios (G&La), compared with our theoretical calculations. The straight lines are, in all cases, the best fit to the corresponding points.
Open with DEXTER


 

 
Table 3: Experimental values of the line depth ratios (G&La; Gray 2001) and those calculated with our CMT models.
STAR C/Fe C/Ti
  exp. theor. exp. theor.
$\sigma $Dra 0.106 0.104 0.116 0.142
$\tau $Cet 0.103 0.105 0.135 0.143
51 Peg 0.330 0.351 0.340 0.344
SUN 0.273 0.279 0.293 0.298
$\iota$Per 0.457 0.400 0.418 0.372
$\upsilon$And 0.672 0.705 0.512 0.513


In Fig. 5 we show the original data of the ratio Fe/C and those calculated by us through the two alternative series of atmospheric models (MLT with $\alpha =1.25$ and CMT with $\alpha $ given by Eq. (13)) vs. the values of $T_{\rm eff}$. The line depths were computed in LTE, by the formal solution of the radiative transfer equation for the emergent flux; the line parameters we used are reported in Table 4. We verified, however, that slight modifications of $\lg(gf)$, $\zeta $ (which is a fudge factor multiplying the Unsöld value of $\gamma $ in the Lorentz part of the absorption profile) or $\xi $ do not have considerable effects on the determination of C0.
 

 
Table 4: Line parameters used for calculation of line profiles. $\zeta $ is a fudge factor multiplying the Unsöld value of $\gamma $ in the Lorentz part of the absorption profile, while $\xi $ is the usual microturbulence term. The values of $\lg(gf)$, $\zeta $ and $\xi $ are those that optimize the comparison with the experimental data of solar flux.
Line lg( gf) $\chi_{\rm ion}\,({\rm eV})$ $\chi_{\rm ex}\,({\rm eV})$ $\zeta $ $\xi $(km s-1)
CI 538.032 nm -1.8 11.26 7.680 1 2
FeI 537.958 nm -1.6 7.87 3.695 7 1
TiII 538.103 nm -2.08 13.58 1.566 40 1


Observing Fig. 5, we see that CMT reproduces the experimental ratios slightly better than MLT, especially for cooler stars. In particular, the CMT models reproduce very well the experimental slope of the Fe/C straight line, with an error of about 1%. Notice that here we plotted all line ratios against our values of $T_{\rm eff}$, in order to test the capability of the models to reproduce simultaneously the colours and the line ratios. In this way, the "experimental'' value of C0 is no longer that reported in G&La, but is now equal to 493, while the theoretical value is 498 with CMT and 514 with MLT models.

The same plot for C/Ti is shown in Fig. 6, where however the agreement is worse: the difference between the "experimental'' value of C0 (619) and the theoretical one (720) is $\approx$15% for CMT and reaches 25% for MLT (770). We note that the cause of the discrepancy can be attributed almost exclusively to an anomalous behavior of the coolest star, for which the reliability of our models might be less. In Table 3 we report explicitly, for the two lines, the experimental depth ratios obtained by G&La and the corresponding values calculated with our CMT models.

We have explored also the effects on C0 of changing the $\alpha $ value, finding a substantial insensitivity ($\approx$3 to 4% for $\alpha $ changing from 1.25 to 2). The corrisponding results obtained by using the Ku94 models provided values of C0 only slightly larger (2-5%) than the Ca97 ones.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{figTi2.eps}\end{figure} Figure 6: Experimental values of C/Ti line-depth ratios (Gray 2001), compared with our theoretical calculations. The straight lines are, in all cases, the best fit to the corresponding points.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{rgT2.eps} \end{figure} Figure 7: Surface $r_{\rm D}(T_{\rm eff}, \log g)$ for the C/Fe line-depth ratio, obtained with a small grid of theoretical CMT models and [Fe/H] = 0.
Open with DEXTER

Finally, calculating through CMT models a grid for $r_{\rm D}$ in the ( $T_{\rm eff}$, $\log g$) plane, we constructed the surface $r(T_{\rm eff}, \log g)$ shown in Fig. 7, as an example, for the C/Fe line-depth ratio.

3.3 Equivalent widths ratios

G&La calibrated also an analogous relation involving the equivalent widths:

 \begin{displaymath}\delta T_{\rm eff} = C_{1} \frac{\delta r_{\rm W}}{r_{\rm W}}\cdot \end{displaymath} (16)

However, they notice that the measures of these observables show larger uncertainties than those of the central depths, especially for the C I line, which is blended in the red wing. Anyway, the comparison between the slope of the G&La experimental relation and that obtained by the $\lambda$ integration of the line profiles calculated with our theoretical (CMT) models is fairly good, as shown in Figs. 8 and 9. The different intercept of the two C/Fe straight lines in Fig. 8 probably derive from a different method adopted for calculating the $\lambda$ integral, that is somewhat difficult for the presence of blends and asymmetries. In spite of that, the C1 values are in good agreement with each other: 567 theoretically, 525 for the experimental data (with a difference of $\approx$8%). The absence of a corresponding shift of the intercept between the C/Ti data shown in Fig. 9 is, instead, purely fictitious, because we had not at our disposal the measures of the Ti II equivalent width and we used, for each star, the value of $\delta r_{\rm W} / r_{\rm W}$ "reconstructed'' from the linear relation in Eq. (16), by using the original values of $T_{\rm eff}$ and C1 given in G&La; therefore the intercept remained undetermined and we chose it arbitrarily. The comparison is, as in the case of the depth ratios, worse for C/Ti than for C/Fe; in particular, the experimental and theoretical values of C1 are 1949 and 1632 respectively (with a difference of $\approx$16%).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{WFe.eps} \end{figure} Figure 8: Experimental values of C/Fe equivalent width ratios (G&La), compared with our theoretical calculations.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{WTi.eps} \end{figure} Figure 9: "Reconstructed'' experimental values of C/Ti equivalent width ratios (G&La), compared with our theoretical calculations.
Open with DEXTER

3.4 Rotation effect

Even if we could already reproduce the G&La experimental data, to obtain a correct stellar calibration of the line-depth ratios vs. $T_{\rm eff}$ variations, we still have to take into account other paramenters that might play an important role in determining line profiles, like the stellar rotation, that produces a line broadening, but does not have any sensible effect on the equivalent widths (Stift & Strassmeier 1995). In this case, our $r_{\rm W}$ calibration should remain, therefore, valid. From this point view the use of the equivalent widths in place of the line depths would be a better choice; unfortunately, as already said, the measurement of the former present, for our lines, larger uncertainties and, above all, their ratios are less sensible to $T_{\rm eff}$ variations (the values of C1 are larger than those of C0, especially in C/Ti case). However, we will show that, even if the rotation modifies the values of the line depths and of their ratios, it has almost no effect on C0, provided that the value of $v\,{\rm sin}\,i$ are small enough and the rotation is the same for all the stars of the sample. More sensible effects would however be present if the sample stars were characterized by a large dispersion in $v\,{\rm sin}\,i$.

The literature data for G&La stars are reported in Table 5, where we see that for three stars (51 Peg, $\upsilon$ And and the Sun) there is not a considerable discrepancy among the data; for one ($\iota$ Per) the difference from the catalogue value (Bernacca & Perinotto 1970) and those taken from more recent works is not negligible but not too large; finally for the first two stars ($\sigma $ Dra and $\tau $ Cet) the data scattering is quite remarkable.

 

 
Table 5: Literature data for the rotation of the stars used in the calibration. Bernacca & Perinotto (1970) is a catalogue of experimental data taken from different sources.
STAR V sin i (km s-1) References
$\sigma $Dra 0.6 Fekel (1997)
  0.8 Gray (1984)
  8 Bernacca & Perinotto (1970)
$\tau $Cet 0 Saar & Osten (1997)
  0.6 Fekel (1997)
  0.9 Gray (1984)
  2 Simon & Landsman (1991)
  2.4 Soderblom (1981)
  8 Smith et al. (1983)
  8 Bernacca & Perinotto (1970)
51 Peg 1.4 Benz & Mayor (1984)
  1.7 Soderblom (1983)
  2 Fuhrmann et al. (1997)
  2 Bernacca & Perinotto (1970)
  2.3 Queloz et al. (1998)
  2.4 Saar & Osten (1997)
  2.6 Melo et al. (2001)
  2.8 Mayor & Queloz (1995)
$\iota$Per 2.9 Benz & Mayor (1984)
  3.5 Soderblom (1983)
  3.5 Schrijver & Pols (1993)
  8 Bernacca & Perinotto (1970)
$\upsilon$And 9 Gray (1986)
  9.2 Soderblom (1983)
  9.3 Benz & Mayor (1984)
c 11 Bernacca & Perinotto (1970)
SUN 1.6 Queloz et al. (1998)
  1.9 Saar & Osten (1997)
  1.7 Simon & Landsman (1991)


Because we have no "a priori'' reason to choose one value rather than another, we can take for the last four stars the mean value of $v\,{\rm sin}\,i$, while for $\sigma $ Dra and $\tau $ Cet we must consider all of the four extreme cases and estimate the corresponding differences with respect to our previous calculation of C0, made without rotation.

To calculate the normalized line profiles in a uniformly rotating star ( $F_{\rm rot}$), we use the following expression

 \begin{displaymath}F_ {\rm rot}= \frac{\int_{-1}^{1} {\rm d}x \int_{0}^{\sqrt{1-... ...1}^{1} {\rm d}x \int_{0}^{\sqrt{1-x^{2}}} I_{0}(x,y) {\rm d}y} \end{displaymath} (17)

where I is the intensity of the radiation originating at the point (x,y) on the disc, $\lambda$ shifted for Doppler effect, while I0 is the intensity of the continuum.

In Fig. 10 we reported the usual plots $\log(r_{\rm D})$ vs. $T_{\rm eff}$ where, for all stars, either $v\,{\rm sin}\,i$ = 0 or $v\,{\rm sin}\,i$ = 8 km s-1; as anticipated, a "constant'' rotation has only the effect of shifting the straight line without changing C0 (the difference is $\approx$3%). This argument remains true also for the ratio C/Ti, that seems even less sensible (the difference is less than 2%).

  \begin{figure} \includegraphics[width=8.8cm,clip]{CFeROTeq.eps} \end{figure} Figure 10: Comparison between the calibrations of the C/Fe line depth-ratio calculated without rotation and with $v\,{\rm sin}\,i$ = 8 km s-1.
Open with DEXTER

This result is not in contradiction with those of Stift and Strassmeier (1995), obtained however for two different lines (Fe I 625.55 nm and V I 625.183 nm). In fact, their curves $r_{\rm D}$ vs. $T_{\rm eff}$, within our $T_{\rm eff}$ range, are not very different from parallel straight lines. The intercept shift, clearly, would become important if we were interested in calibrating the absolute value of $T_{\rm eff}$ rather than its relative variations. The unsensitiveness of C0 to simultaneous changes by the same amount of $v\,{\rm sin}\,i$ is important for the calibration of solar $T_{\rm eff}$ variations along the 11-yr magnetic cycle, where the value of rotation doesn't change, but it is not relevant for the comparison with the G&La experimental data, because the stars of the sample present a nonnegligible dispersion of the rotation values.

In Fig. 11 we plot the straight lines relative to all of the four possible combinations of the extreme $v\,{\rm sin}\,i$ values for $\sigma $ Dra and $\tau $ Cet, that are labelled as follows:
1) $v\,{\rm sin}\,i$($\tau $ Cet) = 0 km s-1 and $v\,{\rm sin}\,i$($\sigma $ Dra) = 8 km s-1;
2) $v\,{\rm sin}\,i$($\tau $ Cet) = 0 km s-1 and $v\,{\rm sin}\,i$($\sigma $ Dra) = 0.6 km s-1;
3) $v\,{\rm sin}\,i$($\tau $ Cet) = 8 km s-1 and $v\,{\rm sin}\,i$($\sigma $ Dra) = 0.6 km s-1;
4) $v\,{\rm sin}\,i$($\tau $ Cet) = 8 km s-1 and $v\,{\rm sin}\,i$($\sigma $ Dra) = 8 km s-1.

  \begin{figure} \par\includegraphics[width=9.2cm,clip]{CFeROTdiff.eps} \end{figure} Figure 11: Comparison between the calibrations of the C/Fe line depth-ratio calculated by associating to the four hotter stars a mean rotation value and considering the two extreme values for the two cooler stars. The four possible combinations are labelled as follows: 1) $v\,{\rm sin}\,i$($\tau $ Cet)=0 and $v\,{\rm sin}\,i$($\sigma $ Dra)=8km s-1; 2) $v\,{\rm sin}\,i$($\tau $ Cet)=0 and $v\,{\rm sin}\,i$($\sigma $ Dra)=0.6 km s-1; 3)  $v\,{\rm sin}\,i$($\tau $ Cet)=8km s-1 and $v\,{\rm sin}\,i$($\sigma $ Dra)=0.6km s-1; 4) $v\,{\rm sin}\,i$($\tau $ Cet)=8km s-1 and $v\,{\rm sin}\,i$($\sigma $ Dra)=8km s-1. The lines corresponding to the two intermediate case (1 and 2) cannot be distinguished in this figure.
Open with DEXTER

The difference on the C0 determination with respect to the nonrotational case is maximum ($\approx$18%) in case (2) (when both $\tau $ Cet and $\sigma $ Dra are very slow rotators) while it's practically negligible (less 2%) in case (3) (when both $\tau $ Cet and $\sigma $ Dra are rather fast rotator); in intermediate cases the error is $\approx$10%. As in the previous calculation, where a "constant'' rotation was included, the situation is better for C/Ti, for which the error is very small in case (1), $\approx$13% in case (2) and $\approx$7% otherwise.

In the light of these results, we believe that our theoretical calibrations of $r_{\rm D}(T_{\rm eff}, \log g)$, for the C0 determination, with or without rotation, remain essentially the same.

4 Conclusions

It seems that one-dimensional photospheric models, when the individual values of $T_{\rm eff}$, g and [Fe/H] for the five stars are used, can satisfactorily reproduce the observed line ratios. However, the problem of temperature calibration is not one-dimensional and we cannot manage every problem with a single biunique relation. The surface gravity appears to be the principal additional parameter that has to be taken into account; we have shown, for example, that the value of C0 is not very sensible to possible differences of the stellar rotation, at least in the $v\,{\rm sin}\,i$ range of our interest. In reality, other parameters, such as the micro or macroturbulence, could play a role (Stift & Strassmeier 1995), but we don't believe they can substantially invalidate our theoretical calibration. If we want to use the line-depth ratios as indicators of $T_{\rm eff}$ variations along the solar cycle, we must then consider, on the surface $r(T_{\rm eff}, \log g)$, the curve at $\log g={\rm const.}$ Calculating, in $T_{\rm eff}=5777$K and $\log g = 4.44$ the partial derivative

 \begin{displaymath}C_0 = (\frac{\partial \ln r_{\rm D}}{\partial T_{\rm eff}})_g \end{displaymath} (18)

we obtain C0=576 for the C/Fe ratio and C0=915 for C/Ti, corresponding to 1.7 and 2 times the values given by G&La.
This result does not allow any longer a simple interpretation of the solar data. G&Lb obtained, for the $T_{\rm eff}$ variation along the solar cycle, an amplitude of 1.5K, equivalent to the whole variation deduced by total irradiance measurements, while it is apparent that at least half of this variation can be explained with the balance of facular excess and sunspot deficit. Our theoretical calibration of the coefficient C0 does not solve the problem; on the contrary it becomes more tangled, because now we obtain $\delta T_{\rm eff} \approx 3$K i.e. twice the experimental value. If we believe in our models (and we have no reason not to do so), this might indicate either that the changes occurring in the Sun during its magnetic cycle are not well simulated by using the modifications of the atmospheric stratification with $T_{\rm eff}$ along the main sequence, or that other phenomena, like multidimensional effects on line formation due to a variable granulation, must also be taken into account (Caccin & Penza 2000). Alternatively, a possible sensitivity of these lines to the presence of faculae and other magnetic structures on the solar disk, which however seems not revealed by G&Lb data, might invalidate the application of both the theoretical and the empirical calibration to solar cycle variations.

Acknowledgements
This work has been supported also by MURST (through Cofin 2000). The authors are indebted with D. F. Gray for valuable comments and for kindly providing additional data; they thank also S. Sofia, I. Mazzitelli, F. Kupka, I. Ermolli and F. Castelli for useful discussions and comments.
The referee, K. G. Strassmeier, suggested discussing the problem of stellar rotation.

References

 

Copyright ESO 2002