A&A 386, 359-378 (2002)
DOI: 10.1051/0004-6361:20020232
D. Huber - D. Pfenniger
Geneva Observatory, 1290 Sauverny, Switzerland
Received 25 July 2001 / Accepted 25 January 2002
Abstract
Observed self-gravitating systems reveal often fragmented,
non-equilibrium structures that feature characteristic long-range
correlations. However, models accounting for non-linear structure
growth are not always consistent with observations and a better
understanding of self-gravitating N-body systems appears
necessary. Because unstable gravitating systems are sensitive to
non-gravitational perturbations, we study the effect of different
dissipative factors as well as different small and large scale
boundary conditions on idealized N-body systems. We find, in the
interval of negative specific heat, equilibrium properties differing
from theoretical predictions made for gravo-thermal systems,
substantiating the importance of microscopic physics and the lack of
consistent theoretical tools to describe self-gravitating gas.
Also, in the interval of negative specific heat, yet outside of
equilibrium, unforced systems fragment and establish transient
long-range correlations. The strength of these correlations
depends on the degree of granularity, which shows that the
mass and force resolution should be coherent. Finally, persistent
correlations appear in model systems subject to an energy flow.
Key words: gravitation - methods: N-body simulations - galaxies: ISM - ISM: structure
Most astrophysical structures result from gravitational instabilities, from large-scale cosmological structures down to planets. Yet, among the least understood topics in astrophysics we find galaxy formation and star formation, which both involve fragmentation and the nonlinear growth of structures occurring during the non-linear phases of gravitational instability.
Perhaps one of the fundamental reasons why fragmentation and structure formation via gravitational instability appears so difficult is that we lack consistent theoretical tools allowing to combine gravity with gas physics. Indeed, it is too often ignored that classical thermodynamics does not hold for gravitating systems, because these are non-extensive in the thermodynamical sense (Landsberg 1972, 1984; Tsallis 1999; Plastino & Plastino 1999). Actually, many other natural systems do not respect the requisites of thermodynamics. Such systems often feature interesting phenomena such as growing long-range correlations or phase transitions. Among the symptoms of a fundamental deep problem in gravitating systems is the appearance of negative specific heat (Lynden-Bell & Lynden-Bell 1977; Lynden-Bell 1998), which was seen for a long time as a paradox in statistical mechanics, since negative specific heat was thought to be impossible.
Presently, the only available approach to follow the nonlinear phases of gravitational instabilities is to carry out numerical simulations. Among all the existing methods, N-body techniques are thought to be the most effective to simulate the continuous case as well as the granular phases of self-gravitating systems.
Yet, despite the considerable success of these methods in reproducing many observed features, many fundamental problems remain. As mentioned above, the fragmentation and structure formation are not clearly understood. Related to this, CDM simulations conflict with observations at galactic scales (Moore 1999; Bullock et al. 2001; Bolatto et al. 2002), and no theory of the ISM is presently able to predict the conditions of star formation. Most of the time the star formation process relies on recipes with few physical constraints.
In situations where N-body simulations are successful (e.g. hot stellar systems), gravitational dynamics is sufficient to account for their main global properties and additional microscopic physics can be neglected. But when gravitational instability via fragmentation involves small-scale physics, the outcome may be strongly dependent on the properties of the small-scale physics. In other words, in situations where the growth on singularities triggered by gravity is allowed, the chaotic nature of gravitating systems make them sensitive to the perturbations induced by non-gravitational physics.
Therefore it is important to understand the properties of N-body systems subjected to various perturbations. For these purposes, a numerical study of perturbed, self-gravitating N-body systems is carried out.
Among the relevant perturbations we expect that boundary conditions at small and large scales, as well as dissipative factors, can play a key role. In order to characterize the individual effects of perturbations, in the tradition of analytical models, one is advised to deliberately use simplified models.
A study of dissipative systems is important because such systems may develop long-range correlations. In the typical ISM, radiative cooling is very effective and induces a temporary energy flow leading the system far from equilibrium (Dyson & Williams 1997). From laboratory experiments it is well known that systems outside of equilibrium may spontaneously develop spatio-temporal structures (Glansdorff & Prigogine 1971; Nicolis & Prigogine 1977; Prigogine 1980; Melo 1994).
A permanent energy flow is induced when energy loss due to dissipation is replenished, that is, when the system is continuously driven, e.g., by time-dependent boundary conditions. Such systems may develop persistent long-range correlations. Astrophysical examples of this are the growth of structures in cosmological simulations or the long-term persistence of filamentary structures in shearing flows (Toomre & Kalnajs 1991; Huber & Pfenniger 2001a; Wisdom & Tremaine 1988; Salo 1995; Pfenniger 1998). Among other things, the effect of time-dependent potential perturbations on dissipative self-gravitating spheres is studied in this paper.
In the next section we briefly review some theoretical results of the thermodynamics of self-gravitating isothermal spheres. The model is presented in Sect. 3 and the applied methods to carry out the structure analysis for the simulated systems are explained in Sect. 4. The results are presented in Sects. 5-7. In Sect. 5 quasi-equilibrium states of N-body models are compared with analytical predictions. Section 6 is dedicated to a study of long-range correlations appearing in the interval of negative specific heat during the collapsing transition of gravitating systems. Finally, in Sect. 7 the evolution of systems subjected to an energy-flow is discussed.
By confining a gravitational system within a sphere, we can compare our numerical work with previous analytical studies using the tools of statistical mechanics and point out some discrepancies. Although the theory, sometimes referred to as gravo-thermal statistics, is not fully consistent, since the applied Gibbs-Boltzmann entropy is derived under the assumption of extensivity (this inconsistency was recalled, e.g., by Taruya & Sakagami 2001), it yields some important and instructive results.
Before we present the model and the results let us here briefly review some theoretical findings (see Padmanabhan 1990 for an extended discussion on the topic).
Antonov (1962) and Lynden-Bell & Wood (1968)
studied theoretically the thermodynamics of self-gravitating
isothermal spheres and found anomalous behavior when compared with
classical thermodynamics of extensive systems. An example of such an
anomalous behavior is the so-called gravo-thermal catastrophe that
occurs when an isothermal gas of energy E(<0) and mass M is
released within a spherical box of radius greater than Antonov's
radius,
![]() .
The analytical model predicts
that for such systems there is no equilibrium to go and nothing can
stop the collapse of the central parts.
.
The analytical model predicts
that for such systems there is no equilibrium to go and nothing can
stop the collapse of the central parts.
Antonov's and Lynden-Bell & Wood's investigations have based on
point-like particles. Since then, several studies have been carried
out with modified (i.e., non point-like) particle potentials. Hertel
& Thirring (1971) modified the gravitational interaction
potential by introducing short-distance repulsive forces due to
quantum degeneracy and Aronson & Hansen (1972)
investigated the behavior of self-gravitating hard-spheres (see also
Chavanis & Sommeria 1998). Finally, Follana & Laliena
(2000) applied softened interaction potentials. They all
found qualitatively the same result: Unlike the model of Lynden-Bell
& Wood, there is always an equilibrium state for finite size
particles. However, a phase transition, separating a high energy
homogeneous phase from a low energy collapsing phase with core-halo
structure, occurs in an energy interval with negative microcanonical
specific heat,
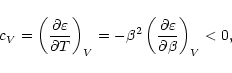 |
(1) |
There are fewer theoretical works done with the grand canonical ensemble (e.g. de Vega et al. 1996) where mass would be allowed to be exchanged with the environment, therefore we limit the scope of this study to the canonical ensemble, that is, energy can be exchanged with the environment, but not the mass and angular momentum.
Note that an ensemble allowing also the exchange of angular momentum would be very relevant for astrophysical situations, but few theoretical works have been made on this important aspect (Laliena 1999; Fliegans & Gross 2001).
A spatially isolated, spherical N-body system is studied. The N particles of the system are accelerated by gravity, and forces induced by boundary conditions and perturbations, respectively. In all, a particle can be accelerated by five force types: 1) confinement 2) energy dissipation due to velocity dependent friction 3) external forcing 4) long-range attraction (self-gravity) and 5) short-range repulsion. The five force types are discussed in detail in Sects. 3.2-3.5.
A steep potential well confines the particles to a sphere of radius
![]() (see Sect. 3.2). The total mass M and the
gravitational constant G equal one as well, G=M=1. The
dimensionless energy is the energy measured in units of GM2/R, that
is in our model
(see Sect. 3.2). The total mass M and the
gravitational constant G equal one as well, G=M=1. The
dimensionless energy is the energy measured in units of GM2/R, that
is in our model ![]() .
Thus energies and other quantities with
energy dimension (like the temperature) can be considered as
dimensionless.
.
Thus energies and other quantities with
energy dimension (like the temperature) can be considered as
dimensionless.
The confinement is realized through a steep potential well
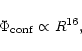 |
(2) |
Unlike non-spherical reflecting enclosures, the applied potential well conserves angular momentum.
The effect of different dissipation schemes is studied: local dissipation, global dissipation and a scheme similar to dynamical friction. For convenience we call the latter hereafter "dynamical friction''.
The local dissipation scheme represents inelastic scattering of interstellar gas constituents. That is, friction forces are added that depend on the relative velocities and positions of the neighboring particles.
A particle is considered as a neighbor if its distance is
![]() ,
where
,
where ![]() is the softening length and
is the softening length and
![]() is a free parameter. The friction force has the form:
is a free parameter. The friction force has the form:
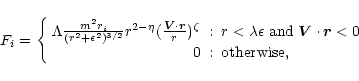 |
(3) |
For
![]() the friction force is
the friction force is
The global dissipation depends not on the relative velocity V, but on
the absolute particle velocity v. The global friction force is
| (5) |
Setting the velocity-dispersion
![]() ,
which is the dispersion of a virialized
self-gravitating system with M=R=1,
Chandrasekhar's dynamical friction formula
can be parameterized to a good approximation by,
,
which is the dispersion of a virialized
self-gravitating system with M=R=1,
Chandrasekhar's dynamical friction formula
can be parameterized to a good approximation by,
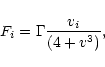 |
(6) |
If the dissipated energy is replenished by a forcing scheme the system
can be subjected to a continuous energy-flow. Here the energy
injection is due to time-dependent boundary conditions, that is, due
to a perturbation potential. This perturbation should on the one hand
be non-periodic and quasi-stochastic, on the other hand it should
provide an approximately regular large-scale energy injection in
time-average. A simple perturbation potential, meeting these
conditions, has the linear form,
![\begin{displaymath}\Phi_{\rm pert}(x,y,z,t)=\gamma [B_x(t) x + B_y(t) y + B_z(t) z],
\end{displaymath}](/articles/aa/full/2002/16/aa1730/img82.gif) |
(7) |
The perturbations are a linear combination of stationary waves that do not inject momentum.
If our system represents a molecular cloud then a perturbation similar
to those described above can be due to star clusters, clouds or other
massive objects passing irregularly in the vicinity. Indeed such
stochastic encounters must be quite frequent in galactic disks and we
assume that the average time between two encounters is,
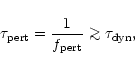 |
(9) |
Such a low frequency forcing scheme induces at first ordered particle motions, which are transformed in the course of time to random thermal motion, due to gravitational particle interaction.
Interaction forces include self-gravity and repulsive
forces whose strength can be adjusted by a parameter.
Repulsive forces may be a result of sub-resolution
processes such as star-formation or quantum degeneracy.
The particle interaction potential reads,
![\begin{figure}
\par\par\includegraphics[angle=90,width=7.4cm,clip]{1730f1.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg102.gif) |
Figure 1:
The potential as a function of r in units of
Gm/R, where m is the particle mass. A test
particle at
|
| Open with DEXTER | |
The interaction forces are computed on the Gravitor Beowulf
Cluster![]() at the Geneva Observatory with a parallel
tree code. This code is based on the Fortran
Barnes & Hut (1986, 1989) tree algorithm,
and has been efficiently parallelized for
a Beowulf cluster. It is available on request.
at the Geneva Observatory with a parallel
tree code. This code is based on the Fortran
Barnes & Hut (1986, 1989) tree algorithm,
and has been efficiently parallelized for
a Beowulf cluster. It is available on request.
The time-integration is the leap-frog algorithm with uniform
time-step, which ensures the conservation of the symplectic structure
of the conservative dynamics. The time-step is,
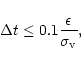 |
(11) |
The accuracy of the force computation is given through the tolerance
parameter, which for the studies presented in this paper is
![]() .
.
In order to test the code, the evolution of the
angular momentum is checked. We find that the angular momentum Jof a system with ![]() particles and local dissipation scheme,
that is initially
particles and local dissipation scheme,
that is initially
![]() in units such that
energy is dimensionless, remains small,
in units such that
energy is dimensionless, remains small,
![]() .
This is illustrated by means of two examples. Two simulations with
equal dissipation strength are carried out. One with short range
repulsion,
.
This is illustrated by means of two examples. Two simulations with
equal dissipation strength are carried out. One with short range
repulsion, ![]() ,
and the other without,
,
and the other without, ![]() .
After 10crossing times the angular momentum is
.
After 10crossing times the angular momentum is
![]() and
and
![]() ,
respectively. The deviation from the initial
value is larger for the simulation without short-range repulsion.
This is because the dissipation leads in this case to a
stronger mass concentration, i.e., to shorter particle distances.
Indeed, the potential energy after 10 crossing times is
,
respectively. The deviation from the initial
value is larger for the simulation without short-range repulsion.
This is because the dissipation leads in this case to a
stronger mass concentration, i.e., to shorter particle distances.
Indeed, the potential energy after 10 crossing times is
![]() and
and
![]() for the simulation with and without short-range
repulsion, respectively.
for the simulation with and without short-range
repulsion, respectively.
The different dissipation schemes, the forcing scheme and the
interaction potential with the short-distance repulsive force, have
several free parameters. In order to do a reasonably sized parameter
study the particle number has to be limited to a maximum of
![]() .
However, the absolute particle number is not important,
but the effect of changing it is. Thus, N also is varied.
.
However, the absolute particle number is not important,
but the effect of changing it is. Thus, N also is varied.
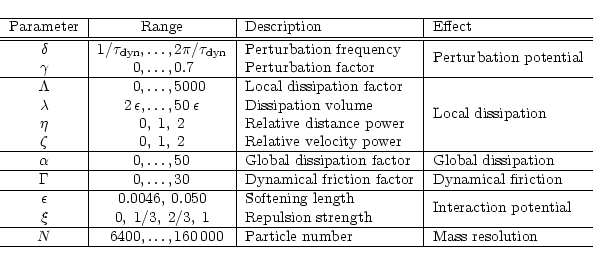
The model parameters and their ranges are indicated in Table 1.
|
|
In order to check if the perturbations of the gravitational system
induce characteristic correlations in phase-space, the indices
D and ![]() of the mass-size
relation and the velocity-dispersion-size relation
are determined.
of the mass-size
relation and the velocity-dispersion-size relation
are determined.
The index of the mass-size relation can be found via,
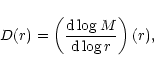 |
(12) |
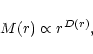 |
(13) |
The index of the velocity-dispersion-size relation is
determined by,
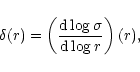 |
(14) |
| (15) |
Here, some N-body gravo-thermal experiments of systems with weak dissipation, i.e., of systems in quasi-equilibrium are presented. The results are compared with theoretical findings.
In order to cover a range of energy with the same experiment, we
introduce a weak global dissipation scheme allowing us to describe a
range of quasi-equilibrium states. Here weak means that
![]() ,
where
,
where
![]() is the dissipation
time-scale. Then, the results can be compared with theoretical
equilibrium states.
is the dissipation
time-scale. Then, the results can be compared with theoretical
equilibrium states.
Follana & Laliena (2000) theoretically examined the
thermodynamics of self-gravitating systems with softened potentials.
They soften the Newtonian potential by keeping n terms of an
expansion in spherical Bessel functions (hereafter such a regularized
potential is called a Follana potential). This regularization allows
the calculation of the thermodynamical quantities of a
self-gravitating system. The form of their potential is similar to a
Plummer potential with a corresponding softening
length. Figure 2 shows a softened Follana
potential with n=10, and a Plummer potential with
![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=7.4cm,clip]{1730f2.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg128.gif) |
Figure 2:
The Follana (n=10) and the Plummer
(
|
| Open with DEXTER | |
In their theoretical work Follana & Laliena found for a mild enough
regularization (n<30) a phase transition below the critical energy
![]() in a region with negative specific
heat. The transition separates a high energy homogeneous phase from a
low energy collapsed phase with a core-halo structure.
in a region with negative specific
heat. The transition separates a high energy homogeneous phase from a
low energy collapsed phase with a core-halo structure.
We want to reproduce these findings by applying
a Plummer potential (![]() ). Furthermore,
the effect of a small-scale repulsive force
(
). Furthermore,
the effect of a small-scale repulsive force
(![]() )
is studied.
)
is studied.
For these purposes, simulations with a weak global dissipation
strength,
![]() ,
are carried out. The dissipation time is
then
,
are carried out. The dissipation time is
then
![]() ,
where the free fall time is
,
where the free fall time is
![]() .
.
Before we discuss the results, let us briefly present some model
properties. The initial state is a relaxed, unperturbed and confined
N-body sphere with total energy
![]() .
.
Assigning a particle a volume of
![]() ,
the
volume filling factor is,
,
the
volume filling factor is,
The applied weak dissipation strength maintains the system
approximately thermalized and virialized (see Fig. 3).
Here a system of N particles is called virialized when the moment of
inertia I is not accelerated,
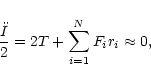 |
(17) |
![\begin{figure}
\par\includegraphics[angle=90,width=7.3cm,clip]{1730f3.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg138.gif) |
Figure 3:
The potential U, kinetic T and
total energy
|
| Open with DEXTER | |
The evolution of the inverse temperature
![]() as a function of the total energy
as a function of the total energy
![]() for two
simulations with
for two
simulations with ![]() and
and ![]() ,
respectively, as well as the
semi-analytical curve calculated by Follana & Laliena are shown in
the left panel of Fig. 4.
,
respectively, as well as the
semi-analytical curve calculated by Follana & Laliena are shown in
the left panel of Fig. 4.
| |
Figure 4:
Comparison of theoretical predictions and simulated
systems. The simulations are carried out with N=8000 and the
softening length is,
|
| Open with DEXTER | |
For the simulation with the Plummer potential the interval of negative
specific heat agrees with theoretical predictions. Also, in
accordance with predictions, a phase transition takes place,
separating a high energy homogeneous phase from a collapsed phase in
a interval with negative specific heat. Yet, the simulated phase
transitions occur at higher energies. To illustrate this the
evolution of the Lagrangian radii ![]() are shown in the middle
and the right panel of Fig. 4.
are shown in the middle
and the right panel of Fig. 4.
In the high energy homogeneous phase the system is insensitive to the short-distance form of the potential. Thus all systems enter the interval of negative specific heat at the same energy. However, the collapsed phase is sensitive to the short-distance form. That is, the system with repulsive short-distance force re-enters the interval of positive specific heat at a higher energy than those without such forces (see left panel of Fig. 4).
Furthermore, the collapsed phase resulting from a simulation with a Plummer potential is hotter and denser than those resulting from a simulation with repulsive small scale forces. This can be seen in Fig. 4 as well.
For a smaller softening length, theory expects a phase transition at higher
energies. Yet, already in simulations with a mild softening
![]() the collapsing transition occurs straight after the
system has entered the interval of negative specific heat, which is
shortly after the system has become self-gravitating. Thus, the
collapsing transition cannot occur at significantly
higher energies for a smaller softening length.
the collapsing transition occurs straight after the
system has entered the interval of negative specific heat, which is
shortly after the system has become self-gravitating. Thus, the
collapsing transition cannot occur at significantly
higher energies for a smaller softening length.
However, for systems with smaller softening length, the energy at which the
system reenters the zone of positive specific heat after the collapse
changes, i.e., it is shifted to smaller energies. This is shown in
Fig. 5, where two simulations with
![]() and
and
![]() resp.
resp.
![]() are compared.
are compared.
![\begin{figure}
\par\includegraphics[angle=90,width=17.8cm,clip]{1730f5.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg142.gif) |
Figure 5:
Same as Fig. 4 for two simulations with
|
| Open with DEXTER | |
Due to the higher particle number the dissipation time is in these
simulations reduced to
![]() .
Thus,
dynamical equilibrium is not as perfect as previously. That is,
the acceleration of the
moment of inertia I attains a maximum value of,
.
Thus,
dynamical equilibrium is not as perfect as previously. That is,
the acceleration of the
moment of inertia I attains a maximum value of,
![]() ,
where T is the kinetic energy. However, in general dynamical
equilibrium is well approximated and we expect, due to the experience
with simulations with varying particle number and dissipation time,
that the effect of the temporal deviation from equilibrium does not
affect qualitatively the results presented in Fig. 5.
,
where T is the kinetic energy. However, in general dynamical
equilibrium is well approximated and we expect, due to the experience
with simulations with varying particle number and dissipation time,
that the effect of the temporal deviation from equilibrium does not
affect qualitatively the results presented in Fig. 5.
The volume filling factor of the systems with
![]() and
and
![]() is
is
![]() ,
meaning that
the mass resolution is a factor 2.7 larger than the force resolution.
Thus the system is less granular than in the previous simulations with
N=8000 and
,
meaning that
the mass resolution is a factor 2.7 larger than the force resolution.
Thus the system is less granular than in the previous simulations with
N=8000 and
![]() (see Fig. 4). Yet, this
does not affect the simulated quasi-equilibrium states and the
deviation from theoretical predictions remains.
(see Fig. 4). Yet, this
does not affect the simulated quasi-equilibrium states and the
deviation from theoretical predictions remains.
Some predictions made by analytical models, such as the interval of
negative specific heat, agree with findings resulting from N-body
models. Yet, discrepancies also appear, such as the way the
collapsing phase transition develops.
| |
Figure 6:
Evolution of the Lagrangian radii
for a system with global dissipation scheme, dynamical
friction and a local dissipation scheme, respectively.
The Lagrangian radii depict, here and in the following figures,
spheres containing the following mass fractions:
|
| Open with DEXTER | |
At first glance the deviating results are surprising. Yet the small scale physics is different in the two models, which may account for the discrepancies. Indeed, thermostatistics assumes a smooth density distribution and is thus not able to account for two-body relaxation effects in granular media. However, a certain degree of granularity is an inherent property of N-body systems. This may then lead to discrepancies, especially in the unstable interval of negative specific heat, where phase transitions may be sensitive to small scale physics.
While thermostatistics is too smooth to account for microscopic physics in granular self-gravitating media such as the interstellar gas, two-body relaxation is often too strong in N-body systems due to computational limitations. This is particularly so in high force resolution simulations where the force resolution is larger than the mass resolution. We refer to this in Sect. 6.1 where we discuss, among other things, the effect of the granularity on long-range correlations appearing in the interval of negative specific heat.
A further discrepancy between nature, analytical models and N-body models may be due to the entropy used in gravo-thermal statistics (Taruya & Sakagami 2001). Indeed, the entropy used in analytical models to find equilibrium states via the maximum entropy principle is the extensive Boltzmann-Gibbs entropy, that is in fact not applicable for non-extensive self-gravitating systems.
Generalized thermostatistics including non-extensivity are currently developed (Tsallis 1988; Sumiyoshi 2001; Latora et al. 2001; Leubner 2001). These formalisms suggest that non-extensivity changes not all but some of the classical thermodynamical results (Tsallis 1999; Boghosian 1999), which agrees with our findings.
Because currently it is a priori not known which thermostatistical properties change in non-extensive systems and consistent theoretical tools are not available, analytical results must be considered with caution.
Properties of equilibrium states differing from theoretical
predictions in the interval of negative specific heat were found (see
above). Let us now study the nonlinear structure growth in this
interval for an increased dissipation strength, i.e., outside of
equilibrium, when
![]() .
.
As previously, a relaxed, unperturbed, confined N-body sphere with
![]() serves as the initial state for the simulations.
serves as the initial state for the simulations.
In order to dissipate the energy different dissipation schemes are applied. Before we discuss the appearance of long-range correlations in unstable dissipative systems let us briefly discuss the effect of the different dissipation schemes on the global system structure.
The different applied dissipation schemes (see Sect. 3.3)
lead to collapsed phases with different global structures. That is,
they have different mass fractions contained in the core and the halo.
A typical ordering is
![]() ,
where
,
where
![]() ,
,
![]() and
and
![]() are the density contrasts
resulting from simulations with a global dissipation scheme, dynamical
friction and a local dissipation scheme, respectively. The density
contrast is,
are the density contrasts
resulting from simulations with a global dissipation scheme, dynamical
friction and a local dissipation scheme, respectively. The density
contrast is,
![]() ,
where
,
where
![]() and
and ![]() are the center of mass density and the
peripheric density, respectively. This means that for a global
dissipation scheme almost all the mass is concentrated in a dense core,
whereas a local dissipation scheme can form a persistent "massive''
halo.
are the center of mass density and the
peripheric density, respectively. This means that for a global
dissipation scheme almost all the mass is concentrated in a dense core,
whereas a local dissipation scheme can form a persistent "massive''
halo.
The evolution of the mass distribution resulting from simulations with
the different dissipation schemes is shown in Fig. 6.
The collapse of the inner shells takes in all systems about the
same time. Yet, the uncollapsed matter distributed in the halo
is for the global dissipation scheme less than ![]() ,
whereas it
is
,
whereas it
is ![]() for the local dissipation scheme.
for the local dissipation scheme.
Next, temporary long-range correlations that develop in unforced
gravitating systems are presented depending on the different
system parameters.
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{1730f7.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg158.gif) |
Figure 7:
Evolution of the index, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=13.8cm,clip]{1730f8.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg159.gif) |
Figure 8: Evolution of the Lagrangian radii (top) and the specific heat (bottom) for three simulations with global dissipation and different dissipation strength. The dashed line marks the moment, when the system becomes fully self-gravitating. The dash-dotted line indicates the moment when the system enters the zone of negative specific heat. The dotted line marks the "end'' of the collapse. The evolution of the corresponding phase-space correlations are shown in Fig. 7. |
| Open with DEXTER | |
A sufficiently strong global dissipation, i.e.,
![]() ,
of a gravitating system leads during the
nonlinear phase of the collapsing transition to fragmentation and
long-range phase-space correlations, so that the index,
,
of a gravitating system leads during the
nonlinear phase of the collapsing transition to fragmentation and
long-range phase-space correlations, so that the index, ![]() ,
of the velocity-dispersion size relation,
,
of the velocity-dispersion size relation,
![]() ,
becomes positive.
,
becomes positive.
Figure 7 shows the evolution of the velocity-dispersion-size
relation, i.e., of ![]() for different dissipation strengths. The
relations result from 3 different simulations with global dissipation
schemes and different dissipation strengths. The dissipation strength is
given through the parameter
for different dissipation strengths. The
relations result from 3 different simulations with global dissipation
schemes and different dissipation strengths. The dissipation strength is
given through the parameter ![]() .
Here
.
Here
![]() .
This corresponds to
.
This corresponds to
![]() .
.
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{1730f9.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg162.gif) |
Figure 9:
Evolution of the index of the
velocity-dispersion-size relation for three simulations with
a local dissipation scheme and different dissipation strengths.
The particle number is
|
| Open with DEXTER | |
| |
Figure 10: Evolution of the Lagrangian radii and the specific heat for three simulations with local dissipation and different dissipation strength. The interval of negative specific heat is depicted by the dash-dotted and dotted line. The dashed line marks the moment when the whole system becomes self-gravitating. Figure 9 shows the evolution of the corresponding long-range correlations. |
| Open with DEXTER | |
While the velocities remain uncorrelated in the simulation with
![]() ,
,
![]() becomes temporarily positive over the whole dynamical
range in the simulations with the stronger dissipation.
becomes temporarily positive over the whole dynamical
range in the simulations with the stronger dissipation.
The velocity correlations start
to develop at largest scales after the system has become
self-gravitating. After the system has entered the interval of
negative specific heat the correlation growth is accelerated.
It attains a maximum and finally disappears when the collapse
ends. The dynamical range over which ![]() during
maximum correlation is
during
maximum correlation is ![]() dex.
dex.
Correlations at small scales straight above the softening length are stronger for a stronger energy dissipation.
The maximum correlation established in the negative specific heat
interval persists for
![]() and is characteristic for
the applied dissipation strength and softening. For instance, the
simulation with the strongest dissipation develops during
and is characteristic for
the applied dissipation strength and softening. For instance, the
simulation with the strongest dissipation develops during
![]() a roughly constant
a roughly constant ![]() over a range of 1.5 dex that
resembles Larson's relation. Yet, correlations at small scales
decay rapidly and the index
over a range of 1.5 dex that
resembles Larson's relation. Yet, correlations at small scales
decay rapidly and the index ![]() even becomes
negative at intermediate scales.
even becomes
negative at intermediate scales.
The end of the collapse and with it the disappearance of the
correlated velocity structure is marked by a diverging
negative specific heat
![]() .
This is shown in Fig. 8.
.
This is shown in Fig. 8.
Systems with dynamical friction and local dissipation also develop velocity correlations.
Figure 9 shows the correlations resulting from simulations with a local dissipation scheme. Contrary to the global dissipation scheme, a strong local dissipation does not extend the collapse of the whole system. Thus, local friction forces that are strong enough to develop correlations lead also to a fast collapse and correlations accordingly persist a short time compared to simulations with global dissipation.
The corresponding evolution of the Lagrangian radii and the interval of negative specific heat are shown in Fig. 10.
In the dynamical friction scheme, energy dissipation depends, as in the global dissipation scheme, on the absolute particle velocity. Thus a strong dynamical friction extends the gravitational collapse and the "lifetime'' of the correlations. Yet, the observed phase-space correlations are weaker, compared to those appearing in simulations with global and local dissipation, respectively, meaning that the reduced dissipation strength for fast particles, accordingly to the dynamical friction scheme, destroys the correlations.
So far the velocity correlations dependent on the different dissipative factors were studied. Next the effect of different short distance regularizations of the Newtonian potential, removing its singularity, are checked. That is, simulations with and without short distance repulsive forces and with different dissipation strengths are carried out. Energy is dissipated via the global dissipation scheme.
In Fig. 11 the velocity correlations resulting from three
simulations with three different regularizations are compared. The
regularizations are characterized by two parameters, namely, the
softening length ![]() and the parameter
and the parameter ![]() that determines
the strength of the repulsive force. The softening length and
that determines
the strength of the repulsive force. The softening length and ![]() of
the three simulations, compared in Fig. 11, are,
(
of
the three simulations, compared in Fig. 11, are,
(
![]() ,
,
![]() ), (
), (
![]() ,
,
![]() and
(
and
(
![]() ,
,
![]() ), where
), where ![]() means that a Plummer
potential is applied and
means that a Plummer
potential is applied and ![]() means that short distance repulsive
forces are at work (see Sect. 3.5). The dissipation strength is
for all three simulations the same,
means that short distance repulsive
forces are at work (see Sect. 3.5). The dissipation strength is
for all three simulations the same, ![]() ,
and the collapsing
time is consequently the same as well (see Fig. 12).
,
and the collapsing
time is consequently the same as well (see Fig. 12).
During the first
![]() long-range correlations resulting
from the three simulations are identical. Then the
long-range correlations resulting
from the three simulations are identical. Then the ![]() starts
to separate. Indeed, the repulsive forces cause an increase of
starts
to separate. Indeed, the repulsive forces cause an increase of
![]() at small scales, compared to the simulation with the same
softening length, but without repulsive forces. Yet, large scales
remain unaffected.
at small scales, compared to the simulation with the same
softening length, but without repulsive forces. Yet, large scales
remain unaffected.
The index ![]() resulting from the simulation with the large
softening length is larger compared to the other two simulations after
one
resulting from the simulation with the large
softening length is larger compared to the other two simulations after
one
![]() .
Also, the
.
Also, the ![]() curve is flatter after
that time.
curve is flatter after
that time.
The large difference between the simulation with the long softening
length and the corresponding simulation with the short softening
length is astonishing, because there is a clear deviation even at large
scales. This may be because the two simulations were carried out with the same
particle number,
![]() .
Consequently, the volume filling factors are
different, namely,
.
Consequently, the volume filling factors are
different, namely,
![]() and
and
![]() ,
meaning that
for the long softening length, i.e., the large
,
meaning that
for the long softening length, i.e., the large
![]() ,
the mass
resolution is greater than the force resolution and vice versa for the
small softening length. Whereas a small volume-filling factor
describes a granular phase, a large volume-filling factor describes
rather a fluid phase. Thus the deviation of the velocity
correlations may mainly be due to the different volume-filling factors
and not due to the different softening lengths.
,
the mass
resolution is greater than the force resolution and vice versa for the
small softening length. Whereas a small volume-filling factor
describes a granular phase, a large volume-filling factor describes
rather a fluid phase. Thus the deviation of the velocity
correlations may mainly be due to the different volume-filling factors
and not due to the different softening lengths.
In order to check this, some complementary numerical experiments are carried out, whose results are presented subsequently.
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{1730f11.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg172.gif) |
Figure 11:
Evolution of the velocity correlations
for three simulations with global dissipation
scheme and different potential regularizations.
That is, the softening
length and the form of the softening, respectively,
change from simulation to simulation. For |
| Open with DEXTER | |
| |
Figure 12: Same as Fig. 10 for three simulations with different potential regularizations, i.e., different softening lengths and forms of the softening potential, respectively. The evolution of the corresponding phase-space correlations are shown in Fig. 11. |
| Open with DEXTER | |
The upper panels in Fig. 13 show the velocity-dispersion-size
relation that develop in simulations with different volume-filling
factors, but equal softening length,
![]() .
The particle
numbers are, N=6400,
.
The particle
numbers are, N=6400, ![]() and
and
![]() .
Thus, the
volume-filling factors are,
.
Thus, the
volume-filling factors are,
![]() ,
,
![]() and
and
![]() ,
respectively. The strongest phase-space correlations
appear in the simulation with the highest mass resolution, i.e., for
the "fluid phase'', and weakest correlations appear in the "granular
phase''. The flattest
,
respectively. The strongest phase-space correlations
appear in the simulation with the highest mass resolution, i.e., for
the "fluid phase'', and weakest correlations appear in the "granular
phase''. The flattest ![]() curve results from the simulation
in which force and mass resolution are equal.
curve results from the simulation
in which force and mass resolution are equal.
This result suggests that the volume filling factor
![]() (and
not the softening length) is the crucial parameter determining the
correlation strength in simulations with equal dissipation strength,
as long as a substantial part of the system forces stem from
interactions of particles with relative distances larger than the
softening length.
(and
not the softening length) is the crucial parameter determining the
correlation strength in simulations with equal dissipation strength,
as long as a substantial part of the system forces stem from
interactions of particles with relative distances larger than the
softening length.
The lower panels in Fig. 13 show, for the same simulations,
the evolution of the index, D(r), of the mass-size relation,
![]() .
The deviation from homogeneity is strongest for
the "granular phase'' and weakest for the "fluid phase''. Thus the
order of the correlation strength in space is inverse to the order of
the correlation strength in phase-space. Such an inverse order is
expected in self-gravitating system with
.
The deviation from homogeneity is strongest for
the "granular phase'' and weakest for the "fluid phase''. Thus the
order of the correlation strength in space is inverse to the order of
the correlation strength in phase-space. Such an inverse order is
expected in self-gravitating system with
![]() ,
where U is
the potential energy and T is the kinetic energy (Pfenniger &
Combes 1994; Pfenniger 1996; Combes
1999).
,
where U is
the potential energy and T is the kinetic energy (Pfenniger &
Combes 1994; Pfenniger 1996; Combes
1999).
The corresponding Lagrangian radii and the interval of negative specific heat are shown in Fig. 14.
![\begin{figure}
\par\includegraphics[width=14.2cm,clip]{1730f13.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg175.gif) |
Figure 13:
Upper panels: Evolution of the
index, |
| Open with DEXTER | |
| |
Figure 14: Same as Fig. 10 for three simulations with different volume filling factor. Figure 13 shows the evolution of the corresponding long-range correlations. |
| Open with DEXTER | |
Assuming a constant softening length, different volume filling
factors
![]() imply different particle numbers N that
introduce different Poisson noise,
imply different particle numbers N that
introduce different Poisson noise, ![]()
![]() .
Then, the
statistical roughness of the initial uniform Poisson particle
distribution decreases as
.
Then, the
statistical roughness of the initial uniform Poisson particle
distribution decreases as ![]()
![]() .
.
Thus the initial roughness of the latter simulations (see Fig. 13)
differ from each other by a factor ![]() 2.2 and one might suppose
that the different correlation strengths in these simulations are
the result of the different inital, statistical roughness.
2.2 and one might suppose
that the different correlation strengths in these simulations are
the result of the different inital, statistical roughness.
![\begin{figure}
\par\includegraphics[width=14.2cm,clip]{1730f15.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg178.gif) |
Figure 15:
Upper panels: Evolution of the
phase-space correlations resulting from two
simulations with identical volume filling factor,
|
| Open with DEXTER | |
| |
Figure 16:
Same as Fig. 10 for two
simulations with identical volume filling factor and
unequal initial roughness, |
| Open with DEXTER | |
In order to check this possibility, long-range correlations, resulting
from two simulations with
![]() and with statistical
roughness differing by a factor of
and with statistical
roughness differing by a factor of ![]() 2.2, are compared. The
results are presented in Fig. 15 and the corresponding
Lagrangian radii are shown in Fig. 16. The simulation with
2.2, are compared. The
results are presented in Fig. 15 and the corresponding
Lagrangian radii are shown in Fig. 16. The simulation with
![]() was already presented in Fig. 13. It is now compared
with a simulation with stronger initial roughness.
was already presented in Fig. 13. It is now compared
with a simulation with stronger initial roughness.
Despite the different initial roughness, long-range correlations in phase-space are almost identical for the two simulations.
As regards
fragmentation, in addition to the parameters of the
mass-size relation, the mass distributions in space were compared.
We actually find a stronger fragmentation for small particle numbers.
Yet
![]() seems to be the crucial parameter for the
fragmentation strength in Fig. 13.
seems to be the crucial parameter for the
fragmentation strength in Fig. 13.
Consequently, the different correlation strengths in Fig. 13 cannot be accounted for by Poisson noise, but are mainly the result of the different volume-filling factors, or more precisely, due to the different ratio of force and mass resolution. Thus, dark matter clustering in high-resolution cosmological N-body simulations in which the force resolution is typically an order of magnitude smaller than the mass resolution, may be too strong compared to the physics of the system (Hamana et al. 2001).
Here, long-range correlations are discussed that develop in cold,
gravitationally unstable systems without energy dissipation. The
correlation strength appearing in such dissipationless systems depends
on the initial ratio between kinetic and potential energy, a=T/|U|,
i.e., on the number of thermal Jeans masses given through
![]() .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1730f17.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg181.gif) |
Figure 17:
Upper panels: Phase-space correlations
that develop during the free fall of three cold,
dissipationless systems. All systems have the same volume
filling factor,
|
| Open with DEXTER | |
This is shown in Fig. 17. For a=0.01 the index ![]() of
the velocity-dispersion-size relation remains zero at small scales
during the entire free fall, whereas for a=0.0 the index becomes
of
the velocity-dispersion-size relation remains zero at small scales
during the entire free fall, whereas for a=0.0 the index becomes
![]() over the whole dynamical range, over a period of
over the whole dynamical range, over a period of ![]()
![]() .
That is, 350
.
That is, 350 ![]() are not sufficient to develop
small-scale phase-space correlations in a dissipationless system.
are not sufficient to develop
small-scale phase-space correlations in a dissipationless system.
In order to show the dependence of the result on the initial
Poisson noise, the absolutely cold simulation with
![]() is
compared with a
is
compared with a ![]() -body simulation. As above, it follows that
the initial roughness of the two systems differs by a factor of
-body simulation. As above, it follows that
the initial roughness of the two systems differs by a factor of ![]() 2.2.
2.2.
Figure 17 shows that the non-equilibrium structures resulting
from the simulations with equal a but unequal particle number differ
from each other during the entire free fall period. Indeed, during the
first half of the free fall time the two initial conditions produce
velocity correlations that differ on small and large scales. After
![]() the differences approximately disappear.
However, the behavior of the spatial correlations (see lower panels of
Fig. 17) is inverse, meaning that differing spatial
correlations appear after
the differences approximately disappear.
However, the behavior of the spatial correlations (see lower panels of
Fig. 17) is inverse, meaning that differing spatial
correlations appear after
![]() and persist for the
rest of the free fall.
and persist for the
rest of the free fall.
These results suggest that non-equilibrium structures appearing in cold systems or in systems with very effective energy dissipation depend more strongly on initial noise than those appearing in warm systems with less effective dissipation (see also Fig. 15).
The evolution of the Lagrangian radii during the free fall of the cold, dissipationless systems are shown in Fig. 18. Because these systems are adiabatic and self-gravitating during the whole simulation, the corresponding intervals are not plotted in the figure.
Long-range spatial and phase-space correlations appear naturally
during the collapsing phase transition in the interval of negative
specific heat if the energy dissipation time is
![]() so that the time-scale of correlation
growth is smaller than the time-scale of chaotic mixing, which
is
so that the time-scale of correlation
growth is smaller than the time-scale of chaotic mixing, which
is
![]() ,
where
,
where ![]() is the maximum Liapunov exponent (Miller 1994).
is the maximum Liapunov exponent (Miller 1994).
Actually, the details of the long-range correlations depend on the
applied dissipation scheme, but there are also some generic
properties. That is, phase space correlations start to grow at large
scales, whereas spatial correlations seem to grow from the bottom-up.
Moreover, there is an upper limit for the index of the
velocity-dispersion-size relation within the dynamical range, namely,
![]() .
.
Besides the dissipation strength and initial conditions, the volume
filling factor
![]() is a crucial parameter for the correlation
strength. That is, phase-space correlations are strong in the fluid
limit and weak for a granular phase. The behavior of the spatial
correlations is exactly the other way around.
is a crucial parameter for the correlation
strength. That is, phase-space correlations are strong in the fluid
limit and weak for a granular phase. The behavior of the spatial
correlations is exactly the other way around.
The softening length does not affect correlations within the dynamical range. Yet, sub-resolution repulsive forces affect correlations on small scales above the resolution scale. Of course, this does not hold for the onset of the correlation growth, but only after sufficient particles have attained sub-resolution distances.
The above considerations suggest that the correlations found are physically relevant and not a numerical artifact.
The long-range spatial and phase-space correlations appearing during the collapsing transition are qualitatively similar to the mass-size and the velocity-dispersion-size relation observed in the ISM (e.g. Blitz & Williams 1999; Chappell & Scalo 2001; Fuller & Myers 1992), showing that in the models, gravity alone can account for ISM-like correlations.
Furthermore, the time-scale of the correlation lifetime is the free
fall time,
![]() ,
which is consistent with a dynamical
scenario in which ISM-structures are highly transient
(Vázquez-Semadeni 2002; Larson 2001; Klessen
et al. 2000), which is related to rapid star formation
and short molecular cloud lifetimes (Elmegreen 2000),
that is, the corresponding time-scales are about an order of magnitude
smaller than in the classical Blitz & Shu (1980) scenario.
,
which is consistent with a dynamical
scenario in which ISM-structures are highly transient
(Vázquez-Semadeni 2002; Larson 2001; Klessen
et al. 2000), which is related to rapid star formation
and short molecular cloud lifetimes (Elmegreen 2000),
that is, the corresponding time-scales are about an order of magnitude
smaller than in the classical Blitz & Shu (1980) scenario.
Here we check if self-gravitating systems can establish persistent long-range correlations if they are maintained continuously outside of equilibrium by a permanent energy-flow. That is, the dissipated energy is continuously replenished by time-dependent potential perturbations.
Both simulations of granular and fluid phases are carried out. A
typical parameter set, describing a granular system is, ![]() ,
,
![]() ,
,
![]() while
while
![]() ,
,
![]() ,
,
![]() are here typical for a fluid phase.
Yet, the parameters are not fixed and the effect on the evolution is
studied when parameters change. Parameters, controlling energy-flow
and interaction potential, as well as their ranges, are indicated in
Table 1.
are here typical for a fluid phase.
Yet, the parameters are not fixed and the effect on the evolution is
studied when parameters change. Parameters, controlling energy-flow
and interaction potential, as well as their ranges, are indicated in
Table 1.
The applied potential perturbations imitate massive objects passing in
the vicinity on time-scales
![]() .
The perturbations induce primarily ordered particle motions.
Then gravitational interactions lead to a conversion of the bulk
kinetic energy to random thermal motion. The energy injection due to
such a forcing scheme can be quite regular until a plateau is reached.
.
The perturbations induce primarily ordered particle motions.
Then gravitational interactions lead to a conversion of the bulk
kinetic energy to random thermal motion. The energy injection due to
such a forcing scheme can be quite regular until a plateau is reached.
Energy injection prevents a system from collapsing and maintains an
approximately statistically steady state for ![]()
![]() when energy dissipation is balanced appropriately by large
scale potential perturbations. These states do not feature any
persistent long-range correlations. Yet, they develop a temperature
structure that is characteristic for the applied dissipation scheme.
This is shown in Fig. 19, where the evolution of two granular
systems subjected to an energy-flow is presented. One system
dissipates its energy by a global dissipation scheme (top), the other
by a local dissipation scheme (bottom).
when energy dissipation is balanced appropriately by large
scale potential perturbations. These states do not feature any
persistent long-range correlations. Yet, they develop a temperature
structure that is characteristic for the applied dissipation scheme.
This is shown in Fig. 19, where the evolution of two granular
systems subjected to an energy-flow is presented. One system
dissipates its energy by a global dissipation scheme (top), the other
by a local dissipation scheme (bottom).
The system with the global dissipation scheme is nearly thermalized
during almost the entire simulation, whereas the local dissipation
scheme leads to a permanent positive temperature gradient that is
inverse compared to stars and resembles those of the ISM where dense,
cool mass condensations are embedded in hotter shells.
| |
Figure 18: Same as Fig. 10 for the free fall of three cold, dissipationless systems with identical volume filling factor but unequal a and initial roughness, respectively. The evolution of the corresponding long-range correlations is shown in Fig. 17. |
| Open with DEXTER | |
| |
Figure 19:
The two left panels: Evolution of the
Lagrangian radii (left) and the Lagrangian
dimensionless temperature (middle left)
of a system subjected to an energy-flow and with global
dissipation scheme. The curves depict certain mass-fractions,
and its temperatures, respectively.
The mass fractions, contained in spheres, centered at the center of
mass, are:
|
| Open with DEXTER | |
If dissipation dominates energy injection the system undergoes in
general a mono-collapse, that is, a collapsed structure is formed in
which a part of the system mass is concentrated in a single dense
core and the rest is distributed in a diffuse halo. However,
systems with a rather fluid phase may develop several dense cores moving
in a diffuse halo, when they are subjected to an appropriate energy
flow. In the course of time the number of clumps varies,
but a non-mono-clump structure persists for some
![]() (see
Fig. 20). These systems may even develop persistent
phase-space correlations (see Fig. 21).
(see
Fig. 20). These systems may even develop persistent
phase-space correlations (see Fig. 21).
![\begin{figure}
\par\includegraphics[angle=-90,width=18cm,clip]{1730f20.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg196.gif) |
Figure 20:
Mass distribution of a system subjected to
an energy-flow. Shown is the projection of the
particle positions onto the xy-plane.
The particle number is, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.2cm,clip]{1730f21.eps}
\end{figure}](/articles/aa/full/2002/16/aa1730/Timg198.gif) |
Figure 21:
The evolution of the phase-space
correlations in a system subjected to an energy-flow and with short
distance repulsive forces (see Fig. 20). During the first
|
| Open with DEXTER | |
However, the clumps result not from a hierarchical fragmentation
process, but are formed sequentially on the free fall time scale.
Furthermore, the clumps are so dense that their evolution is strongly
influenced by the applied regularization. That is, the evolution over
several
![]() depend on the numerical model that does not
represent accurately small-scale physics.
depend on the numerical model that does not
represent accurately small-scale physics.
In order to impede gravitational runaway that may hinder the formation
of complex non-equilibrium structures within the given dynamical range,
different measures are taken, such as short distance repulsion and the
application of the dynamical friction scheme, where the friction force
![]() for
for
![]() .
.
Yet, despite these measure, we find only either nearly homogeneous structures in systems where energy injection prevails, or systems dominated by unphysical clumps in the case of prevailing energy dissipation.
Up to now, the effect of several different dissipation schemes mainly
were discussed. However, the effect of a modified forcing scheme is
also checked. That is, a power-law forcing scheme is applied, which
injects energy at different frequencies. This forcing scheme is a
modification of those presented in Sect. 3.4 and reads,
![]() ,
where
,
where
![]() .
Yet, such a forcing scheme also cannot induce a phase transition to
complex non-equilibrium structures and the resulting mass distribution
corresponds to the those described above.
.
Yet, such a forcing scheme also cannot induce a phase transition to
complex non-equilibrium structures and the resulting mass distribution
corresponds to the those described above.
Actually the "clumpy'' structure in Fig. 20 and the corresponding phase-space correlations shown in Fig. 21 do not represent real physics, nevertheless, they show that it is in principal possible to maintain spatial non-equilibrium structures and long-range phase-space correlations in a perturbed, dissipative, self-gravitating system over several dynamical times. Thus, it cannot be excluded that in the future, with a better representation of microscopic physics and forcing mechanisms at work in the ISM, models including self-gravity may produce complex nonhomogeneous structures in a statistical equilibrium, i.e., persistent patterns formed by transient structures.
However, at present, models of dissipative, self-gravitating systems cannot produce such structures on the scale of Giant Molecular Clouds (e.g. Semelin & Combes 2000; Klessen et al. 2000; Huber & Pfenniger 2001a).
On larger scales, gravity gives rise to persistent non-equilibrium structures in cosmological and shearing box simulations. A common denominator of these models is that their time-dependent boundary conditions are given by a scale-free spatial flow counteracting gravity. Let us discuss this more precisely.
In cosmological and shearing box models, time-dependent boundary
conditions create relative particle velocities that are inverse to
gravitational acceleration and increase with particle distance,
![]() .
In the shearing box model, the relative azimuthal
particle velocity due to the shear flow is
.
In the shearing box model, the relative azimuthal
particle velocity due to the shear flow is
![]() ,
where
,
where ![]() is the radial particle distance in cylinder coordinates.
In cosmological models, the relative particle velocity induced by the
Hubble flow is
is the radial particle distance in cylinder coordinates.
In cosmological models, the relative particle velocity induced by the
Hubble flow is
![]() ,
where r is the relative particle
distance in Cartesian coordinates.
,
where r is the relative particle
distance in Cartesian coordinates.
These relations and consequently the corresponding flows are scale-free. The fact that the shear flow affects only the azimuthal velocity component may then account for the characteristic spiral-arm-like structures found in shearing box experiments, differing from those found in cosmological models, where the isotropic Hubble flow gives rise to, on average, isotropic non-equilibrium structures.
The models studied in this paper are not subject to a scale-free spatial flow counteracting gravity and persistent long-range correlations of astrophysical relevance do not appear. This may suggest that in situations where gravitational runaway is allowed, matter that has passed through a collapsing transition has to be replenished at large scales in order to attain a statistical equilibrium state of transient fragmentation.
First, equilibrium states of N-body models were compared with analytical models. Subsequently, the findings resulting from this comparison were discussed and are summarized as follows:
Second, the collapsing transition was studied in systems with strong dissipation. The findings are:
Finally, systems subject to a permanent energy-flow were studied. We find:
Acknowledgements
This work has been supported by the Swiss National Science Foundation.