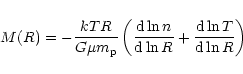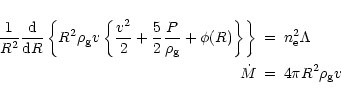A&A 386, 77-96 (2002)
DOI: 10.1051/0004-6361:20020087
XMM-Newton observation of M 87
I. Single-phase temperature structure of intracluster medium
K. Matsushita1 -
E. Belsole2 - A. Finoguenov1 - H. Böhringer1
1 - Max-Planck-Institut für Extraterrestrial Physik, 85748 Garching, Germany
2 - Service d'Astrophysique, CEA Saclay, L'Orme des Merisiers, Bât. 709, 91191 Gif-sur-Yvette Cedex, France
Received 19 June 2001 / Accepted 9 January 2002
Abstract
We report the results of a detailed analysis of the temperature structure of the X-ray
emitting plasma halo of M 87, the cD galaxy of the Virgo Cluster.
Using the MEKAL model,
the data provide strong indications that the intracluster medium
has a single phase structure
locally, except the regions associated with the radio structures.
The deprojected spectrum at each radius is well fitted by a single temperature
MEKAL model, except for the very central region (<2 arcmin) which seems to be
affected by the jet and radio lobe structure.
The temperature of the intracluster plasma is 1 keV at the center and gradually increases
to 2.5 keV at 80 kpc.
We have also fitted spectra using the APEC code. Although the large changes of the strength
of K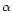 lines causes a discrepancy between the Fe-L and Fe-K lines
for the APEC results,
the overall temperature structure has not changed.
There is no sign of excess absorption in the spectral data.
The single-phase nature of the intracluster medium is in conflict with the standard cooling
flow model which is based on a multi-phase temperature structure.
In addition, the signature of gas cooling below 0.8 keV to zero temperature is not observed
as expected for a cooling flow.
The gravitational mass profile derived from the temperature and density distribution
of the intracluster gas shows two distinct contributions that can be assigned to the
gravitational potential of the cD galaxy and the cluster. The central temperature of
the intracluster medium agrees well with the potential depth and the velocity dispersion of
the cD galaxy. The latter result implies that the central region of the intracluster medium
is equivalent to a virialized interstellar medium in M 87.
lines causes a discrepancy between the Fe-L and Fe-K lines
for the APEC results,
the overall temperature structure has not changed.
There is no sign of excess absorption in the spectral data.
The single-phase nature of the intracluster medium is in conflict with the standard cooling
flow model which is based on a multi-phase temperature structure.
In addition, the signature of gas cooling below 0.8 keV to zero temperature is not observed
as expected for a cooling flow.
The gravitational mass profile derived from the temperature and density distribution
of the intracluster gas shows two distinct contributions that can be assigned to the
gravitational potential of the cD galaxy and the cluster. The central temperature of
the intracluster medium agrees well with the potential depth and the velocity dispersion of
the cD galaxy. The latter result implies that the central region of the intracluster medium
is equivalent to a virialized interstellar medium in M 87.
Key words: X-rays: galaxies - galaxies: ISM - galaxies: individual: M 87
In the cores of many clusters of galaxies, X-ray imaging data show a highly peaked surface
brightness profile (e.g. Fabian et al. 1981).
The radiative cooling time in these regions is much less than a Hubble time.
Without a heating process, the gas cools to low temperature and results in a "cooling flow''
(Fabian 1994 for a review).
The mass flow rate, 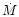 ,
that is deduced in the standard cooling flow model,
is approximately proportional to the radius. This implies that matter is
deposited throughout the entire cooling flow region.
It also implies that the gas in the cooling flow zone is "multi-phase'' on scales small enough
that the inhomogeneities have escaped the observation so far.
ASCA and ROSAT observations confirmed the existence of cooler gas in the cores of cooling flow
clusters as expected (e.g. Allen & Fabian 1994; Ikebe et al. 1999;
Ikebe 2001).
The presence of an intrinsic absorber in excess of the galactic absorption, as
it might be expected to arise from the accumulation of cold gas in the cooling flows,
was also inferred from the analysis of the ASCA spectra (e.g. Allen 2000; Allen et al. 2001).
In fact, the fitting of the "multi-phase'' cooling flow model to the observed spectra including
temperature phases that cool below the X-ray emitting temperature regime,
requires the inclusion of excess absorption to satisfactorily reproduce the observed spectra.
It has also been argued, that inclusion of excess absorption leads to values of the mass flow
rate as obtained from imaging data,
,
that is deduced in the standard cooling flow model,
is approximately proportional to the radius. This implies that matter is
deposited throughout the entire cooling flow region.
It also implies that the gas in the cooling flow zone is "multi-phase'' on scales small enough
that the inhomogeneities have escaped the observation so far.
ASCA and ROSAT observations confirmed the existence of cooler gas in the cores of cooling flow
clusters as expected (e.g. Allen & Fabian 1994; Ikebe et al. 1999;
Ikebe 2001).
The presence of an intrinsic absorber in excess of the galactic absorption, as
it might be expected to arise from the accumulation of cold gas in the cooling flows,
was also inferred from the analysis of the ASCA spectra (e.g. Allen 2000; Allen et al. 2001).
In fact, the fitting of the "multi-phase'' cooling flow model to the observed spectra including
temperature phases that cool below the X-ray emitting temperature regime,
requires the inclusion of excess absorption to satisfactorily reproduce the observed spectra.
It has also been argued, that inclusion of excess absorption leads to values of the mass flow
rate as obtained from imaging data,
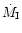 in good agreement with those obtained from
spectral analysis,
in good agreement with those obtained from
spectral analysis,
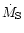 (Allen 2000).
(Allen 2000).
However, without assuming excess absorption, the values of
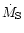 are systematically lower than
are systematically lower than
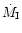 (e.g. Ikebe et al. 1999; Makishima et al. 2001).
Instead of the cooling flow model, a two temperature spectral model can well fit ASCA
spectra of the cooling flow clusters.
The temperatures of the softer component are about half of the hotter component (Ikebe 2001).
The central temperatures of some cD galaxies obtained with the ROSAT PSPC are close to those obtained
from normal elliptical galaxies with the same stellar velocity dispersion (Matsushita 2001).
Since cooling flow clusters always possess central dominant galaxies,
the cool components may reflect the potential structure, rather than cooling gas (Ikebe et al. 1999;
Makishima et al. 2001; Ikebe 2001).
(e.g. Ikebe et al. 1999; Makishima et al. 2001).
Instead of the cooling flow model, a two temperature spectral model can well fit ASCA
spectra of the cooling flow clusters.
The temperatures of the softer component are about half of the hotter component (Ikebe 2001).
The central temperatures of some cD galaxies obtained with the ROSAT PSPC are close to those obtained
from normal elliptical galaxies with the same stellar velocity dispersion (Matsushita 2001).
Since cooling flow clusters always possess central dominant galaxies,
the cool components may reflect the potential structure, rather than cooling gas (Ikebe et al. 1999;
Makishima et al. 2001; Ikebe 2001).
Recently, it was discovered with the RGS instrument onboard XMM-Newton that
there is little X-ray emission from a component with a temperature
below a certain lower cutoff value that differs from object to object (e.g. Tamura et al. 2001; Kaastra et al. 2001).
However, with the RGS one observes only the very central part of the cluster.
M 87 is the cD galaxy of the nearest rich cluster of galaxies, the Virgo Cluster.
It is very luminous in X-rays, and is suggested to have a "cooling flow'' with
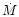 of about 10
of about 10
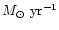 (Stewart et al. 1984; Fabian et al. 1984).
M 87 also hosts a central active galactic nuclei (AGN).
The radio emission is complex and there are two strong lobe structures (e.g. Böhringer et al. 1995).
An enhancement of the X-ray emission around the lobes was discovered with
the EINSTEIN HRI (Feigelson et al. 1987) and ROSAT PSPC (Böhringer et al. 1995).
(Stewart et al. 1984; Fabian et al. 1984).
M 87 also hosts a central active galactic nuclei (AGN).
The radio emission is complex and there are two strong lobe structures (e.g. Böhringer et al. 1995).
An enhancement of the X-ray emission around the lobes was discovered with
the EINSTEIN HRI (Feigelson et al. 1987) and ROSAT PSPC (Böhringer et al. 1995).
In addition to the XMM RGS results mentioned above,
the XMM-Newton observatory offers the possibility to
perform a very detailed spectral and spatial analysis of the cooling flow area.
This is in particular important since the RGS spectrum taken at the very central part of
the intracluster medium (ICM) may be strongly affected by resonance line scattering and
thus the interpretation of the results requires the combined analysis of spectra taken
at different radii from the center.
Early results of the XMM observation of M 87 have already been published (Böhringer et al. 2001;
Belsole et al. 2001).
The projected spectrum is fitted with a single temperature model (Böhringer et al. 2001).
The abundance drop at the central region is interpreted as resonance scattering.
The detailed spectral analysis on the jets and the radio lobe structure is shown in Belsole et al. (2001).
In this paper, we report on the more detailed temperature structure
using a deprojecting analysis,
and apply a cooling flow model to the spectral analysis.
We employ a distance of M 87 of 17 Mpc.
We adopt for the solar iron abundance the "photospheric''
value,
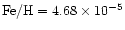 by number (Anders & Grevesse 1989).
Unless otherwise specified, we use 90% confidence error regions.
by number (Anders & Grevesse 1989).
Unless otherwise specified, we use 90% confidence error regions.
M 87 was observed with XMM-Newton on June 19th, 2000.
The thin filter is used for both detectors.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{1597f1.eps}\end{figure}](/articles/aa/full/2002/16/aa1597/Timg22.gif) |
Figure 1:
EPN image of M 87 in the energy range of 0.2 to 10.0 keV.
The effect of the out-of-time events is corrected.
The overlayed contours correspond to the image divided by a azimuthally symmetric
with the same radial profile, smoothed with 20'' Gaussian.
The contour levels are 0.8, 0.9 (white), 1.1, 1.2, 1.3, 1.4, and 1.5 (red).
The regions surrounded by the blue contours are excluded from our spectral analysis as described in Sect. 3.3. |
| Open with DEXTER |
Figure 1 shows the X-ray image of M 87 obtained with the EPN.
The contribution from the out-of-time events is subtracted following the standard analysis package (SAS).
The image divided by an azimuthally symmetric image with the same radial profile
is overlayed in Fig. 1.
The X-ray halo is very smooth and almost spherically symmetric within 20%,
except for the two inner radio lobe regions and the first knot in the jet.
A luminous point source near the south edge of the detector is excised in the further analysis.
We have selected single pattern events.
The background spectrum was calculated for all spectra
by integrating the Lockman-Hole data (observed in the Revolution
70, 71, 73, 81 for the EPN) in the same detector regions.
In the Lockman-Hole field, sources with a luminosity higher than that of
the excluded sources from the M 87 region are excised.
The flare events in the background data were screened in the following way.
We made two count rate histograms of bin width of 200s,
for the corner region in the whole energy band,
and for the whole detector for above 10 keV.
Then, we fitted each histogram with a Gaussian, and selected the time
within 3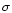 of the mean for both histograms.
The total exposure of the background data is 95 ks.
We have also screened the M 87 data in the same way.
The exposure times of the EPN are 30 ks, 28 ks, 27 ks, 30 ks for the
Chips 1-3, 4-6, 7-9, and 10-12, respectively.
of the mean for both histograms.
The total exposure of the background data is 95 ks.
We have also screened the M 87 data in the same way.
The exposure times of the EPN are 30 ks, 28 ks, 27 ks, 30 ks for the
Chips 1-3, 4-6, 7-9, and 10-12, respectively.
The spectra of each CCD chip
are accumulated within a ring, centered on M 87.
Then, we have subtracted the background and corrected the effect of the vignetting and exposure,
and summed the spectra within annular regions.
The contribution of out-of-time events is subtracted using SAS.
We have selected events with pattern between 0 to 12.
The background spectra are accumulated from the Lockman-Hole data
observed in Revolution 70.
The background flare events are screened in the same way for the EPN.
The exposure times of the background and data are 33 ks and 40 ks, respectively.
Out-of-time events are not subtracted since the contribution is negligible.
Deprojected spectra are calculated by subtracting the contribution from the
outer shell regions for all spectral components, assuming the ICM is spherically symmetric
as done by Nulsen & Böhringer (1995).
Within a each shell, the spectrum per unit volume is assumed to be the same.
In order to calculate the
deprojected spectrum of the outermost (Nth) shell, we subtracted
the emission of the outside of the Nth shell using the brightness
profile derived from the ROSAT All Sky Survey (Böhringer et al. 1994)
assuming that spectral shape outside the Nth shell is the same with that
of the Nth shell.
The deprojected spectrum of the ith shell is then calculated by subtracting
the contributions from i+1th to Nth shell and from outside of the
Nth shell from the annular spectrum of the corresponding radius.
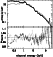 |
Figure 2:
Annular spectra of the EPN (black) and
EMOS (EMOS1+EMOS2; gray) for
r=5.6-8',
fitted with a same single temperature MEKAL model.
Bottom panels show data-to-model ratios. |
| Open with DEXTER |
We employ epn_fs20_sY9_thin.rmf from March 2001, m1_thin1v9q19t5r5_all_15.rsp
from June 2001 for the EPN and the EMOS response files, respectively.
The spectral analysis uses the XSPEC_v11.0.1 package.
Figure 2 shows annular spectra for the radial range
r=5.6-8' of the EPN and the EMOS,
fitted with a same single temperature MEKAL model (Mewe & Gronenschild 1985; Mewe et al. 1986;
Kaastra 1992; Liedahl et al. 1995) but different normalization.
Here, r is the the projected radius.
The EMOS gives about 10% higher normalizations than the EPN.
The response matrices of the EPN and EMOS are mostly consistent.
Below 0.5 keV, EPN data is lower than the EMOS data, and there are
small discrepancies around the tail of the Fe-L lines at 0.8-1.0 keV and around
the instrumental Si edge at 2 keV.
Since the EMOS gives a hydrogen column density,
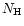 ,
consistent with that of ROSAT (cf. Sect. 6),
we fitted to the EPN and EMOS data in the spectral range of 0.5 to 10 keV and 0.3 to 10 keV, respectively.
For R>8', the energy range between 7.5 and 8.5 keV of the EPN spectra is ignored,
because of strong instrumental emission lines.
,
consistent with that of ROSAT (cf. Sect. 6),
we fitted to the EPN and EMOS data in the spectral range of 0.5 to 10 keV and 0.3 to 10 keV, respectively.
For R>8', the energy range between 7.5 and 8.5 keV of the EPN spectra is ignored,
because of strong instrumental emission lines.
We have fitted the spectra for the region with radius R>0.5'
with a MEKAL model with photoelectric absorption.
Here, R is the three dimensional radius.
For the spectra within 0.5', a power-law component, with the
same absorption,
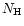 ,
is added.
When fitting the spectra between 0.12' and 0.5', we
fixed the index of the power-law component to the best-fit value obtained
from the spectrum within 0.12' and normalized it using the Point Spread Function.
We grouped several elements
and constrained the elements in each group to have a common abundance.
The first group is C, N, and O, and the second group is Fe and Ni.
The other elements are determined separately.
We also fitted the spectra with a sum of two MEKAL models,
where the two components were constrained to have common abundances.
,
is added.
When fitting the spectra between 0.12' and 0.5', we
fixed the index of the power-law component to the best-fit value obtained
from the spectrum within 0.12' and normalized it using the Point Spread Function.
We grouped several elements
and constrained the elements in each group to have a common abundance.
The first group is C, N, and O, and the second group is Fe and Ni.
The other elements are determined separately.
We also fitted the spectra with a sum of two MEKAL models,
where the two components were constrained to have common abundances.
We have summarized the results in Table 1.
 |
Figure 3:
Deprojected radial profile of the temperature for the EPN (gray crosses) and the
EMOS (gray diamonds), obtained using the single temperature MEKAL model.
We also plotted the same result but excluding the jet and radio lobe
regions (Fig. 1; Sect. 3.3)
for the EPN (black crosses) and the EMOS (black diamonds).
The solid line and the dashed line corresponds to the best-fit power-law relation (excluding the
lobe regions) for the EMOS and EPN, respectively. |
| Open with DEXTER |
Figures 3 and 4 show the radial profile of the temperature obtained by the single temperature model,
and the two temperature model, respectively.
The temperatures derived from the EPN and EMOS are mostly consistent.
Within R<6' and R<13.5' of the EMOS and EPN respectively,
the two temperature model gives significantly lower 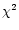 values than the single temperature model.
The temperature of the cooler component is almost constant at
values than the single temperature model.
The temperature of the cooler component is almost constant at 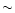 1 keV,
which is the same as the central temperature obtained by the single temperature model fit.
That of the hotter component show a nearly constant value at R<2', whereas
for R>2' it increases gradually.
In Fig. 5, we have plotted the ratio of the emission measure of the cool to the hot component,
assuming the temperature of the former to be 1.0 keV.
The fraction of the cool component is 20% at R=0.5' and drops
below 1% beyond 6' for the EMOS.
Beyond 4', the EPN tends to have 1-2% larger values of the
contribution of the cooler component than the EMOS.
This difference reflects the discrepancy at 0.8-1 keV between the EPN and
the EMOS shown in Fig. 2.
This energy band corresponds to an instrumental low-energy tail of the
Fe-L lines and the effect for the EPN is stronger than that of the EMOS.
The EPN has an additional uncertainty due to the position dependent energy resolution.
Considering that the EMOS spectra of R>6' at 0.7-1.1 keV are well fitted by the
single temperature MEKAL model fit,
the larger amount of 1 keV component observed by EPN may be caused by
the uncertainty of the response matrix of the EPN.
Thus, there is a systematic uncertainty of 1-2% in the
fraction of the 1 keV component.
In summary, within R<6', we detected at least two temperature
components and outside R>6', the upper limit of the second component
is less than a few % even using the EPN.
1 keV,
which is the same as the central temperature obtained by the single temperature model fit.
That of the hotter component show a nearly constant value at R<2', whereas
for R>2' it increases gradually.
In Fig. 5, we have plotted the ratio of the emission measure of the cool to the hot component,
assuming the temperature of the former to be 1.0 keV.
The fraction of the cool component is 20% at R=0.5' and drops
below 1% beyond 6' for the EMOS.
Beyond 4', the EPN tends to have 1-2% larger values of the
contribution of the cooler component than the EMOS.
This difference reflects the discrepancy at 0.8-1 keV between the EPN and
the EMOS shown in Fig. 2.
This energy band corresponds to an instrumental low-energy tail of the
Fe-L lines and the effect for the EPN is stronger than that of the EMOS.
The EPN has an additional uncertainty due to the position dependent energy resolution.
Considering that the EMOS spectra of R>6' at 0.7-1.1 keV are well fitted by the
single temperature MEKAL model fit,
the larger amount of 1 keV component observed by EPN may be caused by
the uncertainty of the response matrix of the EPN.
Thus, there is a systematic uncertainty of 1-2% in the
fraction of the 1 keV component.
In summary, within R<6', we detected at least two temperature
components and outside R>6', the upper limit of the second component
is less than a few % even using the EPN.
ASCA spectra of M 87 are also well fitted with a sum of two Raymond-Smith models (Raymond & Smith 1977).
The temperature of the two components are 3.0 and 1.3 keV, and the
ratio of the emission measure range from
0.2 to 2 within 10' (Matsumoto et al. 1996), although the results of MEKAL model fit with ASCA spectra
are mostly consistent when considering the difference in spatial resolution (Finoguenov & Jones 2000; Shibata 2000).
The contribution of the cooler component plotted in Fig. 5 is
much smaller than that derived from R-S fits.
 |
Figure 4:
The radial temperature profile obtained by fitting the spectra with
a two component MEKAL model.
The meanings of symbols is the same as in Fig. 3.
The solid (EMOS) and dashed line (EPN) corresponds to the best-fit power-law ration of
the single component MEKAL fit, excluding the radio lobe regions. |
| Open with DEXTER |
 |
Figure 5:
The ratio of emission measure of the cool and hot temperature component,
assuming the temperature of the former to be 1.0 keV.
The meanings of symbols is the same as in Fig. 3.
The discrepancies between the EPN and EMOS may be caused by instrumental
problems in the EPN (see text). |
| Open with DEXTER |
In a second step,
in order to study the spatial distribution of the temperature
components in more detail, the EMOS spectra are accumulated within sector regions as
shown in Fig. 6.
The spectral fits used two temperature MEKAL model.
Although the spectra fitted in this section are not the deprojected ones, we
can constrain the spatial distribution of the temperature structure.
Figure 6 shows
EMOS images of the Fe-L (0.6-1.2 keV) and hard (2-10 keV) energy band
with the temperatures obtained for the two components.
It also shows hardness ratio maps for the energy band ratios 2-10 keV/0.6-1.2 keV
and 1.0-1.2 keV/0.8-1.0 keV.
Although the latter is the most sensitive to the 1 keV components
(Fig. 7),
the statistics is not sufficient in the outer regions.
The ratios of the emission measure of the cool to hot components are
overlayed on the hardness ratio maps.
The hard band image is nearly spherically symmetric and
no enhancements of the X-ray emission associated with the radio structure is seen.
The temperature of the hot components is also almost spherically symmetric
within 10%. It tends to be slightly lower in the region around the radio lobes.
In contrast, the spatial distribution of the cool component is far from
symmetry, although its temperature is determined to have an almost
constant value, 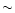 1 keV.
Belsole et al. (2001) found that the softer regions agree well with the
radio structures.
Within R<1', the 1 keV component is detected from all the spectra,
but its contribution ranges from several % to 30%.
In the radial zone R=1-2', where 4 sectors are located outside
the radio lobes, we find a signature of the 1 keV component in two
of these sectors but it is absent in the other two.
Outside 2', we have only detected the 1 keV component
from the two sectors containing the radio lobes.
1 keV.
Belsole et al. (2001) found that the softer regions agree well with the
radio structures.
Within R<1', the 1 keV component is detected from all the spectra,
but its contribution ranges from several % to 30%.
In the radial zone R=1-2', where 4 sectors are located outside
the radio lobes, we find a signature of the 1 keV component in two
of these sectors but it is absent in the other two.
Outside 2', we have only detected the 1 keV component
from the two sectors containing the radio lobes.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{fog6.eps}\end{figure}](/articles/aa/full/2002/16/aa1597/Timg32.gif) |
Figure 6:
Hard (2-10 keV; left panels) and Fe-L blend (0.6-1.2 keV;
middle panels) EMOS images, overlayed by the hard and soft
components temperatures of the two MEKAL component model fit to the projected
sector regions, respectively. The 90% uncertainty of temperatures of
the cool and hot components are typically 0.1 and 0.03 keV, respectively.
The top panels and bottom panels are
 and
and
 regions, respectively.
The right panels show the hardness ratio maps of 2-10 keV/0.6-1.2 keV (top)
and 1.0-1.2 keV/0.8-1.0 keV (bottom), overlayed by the ratio of the
emission measure of the soft to hard components in unit of percent.
White contours corresponds to the regions excluded from spectral
analysis after Sect. 3.3.
regions, respectively.
The right panels show the hardness ratio maps of 2-10 keV/0.6-1.2 keV (top)
and 1.0-1.2 keV/0.8-1.0 keV (bottom), overlayed by the ratio of the
emission measure of the soft to hard components in unit of percent.
White contours corresponds to the regions excluded from spectral
analysis after Sect. 3.3. |
| Open with DEXTER |
For the further analysis,
we have filtered regions with excess emission related to the jet and radio lobes.
We used a spatial filter, excluding those regions where the brightness is larger by 15% than
the azimuthally averaged value (Figs. 1, 6).
The softer regions are not fully excluded within 2',
since it is difficult to filter whole the 1 keV component within 2'
due to its complicated structure and the limited spatial resolution of the XMM telescope.
Assuming spherical symmetry, deprojected spectra are calculated.
We also made deprojected spectra with larger shell width than those in Table 1.
We accumulated spectra within annular regions again and subtracted the contribution
from the outer shells with thin shells width obtained before.
We then fitted the spectra with the single temperature and two temperature MEKAL model,
in the same way as in Sect. 3.1.
In the following sections, we will only use the spectra filtered the
regions with enhance emissions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1597f7.eps}\end{figure}](/articles/aa/full/2002/16/aa1597/Timg34.gif) |
Figure 7:
Deprojected spectra of the EPN (lobes excluded).
The spectrum at R<0.12' is fitted with the double component model, consisting
a MEKAL model and a power-law component and those of
R=0.5-1.0' and
1.0-2.0'are fitted with a two component MEKAL model.
Each component is plotted in dashed lines.
The other spectra are fitted with a MEKAL model.
The bottom panels show residuals of the fit. |
| Open with DEXTER |
The results are summarized in Table 2.
After filtering the regions with excess emissions,
the emission measure of the 1 keV component is reduced (Fig. 5),
and the single temperature model gives reasonable fits at R>2' (Table 2; Fig. 7).
The remaining 1 keV components of the EPN beyond 2' may be due to the
uncertainty of the instrumental low-energy tail of the Fe-L lines.
The radial temperature profile from the single temperature MEKAL model
fit is
approximated as
kT=1.52+0.02-0.02R0.23+0.01-0.01 keV for the EMOS
and
kT=1.51+0.03-0.03R0.21+0.02-0.01 keV for the EPN (Fig. 3),
where R is in units of arcmin.
Within R<2', the two temperature model still gives better fits than
the single temperature model, because of the complex structure of the 1 keV within the region.
When we adopted the hotter component temperature within 2', the radial
temperature profile is approximated as
kT=1.69+0.09-0.08(1+(R/1.6'))0.115+0.011-0.010 keV and
kT=1.68+0.04-0.05(1+(R/1.6'))0.100+0.017-0.016 keV
for the EMOS and EPN, respectively.
There are some residuals at  1.2 keV, which are common to all the deprojected shells.
Any multi-temperature model cannot explain the residual, because the continuum
and the Fe-K line are fitted well with a single MEKAL model.
When the Ni abundance is assumed to be a factor of 2
larger than Fe in solar units, the residuals become smaller
(Finoguenov et al. 2002; Matsushita et al. 2002).
This structure may also be due to a problem with
the Fe-L atomic data, since the APEC code (Smith et al. 2001) does not
need such a high Ni abundance.
1.2 keV, which are common to all the deprojected shells.
Any multi-temperature model cannot explain the residual, because the continuum
and the Fe-K line are fitted well with a single MEKAL model.
When the Ni abundance is assumed to be a factor of 2
larger than Fe in solar units, the residuals become smaller
(Finoguenov et al. 2002; Matsushita et al. 2002).
This structure may also be due to a problem with
the Fe-L atomic data, since the APEC code (Smith et al. 2001) does not
need such a high Ni abundance.
These results indicate that most of the space is occupied by a
component which is nearly spherically symmetrical.
Within relatively small regions associated to the radio structures,
there is an additional component whose temperature is about 1 keV.
In the following sections, we will study the temperature structure in
detail using the filtered spectra.
In spectral fitting the derived temperature and element
abundances are partly dependent on each other.
This is particularly important for the Fe abundance, where the
spectral features of K- and L-shell lines with their temperature
dependent
relative importance are fitted simultaneously. A more detailed report
on the abundances is given in Paper II
(Matsushita et al. 2002) and Finoguenov et al. (2002), however
we briefly discuss here the results on the Fe abundances in relation to
the derived temperature structure.
As derived from the projected spectra (Böhringer et al. 2001; Finoguenov
et al. 2002), the Fe abundance shows a strong negative gradient (Fig. 8).
The two temperature MEKAL fit gives significantly larger abundances than the single temperature MEKAL fit,
although the contributions of the cooler component are small.
For example, at R=0.5-1', including of 10% of the cooler component in units of emission measure
changes Fe abundances by a factor of 2.
The reason for this is the change of the temperature of the hot
component, when the cold component is added, e.g. in the ring taken as
an example, the temperature of the main component increases from 1.47 to
1.72 keV. For a fixed Fe line feature this leads to a higher abundance
required in the fit.
As a result, the central abundance drop that is seen in the single MEKAL fit
is not seen in the result of the two MEKAL fit.
This will be discussed further in Paper II (Matsushita et al. 2002).
 |
Figure 8:
Deprojected Fe profile of the EPN (crosses) and EMOS
(diamonds) fitted with a single temperature MEKAL model (black) and the
two temperature MEKAL model (gray). |
| Open with DEXTER |
There are some problems in the determination of the temperature through X-ray spectral fitting.
The first problem is resonant line scattering,
which should be important in the core of M 87 (Shigeyama 1998; Böhringer et al. 2001).
The second problem is the uncertainties in the Fe-L atomic data (e.g. Masai
1977; Matsushita et al. 2000).
The major uncertainty is the ionization and recombination rates of Fe,
which may change resulting temperature by 20-30%.
(Masai 1997; Matsushita et al. 2000; Arnaud & Rothenflug 1985; Arnaud & Raymond 1992).
In order to avoid these problems, we exclude the Fe-L region below 1.6 keV and fit
the spectra again.
In addition, to compare the temperature obtained to those from the Fe-L lines, we also fitted the data between
0.7 to 1.3 keV with a single temperature MEKAL or Raymond-Smith model (hereafter R-S model).
The R-S model is used for the comparison with the ASCA results.
The result is summarized in Table 3 and Fig. 9.
The derived temperatures using the hard energy band,
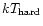 ,
of the EPN and EMOS
are consistent with each other (Table 3).
At R>2', they are consistent to those obtained using the whole energy band and
within
R=0.35-2' they are consistent to the temperatures of the hotter component obtained in
Sects. 3.1 and 3.3.
This indicates that within
R=0.35-2', the 1.7 keV component really
exists and is the dominant phase in the ICM.
,
of the EPN and EMOS
are consistent with each other (Table 3).
At R>2', they are consistent to those obtained using the whole energy band and
within
R=0.35-2' they are consistent to the temperatures of the hotter component obtained in
Sects. 3.1 and 3.3.
This indicates that within
R=0.35-2', the 1.7 keV component really
exists and is the dominant phase in the ICM.
The results for the
Fe-L region using the MEKAL model,
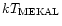 ,
are consistent or slightly higher
than
,
are consistent or slightly higher
than
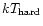 at R>1' because of the residual structure around
at R>1' because of the residual structure around 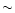 1.2 keV.
Within R<1',
1.2 keV.
Within R<1',
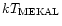 is lower than
is lower than
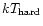 due to the contributions from the 1 keV components.
due to the contributions from the 1 keV components.
The R-S model gives significantly lower temperatures than
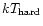 by
by 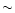 20%.
As a result, when fitted with a R-S model, there remain residuals in the hard energy band.
To explain the residuals, we need an additional R-S component with a high temperature,
20%.
As a result, when fitted with a R-S model, there remain residuals in the hard energy band.
To explain the residuals, we need an additional R-S component with a high temperature,
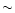 3 keV. This is the reason of the comparable emission measure of
the two temperature R-S components obtained in the ASCA results
(Matsumoto et al. 1996)
3 keV. This is the reason of the comparable emission measure of
the two temperature R-S components obtained in the ASCA results
(Matsumoto et al. 1996)
 |
Figure 9:
Deprojected radial profile of the temperature obtained with EMOS,
by fitting the spectra of 0.7-1.3 keV (black diamonds), above 1.6 keV
(black crosses), 1.8-2.1 keV (gray crosses) and 2.3-2.7 keV (gray
diamonds) with a MEKAL model.
The results obtained by R-S model using 0.7-1.3 keV are also shown (dotted diamonds).
The solid line corresponds to the best fit regression line for the MEKAL
model using the whole energy band of the EMOS. |
| Open with DEXTER |
The ratio of He-like K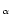 to H-like K
to H-like K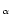 line strengths is sensitive to the gas temperature.
Since the energy resolution of the EMOS is better than that of the EPN, we used only EMOS data here.
We fitted the spectra within the energy range
of 1.8-2.1 keV, and 2.3-2.7 keV with a MEKAL model.
We denote the temperature obtained from the former energy range as
line strengths is sensitive to the gas temperature.
Since the energy resolution of the EMOS is better than that of the EPN, we used only EMOS data here.
We fitted the spectra within the energy range
of 1.8-2.1 keV, and 2.3-2.7 keV with a MEKAL model.
We denote the temperature obtained from the former energy range as
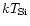 and
from the latter as
and
from the latter as
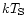 .
The contribution of Fe-L lines at the energy of the He-like
.
The contribution of Fe-L lines at the energy of the He-like 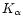 line of Si is considerable,
and the He-like line contains several strong components.
The result is summarized in Table 4.
line of Si is considerable,
and the He-like line contains several strong components.
The result is summarized in Table 4.
Figure 9 also compares the temperatures,
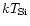 and
and
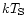 .
These temperatures agree well within 10% with
the deprojected temperature of the corresponding shell, although
.
These temperatures agree well within 10% with
the deprojected temperature of the corresponding shell, although
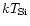 may have some uncertainty, since
around the Si He-K lines, Fe-L and Ni-L lines are also important.
Furthermore, there is an instrumental Si edge in the response matrix and
a strong instrumental Si line, which may cause the discrepancy between
the EPN and EMOS at 2 keV shown in Fig. 2.
may have some uncertainty, since
around the Si He-K lines, Fe-L and Ni-L lines are also important.
Furthermore, there is an instrumental Si edge in the response matrix and
a strong instrumental Si line, which may cause the discrepancy between
the EPN and EMOS at 2 keV shown in Fig. 2.
We also compare the model and data spectra of the Si and S region in Fig. 10.
The two temperature R-S model with the same abundance ratio,
cannot fit the Si and S line ratios, while
a single temperature MEKAL model fits the lines well.
In order to explain the observed line ratios with the two component R-S model,
the harder spectral component should have an abundance of
Si and S a factor of 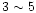 larger than the softer component.
larger than the softer component.
Table 4:
Result of spectral fit of EMOS data, using the energy band around the Si and S lines with a MEKAL model.
| |
1.8-2.1 keV |
2.3-2.8 keV |
| R |
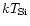 |
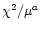 |
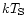 |
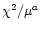 |
| (arcmin) |
(keV) |
|
(keV) |
|
| 0.25-0.50 |
1.28
+0.21-0.16 |
19.2/19 |
1.54
+0.38-0.42 |
18.4/31 |
| 0.50-1.00 |
1.47
+0.13-0.11 |
9.3/19 |
1.65
+0.15-0.15 |
14.6/31 |
| 1.00-2.00 |
1.58
+0.15-0.11 |
17.5/19 |
1.55
+0.13-0.13 |
31.2/31 |
| 2.00-4.00 |
1.85
+0.17-0.14 |
12.8/19 |
1.95
+0.11-0.10 |
20.4/31 |
| 4.00-8.00 |
1.99
+0.23-0.16 |
9.0/19 |
2.21
+0.15-0.12 |
23.0/31 |
| 8.00-11.30 |
2.01
+0.60-0.30 |
12.7/19 |
2.78
+1.26-0.52 |
19.9/31 |
a Degrees of freedom.
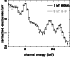 |
Figure 10:
Deprojected EMOS spectrum within
R=1-2.8' in the energy range of Si and S lines,
fitted with a MEKAL model (black line) or
1.4 keV + 3.3 keV R-S model (gray line). |
| Open with DEXTER |
Since the deprojected data have larger uncertainties,
we have also used the S line ratios of the annular spectra.
The strength of the K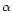 lines are obtained by fitting the annular
spectra within 2.2-2.8 keV with a bremsstrahlung and two Gaussians.
We calculated the projected S line ratio using the deprojected
temperature and density (Sect. 7) profiles and compared with the observed
ones.
We used two temperature relations derived in Sect. 3.3.
One is the best fit relation of the single MEKAL model fit
and the other relation is derived when we adopted the hotter component
temperature of the two temperature MEKAL fit within R<2'.
Outside 1', the observed ratios agree well with the calculated
profiles from single temperature model fit (Fig. 11).
Comparing these results with a profile calculated using a temperature profile shifted by
10% to the data, we can conclude that the temperature profile
inferred from the observed S line ratios is consistent
within several % with the deprojected temperature profile.
Within 1', the observed ratios are close to with those calculated using
the hotter component temperature of the two temperature MEKAL fit, but smaller than those from the single
temperature fit.
This result indicates that S lines are dominated by those of the hotter component
within 2'.
lines are obtained by fitting the annular
spectra within 2.2-2.8 keV with a bremsstrahlung and two Gaussians.
We calculated the projected S line ratio using the deprojected
temperature and density (Sect. 7) profiles and compared with the observed
ones.
We used two temperature relations derived in Sect. 3.3.
One is the best fit relation of the single MEKAL model fit
and the other relation is derived when we adopted the hotter component
temperature of the two temperature MEKAL fit within R<2'.
Outside 1', the observed ratios agree well with the calculated
profiles from single temperature model fit (Fig. 11).
Comparing these results with a profile calculated using a temperature profile shifted by
10% to the data, we can conclude that the temperature profile
inferred from the observed S line ratios is consistent
within several % with the deprojected temperature profile.
Within 1', the observed ratios are close to with those calculated using
the hotter component temperature of the two temperature MEKAL fit, but smaller than those from the single
temperature fit.
This result indicates that S lines are dominated by those of the hotter component
within 2'.
We then compared the strength of the Fe-L and Fe-K lines as follows.
As for the S line ratios, the line brightness profile of Fe-K is
calculated using the deprojected results.
Within 2', we adopted the Fe abundance obtained from the two
temperature model fit.
The Fe abundance from the deprojected data is mainly determined from
the Fe-L lines. For a given temperature, this analysis gives a comparison between the Fe-L and
Fe-K spectral signatures.
Outside 0.5', the observed profile of Fe-K is only 20% larger than the calculated profile
(Fig. 12).
Since the Fe-L atomic data may have uncertainties of 20-30% (e.g. Masai
et al. 1997; Matsushita et al. 2000),
the difference may be due to the uncertainties in the Fe-L atomic data.
If the difference is caused by the temperature structure, it is explained by
only 10% larger temperatures.
 |
Figure 11:
Projected line ratios (EMOS) between K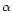 of hydrogen and helium
like S (closed circles). Errors correspond to 68% confidence level.
The solid and dashed lines represent the results using the observed
temperature profile from the single temperature MEKAL model
and that of the hotter component from the two temperature MEKAL model, respectively.
The assumed radial temperature profiles are written in the figure.
We also plotted the profile for temperatures
shifted by 10% (dotted line).
of hydrogen and helium
like S (closed circles). Errors correspond to 68% confidence level.
The solid and dashed lines represent the results using the observed
temperature profile from the single temperature MEKAL model
and that of the hotter component from the two temperature MEKAL model, respectively.
The assumed radial temperature profiles are written in the figure.
We also plotted the profile for temperatures
shifted by 10% (dotted line). |
| Open with DEXTER |
 |
Figure 12:
The projected radial profile of the line brightness of
Fe-K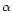 of the EMOS (open circles) and the EPN (crosses).
The solid and dashed lines represent the results using the
temperature profile from the single temperature MEKAL model
and that of the hotter component from the two temperature MEKAL model,
respectively.
The dotted lines corresponds to 10% higher temperatures.
Errors represent the 68% confidence level.
of the EMOS (open circles) and the EPN (crosses).
The solid and dashed lines represent the results using the
temperature profile from the single temperature MEKAL model
and that of the hotter component from the two temperature MEKAL model,
respectively.
The dotted lines corresponds to 10% higher temperatures.
Errors represent the 68% confidence level. |
| Open with DEXTER |
In summary, excluding the regions associated to the radio structures,
at R>1',
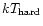 ,
,
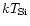 and
and
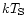 of a
given deprojected spectrum agree within 10%.
of a
given deprojected spectrum agree within 10%.
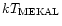 also agrees well with
also agrees well with
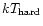 ,
although
,
although
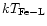 depends on the plasma emission code (e.g. Masai 1997).
These results indicate that at least at R>1', the ICM at a given radius is
dominated by a single temperature component whose temperature is 1.7 keV at R=1' and 2.5 keV at R=15'.
The consistency between Fe-L and Fe-K also supports the single phase
temperature structure.
The difference of these temperatures within 1' reflects that the
contribution of the 1 keV component become significant.
depends on the plasma emission code (e.g. Masai 1997).
These results indicate that at least at R>1', the ICM at a given radius is
dominated by a single temperature component whose temperature is 1.7 keV at R=1' and 2.5 keV at R=15'.
The consistency between Fe-L and Fe-K also supports the single phase
temperature structure.
The difference of these temperatures within 1' reflects that the
contribution of the 1 keV component become significant.
Moreover, the temperature obtained from the MEKAL model seems to be reasonable at least in
the obtained temperature range, when ignoring the residual structure at 1.2 keV.
A new plasma code, APEC (Smith et al. 2001), is now available in
XSPEC.
The residual structures around the Fe-L emission that occurred in the
fits with the MEKAL code
disappeared with the use of the APEC code for Centaurus clusters (Sanders & Fabian 2001).
In this paper, we used the version 1.0 of the APEC in the version 11.0.1 of the XSPEC.
In Fig. 13, we show ratios of a single temperature plasma with
solar abundance calculated with the APEC and MEKAL models, when observed
with the EMOS.
Within the energy resolution of the CCD detectors, the dominant change is not
in the Fe-L lines, but in the K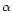 lines.
Using the APEC code, the strength of the K
lines.
Using the APEC code, the strength of the K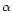 lines of
hydrogen like ions, which are the most fundamental lines,
decrease by several tens of %, and the temperature dependence
also changes.
The 6.7 keV Fe-K lines decrease, by a factor of 2 at 1 keV and 30%
at 4 keV.
The changes of the K
lines of
hydrogen like ions, which are the most fundamental lines,
decrease by several tens of %, and the temperature dependence
also changes.
The 6.7 keV Fe-K lines decrease, by a factor of 2 at 1 keV and 30%
at 4 keV.
The changes of the K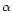 lines of helium like ions of Si, S, Ar and Ca are smaller.
lines of helium like ions of Si, S, Ar and Ca are smaller.
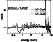 |
Figure 13:
Ratio of theoretical spectra of MEKAL to APEC code for a plasma
temperature of 1 keV (black solid line), 2 keV (gray solid line) and 4
keV (black dashed line) when observed with the EMOS. Abundances are assumed to have solar values. |
| Open with DEXTER |
Figure 14 shows a representative EMOS spectrum of M 87
fitted with the MEKAL and APEC model.
As already shown, the single temperature MEKAL model can well fit the spectra including
the strength of Fe-L, Fe-K and S lines.
The APEC model gives a better fit for the Fe-L/Mg-K structure around 1.2-1.5 keV and
the Fe-L/Si-K structure around 1.8 keV.
However, the single temperature APEC model cannot fit the Fe-L and Fe-K,
as well as the ratio of K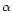 lines of S simultaneously, although the fit to the Fe-L
complex and the continuum is good.
lines of S simultaneously, although the fit to the Fe-L
complex and the continuum is good.
 |
Figure 14:
The deprojected spectrum of EMOS within R=4-8' (crosses) fitted with a
MEKAL model (thin black lines), an APEC model (bold black lines) and a two
temperature APEC model (bold gray lines). The bottom panels shows the
contributions to 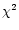 . . |
| Open with DEXTER |
Using the APEC code, we fitted the deprojected spectra of the EMOS
in the same way as described in Sects. 3.3, 5.1 and 5.2.
Figure 15 and Tables 5 summarize the temperatures derived
with the APEC code.
Due to the inconsistency of the S line ratios and the strength of the Fe-K line,
the reduced 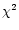 is systematically worse at R>2' compared to those
obtained from the MEKAL model fit.
The temperatures obtained from the whole energy band, the Fe-L complex and
the hard energy band using the APEC code
are consistent with those obtained using the MEKAL model.
The derived Fe abundances, which are mainly determined by Fe-L lines, are also consistent with
those from MEKAL model (Fig. 17).
In contrast, the temperatures from Si and S energy band are 10% larger, due
to the changes of the strength of the K
is systematically worse at R>2' compared to those
obtained from the MEKAL model fit.
The temperatures obtained from the whole energy band, the Fe-L complex and
the hard energy band using the APEC code
are consistent with those obtained using the MEKAL model.
The derived Fe abundances, which are mainly determined by Fe-L lines, are also consistent with
those from MEKAL model (Fig. 17).
In contrast, the temperatures from Si and S energy band are 10% larger, due
to the changes of the strength of the K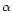 lines of hydrogen like ions.
lines of hydrogen like ions.
The projected radial profile of the S line ratios are also compared with the
calculated profile from the deprojected data (Fig. 16).
Although the deprojected temperatures cannot reproduce the observed line
ratios, the difference is only 10% in temperature.
Therefore, as in the case with MEKAL model,
temperatures derived from whole energy band, the Fe-L, the hard band
Si, and S energy band agree within 10%.
 |
Figure 15:
Deprojected radial profile of the temperature obtained with EMOS,
by fitting the spectra of whole energy band (bold black crosses),
0.7-1.3 keV (black diamonds), above 1.6 keV
(black crosses), 1.8-2.1 keV (gray crosses) and 2.3-2.7 keV (gray
diamonds) with a APEC model.
The solid line corresponds to the best fit regression line for the MEKAL
model using the whole energy band of the EMOS. |
| Open with DEXTER |
 |
Figure 16:
Projected line ratios (EMOS) between K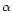 of hydrogen and helium
like S (closed circles). Errors correspond to 68% confidence level.
Solid line and dashed lines represent the results
from deprojected temperature profiles using APEC model,
of hydrogen and helium
like S (closed circles). Errors correspond to 68% confidence level.
Solid line and dashed lines represent the results
from deprojected temperature profiles using APEC model,
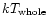 and
and
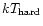 ,
respectively.
We also plotted the profile for temperatures
shifted by 10% (dotted line). ,
respectively.
We also plotted the profile for temperatures
shifted by 10% (dotted line). |
| Open with DEXTER |
 |
Figure 17:
Deprojected profile of Fe abundances obtained from the whole energy band
(diamonds) and above 2 keV (crosses), using the single temperature
MEKAL model (black), APEC model (gray) and the two temperature
MEKAL model (dotted). |
| Open with DEXTER |
However, there is a discrepancy between the Fe-L and Fe-K strength.
Figure 17 also shows the Fe abundances obtained from the deprojected spectra above 2 keV, fitted with a single temperature MEKAL and APEC model.
We denote the derived Fe abundances from >2 keV, as Fe-K
 and Fe-K
and Fe-K
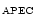 ,
and those from the whole energy band as Fe-L
,
and those from the whole energy band as Fe-L
 and
Fe-L
and
Fe-L
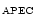 for the MEKAL and APEC codes, respectively.
Outside R>1', Fe-K
for the MEKAL and APEC codes, respectively.
Outside R>1', Fe-K
 ,
Fe-L
,
Fe-L
 ,
and Fe-L
,
and Fe-L
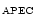 agree
well each other. Within R<1', Fe-K
agree
well each other. Within R<1', Fe-K
 are consistent
with Fe abundances obtained from the two temperature MEKAL model.
However, Fe-K
are consistent
with Fe abundances obtained from the two temperature MEKAL model.
However, Fe-K
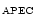 are systematically larger by
are systematically larger by 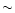 60%.
The strength of the projected Fe-K lines are almost a factor of 2 larger than the
values calculated from the deprojected results (Fig. 18).
In order to obtain the observed Fe-K line profile, the temperature should be
shifted by 30% compared to the deprojected temperatures.
60%.
The strength of the projected Fe-K lines are almost a factor of 2 larger than the
values calculated from the deprojected results (Fig. 18).
In order to obtain the observed Fe-K line profile, the temperature should be
shifted by 30% compared to the deprojected temperatures.
Adding another temperature component, the discrepancy of Fe-K lines
become smaller (Fig. 14).
However, the 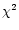 is still worse than the single temperature MEKAL
model, and the radio of S lines cannot be well fitted.
is still worse than the single temperature MEKAL
model, and the radio of S lines cannot be well fitted.
In summary, the changes in the version 1.0 of the APEC code for the
Ly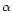 lines (H-like ions) are giving a much less consistent picture
than the results from the MEKAL code.
Therefore, we are not sure that the new atomic data included in
APEC constitute an improvement.
lines (H-like ions) are giving a much less consistent picture
than the results from the MEKAL code.
Therefore, we are not sure that the new atomic data included in
APEC constitute an improvement.
 |
Figure 18:
Projected line brightness profile of Fe-K of the EMOS (open circles) and
EPN (crosses). Errors correspond to 68% confidence level.
Solid line and dashed lines represent the results
using APEC model and deprojected temperature profile,
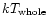 and
and
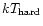 ,
respectively.
We also plotted the profile for temperatures
shifted by 30% (dotted line). ,
respectively.
We also plotted the profile for temperatures
shifted by 30% (dotted line). |
| Open with DEXTER |
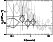 |
Figure 19:
The radial profile of hydrogen column density of EPN (crosses) and EMOS (diamonds)
using the single temperature (gray) and the
two temperature (black) MEKAL model fit.
Holizontal line corresponds to the column density obtained from Nulsen & Böhringer (1995). |
| Open with DEXTER |
The hydrogen column density, 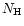 ,
derived from the single MEKAL fit
is almost constant at R>2' (Table 2; Fig. 19).
As summarized in Tables 2 and 5, the
,
derived from the single MEKAL fit
is almost constant at R>2' (Table 2; Fig. 19).
As summarized in Tables 2 and 5, the 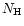 derived from the single APEC model is consistent with
those from the single MEKAL model.
The average value at R>2' is
derived from the single APEC model is consistent with
those from the single MEKAL model.
The average value at R>2' is
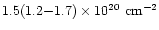 and
and
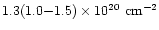 for the EPN and EMOS, respectively.
Within 2 arcmin, the two phase MEKAL model fit gives a consistent value with those at R>2',
although the single MEKAL model fit gives a higher
for the EPN and EMOS, respectively.
Within 2 arcmin, the two phase MEKAL model fit gives a consistent value with those at R>2',
although the single MEKAL model fit gives a higher 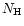 value by
several
value by
several
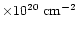 .
The response matrices of the EPN of September 2000 and November 2000 give
systematically different values by
.
The response matrices of the EPN of September 2000 and November 2000 give
systematically different values by
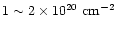 .
Therefore, there may be a systematic uncertainty of a few
.
Therefore, there may be a systematic uncertainty of a few
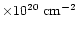 .
.
The value determined by the ROSAT PSPC observation is
about
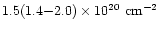 (Nulsen & Böhringer 1995; Böhringer 1999).
The observed HI column density of our Galaxy by Stark et al. (1992) is
(Nulsen & Böhringer 1995; Böhringer 1999).
The observed HI column density of our Galaxy by Stark et al. (1992) is
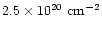 ,
which is slightly reduced to
,
which is slightly reduced to
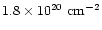 ,
by Lieu et al. (1996).
The observed
,
by Lieu et al. (1996).
The observed 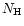 is consistent with the value obtained by ROSAT and also the Galactic column density.
In addition, the power-law component from the central AGN shows no significant excess absorption.
Thus, the intrinsic absorption should be negligible in the M 87 system.
is consistent with the value obtained by ROSAT and also the Galactic column density.
In addition, the power-law component from the central AGN shows no significant excess absorption.
Thus, the intrinsic absorption should be negligible in the M 87 system.
We have assumed 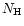 to be the average value of those obtained at R>2',
since the higher
to be the average value of those obtained at R>2',
since the higher 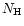 at R<2' from the single MEKAL model may be artificial.
We have fixed the C, N, O abundance to
0.51 (1+(R/0.76')2)-0.09, which is
the best fit
at R<2' from the single MEKAL model may be artificial.
We have fixed the C, N, O abundance to
0.51 (1+(R/0.76')2)-0.09, which is
the best fit 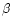 -model of the abundance profile of these elements.
Since the cooler component is distributed around the radio structures, and
the hotter component is almost spherically symmetric, the latter should dominate.
Thus, within 0.35 to 1.4', we fitted the EPN spectra with a two
component MEKAL model and
adopted the electron density of the hotter component.
The electron density (
-model of the abundance profile of these elements.
Since the cooler component is distributed around the radio structures, and
the hotter component is almost spherically symmetric, the latter should dominate.
Thus, within 0.35 to 1.4', we fitted the EPN spectra with a two
component MEKAL model and
adopted the electron density of the hotter component.
The electron density (
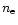 ), profile derived is shown in Table 6 and Fig. 20.
These results are mostly consistent with those obtained by Nulsen & Böhringer (1995),
when considering the difference in the assumption of the abundance.
), profile derived is shown in Table 6 and Fig. 20.
These results are mostly consistent with those obtained by Nulsen & Böhringer (1995),
when considering the difference in the assumption of the abundance.
We fitted the
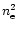 profile with a sum of two
profile with a sum of two 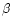 models,
a compact and an extended one, both centered on M 87.
We fixed the
models,
a compact and an extended one, both centered on M 87.
We fixed the 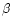 of the extended component to be 0.47.
which is the value obtained by ROSAT All Sky Survey (Böhringer et al. 1994).
The obtained best-fit parameters are shown in Table 7.
The two
of the extended component to be 0.47.
which is the value obtained by ROSAT All Sky Survey (Böhringer et al. 1994).
The obtained best-fit parameters are shown in Table 7.
The two 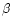 components have distinct parameters,
and cross over at
components have distinct parameters,
and cross over at  ,
or
,
or 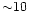 kpc.
kpc.
 |
Figure 20:
Electron density profile.
The solid line is the best-fit double-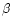 model.
model. |
| Open with DEXTER |
The total mass M(R) within a 3-dimensional radius R, assuming
hydrostatic equilibrium and spherical symmetry, is given by
(e.g. Sarazin 1988),
where 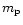 is the proton mass, k is the Boltzmann constant,
G is the constant of gravity, and
is the proton mass, k is the Boltzmann constant,
G is the constant of gravity, and
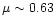 is the mean
particle mass in units of
is the mean
particle mass in units of 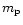 .
.
Based on the deprojected temperature and density profile obtained in Sects. 3.3 and 5,
we have calculated the gravitational mass of the M 87 system, together with the gas mass profile
using the power-law relation in Fig. 3, and the double-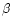 relation approximated as in Table 7.
The upper and lower limit of the mass profile is calculated considering
the uncertainty of the density gradient
and the temperature. The temperature gradient is assumed to be smooth and expressed as the power-law relation.
The upper and lower limit of the density gradient of the ith shell is obtained
from the ratio of the value within i+1th shell to that within i-1th shell.
As plotted in Fig. 21,
our result is mostly consistent with the dynamical mass profiles obtained by stars (Kronawitter
et al. 2000)
and globular clusters (Cohen & Ryzhov 1997).
relation approximated as in Table 7.
The upper and lower limit of the mass profile is calculated considering
the uncertainty of the density gradient
and the temperature. The temperature gradient is assumed to be smooth and expressed as the power-law relation.
The upper and lower limit of the density gradient of the ith shell is obtained
from the ratio of the value within i+1th shell to that within i-1th shell.
As plotted in Fig. 21,
our result is mostly consistent with the dynamical mass profiles obtained by stars (Kronawitter
et al. 2000)
and globular clusters (Cohen & Ryzhov 1997).
The calculated mass-to-blue light ratio (hereafter
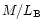 )
of the stellar population ranges between 6 and 10 (e.g. Kronawitter et al. 2000).
Assuming a constant stellar M/LB of 8,
in Fig. 21, we also plotted the stellar mass profile, calculated from the
luminosity profile in Giraud (1999).
Within nearly 0.5
)
of the stellar population ranges between 6 and 10 (e.g. Kronawitter et al. 2000).
Assuming a constant stellar M/LB of 8,
in Fig. 21, we also plotted the stellar mass profile, calculated from the
luminosity profile in Giraud (1999).
Within nearly 0.5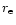 ,
the stellar velocity dispersion profile indicates that the
dynamical M/LB is
,
the stellar velocity dispersion profile indicates that the
dynamical M/LB is 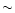 11 (e.g. Kronawitter et al. 2000).
Here,
11 (e.g. Kronawitter et al. 2000).
Here, 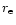 is the effective radius of M 87, which is 7.8 kpc (de Vaucouleurs et al. 1991).
Our mass profile indicates that at
is the effective radius of M 87, which is 7.8 kpc (de Vaucouleurs et al. 1991).
Our mass profile indicates that at
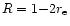 ,
the M/LB is about 17 and beyond this radius,
the slope of the mass profile increases and M/LB reaches
,
the M/LB is about 17 and beyond this radius,
the slope of the mass profile increases and M/LB reaches 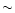 200 at
200 at
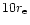 .
.
 |
Figure 21:
(Upper panel) integrated mass profiles of the total gravitating matter (dashed lines for upper and lower limit
and solid line for the double 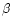 model fit),
the X-ray emitting plasma (dot-dashed line), and the stellar component (dotted line)
assuming stellar M/LB to be 8, in the M 87 system.
The dynamical mass obtained by stars (cross; Kronawitter et al. 2000) and globular clusters
(open circles; Cohen & Ryzhov 1997) are also shown.
(Lower panel) Total mass-to-light ratio (M/LB) of the system.
The meanings of symbols and lines are the same as in the upper panel.
model fit),
the X-ray emitting plasma (dot-dashed line), and the stellar component (dotted line)
assuming stellar M/LB to be 8, in the M 87 system.
The dynamical mass obtained by stars (cross; Kronawitter et al. 2000) and globular clusters
(open circles; Cohen & Ryzhov 1997) are also shown.
(Lower panel) Total mass-to-light ratio (M/LB) of the system.
The meanings of symbols and lines are the same as in the upper panel. |
| Open with DEXTER |
The steady state cooling flow structure in a spherically symmetric cluster is
obtained by,
(e.g. Sarazin 1988),
where
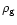 ,
v, and P are, respectively, the gas density, velocity, and pressure,
and
,
v, and P are, respectively, the gas density, velocity, and pressure,
and 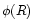 is the gravitational potential,
is the gravitational potential,  is the emissivity.
is the emissivity.
Even within the optical radii of elliptical galaxies,
the X-ray luminosity is a factor of 20 larger
than heating by stellar mass loss (Matsushita 2001). Therefore, we can neglect this component
as a sufficient heat source to balance cooling.
The cooling time is lower than the Hubble time within 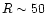 kpc (Fig. 22).
As shown in Fig. 22, the
kpc (Fig. 22).
As shown in Fig. 22, the
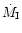 obtained is roughly proportional to the radius.
At
obtained is roughly proportional to the radius.
At 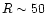 kpc,
kpc,
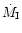 is 10
is 10 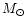 ,
which is consistent to the classical value obtained by
Stewart et al. (1984) from the Einstein observation.
,
which is consistent to the classical value obtained by
Stewart et al. (1984) from the Einstein observation.
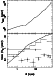 |
Figure 22:
Cooling time (upper panel) and
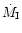 profile (lower panel).
Data corresponds to
profile (lower panel).
Data corresponds to
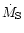 ,
assuming cooling to 0 keV.
The dotted line is the differential of the ,
assuming cooling to 0 keV.
The dotted line is the differential of the
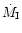 ,
the mass deposition rate in each shell. ,
the mass deposition rate in each shell. |
| Open with DEXTER |
With the RGS we can observe only the very central core of cooling flow clusters.
In contrast, using the EPN, we can accumulate spectra within the entire cooling flow region.
At R=4', the derived cooling time is only a few Gyr and
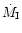 is
is
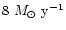 ,
respectively.
The net effect of resonance scattering is negligible for the radiative output in this
integrated circular region.
Without any heating, the gas should cool down to 0 keV, emitting X-rays at intermediate temperatures.
Therefore, the spectral cooling rate,
,
respectively.
The net effect of resonance scattering is negligible for the radiative output in this
integrated circular region.
Without any heating, the gas should cool down to 0 keV, emitting X-rays at intermediate temperatures.
Therefore, the spectral cooling rate,
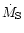 ,
within the radius should be
,
within the radius should be
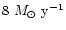 .
.
We fitted the deprojected spectra within R<4' with a cooling flow
model using the MEKAL code modified by photoelectric absorption.
As in other cooling flow clusters observed by RGS,
in order to fit the spectra, we still need a cut-off temperature, lowT, which is found
to be 1.4 keV (Table 8).
Figure 23 shows the EPN spectrum within R<4', fitted with the cooling flow model.
We also plotted in the figure,
another cooling flow model with lowT=0.1 keV, fitted only to the data in the spectral range above 1.2 keV.
The difference in the continuum level between 0.2 and 0.5 keV
is due to the instrumental low-energy tail of Fe-L and O-K lines.
The component cooling radiatively to 0 keV should emit
strong Fe-L lines between 0.6 to 1.0 keV, which are not seen in the spectrum.
When adding an isothermal MEKAL component, we can fit the
spectra with a cooling flow component with lowT=0.1 keV.
However,
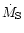 is only
is only
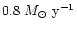 ,
which is a factor of 10 smaller than
,
which is a factor of 10 smaller than
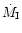 at the same radius.
at the same radius.
 |
Figure 23:
Deprojected spectra within R<4' fitted with a cooling flow model
with a cut-off temperature, lowT=1.44 keV (solid line, a).
The bold dotted line (b) shows the model with cooling to 0.1 keV.
The thin dashed lines of the upper panel, (c1) and (c2), corresponds to the model with
a model with 10 times higher metallicity and a model with low metal
abundance, respectively. The spectral cooling flow rates are
summarized in the panel. The sum of (c1) and (c2) is also plotted.
The dotted lines of the lower panel, (d1) and (d2) are components of another bimodal
metal abundance mdoel, and the solid lines of (e1) and (e2) corresponds
to the model with excess absorption applied for the metal rich components. |
| Open with DEXTER |
Fabian et al. (2001) made a proposal to solve the cooling flow
problem by a scenario in which metals in the ICM are not uniformly distributed.
In this suggestion, a metal poor part of the gas cools without emitting lines and
a metal rich part cools rapidly. In this way, the total strength of Fe-L line emission should be reduced.
A bimodal abundance model, with 0.01 solar abundances and 10 times higher abundances than the
single abundance model and mass deposition rates of 7.3 and
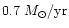 ,
respectively, is shown in Fig. 23.
It is very different from the observed spectrum in the Fe-L structure and
strength of K-
,
respectively, is shown in Fig. 23.
It is very different from the observed spectrum in the Fe-L structure and
strength of K-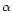 lines (Fig. 23),
since it reduces not only Fe-L lines but also K lines of Si, S, Ar,
Ca, and Fe (see also Böhringer et al. 2002).
In order to obtain the observed strength of K lines with these mass
deposition rates, the abundances in the high metallicity component should be
lines (Fig. 23),
since it reduces not only Fe-L lines but also K lines of Si, S, Ar,
Ca, and Fe (see also Böhringer et al. 2002).
In order to obtain the observed strength of K lines with these mass
deposition rates, the abundances in the high metallicity component should be 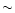 100 solar.
Therefore, we have tried another bimodal metal abundance model,
where the mass deposition rates of the two components are allowed to be free parameters, and
fitted the spectra above 1 keV.
Figure 23 also shows the best fit model, extrapolated to lower energies.
With the mass deposition rates of 4 and
100 solar.
Therefore, we have tried another bimodal metal abundance model,
where the mass deposition rates of the two components are allowed to be free parameters, and
fitted the spectra above 1 keV.
Figure 23 also shows the best fit model, extrapolated to lower energies.
With the mass deposition rates of 4 and
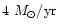 ,
for the metal
rich and metal poor components respectively, the spectra above
,
for the metal
rich and metal poor components respectively, the spectra above 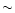 1 keV can be fitted.
Because of the dependence of the cooling function on metallicity,
the Fe-L strength below 0.9 keV is slightly reduced compared to that
of the single abundance model.
However, the model shows very strong Fe-L lines below 0.9 keV.
We then added absorption for the metal rich components and then allowed
the abundances of the metal rich component to vary.
Although including a column density of
1 keV can be fitted.
Because of the dependence of the cooling function on metallicity,
the Fe-L strength below 0.9 keV is slightly reduced compared to that
of the single abundance model.
However, the model shows very strong Fe-L lines below 0.9 keV.
We then added absorption for the metal rich components and then allowed
the abundances of the metal rich component to vary.
Although including a column density of
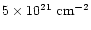 dramatically improved the fit, the fit is much worse compared to the
fit with the cut-off temperature.
In addition, such high absorption heavily reduces the spectra around
the 0.67 keV O line.
Increasing the O abundance of the metal rich components does not solve the problem, since it reduces
the strength of Fe-L lines due to the difference in the cooling function.
Therefore, there must exist an unabsorbed component
whose O abundance is not so peculiar.
For intrinsic absorption, more details are discussed also on
Böhringer et al. (2002).
dramatically improved the fit, the fit is much worse compared to the
fit with the cut-off temperature.
In addition, such high absorption heavily reduces the spectra around
the 0.67 keV O line.
Increasing the O abundance of the metal rich components does not solve the problem, since it reduces
the strength of Fe-L lines due to the difference in the cooling function.
Therefore, there must exist an unabsorbed component
whose O abundance is not so peculiar.
For intrinsic absorption, more details are discussed also on
Böhringer et al. (2002).
In summary, any multi-abundance model cannot explain the observed Fe-L profiles.
In order to explain it, we need a sharp cut off in the temperature distribution.
The observed radial profile of
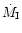 is not constant, but roughly proportional to R.
The differential of
is not constant, but roughly proportional to R.
The differential of
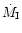 between a shell and next shell
implies that we should observe a cooling flow component in the spectrum of each radial shell.
We thus fitted deprojected spectra with a
cooling flow model with lowT=0.1 keV, and an isothermal MEKAL model.
The result is summarized in Table 8 and Fig. 22.
Within R<1', the fit has improved from the single temperature fit.
However, the
between a shell and next shell
implies that we should observe a cooling flow component in the spectrum of each radial shell.
We thus fitted deprojected spectra with a
cooling flow model with lowT=0.1 keV, and an isothermal MEKAL model.
The result is summarized in Table 8 and Fig. 22.
Within R<1', the fit has improved from the single temperature fit.
However, the
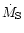 values, are a factor of 10 to 20 lower than
the differential of
values, are a factor of 10 to 20 lower than
the differential of
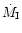 .
Only for the innermost shell,
.
Only for the innermost shell,
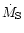 and
and
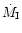 are consistent with each other.
are consistent with each other.
The deprojected spectra of M 87 strongly indicate that excluding the
region associated to the radio structures, the ICM is single phase;
at a given radius, the ICM is dominated by one temperature component.
We cannot detect any multi-phase cooling flow component as seen by Allen et al. (2001).
The ICM is also not characterized by a two-phase structure as suggested by ASCA observations of the Centaurus cluster
(Fukazawa et al. 1994; Ikebe et al. 1999), and M 87 (Matsumoto et al. 1996).
When excluding the regions with the radio structures, the
ICM is nearly spherically symmetric.
Using the MEKAL model,
a single phase model can fit the deprojected spectra well at R>2'.
The temperature profile has a positive temperature gradient,  1.7 keV at R=1'and
1.7 keV at R=1'and  2.5 keV at R=15'.
The consistency of the temperatures obtained by the continuum, Fe-L
region, Si, and S line ratios, Fe-L to Fe-K ratio
indicate that the ICM is dominated by a single temperature component.
The regions associated to the radio structures have an additional
temperature components of 1 keV.
At R<2', since it is
difficult to filter the complicated radio structures within 2' with the XMM
spatial resolution, we observe the major ICM components with the
temperature of 1.7 keV, and small amount of the 1 keV components.
The spatial distribution of the latter component indicates that
the cooler component also relates to the region corresponding to the radio
lobes (see also Belsole et al. 2001).
2.5 keV at R=15'.
The consistency of the temperatures obtained by the continuum, Fe-L
region, Si, and S line ratios, Fe-L to Fe-K ratio
indicate that the ICM is dominated by a single temperature component.
The regions associated to the radio structures have an additional
temperature components of 1 keV.
At R<2', since it is
difficult to filter the complicated radio structures within 2' with the XMM
spatial resolution, we observe the major ICM components with the
temperature of 1.7 keV, and small amount of the 1 keV components.
The spatial distribution of the latter component indicates that
the cooler component also relates to the region corresponding to the radio
lobes (see also Belsole et al. 2001).
The R-S model gives a temperature lower by 20% than MEKAL model.
In order to fit the spectra, the R-S model requires an additional high temperature component.
However, the two temperature R-S model cannot explain the observed Si and S line ratios.
Except for the Fe-K line strength, the APEC temperatures are consistent with the
MEKAL models within 10-15%.
Due to changes of the strength of K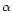 lines,
the single phase APEC model cannot explain the strength of Fe-K lines,
although it can fit the Fe-L and continuum simultaneously. The S line
ratio is discrepancy by a factor of 1.5, but it introduces only a 10% difference
in the temperature structure.
lines,
the single phase APEC model cannot explain the strength of Fe-K lines,
although it can fit the Fe-L and continuum simultaneously. The S line
ratio is discrepancy by a factor of 1.5, but it introduces only a 10% difference
in the temperature structure.
Resonant scattering of line emission should be important in dense core of galaxy clusters.
(Gil'fanov et al. 1987; Tawara et al. 1997).
Shigeyama (1998) calculated the effect on M 87 system, and found that surface brightness profile
considerably decreased within 1-2' because many Fe-L lines are optically thick.
In M 87, Böhringer et al. (2001) suggested that the resonant scattering may
explain the observed sharp abundance drop at center.
This effect may also change the spectra and the Fe-L line profile in the central region.
Part of the 1 keV component may be due to this effect.
Therefore, in order to study the temperature structure within 1-2' arcmin exactly, we have to
consider effect of the resonance scattering.
However, since the temperature obtained from the continuum spectra is close to that
from the whole energy band, the main temperature component should be
similar to the obtained values.
At least using the MEKAL model, the strength of the Fe-L and Fe-K are
consistent with each other, which have a different dependence on the
resonance line scattering.
In addition, most of the 1 keV component should be related to the radio
activity which has a complicated spatial distribution (Belsole et al. 2001).
Most of the resonantly scattered light will be reemitted at slightly larger
projected radii. Therefore integrating over the region, R<4' will reduce the net effect
of scattering and the spectra will hardly be disturbed.
Matsushita (2001) found that normal elliptical galaxies
have
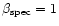 .
The central stellar velocity dispersion of M 87 is 350 km s-1 (Whitmore et al. 1985).
The assumption of
.
The central stellar velocity dispersion of M 87 is 350 km s-1 (Whitmore et al. 1985).
The assumption of
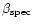 =1 implies a temperature of 0.8 keV, which agrees
well with the observed central ICM temperature of M 87.
The ICM temperature at 10-15' of 2.5 keV also agrees with the
velocity dispersion of early-type galaxies of the Virgo cluster, which is 570 km s-1 (Binggeli & Tammann 1987).
The observed constancy in the temperature suggests that the central cool
temperature mainly reflects the galaxy potential,
even though some part of the cool component may be produced by a small cooling flow in the central region.
=1 implies a temperature of 0.8 keV, which agrees
well with the observed central ICM temperature of M 87.
The ICM temperature at 10-15' of 2.5 keV also agrees with the
velocity dispersion of early-type galaxies of the Virgo cluster, which is 570 km s-1 (Binggeli & Tammann 1987).
The observed constancy in the temperature suggests that the central cool
temperature mainly reflects the galaxy potential,
even though some part of the cool component may be produced by a small cooling flow in the central region.
The hydrogen column density is almost flat within the field of view.
In addition, the spectrum of the central AGN does not show any absorption feature.
Therefore, intrinsic absorption should be negligible in the M 87 system.
If there is excess 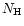 of the order of
of the order of
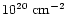 and the absorbing matter is uniformly distributed
within 10 kpc and 50 kpc, the mass of the absorbing matters is
and the absorbing matter is uniformly distributed
within 10 kpc and 50 kpc, the mass of the absorbing matters is
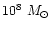 and
and
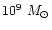 ,
respectively,
which is much smaller than the cooling flow mass deposition rate accumulated over a Hubble time.
,
respectively,
which is much smaller than the cooling flow mass deposition rate accumulated over a Hubble time.
We have determined the gravitational mass profile of the M 87 system, directly from the
observed density and temperature profiles.
At
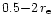 ,
M/LB of the system is constant at
,
M/LB of the system is constant at  17.
Beyond this radius, it starts to increase to
17.
Beyond this radius, it starts to increase to  200 at 80 kpc.
200 at 80 kpc.
This structure is essentially the same feature as seen in the Fornax
cluster (Ikebe et al. 1996), the Centaurus cluster (Ikebe et al. 1999)
and NGC 4636 (Matsushita et al. 1998).
Figure 24 summarizes the gravitational mass profiles of the 3 cD galaxies and NGC 4636.
These galaxies have similar hierarchical mass profiles;
the gravitational mass gradually increases up to several  ,
where the
gravitational to stellar mass ratio is common among galaxies.
Then, M/L start to increase steeply.
,
where the
gravitational to stellar mass ratio is common among galaxies.
Then, M/L start to increase steeply.
Before the total to stellar mass ratio increases steeply,
the total M/LB is 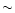 17 at
17 at
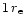 ,
and
,
and 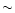 30 even at
30 even at
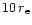 .
This feature should reflect the potential of elliptical galaxies.
The M/LB of the central core of these galaxies obtained by
the dynamics and the same ratio obtained by the stellar population
synthesis models are consistent with each other giving a typical value
of 6-10 (e.g. Kronawitter et al. 2000; Gerhard et al. 2001).
Considering the observed metallicity gradient of stars, the stellar M/LB should be slightly
smaller in the outer regions (e.g. Kodama & Arimoto 1997). Our result suggests that
the dark mass distribution of elliptical galaxies is slightly more extended than those of stars.
It is thought that elliptical galaxies have a 10 times larger amount of dark mass
than stellar mass (e.g. Ciotti et al. 1991).
However, the galaxies themselves may not contain such large amount of mass.
This result should be important for the study of the origin of the dark matter content in elliptical galaxies
and also for the study of the formation and evolution of these galaxies.
.
This feature should reflect the potential of elliptical galaxies.
The M/LB of the central core of these galaxies obtained by
the dynamics and the same ratio obtained by the stellar population
synthesis models are consistent with each other giving a typical value
of 6-10 (e.g. Kronawitter et al. 2000; Gerhard et al. 2001).
Considering the observed metallicity gradient of stars, the stellar M/LB should be slightly
smaller in the outer regions (e.g. Kodama & Arimoto 1997). Our result suggests that
the dark mass distribution of elliptical galaxies is slightly more extended than those of stars.
It is thought that elliptical galaxies have a 10 times larger amount of dark mass
than stellar mass (e.g. Ciotti et al. 1991).
However, the galaxies themselves may not contain such large amount of mass.
This result should be important for the study of the origin of the dark matter content in elliptical galaxies
and also for the study of the formation and evolution of these galaxies.
The scatter of the X-ray to blue luminosity ratio of early-type galaxies has long been a problem
(e.g. Canizares et al. 1987).
Matsushita (2001) found that 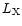 of most of the early-type galaxies
is well explained by a kinematical heating of the gas supplied by stellar mass loss
(
of most of the early-type galaxies
is well explained by a kinematical heating of the gas supplied by stellar mass loss
(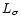 ).
All of the galaxies which have much larger
).
All of the galaxies which have much larger 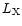 than
than 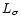 have very extended X-ray emission.
Figure 24 shows that the galaxies with a larger
have very extended X-ray emission.
Figure 24 shows that the galaxies with a larger
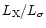 have smaller radii of the starting point of the strong increase of M/L, when scaled
have smaller radii of the starting point of the strong increase of M/L, when scaled 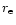 .
In other words, the X-ray luminosity of cD galaxies may be determined in relation to their potential structure,
as indicated by Matsushita (2001).
.
In other words, the X-ray luminosity of cD galaxies may be determined in relation to their potential structure,
as indicated by Matsushita (2001).
 |
Figure 24:
Integrated mass profiles of the total gravitating matter scaled by
LB, and the stellar component (solid line) in the M 87 (solid line;
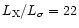 ), the
Centaurus cluster (dotted line; Ikebe et al. 1999; ), the
Centaurus cluster (dotted line; Ikebe et al. 1999;
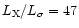 ), NGC 1399 (dashed line; Ikebe et al. 1996; ), NGC 1399 (dashed line; Ikebe et al. 1996;
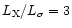 ),
and NGC 4636 (gray line; Matsushita et al. 1998; ),
and NGC 4636 (gray line; Matsushita et al. 1998;
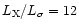 ). ).
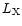 and
and
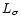 means the ISM luminosity within 4
means the ISM luminosity within 4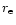 and
kinematical energy input from stellar mass loss (Matsushita 2001).
and
kinematical energy input from stellar mass loss (Matsushita 2001). |
| Open with DEXTER |
The standard cooling flow model indicates that the ICM is multi-temperature on small scales,
since it is thought that mass is deposited within the whole cooling flow region.
The cooling matter should emit strong Fe-L lines below 0.9 keV.
We cannot detect a significant spectral cooling flow component from the whole field of view of the detector
and the ICM at any given radius is dominated by a single temperature component.
The upper limit on
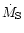 is an order of magnitude smaller than
is an order of magnitude smaller than
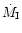 .
A bimodal metal abundance distribution model cannot explain the observed Fe-L profile.
.
A bimodal metal abundance distribution model cannot explain the observed Fe-L profile.
The resonance scattering may reduce the strength of some resonance lines.
However, all the Fe-L lines below 0.9 keV, which includes both resonance lines and non-resonance lines,
are suppressed compared with the expected value for a cooling flow.
In addition, the spectral cooling flow component is also small where the resonance scattering
is not effective.
Therefore, the resonant scattering can not be responsible for the
suppresion of the Fe-L lines below 0.9 keV.
At
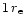 (1.6') of M 87,
(1.6') of M 87,
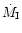 is
is
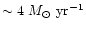 .
In contrast, the upper limit on
.
In contrast, the upper limit on
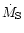 is
is
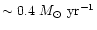 .
This value is close to the stellar mass loss rate within
.
This value is close to the stellar mass loss rate within
 ,
which
is
,
which
is
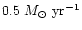 .
At this radius,
.
At this radius,
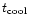 is
is
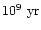 and the gas mass is
and the gas mass is
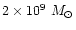 .
Therefore, considering the observed abundance gradient, the standard
cooling flow model indicate that the gas should be diluted
by metal poor surrounding gas.
However, the observed Fe abundance of M 87 within
.
Therefore, considering the observed abundance gradient, the standard
cooling flow model indicate that the gas should be diluted
by metal poor surrounding gas.
However, the observed Fe abundance of M 87 within
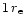 ,
,
 1 solar, is similar to those
of normal X-ray luminous galaxies, which are also
about
1 solar, is similar to those
of normal X-ray luminous galaxies, which are also
about  1 solar (Matsushita et al. 1997, 2000).
Note that the observed ISM abundance of NGC 4636 from the RGS spectra
is 0.9 solar (Xu et al. 2001).
In these systems, the enrichment has to be compared with a mass flow rate of
1 solar (Matsushita et al. 1997, 2000).
Note that the observed ISM abundance of NGC 4636 from the RGS spectra
is 0.9 solar (Xu et al. 2001).
In these systems, the enrichment has to be compared with a mass flow rate of
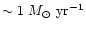 as implied by the standard cooling flow models for these galaxies.
For the case of NGC 4636, the mass flow rate is determined to be
as implied by the standard cooling flow models for these galaxies.
For the case of NGC 4636, the mass flow rate is determined to be
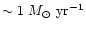 (Bregman et al. 2001).
The effect of the dilution by ICM should be determined by a ratio of
the mass flow rate and the optical luminosity since metals ejected from
a galaxy should be proportional to the stellar luminosity.
Within
(Bregman et al. 2001).
The effect of the dilution by ICM should be determined by a ratio of
the mass flow rate and the optical luminosity since metals ejected from
a galaxy should be proportional to the stellar luminosity.
Within
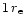 ,
the former rate of NGC 4636 is a factor of 10 smaller
than that of M 87, while the latter is only a factor of 2.5 smaller.
In a much larger cooling flow as exists in M 87 in which the Fe enrichment
is supplied by a stellar population comparable to that of normal
ellipticals, the relative enrichment
will be less and the abundance gradient must be reduced in contrast to the observed data.
Therefore, the overall cooling flow expected from the classical galaxy cluster cooling flow model
should not exist in M 87, although
a small-scale cooling flow, with a mass deposition rate close to the stellar mass loss rate,
may exists in the central core of the classical cooling flow regions.
,
the former rate of NGC 4636 is a factor of 10 smaller
than that of M 87, while the latter is only a factor of 2.5 smaller.
In a much larger cooling flow as exists in M 87 in which the Fe enrichment
is supplied by a stellar population comparable to that of normal
ellipticals, the relative enrichment
will be less and the abundance gradient must be reduced in contrast to the observed data.
Therefore, the overall cooling flow expected from the classical galaxy cluster cooling flow model
should not exist in M 87, although
a small-scale cooling flow, with a mass deposition rate close to the stellar mass loss rate,
may exists in the central core of the classical cooling flow regions.
The major result of this paper is strong evidence that the ICM in the halo of M 87
is isothermal locally, except probably for the very central region, where more
than one temperature component is present.
This could be partly due to the interaction effects of the ICM with the jet and the radio lobes
of M 87. This finding and the fact that no spectral signature of low temperature components
below temperatures of 0.8 keV are observed is in disagreement with the standard cooling flow model
which predicts a strongly multi-phase structure of the ICM and a distinct temperature distribution and
resulting spectrum with a clear signature of low temperature components.
We have also shown that strong inhomogeneities in the metal distribution cannot resolve this problem.
Therefore we conclude that the scenario for the dense gas with short cooling time in the centers of
clusters needs to be revised.
Probably heating processes that can substantially reduce the mass deposition have
to be reconsidered, like the energy input of the central AGN.
The central temperature closely reflects the gravitational potential depth of the central galaxy,
rather than the existence of a cooling flow.
Acknowledgements
This work was supported by the Japan
Society for the Promotion of Science (JSPS) through its Postdoctoral
Fellowship for Research Abroad and Research Fellowships for Young
Scientists.
- Allen, S. W., & Fabian, A. C. 1994, MNRAS, 269, 409
In the text
NASA ADS
- Allen, S. W. 2000, MNRAS, 315, 269
In the text
NASA ADS
- Allen, S. W., Fabian, A. C., Johnstone, R. M., Arnaud, K., & Nulsen, P. H. E. 2001, MNRAS, 322, 589
In the text
NASA ADS
- Anders, E., & Grevesse, N. 1989, Geochimica et Cosmochimica Acta, 53, 197
In the text
NASA ADS
- Arnaud, M., & Rothenflug, M. 1985, A&AS, 60, 425
In the text
NASA ADS
- Arnaud, M., & Raymond, J. 1992, A&A, 398, 394
In the text
- Belsole, E., Sauvageot, J. L., Böhringer, H., et al. 2001, A&A, 365, L188
In the text
NASA ADS
- Binggeli, B., & Tammann, G. A. 1987, AJ, 94, 251
In the text
NASA ADS
- Böhringer, H., Briel, U. G., Schwarz, R. A., et al. 1994, Nature, 368, 828
In the text
NASA ADS
- Böhringer, H., Nulsen, P. E. J., Braun, R., & Fabian, A. C. 1995, MNRAS, 274, 67
In the text
- Böhringer, H. 1999, in Diffuse Thermal and Relativistic Plasma in Galaxy Clusters, ed. H. Böhringer, L. Feretti, & P. Schuecker, MPE Report, 115
In the text
- Böhringer, H., Belsole, E., Kennea, J., et al. 2001, A&A, 365, L181
In the text
NASA ADS
- Böhringer, H., Matsushita, K., Churazov, E., Ikebe, Y., & Chen, Y. 2002, A&A, 382, 804
In the text
NASA ADS
- Bregman, J. N., Miller, E. D., & Irwin, J. A. 2001, ApJ, 553, 125
- Canizares, C. R., Fabbiano, G., & Trinchieri, G. 1987, ApJ, 312, 503
In the text
NASA ADS
- Ciotti, L., Pellegrini, S., Renzini, A., & D'Ercole, A. 1991, ApJ, 376, 380
In the text
NASA ADS
- Cohen, J. G., & Ryzhov, A. 1997, ApJ, 486, 230
In the text
NASA ADS
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr. H. G., et al. 1991,
Third Reference Catalog of Bright Galaxies (RC3 Catalog)
In the text
- Fabian, A. C., Hu, E. M., Cowie, L. L., & Grindlay, J. 1981, ApJ, 248, 47
In the text
NASA ADS
- Fabian, A. C., Stewart, G. C., Nulsen, P. E. J., Itoh, H., & Canizares, C. R. 1984, Nature, 307, 343
In the text
NASA ADS
- Fabian, A. C. 1994, ARA&A, 32, 277
In the text
NASA ADS
- Fabian, A. C., Mushotzky, R. F., Nulsen, P. E. J., & Peterson, J. R. 2001, MNRAS, 321, 20
In the text
- Feigelson, E. D., Wood, P. A. D., Schreier, E. J., Harris, D. E., & Reid, M. J. 1987, 312, 101
In the text
- Finoguenov, A., & Jones, C. 2000, ApJ, 539, 603
In the text
NASA ADS
- Finoguenov, A., Matsushita, K., Böhringer, H., Ikebe, Y., & Arnaud, M. 2002, A&A, 381, 21
In the text
NASA ADS
- Fukazawa, Y., Ohashi, T., Fabian, A. C., et al. 1994, PASJ, 46, L55
In the text
NASA ADS
- Gerhard, O., Kronawitter, A., Saglia, R. P., & Bender, R. 2001, ApJ, 121, 1936
In the text
- Gil'fanov, M. R., Syunyaev, R. A., & Churazov, E. M. 1987, SvAL, 13, 3
In the text
NASA ADS
- Giraud, E. 1999, ApJL, 524, 15
In the text
- Ikebe, Y., Ezawa, H., Fukazawa, Y., et al. 1996, Nature, 379, 427
In the text
NASA ADS
- Ikebe, Y., Makishima, K., Fukazawa, Y., et al. 1999, ApJ, 525, 58
In the text
NASA ADS
- Ikebe, Y. 2001, Proc. of Tracing Cosmic Evolution with Clusters of Galaxies,
Sesto Pusteria, Bolzano, Italy, July 3-6, 2001 [astro-ph/0112132]
In the text
- Kaastra, J. S. 1992, An X-Ray Spectral Code for Optically Thin Plasmas (Internal SRON-Leiden Report, updated version 2.0)
In the text
- Kaastra, J. S., Ferrigno, C., Tamura, T., et al. 2001, A&A, 365, L99
In the text
NASA ADS
- Kodama, T., & Arimoto, N. 1997, 320, 41
In the text
- Kronawitter, A., Saglia, R. P., Gerhard, O., & Bender, R. 2000, A&AS, 144, 53
In the text
NASA ADS
- Lieu, R., Mittaz, J. P. D., Bowyer, S., et al. 1996, ApJL, 458, 5
In the text
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115
In the text
NASA ADS
- Loewenstein, M., & Mathews, W. G. 1991, ApJ, 373, 445
NASA ADS
- Masai, K. 1997, A&A, 324, 410
In the text
NASA ADS
- Makishima, K., Ezawa, H., Fukazawa, Y., et al. 2001, PASJ, 53, 401
In the text
NASA ADS
- Matsumoto, H., Koyama, K., Awaki, H., et al. 1996, PASJ, 48, 201
In the text
NASA ADS
- Matsushita, K., Makishima, K., Rokutanda, E., et al. 1997, ApJ, 488, L125
NASA ADS
- Matsushita, K., Makishima, K., Ikebe, Y., et al. 1998, ApJ, 499, L13
In the text
NASA ADS
- Matsushita, K., Ohashi, T., & Makishima, K. 2000, PASJ, 52, 685
In the text
NASA ADS
- Matsushita, K. 2001, ApJ, 547, 693
In the text
NASA ADS
- Matsushita, K., et al. 2002, in preparation (Paper II)
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197
In the text
NASA ADS
- Mewe, R., Lemen, J. R., & van den Oord, G. H. J. 1986, A&AS, 65, 511
In the text
NASA ADS
- Nulsen, P. E. J., & Böhringer, H. 1995, MNRAS, 274, 1093
In the text
NASA ADS
- Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419
In the text
NASA ADS
- Sanders, J. S., & Fabian, A. C. 2001, MNRAS, in press
In the text
- Sarazin, C. 1988, X-ray emission from clusters of
galaxies (Cambridge University Press)
In the text
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond,
J. S. 2001, ApJ, 556, 91
In the text
- Shibata, R. 2000, Ph.D. Thesis, Gakushuin University
In the text
- Shigeyama, T. 1998, ApJ, 497, 587
In the text
NASA ADS
- Stark, A. A., Gammie, C. F., Wilson, R. W., et al. 1992, ApJS, 79, 77
In the text
NASA ADS
- Stewart, G., Canizares, C. R., Fabian, A. C., & Nulsen, P. E. J. 1984, ApJ, 278, 536
In the text
NASA ADS
- Tamura, T., Kaastra, J. S., Peterson, J. R., et al. 2001, A&A, 365, L87
In the text
NASA ADS
- Tawara, Y., Akimoto, F., Kumada, A., et al. 1997, in X-ray Imaging and Spectroscopy of Cosmic Hot Plasmas, ed. F. Makino, & K. Mitsuda (Universal Academy Press, Tokyo), 87
In the text
- Whitmore, B. C., McElroy, D. B., & Tonry, J. L. 1985, ApJS, 59, 1
In the text
NASA ADS
- Xu, H., Kahn, S., Peterson, J. R., Beher, E., et al. 2001,
ApJ, submitted [astro-ph/0110013)]
In the text
Copyright ESO 2002
![\begin{figure}
\includegraphics[width=8.8cm,clip]{1597f1.eps}\end{figure}](/articles/aa/full/2002/16/aa1597/Timg22.gif)

![\begin{figure}
\par\includegraphics[width=17cm,clip]{fog6.eps}\end{figure}](/articles/aa/full/2002/16/aa1597/Timg32.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1597f7.eps}\end{figure}](/articles/aa/full/2002/16/aa1597/Timg34.gif)