We now consider relativistic Doppler effects due to the motion of
the jet volumes toward the observer.
The relativistic Doppler factor is
![]() where
where ![]() is the Lorentz factor,
is the Lorentz factor, ![]() the plasma velocity in units of the speed of light and
the plasma velocity in units of the speed of light and ![]() the angle
between the trajectory of the volume and the l.o.s.
The observed energies
the angle
between the trajectory of the volume and the l.o.s.
The observed energies ![]() and
luminosities
and
luminosities ![]() of each volume element are
shifted and boosted to the rest frame values (index e),
of each volume element are
shifted and boosted to the rest frame values (index e),
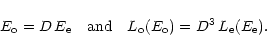 |
(2) |
Figures 3a,b show the effect of boosting and shifting
of the rest frame spectra.
For an angle between the l.o.s. and the jet axis of
![]() ,
the maximum boosting
D3 = D-403 = 6.7 is obtained
for the volume with
T = 106.64K (see also Table 1).
The maximum de-boosting is for the volume at the opposite side of the cone,
D+403 = 0.15.
As in the rest frame, the "hot'' spectra are flatter.
,
the maximum boosting
D3 = D-403 = 6.7 is obtained
for the volume with
T = 106.64K (see also Table 1).
The maximum de-boosting is for the volume at the opposite side of the cone,
D+403 = 0.15.
As in the rest frame, the "hot'' spectra are flatter.
To obtain a total shifted and boosted spectrum
we need to interpolate the single volume luminosity values
since they are shifted to different energies.
Considering the case where the jet axis is along the l.o.s.
(
![]() ,
see Fig. 3c),
we have only a weak effect of shifting,
in fact, we are looking almost perpendicular to an
uncollimated flow.
For a larger jet inclination the Doppler effects become larger.
In this case, one should take into account the fact that the angle
between the velocity and the l.o.s. (
,
see Fig. 3c),
we have only a weak effect of shifting,
in fact, we are looking almost perpendicular to an
uncollimated flow.
For a larger jet inclination the Doppler effects become larger.
In this case, one should take into account the fact that the angle
between the velocity and the l.o.s. (
![]() )
varies
along the jet-torus.
However,
we have considered it reasonable to divide the jet-tori in two regions,
one third containing volume elements for which the Doppler
effect has been calculated using the minimum angle
between the plasma velocity and the l.o.s., and two thirds
containing volume elements for which the Doppler
effect has been calculated using the maximum angle
between the plasma velocity and the l.o.s.
)
varies
along the jet-torus.
However,
we have considered it reasonable to divide the jet-tori in two regions,
one third containing volume elements for which the Doppler
effect has been calculated using the minimum angle
between the plasma velocity and the l.o.s., and two thirds
containing volume elements for which the Doppler
effect has been calculated using the maximum angle
between the plasma velocity and the l.o.s.
The total spectra have been calculated by first considering the blue-shifted and red-shifted parts of the flow and then summing up all the luminosities in each energy bin, where blue and red shifted luminosities are available. The result is shown in Fig. 3d with the luminosity rescaled in order to compare the total spectrum with its components.
Note that the iron line features are considerably shifted also after
the interpolation.
The change in the line shape is due to the fact that for each
of the 5000 volumes along the jet a different Doppler factor must be
considered.
For a larger jet inclination (D-40 , D+40) the lines are
spread out widely because of the larger Doppler shift (not shown).
The de-boosting contribution of the receding counter-jet
has not been taken into account.
| T (K) | 109 | 108 | 107 | 106.64 |
| M (gr) |
|
|
|
|
|
|
|
|
|
|
| 1.014 | 1.179 | 1.428 | 1.494 | |
|
|
82 | 77 | 72 | 70 |
|
|
1.010 | 0.960 | 0.898 | 0.899 |
| D-20 | 1.07 | 1.19 | 1.25 | 1.28 |
| D+20 | 0.96 | 0.79 | 0.68 | 0.67 |
| D-40 | 1.12 | 1.47 | 1.77 | 1.88 |
| D+40 | 0.91 | 0.68 | 0.55 | 0.53 |
Copyright ESO 2002