A&A 385, 1089-1094 (2002)
DOI: 10.1051/0004-6361:20020196

Theoretical thermal X-ray spectra of relativistic MHD jets

E. Memola1,[*] - Ch. Fendt1,2 - W. Brinkmann3


1 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
2 - Universität Potsdam, Institut für Physik, Am Neuen Palais 10, 14469 Potsdam, Germany
3 - Centre for Interdisciplinary Plasma Science, Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse, 85740 Garching, Germany

Received 18 December 2001 / Accepted 4 February 2002

Abstract
Highly relativistic jets are most probably driven by strong magnetic fields and launched from the accretion disk surrounding a central black hole. Applying the jet flow parameters (velocity, density, temperature) calculated from the magnetohydrodynamic (MHD) equations, we derive the thermal X-ray luminosity along the inner jet flow in the energy range 0.2-10.1keV. Here, we concentrate on the case of Galactic microquasars emitting highly relativistic jets. For a $5\,{M}_{\odot }$ central object and a jet mass flow rate of $\dot{M}_{\rm j} = 10^{-8}\,{M}_{\odot}\,{\rm yr}^{-1}$we obtain a jet X-ray luminosity $ L_{\rm X} \approx 10^{33}\,{\rm erg\,s}^{-1}$. Emission lines of Fe XXV and Fe XXVI are clearly visible. Relativistic effects such as Doppler shift and boosting were considered for different inclinations of the jet axis. Due to the chosen geometry of the MHD jet the inner X-ray emitting part is not yet collimated. Therefore, depending on the viewing angle, the Doppler boosting does not play a major role in the total spectra.

Key words: MHD - radiation mechanisms: thermal - X-rays: binaries - ISM: jets and outflows


1 Introduction

Microquasars (Mirabel & Rodr $\acute{\rm {\i}}$guez 1999) are Galactic X-ray binaries where the three basic ingredients of quasars are found - a central black hole, an accretion disk and relativistic jets. Jets are thought to be driven by magnetohydrodynamic (MHD) mechanisms (Blandford & Payne 1982; Camenzind 1986) triggered by the interaction of those three components, although the jet formation process is not yet fully understood (e.g. Fendt 1997). Some microquasars are superluminal sources, e.g. GRS1915+105 at a distance of 7-12kpc (Fender et al. 1999) with a central mass of about $14\,{M}_{\odot}$ (Greiner et al. 2001).

Fendt & Greiner (2001, FG01) presented solutions of the MHD wind equation in Kerr metric with particular application to microquasars. These solutions provide the flow dynamics along a prescribed poloidal magnetic field line. FG01 found temperatures up to more than 1010K in the innermost part of the jet proposing that thermal X-rays might be emitted from this region. Here, we calculate the thermal spectrum of such an optically thin jet flow taking into account one of the solutions of FG01 and considering relativistic Doppler shifting and boosting as well as different inclinations of the jet axis to the line-of-sight (l.o.s.). A similar approach was undertaken by Brinkmann & Kawai (2000, BK00) who have been modeling the two dimensional hydrodynamic outflow of SS 433 applying various initial conditions. However, they do not consider relativistic effects such as Doppler boosting in their spectra.

  \begin{figure} \par\includegraphics[width=3.95cm,clip]{H3366f1a.eps}\hspace*{5mm... ...ps}\hspace*{5mm} \includegraphics[width=3.95cm,clip]{H3366f1d.eps} \end{figure} Figure 1: Dynamical parameters of the MHD jet (see FG01). Shown is the radial dependence of the properly normalized poloidal velocities $u_{\rm p}(x) = \gamma v_{\rm p}/c$, particle densities $\rho (x)$, temperatures T(x) (in K), and size of the emitting volumes V(x) (from left to right) along the chosen magnetic field line. For the calculations in this paper we apply a central mass of $5\,{M}_{\odot }$ and a jet mass flow rate of $ \dot{M}_{\rm jet} = 10^{-10}\,{M}_{\odot}\,{\rm yr}^{-1}$. The units are therefore $r_{\rm g} = 7.4 \times 10^5$cm for all length scales, $r_{\rm g}^3 = 4.1 \times 10^{17}$cm3 for the volumes, and $4.31 \times 10^{16}$cm-3 for the particle densities. Note that the jet injection point is located at $R_{\rm i} = 8.3\,r_{\rm g} $ with a gas temperature of $T_{\rm i} = 10^{10.2}$K. In this solution for the MHD wind equation, the poloidal velocity saturates to a value of $u_{\rm p} = 2.5$ beyond $x\simeq 10^8$. The flow is weakly collimated reaching a half opening angle of $70\hbox {$^\circ $ }$ at about x=250.
Open with DEXTER

2 The model

The axisymmetric, stationary and ideal MHD wind solution provides the density, velocity and temperature for each volume element along the field. Prescribing the jet mass flow rate $\dot{M}_{\rm j}$ together with the shape of the field line, these solutions give a unique set of parameters of the flow defined by the regularity condition across the magnetosonic points (see FG01 for details).

The calculated dynamical parameters are our starting point to obtain the X-ray spectra of the jet. Here, we refer to the solution S3 of FG01 obtained for a collimating field line z(x) = 0.1 (x-x0)6/5, x being the normalized cylindrical radius, x0 the foot point of the field line at the equatorial plane, and z the height above the disk. Length scales are normalized to the gravitational radius $r_{\rm g} = 7.4 \times 10^5$cm $(M/5\,{M}_{\odot})$. For completeness, we show the radial profiles of poloidal velocity, density, temperature, and emitting volume along the field line in Fig. 1.

The jet geometry consists of nested collimating conical magnetic surfaces with sheets of matter accelerating along each surface. The sheet cross section becomes larger for larger distances from the origin. The distribution of the 5000 volume elements along the jet is such that velocity and density gradients are small within the volume. We have 63 volumes in $\phi$ direction defining an axisymmetric torus (i.e. 5000 tori along the magnetic surface).

We distinguish two parts of the inner jet flow. One is for a temperature range T = 106.6-109K, where we calculate the optically thin continuum (bremsstrahlung) and the emission lines. The other is for T = 109-1012K, where only bremsstrahlung is important. Any pair processes are neglected and no ( $\rm e^-e^-$)-bremsstrahlung will be considered, although that might be dominant at the highest temperatures. Such unphysically high temperatures are to a certain degree caused by the use of a non-relativistic equation of state. Employing a relativistically correct equation of state (Synge 1957) one would expect gas temperatures an order of magnitude lower (Brinkmann 1980). These temperatures belong to the intermediate region between disk and jet. The injection radius,which is, in fact, the boundary condition for the jet flow, is located at $R_{\rm i} = 8.3\,r_{\rm g} $and at a height above the disk (and the foot point of the field line) of $0.74\,r_{\rm g}$. For the chosen MHD solution the temperature at this point is $T_{\rm i} = 10^{10.2}$K. With $R_{\rm i} \simeq 6 \times 10^6$cm $(M/5\,{M}_{\odot})$we investigate a region of about $2.5 \times 10^{-5}$ $(M/5\,{M}_{\odot})$AU. Having determined the emissivities of single volume elements, these can be put together obtaining a rest-frame spectrum where any motion is neglected. However, the knowledge of the MHD wind velocities allows us to determine the Doppler shift of the spectral energies and the boosting of the luminosity for each volume. We finally obtain a total spectrum of the inner jet considering these effects in a differential way for each volume element. The final spectra of course depend also from the jet inclination.

We emphasize that our approach is not (yet) a fit to certain observed spectra. In contrary, for the first time, for a jet flow with characteristics defined by the solution of the MHD wind equation, we derive its X-ray spectrum. Our free parameters are the mass of the central object M defining the length scales, the jet mass flow rate $\dot{M}_{\rm j}$ and the shape of the poloidal field lines. In the end, from the comparison of the theoretical spectra with observations, we expect to get information about the internal magnetic structure of the jet close to the black hole and the jet mass flow rate.

  \begin{figure} \par\includegraphics[width=3.9cm,clip]{H3366f2a.eps}\hspace*{8mm}... ...ps}\hspace*{8mm} \includegraphics[width=3.6cm,clip]{H3366f2d.eps} \end{figure} Figure 2: X-ray luminosities of jet-tori of 63 volume elements with different temperatures: T = 106.64K, T = 107K, T = 108K, T = 109K (from left to right). The jet mass flow rate considered here is $ \dot{M}_{\rm j} = 10^{-10}\,{M}_{\odot}\,{\rm yr}^{-1}$ for a $5\,{M}_{\odot }$ central object.
Open with DEXTER

3 X-ray spectra in the rest frame of the volumes

The computation of the continuum spectrum and the emission lines of an optically thin plasma takes into account free-free, free-bound and two-photon processes (Mewe et al. 1985; Kotani et al. 1996; BK00). Cosmic abundances given by Allen (1973) are used for a plasma in equilibrium at the local temperature.

3.1 Luminosities of the fast flow ( $\mathsfsl{T = 10^{6.2}{-}10^9}$K)

Considering the size, density and temperature of each volume, the luminosities ( ${\rm erg\,s^{-1} (0.1\,keV)^{-1}}$) of the jet-tori have been calculated in the energy range 0.2-10.1keV (bin size 0.1keV). Examples are shown for four temperatures in Fig. 2 (see also Table 1). With the increase of the temperature the luminosity range is compressed, therefore those spectra are flatter and the strong cutoff seen for lower temperatures disappears. The luminosity of hot gas volume elements ( $T \simeq 10^9$K), located above the injection point, is higher (factor 100) than the one of the cooler, but faster volume elements. Note that the luminosities shown in Fig. 2 are calculated for $ \dot{M}_{\rm j} = 10^{-10}\,{M}_{\odot}\,{\rm yr}^{-1}$. This quantity is hardly known from observations and, in turn, the calculated luminosities may constrain its value. A mass flow rate 100 times higher increases the luminosity by a factor of 104, for the same magnetic field geometry.

For temperatures T = 106-109K many emission lines are present in the energy range 0.2-10.1keV (Mewe et al. 1985). The 0.5-0.9keV band contains O, N, Fe, Ne, S, Ca lines whereas lines of Ne, Fe, Mg, Ni, Si, S, Ar, Ca are found between 1.0-4.0keV. From 6.6-7.0keV mostly FeXXV (He-like) and FeXXVI (H-like) emission lines are present (BK00). For fully ionized plasma of $T \ge 10^9$K the bremsstrahlung continuum emission is dominant.

The total rest-frame spectrum (neglecting the velocity of the volumes) of a conical sheet of the jet is the integrated luminosity of the single volumes along the field, taking into account also the number of volumes along the jet-tori (Fig. 3c). The emission lines at 6.6 and 6.9keV can be identified as $K\alpha$ lines from He-like and H-like iron, while the one at 8.2keV could be the $K\beta$ from the He-like iron.

3.2 The hot flow close to the disk ( $\mathsfsl{T \geq 10^9}$K)

The thermal continuum of an optically thin fully ionized plasma follows from the formula of bremsstrahlung emission (Rybicki & Lightman 1979),

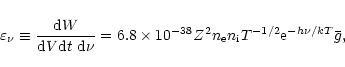\begin{displaymath}\varepsilon_\nu \equiv \frac{{\rm d}W}{{\rm d}V{\rm d}t~{\rm ... ...8} Z^2 n_{\rm e} n_{\rm i} T^{-1/2}{\rm e}^{-h\nu/kT} \bar{g}, \end{displaymath} (1)

(in ${\rm erg\,s^{-1}\,cm^{-3}\,Hz^{-1}}$), with the velocity averaged Gaunt factor $\bar{g}(T, \nu)$[*], the atomic number Z, the electron and ion number densities $n_{\rm e}$ and $n_{\rm i}$, the Planck constant h and the Boltzmann constant k. Considering the calculated volume parameters for temperatures below 109K, we obtain a bremsstrahlung luminosity $L_{\rm br}$comparable to the results in Fig. 2 as expected, in fact, since bremsstrahlung is included in that calculation. Still considering $ \dot{M}_{\rm j} = 10^{-10}\,{M}_{\odot}\,{\rm yr}^{-1}$, for $T \simeq 10^{10}$K we obtain $L_{\rm br} \approx 10^{25}\,{\rm erg\,s^{-1}(0.1\,keV)^{-1}}$, for $T \simeq 10^{11}$K we obtain $L_{\rm br} \approx 10^{27}\,{\rm erg\,s^{-1}(0.1\,keV)^{-1}}$, and when $T \simeq 10^{12}$K the luminosity is $L_{\rm br} \approx 10^{30}\,{\rm erg\,s^{-1}(0.1\,keV)^{-1}}$. Therefore, we expect an increase of the X-ray luminosity due to the bremsstrahlung contribution of the hottest regions in the jet-disk system, if the optically thin condition is still satisfied there.
  \begin{figure} \par\includegraphics[width=6.5cm,clip]{H3366f3a.eps}\hspace*{4mm}... ...eps}\hspace*{4mm} \includegraphics[width=6.5cm,clip]{H3366f3d.eps} \end{figure} Figure 3: Doppler shifted and boosted spectra. Spectra for a volume element with T = 107K a) and T = 109K b) for different jet inclinations. Doppler factor D-40 (triple dotted-dashed line, top), D-20 (dotted-dashed line, top), rest-frame (solid line), $D_{\parallel }$ (dotted line), D+20 (dotted-dashed line, bottom), D+40 (triple dotted-dashed line, bottom). c) Comparison of the total shifted/boosted spectrum $D_{\parallel }$ (thick dotted line) of a conical sheet with the rest-frame spectrum (thin solid line). d) Inclined jet, comparison of the boosted spectra D-20 (thick line top) and D+20 (thick line bottom) with the total spectrum (thick line middle) and the rest-frame spectrum (thin line middle).
Open with DEXTER

4 Relativistic effects - Doppler shift and boosting

We now consider relativistic Doppler effects due to the motion of the jet volumes toward the observer. The relativistic Doppler factor is $ D = (\gamma(1 - \beta \cos\theta))^{-1}, $where $\gamma $ is the Lorentz factor, $\beta$the plasma velocity in units of the speed of light and $\theta$ the angle between the trajectory of the volume and the l.o.s. The observed energies $E_{\rm o}$ and luminosities $L_{\rm o}$ of each volume element are shifted and boosted to the rest frame values (index e),

\begin{displaymath}% E_{\rm o} = D\,E_{\rm e} \quad {\rm and} \quad L_{\rm o}(E_{\rm o}) = D^3 \, L_{\rm e}(E_{\rm e}). \end{displaymath} (2)

Note that the Doppler factor depends on both $\gamma $ and $\theta$ (see also Urry & Padovani 1995) and is unity for $\theta = \arccos \left(\sqrt{(\gamma-1)/(\gamma+1)}\right)$. For larger angles, relativistic de-amplification takes place due to the time lapse in the moving frame of reference. This is the reason for D<1 in our jet (Table 1). Also known as second order Doppler effect, this was first observed in SS 433 (Margon 1984). De-boosting is also present in the asymptotic radio jets (different from the collimation region investigated here) of GRS1915+105 inclined by $70\hbox {$^\circ $ }$ to the l.o.s., actually providing a distance indicator (Mirabel & Rodr $\acute{\rm {\i}}$guez 1994).

4.1 Shifted and boosted spectra

Figures 3a,b show the effect of boosting and shifting of the rest frame spectra. For an angle between the l.o.s. and the jet axis of $40\hbox{$^\circ$ }$, the maximum boosting D3 = D-403 = 6.7 is obtained for the volume with T = 106.64K (see also Table 1). The maximum de-boosting is for the volume at the opposite side of the cone, D+403 = 0.15. As in the rest frame, the "hot'' spectra are flatter.

To obtain a total shifted and boosted spectrum we need to interpolate the single volume luminosity values since they are shifted to different energies. Considering the case where the jet axis is along the l.o.s. ( $\theta _{\parallel }$, see Fig. 3c), we have only a weak effect of shifting, in fact, we are looking almost perpendicular to an uncollimated flow. For a larger jet inclination the Doppler effects become larger. In this case, one should take into account the fact that the angle between the velocity and the l.o.s. ( $\theta _{\parallel }$) varies along the jet-torus. However, we have considered it reasonable to divide the jet-tori in two regions, one third containing volume elements for which the Doppler effect has been calculated using the minimum angle between the plasma velocity and the l.o.s., and two thirds containing volume elements for which the Doppler effect has been calculated using the maximum angle between the plasma velocity and the l.o.s.

The total spectra have been calculated by first considering the blue-shifted and red-shifted parts of the flow and then summing up all the luminosities in each energy bin, where blue and red shifted luminosities are available. The result is shown in Fig. 3d with the luminosity rescaled in order to compare the total spectrum with its components.

Note that the iron line features are considerably shifted also after the interpolation. The change in the line shape is due to the fact that for each of the 5000 volumes along the jet a different Doppler factor must be considered. For a larger jet inclination (D-40 , D+40) the lines are spread out widely because of the larger Doppler shift (not shown). The de-boosting contribution of the receding counter-jet has not been taken into account.

 

 
Table 1: Dynamical parameters for four example volume elements. Quoted are temperature T, mass M, particle density $\rho $ and the Lorentz factor $\gamma $. The angle $\theta _{\parallel }$ is the angle between the plasma velocity and the l.o.s., if the l.o.s. is parallel to the jet axis. The corresponding Doppler factor is $D_{\parallel }$. If the l.o.s. is inclined $20^{\circ }$ to the jet axis, the minimum (maximum) angle between the plasma velocity and the l.o.s. is $\theta _{\parallel } - 20^{\circ }$ ( $\theta _{\parallel } + 20^{\circ }$) with a corresponding Doppler factor D-20 (D+20) and similarly for an inclination of $40^{\circ }$.
T (K) 109 108 107 106.64
M (gr) $ 7 \times 10^7$ $ 2 \times 10^7$ $1.1 \times 10^7$ $ 0.97 \times 10^7$
$\rho $ (cm-3) $ 6 \times 10^{13}$ $ 2 \times 10^{12}$ $ 6 \times 10^{11}$ $ 2 \times 10^{11}$
$\gamma $ 1.014 1.179 1.428 1.494
$\theta _{\parallel }$ $(^\circ)$ 82 77 72 70
$D_{\parallel }$ 1.010 0.960 0.898 0.899
D-20 1.07 1.19 1.25 1.28
D+20 0.96 0.79 0.68 0.67
D-40 1.12 1.47 1.77 1.88
D+40 0.91 0.68 0.55 0.53


5 Discussion

5.1 X-ray luminosities

We find a total rest-frame X-ray luminosity of the jet $ L_{\rm X} = 3.8 \times 10^{31}$ $(\dot{M}_{\rm j}/10^{-8}\,{M}_{\odot}\,{\rm yr}^{-1})\,{\rm erg\,s^{-1}}$. The total kinematic luminosity for this jet mass flow rate is $L_{\rm k} = \gamma \dot{M}_{\rm j} c^2 \approx 10^{39}\,{\rm erg\,s^{-1}} \gg L_{\rm X} $. This proves a posteriori that the assumption of a polytropic gas law used to obtain the MHD wind solution is consistent with the amount of radiation losses.

Considering the Doppler factor $D_{\parallel }$, the total X-ray luminosity of the jet is $L_{\rm X} = 6.4 \times 10^{32}~(\dot{M}_{\rm j}/10^{-8}\,{M}_{\odot}\,{\rm yr}^{-1})\,{\rm erg\,s^{-1}}$. In the case of an inclined jet axis (D-20, D+20) we have $L_{\rm X} = 1.4 \times 10^{33}~(\dot{M}_{\rm j}/10^{-8}\,{M}_{\odot}\,{\rm yr}^{-1})\,{\rm erg\,s^{-1}}$. For D-40 and D+40 we obtain $L_{\rm X} = 1.1 \times 10^{33}~(\dot{M}_{\rm j}/10^{-8}\,{M}_{\odot}\,{\rm yr}^{-1})\,{\rm erg\,s^{-1}}$. These values can be increased by the contribution of bremsstrahlung from the high temperature ( $T \geq 10^9$K) volumes till about $L_{\rm X} \approx 10^{34}\,{\rm erg\,s^{-1}}$.

In comparison, the X-ray luminosity of GRS1915+105 is $10^{38}\,{\rm erg\,s^{-1}}$ in low-state and $10^{39}\,{\rm erg\,s^{-1}}$ in high-state (Greiner et al. 1996), and larger than the one we obtain. Such a luminosity might be obtained from the jet for an increased mass flow rate. The jet inclination of $70\hbox {$^\circ $ }$ implies a maximum boosting of about 20 for some volumes. Further, also the accretion disk contributes to the X-ray flux. In SS433 we have $ L_{\rm X} > 10^{35}\,{\rm erg\,s^{-1}}$ (Brinkmann et al. 1996) but no broad Fe-lines are observed. This might be either due to a very low mass flow rate (low jet luminosity) or to a very high mass flow rate (self-absorption of the emission lines).

Higher jet velocities ($\gamma >2$) may increase the Doppler boosting. Such velocities can be easily obtained for a higher flow magnetization, i.e. for a stronger magnetic field strength or a lower jet mass flow rate (see FG01; Fendt & Camenzind 1996). However, for the same mass flow rate, a higher velocity implies a lower gas density, which may lead, instead, to a decrease of the luminosity. The interplay of these effects is rather complex. The rest frame emissivity depends on the density as $\sim$$\rho^2$ and is also proportional to the emitting volume. The maximum Doppler boosting increases with the Lorentz factor, $D^3 (\cos\theta = 1) \simeq (2\gamma^2\,(1 + \sqrt{1 - \gamma^{-2}}))^{3/2} $, whereas the real boosting parameter also depends on the inclination of the velocity vector to the l.o.s. Answering the question how these effects determine the observed X-ray luminosity, would require a detailed study of various MHD wind solutions and their derived spectra investigating different magnetic field geometries (degree of collimation), jet mass flow rates (the flow magnetization), and also possible masses of the central black hole. We will return to this important point in a future paper.

Markoff et al. (2001) have recently shown (for XTE J1118+480) that synchrotron emission from the jet may play a role also in the X-ray band. Their model differs from ours in some respects, especially the initial jet acceleration is not treated and the jet nozzle geometry is more concentrated along the axis with a jet radius of only 10 Schwarzschild radii (in our model the jet is much wider and collimates later). As a consequence, the densities become higher and it is questionable whether a more reasonable jet geometry will deliver the same amount of X-ray flux.

5.2 Jet plasma composition

At this point we should note that the fundamental question of the plasma composition in relativistic jets has not yet been answered. In the case of microquasars we do not really know whether the jet consists of a $\rm e^-p^+$ or a $\rm e^-e^+$ plasma (see e.g. Fender et al. 2000). It could be possible that these jets are "light'' jets, i.e. made of a pair plasma only, and we would not expect to observe an iron line emission from such jets. Instead, the iron line emission would then arise from processes connected to the accretion disk or an accretion column. Such models were discussed for example in the case of XTEJ1748-288 (Kotani et al. 2000; Miller et al. 2001).

On the other hand, the theoretical spectra derived in our paper provide an additional information needed in order to interpret the observed emission lines. A deeper understanding will, however, require a more detailed investigation of different jet geometries, viewing angles and mass flow rates. In the end, this might answer the question whether the line emission, or at least part of it, comes from the highly relativistic jet motion or from a rapidly rotating (i.e. also relativistic) accretion disk. For example, we expect the emission lines of a collimated jet being narrower, and probably shifted by a larger Doppler factor, due to the strong beaming. One should also keep in mind that the direction of motion of the jet material is inclined (if not perpendicular) to the disk rotation.

Evidently, if the observations would tell us that the Doppler shifted Fe lines which are visible in our theoretical spectra arise in the jet material, this would also prove the existence of a baryonic component in these jets.

Nevertheless, observations in the radio and shorter wavelengths give clear indication for synchrotron emission from highly relativistic electrons. Whether this non thermal particle population contributes to all of the observed emission is not clear, a hot thermal plasma may also exist besides the non thermal electrons.

A similar discussion concerning the plasma composition is present in the context of extragalactic jets (e.g. Mukherjee et al. 1997). The non thermal emission from blazars can be explained by inverse Compton scattering of low-energy photons by the relativistic electrons in the jet. However, two main issues remain unsolved: the source of the soft photons that are inverse Compton scattered, and the structure of the inner jet, which cannot be imaged directly. The soft photons can originate as synchrotron emission either within the jet (see e.g. Bloom & Marscher 1996) or nearby the accretion disk, or they can be disk radiation reprocessed in broad emission line clouds (see e.g. Ghisellini & Madau 1996). In contrast to these leptonic jet models, the proton-initiated cascade model (see e.g. Mannheim & Biermann 1989) predicts that the high-energy emission comes from knots in jets as a consequence of diffusive shock acceleration of protons to energies so high that the threshold of secondary particle production is exceeded.

Comparison of our calculated Fe emission lines to the observed ones potentially give some hints on the plasma composition ( $\rm e^-p^+$ or $\rm e^-e^+$) in relativistic jets.

6 Summary

For the first time, theoretical thermal X-ray spectra were obtained for the dynamical parameters of a relativistic jet calculated from the MHD wind equation. The total spectra were derived as composition of the spectral contributions of the single volume elements accelerating along the jet with relativistic speed. Our results are the following.

1.
We find X-ray emission from the hot inner part of the jet originating in a region of $2.5 \times 10^{-5}$AU diameter close to the center of a 5 ${M}_{\odot}$ jet source. The jet X-ray luminosity is $ L_{\rm X} \sim 10^{33}~(\dot{M}_{\rm j}/10^{-8}\,{M}_{\odot}\,{\rm yr}^{-1})\,{\rm erg\,s^{-1}}$.

2.
Emission lines of Fe XXV and Fe XXVI are clearly visible in our spectra. Interestingly, the $K\!\alpha$ iron emission line has been probably observed in GRS 1915+105 (Ebisawa et al. 1998) and XTE J1748-288 (Kotani et al. 2000). The absence of broad Fe-lines in the spectrum of SS433 might tell us something on the "invisibility'' of the acceleration region above the disk. Comparison of our calculated emission lines to observed ones may give some hints on the plasma composition in relativistic jets.

3.
From the MHD jet underlying the spectra we find a maximum Doppler boosting of about 7. Minimum boosting is present along the opposite side of the jet cone (Doppler factor 0.53). The shift of the emission lines is always visible. The boosting, however, does not play a major role in the total spectra, because of the uncollimated geometry of the innermost part of the jet emitting the X-rays and the combined effect of boosting and de-boosting around the jet cone.
If jets from X-ray binaries indeed contain matter of baryonic composition, our model will have a broad application. Indication of that is probably given by the observation of iron emisson lines in some sources (see above). However, it is not yet clear, whether the line emission originates in the jet or in the accretion disk. Our calculated Fe emission lines may help to interpret the observed spectra and potentially give some clue on the plasma composition in relativistic jets.

This study will be extended in a future work investigating spectra of jets with different magnetic geometry, mass flow rates and central masses. In the end, this might also allow to constrain the intrinsic parameters of jet formation itself (such as mass loading or opening angle) from the observation of the large-scale, asymptotic jet.

Acknowledgements
This work was partly supported by the German Science Foundation (Deutsche Forschungsgemeinschaft) as project DFG/FE490. We thank an anonymous referee for useful comments.

References

 

Copyright ESO 2002