A&A 385, 968-985 (2002)
DOI: 10.1051/0004-6361:20020164

Spectroscopic diagnostics of stellar transition regions
and coronae in the XUV: AU Mic in quiescence

G. Del Zanna ¹ - M. Landini ² - H. E. Mason ¹

1 - Department of Applied Mathematics and Theoretical Physics, University of Cambridge, UK
2 - Dipartimento di Astronomia e Scienza dello Spazio, Università di Firenze, Italy

Received 17 October 2001 / Accepted 29 January 2002

Abstract
In this paper we review the spectroscopic diagnostic techniques that can be applied to XUV observations of active stars. In particular, we discuss methods for the determination of electron densities, emission measures and the chemical composition of the stellar transition regions and coronae. We pay particular attention to the atomic data used and we revise several previous analyses with the most recent atomic data (from CHIANTI). We find severe limitations to some of the commonly used methods and atomic data and we obtain results which are significantly different from other authors. We illustrate this with a number of examples. We analyse a combined set of multi-wavelength observations (EUVE, HST/STIS, FUSE) for the quiescent phase of the dMe star AU Mic. A major conclusion of this paper is that the use of spectral lines from the Li and Na isoelectronic sequences, common in previous literature, produces erroneous results in the determination of emission measures, elemental abundances and transition region densities.

Key words: techniques: spectroscopic - atomic data - stars: atmospheres - stars: individual: AU Mic

1 Introduction

Many of the bright sources in the XUV are late-type dwarf active stars with very strong chromospheric emission. These stars have quiescent XUV/bolometric luminosity ratios many orders of magnitude greater than the Sun. They also present recurrent flares. The physical characteristics of the stellar transition regions (TRs) and coronae provide important observational constraints on the modeling of the thermal structure of their outer atmospheres (see, e.g., Jordan 2000). It is important to determine: the thermal structure of the stellar outer atmospheres, in terms of the differential emission measure DEM or emission measure EM; the chemical composition of the TR and corona; electron densities (or pressures); radiative losses. At present, these physical characteristics are poorly known for active stars. It is important to measure them, because they seem to vary from star to star, and to be different from the Sun. For example, EUV observations indicate that some stars have coronal abundances similar to the Sun, while other stars do not (see, e.g., the review of Feldman & Laming 2000). This could have important implications for our understanding of the various processes taking place in stellar atmospheres.

Spectroscopic diagnostics can be applied to XUV observations to determine the above physical characteristics. Until recently, low- to medium-resolution XUV spectroscopy provided measurements which were subject to large uncertainties, with approximate methods being used to analyse them. For example: electron densities were estimated from emission measures; the emission measures were estimated assuming an isothermal or a two-temperature coronal plasma; elemental abundances were estimated using global fits to the spectra. The advent of high-resolution XUV spectroscopy in the past few years (summarised in Sect. 2) provides an excellent opportunity to determine these physical parameters more directly and more accurately.

A large body of literature has been written on the subject of spectroscopic diagnostics (for a general review see, e.g., Mason & Monsignori Fossi 1994) and applications to solar and stellar observations. Unfortunately, in many studies, particularly those based on stellar observations, incorrect physical parameters have been obtained. This has in turn led to unnecessary physical conjectures that we believe should now be revisited. In this paper, we are primarily concerned with pointing out the reasons why wrong results have been obtained. We illustrate this with some examples and suggest the correct methodologies that should be applied to high-resolution XUV stellar spectra. In many cases, inaccurate atomic calculations have been used. The problematics discussed here are more generally applicable, both for solar and stellar atmospheres.

It is important to realise that some of the physical parameters are inter-related. For example, an accurate knowledge of the DEM is necessary to estimate elemental abundances (see Sect. 3), and both the DEM and the chemical composition are important factors in the calculation of the radiative losses (cf. Cook et al. 1989). The DEM and the relative element abundances can only be directly obtained to a high accuracy from the line intensities if the spectral lines:

(a) are obtained from high signal to noise (S/N) observations with a high resolving power;
(b) are optically thin;
(c) are density-insensitive;
(d) cover a large temperature range, from transition region up to coronal and flare temperatures;
(e) cover a large range of elements and ions;
(f) are from various isoelectronic sequences;
(g) have corresponding accurate atomic data.

Point (a) is self evident. Point (b) does not mean that lines that are not optically thin cannot be used for diagnostics. If the optical depths can be estimated (see Sect. 5.1) and are not large, then the lines can still be used without the need for full radiative transfer calculations. Point (c) is often overlooked. Point (d) is particularly important for an accurate calculation of the radiative losses. A major problem with past and present spectroscopic data from various satellites is that they observe spectral lines that are emitted over a restricted temperature range, and do not usually satisfy all the above requirements (see Sect. 2). Point (e) is important for the derivation of elemental abundances.

Regarding point (f), anomalous behaviour of lines emitted by some ions from the Li and Na isoelectronic sequences has now been reported by several authors (see Sect. 3.1). However, in most of the literature (see, e.g., Brown et al. 1984b; Brown et al. 1984a; Hartmann et al. 1985; Jordan et al. 1985; Byrne et al. 1987; Jordan et al. 1987; Linsky et al. 1989; Quin et al. 1993; Maran et al. 1994; Linsky et al. 1995; Doschek 1997; Griffiths & Jordan 1998; Brandt et al. 2001), these lines have been used for solar and stellar emission measure analyses, since they are among the most prominent ones in the FUV. In this paper we show that erroneous results are obtained if these lines are used, in particular in terms of DEM, elemental abundances and electron densities. For example, many authors have used the EM loci method (see Sect. 3.3 for details) and lines with anomalous behaviour to determine electron densities. The values derived from the EM loci method are often one order of magnitude higher than those derived with the line ratio technique. In the majority of cases the authors adopt the results obtained from the EM loci method, because of the weakness of the lines used in the density-sensitive line ratios, and the various uncertainties due to blending and atomic data. The discrepancy in the electron densities derived from the two different methods is often explained with unnecessary conjectures, for example by assuming that the emission was formed in distinct types of atmospheric structures, having different densities (see, e.g., Linsky et al. 1995; Pagano et al. 2000). In this paper we show that the lower densities found by the line ratio technique should be adopted and that the two methods are fully consistent if the correct EM is obtained.

In Sect. 2 we briefly discuss some of the limitations and diagnostic possibilities offered by observations with previous and current XUV spectroscopic instruments, from the the TR through to the corona. Section 3 contains a discussion of diagnostics in the far ultraviolet spectral region (FUV: 900-1700 Å) for the determination of the physical parameters of the transition regions in active stars. In Sect. 4 we consider multi-wavelength observations of the quiescent phase of the dMe star AU Mic as a benchmark case. Section 5 presents the results, including a detailed discussion of densities, and a revision of some previous solar and stellar measurements. Section 6 draws the conclusions.

2 Diagnostic possibilities in the XUV

Until the launch of the recent XUV satellites, the spectral information available from stars was limited and only provided a few diagnostic possibilities. Some diagnostics of stellar coronae were possible with the Extreme Ultraviolet Explorer (EUVE) spectrometers (SW: 70-190 Å; MW: 140-380 Å; LW: 280-760 Å). EUVE spectra had moderate resolutions ( $\Delta\lambda \approx 0.5$ , 1 and 2 Å) but could be used to get estimates of coronal densities from line ratios, and to constrain the DEM at temperatures above a million degrees. Only a few weak lines were available at lower temperatures and for element abundance analyses (cf. Drake et al. 1995). The XMM-Newton and Chandra gratings are now providing a wealth of high-resolution X-ray spectra in the 3-170 Å range. Direct estimates of temperatures, densities and element abundances are now possible using the X-ray spectra, although all the spectroscopic diagnostics are limited to the high-temperature coronal plasma. In fact, only coronal lines emitted at temperatures above a million degrees are observed, with the exception of a few weak transition region C V lines (formed at $\log\, T=5.5$ ) observed by one of the Chandra gratings.

Information on the TR can be obtained from observations in the FUV spectral region. The IUE mission observed in the FUV with two channels (SWP: 1175-2000 Å; LWR: 2000-3200 Å). Unfortunately, IUE spectra had severely limited diagnostic capabilities, since the available lines do not simultaneously satisfy conditions (a), (b), (d), (e). IUE only observed lines formed in the chromosphere and lower TR, many of which are emitted by neutrals or singly-ionised atoms and are not optically-thin. The exceptions are a few lines of Si IV, C IV, and N V which unfortunately all belong to the class of anomalous behaviour. Another limiting factor was the fact that most lines were heavily blended, since the majority of observations were done with the SWP channel at low resolution ( $\simeq$ 6 Å).

The Goddard High Resolution Spectrograph (GHRS) and Space Telescope Imaging Spectrograph (STIS) instruments on board the NASA/ESA Hubble Space Telescope (HST) have produced very good spectroscopic data in the 117-1700 Å range, with much higher S/N and spectral resolution compared to IUE. This has allowed a large number of diagnostics (in particular density) to be applied to stellar observations. However, the GHRS and STIS instruments cover similar spectral ranges to IUE, and therefore their data share some of the limitations as the IUE spectra. In fact, the lines in the GHRS and STIS spectra do not satisfy conditions (b), (c), (d), (e), (f), as discussed below. Only lines that are formed at temperatures up to log T = 5.4 are observed, with the exception of the Fe XXI 1354 Å coronal line ( $\log\, T =7$ ). Strictly, the HST spectra on their own cannot directly provide accurate DEM and elemental abundance diagnostics. Even dropping conditions (d) and (f) leaves us with just a few lines.

The Far Ultraviolet Spectroscopic Explorer (FUSE), launched in 1999, covers the 905-1187 Å region with a high resolving power (20000-25000). For cool stars, the FUSE spectral range is more useful than the HST/STIS one, since it is rich in lines from different isoelectronic sequences which cover a large temperature range, from chromospheric to coronal temperatures (Fe XVIII, Fe XIX). FUSE is also the only instrument which observes the O VI doublet, important for bridging the gap between transition region and coronal temperatures. Note that also other instruments, such as the Hopkins Ultraviolet Telescope (HUT) and the Orbiting Retrievable Far and Extreme Ultraviolet Spectrometers (ORFEUS), flown on the Space Shuttle, have provided a few spectra in the FUSE spectral region, although with much lower resolution.

3 Spectroscopic techniques for the determination of densities, temperatures and elemental abundances

The flux $I(\lambda_{ij})$ (ergs cm^-2 s^-1), of an optically thin spectral line of wavelength $\lambda_{ij}$ is

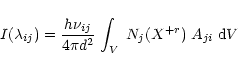$\begin{displaymath}% I(\lambda_{ij})={h \nu_{ij} \over{4\pi d^2} }\;{\int_V \; N_j(X^{+r}) \;A_{ji}\;{\rm d}V} \end{displaymath}$

(1)

where: i, j are the lower and upper levels; A_ji is the spontaneous transition probability; N_j(X^+r) is the number density of the upper level j of the emitting ion X^+r; d is the star's distance; dV is the volume element, and V is the entire source volume. The flux can be written:

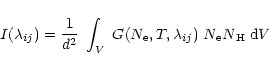$\begin{displaymath}% I(\lambda_{ij})= {1 \over d^2} ~ \int_V \; G(N_{\rm e}, T, \lambda_{ij}) \; N_{\rm e} N{\rm _H} \;{\rm d}V \end{displaymath}$

(2)

having defined $N_{\rm e}$ and $N_{\rm H}$ (cm^-3) as the electron and hydrogen number densities, and the contribution function $G(T,\lambda_{ij},N_{\rm e})$ (ergs cm³ s^-1) of each line:

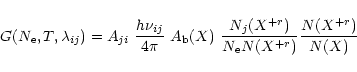$\begin{displaymath}% G(N_{\rm e},T,\lambda_{ij}) = A_{ji} ~{h \nu_{ij} \over{4\p... ...N_j(X^{+r})\over N_{\rm e} N(X^{+r})} { N(X^{+r}) \over N(X)} \end{displaymath}$

(3)

where: $A_{\rm b}(X)=N(X) / N_{\rm H}$ is the element abundance relative to hydrogen; N_j(X^+r) / N(X^+r)is the population of level j relative to the total N(X^+r)number density of the ion X^+r and is a function of the electron temperature and density; N(X^+r) / N(X) is the ionisation ratio, and is predominantly a peaked function of the temperature, confining the emission to a limited temperature range. It is common to assume that the abundance of the element $A_{\rm b}(X)$ is constant over the source volume, and to define a differential emission measure $DEM (T) = ~N_{\rm e} N_{\rm H} {{\rm d}h \over {\rm d}T}$ (cm^-5 K^-1) in order to write:

$\begin{displaymath}% {I(\lambda_{ij})}= {A_{\rm b}(X)}{\int ~{C(T,\lambda_{ij},N_{\rm e})} ~DEM (T) {\rm d}T} \end{displaymath}$

(4)

where we have defined $G(T, N_{\rm e}) = {A_{\rm b}(X)} \times {C(T, N_{\rm e})}$ , and assumed filling factors of unity and spherical symmetry, i.e. d $V=4\pi R^2_* {\rm d}h$ (h is the coordinate along the line of sight and R_* is the star's radius). Given a set of observed fluxes, the problem is to invert a set of integral equations like Eq. (4). In this paper, the DEM analysis was performed using a modified version of the Arcetri inversion code (Monsignori Fossi & Landini 1991). The CHIANTI atomic database (Dere et al. 1997) has been used to calculate the contribution functions of the observed lines, assuming collisional ionisation equilibrium. In particular, Version 3 of the database (Dere et al. 2001) was used, together with an update for O V that is described below.

Note that the determination of the DEM(T) distribution is an ill-posed problem (see, e.g. Craig & Brown 1986; McIntosh 2000, and references therein) where solutions are not unique. However, improvements can be made with a careful selection of lines, and the larger uncertainties become those associated with either the observational data or the atomic physics calculations. Also note that the DEM(T) does not necessarily have a direct physical significance (in terms of e.g. a temperature gradient), unless other factors are taken into account. For example, filling factors (cf. Judge 2000) are known to be small in the transition region, and probably different from those of the low corona.

Once the DEM is derived from a set of observed fluxes, it is possible to calculate an emission measure value $EM_{\Delta T}(T_i)$ for each temperature T_i, once a temperature interval $\Delta T$ is defined:

$\begin{displaymath}% EM_{\Delta T} (T_i) \equiv \int_{T_i- {\Delta T \over 2}}^{T_i+{\Delta T \over 2}} DEM(T)\; {\rm d}T . \end{displaymath}$

(5)

Note that many different definitions of DEM and EM are found in the literature, that, together with some confusion in the terminology adopted, can create some difficulties when comparing results from different papers. For the sake of clarity, we therefore now briefly summarise other common definitions. In order to avoid the use of spherical symmetry and of the star's radius (a parameter not always well known), a volume differential emission measure $DEM (T) = ~N_{\rm e} N_{\rm H} {{\rm d}V \over {\rm d}T}$ (cm^-3 K^-1) and a corresponding emission measure EM are often defined. The ionisation state is often assumed known by assigning a value to the ratios of the electron and hydrogen number densities (e.g. ${N_{\rm H} / N_{\rm e}} \simeq 0.8$ by assuming that H and He are fully ionised and $A_{\rm b}{\rm (He)}=0.1$ ).

Another definition that is commonly used (see, e.g. Griffiths & Jordan 1998, and references therein) involves differentiation over the logarithm of the temperature: $DEM_{\rm log} (T) = N_{\rm e} N_{\rm H} {{\rm d}V \over {\rm d}\; {\rm log} \,T}$ . This definition is more convenient when an approximation for the volume emission measure is sought. In fact, if one defines an average temperature T₀ such as log $T_0 = \int G(T) \log\, T {\rm d} \log\, T\,/\,\int G(T) {\rm d} \log\, T$ , and assumes that $DEM_{\rm log} (T)$ varies linearly with $\log\, T$ , the total emission measure over an interval $\Delta {\rm log}\, T=0.3$ centred at T₀ can be approximated with what is generally termed the EM(0.3) value (cf. Griffiths & Jordan 1998):

$\begin{displaymath}% EM_{\Delta {\rm log}\, T=0.3} (T_0) \simeq EM(0.3) \equiv ... ...d^2 \; I_{\rm ob} \over \int G(T) \; {\rm d}\, {\rm log}\, T } \end{displaymath}$

(6)

where $I_{\rm ob}$ is the observed flux at Earth. The EM(0.3) points are often used instead of the $EM_{\Delta T}$ values. Note that in the definition of EM(0.3) in Eq. (8) of Griffiths & Jordan (1998) F_* should read $4\pi d^2 F_{\rm obs}$ according to their previous definitions. Also note that the EM(0.3) values are generally plotted at the temperature $T\mbox{$\rm _{max}$ }$ where C(T) has a maximum, and not at T₀, as they should.

Another different and common approach (see Fig. 8) is to plot the ratio $I\mbox{$\rm _{ob}$ } / G(T)$ for each line as a function of temperature and consider the loci of these curves to constrain the shape of the emission measure distribution. In fact, for each line and temperature T_i the value $I\mbox{$\rm _{ob}$ } / G(T_i)$ represents an upper limit to the value of the emission measure at that temperature (assuming that all the observed emission $I\mbox{$\rm _{ob}$ }$ is produced by plasma at temperature T_i).

3.1 Anomalous behaviour of Li- and Na-like ions

It should be noted that the ionisation equilibrium plays a major role not only in the derivation of the DEM, but also in that one of the elemental abundances.

The anomalous behaviour of the ions of the Li and Na isoelectronic sequences has been known for more than 30 years. For anomalous behaviour we mean that once a DEM analysis is performed using lines from different isoelectronic sequences, the theoretical intensities of the lines of the anomalous ions are consistently under- or over-estimated by large factors. Burton et al. (1971) reported this anomalous behaviour based on a solar spectrum from a rocket flight. Dupree (1972) confirmed this anomaly, using OSO-IV solar spectra. A possible explanation of this anomaly resides in the density dependence of the ionisation fractions. Burgess & Summers (1969) showed that the density dependence of the dielectronic recombination, together with the collisional ionisations from metastable levels produce significant changes in the ionisation fractions. Vernazza & Raymond (1978) took into account these effects and showed that significant increases in the line intensities of the Li-like ions occur at high densities. The same applies to the Na-like ions, and, to a lesser extent, to other ions as well. Raymond & Doyle (1981a, 1981b) applied the ionisation equilibrium calculations of Vernazza & Raymond (1978) to Skylab data and found a good agreement between lines of different isoelectronic sequences. The problem appeared to be resolved.

However, the same authors (Doyle & Raymond 1984), among others, presented cases where these density effects were not enough to explain the anomalous behaviour. At that time, uncertainties in the atomic data and instrument's calibration were a major concern. Judge et al. (1995) presented a DEM analysis of a rocket spectrum of the entire Sun, obtained with a good photometric accuracy of 15%. They used more recent atomic data, and calculated the ionisation equilibrium taking into account the density effects. They found "very significant and systematic differences'' between the line intensities of the Li and Na isoelectronic sequences and those of the other ions. C IV, N V, and O VI lines were underestimated by factors of 2 to 5. Regarding the Na sequence, only Si IV was observed, with an underestimation by a factor of 2.

Another difficulty in investigating these effects was due to the fact that the majority of the strong lines that could be used for DEM analyses were from the anomalous class. For example, Raymond & Doyle (1981b) used Li-like lines (O VI, Ne VIII, Mg X, Si XII, S XIV), with the exception of Ar VII and Ca X, to constrain the million-degree peak of the DEM. The same argument applies to the Judge et al. (1995) results.

The problems of the paucity of the observed lines and uncertainty in the instrument's calibration have been overcomed with the spectroscopic instruments on board SOHO. Del Zanna (1999) has presented many DEM analyses of different solar regions, using SOHO/Coronal Diagnostic Spectrometer (CDS) spectra. The CDS instrument covers almost entirely the 150-800 Å spectral region, and is rich in emission lines from a large number of highly ionised ions of many different isoelectronic sequences. The CDS instrument has a good in-flight calibration (see Del Zanna et al. 2001a and references therein). The lines from the following ions have presented significant deviations (factors of 2 to 10): Ne VIII, Na IX, Mg X, Al XI, Si XII (Li-like); Ca X (Na-like). Del Zanna (1999) also found similar deviations with re-analyses of solar spectra from various instruments (including SERTS, Skylab). These discrepancies cannot be ascribed to elemental abundance anomalies, nor to instrumental effects.

Furthermore, progress in the theoretical models for ionisation and recombination processes has led to significant changes in the ionisation and recombination rates over the years. The compilation of Mazzotta et al. (1998) is the best available to date, computed for the low density limit. The Mazzotta et al. results have been used here. They are close to those of Arnaud & Raymond (1992) for the Fe ions. For the other elements the differences from the older calculations of Arnaud & Rothenflug (1985) are quite substantial, as discussed by Del Zanna (1999). Del Zanna et al. (2001b) have reanalysed Skylab data using the Mazzotta et al. (1998) ionisation fractions and up-to-date atomic data to show the extent of the anomalous behavior. The results are that lines of the Li-like N V and C IV are underestimated by factors of 3 and 10, while those of Ne VIII and Mg X are overestimated by factors of 5 and 10, respectively. The S VI 933.3 Å (Na-like) is also underestimated by a factor of 3.

We conclude that all the spectral lines of the Li and Na isoelectronic sequences observed in EUV solar spectra present significant deviations from other isoelectronic sequences. The analyses presented in Del Zanna (1999) also indicate a new characteristic. All lines in the lower transition region (e.g. C IV) are consistently underestimated, while those in the upper transition region (e.g. Ne VIII) are consistently overestimated. The deviations vary, depending on the source region observed. This suggests to us that one of the main inaccuracy in the ion balance calculations is the temperature corresponding to the peak emission. Until the reasons for these discrepancies are fully understood, and all the relevant physical effects taken into account, the lines of the Li and Na isoelectronic sequences should not be used for DEM, density and elemental abundance analyses.

3.2 Elemental abundances

Stellar coronal abundances are still poorly known, but are important to measure, because they affect our understanding of the stellar atmospheres. Comparisons with the solar case are difficult, since a large variety of solar coronal abundances have been reported, with variations from the photospheric values up to an order of magnitude (cf. the reviews of Feldman 1992; Raymond et al. 2001). These differences appear to be related to the first ionisation potential (FIP) of the various elements. The abundances of elements with low FIP (<10 eV, e.g. Fe) appear enhanced compared to those of the high FIP (>10 eV, e.g. Ne) elements, using the solar photospheric values as a standard reference. Sulfur is an important element since it lies in the middle of these two classes. This "FIP effect'' can be used as an important diagnostic of the physical processes that occur in the chromosphere and TR of active stars.

In principle, it is possible to derive a relative element abundance $A_{\rm b}(X_1)/A_{\rm b}(X_2)$ of two elements X₁ and X₂ from any observed intensity ratio $I\mbox{$\rm _{1}$ } / I\mbox{$\rm _{2}$ }$ :

$\begin{displaymath}% {A_{\rm b}(X_1) \over A_{\rm b}(X_2)} = { {I_1 \times ~\int... ..._2 \times ~\int C_1(T, N_{\rm e}) ~DEM (T) \,{\rm d}T} }\cdot \end{displaymath}$

(7)

In practice, the ionisation balance, the selection of lines, and the spectroscopic method used can each account for a variation of a factor of two or more in the derived element abundances. Various examples are given in Del Zanna (1999) and Del Zanna et al. (2001b).

In the investigation of elemental abundances and the FIP effect it has been common to use ratios of low- vs. high-FIP lines that are emitted over the same temperature range and have similar contribution functions. In the solar case lines of Mg VI and Ne VI have been widely used. In the FUSE spectra the following ions present some temperature overlap: S III, S IV vs. N III; C III vs. N III; Si III vs. S III and C III; Ne VI vs. O VI; Ne V vs. S VI. The FUSE observations are complementary to those of Chandra and XMM, which observe coronal ions.

In the literature it is common to assume that any intensity ratio is directly proportional to the relative abundances of the two elements involved. A common approach, proposed by Widing & Feldman (1989), is to approximate Eq. (4) by defining for each spectral line a single differential emission measure $DEM_{\rm L}$ value for the temperature range over which the line forms:

$\begin{displaymath}% DEM_{\rm L} \equiv \left\langle N_{\rm e} N_{\rm H} {{\rm d... ...m _{ob}$ } \over A_{\rm b}(X) ~ {\int ~{C(T) {\rm d}T }}}\cdot \end{displaymath}$

(8)

The relative elemental abundances are then adjusted in order to make the $A_{\rm b}(X) ~ DEM_{\rm L} = I\mbox{$\rm _{ob}$ } / {\int ~{C(T) {\rm d}T }}$ points lie along a common smooth curve. These points are displayed at the temperatures $T\mbox{$\rm _{max}$ }$ , defined as the temperature where C(T) has a maximum. This method can be misleading. First, the use of $T\mbox{$\rm _{max}$ }$ is problematic, since this temperature can in some cases be quite different from the temperature where the bulk of the plasma is emitted. An effective temperature $T_{\rm eff}$ , defined as $\log\, T_{\rm eff} = \int C{\left({T}\right)}~ DEM{\left({T}\right)} \log\, T~{\rm d}T / ({\int C{\left({T}\right)}~DEM{\left({T}\right)}~{\rm d}T}$ ) is more appropriate. Second, this method neglects the shape of the DEM distribution (which is not known a priori) and can therefore lead to a large under- or over-estimation of the relative abundance. This can occur if for example the DEM(T) has a steep gradient in the temperature range where C₁(T)and C₂(T) have some differences (see Del Zanna et al. 2001b for details).

The approach adopted here is to use the largest possible number of lines, calculate the line emissivities at the measured TR densities, and then determine the relative element abundances and the DEM(T) at the same time. The scaling between the high and low-FIP elements is done using lines that overlap in temperature. More details of the technique can be found in Del Zanna & Bromage (1999). In this way, most of the uncertainties will be reduced, and any systematic effects, such as those occurring with the Na- and Li-like lines will be highlighted. The use of line ratio methods for abundance diagnostics of solar and stellar coronae, in particular when lines of the Na and Li isoelectronic sequences are used, as recently suggested by e.g. Laming & Feldman (1999), is inadvisable.

3.3 Electron density

The most accurate density diagnostics are those obtained by considering the ratios of lines emitted by the same ion which are sensitive to density. However, owing to the paucity of the observed density-sensitive line pairs from the same ion, other methods have often been adopted in solar and stellar physics. One method is to compare the emission measures of the forbidden lines with those of the allowed ones. One of the first applications of this method was due to Feldman et al. (1977). A variation of this method is to compare the emission measure loci of the two groups of lines, and is the most commonly used (see, e.g., Brown et al. 1984b; Byrne et al. 1987; Jordan et al. 1987; Linsky et al. 1989; Maran et al. 1994; Linsky et al. 1995; Griffiths & Jordan 1998; Pagano et al. 2000). In most cases, large inconsistencies between the densities obtained using this method with those derived from line ratios have been reported. These inconsistencies are caused by the use of lines with anomalous behaviour, as shown below in Sect. 5.3.

Diagnostics based on line ratios have been extensively used in solar and stellar physics. In many cases, discrepancies between densities derived using different line ratios or different ions have been reported, thus leading to suggestions that the derived values might not have any physical significance (Judge & McIntosh 1999). It is well known that significant effects on the line ratios can be caused by inhomogeneities in the atmosphere (see e.g., Doschek 1984) or by plasma flows (cf. Raymond & Dupree 1978). However, we would like to stress that some of these discrepancies could also be due to un-accounted blending and/or inaccurate atomic calculations, as shown below in Sect. 5.2 with some examples. In addition, that misleading results can easily be obtained by using line ratios that have a very small sensitivity at the observed densities or when temperature effects are not taken into account. In some cases, it is possible to obtain consistent measurements, although it should be born in mind that the derived densities are in any case averaged values over the entire stellar disk and along the line of sight.

Finally, it is common in the literature to use only a few well-behaved line ratios, without considering all the observed lines. A different approach, preferable when more than two lines from an ion are observed, is to plot the values of

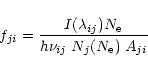$\begin{displaymath}% f_{ji}= { I(\lambda_{ij}) N_{\rm e} \over {h \nu_{ij}}\; N_j(N_{\rm e}) \;A_{ji}} \end{displaymath}$

(9)

as a function of electron density, calculated at a fixed temperature. All the curves should cross at one point, if the plasma is isodensity (a description of this method, termed L-function, can be found in Landi & Landini 1998). The f_ji curves should be calculated at the effective temperature, i.e. at the temperature where the bulk of the ion emission is. This can be quite substantially different from the temperature of the maximum ionisation fraction, in particular when the DEM has a steep gradient at the temperatures where the ion is emitted. This method has the following advantages over the line ratio technique: a) it gives an overall view of all lines; b) it shows any discrepancies even when considering lines that are not density-sensitive; c) it clearly shows which lines (and not ratios) are more suitable in a particular density regime; d) it clearly shows when lines are at the limit of their density sensitive regime. We use this method in Sect. 5.2 to discuss individual cases.

4 AU Mic multi-wavelength observations

The value of using multi-wavelength observations is evident from the above. Unfortunately it is difficult to obtain simultaneous observations with different satellites, and most authors merge observations that can be even years apart. This procedure has some limitations, since active stars are known to present high variability in the XUV on all time scales, from minutes (due to flaring) to years (possibly due to stellar cycles). In this paper we consider FUSE, STIS and EUVE observations of the dMe star AU Mic as a benchmark study. AU Mic is a nearby (9.94 pc) dM1e star smaller than the Sun (0.59 $R_{\odot}$ ). We have selected AU Mic for two main reasons.

The first is that AU Mic is one of the brightest ultraviolet and X-ray sources, observed by several satellites. EUVE observed AU Mic in quiescent and flaring state on July 14-17, 1992. A detailed analysis of the main plasma parameters during both phases was presented by Monsignori Fossi et al. (1996). AU Mic was also observed on July 22-23, 1993 (Del Zanna et al. 1995) during a quiet phase, with count rates very similar to those measured during the quiescent phase of the July 1992 observation. We have therefore adopted the July 1993 EUVE observation as representative of AU Mic in quiescence. STIS observed AU Mic on September 6, 1998 in both quiescent and flaring state. An analysis of the quiescent part of this observation (totaling to 9200s) has been presented by Pagano et al. (2000), while Robinson et al. (2001) discusses the flaring part.

The second reason is that the spectroscopic diagnostics that have been applied to AU Mic by other authors present some of the problems that we highlight in this paper. DEM analyses and calculations of radiative losses for AU Mic in quiescence have been presented by Quin et al. (1993, using IUE spectra) and by Pagano et al. (2000). The latter measured densities using different methods and ions and found some of the commonly known inconsistencies. In particular, Pagano et al. found a quite substantial discrepancy between the density derived from O IV ratios ( $\log N_{\rm e} \simeq 10.8$ ) and that deduced with the emission measure loci method ( $\log N_{\rm e} = 11.5{-}12$ ). We use a new FUSE observation of AU Mic in order to complement those of STIS and EUVE, and revise the results of Quin et al. and Pagano et al. in terms of densities, DEM and elemental abundances.

4.1 FUSE observations of AU Mic

AU Mic was observed in August 2000 with the FUSE large square aperture (LWRS: $30\hbox{$^{\prime\prime}$ }\times 30\hbox{$^{\prime\prime}$ }$ ), starting at 19:35:47 UT on the 26th and ending at 09:21:52 UT on the 27th, with a total of 9 observations (one for each orbit) of about 30 min each. We have used the publicly available data, processed with the standard FUSE pipeline package (CALFUSE version 1.7.7). Among all the channels, the SiC 2A, LiF 1A, and LiF 2A present the highest effective areas and are those that have been considered here. The standard wavelength calibration required some corrections. Normally, the wavelength scale for a given observation has a variable zero point offset. The single observations did not require any wavelength adjustments. On the other hand, large wavelength shifts of -0.25, -0.3, and -0.15 Å were required to adjust the calibration of the SiC 2A, LiF 1A, and LiF 2A channels, respectively (similar to what found by others, see, e.g., Harper et al. 2001). These shifts produce a good representation of the lines observed, as can be seen from a comparison with the theoretical wavelengths obtained from the CHIANTI database, and shown in Table 3 (note that the theoretical wavelengths are given with three decimal places for easier comparison with the observations, although they are not always known with such accuracy).

$\begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{H3236_1.ps} \end{figure}$	Figure 1: Fluxes of a selection of lines observed by FUSE during the AU Mic observation. Note the presence of a flare during the last observation.
Open with DEXTER

First, an analysis of the 9 observations has been performed. The S/N is such that only the fluxes of the brightest lines could be measured, for each observation. Figure 1 shows the time variation of the fluxes of a selection of lines during the 9 observations. The star was obviously in a quiescent state during the first 8 orbits, while during the last observation a large flare occurred. All the transition region lines increased their intensities by factors of 2 to 5. The C III, Si IV lines presented the largest increase, while lines emitted at lower (e.g. C II, Ly $_\gamma$ ) or higher (e.g. O VI) temperatures were only slightly affected. Lines emitted at coronal temperatures (Fe XVIII, Fe XIX) did not show any significant enhancement. This event cannot be classified as a classical stellar flare, but instead as a transition region explosive event. The paper by Robinson et al. (2001) focuses on brightenings with similar characteristics, although of much smaller amplitude. Something similar was also observed with STIS by Ayres (2001) during a multi-wavelength (EUVE, Chandra, STIS) campaign on the RS CVn binary HR 1099. It is possible that these types of stellar transition region events are very common in active stars. The lower sensitivity of previous instruments only allowed the observation of the long duration flares.

$\begin{figure} \par\includegraphics[angle=90,width=12cm,clip]{H3236_2.ps}\end{figure}$	Figure 2: A selection of FUSE wavelength ranges, with the AU Mic observed spectra.
Open with DEXTER

Aside from the flare, all the previous 8 observations present a remarkable constancy in fluxes. We therefore proceeded by averaging the first 8 spectra of each channel, for a total of 15686 s. In order to further increase the S/N, the spectra have also been rebinned. The line fluxes have been measured with multiple profile fitting and removal of the background. The errors have been calculated according to the S/N in the line, and derived directly from the extracted spectra in counts. The results are shown in Table 3.

Taking into account the relatively short exposure time, a considerable number of lines are clearly detected (see Fig. 2). All lines are formed in the chromosphere and transition region, with the exception of two coronal lines. In fact, we can positively identify not only the Fe XVIII 974.86 Å line (already observed in the Capella spectrum by Young et al. 2001), but also the bright Fe XIX 1118.06 Å line. The blending of C I lines with the Fe XIX line can be excluded, since C I lines are very weak in the spectrum. The identification of the Fe XIX line as well as the others is further confirmed by the DEM analysis (see Sect. 5.3 and Table 3).

4.2 Merging of the datasets

First, we have verified that the fluxes in the TR lines observed by STIS and FUSE during quiescence are consistent. In particular, the fluxes of the C III multiplet at 1175 Å as measured by both instruments are similar, with a deviation of only 7%, well within the statistical and calibration errors. Second, it is interesting to note that the fluxes of the TR lines observed by STIS and FUSE during quiescence are consistent with those obtained by IUE (Linsky et al. 1982; Ayres et al. 1983; Butler et al. 1987; Quin et al. 1993). This gives us confidence in the merging of the two datasets, that should be representative of the AU Mic quiescent "average transition region''. We have used the line fluxes of Pagano et al. (2000), assuming for the DEM analysis an indicative 20% error, since no error estimates were presented.

In this paper, we are mainly interested in the diagnostics applied to the transition region. However, we have complemented the STIS and FUSE data with the EUVE ones. We have verified that the Fe XXI 1354 Å emission observed by STIS is consistent with the Fe XXI emission measured by EUVE, and that the EUVE fluxes are broadly consistent with the FUSE data (see Sect. 5.3), thus giving us confidence in the similarity of the coronal activity during these observations years apart.

5 Results

It is important to check that the observed lines are optically thin, before performing any density estimate or emission measure modeling.

5.1 Optical depth

Fortunately, it is possible in a number of cases to check which lines are optically thick, and to what extent. We can identify two groups of lines in the AU Mic STIS and FUSE observations (see Table 1). The first are the doublets of Si IV, C IV, N V, and O VI. In the optically thin case, the ratios of the two lines of the doublet should be equal to the ratio of the oscillator strengths, i.e. 2. If opacity effects are present, the ratio would decrease, with the brightest component ²S_1/2-²P_3/2 being more affected, having a higher oscillator strength. In this case, the ratio is a direct measure of the ratio of the photon escape probabilities, from which the optical depths of the lines can be obtained (see e.g. Mathioudakis et al. 1999). The observed C IV, N V and O VI ratios indicate that the lines are optically thin. Only Si IV shows an opacity effect, with the ²S_1/2-²P_1/2 line having an optical depth of about 0.3, corresponding to a very small correction factor (a 15% increase).

Table 1: The line ratios in the STIS and FUSE spectral ranges useful for optical depth estimates. The last two columns indicate the theoretical (optical thin case) and the observed ratio values.
Ion Terms Wavelengths (Å) Th. Ob.

C II ²P_3/2-²S_1/2 /

²P_1/2-²S_1/2 1037.020/1036.332 2 1.5

Si II $\prime\prime$ 1533.430/1526.706 2 1.2

C III ³P₀-³P₁ /

³P₂-³P₁ 1175.265/1176.372 0.8 1.0

Si III $\prime\prime$ 1296.726/1303.323 0.8 0.5

C III ³P₂-³P₂ /

³P₁-³P₂ 1175.713/1174.935 3 1.9

Si III $\prime\prime$ 1298.944/1294.543 3 2

Si IV ²S_1/2-²P_3/2 /

²S_1/2-²P_1/2 1393.755/1402.770 2 1.7

C IV $\prime\prime$ 1548.201/1550.772 2 2

N V $\prime\prime$ 1238.821/1242.804 2 2

O VI $\prime\prime$ 1031.914/1037.615 2 2

**Table 1:** The line ratios in the STIS and FUSE spectral ranges useful for optical depth estimates. The last two columns indicate the theoretical (optical thin case) and the observed ratio values.
Ion	Terms	Wavelengths (Å)	Th.	Ob.
C II	²P_3/2-²S_1/2 /
	²P_1/2-²S_1/2	1037.020/1036.332	2	1.5
Si II	$\prime\prime$	1533.430/1526.706	2	1.2
C III	³P₀-³P₁ /
	³P₂-³P₁	1175.265/1176.372	0.8	1.0
Si III	$\prime\prime$	1296.726/1303.323	0.8	0.5
C III	³P₂-³P₂ /
	³P₁-³P₂	1175.713/1174.935	3	1.9
Si III	$\prime\prime$	1298.944/1294.543	3	2
Si IV	²S_1/2-²P_3/2 /
	²S_1/2-²P_1/2	1393.755/1402.770	2	1.7
C IV	$\prime\prime$	1548.201/1550.772	2	2
N V	$\prime\prime$	1238.821/1242.804	2	2
O VI	$\prime\prime$	1031.914/1037.615	2	2

The other groups of lines that can be used to estimate the opacity are those where there are ratios of lines that originate from a common upper level (a branching ratio). In the optically thin case, the ratios are equal to the ratios of the A-values (see, e.g. Jordan 1967). The STIS and FUSE spectra contain a number of useful ratios, of C II, Si II, Si III, and C III. The C II ratio indicates the presence of opacity effects, although of smaller amplitudes than those reported on the Sun (see, e.g. Brooks et al. 2000). Also Si II appears to be affected by opacity. The Si III is the worst case, since the 1296.726 Å line is very weak in the spectrum, and the 1298.944 Å line is blended with another line of the multiplet. If the blend is accounted for, the observed ratio indicates some opacity in the 1298.944 Å line, similarly to the solar case (cf. Keenan & Kingston 1986).

The first C III ratio is consistent with the theoretical value, while the second one is lower than the predicted one, suggesting some opacity. The latter result is more uncertain, because the measurement of the 1175.713 Å line is difficult, owing to the presence of the 1175.592 Å line. Even with the high spectral resolution of FUSE these two lines are difficult to deblend with a multiple profile fitting. In any case, these C III results are similar to those obtained from solar observations (see, e.g., Doyle & McWhirter 1980; Brooks et al. 2000) and indicate that within the multiplet the 1175.713 Å line has the highest optical thickness, as expected. It is worth noting that the Si III and C III line ratios can be affected by any inhomogeneities of the atmosphere (see, e.g. Doschek & Feldman 1977) because of their density and temperature sensitivity.

In conclusion, we can say that only a small number of lines are somewhat affected by opacity. However, no corrections to the line fluxes have been applied, since they would only slightly affect the lines at the lower temperatures and would not change the main results discussed in the DEM analysis (Sect. 5.3).

5.2 Electron density

In what follows, we review the density diagnostics relevant to active stars in the STIS and FUSE spectral regions, by comparing observations with the best atomic data available.

5.2.1 O IV and S IV

The O IV and S IV lines around 1400 Å (see Table 2) are well known density diagnostics in both solar and stellar spectra (cf. Linsky et al. 1995; Cook et al. 1995; Brage et al. 1996; Harper et al. 1999; Teriaca et al. 2001, and references therein). They are considered to be the best diagnostics in the FUV wavelength range because their temperature sensitivity is very small, compared to other cases such as C III, O V and Si III (see below). However, a number of problems and inconsistencies have been reported in the literature, leading to a degree of confusion on the reliability of the O IV and S IV lines. In what follows, we will discuss several issues, complementing the AU Mic observations with those of Cook et al. (1995) and Linsky et al. (1995). Cook et al. (1995) presented a comprehensive list of O IV and S IV solar observations (including active regions, flares), while Linsky et al. (1995) published one of the best spectrum in the FUV, based on HST/GHRS observations of Capella.

Table 2: The O IV and S IV transitions in the STIS spectral range and some of the density-sensitive ratios commonly used.
Ion Terms Wavelength (Å) Ratio

O IV ²P_1/2-⁴P_3/2 1397.217

O IV ²P_1/2-⁴P_1/2 1399.779

O IV ²P_3/2-⁴P_5/2 1401.171

O IV ²P_3/2-⁴P_3/2 1404.793 (bl)

O IV ²P_3/2-⁴P_1/2 1407.383

O IV 1401.171/1399.779 R₁

O IV 1401.171/1407.383 R₂

O IV 1401.171/1404.793 R₃

O IV 1404.793/1407.383 R₄

O IV 1404.793/1399.779 R₅

S IV ²P_1/2-⁴P_3/2 1398.040

S IV ²P_1/2-⁴P_1/2 1404.808 (bl)

S IV ²P_3/2-⁴P_5/2 1406.016

S IV ²P_3/2-⁴P_3/2 1416.887

S IV ²P_3/2-⁴P_1/2 1423.839

S IV 1416.887/1406.016 R₆

S IV 1423.839/1416.887 R₇

**Table 2:** The O IV and S IV transitions in the STIS spectral range and some of the density-sensitive ratios commonly used.
Ion	Terms	Wavelength (Å)	Ratio
O IV	²P_1/2-⁴P_3/2	1397.217
O IV	²P_1/2-⁴P_1/2	1399.779
O IV	²P_3/2-⁴P_5/2	1401.171
O IV	²P_3/2-⁴P_3/2	1404.793 (bl)
O IV	²P_3/2-⁴P_1/2	1407.383
O IV		1401.171/1399.779	R₁
O IV		1401.171/1407.383	R₂
O IV		1401.171/1404.793	R₃
O IV		1404.793/1407.383	R₄
O IV		1404.793/1399.779	R₅
S IV	²P_1/2-⁴P_3/2	1398.040
S IV	²P_1/2-⁴P_1/2	1404.808 (bl)
S IV	²P_3/2-⁴P_5/2	1406.016
S IV	²P_3/2-⁴P_3/2	1416.887
S IV	²P_3/2-⁴P_1/2	1423.839
S IV		1416.887/1406.016	R₆
S IV		1423.839/1416.887	R₇

Let us consider O IV first. The 1397.217 Å is very weak and is rarely observed even in solar spectra. The 1399.779 Å line is also very weak, and usually has a large observational error associated with it. The 1399.779/ 1407.383 Å is a branching ratio, and excellent agreement between theory and observations is normally found (e.g. Cook et al. 1995). The ratios that include the 1401.171 Å line (R₁, R₂, R₃) have often been used to estimate the density, even though they have a very small density sensitivity as already noted by Feldman & Doschek (1979) and as can be judged from Fig. 3. Even with accurate measurements, large errors should be expected, particularly for densities higher than 10¹⁰ cm^-3. On the other hand, ratios including the 1404.793 Å line (R₄, R₅) have a much better density sensitivity, and have therefore often been preferred. Unfortunately, the 1404.793 Å line is a well-known blend with S IV (1404.808 Å) and with another unknown line (as described below), and therefore its use cannot preclude an understanding of the S IV emission.

The S IV 1416.887 Å and 1423.839 Å lines are weak and are often not detected, even in solar spectra. The 1398.040 Å line is even weaker. It is common practice in both solar and stellar physics to use the theoretical ratio of the 1404.808 Å and 1406.016 Å lines to infer the contribution of the 1404.808 Å line to the observed blend with O IV. The first problem with this method is that the 1404.808/1406.016 Å ratio is density sensitive, and therefore, unless there is an independent way of measuring the density, it should not be used. The second problem is in explaining the S IV emission, as discussed below.

In previous publications, the S IV atomic calculations by Dufton et al. (1982) have normally been used. These calculations predict that the intensity of the 1404.808 Å line is about 0.2 the intensity of the 1406.016 Å line, up to densities of $3 \times 10^{11}$ cm^-3. This results in a contribution to the observed blend that is normally only of the order of 5-10%, i.e. it is generally assumed that the observed blend is mostly O IV 1404.793 Å. Now, a further problem is that many authors report inconsistencies between the densities obtained by using different line ratios. For example, Cook et al. (1995) report that densities derived from the R₄ ratio are consistently more than an order of magnitude smaller than those derived from the R₂ ratio, for a wide range of cases (Quiet Sun, Active Regions, Sunspots, Flares). Similarly, many authors found inconsistencies with the densities derived from S IV lines. For example, Cook et al. (1995) pointed out that the densities derived from the R₆, R₇ ratios are beyond the low- or high-density limit, and no comparisons with the densities derived from O IV could be made. These inconsistencies in the O IV and S IV lines therefore suggest various possibilities:

1.: the atomic data for O IV are inaccurate;
2.: the atomic data of Dufton et al. for S IV are inaccurate;
3.: the blend observed at 1404.8 Å is mostly due to an unidentified line, and not to either O IV or S IV or a combination of the two;

among with other more subtle explanations, such as fluorescence, suggested by Cook et al. (1995). Regarding option (1), we note that Cook et al. (1995) used the collisional R-matrix calculations of Zhang et al. (1994) for O IV. Brage et al. (1996) presented new O IV atomic structure calculations. They compared their O IV model with a wide range of solar and stellar observations, including the same data presented by Cook et al. (1995), and removing the S IV contribution to the 1404.8 Å blend according to the Dufton et al. (1982) calculations. Brage et al. (1996) claimed that in most cases no inconsistencies were found, in contrast to previous studies such as in Cook et al. (1995). However, it should be noted that Brage et al. considered different line ratios (R₂, R₃, R₅), and their results are therefore not directly comparable with those of Cook et al. (1995). We used the CHIANTI v3.02 atomic model for O IV, which includes the collisional R-matrix calculations of Zhang et al. (1994), together with A-values from Flower & Nussbaumer (1975). The model gives results that are very close to those of Brage et al. (1996), as shown by Teriaca et al. (2001).

$\begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{H3236_3.ps}\par\includegraphics[angle=90,width=7.5cm,clip]{H3236_4.ps}\end{figure}$	Figure 3: The f_ji curves of the S IV and O IV lines observed by HRTS I during a solar flare - 1973 Sep. 7 12:21 UT (Cook et al. 1995). We have assumed here that 50% of the intensity of the observed blend at 1404.8 Å is due to the S IV 1404.808 Å line, while the other 50% is due to O IV 1404.793 Å.
Open with DEXTER

Regarding option (2), there is now substantial evidence for the inaccuracy of the Dufton et al. calculations. Aside from the studies already mentioned, Harper et al. (1999) used the same S IV ratios and atomic data of Cook et al. and found inconsistencies with the HST/GHRS spectra of the RR Tel nebula. Doschek et al. (1999) reported SOHO/SUMER measurements of S IV over a wide wavelength range (661-1406 Å), and found very large disagreements with the Dufton et al. calculations, of up to a factor of 6. We used the CHIANTI version 3.02 model for S IV, that includes the recent R-matrix calculations of Tayal (2000). We have considered a large number of published solar and stellar observations, and found that the new atomic data for S IV gives very different results, in most cases in good agreement with the observations. A detailed discussion is beyond the scope of this paper. Here, we only mention that in the 661-900 Å range the agreement with the Doschek et al. (1999) data is now excellent, and provide two examples to illustrate this point.

$\begin{figure} \par\includegraphics[angle=90,width=7cm,clip]{H3236_5.ps}\par\includegraphics[angle=90,width=7cm,clip]{H3236_6.ps}\end{figure}$	Figure 4: The f_ji curves of the S IV and O IV lines observed by HST/GHRS on Capella (Linsky et al. 1995).
Open with DEXTER

The first example is presented in Fig. 3, and shows the f_ji curves of the O IV and S IV measurements of Cook et al. (1995) during a solar flare. Contrary to what Cook et al. found, it can be seen that the three unblended S IV lines do indicate a consistent density ( $5 \times 10^{11}$ cm^-3). Agreement with the 1404.808 Å line is also found by assuming that the S IV line contributes to 50% of the observed blend. If one assumes that the other 50% is all O IV 1404.793 Å, agreement is also found with the other O IV lines, although all lines are in the high density limit and therefore no reliable density measurement can be established (contrary to what Cook et al. found). The problem with the O IV and S IV lines appears to have been resolved.

$\begin{figure} \par\includegraphics[angle=90,width=7cm,clip]{H3236_7.ps}\par\includegraphics[angle=90,width=7cm,clip]{H3236_8.ps}\end{figure}$	Figure 5: The f_ji curves of the S IV and O IV lines observed by STIS and FUSE. The intensity of the S IV 1404.808 Å line has been assumed equal to 20% the intensity of the observed blend.
Open with DEXTER

However, we found a number of cases in both solar and stellar spectra where additional blending in the 1404.8 Å line seems to occur. Figure 4 shows the second example: the f_ji curves of the O IV and S IV lines of one of the best stellar spectra (Capella - Linsky et al. 1995). The S IV 1404.808 Å line is in agreement with the other S IV lines only if its intensity is 9% that of the observed line. If one assumes that the rest (91%) is all due to O IV 1404.793 Å, no agreement is found with the other O IV lines. Instead, the contribution of the O IV line should be about 50%. This leaves about 40% of the observed line due to an unknown blend. The measurements have very small errors, indicated in the figure. Figure 4 also shows that no conclusive density measurement based on S IV can be obtained, while the O IV indicates a density of $4 \times 10^{10}$ cm^-3, a value almost an order of magnitude higher than the value indicated by Linsky et al.

Let us now consider the FUSE and STIS AU Mic observations of S IV and O IV (see Fig. 5). To reach consistency with the other lines, the intensity of the S IV 1404.808 Å line has been assumed equal to 20% the intensity of the observed blend. If we assume that the rest (80%) of the observed blend is due to the O IV 1404.7 Å line, we can see that the O IV f_ji curves are consistent with a density of the order of $5{-}9 \times 10^{10}$ cm^-3. The measurement of the 1399.779 Å line is in obvious disagreement, and might be due to weakness of this line. The same holds for the S IV 1406.016 Å line.

5.2.2 O V

$\begin{figure} \par\includegraphics[angle=90,width=7cm,clip]{H3236_9.ps}\par\includegraphics[angle=90,width=7cm,clip]{H3236_10.ps}\end{figure}$	Figure 6: The f_ji curves of the O V lines observed in the STIS spectrum of AU Mic. Top: values calculated with the Zhang & Sampson (1992 - CHIANTI v. 3.01) and Berrington et al. (1985 - CHIANTI v. 3.02) atomic data at the same temperature. Note the large difference. Bottom: values calculated at two temperatures. Note the large temperature effect.
Open with DEXTER

The Be-like O V is particularly important for the STIS spectral range, since the ratio of the 1218.390 and 1371.292 Å lines is an excellent diagnostic at the densities of active stars. However, many authors in the past reported discrepancies between the densities derived from this ratio with those obtained from other ions. For example, Pagano et al. (2000) used the Zhang & Sampson (1992) collisional data and obtained from this ratio a density of $5 \times 10^{11}$ cm^-3, at odds with what derived from the O IV ratios. If the R-Matrix calculations of Berrington et al. (1985) are used (CHIANTI version 3.02), large differences are found for some transitions, and the densities derived from O V become consistent with those obtained from other ions, as shown in Fig. 6. In fact, at the effective temperature $T_{\rm eff} = 2.7 \times 10^{5}$ K (see Table 3), the observed ratio indicates an electron density of $5 \times 10^{10}$ cm^-3. Note that this $T_{\rm eff}$ is quite different from the temperature of maximum ionisation fraction ( $T = 2.5 \times 10^{5}$ K according to Mazzotta et al. 1998) and that a small difference in temperature has a large effect on the ratio (Fig. 6).

5.2.3 Si III

There are a few Si III lines visible in the FUSE and STIS spectral ranges that could be used for density diagnostics. For example, the resonance 3s² ¹S₀-3s 3p ¹P₁ line at 1206.499 Å has a density dependence different compared to the lines of the 3s 3p ³P-3p² ³P multiplet. All the measurements are consistent with the density derived from O V, with two exceptions, the ³P₁-³P₀ (1301.147 Å) and the ³P₁-³P₂ (1294.543 Å) lines observed by STIS, which are probably blended. However, the Si III results have a large uncertainty, since the density dependence is small, and temperature effects are even greater than in the O V case. This occurs because the DEM of AU Mic presents a a steep gradient at the Si III temperatures (see Sect. 5.3), larger than for O V.

5.2.4 C III

Densities could be obtained using the well-known ratio of the resonance 2s² ¹S₀-2s 2p ¹P₁ line at 977.022 Å with the total intensity of the 2s 2p ³P-2p² ³P multiplet at 1175 Å. However, this diagnostic is only sensitive up to log $N_{\rm e}=10$ (cm^-3) and is therefore not useful for active stars, that normally have higher densities. Moreover, temperature and opacity effects can be large. The C III 977/1176 Å ratio as measured from FUSE spectra is 1.0, much lower than the high-density limit (1.7), according to the C III CHIANTI model and calculated at $T= 6.3 \times 10^4$ K. This discrepancy can be interpreted in terms of opacity effects in the resonance line. The ratio is therefore not useful for density diagnostic for AU Mic, nor probably for diagnostic of other active stars. Young et al. (2001) and Ake et al. (2000) report FUSE measurements of Capella and AB Dor, a rapidly rotating active star. They report ratios of $2.0 (N_{\rm e} = 2 \times 10^{10}$ cm^-3) and 1.5, close to the high-density limit, but also point out the uncertainties related to opacity effects. Schmitt et al. (1998) report ORFEUS observations of AB Dor, but measured a ratio in the range 1.0-1.3. The authors conclude that the AB Dor TR had densities in excess of 10¹¹ cm^-3. However, these ratio values are much lower than the high-density limit, and we believe that opacity effects are probably significant also in the ORFEUS spectrum, and no conclusions can be drawn.

5.2.5 Summary of density diagnostics

If we restrict to the FUV spectral range and consider the Capella and AU Mic observations as typical for active stars ( $N_{\rm e} = 5{-}10 \times 10^{10}$ cm^-3), we can conclude that: a) the best diagnostic is O V, although with some uncertainties, due to the weakness of the 1371.292 Å line and the temperature effects; b) results based on the O IV diagnostic should be treated with caution given the low density sensitivity and blending; c) the C III diagnostic is only useful at lower densities, and should be treated with caution because of opacity and temperature effects; d) the S IV diagnostic is only useful at higher densities; e) the Si III diagnostic has large temperature effects. Any measurement involving these ions should therefore be treated with caution and complemented with other methods. One possibility (see Sect. 5.3 below) is to use the EM loci method and the O III 1666.142 Å and N IV 1486.496 Å lines, that are density-sensitive (relative to dipole allowed transitions) in the 10¹⁰-10¹¹ cm^-3 regime.

Another method, frequently adopted in the literature, is to use ratios of lines emitted by different elements. This leads to uncertain results unless independent methods for checking the ionisation state and the relative elemental abundances can be used. Temperature effects can also be important. For example, Doschek et al. (1978) and following authors (e.g. Cook & Nicholas 1979) suggest the use of the Si III 1892 Å/C III 1908 Å ratio. As already mentioned, both C III and Si III lines have large temperature effects and therefore can only be used not only when the relative C/Si abundance is known, but also when the DEM is independently estimated. Cook & Nicholas (1979) and following authors (e.g. Byrne et al. 1987) also suggest the use of the Si IV 1402 Å/C III 1908 Å ratio. In this case, aside from the same problems that the Si III/C III ratio has, this ratio is unreliable because the Si IV lines belong to the anomalous class.

5.3 The $\mathsfsl{DEM}$ of AU Mic in quiescence

$\begin{figure} \par\includegraphics[angle=90,width=10cm,clip]{H3236_11.ps}\end{figure}$	Figure 7: The DEM of AU Mic in quiescence, as derived from FUSE, STIS and EUVE spectra. Note the large deviations of the lines of the Li-like (C IV, N V) and Na-like (Si IV) ions.
Open with DEXTER

We have used the observations detailed in Sect. 4 to derive a DEM. As a first attempt, the photospheric abundances of Grevesse & Sauval (1998) have been used, with a correction for the oxygen abundance to a value of 8.73 (in the usual dex notation, with H fixed at 12), as recently revised by Grevesse (2002). Note that this value is much lower than the value of 8.93 published in Grevesse & Anders (1991), which has been used as a reference in many previous studies. The contribution functions have been calculated at a constant electron pressure $P_{\rm e}=1 \times 10^{16}$ cm^-3 K, for reasons that are explained below. The resulting DEM is plotted in Fig. 7, while Table 3 presents the line list with the details and line identifications. Each experimental data point is over-plotted in Fig. 7 at the effective temperature $T_{\rm eff}$ and at a value equal to the product $DEM(T\mbox{$\rm _{eff}$ }) \times (I_{\rm ob}/I_{\rm th})$ . The error bars refer to the combination of observational and theoretical (10%) errors and give an idea of the uncertainties in the derived DEM values.

First, let us examine the DEM at lower temperatures. The DEM is well constrained in the log T =4-6range by all the lines observed by STIS and FUSE. The general agreement between the two sets of lines is very good, considering the lack of simultaneity. The DEM at temperatures as high as 10⁶ K is well constrained by the O VI lines, that have a long tail in their contribution function at high-temperatures. As in the case of the Sun, the DEM has a minimum around $\log\, T = 5.2$ , and presents the usual increase toward million-degrees temperatures (see, e.g., Del Zanna & Bromage 1999, for solar DEM distributions). The exact position of the minimum is not well constrained, since there are no observed allowed lines between the temperatures where S IV and O V are emitted. However, further constraints are given by N IV] and O IV], as discussed below. The S III, N III, S IV lines observed by FUSE confirm the anomalous behaviour of the lines of the Li and Na isoelectronic sequences. This anomalous behaviour is quite striking. The Li-like N V and C IV lines are underestimated by factors larger than 3 and 5, respectively. The Na-like Si IV lines are also underestimated by a factor larger than 5. The S VI 933.3 Å (Na-like) is overestimated (only by a 40%), while the O VI lines are the only ones that do not seem to present anomalous behaviour. This confirms the problems with these ions already found in the solar spectra.

In order to estimate the importance of density effects in the ion balance calculations for this case, we have performed a DEM analysis using ionisation fractions calculated at a density $N_{\rm e}=10^{10}$ cm^-3 (J. Raymond 2001, priv. comm.). As already shown by Vernazza & Raymond (1978), density effects can be quite large. Indeed, we have found significant changes, not only to the calculated fluxes, but also to the effective temperatures. The fluxes of the Li- and Na-like lines increase (e.g. by factors of 2 for C IV and 3 for Si IV), suggesting that these density effects are in fact very important, although still not sufficient to completely remove the discrepancy in this particular case.

Our DEM distribution is in stark contrast with those obtained by Quin et al. (1993) and Pagano et al. (2000). The latter found a minimum in the DEM at $\log\, T = 4.7$ , with a nearly flat DEM until $\log\, T = 5.4$ , and concluded that the energy balance in the transition region of AU Mic is very different from that of the Sun. The large discrepancy in the results obtained by Pagano et al. (2000) is due to the fact that they used the Si III, Si IV, C IV, N V lines observed by STIS to constrain the log T = 4.5-5.5 region. Pagano et al. presented the results in terms of the $I\mbox{$\rm _{ob}$ } / (A_{\rm b} \times C(N_{\rm e}, T))$ curves. For comparison, we show in Fig. 8 (top) these curves, together with the $EM_{\Delta {\rm log}\, T=0.3}$ values, i.e. the emission measures calculated with a $\Delta {\rm log}\, T=0.3$ , for all the allowed lines, excluding those of the Li and Na isoelectronic sequences, that are plotted in Fig. 8 (middle). The erroneous DEM derived by Pagano et al. (2000) resulted in the particularly high densities required to explain the fluxes of the density-sensitive lines of O III, N IV, O IV, O V (log $N_{\rm e} = 11.5{-}12$ ) by using the emission measure loci. Figure 8 (bottom) clearly shows that the much lower densities found here are perfectly consistent with the emission measure values. We note that the use of the emission measure loci method can provide misleading results, since the $I\mbox{$\rm _{ob}$ } / (A_{\rm b} \times C(T))$ curves only provide upper limits to the emission measure. Instead it is important to calculate the line fluxes, i.e. the emissivities integrated over the DEM distribution. In this respect, it is interesting to examine the behaviour of the line fluxes when the emissivities are calculated at different densities (or pressures). Figure 9 shows the results obtained when the emissivities are calculated at two constant densities ( $N_{\rm e}= 3.5$ and $14 \times 10^{10}$ cm^-3) and at constant pressure ( $P_{\rm e}= 10^{16}$ cm^-3 K). Figure 9 shows that:

a) the O III] and N IV] lines are very sensitive to small density variations;

b) the Si III] lines are very sensitive to both density and temperature effects;

c) it is impossible to reproduce all the intensities of the density sensitive lines if the emissivities are calculated at constant density;

d) a constant pressure $P_{\rm e}= 10^{16}$ cm^-3 K produces good agreement for all the transition region lines in the $\log\, T = 4.5{-}5.5$ range (Si III], O III], N IV], O IV], O V], with the exception of S IV] 1406.016 Å, that probably has an erroneous observed flux, see Sect. 4.2.1) and confirms the densities derived from the L-function method;

e) with this constant pressure, the N IV and O IV lines confirm the presence of a minimum at $\log\, T = 5.2$ in the DEM.

At higher temperatures, the DEM is not well constrained between log T = 6-6.7. The EUVE measurements suggest a peak at log $T \simeq 6.1$ and a decrease at log T = 6.5. It is interesting to note that the Chandra and XMM gratings observe only few lines that cover this important temperature range, where the bulk of the quiet Sun emission is. The DEM has a peak at log T = 6.9, well constrained by the FUSE and STIS data, together with the EUVE ones. This peak is typical of the coronae of active stars and of solar flares.

Regarding elemental abundances, no significant departures from the adopted solar photospheric abundances are found. This includes low-FIP elements (Si), medium-FIP elements (S), and high-FIP ones (C, N, O, Ne). This is in stark contrast to the result obtained by Quin et al. (1993), where solar coronal abundances were found to be satisfactory. Again, this erroneous result was due to the use of the Si IV, C IV, N V lines in the DEM analysis.

Finally, it should be noted that erroneous DEM distributions and chemical abundances such as those found for the AU Mic transition region by Quin et al. (1993) and Pagano et al. (2000) lead to inaccurate calculations of the radiative losses, and to misconceptions about physical processes that are derived from them.

6 Conclusions

We have discussed diagnostic methods and atomic data for the determination of densities, the DEM and the chemical composition of the transition regions and coronae of the Sun and active stars. We have described the severe limitations which some of the commonly used methods have. We have illustrated several issues with examples, mainly focusing on the diagnostic methods for the transition region using FUV (900-1700 Å - HST/STIS, FUSE) observations of AU Mic. We have complemented them with FUV observations of the Sun and Capella. We have revised some previous analyses and obtained results that are significantly different from those of other authors.

The problems highlighted are quite general and apply to other stellar transition regions (including the Sun) and to other wavelength ranges. In terms of emission measure analysis, we have indicated what we think is the best approach, which avoids frequently used approximations. We have described the main problems related to the direct determination of the relative elemental abundances, giving warnings about the use of emission measures and line ratio methods.

$\begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{H3236_12.ps}\par\... ...6_13.ps}\par\includegraphics[angle=90,width=7.5cm,clip]{H3236_14.ps}\end{figure}$	Figure 8: The emission measures $EM_{\Delta {\rm log}\, T=0.3}$ values, together with the $I\mbox{$\rm _{ob}$ } / (A_{\rm b} \times C(T))$ curves, calculated at constant pressure $P_{\rm e}= 10^{16}$ cm^-3 K. From top to bottom: the curves for the allowed lines; the curves for the anomalous allowed lines of the Li- and Na-like sequences; the curves for the forbidden lines.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=90,width=7.6cm,clip]{H3236_15.ps}\par\... ...6_16.ps}\par\includegraphics[angle=90,width=7.6cm,clip]{H3236_17.ps}\end{figure}$

Figure 9: The DEM of the AU Mic in quiescence (same as Fig. 7), but with the emissivities calculated, from top to bottom: at constant density $N_{\rm e}= 3.5 \times 10^{10}$ cm^-3; $N_{\rm e}= 14 \times 10^{10}$ cm^-3; at constant pressure $P_{\rm e}= 10^{16}$ cm^-3 K. Note the large variations in the forbidden lines Si III], O III], N IV], O IV], O V], and the fact that a constant pressure $P_{\rm e}= 10^{16}$ cm^-3 K produces the best agreement in the temperature range shown.

Open with DEXTER

Regarding electron densities, we have discussed the limitations of using single line ratios, and recommended the use of the L-function method, which gives a better overall view of the results. We have presented the limitations in the use of lines that have a small density sensitivity, providing a discussion of the O IV lines at 1400 Å as an example. The use of these lines is further complicated by the presence of an unknown blend.

We have shown the importance of revising earlier results by using more up-to-date atomic calculations. As an example, we have shown that the latest S IV calculations of Tayal (2000) provide density estimates that are significantly different from those reported in the previous literature.

The anomalous behaviour of lines from the Li and Na isoelectronic sequences has been neglected too often in previous solar and stellar publications. We have shown that the use of these lines produces erroneous results in the determination of: a) the DEM; b) the elemental abundances; c) the densities using the emission measure loci method. Note that in most papers these lines have been the primary means of determining the physical characteristics of the solar and stellar transition regions.

In light of the above, we believe that a large body of work in terms of spectroscopic diagnostics of the solar and stellar outer atmospheres (and their application to physical modeling) should be revisited, now that more accurate atomic and observational data are available.

Table 3: Results of the DEM analysis. The columns consist of: (1) the ion; (2) the theoretical wavelength $\lambda _{\rm th}$ ; (3) the observed wavelength $\lambda _{\rm ob}$ ; (4) configuration and term description; (5) observed flux $I_{\rm ob}$ (10^-14 ergs cm^-2 s^-1); (6) ratio between the theoretical $I_{\rm th}$ and the observed flux; (7) the estimated error on the ratio value; (8) the effective temperature (log values); (9) $T_{\rm max}$ (log values); (10) the contribution of each transition to the total calculated intensity of the line. (11) the instrument. The last column indicates: (*) a selection of the observed allowed lines; (a) the anomalous allowed lines of the Li- and Na-like sequences; (d) the forbidden lines. The lines marked in the last column are plotted in Fig. 8.
Ion $\lambda _{\rm th}$ $\lambda _{\rm ob}$ Transition $I_{\rm ob}$ $I_{\rm th}$ / +/- log log frac

(Å) (Å) (10^-14) $I_{\rm ob}$ $T_{\rm eff}$ $T_{\rm max}$

Si II 1533.430 1533.406 3s² (¹S) 3p ²P_3/2-3s² (¹S) 4s ²S_1/2 0.69 1.09 0.24 4.28 4.43 STIS

Si II 1526.706 1526.687 3s² (¹S) 3p ²P_1/2-3s² (¹S) 4s ²S_1/2 0.58 0.66 0.15 4.28 4.43 STIS

Si II 1304.369 1304.355 3s² (¹S) 3p ²P_1/2-3s 3p² ²S_1/2 0.12 1.05 0.23 4.33 4.48 STIS *

Si II 1309.274 1309.287 3s² (¹S) 3p ²P_3/2-3s 3p² ²S_1/2 0.32 0.78 0.17 4.33 4.48 STIS

Si II 1264.737 1264.725 3s² (¹S) 3p ²P_3/2-3s² (¹S) 3d ²D_5/2 0.48 2.01 0.45 4.35 4.49 STIS

Si II 1265.001 1264.986 3s² (¹S) 3p ²P_3/2-3s² (¹S) 3d ²D_3/2 0.21 0.55 0.12 4.35 4.49 STIS

S II 1253.811 1253.808 3s² 3p³ ⁴S_3/2-3s 3p⁴ ⁴P_3/2 0.12 1.65 0.37 4.34 4.45 STIS

S II 1259.519 1259.495 3s² 3p³ ⁴S_3/2 -3s 3p⁴ ⁴P_5/2 0.14 0.80 0.18 4.35 4.45 STIS *

C II 1334.524 1334.535 2s² (¹S) 2p ²P_1/2-2s 2p² ²D_3/2 6.89 1.00 0.22 4.44 4.58 STIS

C II 1335.709 1335.692 2s² (¹S) 2p ²P_3/2-2s 2p² ²D_5/2 14.39 0.96 0.21 4.44 4.58 STIS *

C II 1036.332 1036.302 2s² (¹S) 2p ²P_1/2-2s 2p² ²S_1/2 0.73 1.06 0.17 4.53 4.63 FUSE

C II 1037.020 1036.982 2s² (¹S) 2p ²P_3/2-2s 2p² ²S_1/2 1.1 1.39 0.18 4.53 4.63 FUSE

C II 1323.952 1323.929 2s 2p² ²D_5/2-2p³ ²D_5/2 0.14 0.95 0.21 4.63 4.69 0.56 STIS

C II 1323.907 2s 2p² ²D_3/2-2p³ ²D_3/2 4.69 0.36

Si III 1206.499 1206.496 3s² ¹S₀-3s 3p ¹P₁ 7.9 1.09 0.24 4.64 4.78 STIS *

Si III 1301.147 1301.139 3s 3p ³P₁-3p² ³P₀ 0.17 0.65 0.14 4.66 4.77 STIS

Si III 1303.323 1303.325 3s 3p ³P₂-3p² ³P₁ 0.15 1.05 0.23 4.66 4.77 STIS

Si III 1298.944 1298.938 3s 3p ³P₂-3p² ³P₂ 0.51 1.11 0.25 4.67 4.77 0.83 STIS d

Si III 1298.892 3s 3p ³P₁-3p² ³P₁ 4.77 0.17

Si III 1294.543 1294.537 3s 3p ³P₁-3p² ³P₂ 0.21 0.76 0.17 4.67 4.77 STIS

Si III 1296.726 1296.713 3s 3p ³P₀-3p² ³P₁ 0.08 1.60 0.36 4.67 4.77 STIS

Si III 1109.969 1110.006 3s 3p ³P₁-3s 3d ³D₂ 0.25 1.27 0.28 4.69 4.78 0.74 FUSE

Si III 1109.939 3s 3p ³P₁-3s 3d ³D₁ 4.78 0.26

Si III 1108.357 1108.370 3s 3p ³P₀-3s 3d ³D₁ 0.083 1.32 0.68 4.69 4.78 FUSE

Si III 1113.229 1113.270 3s 3p ³P₂-3s 3d ³D₃ 0.31 2.00 0.39 4.69 4.78 0.87 FUSE

Si III 1113.203 3s 3p ³P₂-3s 3d ³D₂ 4.78 0.13

S III 1021.321 1021.357 3s² 3p² ³P₂-3s 3p³ ³P₂ 0.083 1.38 0.48 4.71 4.79 FUSE *

S III 1077.171 1077.017 3s² 3p² ¹D₂-3s² 3p 3d ¹D₂ 0.13 1.10 0.56 4.72 4.80 FUSE *

C III 977.022 977.015 2s² ¹S₀-2s 2p ¹P₁ 12 1.49 0.16 4.81 4.92 FUSE

C III 1174.935 1174.939 2s 2p ³P₁-2p² ³P₂ 2 0.70 0.10 4.82 4.92 FUSE

C III 1175.265 1175.281 2s 2p ³P₀-2p² ³P₁ 1.6 0.70 0.10 4.82 4.92 FUSE

C III 1175.592 1175.570 2s 2p ³P₁-2p² ³P₁ 1.1 0.76 0.11 4.82 4.92 FUSE

C III 1175.713 1175.709 2s 2p ³P₂-2p² ³P₂ 3.8 1.10 0.16 4.82 4.92 FUSE *

C III 1175.989 1175.986 2s 2p ³P₁-2p² ³P₀ 1.8 0.62 0.09 4.82 4.92 FUSE

C III 1176.372 1176.366 2s 2p ³P₂-2p² ³P₁ 1.6 0.87 0.12 4.82 4.92 FUSE

C III 1175.713 1175.694 2s 2p ³P₂-2p² ³P₂ 3.98 1.05 0.24 4.82 4.92 STIS

Si IV 1402.770 1402.747 3s ²S_1/2-3p ²P_1/2 2.92 0.18 0.04 4.88 4.87 STIS a

Si IV 1393.755 1393.744 3s ²S_1/2-3p ²P_3/2 4.93 0.21 0.05 4.88 4.88 STIS a

Si IV 1128.325 1128.350 3p ²P_3/2-3d ²D_5/2 0.2 0.12 0.04 4.95 4.90 0.90 FUSE a

Si IV 1128.340 3p ²P_3/2-3d ²D_3/2 4.90 0.10

Si IV 1122.500 1122.578 3p ²P_1/2-3d ²D_3/2 0.11 0.12 0.05 5.20 4.90 FUSE a

N III 989.787 989.752 2s² 2p ²P_1/2-2s 2p² ²D_3/2 0.46 1.16 0.40 4.88 4.94 FUSE *

N III 991.564 991.538 2s² 2p ²P_3/2-2s 2p² ²D_5/2 1.2 0.87 0.16 4.88 4.94 0.90 FUSE *

N III 991.495 2s² 2p ²P_3/2-2s 2p² ²D_3/2 4.94 0.10

O III 1666.142 1666.109 2s² 2p² ³P₂-2s 2p³ ⁵S₂ 0.13 1.02 0.23 4.94 4.98 STIS d

S IV 1406.016 1406.031 3s² 3p ²P_3/2-3s 3p² ⁴P_5/2 0.04 2.76 0.62 4.95 5.00 STIS d

S IV 1072.974 1072.930 3s² 3p ²P_3/2-3s 3p² ²D_5/2 0.23 1.18 0.32 4.98 5.03 FUSE *

S IV 1062.664 1062.572 3s² 3p ²P_1/2-3s 3p² ²D_3/2 0.19 0.93 0.23 4.99 5.03 FUSE *

N IV 1486.496 1486.510 2s² ¹S₀-2s 2p ³P₁ 0.09 0.72 0.16 5.15 5.16 STIS d

C IV 1550.772 1550.746 1s² 2s ²S_1/2-1s² 2p ²P_1/2 11.34 0.20 0.04 5.19 5.03 STIS a

C IV 1548.201 1548.181 1s² 2s ²S_1/2-1s² 2p ²P_3/2 21.36 0.21 0.05 5.19 5.03 STIS a

O IV 1404.793 1404.811 2s² 2p ²P_3/2-2s 2p² ⁴P_3/2 0.11 1.15 0.26 5.22 5.21 0.79 STIS

S IV 1404.808 3s² 3p ²P_1/2-3s 3p² ⁴P_1/2 4.99 0.21

O IV 1399.779 1399.765 2s² 2p ²P_1/2-2s 2p² ⁴P_1/2 0.07 1.72 0.39 5.24 5.18 STIS

O IV 1407.383 1407.361 2s² 2p ²P_3/2-2s 2p² ⁴P_1/2 0.12 0.93 0.21 5.24 5.18 STIS d

O IV 1401.171 1401.140 2s² 2p ²P_3/2-2s 2p² ⁴P_5/2 0.4 1.14 0.25 5.26 5.20 STIS d

O V 1218.390 1218.322 2s² ¹S₀-2s 2p ³P₁ 1.83 1.01 0.23 5.42 5.37 STIS d

O V 1371.292 1371.285 2s 2p ¹P₁-2p² ¹D₂ 0.35 0.90 0.20 5.44 5.38 STIS *

**Table 3:** Results of the *DEM* analysis. The columns consist of: (1) the ion; (2) the theoretical wavelength $\lambda _{\rm th}$ ; (3) the observed wavelength $\lambda _{\rm ob}$ ; (4) configuration and term description; (5) observed flux $I_{\rm ob}$ (10^-14 ergs cm^-2 s^-1); (6) ratio between the theoretical $I_{\rm th}$ and the observed flux; (7) the estimated error on the ratio value; (8) the effective temperature (log values); (9) $T_{\rm max}$ (log values); (10) the contribution of each transition to the total calculated intensity of the line. (11) the instrument. The last column indicates: (*) a selection of the observed allowed lines; (a) the anomalous allowed lines of the Li- and Na-like sequences; (d) the forbidden lines. The lines marked in the last column are plotted in Fig. 8.
Ion	$\lambda _{\rm th}$	$\lambda _{\rm ob}$	Transition	$I_{\rm ob}$	$I_{\rm th}$ /	+/-	log	log	frac
	(Å)	(Å)		(10^-14)	$I_{\rm ob}$		$T_{\rm eff}$	$T_{\rm max}$
Si II	1533.430	1533.406	3s² (¹S) 3p ²P_3/2-3s² (¹S) 4s ²S_1/2	0.69	1.09	0.24	4.28	4.43		STIS
Si II	1526.706	1526.687	3s² (¹S) 3p ²P_1/2-3s² (¹S) 4s ²S_1/2	0.58	0.66	0.15	4.28	4.43		STIS
Si II	1304.369	1304.355	3s² (¹S) 3p ²P_1/2-3s 3p² ²S_1/2	0.12	1.05	0.23	4.33	4.48		STIS	*
Si II	1309.274	1309.287	3s² (¹S) 3p ²P_3/2-3s 3p² ²S_1/2	0.32	0.78	0.17	4.33	4.48		STIS
Si II	1264.737	1264.725	3s² (¹S) 3p ²P_3/2-3s² (¹S) 3d ²D_5/2	0.48	2.01	0.45	4.35	4.49		STIS
Si II	1265.001	1264.986	3s² (¹S) 3p ²P_3/2-3s² (¹S) 3d ²D_3/2	0.21	0.55	0.12	4.35	4.49		STIS
S II	1253.811	1253.808	3s² 3p³ ⁴S_3/2-3s 3p⁴ ⁴P_3/2	0.12	1.65	0.37	4.34	4.45		STIS
S II	1259.519	1259.495	3s² 3p³ ⁴S_3/2 -3s 3p⁴ ⁴P_5/2	0.14	0.80	0.18	4.35	4.45		STIS	*
C II	1334.524	1334.535	2s² (¹S) 2p ²P_1/2-2s 2p² ²D_3/2	6.89	1.00	0.22	4.44	4.58		STIS
C II	1335.709	1335.692	2s² (¹S) 2p ²P_3/2-2s 2p² ²D_5/2	14.39	0.96	0.21	4.44	4.58		STIS	*
C II	1036.332	1036.302	2s² (¹S) 2p ²P_1/2-2s 2p² ²S_1/2	0.73	1.06	0.17	4.53	4.63		FUSE
C II	1037.020	1036.982	2s² (¹S) 2p ²P_3/2-2s 2p² ²S_1/2	1.1	1.39	0.18	4.53	4.63		FUSE
C II	1323.952	1323.929	2s 2p² ²D_5/2-2p³ ²D_5/2	0.14	0.95	0.21	4.63	4.69	0.56	STIS
C II	1323.907		2s 2p² ²D_3/2-2p³ ²D_3/2					4.69	0.36
Si III	1206.499	1206.496	3s² ¹S₀-3s 3p ¹P₁	7.9	1.09	0.24	4.64	4.78		STIS	*
Si III	1301.147	1301.139	3s 3p ³P₁-3p² ³P₀	0.17	0.65	0.14	4.66	4.77		STIS
Si III	1303.323	1303.325	3s 3p ³P₂-3p² ³P₁	0.15	1.05	0.23	4.66	4.77		STIS
Si III	1298.944	1298.938	3s 3p ³P₂-3p² ³P₂	0.51	1.11	0.25	4.67	4.77	0.83	STIS	d
Si III	1298.892		3s 3p ³P₁-3p² ³P₁					4.77	0.17
Si III	1294.543	1294.537	3s 3p ³P₁-3p² ³P₂	0.21	0.76	0.17	4.67	4.77		STIS
Si III	1296.726	1296.713	3s 3p ³P₀-3p² ³P₁	0.08	1.60	0.36	4.67	4.77		STIS
Si III	1109.969	1110.006	3s 3p ³P₁-3s 3d ³D₂	0.25	1.27	0.28	4.69	4.78	0.74	FUSE
Si III	1109.939		3s 3p ³P₁-3s 3d ³D₁					4.78	0.26
Si III	1108.357	1108.370	3s 3p ³P₀-3s 3d ³D₁	0.083	1.32	0.68	4.69	4.78		FUSE
Si III	1113.229	1113.270	3s 3p ³P₂-3s 3d ³D₃	0.31	2.00	0.39	4.69	4.78	0.87	FUSE
Si III	1113.203		3s 3p ³P₂-3s 3d ³D₂					4.78	0.13
S III	1021.321	1021.357	3s² 3p² ³P₂-3s 3p³ ³P₂	0.083	1.38	0.48	4.71	4.79		FUSE	*
S III	1077.171	1077.017	3s² 3p² ¹D₂-3s² 3p 3d ¹D₂	0.13	1.10	0.56	4.72	4.80		FUSE	*
C III	977.022	977.015	2s² ¹S₀-2s 2p ¹P₁	12	1.49	0.16	4.81	4.92		FUSE
C III	1174.935	1174.939	2s 2p ³P₁-2p² ³P₂	2	0.70	0.10	4.82	4.92		FUSE
C III	1175.265	1175.281	2s 2p ³P₀-2p² ³P₁	1.6	0.70	0.10	4.82	4.92		FUSE
C III	1175.592	1175.570	2s 2p ³P₁-2p² ³P₁	1.1	0.76	0.11	4.82	4.92		FUSE
C III	1175.713	1175.709	2s 2p ³P₂-2p² ³P₂	3.8	1.10	0.16	4.82	4.92		FUSE	*
C III	1175.989	1175.986	2s 2p ³P₁-2p² ³P₀	1.8	0.62	0.09	4.82	4.92		FUSE
C III	1176.372	1176.366	2s 2p ³P₂-2p² ³P₁	1.6	0.87	0.12	4.82	4.92		FUSE
C III	1175.713	1175.694	2s 2p ³P₂-2p² ³P₂	3.98	1.05	0.24	4.82	4.92		STIS
Si IV	1402.770	1402.747	3s ²S_1/2-3p ²P_1/2	2.92	0.18	0.04	4.88	4.87		STIS	a
Si IV	1393.755	1393.744	3s ²S_1/2-3p ²P_3/2	4.93	0.21	0.05	4.88	4.88		STIS	a
Si IV	1128.325	1128.350	3p ²P_3/2-3d ²D_5/2	0.2	0.12	0.04	4.95	4.90	0.90	FUSE	a
Si IV	1128.340		3p ²P_3/2-3d ²D_3/2					4.90	0.10
Si IV	1122.500	1122.578	3p ²P_1/2-3d ²D_3/2	0.11	0.12	0.05	5.20	4.90		FUSE	a
N III	989.787	989.752	2s² 2p ²P_1/2-2s 2p² ²D_3/2	0.46	1.16	0.40	4.88	4.94		FUSE	*
N III	991.564	991.538	2s² 2p ²P_3/2-2s 2p² ²D_5/2	1.2	0.87	0.16	4.88	4.94	0.90	FUSE	*
N III	991.495		2s² 2p ²P_3/2-2s 2p² ²D_3/2					4.94	0.10
O III	1666.142	1666.109	2s² 2p² ³P₂-2s 2p³ ⁵S₂	0.13	1.02	0.23	4.94	4.98		STIS	d
S IV	1406.016	1406.031	3s² 3p ²P_3/2-3s 3p² ⁴P_5/2	0.04	2.76	0.62	4.95	5.00		STIS	d
S IV	1072.974	1072.930	3s² 3p ²P_3/2-3s 3p² ²D_5/2	0.23	1.18	0.32	4.98	5.03		FUSE	*
S IV	1062.664	1062.572	3s² 3p ²P_1/2-3s 3p² ²D_3/2	0.19	0.93	0.23	4.99	5.03		FUSE	*
N IV	1486.496	1486.510	2s² ¹S₀-2s 2p ³P₁	0.09	0.72	0.16	5.15	5.16		STIS	d
C IV	1550.772	1550.746	1s² 2s ²S_1/2-1s² 2p ²P_1/2	11.34	0.20	0.04	5.19	5.03		STIS	a
C IV	1548.201	1548.181	1s² 2s ²S_1/2-1s² 2p ²P_3/2	21.36	0.21	0.05	5.19	5.03		STIS	a
O IV	1404.793	1404.811	2s² 2p ²P_3/2-2s 2p² ⁴P_3/2	0.11	1.15	0.26	5.22	5.21	0.79	STIS
S IV	1404.808		3s² 3p ²P_1/2-3s 3p² ⁴P_1/2					4.99	0.21
O IV	1399.779	1399.765	2s² 2p ²P_1/2-2s 2p² ⁴P_1/2	0.07	1.72	0.39	5.24	5.18		STIS
O IV	1407.383	1407.361	2s² 2p ²P_3/2-2s 2p² ⁴P_1/2	0.12	0.93	0.21	5.24	5.18		STIS	d
O IV	1401.171	1401.140	2s² 2p ²P_3/2-2s 2p² ⁴P_5/2	0.4	1.14	0.25	5.26	5.20		STIS	d
O V	1218.390	1218.322	2s² ¹S₀-2s 2p ³P₁	1.83	1.01	0.23	5.42	5.37		STIS	d
O V	1371.292	1371.285	2s 2p ¹P₁-2p² ¹D₂	0.35	0.90	0.20	5.44	5.38		STIS	*

Table 3: continued.
Ion $\lambda _{\rm th}$ $\lambda _{\rm ob}$ Transition $I_{\rm ob}$ $I_{\rm th}$ / +/- log log frac

(Å) (Å) (10^-14) $I_{\rm ob}$ $T_{\rm eff}$ $T_{\rm max}$

Ne V 1145.596 1145.624 2s² 2p² ³P₂-2s 2p³ ⁵S₂ 0.15 1.05 0.36 5.52 5.46 FUSE *

S VI 933.378 933.397 3s ²S_1/2-3p ²P_3/2 0.48 1.38 0.48 5.55 5.30 FUSE a

N V 1242.804 1242.794 1s² 2s ²S_1/2-1s² 2p ²P_1/2 2.11 0.31 0.07 5.57 5.27 STIS a

N V 1238.821 1238.799 1s² 2s ²S_1/2-1s² 2p ²P_3/2 4.52 0.29 0.07 5.57 5.27 STIS a

Ne VI 999.182 999.181 2s² 2p ²P_3/2-2s 2p² ⁴P_5/2 0.45 0.75 0.38 5.64 5.60 FUSE *

O VI 1037.615 1037.583 1s² 2s ²S_1/2-1s² 2p ²P_1/2 9.6 1.07 0.11 5.72 5.47 FUSE *

O VI 1031.914 1031.920 1s² 2s ²S_1/2-1s² 2p ²P_3/2 19 1.09 0.11 5.72 5.47 FUSE *

Fe IX 171.073 171.000 3p6 ¹S₀-3p5.3d ¹P₁ 22.9 1.08 0.48 5.92 5.85 EUVE *

Fe XV 284.160 284.200 3s2 ¹S₀-3s3p ¹P₁ 40.8 0.76 0.33 6.42 6.32 EUVE *

Fe XVI 335.410 335.300 3s ²S_1/2-3p ²P_3/2 27.9 1.02 0.70 6.61 6.41 EUVE *

Fe XVIII 93.923 94.100 2s² 2p⁵ ²P_3/2-2s 2p⁶ ²S_1/2 8.7 1.03 0.58 6.85 6.83 EUVE *

Fe XVIII 974.860 974.810 2s² 2p⁵ ²P_3/2-2s² 2p⁵ ²P_1/2 0.48 0.94 0.48 6.85 6.83 EUVE *

Fe XIX 1118.057 1118.013 2s² 2p⁴ ³P₂-2s² 2p⁴ ³P₁ 0.22 1.28 0.29 6.90 6.90 FUSE *

Fe XIX 108.355 108.500 2s² 2p⁴ ³P₂-2s 2p⁵ ³P₂ 7.96 0.69 0.25 6.92 6.90 EUVE *

Fe XX 121.845 121.700 2s² 2p³ ⁴S_3/2-2s 2p⁴ ⁴P_3/2 6.2 0.98 0.41 6.97 6.97 EUVE *

Fe XXI 1354.080 1354.045 2p² ³P₀-2p² ³P₁ 0.77 0.93 0.21 7.02 7.02 STIS *

Fe XXI 128.752 128.600 2p² ³P₀-2s 2p³ ³D₁ 8.7 1.05 0.57 7.02 7.02 EUVE *

Fe XXII 135.755 135.800 2s² 2p ²P_1/2-1s² 2s 2p² ²D_3/2 7.8 0.70 0.28 7.09 7.08 EUVE *

Fe XXI 117.499 117.600 2p² ³P₁-2s 2p³ ³P₁ 3.2 0.89 0.56 7.11 7.02 0.50 EUVE

Ni XXV 117.911 2s² ¹S₀-2s 2p ¹P₁ 7.24 0.28

Ni XXII 117.918 2s² 2p³ ⁴S_3/2-2s 2p⁴ ⁴S_5/2 7.05 0.11

Fe XXIII 132.906 132.800 2s² ¹S₀-2s 2p ¹P₁ 22.6 1.09 0.29 7.13 7.14 0.67 EUVE *

Fe XX 132.840 2s² 2p³ ⁴S_3/2-2s 2p⁴ ⁴P_5/2 6.97 0.31

Fe XXIV 192.029 191.700 1s² 2s ²S_1/2-1s² 2p ²P_3/2 10.4 0.90 0.61 7.24 7.23 0.84 EUVE *

S XI 191.266 2s22p2 ³P₂-2s2p3 ³S₁ 6.28 0.14

**Table 3:** continued.
Ion	$\lambda _{\rm th}$	$\lambda _{\rm ob}$	Transition	$I_{\rm ob}$	$I_{\rm th}$ /	+/-	log	log	frac
	(Å)	(Å)		(10^-14)	$I_{\rm ob}$		$T_{\rm eff}$	$T_{\rm max}$
Ne V	1145.596	1145.624	2s² 2p² ³P₂-2s 2p³ ⁵S₂	0.15	1.05	0.36	5.52	5.46		FUSE	*
S VI	933.378	933.397	3s ²S_1/2-3p ²P_3/2	0.48	1.38	0.48	5.55	5.30		FUSE	a
N V	1242.804	1242.794	1s² 2s ²S_1/2-1s² 2p ²P_1/2	2.11	0.31	0.07	5.57	5.27		STIS	a
N V	1238.821	1238.799	1s² 2s ²S_1/2-1s² 2p ²P_3/2	4.52	0.29	0.07	5.57	5.27		STIS	a
Ne VI	999.182	999.181	2s² 2p ²P_3/2-2s 2p² ⁴P_5/2	0.45	0.75	0.38	5.64	5.60		FUSE	*
O VI	1037.615	1037.583	1s² 2s ²S_1/2-1s² 2p ²P_1/2	9.6	1.07	0.11	5.72	5.47		FUSE	*
O VI	1031.914	1031.920	1s² 2s ²S_1/2-1s² 2p ²P_3/2	19	1.09	0.11	5.72	5.47		FUSE	*
Fe IX	171.073	171.000	3p6 ¹S₀-3p5.3d ¹P₁	22.9	1.08	0.48	5.92	5.85		EUVE	*
Fe XV	284.160	284.200	3s2 ¹S₀-3s3p ¹P₁	40.8	0.76	0.33	6.42	6.32		EUVE	*
Fe XVI	335.410	335.300	3s ²S_1/2-3p ²P_3/2	27.9	1.02	0.70	6.61	6.41		EUVE	*
Fe XVIII	93.923	94.100	2s² 2p⁵ ²P_3/2-2s 2p⁶ ²S_1/2	8.7	1.03	0.58	6.85	6.83		EUVE	*
Fe XVIII	974.860	974.810	2s² 2p⁵ ²P_3/2-2s² 2p⁵ ²P_1/2	0.48	0.94	0.48	6.85	6.83		EUVE	*
Fe XIX	1118.057	1118.013	2s² 2p⁴ ³P₂-2s² 2p⁴ ³P₁	0.22	1.28	0.29	6.90	6.90		FUSE	*
Fe XIX	108.355	108.500	2s² 2p⁴ ³P₂-2s 2p⁵ ³P₂	7.96	0.69	0.25	6.92	6.90		EUVE	*
Fe XX	121.845	121.700	2s² 2p³ ⁴S_3/2-2s 2p⁴ ⁴P_3/2	6.2	0.98	0.41	6.97	6.97		EUVE	*
Fe XXI	1354.080	1354.045	2p² ³P₀-2p² ³P₁	0.77	0.93	0.21	7.02	7.02		STIS	*
Fe XXI	128.752	128.600	2p² ³P₀-2s 2p³ ³D₁	8.7	1.05	0.57	7.02	7.02		EUVE	*
Fe XXII	135.755	135.800	2s² 2p ²P_1/2-1s² 2s 2p² ²D_3/2	7.8	0.70	0.28	7.09	7.08		EUVE	*
Fe XXI	117.499	117.600	2p² ³P₁-2s 2p³ ³P₁	3.2	0.89	0.56	7.11	7.02	0.50	EUVE
Ni XXV	117.911		2s² ¹S₀-2s 2p ¹P₁					7.24	0.28
Ni XXII	117.918		2s² 2p³ ⁴S_3/2-2s 2p⁴ ⁴S_5/2					7.05	0.11
Fe XXIII	132.906	132.800	2s² ¹S₀-2s 2p ¹P₁	22.6	1.09	0.29	7.13	7.14	0.67	EUVE	*
Fe XX	132.840		2s² 2p³ ⁴S_3/2-2s 2p⁴ ⁴P_5/2					6.97	0.31
Fe XXIV	192.029	191.700	1s² 2s ²S_1/2-1s² 2p ²P_3/2	10.4	0.90	0.61	7.24	7.23	0.84	EUVE	*
S XI	191.266		2s22p2 ³P₂-2s2p3 ³S₁					6.28	0.14

Acknowledgements

G. Del Zanna and H. E. Mason acknowledge support from PPARC (UK). M. Landini and G. Del Zanna acknowledge support from ASI and MIUR (Italy). We thank R. Mewe for his helpful suggestions.

References

Ake, T. B., Dupree, A. K., Young, P. R., et al. 2000, ApJ, 538, L87 In the text NASA ADS
Arnaud, M., & Raymond, J. 1992, ApJ, 398, 394 In the text NASA ADS
Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 In the text NASA ADS
Ayres, T. R., Brown, A., Osten, R. A., et al. 2001, ApJ, 549, 554 In the text NASA ADS
Ayres, T. R., Eriksson, K., Linsky, J. L., & Stencel, R. E. 1983, ApJ, 270, L17 In the text NASA ADS
Berrington, K. A., Burke, P. G., Dufton, P. L., & Kingston, A. E. 1985, Atomic Data and Nuclear Data Tables, 33, 195 In the text NASA ADS
Brage, T., Judge, P. G., & Brekke, P. 1996, ApJ, 464, 1030 In the text NASA ADS
Brandt, J. C., Heap, S. R., Walter, F. M., et al. 2001, AJ, 121, 2173 In the text NASA ADS
Brooks, D. H., Fischbacher, G. A., Fludra, A., et al. 2000, A&A, 357, 697 In the text NASA ADS
Brown, A., de M. Ferraz, M. C., & Jordan, C. 1984a, MNRAS, 207, 831 In the text NASA ADS
Brown, A., Jordan, C., Stencel, R. E., Linsky, J. L., & Ayres, T. R. 1984b, ApJ, 283, 731 In the text NASA ADS
Burgess, A., & Summers, H. P. 1969, ApJ, 157, 1007 In the text NASA ADS
Burton, W. M., Jordan, C., Ridgeley, A., & Wilson, R. 1971, Phil. Trans. Roy. Soc. Lon. A, 270, 81 In the text
Butler, C. J., Doyle, J. G., Andrews, A. D., et al. 1987, A&A, 174, 139 In the text NASA ADS
Byrne, P. B., Doyle, J. G., Brown, A., Linsky, J. L., & Rodono, M. 1987, A&A, 180, 172 In the text NASA ADS
Cook, J. W., Cheng, C.-C., Jacobs, V. L., & Antiochos, S. K. 1989, ApJ, 338, 1176 In the text NASA ADS
Cook, J. W., Keenan, F. P., Dufton, P. L., et al. 1995, ApJ, 444, 936 In the text NASA ADS
Cook, J. W., & Nicolas, K. R. 1979, ApJ, 229, 1163 In the text NASA ADS
Craig, I. J. D., & Brown, J. C. 1986, Inverse problems in astronomy: A guide to inversion strategies for remotely sensed data (Research supported by SERC. Bristol, England and Boston, MA, Adam Hilger, Ltd., 1986, 159 p.) In the text
Del Zanna, G. 1999, Ph.D. Thesis, Univ. of Central Lancashire, UK In the text
Del Zanna, G., & Bromage, B. J. I. 1999, J. Geophys. Res., 104, 9753 In the text NASA ADS
Del Zanna, G., Bromage, B. J. I., Landi, E., & Landini, M. 2001a, A&A, 379, 708 In the text NASA ADS
Del Zanna, G., Bromage, B. J. I., & Mason, H. E. 2001b, in Solar and Galactic Composition, AIP Conf. Proc., 598, 59 In the text
Del Zanna, G., Landini, M., Migliorini, S., & Monsignori Fossi, B. 1995, in PASP Conf. Ser., 109, 261 In the text
Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 In the text NASA ADS
Dere, K. P., Landi, E., Young, P. R., & Del Zanna, G. 2001, ApJS, 134, 331 In the text NASA ADS
Doschek, E. E., Laming, J. M., Doschek, G. A., Feldman, U., & Wilhelm, K. 1999, ApJ, 518, 909 In the text NASA ADS
Doschek, G. A. 1984, ApJ, 279, 446 In the text NASA ADS
Doschek, G. A. 1997, ApJ, 476, 903 In the text NASA ADS
Doschek, G. A., & Feldman, U. 1977, A&A, 58, L13 In the text NASA ADS
Doschek, G. A., Feldman, U., Mariska, J. T., & Linsky, J. L. 1978, ApJ, 226, L35 In the text NASA ADS
Doyle, J. G., & McWhirter, R. W. P. 1980, MNRAS, 193, 947 In the text NASA ADS
Doyle, J. G., & Raymond, J. C. 1984, Sol. Phys., 90, 97 In the text NASA ADS
Drake, J. J., Laming, J. M., & Widing, K. G. 1995, ApJ, 443, 393 In the text NASA ADS
Dufton, P. L., Hibbert, A., Kingston, A. E., & Doschek, G. A. 1982, ApJ, 257, 338 In the text NASA ADS
Dupree, A. K. 1972, ApJ, 178, 527 In the text NASA ADS
Feldman, U. 1992, Phys. Scr., 46, 202 In the text
Feldman, U., & Doschek, G. A. 1979, A&A, 79, 357 In the text NASA ADS
Feldman, U., Doschek, G. A., & Rosenberg, F. D. 1977, ApJ, 215, 652 In the text NASA ADS
Feldman, U., & Laming, J. M. 2000, Phys. Scr., 61, 222 In the text
Flower, D. R., & Nussbaumer, H. 1975, A&A, 45, 145 In the text NASA ADS
Grevesse, N. 2002, Adv. Space Res., in press In the text
Grevesse, N., & Anders, E. 1991 Solar interior and atmosphere (Tucson, AZ, University of Arizona Press), 1227 In the text
Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 In the text NASA ADS
Griffiths, N. W., & Jordan, C. 1998, ApJ, 497, 883 In the text NASA ADS
Harper, G. M., Jordan, C., Judge, P. G., et al. 1999, MNRAS, 303, L41 In the text NASA ADS
Harper, G. M., Wilkinson, E., Brown, A., Jordan, C., & Linsky, J. L. 2001, ApJ, 551, 486 In the text NASA ADS
Hartmann, L., Dupree, A. K., Jordan, C., & Brown, A. 1985, ApJ, 296, 576 In the text NASA ADS
Jordan, C. 1967, Sol. Phys., 2, 441 In the text NASA ADS
Jordan, C. 1985, MNRAS, 214, 1P In the text NASA ADS
Jordan, C. 2000, Plasma Physics and Controlled Fusion, 42, 415 In the text NASA ADS
Jordan, C., Ayres, T. R., Brown, A., Linsky, J. L., & Simon, T. 1987, MNRAS, 225, 903 In the text NASA ADS
Judge, P. G. 2000, ApJ, 531, 585 In the text NASA ADS
Judge, P. G., & McIntosh, S. W. 1999, Sol. Phys., 190, 331 In the text NASA ADS
Judge, P. G., Woods, T. N., Brekke, P., & Rottman, G. J. 1995, ApJ, 455, L85 In the text NASA ADS
Keenan, F. P., & Kingston, A. E. 1986, MNRAS, 220, 493 In the text NASA ADS
Laming, J. M., & Feldman, U. 1999, ApJ, 527, 461 In the text NASA ADS
Landi, E., & Landini, M. 1998, A&A, 340, 265 In the text NASA ADS
Linsky, J. L., Bornmann, P. L., Carpenter, K. G., et al. 1982, ApJ, 260, 670 In the text NASA ADS
Linsky, J. L., Neff, J. E., Brown, A., et al. 1989, A&A, 211, 173 In the text NASA ADS
Linsky, J. L., Wood, B. E., Judge, P., et al. 1995, ApJ, 442, 381 In the text NASA ADS
Maran, S. P., Robinson, R. D., Shore, S. N., et al. 1994, ApJ, 421, 800 In the text NASA ADS
Mason, H. E., & Monsignori Fossi, B. C. M. 1994, A&AR, 6, 123 In the text
Mathioudakis, M., McKenny, J., Keenan, F. P., Williams, D. R., & Phillips, K. J. H. 1999, A&A, 351, L23 In the text NASA ADS
Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 In the text NASA ADS
McIntosh, S. W. 2000, ApJ, 533, 1043 In the text NASA ADS
Monsignori Fossi, B. C., & Landini, M. 1991, Advances in Space Research, 11, 281 In the text NASA ADS
Monsignori Fossi, B. C., Landini, M., Del Zanna, G., & Bowyer, S. 1996, ApJ, 466, 427 In the text NASA ADS
Pagano, I., Linsky, J. L., Carkner, L., et al. 2000, ApJ, 532, 497 In the text NASA ADS
Quin, D. A., Doyle, J. G., Butler, C. J., Byrne, P. B., & Swank, J. H. 1993, A&A, 272, 477 In the text NASA ADS
Raymond, J. C., Mazur, J. E., Allegrini, F., et al., 2001, in Solar and Galactic Composition, AIP Conf. Proc., 598, 49 In the text
Raymond, J. C., & Doyle, J. G. 1981a, ApJ, 245, 1141 In the text NASA ADS
Raymond, J. C., & Doyle, J. G. 1981b, ApJ, 247, 686 In the text NASA ADS
Raymond, J. C., & Dupree, A. K. 1978, ApJ, 222, 379 In the text NASA ADS
Robinson, R. D., Linsky, J. L., Woodgate, B. E., & Timothy, J. G. 2001, ApJ, 554, 368 In the text NASA ADS
Schmitt, J. H. M. M., Cutispoto, G., & Krautter, J. 1998, ApJ, 500, L25 In the text NASA ADS
Tayal, S. S. 2000, ApJ, 530, 1091 In the text NASA ADS
Teriaca, L., Madjarska, M. S., & Doyle, J. G. 2001, Sol. Phys., in press In the text
Vernazza, J. E., & Reeves, E. M. 1978, ApJS, 37, 485 In the text NASA ADS
Widing, K. G., & Feldman, U. 1989, ApJ, 344, 1046 In the text NASA ADS
Young, P. R., Dupree, A. K., Wood, B. E., et al. 2001, ApJ, 555, L121 In the text NASA ADS
Zhang, H. L., Graziani, M., & Pradhan, A. K. 1994, A&A, 283, 319 In the text NASA ADS
Zhang, H. L., & Sampson, D. H. 1992, Atomic Data and Nuclear Data Tables, 52, 143 In the text NASA ADS

Spectroscopic diagnostics of stellar transition regions and coronae in the XUV: AU Mic in quiescence