A&A 385, 816-846 (2002)
DOI: 10.1051/0004-6361:20020080
W. J. G. de Blok1 - A. Bosma2
1 - ATNF, CSIRO, PO Box 76, Epping NSW 1710, Australia
2 -
Observatoire de Marseille,
2 place Le Verrier,
13248 Marseille Cedex 4, France
Received 18 July 2001 / Accepted 15 January 2002
Abstract
We present high-resolution rotation curves of a sample of 26
low surface brightness galaxies. From these curves we derive mass
distributions using a variety of assumptions for the stellar
mass-to-light ratio. We show that the predictions of current Cold
Dark Matter models for the density profiles of dark matter halos are
inconsistent with the observed curves. The latter indicate a
core-dominated structure, rather than the theoretically preferred
cuspy structure.
Key words: galaxies: structure - galaxies: kinematics and dynamics - galaxies: halos
Despite much effort, it is still unclear to what extent rotation curves can give clues about the distribution of the visible and dark matter in bright spiral galaxies (e.g. Bosma 1999; Sellwood 1999). It is thought, however, that low surface brightness (LSB) galaxies and dwarf galaxies are dark matter dominated, and that therefore the analysis of their rotation curves can yield directly important information about the properties and distribution of their associated dark matter halos (de Blok & McGaugh 1997; Verheijen 1997; Swaters 1999).
This implication has far-reaching consequences, as early results by e.g. Moore (1994) already showed. Predictions from cold dark matter (CDM) simulations were found to disagree with observations of rotation curves of several dwarf galaxies; the data indicating much less cuspy distributions of matter than the simulations. It was thought at the time that this problem could be solved once the effect of feedback due to star formation was understood. However, the behaviour of the rotation curves of low surface brightness (LSB) galaxies is rather similar, and their low star formation rate at present and in the past indicate that star formation in such galaxies might never have been important enough to modify their structure drastically.
Early work on LSB galaxies used 21-cm H Iwork to determine the
rotation curves (e.g. van der Hulst et al. 1993; de Blok et al. 1996), and as such the results are likely to suffer from modest angular resolution effects (commonly
called beam smearing). Even though these can be partly modelled,
experience shows that direct measurements are preferable (cf. discussions in Bosma 1978; Begeman 1987); in particular, supplementary data
in the optical emission lines, such as H![]() and [N II] are
always useful
(cf. Van der Kruit & Bosma 1978; Rubin et al. 1989; Corradi et al. 1991; Swaters et al. 2000). Thus a whole industry
has sprung up to combine optical and 21-cm line rotation curves of all
sorts of gas rich galaxies.
and [N II] are
always useful
(cf. Van der Kruit & Bosma 1978; Rubin et al. 1989; Corradi et al. 1991; Swaters et al. 2000). Thus a whole industry
has sprung up to combine optical and 21-cm line rotation curves of all
sorts of gas rich galaxies.
For the particular problem of the dark matter distribution in LSB
galaxies Swaters et al. (2000) presented supplementary H![]() data for five
LSB galaxies already observed in H Ide Blok et al. (1996), and
concluded that the influence of beam smearing on the H Iwas
severe enough to question earlier conclusions regarding dark matter
content and rotation curve shape of LSB galaxies.
McGaugh et al. (2001) and de Blok et al. (2001a) (hereafter dBMR) reanalysed these data,
and concluded that the discrepancy between H
data for five
LSB galaxies already observed in H Ide Blok et al. (1996), and
concluded that the influence of beam smearing on the H Iwas
severe enough to question earlier conclusions regarding dark matter
content and rotation curve shape of LSB galaxies.
McGaugh et al. (2001) and de Blok et al. (2001a) (hereafter dBMR) reanalysed these data,
and concluded that the discrepancy between H![]() and H Iis
only really significant for one of these five galaxies. Conclusions
regarding the dark matter content and the shape of the dark matter
distribution in LSB galaxies are thus not affected.
and H Iis
only really significant for one of these five galaxies. Conclusions
regarding the dark matter content and the shape of the dark matter
distribution in LSB galaxies are thus not affected.
In a comparison of pseudo-isothermal and CDM halo models using high-resolution rotation curves of a sample of a further 29 LSB galaxies dBMR show that the so-called "universal'' CDM halo-profile as parameterised in Navarro et al. (1996) is not a good description of the data: the rotation curves generally show linear solid-body rise in the inner parts, which is inconsistent with the steeper rise necessary for the CDM rotation curves. Rather, the rotation curves prefer a pseudo-isothermal (i.e. core-dominated) halo model. de Blok et al. (2001b) furthermore showed that all rotation curves of LSB galaxies measured so far are consistent with a pseudo-isothermal core model. Analyses that show that these rotation curves confirm the CDM NFW halo model (e.g. van den Bosch & Swaters 2001) can be traced back to the fact that at lower resolutions the NFW and pseudo-isothermal models look sufficiently similar and the errors are large enough that a NFW model can be made to fit the data. The higher-resolution data presented in de Blok et al. (2001b) now seem to have settled the observational side of the debate in favour of core-dominated LSB galaxy halos. These results are independent of the stellar mass-to-light ratios one assumes in constructing these mass models.
It would therefore seem that current models of structure formation and galaxy evolution need to take into account the fact that most late-type galaxies have a constant density dark matter core rather than a cusp (see also results by Borriello & Salucci 2001; Salucci & Burkert 2000; Salucci 2001 for HSB galaxies).
As the signature of the core is clearest at small radii it is important to find galaxies where these inner parts are well-resolved and well-sampled. In this paper we thus supplement the collection of high-resolution rotation curves of LSB galaxies from de Blok et al. (2001a) with curves for an additional 26 galaxies, of which 12 are entirely new and 14 were already used in the analysis by de Blok et al. (2001b). The 12 new galaxies in our sample have been specifically chosen to have small distances so that we can easily verify the discrepancies between the NFW model and the observations.
This paper is organised as follows: we describe our data in Sect. 2, and present the rotation curves in Sect. 3. Section 4 describes individual galaxies. In Sect. 5 we describe the derivation of the final rotation curves. The mass models are then presented in Sect. 6. In Sect. 7 we discuss these models. Section 8 digresses into the consequences that systematic observational effects may or may not have on the data. In Sect. 9 we discuss the mass densities profiles inferred from the rotation curves. Section 10 summarises the paper.
We constructed a sample of galaxies to observe in H![]() from lists
of LSB galaxies already observed in the 21-cm H Iby
van der Hulst et al. (1993) and
de Blok et al. (1996). A representative sample of nearby dwarf galaxies from
the theses of Swaters (1999) and Stil (1999) was also included (see
also Swaters et al. 2002a,b). The sample was supplemented by two
well-known nearby dwarf galaxies (NGC 1560 and NGC 100) and a galaxy
(UGC 711) from the Flat Galaxy Catalog
(Karachentsev et al. 1993). H Ifields were available for all galaxies
(except U711 and N100).
Since we observed with a long-slit spectrograph, we determined for
each galaxy the position angle of the major axis of the velocity
field, using the position angle of the major axis of the light
distribution as an additional check. For U711 and N100 we only used
the position angle of the light distribution: since these are edge-on
galaxies these angles are well determined.
from lists
of LSB galaxies already observed in the 21-cm H Iby
van der Hulst et al. (1993) and
de Blok et al. (1996). A representative sample of nearby dwarf galaxies from
the theses of Swaters (1999) and Stil (1999) was also included (see
also Swaters et al. 2002a,b). The sample was supplemented by two
well-known nearby dwarf galaxies (NGC 1560 and NGC 100) and a galaxy
(UGC 711) from the Flat Galaxy Catalog
(Karachentsev et al. 1993). H Ifields were available for all galaxies
(except U711 and N100).
Since we observed with a long-slit spectrograph, we determined for
each galaxy the position angle of the major axis of the velocity
field, using the position angle of the major axis of the light
distribution as an additional check. For U711 and N100 we only used
the position angle of the light distribution: since these are edge-on
galaxies these angles are well determined.
Table 1 lists parameters of these galaxies for which we managed to
obtain useful, high S/N data that will be used in our mass modelling.
The last column in Table 1 gives references to the data presented in
Table 1 not derived in this paper. Images and surface brightness
profiles can also be found in these references. See also Sect. 2.4.
Table 2 gives a brief
summary of those galaxies that we did observe, but which for various
reasons were deemed to be of insufficient quality to warrant mass
modelling. Our main sample therefore consists of the galaxies listed
in Table 1.
| UGC | Other | D | MR | hR | i |
|
|
|
|
PA | bin | Obs. | Refs. | |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | (15) |
| -- | F563-1 | 45 | -18. | 22.6 | 3.5 | 25 | 17.5 | 114 | 3495 | 3492 | 161 | 5.4 | Jan. 00 | (1)(2) |
| U231 | N100 | 11.2 | -17.7a | - | - | 89 | 8.3 | 97 | 841 | -- | 236 | 1.8 | Jan. 00 | -- |
| U628 | -- | 65 | -19.2 | 22.1 | 4.7 | 56 | 13.8 | 142 | 5451 | -- | 139 | 1.8 | Jan. 00 | (2)(4) |
| U711 | -- | 26.4 | -17.7a | - | - | 90 | 15.4 | 92 | 1984 | -- | 118 | 1.8 | Jan. 00 | -- |
| U731 | DDO 9 | 8.0 | -16.6 | 23.0 | 1.7 | 57 | 7.0 | 75 | 637 | 638 | 257 | 1.8 | Jan. 00 | (5) |
| U1230 | -- | 51 | -19.1 | 22.6 | 4.5 | 22 | 34.7 | 103 | 3837 | 3835 | 112 | 1.8 | Jan. 00 | (2)(4) |
| U1281 | -- | 5.5 | -16.2 | 22.7 | 1.7 | 90 | 5.2 | 57 | 157 | 157 | 218 | 1.8 | Jan. 00 | (5) |
| U3060 | N1560 | 3.0 | -15.9a | 23.2a | 1.3a | 82 | 8.3 | 78 | -36 | -36 | 203 | 1.8 | Jan. 00 | (3) |
| U3137 | -- | 18.4 | -18.7 | 23.2 | 2.0 | 90 | 30.9 | 100 | 982 | 993 | 255 | 1.8 | Jan. 00 | (5) |
| U3371 | DDO 39 | 12.8 | -17.7 | 23.3 | 3.1 | 49 | 10.3 | 86 | 819 | 818 | 133 | 5.4 | Jan. 00 | (5) |
| U4173 | -- | 16.8 | -17.8 | 24.3 | 4.5 | 40 | 12.2 | 57 | 861 | 865 | 168 | 5.4 | Jan. 00 | (5) |
| U4325 | N2552 | 10.1 | -18.1 | 21.6 | 1.6 | 41 | 4.6 | 123 | 523 | 523 | 231 | 1.8 | Jan. 00 | (5) |
| U5005 | -- | 52 | -18.6 | 22.9 | 4.4 | 41 | 27.7 | 99 | 3830 | 3844 | 226 | 5.4 | Jan. 00 | (2)(4) |
| U5750 | -- | 56 | -19.5 | 22.6 | 5.6 | 64 | 21.8 | 79 | 4169 | 4168 | 167 | 1.8 | Jan. 00 | (2)(4) |
| U3851 | N2366 | 3.4 | -16.9 | 22.6 | 1.5 | 59 | 5.4 | 55 | 102 | 104 | 42 | 1.8 | Feb. 01 | (5) |
| U3974 | DDO47 | 4b | -14.9a | - | 1.0 | 30 | 3.2 | 67 | 282 | 274 | 319 | 5.4 | Feb. 01 | (6) |
| U4278 | I2233 | 10.5 | -17.7 | 22.5 | 2.3 | 90 | 7.4 | 93 | 556 | 559 | 173 | 1.8 | Feb. 01 | (5) |
| U4426 | DDO52 | 5.3 | -13.8a | - | 0.6 | 60 | 3.1 | 50 | 382: | 395 | 185 | 1.8 | Feb. 01 | (6) |
| U5272 | DDO64 | 6.1 | -14.7a | - | 1.2 | 60 | 2.7 | 47 | 520 | 525 | 97 | 1.8 | Feb. 01 | (6) |
| U5721 | N3274 | 6.7 | -16.7 | 20.2 | 0.5 | 61 | 7.3 | 79 | 542 | 542 | 279 | 1.8 | Feb. 01 | (5) |
| U7524 | N4395 | 3.5 | -18.1 | 22.2 | 2.3 | 46 | 7.9 | 83 | 319 | 320 | 327 | 1.8 | Feb. 01 | (5) |
| U7603 | N4455 | 6.8 | -16.9 | 20.8 | 0.7 | 78 | 5.9 | 64 | 655 | 644 | 197 | 1.8 | Feb. 01 | (5) |
| U8286 | N5023 | 4.8 | -17.2 | 20.9 | 0.8 | 90 | 5.9 | 84 | 403 | 407 | 208 | 1.8 | Feb. 01 | (5) |
| U8837 | DDO185 | 5.1 | -15.7 | 23.2 | 1.2 | 80 | 2.1 | 50 | 148 | 135 | 22 | 1.8 | Feb. 01 | (5) |
| U9211 | DDO189 | 12.6 | -16.2 | 22.6 | 1.2 | 44 | 8.3 | 64 | 685 | 686 | 287 | 5.4 | Feb. 01 | (5) |
| U10310 | Arp 2 | 15.6 | -17.9 | 22.0 | 1.9 | 34 | 9.0 | 75 | 720 | 718 | 202 | 1.8 | Feb. 01 | (5) |
The emission line observations have been made with the 193-cm
telescope at the Observatoire de Haute Provence and its long-slit
Carelec spectrograph from 2-9 Jan. 2000 and 22-27 Feb. 2001. The
spectrograph has been described in detail by Lemaître et al. (1991). As a
detector, we used a EEV 2048 ![]() 1024 CCD chip. The slit length on the
sky was about 5.5
1024 CCD chip. The slit length on the
sky was about 5.5![]() ,
and we used a 2.0
,
and we used a 2.0
![]() slit-width. This
works out to a pixel size of 0.6
slit-width. This
works out to a pixel size of 0.6
![]()
![]() 45.7 km
s-1. Spectral resolution was 54 km s-1 FWHM. Typical
exposure times were 1 hour per spectrum, preceded and followed by
calibration spectra from a neon arc lamp. The typical seeing during
the observations was
45.7 km
s-1. Spectral resolution was 54 km s-1 FWHM. Typical
exposure times were 1 hour per spectrum, preceded and followed by
calibration spectra from a neon arc lamp. The typical seeing during
the observations was
![]() .
Care was taken to align the
slit with the optical centre of the galaxy. This was done with
off-set pointing from nearby stars. In many cases the central part of
the galaxy was visible in the guiding camera, and the accuracy of the
off-set procedure could be verified. For a few of these galaxies we
repeated the off-set procedure a few times, and found that the galaxy
acquisition was indeed repeatable, with an error of less than
1''. See Sect. 8 for a full discussion of the effects of
(mis-)pointing.
.
Care was taken to align the
slit with the optical centre of the galaxy. This was done with
off-set pointing from nearby stars. In many cases the central part of
the galaxy was visible in the guiding camera, and the accuracy of the
off-set procedure could be verified. For a few of these galaxies we
repeated the off-set procedure a few times, and found that the galaxy
acquisition was indeed repeatable, with an error of less than
1''. See Sect. 8 for a full discussion of the effects of
(mis-)pointing.
The data were corrected for instrumental effects (bias, flat-field, etc.) in the standard manner. The spectra were then further reduced with the Figaro package: the calibration spectra were averaged, and for each of the spectra a wavelength solution was found and the wavelength calibration applied. Cosmic rays were corrected with an automated method, which was verified interactively.
The data were then further processed using the EMSAO programme
of the RVSAO package (Kurtz & Mink 1998) within the IRAF
environment. Emission lines were traced and their wavelengths determined
using known night sky lines. Spectral shifts were then converted into
barycentric radial velocities. The spectra were averaged every 3 pixels
in spatial direction (1.8
![]() ). Some spectra with low S/N were
averaged every 9 pixels (5.4
). Some spectra with low S/N were
averaged every 9 pixels (5.4
![]() )
as indicated in Table 1.
)
as indicated in Table 1.
| Name | Reason for rejection |
| Jan 2000 observations | |
| F561-1 | low S/N |
| F564-V3 | no H |
| F568-6 | only bulge visible |
| U5999 | suspect slit position |
| DDO154 | low S/N, suspect slit position |
| DDO127 | low S/N |
| Feb 2001 observations | |
| N4214 | suspect slit position |
| DDO125 | low S/N |
| DDO43 | low S/N |
| DDO168 | low S/N |
For U628 we only have R-band photometry and H![]() velocity data.
For two galaxies (U711 and N100) we only have H
velocity data.
For two galaxies (U711 and N100) we only have H![]() data. For
U10310 we only have H I - H
data. For
U10310 we only have H I - H![]() data. For these four galaxies
we can construct only limited mass models.
data. For these four galaxies
we can construct only limited mass models.
Generally we adopted the distances given in the source papers
(corrected to H0 = 75 km s-1 Mpc-1), except for DDO 47
where we used the revised distance given in Walter & Brinks (2001), and for
U711 where we used the recession velocity. Inclinations were also
adopted from the source papers. These inclinations are for the major
part kinematically derived and as such only have a few degrees error
at most. It should be emphasised that the shape of the rotation curve
and hence applicability of any particular model does not depend on
inclination, and thus an uncertainty of a few degrees does not affect
our main conclusions.
The scale lengths and surface brightnesses were
are also taken from the references listed in Table 1. We refer to
these papers for precise details. Here it suffices to say that they
were derived using a simple straight-line fit to the exponential part
of the profile (most of the sample galaxies are dominated by an
exponential disk).
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3018F1A.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg19.gif) |
Figure 1:
Raw H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3018F1B.PS}
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg20.gif) |
Figure 1: continued. |
| Open with DEXTER | |
Figure 3 presents overlays of the H![]() data on a major axis
position-velocity diagram from the H I. Such a presentation has
the advantage of immediately showing any discrepancies between the two
datasets, if they exist. The H Iare taken from the literature,
with references given in Table 1. Also indicated is the H I
curve as derived from the position-velocity diagram.
These overlays will be discussed in more detail in Sect. 4.
data on a major axis
position-velocity diagram from the H I. Such a presentation has
the advantage of immediately showing any discrepancies between the two
datasets, if they exist. The H Iare taken from the literature,
with references given in Table 1. Also indicated is the H I
curve as derived from the position-velocity diagram.
These overlays will be discussed in more detail in Sect. 4.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{H3018F2.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg21.gif) |
Figure 2:
Raw H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H3018F3A.PS}\par\par\end{figure}](/articles/aa/full/2002/15/aah3018/Timg22.gif) |
Figure 3:
Overlay of the raw H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H3018f3br.eps}\par
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg23.gif) |
Figure 3: continued. |
| Open with DEXTER | |
In most cases the continuum emission from the central parts of the
galaxies was visible in the spectra. This was used to determine the
central position in the spectra and the systemic velocities. In a few
cases (DDO185, U10310, U5999) the centre was not seen and we varied
the central position and systemic velocity over a small range until we
found the values that gave the maximum symmetry. The systemic
velocities based on the H![]() data are given in Table 1. A
comparison with the systemic velocities derived from the H I(also
listed in Table 1 and taken from the source papers) shows a good
correspondence with the H
data are given in Table 1. A
comparison with the systemic velocities derived from the H I(also
listed in Table 1 and taken from the source papers) shows a good
correspondence with the H![]() velocities. The absolute difference
is 5 km s-1 or less, except in 6 cases where the difference lies
between 10 and 14 km s-1. In 4 of the 6 cases the H Iwere
obtained using a velocity resolution of over 20 km s-1, implying
that the comparison with H
velocities. The absolute difference
is 5 km s-1 or less, except in 6 cases where the difference lies
between 10 and 14 km s-1. In 4 of the 6 cases the H Iwere
obtained using a velocity resolution of over 20 km s-1, implying
that the comparison with H![]() is still very favourable. Only for
DDO 47 and DDO 52 do we find a difference of
is still very favourable. Only for
DDO 47 and DDO 52 do we find a difference of ![]() 1.5 H I
widths. Given the limited spatial and velocity resolution of the H I data it is not clear where this difference originates.
1.5 H I
widths. Given the limited spatial and velocity resolution of the H I data it is not clear where this difference originates.
Figure 4 shows the folded and symmetrised rotation curves, corrected for inclination.
Figure 5 compares the folded H![]() rotation curves with the
H Icurves as presented in the literature
(see Table 1 for references). It is clear that grosso modo
there is reasonable agreement. A small number of galaxies were
obviously affected by beam-smearing, just as for some galaxies the
H
rotation curves with the
H Icurves as presented in the literature
(see Table 1 for references). It is clear that grosso modo
there is reasonable agreement. A small number of galaxies were
obviously affected by beam-smearing, just as for some galaxies the
H![]() rotation curve shows signs of non-circular motion.
rotation curve shows signs of non-circular motion.
In this section we describe the various rotation curves of each galaxy
in some detail. We will compare the H I - the H![]() data, as
well as the H I - H
data, as
well as the H I - H![]() rotation curves as presented in Figs. 1
and 3-5. For some galaxies we make a comparison with independent data
from the literature.
rotation curves as presented in Figs. 1
and 3-5. For some galaxies we make a comparison with independent data
from the literature.
F563-1: The H![]() data show reasonable agreement with the
H I, showing that beamsmearing is not a major problem. At the
receding side the H
data show reasonable agreement with the
H I, showing that beamsmearing is not a major problem. At the
receding side the H![]() data disagree slightly with the H I curve. An independent observation by dBMR of this galaxy is available
and agrees with our observation (see Fig. 6); any systematic
differences between the data sets is less than the uncertainties in
individual data points. Obtaining high-resolution H
data disagree slightly with the H I curve. An independent observation by dBMR of this galaxy is available
and agrees with our observation (see Fig. 6); any systematic
differences between the data sets is less than the uncertainties in
individual data points. Obtaining high-resolution H![]() rotation
curves of LSB galaxies is thus a repeatable exercise.
rotation
curves of LSB galaxies is thus a repeatable exercise.
U5005: The H![]() data agree with the H I-velocity
diagram, but the resulting high-resolution curve rises less steeply
than the H I. The H Ihave only a low spatial resolution
of
data agree with the H I-velocity
diagram, but the resulting high-resolution curve rises less steeply
than the H I. The H Ihave only a low spatial resolution
of
![]() (van der Hulst et al. 1993) and uncertain corrections for beam
smearing are thus unavoidable.
(van der Hulst et al. 1993) and uncertain corrections for beam
smearing are thus unavoidable.
U1230: The H![]() data are of high-quality, and shows that
beamsmearing has affected the 40''-resolution H I
(van der Hulst et al. 1993). The high-resolution curve rises more steeply,
though still with a solid-body signature.
data are of high-quality, and shows that
beamsmearing has affected the 40''-resolution H I
(van der Hulst et al. 1993). The high-resolution curve rises more steeply,
though still with a solid-body signature.
U5750: The H Iare poor, but in agreement with the
H![]() data. The linearly rising H Ialso shows reasonable
agreement with the H
data. The linearly rising H Ialso shows reasonable
agreement with the H![]() data. For this galaxy an independent
observation of dBMR is available and shows excellent agreement
(Fig. 6), again showing that systematic effects due to telescope pointing
etc. are negligible.
data. For this galaxy an independent
observation of dBMR is available and shows excellent agreement
(Fig. 6), again showing that systematic effects due to telescope pointing
etc. are negligible.
U731/DDO9: The H![]() is weak at the receding side and
superimposed on a night sky line. This makes it virtually impossible
to say anything about the H
is weak at the receding side and
superimposed on a night sky line. This makes it virtually impossible
to say anything about the H![]() velocities between +0.5' and
+2'. The H
velocities between +0.5' and
+2'. The H![]() is stronger at the approaching side, and agrees
well with the ridge in the H I
is stronger at the approaching side, and agrees
well with the ridge in the H I
pV diagram. The H![]() curve
rises more steeply than the H I
curve
rises more steeply than the H I
curve, which turns over too
quickly. U731 is a "kinematically lopsided'' galaxy
(Swaters et al. 1999), and the H I
rotation curve of the approaching side
is different from that of the receding side. The H![]() data
agrees well with the steep approaching side of the
H I
data
agrees well with the steep approaching side of the
H I
position-velocity diagram. The H![]() curve is however
significantly steeper than the H I
curve is however
significantly steeper than the H I
curve. This discrepancy
cannot be explained by lopsidedness effects, which are much smaller
than the difference shown here. The H I
curve extends over ![]() 8
beams in radius, and this galaxy thus demonstrates that even for
well-resolved galaxies corrections for beam-smearing are ambiguous,
and do not always yield the correct outcome.
8
beams in radius, and this galaxy thus demonstrates that even for
well-resolved galaxies corrections for beam-smearing are ambiguous,
and do not always yield the correct outcome.
U1281, U3137, U3371/DDO39, U4325/N2552: For these four galaxies
there is excellent agreement between the H Ivelocity data
and the H![]() curve. There is some disagreement between the H I and H
curve. There is some disagreement between the H I and H![]() rotation curves for U4325 and U3371. In these cases the
H Irise more steeply than the H
rotation curves for U4325 and U3371. In these cases the
H Irise more steeply than the H![]() data. The agreement
between the raw H I - H
data. The agreement
between the raw H I - H![]() data suggests that the cause
of this disagreement is likely an overcorrection for beamsmearing in
the H I. While suited for correcting for large-scale resolution
effects, beam smearing corrections thus give non-unique solutions on
small scales - a rotation curve that looks like it has linear rise,
can in reality be a steeply rising rotation curve (as the
beam-smearing corrections in this case usually assume),
or it can be an intrinsically linearly rising curve, as the
H
data suggests that the cause
of this disagreement is likely an overcorrection for beamsmearing in
the H I. While suited for correcting for large-scale resolution
effects, beam smearing corrections thus give non-unique solutions on
small scales - a rotation curve that looks like it has linear rise,
can in reality be a steeply rising rotation curve (as the
beam-smearing corrections in this case usually assume),
or it can be an intrinsically linearly rising curve, as the
H![]() data in this case show.
data in this case show.
U4173: The H![]() data are rather poor in quality, but do
seem to agree with the H I.
data are rather poor in quality, but do
seem to agree with the H I.
N100/U231: Good agreement between the data sets. Given the edge-on orientation of the galaxy, it reaffirms the transparency of this small galaxy, cf. Bosma et al. (1992).
N1560/U3060: Excellent agreement between H I - H![]() .
This curve
is a combination of three spectra covering the entire extent of the
optical disk of N1560. The H
.
This curve
is a combination of three spectra covering the entire extent of the
optical disk of N1560. The H![]() curve shows clear signs of
non-circular motions in the disk of N1560 (high-velocity gas near star
forming regions, etc.).
curve shows clear signs of
non-circular motions in the disk of N1560 (high-velocity gas near star
forming regions, etc.).
N2366/U3851/DDO42: The H![]() rotation-curve is dominated at the
approaching side by the effects of non-circular motions. This position
corresponds to a large star forming region (Hunter et al. 2001), that
is disturbing the dynamics on that side of the galaxy. The
unaffected
raw H
rotation-curve is dominated at the
approaching side by the effects of non-circular motions. This position
corresponds to a large star forming region (Hunter et al. 2001), that
is disturbing the dynamics on that side of the galaxy. The
unaffected
raw H![]() data
show excellent agreement with the H I-velocity diagram, the
H
data
show excellent agreement with the H I-velocity diagram, the
H![]() rotation curve, however, rises steeper than the H I.
rotation curve, however, rises steeper than the H I.
N3274/U5721, N4395/U7524: In general there is excellent
agreement
between the
various raw data sets. The H![]() curves rise a bit faster than
the H I.
curves rise a bit faster than
the H I.
N4455/U7603: The H![]() agrees well with the H Ivelocity
diagram. The H Icurve seems to over-estimate the rotation
velocity in the outer parts by a significant amount. For this galaxy
we found a
agrees well with the H Ivelocity
diagram. The H Icurve seems to over-estimate the rotation
velocity in the outer parts by a significant amount. For this galaxy
we found a ![]() 10 km s-1 difference between the systemic
velocities of the H I - H
10 km s-1 difference between the systemic
velocities of the H I - H![]() curves. The velocity resolution of
the H Iis, however, 25
curves. The velocity resolution of
the H Iis, however, 25
![]() ,
so this difference may not be significant.
,
so this difference may not be significant.
N5023/U8286: Excellent agreement between the data sets, except between
![]() and
and
![]() where the H I
overestimates the
velocity.
The good agreement in the inner parts of this edge-on galaxy confirm again
that these late-type galaxies are virtually transparent.
where the H I
overestimates the
velocity.
The good agreement in the inner parts of this edge-on galaxy confirm again
that these late-type galaxies are virtually transparent.
U10310/Arp2: The H![]() data of this galaxy is rather poorer
in quality than the previous couple of data sets. Nevertheless the
data sets are in good agreement, except perhaps the H Icurve
which seems to overestimate the true rotation velocity.
data of this galaxy is rather poorer
in quality than the previous couple of data sets. Nevertheless the
data sets are in good agreement, except perhaps the H Icurve
which seems to overestimate the true rotation velocity.
DDO47/U3974: The H![]() curve is rather poor in quality, but shows
reasonable agreement with the H I.
curve is rather poor in quality, but shows
reasonable agreement with the H I.
DDO52/U4426: Rather poor H![]() data but a reasonable match with the
H I
data but a reasonable match with the
H I
curve, except in the outer parts, where beam smearing effects presumable
cause a small discrepancy.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{H3018F4.PS}\par\par\end{figure}](/articles/aa/full/2002/15/aah3018/Timg28.gif) |
Figure 4: Symmetrised and folded rotation curves. Different symbols indicate different sides of the galaxies. The rotation velocities have been corrected for inclination. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{H3018F5.PS}\par\end{figure}](/articles/aa/full/2002/15/aah3018/Timg29.gif) |
Figure 5:
Comparison of the folded H |
| Open with DEXTER | |
DDO64/U5272: Good H![]() data show that the H Isuffers from
slight beam smearing effects. Non-circular motions presumably cause the
difference between approaching and receding sides at
data show that the H Isuffers from
slight beam smearing effects. Non-circular motions presumably cause the
difference between approaching and receding sides at
![]() .
.
DDO185/U8837: The H![]() data are of good quality, but do not
correspond very well with the H I-velocity overlay nor the
H I. The most likely explanation is non-circular motions in
especially the approaching side, where the DSS image shows what is
likely a large star formation complex. The receding side does show a
linear rise. We do find an H
data are of good quality, but do not
correspond very well with the H I-velocity overlay nor the
H I. The most likely explanation is non-circular motions in
especially the approaching side, where the DSS image shows what is
likely a large star formation complex. The receding side does show a
linear rise. We do find an H![]() systemic velocity that differs
systemic velocity that differs
![]() 15 kms-1 from the H Ivelocity. Alternatively,
as this is one of the galaxies where the continuum emission of the
central part could not be detected, we may have chosen the wrong
systemic velocity. This curve is therefore rather uncertain.
15 kms-1 from the H Ivelocity. Alternatively,
as this is one of the galaxies where the continuum emission of the
central part could not be detected, we may have chosen the wrong
systemic velocity. This curve is therefore rather uncertain.
DDO189/U9211: The H![]() data are of average quality. The various
data sets are all consistent with each other.
data are of average quality. The various
data sets are all consistent with each other.
In summary the comparison between H I - H![]() shows that the H I curves in this sample tend to suffer from two systematic effects. The
low-resolution curves clearly suffer from beam-smearing which
underestimates the rotation velocities. This is apparent in e.g. U1230. A second effect is apparent for a small number of galaxies
where the raw H I - H
shows that the H I curves in this sample tend to suffer from two systematic effects. The
low-resolution curves clearly suffer from beam-smearing which
underestimates the rotation velocities. This is apparent in e.g. U1230. A second effect is apparent for a small number of galaxies
where the raw H I - H![]() data are an excellent match,
but where the H I
data are an excellent match,
but where the H I
emphcurve overestimates the true rotation
velocity. Because of the good match between the raw data sets, this
systematic effect must have been introduced as a result of
beam-smearing corrections; U4325 is a good example.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{H3018F6.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg31.gif) |
Figure 6: Comparison of the data obtained by dBMR (open circles) and our data (filled circles), for two galaxies in common. At left is the folded original data, and at right the final adopted smooth rotation curves. The agreement is reasonable for UGC 5750 and F563-1. |
| Open with DEXTER | |
This comparison underscores the need for this kind of high-resolution
H![]() data even in moderately well-resolved
galaxies. Beam-smearing corrections are useful in deriving the general
properties of rotation curves. For example, they can tell us what
the general shape of the original curve was, or how likely it is that
a particular rotation curve shape can give rise to the observed
data. When it comes to determining an accurate slope or detailed shape
for an individual galaxy, beam smearing correction are frequently
ambiguous.
data even in moderately well-resolved
galaxies. Beam-smearing corrections are useful in deriving the general
properties of rotation curves. For example, they can tell us what
the general shape of the original curve was, or how likely it is that
a particular rotation curve shape can give rise to the observed
data. When it comes to determining an accurate slope or detailed shape
for an individual galaxy, beam smearing correction are frequently
ambiguous.
In many cases the H Iextend further out than the H![]() data. Due to the flattening of the H Itowards larger radii,
resolution effects become less important, and to get a more extended
rotation curve it therefore makes sense to combine the H I -
H
data. Due to the flattening of the H Itowards larger radii,
resolution effects become less important, and to get a more extended
rotation curve it therefore makes sense to combine the H I -
H![]() data. We have defined hybrid H I/H
data. We have defined hybrid H I/H![]() curves,
always giving preference to H
curves,
always giving preference to H![]() data where available. In
practice this meant that we simply adopt the H
data where available. In
practice this meant that we simply adopt the H![]() rotation
velocities interior to a radius
rotation
velocities interior to a radius
![]() ,
usually
corresponding to the outermost point of the H
,
usually
corresponding to the outermost point of the H![]() rotation curve,
and the H Ioutside that radius. Table 3
lists these radii, along with supplementary notes.
rotation curve,
and the H Ioutside that radius. Table 3
lists these radii, along with supplementary notes.
In order to combine the H I - H![]() rotation curves one should
in principle correct for the pressure gradients in the gas. This
correction for asymmetric drift is given by
rotation curves one should
in principle correct for the pressure gradients in the gas. This
correction for asymmetric drift is given by
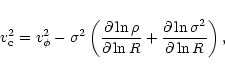
| Name |
|
Name |
|
| F563-1 | 60 | N1560 | 200 |
| U628 | --a | IC2233 | --b |
| U711 | --a | N2366 | 200 |
| U731 | 40 | N3274 | 70 |
| U1230 | 90 | DDO64 | 80 |
| U1281 | 115 | DDO52 | 80 |
| U3137 | 88 | DDO47 | 100 |
| U3371 | 104 | DDO185 | --b |
| U4173 | 10 | DDO189 | 60 |
| U4325 | --b | N5023 | 180 |
| U5005 | 65 | N4455 | 100 |
| U5750 | 39 | N4395 | 250 |
| N100 | --a | U10310 | 70 |
Some of the main assumptions that are made when deriving mass models
from rotation curves is that there is symmetry, that all mass is on
circular orbits and there is continuity with radius. The raw data
still show some scatter and non-circular motions, which can
occasionally result in virtual or ambiguous rotation velocities. In
order to estimate the (smooth) radial run of the potential we want to
represent the data by a curve whose velocity and velocity-derivative
change smoothly, retaining small-scale details. As we are combining
H I - H![]() points we also want the density of the different
data points to be approximately equal, in order to prevent the densely
sampled H
points we also want the density of the different
data points to be approximately equal, in order to prevent the densely
sampled H![]() curves from dominating the fits. We have used a
local regression method to derive the smooth curve (Loader 1999). This
method fits polynomial pieces locally to subsets of data but
does not impose any global functional description (see dBMR for
a more extensive description). As this process inevitably introduces
a small degree of correlation between adjacent data points, the smooth
(H
curves from dominating the fits. We have used a
local regression method to derive the smooth curve (Loader 1999). This
method fits polynomial pieces locally to subsets of data but
does not impose any global functional description (see dBMR for
a more extensive description). As this process inevitably introduces
a small degree of correlation between adjacent data points, the smooth
(H![]() )
curves were resampled every 6''.
)
curves were resampled every 6''.
The final errorbar in these resampled data points consists of two components: (i) the average measurement uncertainty, derived from the average weighted measurement error in each 6'' interval; (ii) an error estimate due to large-scale asymmetries and non-circular motions. We used the difference between the weighted mean velocity and the smooth curve in each interval as an estimate. These two uncertainties were added quadratically giving a conservative estimate for the uncertainty.
A general problem with H![]() rotation curves is that the formal
errorbars of well-sampled, high S/N data points become unrealistically
small (sometimes less than 1 km s-1). These errorbars no longer
have any physical significance but simply indicate that the Gaussian
fit to the profile was well-determined. A similar problem also exists
with H Iwhere the tilted-ring fitting programs produce error
bars that give the uncertainty in the fit and not the actual
uncertainty due to profile width etc. Realistically, observational
and physical uncertainties make it difficult to determine a meaningful
rotation velocity with an accuracy more than a few km s-1. As
the final step in our derivation of the rotation curves we have
imposed a minimum error of 4 km s-1 (prior to inclination
correction) on each data point.
rotation curves is that the formal
errorbars of well-sampled, high S/N data points become unrealistically
small (sometimes less than 1 km s-1). These errorbars no longer
have any physical significance but simply indicate that the Gaussian
fit to the profile was well-determined. A similar problem also exists
with H Iwhere the tilted-ring fitting programs produce error
bars that give the uncertainty in the fit and not the actual
uncertainty due to profile width etc. Realistically, observational
and physical uncertainties make it difficult to determine a meaningful
rotation velocity with an accuracy more than a few km s-1. As
the final step in our derivation of the rotation curves we have
imposed a minimum error of 4 km s-1 (prior to inclination
correction) on each data point.
We compare the resampled smooth curves with the raw data in Fig. 7. To avoid cluttering the plot we represent the smooth curves as a line. The full curves, complete with data points, are also shown in Fig. 8. It is evident that the method does not introduce any systematic effects that affect the shape of the curve. For an extensive discussion see dBMR. The curves shown in Fig. 7 will be used as the basis for our mass modelling.
In order to find the signature of the dark matter halo one needs to decompose the observed rotation curve in a number of separate dynamical components, described below.
For the stellar disk the R-band photometry presented in de Blok et al. (1995) and Swaters (1999) (see also Swaters et al. 2002a) was used. For NGC 1560 we used the B-band photometry presented in Broeils (1992). For DDO47 and DDO64 we used the radial surface brightness profiles from Stil (1999). These profiles are presented as relative to the sky-level without absolute calibration and we therefore used the surface photometry presented in Hopp & Schulte-Ladbeck (1991) and Makarova (1999) to put the profiles on an absolute R-band surface brightness scale. (Since the Stil photometry is in the I-band, this assumes that there are no strong R-I gradients.) See Table 1 for more details.
The rotation curve of
the disk was computed using the ROTMOD task in GIPSY. The
disk was assumed to have a vertical sech2 distribution with a scale
height z0 = h/6 (van der Kruit & Searle 1981). The rotation curves of the
stellar component were resampled at the same radii as the smooth
curves. We assume
![]() constant with radius, which is a
reasonable assumption for the range of variation expected from
plausible stellar populations (de Jong 1996).
constant with radius, which is a
reasonable assumption for the range of variation expected from
plausible stellar populations (de Jong 1996).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{H3018F7.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg38.gif) |
Figure 7:
Final hybrid smooth rotation curves (full and dashed line) overlaid on
original raw hybrid H |
| Open with DEXTER | |
For the gas component we used the H Idensities from the references given in Table 1. They were scaled by a factor of 1.4 to take into account the contribution of helium and metals. Their rotation curve was derived assuming the gas is distributed in a thin disk. For a few nearby galaxies we had to slightly smooth the H I radial profile, mainly because small-scale structure at small radii cause unrealistically large fluctuations in the gas rotation curve and hence the potential. At large radii this small-scale structure is averaged out so the H Ithere is a good description of the global H I.
After subtraction of the above components from the observed rotation curve, any residuals are usually taken to indicate the presence of a dark matter halo. The halos are usually parametrised by fitting a model to these residuals. The quality of the fit tells us something about the applicability of any particular model. Here we restrict ourselves to two well-known models: the pseudo-isothermal halo, used in most of the classic rotation curve studies, and the CDM NFW halo.
We assume a spherical pseudo-isothermal
halo with a density profile
![\begin{displaymath}%
\rho_{\rm ISO}(R) = \rho_0 \Bigl[ 1 + \Bigl( {{R}\over{R_{\rm C}}} \Bigr)^2 \Bigr]^{-1},
\end{displaymath}](/articles/aa/full/2002/15/aah3018/img39.gif) |
(1) |
![\begin{displaymath}%
V_{\rm halo}(R) = \sqrt{ 4\pi G\rho_0 R_{\rm C}^2 \Bigl[ 1 ...
...r{R}}\arctan \Bigl( {{R}\over{R_{\rm C}}} \Bigr) \Bigr] }\cdot
\end{displaymath}](/articles/aa/full/2002/15/aah3018/img42.gif) |
(2) |
The asymptotic velocity of the halo,
![]() ,
is given by
,
is given by
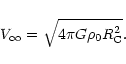 |
(3) |
The NFW mass density distribution (Navarro et al. 1996; Navarro et al. 1997) takes the form
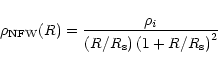 |
(4) |
![\begin{displaymath}%
V(R) = V_{200} \left[\frac{\ln(1+cx)-cx/(1+cx)}
{x[\ln(1+c)-c/(1+c)]}\right]^{1/2},
\end{displaymath}](/articles/aa/full/2002/15/aah3018/img50.gif) |
(5) |
One of largest uncertainties in any mass model is the precise value of
![]() .
Though broad trends in
.
Though broad trends in
![]() have been measured and
modelled (Bottema 1997; Bell & de Jong 2000), the precise value from
galaxy to galaxy is unknown, and depends on extinction, star formation
history, initial mass function, etc. Because of this problem we
present disk-halo decompositions using four different assumptions for
have been measured and
modelled (Bottema 1997; Bell & de Jong 2000), the precise value from
galaxy to galaxy is unknown, and depends on extinction, star formation
history, initial mass function, etc. Because of this problem we
present disk-halo decompositions using four different assumptions for
![]() for those galaxies with photometry available. For the
galaxies without photometry only the first (minimum-disk) model is
presented.
for those galaxies with photometry available. For the
galaxies without photometry only the first (minimum-disk) model is
presented.
The results of the modelling are presented in Fig. 8 and
Tables 4 and 5. Figure 8 displays
the models for the four
![]() assumptions, or, if no photometry
was available, only the minimum disk model. The NFW and
pseudo-isothermal ("ISO'') halo fits are shown side by side. The
values of the halo parameters are given in Table 4 for
the NFW model and Table 5 for the pseudo-isothermal halo model. Both figure and tables
also list the reduced
assumptions, or, if no photometry
was available, only the minimum disk model. The NFW and
pseudo-isothermal ("ISO'') halo fits are shown side by side. The
values of the halo parameters are given in Table 4 for
the NFW model and Table 5 for the pseudo-isothermal halo model. Both figure and tables
also list the reduced ![]() goodness-of-fit values. We have also
done a simple
goodness-of-fit values. We have also
done a simple ![]() test to compute the chance p that the data
and the models could originate from the same distribution. We regard
p>0.95 as a good fit, indicating that the data and the model
match. Values of p<0.05 generally indicate that the wrong model is
used to describe the data. Derived values for p are shown in
Fig. 8.
test to compute the chance p that the data
and the models could originate from the same distribution. We regard
p>0.95 as a good fit, indicating that the data and the model
match. Values of p<0.05 generally indicate that the wrong model is
used to describe the data. Derived values for p are shown in
Fig. 8.
For the NFW fits the fitting routine often preferred very small or
negative c values. These are obviously unphysical, and we have
restricted the parameter space for c to values ![]() 0.1. When the
fit preferred a value less than 0.1 we set c simply equal to 0.1,
and found the best fitting value for V200. This is indicated in
Table 4 by giving the values in italics.
0.1. When the
fit preferred a value less than 0.1 we set c simply equal to 0.1,
and found the best fitting value for V200. This is indicated in
Table 4 by giving the values in italics.
![\begin{figure}
\par\includegraphics[width=4.1cm,height=11.4cm,clip]{3018F8AA.PS}...
...\includegraphics[width=4.1cm,height=11.4cm,clip]{3018F8AH.PS}\par %
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg54.gif) |
Figure 8:
Mass models for F563-1, U628, U731 and U1230. First and third
column show fits using the NFW halo model; second and fourth column
show models using the pseudo-isothermal halo model. Reduced |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,height=11.4cm,clip]{3018F8AI.PS}...
...{4mm}
\includegraphics[width=4.1cm,height=11.4cm,clip]{3018F8AP.PS}
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg55.gif) |
Figure 8: continued. Mass models for U3371, U4173, U4325 and U5005. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,height=11.4cm,clip]{3018F8AQ.PS}...
...}
\includegraphics[width=4.1cm,height=11.4cm,clip]{3018F8AX.PS}\par
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg56.gif) |
Figure 8: continued. Mass models for U5750, N1560, DDO185 and DDO189. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{3018F8AY.PS}\hspace*{4mm}
...
...S}\hspace*{4mm}
\includegraphics[width=4.1cm,clip]{3018F8BF.PS}\par
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg57.gif) |
Figure 8: continued. Mass models for DDO47, DD064, N2366 and N3274. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{3018F8BG.PS}\hspace*{4mm}
...
....PS}\hspace*{4mm}
\includegraphics[width=4.1cm,clip]{3018F8BJ.PS} %
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg58.gif) |
Figure 8: continued. Mass models for N4395 and N4455. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{3018F8BK.PS}\hspace*{4mm}
...
...BY.PS}\hspace*{4mm}
\includegraphics[width=4.1cm,clip]{3018F8BZ.PS}
\end{figure}](/articles/aa/full/2002/15/aah3018/Timg59.gif) |
Figure 8: continued. Mass models for galaxies with only minimum disk fits. |
| Open with DEXTER | |
F563-1: The pseudo-isothermal halo fits are comparable in quality to
the NFW fits. We can compare our results with the independent fits by
dBMR. For the minimum disk pseudo-isothermal halo we find
![]() and
and
![]() .
dBMR find
.
dBMR find
![]() and
and
![]() .
These
values thus agree within their
.
These
values thus agree within their ![]() errors. For the NFW models
our values of
errors. For the NFW models
our values of
![]() and
and
![]() compare
well with the dBMR values of
compare
well with the dBMR values of
![]() and
and
![]() .
The c values agree at the 1.1
.
The c values agree at the 1.1![]() level, whereas the
V200 values agree within the
level, whereas the
V200 values agree within the ![]() errorbars. Two completely
independent analyses of different observations on different telescopes
are thus able to reproduce the same parameters, showing that systematic effects
due to telescope pointing, smoothing etc. are small.
errorbars. Two completely
independent analyses of different observations on different telescopes
are thus able to reproduce the same parameters, showing that systematic effects
due to telescope pointing, smoothing etc. are small.
U628: The pseudo-isothermal and NFW fits are comparable. One
should note that for this galaxy no H Iare available, and that
the "minimum disk'' and "minimum disk+gas'' fits are identical. Also
no gas rotation curve is included in the "constant
![]() '' and
"maximum disk'' cases. The gas rotation curve does however usually
have only a small impact on the fit parameters, and the values
presented here will be close to the true ones.
'' and
"maximum disk'' cases. The gas rotation curve does however usually
have only a small impact on the fit parameters, and the values
presented here will be close to the true ones.
U731: The pseudo-isothermal models and NFW fits are comparable
except that the latter overestimate the rotation velocity in the inner
parts. Both models have trouble fitting the sharp kink at ![]() kpc. This kink is artificial and caused by a lack of data between 0.8
and 4.2 kpc due to the presence of a strong night-sky line at these
velocities.
kpc. This kink is artificial and caused by a lack of data between 0.8
and 4.2 kpc due to the presence of a strong night-sky line at these
velocities.
U1230: For both models maximum disk is the best fit. This comes
at the cost, however, of a high
![]() which is hard to
explain in term of reasonable population synthesis
which is hard to
explain in term of reasonable population synthesis
![]() values,
which usually find values between
values,
which usually find values between ![]() 0.5 and
0.5 and ![]() 2 for LSB
galaxies (van den Hoek et al. 2000).
2 for LSB
galaxies (van den Hoek et al. 2000).
U4173: This rotation curve is virtually identical to the H I curve as the H![]() data do not add much extra constraint. Both
models fit equally well. The H Idensity profile given in
Swaters (1999) gives rise to large fluctuations in the inner gas
rotation curve and was therefore smoothed slightly as explained above.
data do not add much extra constraint. Both
models fit equally well. The H Idensity profile given in
Swaters (1999) gives rise to large fluctuations in the inner gas
rotation curve and was therefore smoothed slightly as explained above.
U4325: Good fits for the pseudo-isothermal models, bad ones for the NFW models.
U5005: Both sets of fits are comparable. The data are however not of high enough quality to constrain either model.
U5750: This galaxy can again be compared with independent
observations by dBMR. We first compare the fitting parameters. For the
isothermal model we find
![]() and
and
![]() .
dBMR find
.
dBMR find
![]() and
and
![]() (again
minimum disk). These agree within the
(again
minimum disk). These agree within the ![]() level. For the NFW
model we find
level. For the NFW
model we find
![]() and
and
![]() ,
compared to their
,
compared to their
![]() and
and
![]() ,
again
in good agreement. The large uncertainties in the NFW parameters
indicate that the rotation curve of U5750 cannot be adequately
described by that model. This is mainly caused by the very linear rise
of the inner rotation curve. For the NFW model the only constraint is
imposed by the two H Iat the flat part of the curve. Without
these the fit would diverge to c=0 and
,
again
in good agreement. The large uncertainties in the NFW parameters
indicate that the rotation curve of U5750 cannot be adequately
described by that model. This is mainly caused by the very linear rise
of the inner rotation curve. For the NFW model the only constraint is
imposed by the two H Iat the flat part of the curve. Without
these the fit would diverge to c=0 and
![]() .
Clearly,
higher-resolution H Iof the outer parts are
needed further fill in the flat part of the curve and bring down the
uncertainties of the fit parameters. This would however not change the
conclusion that this galaxy is very hard to fit with the NFW
model. Again we see that independent observations are capable of
reproducing the same set of parameters at the
.
Clearly,
higher-resolution H Iof the outer parts are
needed further fill in the flat part of the curve and bring down the
uncertainties of the fit parameters. This would however not change the
conclusion that this galaxy is very hard to fit with the NFW
model. Again we see that independent observations are capable of
reproducing the same set of parameters at the ![]() level.
level.
N1560: Due to the large number of data points and the small
scale structure present in the rotation curve, the ![]() values are
high. The pseudo-isothermal and NFW models seem to perform equally
well, though there is still a slight tendency of the NFW models to
overestimate the inner parts. Whereas the problem with rotation curves
is usually that there is not enough resolution, NGC 1560 illustrates
the opposite: the non-circular motions in the H
values are
high. The pseudo-isothermal and NFW models seem to perform equally
well, though there is still a slight tendency of the NFW models to
overestimate the inner parts. Whereas the problem with rotation curves
is usually that there is not enough resolution, NGC 1560 illustrates
the opposite: the non-circular motions in the H![]() data are
large. For the pseudo-isothermal model maximum disk fits best, but
again with a value
data are
large. For the pseudo-isothermal model maximum disk fits best, but
again with a value
![]() which is much higher than one
would find on the basis of reasonable star formation histories and
stellar initial mass functions.
which is much higher than one
would find on the basis of reasonable star formation histories and
stellar initial mass functions.
DDO185: This is a very linear curve that is reasonably fitted by pseudo-isothermal models, but poorly by NFW models. The curve is however only of average quality, and better observations are needed to constrain the models further.
DDO189: This curve is equally well fitted by pseudo-isothermal and NFW models.
DDO64: This curve shows a bump in the inner parts, that is very well fitted by the stellar disk in the maximum disk model, perhaps indicating that the inner part of this galaxy is dominated by stars. Similar bumps have been found in other highly resolved observations of dwarf galaxies (e.g. Blais-Ouellette et al. 2001). The pseudo-isothermal model is a better fit.
N2366: This curve is a challenge for both ISO and NFW models. The very linear rise in the inner parts rapidly changes in a flat part at larger radii. It is hard to reproduce such a sharp change in slope. It is possible that the H Ion which the outer points are based underestimates the rotation velocity as a comparison with the H I-velocity diagram perhaps suggests. Another possible explanation would be that non-circular motions due to the bar-like structure in the centre affect the curve. In their study of NGC 2366 Hunter et al. (2001) find some weak evidence for this from the H I field, but they also note that the rotation curve does not seem to be affected. Clearly there is room for additional high-resolution velocity measurements.
N3274, N4395, N4455: The NFW models fit as well as the ISO models. Parts of the rotation curve of N4395 are dominated by effects of star formation.
U1281, U3137, U711, N100, DDO52, N5023, IC2233 and U10310: For
these eight galaxies only minimum disk models are presented. For U711,
N100, DDO52 and U10310 this is because no surface photometry is
available. U1281, U3137, N100, IC2233, and N5023 are edge-on galaxies
and deriving their face-on surface brightness profiles depends on
various assumptions about the properties of their disk which would
introduce additional uncertainties in the models.
| Name | c | V200 | p | c | V200 | p |
|
|||||||
| Minimum disk | Minimum disk + gas | |||||||||||||
| F5631 | 7.8 | 1.4 | 106.8 | 10.3 | 0.343 | 0.915 | 8.1 | 1.5 | 99.7 | 9.4 | 0.358 | 0.906 | ||
| U5750 | 1.9 | 2.1 | 145.7 | 122.9 | 3.288 | 0.000 | 2.1 | 2.1 | 122.6 | 92.0 | 3.129 | 0.001 | ||
| U5005 | 3.3 | 0.6 | 124.6 | 13.5 | 0.191 | 0.991 | 3.5 | 0.6 | 107.9 | 10.2 | 0.191 | 0.995 | ||
| U1230 | 12.1 | 2.1 | 86.4 | 6.2 | 1.143 | 0.328 | 13.0 | 2.6 | 79.5 | 6.5 | 1.244 | 0.262 | ||
| U731 | 18.6 | 1.9 | 53.1 | 2.8 | 0.684 | 0.740 | 20.2 | 2.2 | 48.9 | 2.6 | 0.760 | 0.668 | ||
| U4173 | 0.1 | - | 319.6 | - | 0.058 | 1.000 | 2.0 | 0.7 | 74.4 | 17.4 | 0.116 | 0.999 | ||
| U4325 | 0.1 | - | 3331.6 | - | 1.330 | 0.132 | 0.1 | - | 3203.9 | - | 1.132 | 0.257 | ||
| N1560 | 5.3 | 0.5 | 106.1 | 8.8 | 2.969 | 0.000 | 5.4 | 0.5 | 92.9 | 7.3 | 2.630 | 0.000 | ||
| U3371 | 0.1 | - | 875.6 | - | 0.287 | 0.996 | 0.1 | - | 814.7 | - | 0.273 | 0.997 | ||
| U628 | 12.9 | 1.2 | 101.2 | 5.7 | 0.347 | 0.912 | 12.9 | 1.2 | 101.2 | 5.7 | 0.346 | 0.912 | ||
| DDO185 | 0.1 | - | 784.5 | - | 2.677 | 0.005 | 0.1 | - | 651.1 | - | 2.326 | 0.012 | ||
| DDO189 | 9.9 | 1.3 | 59.2408 | 4.3 | 0.171 | 0.997 | 11.0 | 1.2 | 50.6 | 2.8 | 0.119 | 0.999 | ||
| DDO47 | 0.1 | - | 1332.5 | - | 0.320 | 0.897 | 0.1 | - | 1248.2 | - | 0.250 | 0.941 | ||
| DDO64 | 0.1 | - | 1182.3 | - | 0.838 | 0.539 | - | - | - | - | - | - | ||
| N2366 | 11.2 | 2.4 | 50.8487 | 7.5 | 2.154 | 0.001 | 12.8 | 2.8 | 41.1 | 5.8 | 2.240 | 0.000 | ||
| N3274 | 30.4 | 2.1 | 49.6296 | 1.6 | 0.894 | 0.600 | 31.0 | 2.2 | 47.7 | 1.5 | 0.830 | 0.685 | ||
| N4395 | 12.1 | 0.9 | 69.7218 | 3.8 | 0.762 | 0.898 | 13.2 | 1.0 | 63.3 | 3.2 | 0.733 | 0.927 | ||
| N4455 | 5.2 | 1.0 | 99.7369 | 19.3 | 0.452 | 0.976 | 5.4 | 1.0 | 86.8 | 14.7 | 0.393 | 0.990 | ||
| K124 | 0.2 | 6.0 | 661.1 | 4320.4 | 1.668 | 0.034 | - | - | - | - | - | - | ||
| N100 | 8.3 | 1.2 | 104.7 | 13.2 | 0.939 | 0.018 | - | - | - | - | - | - | ||
| U1281 | 0.1 | - | 785.0 | - | 1.376 | 0.080 | - | - | - | - | - | - | ||
| U3137 | 10.0 | 0.8 | 88.2 | 2.6 | 2.188 | 0.000 | - | - | - | - | - | - | ||
| DDO52 | 0.1 | - | 991.0 | - | 2.921 | 0.004 | - | - | - | - | - | - | ||
| IC2233 | 0.1 | - | 1135.0 | - | 1.256 | 0.145 | - | - | - | - | - | - | ||
| N5023 | 11.4 | 1.1 | 84.6 | 7.3 | 1.044 | 0.398 | - | - | - | - | - | - | ||
| U10310 | 2.6 | 2.5 | 181.3 | 160.9 | 0.590 | 0.873 | - | - | - | - | - | - | ||
| Constant
|
Maximum disk | |||||||||||||
| F5631 | 6.8 | 1.6 | 103.5 | 12.9 | 0.360 | 0.904 | 1.6 | 2.8 | 220.3 | 282.0 | 0.373 | 0.895 | 5.9 | |
| U5750 | 0.8 | 3.6 | 187.7 | 474.3 | 3.110 | 0.000 | 0.6 | 4.3 | 215.5 | 772.3 | 3.118 | 0.000 | 1.6 | |
| U5005 | 2.3 | 0.6 | 127.2 | 19.7 | 0.170 | 0.997 | 0.1 | - | 307.1 | - | 0.557 | 0.475 | 5.4 | |
| U1230 | 11.7 | 2.4 | 77.7 | 6.6 | 1.091 | 0.365 | 6.6 | 2.0 | 73.0 | 8.7 | 0.724 | 0.687 | 6.1 | |
| U731 | 19.5 | 2.3 | 47.6 | 2.8 | 0.728 | 0.699 | 9.3 | 4.0 | 31.8 | 6.6 | 0.562 | 0.847 | 13.5 | |
| U4173 | 0.1 | - | 176.2 | - | 0.129 | 1.000 | 0.1 | - | 128.9 | - | 0.236 | 0.993 | 2.4 | |
| U4325 | 0.1 | - | 2655.1 | - | 1.157 | 0.237 | 0.1 | - | 1724.1 | - | 1.225 | 0.172 | 4.6 | |
| N1560 | 1.8 | 1.0 | 218.9 | 105.2 | 2.243 | 0.000 | 0.1 | - | 520.6 | - | 8.859 | 0.000 | 4.9 | |
| U3371 | 0.1 | - | 735.3 | - | 0.278 | 0.997 | 0.1 | - | 533.1 | - | 0.391 | 0.980 | 5.0 | |
| U628 | 12.0 | 1.3 | 97.2 | 6.3 | 0.341 | 0.915 | 0.1 | - | 273.5 | - | 0.619 | 0.689 | 9.8 | |
| DDO185 | 0.1 | - | 575.0 | - | 2.269 | 0.014 | 0.1 | - | 382.9 | - | 2.137 | 0.021 | 5.0 | |
| DDO189 | 9.6 | 1.1 | 52.3 | 3.3 | 0.099 | 1.000 | 1.5 | 3.0 | 148.6 | 220.0 | 0.156 | 0.998 | 8.3 | |
| DDO47 | 0.1 | - | 1178.0 | - | 0.307 | 0.905 | 0.1 | - | 1029.8 | - | 0.455 | 0.785 | 4.4 | |
| DDO64 | 0.1 | - | 966.0 | - | 0.770 | 0.615 | 0.1 | - | 562.1 | - | 0.739 | 0.651 | 4.1 | |
| N2366 | 11.9 | 3.0 | 36.4 | 5.8 | 1.932 | 0.003 | 8.6 | 7.3 | 14.9 | 7.0 | 1.245 | 0.181 | 5.4 | |
| N3274 | 23.7 | 2.1 | 50.4 | 2.2 | 0.928 | 0.554 | 12.6 | 2.6 | 61.8 | 7.7 | 1.804 | 0.013 | 3.9 | |
| N4395 | 12.6 | 1.1 | 58.0 | 3.1 | 0.646 | 0.979 | 11.9 | 1.2 | 50.8 | 3.1 | 0.577 | 0.994 | 3.0 | |
| N4455 | 0.1 | - | 708.3 | 32.1 | 0.630 | 0.849 | 0.1 | - | 602.4 | - | 1.495 | 0.056 | 2.3 | |
| Name |
|
p |
|
p |
|
|||||||||
| Minimum disk | Minimum disk + gas | |||||||||||||
| F5631 | 2.0 | 0.2 | 70.4 | 13.1 | 0.203 | 0.976 | 1.9 | 0.2 | 73.3 | 14.9 | 0.217 | 0.971 | ||
| U5750 | 5.0 | 0.9 | 7.9 | 1.6 | 1.026 | 0.321 | 4.8 | 1.0 | 7.4 | 1.8 | 1.148 | 0.260 | ||
| U5005 | 4.7 | 0.2 | 11.5 | 0.8 | 0.062 | 1.000 | 4.2 | 0.2 | 11.7 | 0.9 | 0.047 | 1.000 | ||
| U1230 | 1.5 | 0.3 | 103.5 | 38.6 | 0.774 | 0.640 | 1.4 | 0.4 | 114.5 | 55.2 | 1.030 | 0.413 | ||
| U731 | 0.6 | 0.1 | 333.9 | 46.0 | 0.313 | 0.976 | 0.5 | 0.1 | 381.8 | 69.9 | 0.439 | 0.928 | ||
| U4173 | 3.5 | 0.2 | 7.3 | 0.7 | 0.066 | 1.000 | 2.6 | 0.2 | 7.9 | 0.8 | 0.041 | 1.000 | ||
| U4325 | 2.7 | 0.1 | 100.1 | 2.1 | 0.017 | 1.000 | 2.5 | 0.1 | 100.6 | 2.0 | 0.015 | 1.000 | ||
| N1560 | 1.6 | 0.1 | 57.1 | 4.3 | 4.343 | 0.000 | 1.5 | 0.1 | 54.6 | 4.8 | 4.306 | 0.000 | ||
| U3371 | 3.7 | 0.1 | 18.0 | 0.3 | 0.003 | 1.000 | 3.3 | 0.1 | 19.2 | 0.6 | 0.009 | 1.000 | ||
| U628 | 1.5 | 0.2 | 151.9 | 27.8 | 0.392 | 0.883 | 1.5 | 0.2 | 151.9 | 27.8 | 0.392 | 0.883 | ||
| DDO185 | - | 22.4 | 2.0 | 0.669 | 0.672 | - | 20.7 | 2.5 | 1.020 | 0.372 | ||||
| DDO189 | 1.0 | 0.1 | 97.9 | 11.3 | 0.064 | 1.000 | 0.8 | 0.1 | 115.0 | 13.7 | 0.053 | 1.000 | ||
| DDO47 | 2.1 | 0.5 | 47.5 | 10.2 | 0.205 | 0.975 | 1.9 | 0.4 | 48.4 | 10.4 | 0.173 | 0.984 | ||
| DDO64 | 1.2 | 0.2 | 72.7 | 11.9 | 0.423 | 0.955 | 1.2 | 0.2 | 72.7 | 11.9 | 0.423 | 0.955 | ||
| N2366 | 0.7 | 0.1 | 147.3 | 26.4 | 1.043 | 0.402 | 0.6 | 0.1 | 154.7 | 37.2 | 1.316 | 0.129 | ||
| N3274 | 0.3 | 0.1 | 1259.4 | 255.6 | 0.918 | 0.565 | 0.3 | 0.1 | 1340.2 | 290.2 | 0.906 | 0.582 | ||
| N4395 | 0.9 | 0.1 | 175.6 | 18.9 | 0.601 | 0.991 | 0.8 | 0.1 | 202.0 | 21.8 | 0.513 | 0.999 | ||
| N4455 | 1.3 | 0.1 | 63.2 | 5.1 | 0.299 | 0.998 | 1.2 | 0.1 | 61.0 | 5.4 | 0.283 | 0.999 | ||
| K124 | 4.4 | 0.2 | 13.5 | 0.8 | 0.236 | 1.000 | - | - | - | - | - | - | ||
| N100 | 1.4 | 0.1 | 105.3 | 4.1 | 0.106 | 0.688 | - | - | - | - | - | - | ||
| U1281 | 2.2 | 0.1 | 28.0 | 1.7 | 0.169 | 1.000 | - | - | - | - | - | - | ||
| U3137 | 2.0 | 0.2 | 61.2 | 8.7 | 1.491 | 0.278 | - | - | - | - | - | - | ||
| DDO52 | 0.7 | 0.3 | 123.8 | 69.0 | 2.193 | 0.052 | - | - | - | - | - | - | ||
| IC2233 | 3.7 | 0.5 | 23.0 | 2.9 | 1.532 | 0.049 | - | - | - | - | - | - | ||
| N5023 | 0.9 | 0.1 | 200.7 | 10.7 | 0.277 | 1.000 | - | - | - | - | - | - | ||
| U10310 | 2.5 | 0.2 | 27.2 | 2.2 | 0.081 | 1.000 | - | - | - | - | - | - | ||
| Constant
|
Maximum disk | |||||||||||||
| F5631 | 2.0 | 0.3 | 57.4 | 14.3 | 0.261 | 0.955 | 3.9 | 1.4 | 15.3 | 8.4 | 0.427 | 0.861 | 5.9 | |
| U5750 | 5.9 | 1.7 | 4.7 | 1.4 | 1.311 | 0.144 | 6.1 | 1.8 | 4.5 | 1.4 | 1.349 | 0.128 | 1.6 | |
| U5005 | 5.4 | 0.3 | 7.4 | 0.5 | 0.041 | 1.000 | 16.0 | 4.2 | 1.5 | 0.3 | 0.150 | 0.998 | 5.4 | |
| U1230 | 1.5 | 0.4 | 90.2 | 43.1 | 0.825 | 0.593 | 2.2 | 0.7 | 27.8 | 14.9 | 0.452 | 0.907 | 6.1 | |
| U731 | 0.5 | 0.1 | 346.4 | 68.0 | 0.433 | 0.931 | 0.7 | 0.3 | 63.4 | 42.7 | 0.476 | 0.906 | 13.5 | |
| U4173 | 4.2 | 0.6 | 3.2 | 0.5 | 0.062 | 1.000 | 7.0 | 2.2 | 1.4 | 0.4 | 0.118 | 1.000 | 2.4 | |
| U4325 | 3.2 | 0.1 | 72.2 | 1.1 | 0.006 | 1.000 | 9.1 | 4.7 | 35.2 | 2.4 | 0.076 | 1.000 | 3.8 | |
| N1560 | 2.1 | 0.2 | 29.4 | 2.9 | 4.298 | 0.000 | 13.2 | 4.2 | 4.8 | 0.4 | 2.445 | 0.000 | 4.9 | |
| U3371 | 3.7 | 0.1 | 14.7 | 0.7 | 0.016 | 1.000 | 5.9 | 0.8 | 6.5 | 0.8 | 0.080 | 1.000 | 5.0 | |
| U628 | 1.5 | 0.2 | 132.0 | 29.3 | 0.447 | 0.847 | 0.4 | 0.8 | 223.6 | 893.1 | 0.946 | 0.460 | 9.8 | |
| DDO185 | - | 16.9 | 2.4 | 1.043 | 0.392 | - | 11.6 | 2.7 | 1.321 | 0.257 | 5.0 | |||
| DDO189 | 0.9 | 0.1 | 88.6 | 10.3 | 0.042 | 1.000 | 2.8 | 0.4 | 11.9 | 2.4 | 0.047 | 1.000 | 8.3 | |
| DDO47 | 2.4 | 0.7 | 37.6 | 7.8 | 0.152 | 0.989 | 7.7 | 9.1 | 21.3 | 3.5 | 0.101 | 0.996 | 4.4 | |
| DDO64 | 1.4 | 0.3 | 52.7 | 10.1 | 0.413 | 0.959 | 2.7 | 1.9 | 22.0 | 6.5 | 0.439 | 0.948 | 4.1 | |
| N2366 | 0.6 | 0.1 | 126.0 | 37.5 | 1.258 | 0.171 | 0.5 | 0.4 | 35.5 | 46.5 | 1.165 | 0.256 | 5.4 | |
| N3274 | 0.4 | 0.1 | 585.3 | 120.7 | 0.787 | 0.738 | 1.0 | 0.2 | 132.0 | 33.2 | 1.064 | 0.376 | 4.0 | |
| N4395 | 0.8 | 0.1 | 184.2 | 23.2 | 0.478 | 1.000 | 0.7 | 0.1 | 167.1 | 27.0 | 0.454 | 1.000 | 3.0 | |
| N4455 | 2.4 | 0.2 | 22.6 | 2.0 | 0.225 | 1.000 | 4.0 | 0.7 | 12.4 | 1.7 | 0.400 | 0.988 | 2.3 | |
The ![]() values of the pseudo-isothermal models are generally
smaller than those of the NFW models. This is illustrated in
Fig. 9 where we plot both sets of
values of the pseudo-isothermal models are generally
smaller than those of the NFW models. This is illustrated in
Fig. 9 where we plot both sets of ![]() values
against each other for the four different
values
against each other for the four different
![]() scenarios. In all
cases the NFW models are either comparable or worse than the
isothermal models. We emphasise this point again in
Table 6. Here we list the number of galaxies with
good (p>0.95) and bad (p>0.05) fits for the two models under the
four
scenarios. In all
cases the NFW models are either comparable or worse than the
isothermal models. We emphasise this point again in
Table 6. Here we list the number of galaxies with
good (p>0.95) and bad (p>0.05) fits for the two models under the
four
![]() assumptions.
assumptions.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{H3018F9A.PS}\par\includegraphics[width=6.4cm,clip]{H3018F9B.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg88.gif) |
Figure 9:
Top: Comparison of the reduced |
| Open with DEXTER | |
We note that the ![]() values given here should not be regarded as
absolute. As described in Sect. 5, the combination of
H
values given here should not be regarded as
absolute. As described in Sect. 5, the combination of
H![]() and H I data, the symmetrization of the curves, the
definition of the subsequent error and the imposition of a minimum
error result in a conservative estimate of the uncertainty. The
errorbars we give here are likely an overestimate of the true
uncertainty. This at least partly explains the very low
and H I data, the symmetrization of the curves, the
definition of the subsequent error and the imposition of a minimum
error result in a conservative estimate of the uncertainty. The
errorbars we give here are likely an overestimate of the true
uncertainty. This at least partly explains the very low ![]() values found for some curves.
values found for some curves.
The bottom panel in Fig. 9 compares the ![]() values for the
minimum disk case, but measured separately for the inner and outer
halves of the rotation curves, respectively. The largest discrepancies
between pseudo-isothermal and NFW are found in the inner parts, as
expected, but it is clear that also in the outer parts
pseudo-isothermal models generally provide better fits. It is
remarkable that despite the large errorbars, there is still an obvious
preference for the pseudo-isothermal model. This conclusion is
independent of any over- or underestimate of the true error: a less conservative
estimate would even strengthen the trends observed here.
values for the
minimum disk case, but measured separately for the inner and outer
halves of the rotation curves, respectively. The largest discrepancies
between pseudo-isothermal and NFW are found in the inner parts, as
expected, but it is clear that also in the outer parts
pseudo-isothermal models generally provide better fits. It is
remarkable that despite the large errorbars, there is still an obvious
preference for the pseudo-isothermal model. This conclusion is
independent of any over- or underestimate of the true error: a less conservative
estimate would even strengthen the trends observed here.
| NFW | ISO | |||
| p>0.95 | p<0.05 | p>0.95 | p<0.05 | |
| min | 5 | 4 | 11 | 0 |
| min+gas | 5 | 5 | 10 | 0 |
| con | 5 | 4 | 10 | 0 |
| max | 5 | 2 | 8 | 0 |
The pseudo-isothermal model has no bad (p<0.05) fits, in contrast
with NFW. The absolute number of good fits is a factor 2 larger for
the pseudo-isothermal model. The proportion of "average'' fits (
![]() )
is larger in the NFW case. The conclusion is that the
pseudo-isothermal halo gives a better description of the data.
)
is larger in the NFW case. The conclusion is that the
pseudo-isothermal halo gives a better description of the data.
The mass and concentration of (numerically simulated) CDM halos depend
on the cosmological assumptions that are used as input to the
simulations. NFW halos follow a specific relation between c and
V200 (Navarro et al. 1997). Independent simulations have also given a
reasonable idea of the scatter one expects at fixed halo mass
(Jing 2000; Bullock et al. 2001), even though they do not agree on the
details. In Fig. 10 we compare our results with these
predictions.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{H3018F10.PS}\par\end{figure}](/articles/aa/full/2002/15/aah3018/Timg90.gif) |
Figure 10:
The NFW halo concentration parameter c plotted
against the halo rotation velocity V200 for the four different
|
| Open with DEXTER | |
Shown as the full line is the prediction for a ![]() dominated
flat universe (
dominated
flat universe (
![]() ,
,
![]() ). There is a
general trend of increasing c values towards lower V200. There
is some disagreement regarding the theoretical scatter in the c-values.
Bullock et al. (2001) quotes a scatter in
). There is a
general trend of increasing c values towards lower V200. There
is some disagreement regarding the theoretical scatter in the c-values.
Bullock et al. (2001) quotes a scatter in ![]() of 0.18, while Jing (2000) derives a smaller scatter in
of 0.18, while Jing (2000) derives a smaller scatter in ![]() of 0.08. Here we adopt the larger value
from Bullock et al. (2001) in order to give the CDM models as much leeway
as possible. The dotted lines in Fig. 10 indicate the
1
of 0.08. Here we adopt the larger value
from Bullock et al. (2001) in order to give the CDM models as much leeway
as possible. The dotted lines in Fig. 10 indicate the
1![]() (grey area) and
(grey area) and ![]() scatter where
scatter where
![]() .
The small dots represent the values for other LSB and dwarf galaxies
derived in dBMR. Our data show a similar behaviour, though the locus
of our data seems to be better defined than that of the dBMR
data. The spread in c larger than the models predict, which is best
illustrated by the excess of low-c points.
.
The small dots represent the values for other LSB and dwarf galaxies
derived in dBMR. Our data show a similar behaviour, though the locus
of our data seems to be better defined than that of the dBMR
data. The spread in c larger than the models predict, which is best
illustrated by the excess of low-c points.
In an analysis of this nature it is crucial that the slit is aligned with the center of the galaxy. Any off-set from center will lead to a rotation curve that is less steep than a properly centered rotation curve unless the entire galaxy is a pure solid body rotator. It is therefore theoretically conceivable that systematic effects may have caused us to underestimate the inner slope of the rotation curve, thus mistaking the incorrectly lowered slope of the NFW profile for that of an isothermal halo.
Here we present several arguments why this is not the case, and why the observationally derived slopes are very close to the true slopes.
As already mentioned in Sect. 2, we took considerable care when acquiring the galaxy at the telescope. Most of the nearby galaxies in our sample were visible in the guiding-camera, and they were used to test our off-set procedure. This involved re-acquiring a galaxy several times in order to test the stability of the procedure, as well as moving back and forth to the acquisition star to test for repeatability. We found the stability of the system to be better than 1''. Of course, for the faintest galaxies, we rely entirely on the position given for the center, which we took from Swaters (1999) or Stil (1999) or the NED database.
There are no systematic differences between the rotation curves
acquired by us at the 1.93 m telescope at OHP, by McGaugh et al. (2001) at the
Kitt-Peak 4 m telescope, and the Las Campanas du Pont 2.5 telescope, by
Swaters et al. (2000) at the 200'' Hale Telescope at Mt. Palomar and
by Pickering et al. (1998) at the MMT. This indicates that either all or none
of the data sets suffer from systematic effects due to mispointing. A
number of galaxies have been observed multiple times by different
observers, and similarly show no systematic differences. This is
illustrated in Fig. 11 where the raw data of four LSB
galaxy rotation curves are compared. In one case there are three
independent data sets available, all agreeing with each other. It is
unlikely that independent observers miss the center of the
galaxy by the same amount in the
same direction every time.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{H3018F11.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg96.gif) |
Figure 11:
The rotation curves derived from independent H |
| Open with DEXTER | |
If the true rotation curves were really bona-fide NFW curves we would
expect that with the increased resolution of the H![]() data, at
least some of them should start to look more like NFW curves. After
all, the combined samples in this paper and McGaugh et al. (2001) contain a few
dozen rotation curves. Even in the presence of (hypothetical) pointing
effects, some should have hit the nucleus and have shown the
characteristic NFW shape. This has not happened. The situation is
quite the reverse: the best resolved rotation curves show the flattest
cores (see Sect. 9 and de Blok et al. 2001b).
data, at
least some of them should start to look more like NFW curves. After
all, the combined samples in this paper and McGaugh et al. (2001) contain a few
dozen rotation curves. Even in the presence of (hypothetical) pointing
effects, some should have hit the nucleus and have shown the
characteristic NFW shape. This has not happened. The situation is
quite the reverse: the best resolved rotation curves show the flattest
cores (see Sect. 9 and de Blok et al. 2001b).
This leads to an interesting contradiction: if indeed we imagine that
a pointing offset leads to a systematic under estimate of the slope,
we ought to see a trend of rotation curve shape with distance. This is
not seen. A pointing offset of a given number of arcseconds
corresponds to a different physical scale in each galaxy, depending on
its distance. Our sample and that of McGaugh et al. (2001) span a range in
distance of a factor of ![]() 200. If we imagine that a pointing
offset of, say, 0.5'' causes us to mistake an NFW halo for a
pseudo-isothermal one in the distant galaxies in our sample, then this
implies that in order to mislead ourselves in a similar way, we ought
to be making an error of almost 1.5' in our pointing when observing
the nearest galaxies. Though this is an extreme example, it is highly
improbably that systematic effects in target acquisition at the
telescope depend on the distance of the target.
200. If we imagine that a pointing
offset of, say, 0.5'' causes us to mistake an NFW halo for a
pseudo-isothermal one in the distant galaxies in our sample, then this
implies that in order to mislead ourselves in a similar way, we ought
to be making an error of almost 1.5' in our pointing when observing
the nearest galaxies. Though this is an extreme example, it is highly
improbably that systematic effects in target acquisition at the
telescope depend on the distance of the target.
Assuming then that we managed in the large majority of the cases to
indeed home in on the center of the light distribution of the galaxy,
one could still assume that the dynamical center of the galaxy does
not coincide with the center of the light distribution. Centering on
the light distribution would thus not give us the true rotation
curve. This has of course just the same effect of mis-pointing, but
now the fault lies with the galaxy, rather than the observer.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3018F12A.PS}\par\includegr...
...lip]{3018F12C.PS}\par\includegraphics[width=8.6cm,clip]{3018F12D.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg97.gif) |
Figure 12: Top panel: NFW model curves assuming D=10 Mpc, V200=100 km s-1, and c=4 (left), 9 (middle) and 20 (right). For each c we derived curves for various offsets: 0'' (full line), 2'' (dotted), 5'' (short-dashed) and 10''(long-dashed). The other panels show the rotation curves for each combination of c and offset (thick curve). Overplotted are the best fitting pseudo-isothermal models (thin curve). Also shown are the differences between the two models. |
| Open with DEXTER | |
To test this one needs high-resolution velocity fields, to which one
can then fit a tilted ring model. The tilted ring model has the
central position of the rings as a free parameter, and will thus
immediately show whether there is a significant discrepancy between
the optical and the dynamical center or not. This is precisely what
Blais-Ouellette et al. (2001) have done. They have derived H![]() rotation curves for a number of late-type galaxies using full 2D
Fabry-Perot velocity fields. They find the same slowly-rising rotation
curves, and conclude that NFW models are incompatible with their data,
which prefer a core-dominated halo or a model with a shallow inner
density slope.
rotation curves for a number of late-type galaxies using full 2D
Fabry-Perot velocity fields. They find the same slowly-rising rotation
curves, and conclude that NFW models are incompatible with their data,
which prefer a core-dominated halo or a model with a shallow inner
density slope.
This is the same conclusion as reached by Bolatto et al. (2002), who obtained high-resolution 5'' CO observations of the nearby dwarf galaxy NGC 4605. They derived a rotation curve from a 3D data cube, again using a tilted ring model, and find a slowly rising rotation curve incompatible with NFW.
A number of galaxies in our sample is edge-on, and it is conceivable
that, despite contrary evidence, these data are affected by optical
depth or projection effects. These edge-on galaxies are however only a
small fraction of the galaxies investigated. For example, of the 56
galaxies presented here and in de Blok et al. (2001a), only 16 have inclinations
larger than 70![]() .
Though there are no systematic differences
between the
.
Though there are no systematic differences
between the ![]() 30 per cent with
30 per cent with
![]() and the
and the ![]() 70 per cent with
70 per cent with
![]() ,
one could easily disregard the
high-inclination galaxies without affecting any of the
conclusions. There are no significant trends of c or slope with
inclination.
,
one could easily disregard the
high-inclination galaxies without affecting any of the
conclusions. There are no significant trends of c or slope with
inclination.
In summary, there is no evidence that the data set presented in this paper suffers from significant systematic effects, nor is it inconsistent with any other relevant data set in the literature. Pointing effects play no significant role, and the observed rotation curves represent the overall dynamics of our galaxies well.
To quantify the effects of mispointing we have created model NFW
velocity fields and have derived rotation curves for various pointing
offsets. We consider model velocity fields assuming NFW halos with
![]() ,
V200 = 100 km s-1 and
c=4, 9, 20,
respectively. Each of these three velocity fields is "observed'' with
a 1'' wide slit, offset by
d = 0'', 2'', 5'', 10'' from the
center, parallel to the major axis. We assume a distance of 10 Mpc,
which is the average distance of the large majority of galaxies in our
sample (disregarding the 4 galaxies with D>40 Mpc.)
,
V200 = 100 km s-1 and
c=4, 9, 20,
respectively. Each of these three velocity fields is "observed'' with
a 1'' wide slit, offset by
d = 0'', 2'', 5'', 10'' from the
center, parallel to the major axis. We assume a distance of 10 Mpc,
which is the average distance of the large majority of galaxies in our
sample (disregarding the 4 galaxies with D>40 Mpc.)
The top panel in Fig. 12 shows the rotation curves, for each combination of c and d. The most important question we want to answer here is under what conditions an NFW velocity field can produce a rotation curve that mimics a pseudo-isothermal curve.
The three bottom panels in Fig. 12 show the derived offset
NFW curves, with the best fitting pseudo-isothermal models
overplotted. Also shown are the differences between both types of
curves. It is clear that in almost all cases the shape of the
pseudo-isothermal halo curve is distinctly different from that of the
NFW curve. The only cases where one might mistake an offset NFW curve
for a pseudo-isothermal curve are those for (c=9; d=10'') and
(c=20;
d=5'', 10''). Pointing errors of this magnitude are simply
not present in the data. If we accept an uncertainty of at most a few
tenths of an arcsecond, it is easy to see that pointing effects are
only likely to affect galaxies at distances
![]() 100 Mpc.
100 Mpc.
We can also regard the NFW curves in Fig. 12 as best fits
to the plotted pseudo-isothermal curves. In this case we can make a
direct comparison with the fits plotted in Fig. 8, and see
that the characteristic overprediction of the inner part of the curve
is also present in the data. Except for the three cases mentioned
above, Fig. 12 shows that in all cases the difference
between NFW and pseudo-isothermal is most pronounced in the inner 2
kpc with residuals between ![]() 5 and
5 and ![]() 20 km s-1. The
majority of galaxies in Fig. 8 does show such residuals,
meaning that even in the presence of (hypothetical) modest pointing
offsets, NFW curves would look different from the curves observed and
shown in Fig. 8.
20 km s-1. The
majority of galaxies in Fig. 8 does show such residuals,
meaning that even in the presence of (hypothetical) modest pointing
offsets, NFW curves would look different from the curves observed and
shown in Fig. 8.
In summary, for the galaxies in this sample the effect of missing the
centers of the galaxies would not be strong enough to masquerade NFW
curves as pseudo-isothermal curves, except in the case of very
(unrealistically) large offsets (
![]() ). This conclusion, combined
with the conclusion from Sect. 8.1 that any pointing errors must be
below the 1'' level, shows that the observed rotation curves must be
close to the true rotation curves. Systematic observational effects
cannot hide NFW halos in LSB galaxies.
). This conclusion, combined
with the conclusion from Sect. 8.1 that any pointing errors must be
below the 1'' level, shows that the observed rotation curves must be
close to the true rotation curves. Systematic observational effects
cannot hide NFW halos in LSB galaxies.
In de Blok et al. (2001b) (hereafter dBMBR) the rotation curve sample presented in dBMR and part of the sample (the Jan00 galaxies) presented in this work were used to calculate the mass-density profiles that give rise to the observed rotation curves. As the different halo models predict different shapes of the mass distribution this gives one a direct test of the applicability of a particular model.
The mass density profile is derived by assuming a spherical mass
distribution. Then, from
![]() and
and
![]() one can derive the mass density
one can derive the mass density ![]() :
:
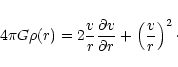 |
(6) |
This inversion is only valid if the contribution by the gas and stars is negligible, i.e. one implicitly assumes a situation (close to) minimum disk. It is well-established that this is a reasonable assumption for LSB (dwarf) galaxies. A minimum disk also provides an upper limit on the steepness of the slopes of the halo mass-density profiles: inclusion of gas and stars will necessarily tend to flatten the slopes.
dBMBR find that the shape of the minimum-disk halo profiles can
usually be characterised by two power-law components of the form
![]() .
The outer slope has a value close to
.
The outer slope has a value close to
![]() ,
whereas the inner slope is more shallow. The models tested here make
distinct predictions regarding the value of the inner slope: the
pseudo-isothermal halo predicts
,
whereas the inner slope is more shallow. The models tested here make
distinct predictions regarding the value of the inner slope: the
pseudo-isothermal halo predicts
![]() ,
the NFW halo predicts
,
the NFW halo predicts
![]() ,
and more recent CDM simulations (Moore et al. 1999) find
even steeper values of
,
and more recent CDM simulations (Moore et al. 1999) find
even steeper values of
![]() .
.
dBMBR find that the distribution of the inner slopes ![]() is
asymmetric, with a well-defined peak at
is
asymmetric, with a well-defined peak at
![]() ,
inconsistent with CDM predictions. This distribution has a broad wing
however, extending to values of
,
inconsistent with CDM predictions. This distribution has a broad wing
however, extending to values of
![]() ,
seemingly consistent
with the steep slopes demanded by CDM. dBMBR show that the inner
slope one derives depends on the radius of the innermost sampled point
,
seemingly consistent
with the steep slopes demanded by CDM. dBMBR show that the inner
slope one derives depends on the radius of the innermost sampled point
![]() of the rotation curve. Larger values of
of the rotation curve. Larger values of
![]() sample the range of radii where the NFW profile and the
pseudo-isothermal profile have similar slopes (which does not imply
they have similar shapes!). Small values of
sample the range of radii where the NFW profile and the
pseudo-isothermal profile have similar slopes (which does not imply
they have similar shapes!). Small values of
![]() probe
the region where the predicted slopes are distinctly different. The
galaxies with small values for
probe
the region where the predicted slopes are distinctly different. The
galaxies with small values for
![]() indeed show the clearest
evidence for the presence of a constant-density core (i.e.
indeed show the clearest
evidence for the presence of a constant-density core (i.e.
![]() ). dBMBR conclude that all data are consistent with LSB
galaxies having core-dominated halos with core-radii of a few kpc.
). dBMBR conclude that all data are consistent with LSB
galaxies having core-dominated halos with core-radii of a few kpc.
The implication is that galaxies with large values of
![]() and
consequently with steep slopes, should show much shallower slopes once
the resolution is increased (and
and
consequently with steep slopes, should show much shallower slopes once
the resolution is increased (and
![]() decreased).
The current data set puts us in an excellent position to test this
prediction. For a large number of galaxies we now have
high-resolution rotation curves, as well as independent
lower-resolution curves from Swaters (1999). We should thus see a
systematic decrease in inner slope when moving from the pure H I
to the high-resolution data.
decreased).
The current data set puts us in an excellent position to test this
prediction. For a large number of galaxies we now have
high-resolution rotation curves, as well as independent
lower-resolution curves from Swaters (1999). We should thus see a
systematic decrease in inner slope when moving from the pure H I
to the high-resolution data.
Figure 13 plots the derived mass profiles for our
complete sample. It is clear that most of the galaxies from our Feb. 01
run, which were specifically chosen to be nearby objects, are also
characterised by an almost flat inner core with a radius of a few kpc,
in contrast with the steep
![]() power-law slope demanded by
CDM, or even the inner
power-law slope demanded by
CDM, or even the inner
![]() power-law slope of the NFW
profile.
power-law slope of the NFW
profile.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3018F13.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg116.gif) |
Figure 13:
Mass profiles of our sample galaxies derived from the
high-resolution rotation curves. The profiles can be characterised by
a steep r-2 outer component, and a more shallow inner component
("core''). Also shown are the mass density profiles implied by the
best-fitting minimum disk models. Shown are the pseudo-isothermal halo
(full line) and the NFW halo (long-dashed line). We have also fitted a
power-law to the inner shallow part (thick short-dashed line). The
slope |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H3018F14.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg117.gif) |
Figure 14:
Value of the inner slope |
| Open with DEXTER | |
Table 7 lists the values of the slopes derived using
the method described in dBMBR. In short, after determining the
"break-radius'' where the slope changes most rapidly, we determined
the slope of the inner component using a weighted least-squares
fit. The uncertainty was determined by re-measuring the slope twice,
once by including the first data point outside the break-radius, and
once by omitting the data point at the break-radius. The maximum
difference between these two values and the original slope was adopted
as the uncertainty. Following dBMBR we re-plot the values of the
inner slope against the value of
![]() ,
this time also including
the Feb. 01 data (see Fig. 14). The new galaxies are
consistent with a core, not a cusp, and the galaxies with small values
of
,
this time also including
the Feb. 01 data (see Fig. 14). The new galaxies are
consistent with a core, not a cusp, and the galaxies with small values
of
![]() have flat mass density slopes.
have flat mass density slopes.
The only exception seems to be N3274 which shows a slope close to -1even though its value for
![]() is quite small. The
pseudo-isothermal halo fit shows that this galaxy has the smallest
(minimum disk) core-radius and highest central density of the entire
sample. Though seemingly consistent with the NFW profile, it is also
consistent with a pseudo-isothermal halo profile with a small core
radius. Furthermore, it has by far the highest surface brightness and
smallest scale-length of the entire sample, and in this case it is
very likely that the minimum disk assumption breaks down and the
stellar component is important in the inner parts.
is quite small. The
pseudo-isothermal halo fit shows that this galaxy has the smallest
(minimum disk) core-radius and highest central density of the entire
sample. Though seemingly consistent with the NFW profile, it is also
consistent with a pseudo-isothermal halo profile with a small core
radius. Furthermore, it has by far the highest surface brightness and
smallest scale-length of the entire sample, and in this case it is
very likely that the minimum disk assumption breaks down and the
stellar component is important in the inner parts.
| Name |
|
|
|
|
|
| F563-1 | -0.01 | 0.70 | 0.55 | 0.21 | 1.38 |
| U628 | -1.29 | 0.08 | 0.95 | -1.37 | 1.37 |
| U711 | -0.12 | 0.07 | 0.38 | - | - |
| U731 | -0.52 | 0.45 | 0.35 | -0.44 | 0.15 |
| U1230 | -0.13 | 0.26 | 0.74 | 0.08 | 0.47 |
| U1281 | -0.04 | 0.01 | 0.08 | - | - |
| U3137 | -0.20 | 0.10 | 0.27 | - | - |
| U3371 | -0.16 | 0.10 | 0.56 | -0.02 | 0.19 |
| U4173 | -0.77 | 0.13 | 0.73 | -0.26 | 0.46 |
| U4325 | -0.33 | 0.03 | 0.15 | -0.24 | 0.06 |
| U5005 | -0.58 | 0.09 | 0.76 | -0.53 | 0.24 |
| U5750 | -0.17 | 0.27 | 0.81 | 0.26 | 0.71 |
| N100 | -0.19 | 0.17 | 0.19 | - | - |
| N1560 | -0.26 | 0.26 | 0.04 | -0.04 | 0.24 |
| N2366 | 0.24 | 0.13 | 0.09 | 0.45 | 0.45 |
| N4395 | -0.40 | 0.07 | 0.05 | -0.52 | 0.02 |
| N3274 | -0.90 | 0.13 | 0.10 | -0.67 | 0.17 |
| N4455 | -0.57 | 0.21 | 0.10 | -0.70 | 0.25 |
| U10310 | 0.10 | 0.36 | 0.22 | - | - |
| N5023 | -0.39 | 0.14 | 0.07 | - | - |
| IC2233 | -0.20 | 0.22 | 0.15 | - | - |
| DDO52 | 0.34 | 0.50 | 0.14 | - | - |
| DDO64 | -0.21 | 0.11 | 0.09 | -0.16 | 0.58 |
| DDO47 | -0.42 | 0.25 | 0.27 | -0.28 | 0.30 |
| DDO185 | -0.18 | 0.29 | 0.07 | -0.23 | 0.61 |
| DDO189 | -0.82 | 0.05 | 0.46 | -0.87 | 0.35 |
We tested this by re-deriving the slopes for the constant
![]() case (see dBMR for a justification of this value). The halo
rotation curve was found by quadratically subtracting the gas-rotation
curve and the rotation curve of the stars. This treatment is likely to
be too naive, as in a non-minimum disk case one expects the disk to
influence the dark matter distribution to some degree (though perhaps
not for LSB galaxies). A full treatment of this problem is beyond the
scope of this paper, and the naive procedure suffices to illustrate
the main point: as the stellar mass-to-light ratio is increased the
inner slope of the halo mass-density profile becomes flatter.
case (see dBMR for a justification of this value). The halo
rotation curve was found by quadratically subtracting the gas-rotation
curve and the rotation curve of the stars. This treatment is likely to
be too naive, as in a non-minimum disk case one expects the disk to
influence the dark matter distribution to some degree (though perhaps
not for LSB galaxies). A full treatment of this problem is beyond the
scope of this paper, and the naive procedure suffices to illustrate
the main point: as the stellar mass-to-light ratio is increased the
inner slope of the halo mass-density profile becomes flatter.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H3018F15.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg123.gif) |
Figure 15:
The inner power-law slopes |
| Open with DEXTER | |
The slopes for the constant
![]() case are listed in
Table 7. In Fig. 15 we again plot the
derived slopes against the inner radii for the galaxies in our sample
where a constant
case are listed in
Table 7. In Fig. 15 we again plot the
derived slopes against the inner radii for the galaxies in our sample
where a constant
![]() model was available. A comparison with
Fig. 14 shows that the data points have all moved up,
as expected. In a number of cases we found rather large positive
slopes, which would imply that these galaxies have hollow halos. This
is rather improbable, and a more realistic explanation is that the
value
model was available. A comparison with
Fig. 14 shows that the data points have all moved up,
as expected. In a number of cases we found rather large positive
slopes, which would imply that these galaxies have hollow halos. This
is rather improbable, and a more realistic explanation is that the
value
![]() is an overestimate of the true M/L*.
is an overestimate of the true M/L*.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3018F16.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg124.gif) |
Figure 16: Comparison of mass density profiles for a number of galaxies as derived from the high-resolution curves (grey data points) and from medium resolution H I(black points). The dashed lines indicate the range over which the inner slope is fitted. Derived values are indicated in each panel. |
| Open with DEXTER | |
N3274 has a slope of -0.66 in the constant
![]() case, which is
consistent with the slope one would expect for a halo with a
core-radius of a few tenths of a kpc. Though this galaxy obviously
cannot be used to prove or disprove either model, it is clear that
galaxies which show steep inner slopes are likely to be of high
surface brightness with inner regions dominated by stars. In order to
unambiguously prove that a galaxy has a bona-fide NFW halo and is
inconsistent with the pseudo-isothermal halo model, it needs
to have a steep inner slope, and a small value of
case, which is
consistent with the slope one would expect for a halo with a
core-radius of a few tenths of a kpc. Though this galaxy obviously
cannot be used to prove or disprove either model, it is clear that
galaxies which show steep inner slopes are likely to be of high
surface brightness with inner regions dominated by stars. In order to
unambiguously prove that a galaxy has a bona-fide NFW halo and is
inconsistent with the pseudo-isothermal halo model, it needs
to have a steep inner slope, and a small value of
![]() and a low surface brightness. Such galaxies have not been found yet.
and a low surface brightness. Such galaxies have not been found yet.
One of the conclusions of dBMBR is that as the resolution of rotation
curves ) is increased (i.e.
![]() is decreased), the derived
inner slope should become shallower. We test this by comparing the
slopes and inner radii for a number of curves for which we have
high-resolution curves and medium-resolution (
is decreased), the derived
inner slope should become shallower. We test this by comparing the
slopes and inner radii for a number of curves for which we have
high-resolution curves and medium-resolution (![]() )
H I.
We determined the slopes of both the high-resolution curves and the
H I.
)
H I.
We determined the slopes of both the high-resolution curves and the
H I.
In Fig. 16 we plot the inversions of the high-resolution
hybrid curves and the lower-resolution H I. The slopes as
derived from these curves are shown in the figure. Those derived from
the H Itend to be steeper than those from the equivalent
high-resolution curves. The values of the slopes in
Fig. 16 are slightly different from those given in
Fig. 13. This is because the H Igenerally
did not extend as far inward as the hybrid profiles, and we had to
choose a larger upper fitting radius. In Fig. 17 we
plot the positions that the high-resolution and H Ioccupy in
the
![]() diagram. The general trend is indeed that as
the resolution is increased, the galaxies move towards smaller slopes,
more or less along the pseudo-isothermal halo model curves.
diagram. The general trend is indeed that as
the resolution is increased, the galaxies move towards smaller slopes,
more or less along the pseudo-isothermal halo model curves.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{H3018F17.PS}\end{figure}](/articles/aa/full/2002/15/aah3018/Timg127.gif) |
Figure 17:
Comparison of the inner slopes |
| Open with DEXTER | |
It is interesting to compare our analysis with that of van den Bosch & Swaters (2001)
(hereafter vdBS), who investigated the H Iof a number of
galaxies for which we now have high-resolution data. Their conclusion
was that the majority of the galaxies they investigated was consistent
with a ![]() CDM scenario, but they also noted that it is difficult
to distinguish between a cusp and a core model at the typical
resolution of the H I. It is clear that this was because the
lower spatial and velocity resolution makes it possible to force a NFW
fit on the data, even though it is not always of the shape preferred
by the data. We will discuss the galaxies they consider in turn.
CDM scenario, but they also noted that it is difficult
to distinguish between a cusp and a core model at the typical
resolution of the H I. It is clear that this was because the
lower spatial and velocity resolution makes it possible to force a NFW
fit on the data, even though it is not always of the shape preferred
by the data. We will discuss the galaxies they consider in turn.
U731: The H Idiffers substantially from the
high-resolution curve. Though our NFW fit gives similar parameters to
the vdBS fit (![]() versus their
versus their ![]() ), our curve provides
a much inferior fit. This is mainly caused by the more linear inner
curve. The inner slope of the high-resolution mass density profile
shows a large change away from the optimum CDM value.
), our curve provides
a much inferior fit. This is mainly caused by the more linear inner
curve. The inner slope of the high-resolution mass density profile
shows a large change away from the optimum CDM value.
U3371: The high-resolution curve is more linear and rises less
steeply than the H I. The slope of the inner curve again shows a
large change: the H I 0is
![]() and consistent with
CDM, the new value is
and consistent with
CDM, the new value is
![]() and consistent with a
constant-density core. We were unable to derive a sensible NFW model
fit.
and consistent with a
constant-density core. We were unable to derive a sensible NFW model
fit.
U4325: This galaxy shows the same behaviour as U3371: the slope derived from the H Iis optimum for CDM, whereas the slope derived from the high-resolution data is consistent with a constant density core.
N4395 (U7524): This is the best-resolved H Iin the vdBS sample, but here we also see the same trends noted above: the slope of the H Iis steeper than the slope of the high-resolution curve. The new curve also differs markedly from the H I. The difference between NFW and pseudo-isothermal is most marked in the inner parts. The increase in resolution has made this galaxy less consistent with CDM.
N4455 (U7603): vdBS note that for this galaxy no meaningful CDM
fit could be derived. We find identical slopes for both sets of data.
As a note of interest, we note that the NFW fit to the H I
presented in vdBS shows the same systematic residuals as the H![]() LSB rotation curves presented in dBMR.
LSB rotation curves presented in dBMR.
DDO189 (U9211): We find similar slopes as vdBS and also the models are of similar quality. The new data does not prefer one model over the other.
Of the 6 galaxies in this small subsample vdBS find that 5 are consistent with CDM, with one dubious case. The increased resolution suggests that only one of these 6 galaxies (DDO189) is still consistent with CDM (this is also the galaxy with the poorest high-resolution data in the subsample). For two galaxies CDM is perhaps inconsistent with the data (U731 and N4455), whereas for the remaining three the data are clearly inconsistent with the CDM models. In summary, we conclude that the slopes of rotation curves are best described by a pseudo-isothermal halo model.
We have presented high-resolution H![]() /H Icurves of a
sample of 26 LSB and dwarf galaxies. We have fitted mass-models to
these rotation curves assuming both a pseudo-isothermal
(core-dominated) halo and a CDM NFW (cusp-dominated) halo. We find
that the pseudo-isothermal halos generally provide better fits, though
the difference is maybe not as pronounced as in dBMR, which can be
traced back to the fact that our sample contains more galaxies of
higher surface brightness than the dBMR sample.
/H Icurves of a
sample of 26 LSB and dwarf galaxies. We have fitted mass-models to
these rotation curves assuming both a pseudo-isothermal
(core-dominated) halo and a CDM NFW (cusp-dominated) halo. We find
that the pseudo-isothermal halos generally provide better fits, though
the difference is maybe not as pronounced as in dBMR, which can be
traced back to the fact that our sample contains more galaxies of
higher surface brightness than the dBMR sample.
We find more galaxies with low concentration parameters than predicted
by numerical CDM simulations. An analysis of the mass-density profiles
of the halos, as derived from minimum-disk rotation curves, shows that
the galaxies in our sample are dominated by more-or-less constant
density cores. As shown in dBMBR the few galaxies that show slopes
consistent with CDM are usually the ones that are not well-resolved,
so that one traces the edges of the constant-density cores rather than
the cores themselves. We have illustrated this explicitly by comparing
the mass-density profiles of a number of galaxies for which we have
both high-resolution H![]() curves and
medium-resolution H I. In general the slopes
derived from the high-resolution curves are less steep than those from
the H I.
curves and
medium-resolution H I. In general the slopes
derived from the high-resolution curves are less steep than those from
the H I.
In conclusion, our high resolution rotation data on nearby dwarfs and LSB galaxies show that the halos of late-type LSB and dwarf galaxies are dominated by kpc-sized constant density cores inconsistent with the predictions of cuspy dark matter halos in cosmological numerical simulations.
Acknowledgements
EdB would like to thank ANSTO for their financial support which made attending the February 2001 observing run possible. AB thanks the Programme National Galaxies for financial support of his observing runs at the Observatoire de Haute Provence. We thank Stacy McGaugh for useful discussions.