The photometric modal discrimination relies on model atmosphere calculations (e.g. Garrido 2000), which
suffer from our lack of understanding of the physical conditions in ![]() Scuti stars. The "regions of interest''
used in the photometric discrimination are not only partially overlapping, but also strongly dependent on
model parameters.
Scuti stars. The "regions of interest''
used in the photometric discrimination are not only partially overlapping, but also strongly dependent on
model parameters.
Another method has been the calculation of thousands of models to try to reproduce the frequencies (e.g. Pamyatnykh et al. 1998 for the case of XX Pyx), but without any convincing results. In fact, no stellar model has yet provided a unique fit to any set of observed frequencies.
The detection of line-profile variations caused by non-radial pulsation modes has been made possible by detailed spectroscopic studies.
High resolution spectroscopy combined with high time resolution provides the ultimate information and
works for low as well as high degree modes. In this case, large telescopes with efficient spectrographs are needed.
For a recent review consult Mantegazza (2000).
A different approach is the moment method introduced by Balona and discussed by Aerts & Eyer (2000)
where references are given. Both methods work well when there are only a small number of
modes (i.e. for a star like ![]() Pup with one radial mode), but when trying to fit a number of closely spaced modes,
these spectroscopic methods are less powerful and
often leave a lot of ambiguity in the classification.
None of them has ever been applied to
Pup with one radial mode), but when trying to fit a number of closely spaced modes,
these spectroscopic methods are less powerful and
often leave a lot of ambiguity in the classification.
None of them has ever been applied to ![]() Scuti stars as
faint as BN Cnc.
Scuti stars as
faint as BN Cnc.
Detailed studies of line profile variations have been carried out for
![]() Cephei stars (e.g. Telting & Schrijvers 1997 or
Schrijvers et al. 1997).
If the S/N of the spectra is sufficiently high, good indications of
the mode type can be derived. This type of analysis is more difficult
for
Cephei stars (e.g. Telting & Schrijvers 1997 or
Schrijvers et al. 1997).
If the S/N of the spectra is sufficiently high, good indications of
the mode type can be derived. This type of analysis is more difficult
for ![]() Scuti stars, where the Doppler velocities are smaller.
Scuti stars, where the Doppler velocities are smaller.
A more efficient technique in terms of photon efficiency, which can work with a modest resolution spectrum, is the use of
ratios between the amplitude of the variation of the equivalent width
(EW) of the Balmer lines divided by a
photometric amplitude (e.g. Dall 1998;
Frandsen 2000). The EW can be measured with "FOSC''
(Faint Object Spectroscopic Camera) type instruments which are
very efficient (>20%) and easy to use.
One can replace the EW by line-indices which rely on the temperature
sensitivity and spatial sensitivity of the equivalent widths of
spectral lines. It is a promising new technique, which has been successfully
applied to a number of pulsating stars of different classes;
the ![]() Scuti star FG Vir (Viskum et al. 1997, 1998),
the roAp star
Scuti star FG Vir (Viskum et al. 1997, 1998),
the roAp star ![]() Cir (Baldry et al. 1998, 1999) and
the EC14026 star PG1605+072 (O'Toole et al. 2000).
It was suggested as a way to observe oscillations in solar-type stars by Bedding & Kjeldsen (1996) and
has been theoretically explored for early type stars by Balona (2000).
The variation of the EW basically tracks the changes in temperature and gravity.
In
Cir (Baldry et al. 1998, 1999) and
the EC14026 star PG1605+072 (O'Toole et al. 2000).
It was suggested as a way to observe oscillations in solar-type stars by Bedding & Kjeldsen (1996) and
has been theoretically explored for early type stars by Balona (2000).
The variation of the EW basically tracks the changes in temperature and gravity.
In ![]() Scuti stars the temperature dominates, while in EC14026 stars the
gravity changes contribute at a similar level.
Scuti stars the temperature dominates, while in EC14026 stars the
gravity changes contribute at a similar level.
The modest resolution of the "FOSC'' type instruments and the instrumental flexures caused by the mounting in the Cassegrain focus means that radial velocity measurements are difficult. This is the reason that radial velocities are not discussed in the present project, as the data from the other sites alone is not enough to derive a decent power spectrum of the radial velocity variations.
| (1) |
The general idea is to integrate the counts in the line, using a suitable weight function,
![]() ,
which
we will call a filter-function or just filter. A broad filter
,
which
we will call a filter-function or just filter. A broad filter
![]() is used for the continuum.
is used for the continuum.
First the centre of the line is defined by moving an integration weight filter across the line, and choosing
the point of maximum total counts as the line centre. The line centre is thus the position that
maximises the counts in the filter, see Fig. 1.
With the line centre pinned the continuum Cx is calculated from two adjacent areas on each side of the line, which appears to have a well defined continuum between weak lines. This is done by rejection iterations, fitting a straight line to the continuum. Even if the continuum is not well defined e.g. because of a continuous blend of weak lines, it is still possible to obtain a continuum measure from this blend, only will this give a lower value for the continuum. The effect will be to diminish each value of the line index by the same amount, which will in turn tend to make the apparent oscillation amplitude insignificantly larger.
With the chosen filter function
![]() for the line in question, the integration is carried out
across the line, yielding the line-index;
for the line in question, the integration is carried out
across the line, yielding the line-index;
The justification of the term "line index'' as an analogue to a colour index can be seen as follows: we define an
index
![]() as the difference between a narrow and a broad flux band centred on the line, analogous
to the
as the difference between a narrow and a broad flux band centred on the line, analogous
to the ![]() -index:
-index:
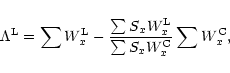 |
(4) |
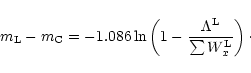 |
(5) |
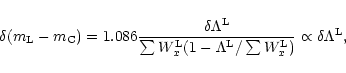 |
(6) |
One may of course define any number of line-indices for any spectral line
by varying the filter-function used, hereby gaining information
from different parts of the line. The choice of filter shape is not critical. We have used a so-called
super-Gaussian filter with exponent 8, i.e.:
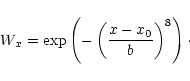 |
(7) |
The mode identification proposed here relies on the investigation by Bedding et al. (1996)
of the sensitivity of different absorption lines to pulsation modes
with different ![]() .
For non-rotating stars they showed that the Balmer lines have sensitivity
similar to radial velocity measurements because of the strong
limb darkening in these lines.
Photometry on the other hand has very weak centre-to-limb variation.
.
For non-rotating stars they showed that the Balmer lines have sensitivity
similar to radial velocity measurements because of the strong
limb darkening in these lines.
Photometry on the other hand has very weak centre-to-limb variation.
Thus photometry and the line-indices of Balmer lines show different response to spatial variations across the
stellar disk (i.e. to the ![]() value), because the Balmer lines sample the
centre of the disk stronger than the limb while photometry
smears out spatial variations across the disk. It follows that the ratio R between
the amplitudes of
the Balmer line-index and the photometry should be an increasing
function of
value), because the Balmer lines sample the
centre of the disk stronger than the limb while photometry
smears out spatial variations across the disk. It follows that the ratio R between
the amplitudes of
the Balmer line-index and the photometry should be an increasing
function of ![]() ,
so that modes with different
,
so that modes with different ![]() should be grouped in
an amplitude ratio diagram. This applies only to a slowly rotating star.
should be grouped in
an amplitude ratio diagram. This applies only to a slowly rotating star.
Some concern about the ability of the method to discriminate between modes of different spherical degree has been raised
by Balona (2000), who used stellar models to investigate the sensitivity of R on ![]() .
He finds in addition
a strong dependence on
.
He finds in addition
a strong dependence on ![]() and m. His results will be addressed later.
Indeed, for rotating
stars the picture becomes much more complicated (Kjeldsen et al. 1998):
as rotation increases, gravitational
darkening becomes more important. This effect causes a stronger sensitivity to the azimuthal number m, because
the orientational degeneracy is lifted. So we get in turn a dependence on the inclination angle. As
shown by Hansen (1999) and Frandsen (2000), the m dependence
is as least as strong as the
and m. His results will be addressed later.
Indeed, for rotating
stars the picture becomes much more complicated (Kjeldsen et al. 1998):
as rotation increases, gravitational
darkening becomes more important. This effect causes a stronger sensitivity to the azimuthal number m, because
the orientational degeneracy is lifted. So we get in turn a dependence on the inclination angle. As
shown by Hansen (1999) and Frandsen (2000), the m dependence
is as least as strong as the ![]() dependence, with the values of amplitude ratios
between photometry and line-index varying
strongly with
dependence, with the values of amplitude ratios
between photometry and line-index varying
strongly with ![]() .
Thus, to disentangle the
.
Thus, to disentangle the ![]() and m dependencies, knowledge of the inclination
angle is essential, which in turn means that the rotation period and
and m dependencies, knowledge of the inclination
angle is essential, which in turn means that the rotation period and ![]() must be known independently.
must be known independently.
Viskum et al. (1998) conducted a detailed analysis of FG Vir that
resulted in a suggestion of mode identification for the 8 strongest modes.
This suggestion was later found to agree with an independent mode identification
by Breger et al. (1999). In FG Vir a long period variation in the H![]() and Fe I line-indices,
found by Viskum et al. was attributed to stellar activity and thus gave directly the rotation period of the star and, with
the observed value of
and Fe I line-indices,
found by Viskum et al. was attributed to stellar activity and thus gave directly the rotation period of the star and, with
the observed value of ![]() ,
also the inclination angle.
,
also the inclination angle.
Copyright ESO 2002