A&A 385, L19-L22 (2002)
DOI: 10.1051/0004-6361:20011764
Timing diagrams and correlations in gamma-ray bursts signal jets
from accretion into black holes
S. McBreen -
B. McBreen -
F. Quilligan -
L. Hanlon
Department of Experimental Physics, University
College Dublin, Dublin 4, Ireland
Received 22 October 2001 / Accepted 10 December 2001
Abstract
The temporal properties of a sample of 498 bright
gamma-ray bursts (GRBs) with durations between 0.05 s and 674 s
were analysed. The large range in duration (T90) is
accompanied by a similarly large range in the median values of
the pulse timing properties including rise time, fall time, FWHM
and separation between the pulses. Four timing diagrams relating
these pulse properties to T90 are presented and show the
power law relationships between the median values of the 4 pulse
timing properties and T90, but also that the power laws
depend in a consistent manner on the number of pulses per GRB.
The timing diagrams are caused by the correlated properties of
the pulses in the burst and can be explained by a combination of
factors including the Doppler boost factor 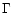 ,
a viewing
effect caused by a jet and different progenitors. GRBs with
similar values of T90 have a wide range in the number of
pulses. GRBs with the large number of short and spectrally hard
pulses may occur either from a homogeneous jet with a higher
average value of
,
a viewing
effect caused by a jet and different progenitors. GRBs with
similar values of T90 have a wide range in the number of
pulses. GRBs with the large number of short and spectrally hard
pulses may occur either from a homogeneous jet with a higher
average value of 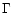 or close to the axis of an
inhomogeneous jet with higher values of
or close to the axis of an
inhomogeneous jet with higher values of 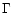 near the
rotation axis. The less luminous GRBs with fewer pulses may
originate further from the axis of the inhomogeneous jet. The
pulses in GRBs have six distinctive statistical properties
including correlations between time intervals, correlations
between pulse amplitudes, an anticorrelation between pulse
amplitudes and time intervals, and a link to intermittency in GRS
1915+105. The timing diagrams and correlated pulses suggest that
GRBs are powered by accretion processes signalling jets from the
formation of black holes.
near the
rotation axis. The less luminous GRBs with fewer pulses may
originate further from the axis of the inhomogeneous jet. The
pulses in GRBs have six distinctive statistical properties
including correlations between time intervals, correlations
between pulse amplitudes, an anticorrelation between pulse
amplitudes and time intervals, and a link to intermittency in GRS
1915+105. The timing diagrams and correlated pulses suggest that
GRBs are powered by accretion processes signalling jets from the
formation of black holes.
Key words: gamma rays - bursts: gamma rays - observations:
methods - data analysis: methods - statistical
The cosmological origin of gamma-ray bursts (GRBs) requires an
extraordinary amount of energy to be emitted in gamma-rays
(Piran 1999). The source of this energy is thought to be a
cataclysmic event involving mergers of compact objects such as
neutron stars or a neutron star and black hole
(Paczynski 1991; Ruffert & Janka 1999) or the formation of a black hole
in massive stars (MacFadyen & Woosley 1999; Popham et al. 1999). GRB light
curves are complex and irregular (Fishman & Meegan 1995) and a range
of techniques have been developed to elucidate their structure
(McBreen et al. 1994; Norris et al. 1996; Lee et al. 2000; Beloborodov et al. 2000; Quilligan et al. 2002). In
this paper we present the results of the analysis of pulses in a
large sample including long and short GRBs. The main results are
presented in Sect. 3 including four timing diagrams and our
analysis of pulse properties. These results along with the unique
properties of the pulses in GRBs are interpreted in Sect. 4 and
used to provide additional insights to the emission process and
the central engine that support jets from accretion into newly
formed black holes.
![\begin{figure}
\par\includegraphics[angle=-90,width=11.5cm,clip]{Dj223_f1.eps}\end{figure}](/articles/aa/full/2002/15/aadj223/Timg11.gif) |
Figure 1:
The timing
diagrams in GRBs. The median values obtained from the lognormal
distributions for the pulse timing parameters a) 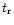 ,
b) ,
b)
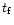 ,
c) FWHM and d) ,
c) FWHM and d) 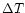 are plotted versus
duration T90 for GRBs in three categories i.e.
are plotted versus
duration T90 for GRBs in three categories i.e.
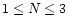 (blue),
(blue),
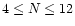 (red) and N > 12 (green).
The crosses signify the range covered in T90 and
(red) and N > 12 (green).
The crosses signify the range covered in T90 and
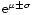 for the lognormal distribution which includes 16% to
84% of the pulse values for that T90 bin. The upper
diagonal line is the limit where the pulse parameter is equal to
T90 and the lower lines by the limited time resolution i.e.
5 ms, 64 ms and 256 ms. In some GRBs with few pulses separated by
a long
for the lognormal distribution which includes 16% to
84% of the pulse values for that T90 bin. The upper
diagonal line is the limit where the pulse parameter is equal to
T90 and the lower lines by the limited time resolution i.e.
5 ms, 64 ms and 256 ms. In some GRBs with few pulses separated by
a long 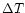 the value of T90 which goes from 5% to
95% of the counts may not include a small peak before or after
the
the value of T90 which goes from 5% to
95% of the counts may not include a small peak before or after
the 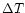 yielding a value of
yielding a value of
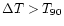 .
This
effect is seen in d). Small corrections were applied to the
pulse timing locations of the crosses that took into account the
truncation of the distributions by the limited time resolution.
The lines are the best fits to the median values and the power
law indices are listed in Table 1. The timing values were
obtained for pulses that were isolated from neighbouring pulses
at .
This
effect is seen in d). Small corrections were applied to the
pulse timing locations of the crosses that took into account the
truncation of the distributions by the limited time resolution.
The lines are the best fits to the median values and the power
law indices are listed in Table 1. The timing values were
obtained for pulses that were isolated from neighbouring pulses
at 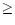 50% whereas all pulses above 5 50% whereas all pulses above 5 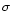 were used for
were used for
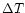 . . |
| Open with DEXTER |
The BATSE experiment has provided the most uniform collection of
GRBs available. A large sample of the brightest GRBs with data
combined from the four energy channels was analysed using either
wavelets or median filters. A detailed account of this process
has been described elsewhere (Quilligan et al. 2002; McBreen et al. 2001).
An automated pulse selection algorithm was used to detect pulses
in the denoised signals. The samples included the brightest 319 GRBs with
T90
> 2 s analysed at 64 ms resolution and 100 GRBs with
T90 <
2 s analysed at 5 ms resolution. To extend the sample to include
GRBs with T90 well beyond 100 s, a further 79 bright GRBs
were included and analysed at 256 ms resolution.
Pulses that were isolated from neighbouring pulses at 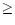 50%
level were selected and the rise times
50%
level were selected and the rise times 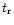 ,
fall times
,
fall times 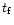 and FWHM were measured. The time intervals between pulses
and FWHM were measured. The time intervals between pulses
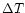 ,
above the 5
,
above the 5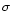 threshold, were determined. The
individual distributions of
threshold, were determined. The
individual distributions of 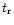 ,
,
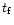 ,
FWHM and
,
FWHM and 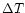 have a wide range and are consistent with lognormal
distributions. The bursts were split into T90categories with comparable number of pulses and typical lower boundaries
0, 0.5, 2, 15, 30 and greater than 100 s for the GRBs at 256 ms resolution.
The latter GRBs were binned separately despite the overlap with
T90 because they are from a dimmer sample that was included
to extend the range in duration to ultra-long GRBs. The GRBs were
further split into three categories based on the number of pulses
have a wide range and are consistent with lognormal
distributions. The bursts were split into T90categories with comparable number of pulses and typical lower boundaries
0, 0.5, 2, 15, 30 and greater than 100 s for the GRBs at 256 ms resolution.
The latter GRBs were binned separately despite the overlap with
T90 because they are from a dimmer sample that was included
to extend the range in duration to ultra-long GRBs. The GRBs were
further split into three categories based on the number of pulses
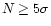 i.e.
i.e.
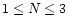 ,
,
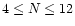 and
and 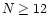 .
The median
.
The median 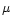 and standard deviation
and standard deviation 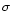 of each lognormal distribution was determined
(Quilligan et al. 2002).
of each lognormal distribution was determined
(Quilligan et al. 2002).
The diagrams of 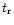 ,
,
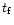 ,
FWHM and
,
FWHM and 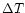 versus T90 are presented in Fig. 1 for three categories
based on the number of pulses in the GRBs. The crosses in Fig. 1
are not error bars but show the range in T90 over which the
pulses in the bursts were combined and the range of the lognormal
distribution that includes 67% of the values for the relevant
pulse property. The indices of the best fit power-laws to the
median values in Fig. 1 are listed in Table 1 and all have values
close to unity. The values of
versus T90 are presented in Fig. 1 for three categories
based on the number of pulses in the GRBs. The crosses in Fig. 1
are not error bars but show the range in T90 over which the
pulses in the bursts were combined and the range of the lognormal
distribution that includes 67% of the values for the relevant
pulse property. The indices of the best fit power-laws to the
median values in Fig. 1 are listed in Table 1 and all have values
close to unity. The values of 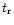 ,
,
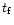 ,
FWHM and
,
FWHM and
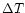 are well correlated with each other
(Quilligan et al. 2002) which explains the similarity of the
diagrams when plotted versus T90. All four figures are
presented to emphasise this result. For the two categories with
are well correlated with each other
(Quilligan et al. 2002) which explains the similarity of the
diagrams when plotted versus T90. All four figures are
presented to emphasise this result. For the two categories with
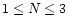 and
and
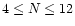 the power-laws between
the median values of
the power-laws between
the median values of 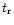 ,
,
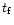 ,
FWHM,
,
FWHM, 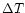 and T90 extend over a range of more than 103 and
includes GRBs from both sub-classes. The GRBs with N > 12include only those with
T90 > 2 s because N = 9 is the
largest value for GRBs with
T90 < 2 s. The data are
displaced from the two catagories of GRBs with fewer pulses and
display flattening for
T90 < 50 s which may be caused by a
selection effect because of pulse amalgamation by the 64 ms
resolution of the data.
and T90 extend over a range of more than 103 and
includes GRBs from both sub-classes. The GRBs with N > 12include only those with
T90 > 2 s because N = 9 is the
largest value for GRBs with
T90 < 2 s. The data are
displaced from the two catagories of GRBs with fewer pulses and
display flattening for
T90 < 50 s which may be caused by a
selection effect because of pulse amalgamation by the 64 ms
resolution of the data.
The properties of the isolated pulses in GRBs with
T90 > 2 s,
at 64 ms resolution, were compared with the preceding
(
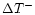 )
and subsequent (
)
and subsequent (
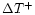 )
values of
)
values of
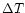 .
The pulse amplitudes (PA) are more anticorrelated with
.
The pulse amplitudes (PA) are more anticorrelated with
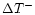 than
than
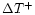 with Spearman rank order
correlation coefficients of -0.39 and -0.33. The peak to peak
values of
with Spearman rank order
correlation coefficients of -0.39 and -0.33. The peak to peak
values of 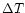 were then corrected for the strong
correlation between
were then corrected for the strong
correlation between 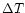 and the pulse rise and fall times
(Quilligan et al. 2002). The amended values of the correlation
coefficients are -0.27 and -0.16 with probabilities that the
anti-correlations arose by chance of 10-15 and 10-6.
This difference did not depend on the isolation level of the
pulses which was varied from 30% to 80%. The FWHM of the
pulses were also compared with
and the pulse rise and fall times
(Quilligan et al. 2002). The amended values of the correlation
coefficients are -0.27 and -0.16 with probabilities that the
anti-correlations arose by chance of 10-15 and 10-6.
This difference did not depend on the isolation level of the
pulses which was varied from 30% to 80%. The FWHM of the
pulses were also compared with
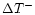 and
and
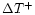 and found to be strongly correlated. The
correlations were marginally stronger for
and found to be strongly correlated. The
correlations were marginally stronger for
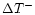 than
than
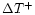 .
.
The data in Fig. 1 shows that the median values of 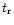 ,
,
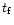 ,
FWHM and
,
FWHM and 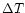 depend strongly on T90 and
also on the number of pulses. GRBs with the same durations can
have a wide variation in the number of pulses and the pulse
properties. GRBs with a small number of pulses generally have
slow pulses that are further apart while bursts with larger
number of pulses have faster and spectrally harder pulses that
are closer together (Norris et al. 2001). In both cases the same
pattern is observed except that the median values of
depend strongly on T90 and
also on the number of pulses. GRBs with the same durations can
have a wide variation in the number of pulses and the pulse
properties. GRBs with a small number of pulses generally have
slow pulses that are further apart while bursts with larger
number of pulses have faster and spectrally harder pulses that
are closer together (Norris et al. 2001). In both cases the same
pattern is observed except that the median values of 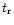 ,
,
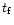 ,
FWHM and
,
FWHM and 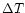 scale with T90. Bursts with
only one pulse and correlated pulse properties would lie on a
line of slope unity, while bursts with many pulses lie on
parallel lines if the pulse properties and
scale with T90. Bursts with
only one pulse and correlated pulse properties would lie on a
line of slope unity, while bursts with many pulses lie on
parallel lines if the pulse properties and 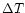 are
correlated. The correlated nature of the pulse parameters and
are
correlated. The correlated nature of the pulse parameters and
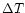 provide additional information on the central engine
and the emission process.
provide additional information on the central engine
and the emission process.
The separation of GRBs based on N (Fig. 1) suggests a kinematic
origin because the median values of the pulse timing parameters
and 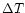 scale in the same way and by about the same amount.
In the internal shock model, an effect of this type may occur in
homogeneous jet models where the degree of collimation and range
in
scale in the same way and by about the same amount.
In the internal shock model, an effect of this type may occur in
homogeneous jet models where the degree of collimation and range
in 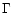 depends on the mass at the explosion
(Kobayashi et al. 2001) or in an inhomogeneous jet model by a viewing
effect caused by collimated emission with higher average values of
depends on the mass at the explosion
(Kobayashi et al. 2001) or in an inhomogeneous jet model by a viewing
effect caused by collimated emission with higher average values of
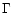 close to the rotation axis, where there is lower baryon
pollution (Rees & Mészáros 1994; Rees 1999; Salmonson 2000). The
transparency radius of the fireball
close to the rotation axis, where there is lower baryon
pollution (Rees & Mészáros 1994; Rees 1999; Salmonson 2000). The
transparency radius of the fireball 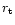 varies as
varies as
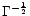 .
The profiles of pulses in bursts from
off-axis will be slowed by (1) the reduced value of
.
The profiles of pulses in bursts from
off-axis will be slowed by (1) the reduced value of 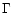 and
(2) the longer time for faster shocks to catch slower ones before
reaching
and
(2) the longer time for faster shocks to catch slower ones before
reaching 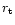 .
There will be fewer shocks to collide outside
.
There will be fewer shocks to collide outside
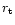 and hence generate lower luminosity bursts with slower
and softer pulses because the additional shock amalgamation
produces a narrower range in
and hence generate lower luminosity bursts with slower
and softer pulses because the additional shock amalgamation
produces a narrower range in 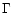 .
Indeed this process may be
a key factor in controlling the spread in
.
Indeed this process may be
a key factor in controlling the spread in 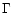 in GRBs.
in GRBs.
The luminosity of BATSE bursts is not determined but several
factors imply that GRBs with faster and harder pulses are more
luminous. The luminosity-variability and luminosity-lag
correlations for GRBs with known z infer that the more variable
and spectrally harder bursts are more luminous
(Norris et al. 2000; Salmonson 2000; Fenimore & Ramirez-Ruiz 2001; Schaefer et al. 2001; Ioka & Nakamura 2001; Schmidt 2001).
These correlations can be explained in an inhomogeneous jet model
where the more luminous and variable bursts with higher N occur
close to the axis and the slower, softer and less luminous bursts
from further off-axis (Quilligan et al. 2002). In addition, there
is the strong case for jets in GRBs based on the impressive range
of afterglow studies (Frail et al. 2001). The unexpected effect is
that the jet has left its imprint on the timing profile of the
burst.
The power laws in Fig. 1 connect the pulse data in the two
sub-classes for
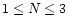 and
and
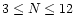 .
The
median values of the pulse timing parameters and
.
The
median values of the pulse timing parameters and 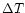 scale
with T90 by about a factor of 103. This result may
indicate a direct connection between the two sub-classes of
bursts or that they coincidentally lie on the same power laws in
the absence of sufficient data to independently determine the
slopes for the short bursts. The popular progenitors of GRBs
range from mergers of compact objects such as neutron stars and
black holes to collapsars and hypernovae in massive stars. A neat
feature of most progenitor models is that they provide a generic
scenario based on the formation of a black hole with a massive
debris torus that is rapidly accreted and energises the jet by
neutrino transport and magnetohydrodynamic processes.
scale
with T90 by about a factor of 103. This result may
indicate a direct connection between the two sub-classes of
bursts or that they coincidentally lie on the same power laws in
the absence of sufficient data to independently determine the
slopes for the short bursts. The popular progenitors of GRBs
range from mergers of compact objects such as neutron stars and
black holes to collapsars and hypernovae in massive stars. A neat
feature of most progenitor models is that they provide a generic
scenario based on the formation of a black hole with a massive
debris torus that is rapidly accreted and energises the jet by
neutrino transport and magnetohydrodynamic processes.
The variation of the pulse parameters with T90 maybe caused
by the same emission mechanisms and progenitors. If GRBs have
the same progenitors, the short GRBs must have very high values of
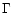 to produce the short durations (Piran 1999). The
high value of
to produce the short durations (Piran 1999). The
high value of 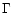 is close to the upper bound allowed by the
internal shock model (Sari & Piran 1997; Lazzati et al. 1999) but well
below what can in principle be produced in a very low baryon
environment (Mészáros & Rees 1997). An alternative interpretation
is that there are two types of progenitors with pulses that
coincidentally lie on the same power laws. The progenitors that
arise from massive stars may not be capable of producing short
GRBs. The short bursts may come from mergers of neutron stars or
neutron stars and black holes (Ruffert & Janka 1999) where the time
structure in the bursts reflects the interaction of thin
relativistic shocks with
is close to the upper bound allowed by the
internal shock model (Sari & Piran 1997; Lazzati et al. 1999) but well
below what can in principle be produced in a very low baryon
environment (Mészáros & Rees 1997). An alternative interpretation
is that there are two types of progenitors with pulses that
coincidentally lie on the same power laws. The progenitors that
arise from massive stars may not be capable of producing short
GRBs. The short bursts may come from mergers of neutron stars or
neutron stars and black holes (Ruffert & Janka 1999) where the time
structure in the bursts reflects the interaction of thin
relativistic shocks with
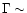 100 and duration of
100 and duration of 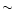 50 ms. In this two progenitor scenario the high values of
50 ms. In this two progenitor scenario the high values of
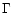 can be reduced by about an order of magnitude. In
addition the central engine and the environment before the
photosphere may combine to smooth the shocks in a way that is a
function of T90.
can be reduced by about an order of magnitude. In
addition the central engine and the environment before the
photosphere may combine to smooth the shocks in a way that is a
function of T90.
There are a number of new results on pulses, from short and long
GRBs, that constrain the emission process. These include (1) the
distributions of values of 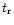 ,
,
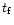 ,
FWHM, pulse
amplitude (PA) and pulse area of isolated pulses are not random
but have lognormal distributions
(Quilligan et al. 2002; McBreen et al. 2001; Nakar & Piran 2001), (2) the values of
,
FWHM, pulse
amplitude (PA) and pulse area of isolated pulses are not random
but have lognormal distributions
(Quilligan et al. 2002; McBreen et al. 2001; Nakar & Piran 2001), (2) the values of
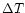 are lognormally distributed with a power-law excess of
long time intervals or a Pareto-Levy tail for GRBs with
T90
> 2 s (Quilligan et al. 2002; McBreen et al. 2001; Nakar & Piran 2001), (3) there is an
anticorrelation between the values of PA and FWHM
(Ramirez-Ruiz & Fenimore 2000; Quilligan et al. 2002), (4) there is a positive
correlation between the values of the PA that extend over many
pulses (Quilligan et al. 2002; McBreen et al. 2001), (5) there is also a
positive correlation between the values of
are lognormally distributed with a power-law excess of
long time intervals or a Pareto-Levy tail for GRBs with
T90
> 2 s (Quilligan et al. 2002; McBreen et al. 2001; Nakar & Piran 2001), (3) there is an
anticorrelation between the values of PA and FWHM
(Ramirez-Ruiz & Fenimore 2000; Quilligan et al. 2002), (4) there is a positive
correlation between the values of the PA that extend over many
pulses (Quilligan et al. 2002; McBreen et al. 2001), (5) there is also a
positive correlation between the values of 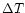 (Quilligan et al. 2002; McBreen et al. 2001), (6) the PA of isolated pulses
in GRBs with
T90
> 2 s and 64 ms resolution were compared with
(Quilligan et al. 2002; McBreen et al. 2001), (6) the PA of isolated pulses
in GRBs with
T90
> 2 s and 64 ms resolution were compared with
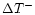 and
and
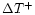 because of a strong correlation between the pulse
width and
because of a strong correlation between the pulse
width and
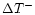 in the galactic superluminal source GRS
1915+105 where outbursts are powered by accretion into a black
hole (Belloni et al. 1997) and a correlation between long quiescent
periods in GRBs and subsequent intervals of emission
(Ramirez-Ruiz & Merloni 2001). The PAs were found to be anticorrelated with
in the galactic superluminal source GRS
1915+105 where outbursts are powered by accretion into a black
hole (Belloni et al. 1997) and a correlation between long quiescent
periods in GRBs and subsequent intervals of emission
(Ramirez-Ruiz & Merloni 2001). The PAs were found to be anticorrelated with
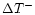 and
and
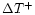 with a slightly larger
anticorrelation for
with a slightly larger
anticorrelation for
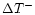 .
Any additional correlations
between the pulse properties and
.
Any additional correlations
between the pulse properties and
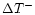 would be
expected to be much weaker than in GRS 1915+105 because a similar
intermittent pattern in the outbursts from the central engine
would have to persist after shock interactions generated the
outbursts. The combination of the six results make the pulses in
GRBs quite unique. In addition long pulses are asymmetric and
reach their maximum earlier in higher energy bands while shorter
pulses tend to be more symmetric with negligible time lags
between energy channels (Norris et al. 1996).
would be
expected to be much weaker than in GRS 1915+105 because a similar
intermittent pattern in the outbursts from the central engine
would have to persist after shock interactions generated the
outbursts. The combination of the six results make the pulses in
GRBs quite unique. In addition long pulses are asymmetric and
reach their maximum earlier in higher energy bands while shorter
pulses tend to be more symmetric with negligible time lags
between energy channels (Norris et al. 1996).
The three results discussed above seem to favour an internal
shock model powered by a hyper-accretion process into a newly
formed black hole (Ruffert & Janka 1999; Popham et al. 1999; Zhang & Fryer 2001).
The accretion process has been modelled and is sensitive to the
rate at which material piles up around the black hole and the
accretion time scale of the particles. The accretion rate might
provide the overall control on the process that
eventually
generates the correlated outbursts from the jet. The
pulse
amplitudes and time intervals can be coupled because higher
accretion rates cause larger outbursts that are closer in time,
while lower accretion rates produce smaller and slower events that
are further apart. It appears that variation in the rate of
accretion, the thickness of the relativistic shocks and the
viewing angle of the jet may be key factors in accounting for the
observed durations and pulse properties in GRBs. There are many
uncertain factors that influence the process. These include the
viscosity of the particles, the mass and angular momentum of the
disk, the mass and spin of the black hole and the energy
extraction and collimation process.
-
Belloni, T., Mendez, M., King, A. R., van der Klis,
M., & van Paradijs, J. 1997, ApJ, 488, L109
In the text
NASA ADS
-
Beloborodov, A. M., Stern, B. E., & Svensson, R. 2000, ApJ, 535, 158
In the text
NASA ADS
-
Fenimore, E. E., & Ramirez-Ruiz, E. 2001, ApJ, submitted [astro-ph/0004176]
In the text
-
Fishman, G. J., & Meegan, C. A. 1995, ARA&A, 33, 415
In the text
NASA ADS
-
Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2001, ApJ, 562, L55
In the text
NASA ADS
-
Ioka, K., & Nakamura, T. 2001, ApJ, 554, L163
In the text
NASA ADS
-
Kobayashi, S., Ryde, F., & MacFadyen, A. 2001 [astro-ph/0110080]
In the text
-
Lazzati, D., Ghisellini, G., & Celotti, A. 1999, MNRAS, 309, L13
In the text
NASA ADS
-
Lee, A., Bloom, E., & Petrosian, V. 2000, ApJS, 131, 1
In the text
NASA ADS
-
MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262
In the text
NASA ADS
-
McBreen, B., Hurley, K. J., Long, R., & Metcalfe, L. 1994, MNRAS, 271,
662
In the text
NASA ADS
-
McBreen, S., Quilligan, F., McBreen, B., Hanlon, L., & Watson, D. 2001, A&A, 380, L31
In the text
NASA ADS
-
Mészáros, P., & Rees, M. J. 1997, ApJ, 482, L29
In the text
NASA ADS
-
Nakar, E., & Piran, T. 2001 [astro-ph/0103210]
In the text
-
Norris, J. P., Nemiroff, R. J., Bonnell, J. T., et al. 1996, ApJ, 459,
393
In the text
NASA ADS
-
Norris, J. P., Marani, G. F., & Bonnell, J. T. 2000, ApJ, 534, 248
In the text
NASA ADS
-
Norris, J. P., Scargle, J. D., & Bonnell, J. T. 2001t [astro-ph/0105052]
In the text
-
Paczynski, B. 1991, Acta Astron., 41, 257
In the text
NASA ADS
-
Piran, T. 1999, Phys. Rep., 314, 575
In the text
NASA ADS
-
Popham, R., Woosley, S. E., & Fryer, C. 1999, ApJ, 518, 356
In the text
NASA ADS
-
Quilligan, F., McBreen, B., Hanlon, L., et al. 2002, A&A,
385, 377
In the text
-
Ramirez-Ruiz, E., & Fenimore, E. E. 2000, ApJ, 539, 712
In the text
NASA ADS
-
Ramirez-Ruiz, E., & Merloni, A. 2001, MNRAS, 320, L25
In the text
NASA ADS
-
Rees, M. J. 1999, A&AS, 138, L491
In the text
-
Rees, M. J., & Mészáros, P. 1994, ApJ, 430, L93
In the text
NASA ADS
-
Ruffert, M., & Janka, H.-T. 1999, A&A, 344, 573
In the text
NASA ADS
-
Salmonson, J. D. 2000, ApJ, 544, L115
In the text
NASA ADS
-
Sari, R., & Piran, T. 1997, MNRAS, 287, 110
In the text
NASA ADS
-
Schaefer, B. E., Deng, M., & Band, D. L. 2001, ApJ, 563, L123
In the text
NASA ADS
-
Schmidt, M. 2001, ApJ, 552, 36
In the text
NASA ADS
-
Zhang, W., & Fryer, C. L. 2001, ApJ, 550, 357
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[angle=-90,width=11.5cm,clip]{Dj223_f1.eps}\end{figure}](/articles/aa/full/2002/15/aadj223/Timg11.gif)