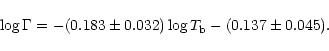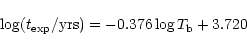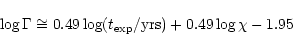A&A 385, 1008-1013 (2002)
DOI: 10.1051/0004-6361:20020031
A possible observational measure of evolution in bipolar nebulae
J. P. Phillips
Instituto de Astronomia y Meteorologia, Avenida
Vallarta No. 2602, Col. Arcos Vallarta, C.P. 44130 Guadalajara, Jalisco, Mexico
Received 30 November 2001 / Accepted 4 January 2002
Abstract
Bipolar planetary nebulae (BPNe) possess a broad range of shapes,
ranging from narrow-waisted butterfly-like structures, through to those
which are more nearly cylindrical. We point out that these morphologies
appear to be correlated with radio surface brightness  ,
in the sense
that higher values of
,
in the sense
that higher values of  are associated with envelopes having narrower
waists. If one interprets the variation in
are associated with envelopes having narrower
waists. If one interprets the variation in  as arising from shell evolution,
as is usually assumed for other planetaries, this would then imply that
shell morphology varies with time in a manner which appears not to be
consistent with evolutionary models. It also remains possible, however,
that different BPNe morphologies arise as a result of differing
mechanisms of formation, and that the pre-collimation of high velocity
central winds gives rise to narrower waists, and higher surface
brightness nuclei. Our results, if this is true, may then imply that central
winds possess a broad range of collimations.
as arising from shell evolution,
as is usually assumed for other planetaries, this would then imply that
shell morphology varies with time in a manner which appears not to be
consistent with evolutionary models. It also remains possible, however,
that different BPNe morphologies arise as a result of differing
mechanisms of formation, and that the pre-collimation of high velocity
central winds gives rise to narrower waists, and higher surface
brightness nuclei. Our results, if this is true, may then imply that central
winds possess a broad range of collimations.
Key words: ISM: planetary nebulae: general - ISM: jets and outflows
It is generally believed that post-main-sequence bipolar nebulae (BPNe)
arise through the interaction of stellar winds with collimating disks (e.g.
Corradi & Schwarz 1995; Cuesta et al. 1995). The resulting shocked
bubbles of high temperature gas then drive the lobal structures to
velocities of  150 kms-1 or so (Corradi & Schwarz 1995).
150 kms-1 or so (Corradi & Schwarz 1995).
Beyond this, our understanding of the formation and evolution of such
sources is extremely restricted, whether regarded in theoretical or
observational terms. Modeling of such sources appears to indicate that
BPNe morphologies are sensitive to the presence of magnetic fields,
wind rotation, density contrasts within the slower AGB wind, the rate of
evolution (i.e. the mass) of the central star, the level of pre-collimation of
the fast wind (see discussion in Sect. 3), and various other parameters
(e.g. Garcia-Segura et al. 1999; Frank et al. 1993; Mellema 1995; Soker
& Rappaport 2000). The relative importance of these mechanisms is
however uncertain. The time evolution of such sources has been
considered by Mellema et al. (1991) and Mellema & Frank (1995),
whence it is clear that morphologies are expected to vary considerably
during the initial phases of expansion. Mellema (1997) and Mellema &
Frank (1995), however, suggest that much of this development may be
confined to the earliest stages of expansion. Later expansion of the I-fronts would be expected to reduce density contrasts within the exterior,
aspherical AGB wind, and result in an invariant morphology during
subsequent phases of evolution.
There is some observational evidence to support this presumption. Thus
Corradi et al. (2001) find evidence for "ballistic" expansion in the lobes of
He 2-104, a trend that appears also to be present in other BPNe
(Corradi & Schwarz 1993a; Corradi & Schwarz 1993b; Redman et al.
2000), and has been noted in more spherically symmetric nebulae as
well (e.g. Weedman 1968; Wilson 1958). This is interpreted as arising
from self-similar evolution of the lobes (i.e. evolution with constant
morphology) subsequent to the phase in which lobes are confined and
shaped within the AGB envelopes. This, if true, would conflict with
certain earlier models of BPNe evolution, in which it was presumed that
the ratio between disk and lobal dimensions decreases with time (Balick
1987).
Table 1:
Summary of spatial and surface brightness paramaeters for bipolar sources.
![\begin{table}
{\includegraphics[width=12cm,clip]{table1.eps} }
\end{table}](/articles/aa/full/2002/15/aa2156/img5.gif) |
Refs: 1. Milne & Aller (1975); 2. Milne & Aller (1982); 3. Isaacman
(1984); 4. Phillips & Mampaso (1988); 5. Zijlstra et al.
(1989); 6. Milne (1979); 7. Cahn & Rubin (1974); 8. Kaftan-Kassim
(1969); 9. Zhang (1995); 10. Calabretta (1982); 11. Rodriguez
et al. (1985); 12. Cahn & Kaler (1971); 14. Chu et al. (1987); 15
Perek & Kohoutek (1967).
Much here depends, however, upon a narrow observational data base,
and the parameters and codes which are employed for hydrodynamical
modeling. It also, in the latter cases, depends upon whether the
analyses are fully three dimensional, include the effects of central star
evolution, the degree to which radiative transfer is incorporated, and the
manner in which non-ionized regions are treated; it is sensitive, in short,
to the level of analytical sophistication which is employed. Taking all of
this into account, it is probably fair to state that our understanding of
such evolution remains in its infancy, and that our ideas may still be
open to considerable revision.
With this in mind, we have therefore investigated whether there may be
further ways in which the evolution of BPNe may be assessed. In
particular, we shall investigate whether trends may be discerned
between the relative sizes of collimation disks and lobes.
We have, for the purposes of this analysis, evaluated a parameter
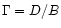 for some 24 BPNe, where B corresponds to the maximum width of
the bilobal structures, and D is the diameter of the collimating disks -
both of these assessed along directions perpendicular to the primary
outflows (see Table 1). This total of sources represents approximately 30% of known BPNe, and corresponds to nebulae for which it was possible
to identify and measure central collimating disks (see below).
for some 24 BPNe, where B corresponds to the maximum width of
the bilobal structures, and D is the diameter of the collimating disks -
both of these assessed along directions perpendicular to the primary
outflows (see Table 1). This total of sources represents approximately 30% of known BPNe, and corresponds to nebulae for which it was possible
to identify and measure central collimating disks (see below).
The parameter  has the merit of being relatively independent of bipolar
inclination i. By contrast, the use of lobe dimensions L along the
principal axes of the outflows (in place of the perpendicular dimensions
B) would suffer from two primary disadvantages; that the size of L varies
as sin i (where i is usually poorly known), and that the major axis limits
of the lobes are often faint, fragmentary, and extremely ill-defined.
has the merit of being relatively independent of bipolar
inclination i. By contrast, the use of lobe dimensions L along the
principal axes of the outflows (in place of the perpendicular dimensions
B) would suffer from two primary disadvantages; that the size of L varies
as sin i (where i is usually poorly known), and that the major axis limits
of the lobes are often faint, fragmentary, and extremely ill-defined.
Most if not all BPNe contain bright central condensations, out of which
the primary outflows appear frequently to be emerging. We take these
structures to represent the central collimating disks. There are several
indicators to support this presumption. The first is that many of these
features appear (where inclinations permit) to possess ring-like
morphologies (e.g. Phillips 2001). It is also clear that most (and possibly
all) of these structures are elongated perpendicularly to the bipolar
outflows, as would be expected for tilted collimating disks.
Finally, it is apparent that several of these regions are associated with
bands of extinction (cf. NGC 6302, M 2-48 and Hen 3-401) and toroids
of molecular emission (Sahai et al. 1991; Bachiller et al. 1989; Zweigle
et al. 1997), implying the presence of collimating disks with high
contents of neutral gas.
We have been able to evaluate values of  from imaging published by
Manchado et al. (1996), Corradi & Schwarz (1995), Schwarz et al.
(1992), Perek & Kohoutek (1967), Balick (1987), at the web sites
http://ad.usno.navy.mil/pne/ and http://astro.uni-tuebingen.de/groups/pn/, and from individual images published in the scientific literature.
These are indicated in Table 1; where it should be noted that we have
listed only those sources having measured 5 GHz brightness
temperatures
from imaging published by
Manchado et al. (1996), Corradi & Schwarz (1995), Schwarz et al.
(1992), Perek & Kohoutek (1967), Balick (1987), at the web sites
http://ad.usno.navy.mil/pne/ and http://astro.uni-tuebingen.de/groups/pn/, and from individual images published in the scientific literature.
These are indicated in Table 1; where it should be noted that we have
listed only those sources having measured 5 GHz brightness
temperatures  (see discussion below).
(see discussion below).
The errors in  are difficult to assess precisely, but arise (for the most
part) where nebular structures are ill-defined; where shells fade
gradually, without sharply defined limits; where the lobal structures are
complex and/or filamentary; and where seeing disk sizes are
comparable to the sizes of the nebulae, leading to smoothing of the
apparent shell structures. None of these factors are likely to be
important for the nebulae considered here, although they may all play
their part in contributing to overall errors. All of the nebular images are,
for instance, considerably larger than those of nearby field stars, and
appear (for the larger part) to be reasonably sharply defined. Similarly,
we note that images of the central collimating disks are in all cases
reasonably deep (the disks are often much brighter than the bipolar
extensions), and reasonably well defined. It is unlikely that deeper
exposures would yield significant changes in apparent dimensions.
Although certain of the disks are enveloped by more extended emission,
this is usually very much fainter, and unlikely to be associated with the
primary disk structures.
are difficult to assess precisely, but arise (for the most
part) where nebular structures are ill-defined; where shells fade
gradually, without sharply defined limits; where the lobal structures are
complex and/or filamentary; and where seeing disk sizes are
comparable to the sizes of the nebulae, leading to smoothing of the
apparent shell structures. None of these factors are likely to be
important for the nebulae considered here, although they may all play
their part in contributing to overall errors. All of the nebular images are,
for instance, considerably larger than those of nearby field stars, and
appear (for the larger part) to be reasonably sharply defined. Similarly,
we note that images of the central collimating disks are in all cases
reasonably deep (the disks are often much brighter than the bipolar
extensions), and reasonably well defined. It is unlikely that deeper
exposures would yield significant changes in apparent dimensions.
Although certain of the disks are enveloped by more extended emission,
this is usually very much fainter, and unlikely to be associated with the
primary disk structures.
The values of  may also depend upon stratification effects, and upon
which ionic transitions are contained within the filter passbands. Thus,
low excitation lines (such as [NII], [SII] and so forth) are likely derive
from differing regimes of the outflows than those of higher excitation
transitions ([OIII], [Ar IV] and etc.). It is at least plausible, therefore, to
suppose that differing images may give rise to differing values of
may also depend upon stratification effects, and upon
which ionic transitions are contained within the filter passbands. Thus,
low excitation lines (such as [NII], [SII] and so forth) are likely derive
from differing regimes of the outflows than those of higher excitation
transitions ([OIII], [Ar IV] and etc.). It is at least plausible, therefore, to
suppose that differing images may give rise to differing values of  .
We
find little evidence for this in the images used here, but have
nevertheless chosen to evaluate
.
We
find little evidence for this in the images used here, but have
nevertheless chosen to evaluate  using images in HI where at all
possible. The effects of this uncertainty (both random and systematic)
are likely to be extremely modest, and dwarfed by the intrinsic scatter in
using images in HI where at all
possible. The effects of this uncertainty (both random and systematic)
are likely to be extremely modest, and dwarfed by the intrinsic scatter in
 between differing sources.
between differing sources.
Given the various comments above, we therefore believe that errors in  are likely to be small. Comparisons between values of
are likely to be small. Comparisons between values of  determined
from independent images suggests a typical uncertainty of
determined
from independent images suggests a typical uncertainty of
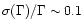 .
.
Finally, we wish to take note of a possible ambiguity in the analysis of M
2-9. We have, for this source, taken the size of the disk to be 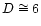 arcsec, corresponding to the maximum dimension of the central optical
condensation (Kohoutek & Surdej 1980). This approach is consistent
with the methodology applied for other sources in this study. The use of
this value is also supported through measurements at millimetric
wavelengths, which indicate the presence of a toroidal structure of
precisely this dimension (Zweigle et al. 1997). It seems clear however
that the source also possesses much smaller structures close to the
central star(s); structures which are detectable at radio and optical
wavelengths, and appear (at most) to be a few tenths of an arcsecond in
size (Kwok et al. 1985; Balick et al. 1997). If these structures
correspond to the true collimating disk, then the value of
arcsec, corresponding to the maximum dimension of the central optical
condensation (Kohoutek & Surdej 1980). This approach is consistent
with the methodology applied for other sources in this study. The use of
this value is also supported through measurements at millimetric
wavelengths, which indicate the presence of a toroidal structure of
precisely this dimension (Zweigle et al. 1997). It seems clear however
that the source also possesses much smaller structures close to the
central star(s); structures which are detectable at radio and optical
wavelengths, and appear (at most) to be a few tenths of an arcsecond in
size (Kwok et al. 1985; Balick et al. 1997). If these structures
correspond to the true collimating disk, then the value of  would require
increasing by at least an order of magnitude. This would, in turn, take
the nebula well outside of the sequence for BPNe to be discussed in
Sect. 3.
would require
increasing by at least an order of magnitude. This would, in turn, take
the nebula well outside of the sequence for BPNe to be discussed in
Sect. 3.
Having established a reasonable corpus of values  ,
it is now of interest
to evaluate the evolutionary status of the nebulae. One common way of
doing this is to determine the radii R of the nebulae, on the supposition
that older nebulae are intrinsically larger. The problem in this case,
however, is how to determine reliable values for R. Whilst the angular
dimensions of planetaries can be determined to a tolerable level of
accuracy (although bipolar sources are particularly problematic in this
regard) their distances cannot. Similarly, whilst statistical distances are available
for many of the sources in our list (van de Steene & Zijlstra 1994; Zhang
1995; Cahn et al. 1992; and etc.), none of these estimates can be
regarded as secure.
,
it is now of interest
to evaluate the evolutionary status of the nebulae. One common way of
doing this is to determine the radii R of the nebulae, on the supposition
that older nebulae are intrinsically larger. The problem in this case,
however, is how to determine reliable values for R. Whilst the angular
dimensions of planetaries can be determined to a tolerable level of
accuracy (although bipolar sources are particularly problematic in this
regard) their distances cannot. Similarly, whilst statistical distances are available
for many of the sources in our list (van de Steene & Zijlstra 1994; Zhang
1995; Cahn et al. 1992; and etc.), none of these estimates can be
regarded as secure.
We have therefore chosen to take note of an evolutionary trend in most
(non-bipolar) nebulae, and apply this to the case of the BPNe.
Specifically, it has been found that where nebular distances are
evaluated through more-or-less reliable procedures (i.e. using
trigonometric and spectroscopic distances, expansion distances and so
forth), then the surface brightnesses of the sources appear to be
monotonically related to their radii (e.g. Phillips 2001b; Zhang 1995;
van de Steene & Zijlstra 1994). Put at its most simple, the younger
sources have high brightness temperatures, and the older sources have
low brightness temperatures. The deduced correlation between  (5 GHz) and R appears to be reasonably well defined.
(5 GHz) and R appears to be reasonably well defined.
It is important, on the other hand, to note that radio surface brightnesses
in BPNe are not quite the same as in other planetary nebulae. Thus,
whilst the radio and optical diameters of "normal" PNe are broadly
comparable, and representative of the overall sizes of the sources, this
is not the case with BPNe. On the contrary, much of the radio emission
appears to come from the interiors of these sources, and is confined
within regions which are very much smaller than the overall nebular
dimensions (e.g. Phillips & Mampaso 1988).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2156f1.eps}\end{figure}](/articles/aa/full/2002/15/aa2156/Timg10.gif) |
Figure 1:
Variation of brightness temperature with radius for bipolar nebulae at
known distances. The two diagonal lines correspond to the calibrations
of Zhang (1995) and Phillips (2001), determined using general
populations of PNe. |
| Open with DEXTER |
It is likely, in brief, that the radio dimensions of most (if not all) of these
sources refers to the central higher density, higher emission measure
collimating regimes.
Nevertheless, and insofar as it can be assessed, it appears that the
trend of  with R is similar for both BPNe and other planetary nebulae.
This is illustrated in Fig. 1, where we have taken values of "known" (i.e.
model independent) BPNe distances from papers by Zhang (1995) and
Phillips (2001). It is clear from this that although distances remain
uncertain; that the scatter is large; and that the total number of sources
is restricted, there is nevertheless a close correspondence between the
mean trends for other PNe (represented by the diagonal lines) and that
for BPNe. It appears, in short, that the central collimating regimes of
BPNe follow a closely similar relation to that noted for the generality of
sources. This, in turn, suggests that a similar interpretation is relevant,
and that lower surface brightness BPNe are also older.
with R is similar for both BPNe and other planetary nebulae.
This is illustrated in Fig. 1, where we have taken values of "known" (i.e.
model independent) BPNe distances from papers by Zhang (1995) and
Phillips (2001). It is clear from this that although distances remain
uncertain; that the scatter is large; and that the total number of sources
is restricted, there is nevertheless a close correspondence between the
mean trends for other PNe (represented by the diagonal lines) and that
for BPNe. It appears, in short, that the central collimating regimes of
BPNe follow a closely similar relation to that noted for the generality of
sources. This, in turn, suggests that a similar interpretation is relevant,
and that lower surface brightness BPNe are also older.
We shall be assuming this in the proceeding analysis, whilst noting a
possible alternative explanation later in Sect. 3.
Values of  have been assessed using radio interferometric source
dimensions wherever available (i.e. in a little over 40% of the sources
considered here; see Isaacman 1984; Phillips & Mampaso 1988; and
Zijlstra et al. 1989). We have, otherwise, employed optical diameters
based upon the listings of Cahn et al. (1992), Cahn & Kaler (1971) and
others (see references in Table 1). Column 6 of Table 1 indicates the
type of measurement employed (optical (O) and/or radio (R)). These
optical values apply to the brightest central parts of the BPNe; to
regions, that is, which are smaller than the overall source sizes, and
similar to the areas mapped through radio interferometry. The optical
and radio dimensions are therefore expected to be comparable. A
comparison between source diameters
have been assessed using radio interferometric source
dimensions wherever available (i.e. in a little over 40% of the sources
considered here; see Isaacman 1984; Phillips & Mampaso 1988; and
Zijlstra et al. 1989). We have, otherwise, employed optical diameters
based upon the listings of Cahn et al. (1992), Cahn & Kaler (1971) and
others (see references in Table 1). Column 6 of Table 1 indicates the
type of measurement employed (optical (O) and/or radio (R)). These
optical values apply to the brightest central parts of the BPNe; to
regions, that is, which are smaller than the overall source sizes, and
similar to the areas mapped through radio interferometry. The optical
and radio dimensions are therefore expected to be comparable. A
comparison between source diameters 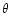 (optical) measured in the
visible, and those (
(optical) measured in the
visible, and those (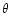 (radio)) measured in the radio suggests that this is,
in fact, broadly the case, although optical diameters are somewhat
larger; we determine that
(radio)) measured in the radio suggests that this is,
in fact, broadly the case, although optical diameters are somewhat
larger; we determine that
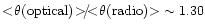 .
This may, in
turn, imply that values of
.
This may, in
turn, imply that values of  based upon optical dimensions are typically
0.23 dex too small.
based upon optical dimensions are typically
0.23 dex too small.
A further important factor to consider is that single dish and radio
interferometric estimates of F(5 GHz) appear to differ in the mean, with
interferometric measures being 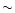 12% lower where
12% lower where
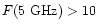 mJy.
Fainter sources appear to display even greater anomalies, with
interferometric fluxes often being less than half as great as those
measured using single dishes. This tendency has already been
discussed in the literature, with Zijlstra et al. (1989) mentioning the
possibility that single dish measures are affected by extraneous sources.
It seems more likely, however, that single beam fluxes are reasonably
accurate (Tylenda et al. 1992), and that interferometric results
underestimate emission associated with lower spatial frequencies (e.g.
emission arising from larger scale nebular structures, halos and etc.).
mJy.
Fainter sources appear to display even greater anomalies, with
interferometric fluxes often being less than half as great as those
measured using single dishes. This tendency has already been
discussed in the literature, with Zijlstra et al. (1989) mentioning the
possibility that single dish measures are affected by extraneous sources.
It seems more likely, however, that single beam fluxes are reasonably
accurate (Tylenda et al. 1992), and that interferometric results
underestimate emission associated with lower spatial frequencies (e.g.
emission arising from larger scale nebular structures, halos and etc.).
It transpires, in fact, that the use of single dish or interferometric results
makes little difference to our results. However, we have preferred to use
interferometric results where at all possible, since these are more
closely related to the radio and optical dimensions used here.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2156f2.eps}\end{figure}](/articles/aa/full/2002/15/aa2156/Timg14.gif) |
Figure 2:
Variation of the outflow aspect ratio  (see text for details) with 5 GHz
surface brightness. The representative error bars indicate the mean
levels of uncertainty that are likely to be associated with
(see text for details) with 5 GHz
surface brightness. The representative error bars indicate the mean
levels of uncertainty that are likely to be associated with  and
and  . . |
| Open with DEXTER |
It is therefore clear that the values of  are open to various
uncertainties - use of single dish fluxes may artificially enhance
temperatures in the brighter nebular structures, whilst the use of optical
dimensions may systematically reduce them. It is possible, therefore,
that errors in log(
are open to various
uncertainties - use of single dish fluxes may artificially enhance
temperatures in the brighter nebular structures, whilst the use of optical
dimensions may systematically reduce them. It is possible, therefore,
that errors in log( )
may be as high as
)
may be as high as 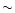 0.6 in individual cases, and
differ markedly between the various sources. A bar indicating the likely
mean error is illustrated in Fig. 2.
0.6 in individual cases, and
differ markedly between the various sources. A bar indicating the likely
mean error is illustrated in Fig. 2.
If one accepts that the radio surface brightnesses of BPNe vary with
shell lifetime (see Sect. 2.2), then the variation of  with
with  may be
interpreted as indicating the evolution of morphology with time. Such a
variation is illustrated in Fig. 2 for the sources listed in Table 1.
may be
interpreted as indicating the evolution of morphology with time. Such a
variation is illustrated in Fig. 2 for the sources listed in Table 1.
However one interprets  (and alternative reasons for these trends will
be discussed below), it is clear that there is a correlation between
(and alternative reasons for these trends will
be discussed below), it is clear that there is a correlation between  and
and
 ,
in the sense that
,
in the sense that  increases as
increases as  decreases. The least squares
relation between these parameters is given through
decreases. The least squares
relation between these parameters is given through
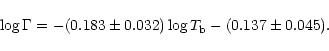 |
(1) |
The scatter about this trend is appreciable, with much of this arising from
uncertainties in  and
and  (note the representative error bars in Fig. 2). It
is very probable, therefore, that the intrinsic distribution would display an
even higher correlation. Even given this, however, it is clear that the
deduced least-squares trend appears to be highly significant, with
gradients
(note the representative error bars in Fig. 2). It
is very probable, therefore, that the intrinsic distribution would display an
even higher correlation. Even given this, however, it is clear that the
deduced least-squares trend appears to be highly significant, with
gradients
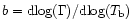 of order
of order 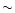 6
6
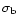 .
The correlation coefficient
.
The correlation coefficient
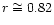 .
.
Where this trend is interpreted in evolutionary terms, then it would
appear that bipolar sources become more "circularized" or
"cylindrasized" with advancing age. The belt of material responsible for
flow collimation swells in size relative to the lobal extremities - leading
first to cylindrical structures such as IC 4406 and He 2-114, and then
(possibly) more circular morphologies such as JnEr 1, where an
essentially circular (low surface-brightness) shell contains two interior
and much brighter condensations (e.g. Manchado et al. 1996). Such a
scenario is somewhat different from that postulated by Balick (1987), in
which it is presumed that the lobes increase in size relative to the central
collimating disks. It would also be inconsistent with the ballistic models
discussed in Sect. 1, whereby BPNe are assumed to expand self-similarly.
Much here depends, of course, upon how one interprets the variation in
 ,
and upon whether the evolution in this parameter is as assumed in
other PNe (see Sect. 2). Presuming however that this is the case, then
the present results may be open to a variety of interpretations. It is
perhaps relevant, for instance, to note that mass densities within the
disks appear to be appreciable, and sufficient to retain molecular
material in the face of fierce central star UV fluxes (e.g. Sahai et al.
1991; Bachiller et al. 1989; although the formation and maintenance of
such molecules may also be aided through occasional high levels of
nuclear dust extinction (e.g. Phillips 1984)). Such higher mass densities
may moderate the level of disk acceleration, and result in lower initial
velocities of expansion than are found in the lobes. Only later, with full
ionization (and further expansion) of the disks, together with increasing
central star ionizing fluxes, would velocities of expansion increase and
lead to increasing values of
,
and upon whether the evolution in this parameter is as assumed in
other PNe (see Sect. 2). Presuming however that this is the case, then
the present results may be open to a variety of interpretations. It is
perhaps relevant, for instance, to note that mass densities within the
disks appear to be appreciable, and sufficient to retain molecular
material in the face of fierce central star UV fluxes (e.g. Sahai et al.
1991; Bachiller et al. 1989; although the formation and maintenance of
such molecules may also be aided through occasional high levels of
nuclear dust extinction (e.g. Phillips 1984)). Such higher mass densities
may moderate the level of disk acceleration, and result in lower initial
velocities of expansion than are found in the lobes. Only later, with full
ionization (and further expansion) of the disks, together with increasing
central star ionizing fluxes, would velocities of expansion increase and
lead to increasing values of  .
Whilst the kinematics of disks are
handled in extant modeling of bipolar evolution, much depends upon the
density contrasts which are assumed; the nature of the assumed
asphericities in the AGB envelopes; the presence or otherwise of neutral
gas, dust, and gas clumping; the relative velocities of the exterior and
interior winds, and so forth. In brief, the structures and properties of the
exterior disks are essentially unknown, and may have a strong bearing
upon nebular evolution, and the timescale over which this occurs.
.
Whilst the kinematics of disks are
handled in extant modeling of bipolar evolution, much depends upon the
density contrasts which are assumed; the nature of the assumed
asphericities in the AGB envelopes; the presence or otherwise of neutral
gas, dust, and gas clumping; the relative velocities of the exterior and
interior winds, and so forth. In brief, the structures and properties of the
exterior disks are essentially unknown, and may have a strong bearing
upon nebular evolution, and the timescale over which this occurs.
Alternatively, or in addition, we note that the bubble driven lobes will
likely decelerate as a result of cooling of the cavity gas; through
disruption of the walls of the lobes, leading to escape of cavity material
near the radial limits of the outflow; and from a species of snow-plow
effect, whereby the lobes shovel-up increasing amounts of superwind
material as they increase in size. These factors, too, might contribute to
secularly increasing values of  .
Some, if not all of these effects have
been considered in extant evolutionary modeling - although here again,
the precise degree to which they are important depends upon the (as yet
uncertain) properties of bipolar winds. An example of this is cited below,
where it is noted that prior collimation of the interior winds is at least
plausible, if not yet confirmed.
.
Some, if not all of these effects have
been considered in extant evolutionary modeling - although here again,
the precise degree to which they are important depends upon the (as yet
uncertain) properties of bipolar winds. An example of this is cited below,
where it is noted that prior collimation of the interior winds is at least
plausible, if not yet confirmed.
It appears therefore that various mechanisms might, in principle, explain
the evolutionary trends noted above, although whether they are in fact
relevant depends strongly upon the wind properties of the BPNe. It
would, in particular, be interesting to determine whether winds can be
made to continue forming and shaping BPNe towards later phases of
their evolution.
It would also be of interest to attempt to correlate  with the evolutionary
time-scale
with the evolutionary
time-scale
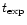 ,
although such an analysis is open to considerable
uncertainty. As a first approximation, however, and assuming a mean
expansion velocity of
,
although such an analysis is open to considerable
uncertainty. As a first approximation, however, and assuming a mean
expansion velocity of 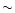 25 kms-1, we note that non-bipolar sources are
expected to follow a trend
25 kms-1, we note that non-bipolar sources are
expected to follow a trend
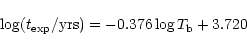 |
(2) |
where we have employed the variation between nebular radius R and  deduced by Phillips (2001b). It is likely that the relation for BPNe will be
somewhat similar, apart from scaling factors of order a few. Given that
this is so, then one anticipates that
deduced by Phillips (2001b). It is likely that the relation for BPNe will be
somewhat similar, apart from scaling factors of order a few. Given that
this is so, then one anticipates that
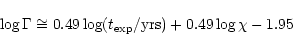 |
(3) |
where 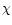 is the fraction by which bipolar expansion velocities exceed
those of non-BPNe. Inspection of the values summarized by Corradi &
Schwarz (1995) suggests that
is the fraction by which bipolar expansion velocities exceed
those of non-BPNe. Inspection of the values summarized by Corradi &
Schwarz (1995) suggests that
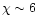 .
.
Finally, we note that such trends between  and
and  may also arise
through other means. Soker & Rappaport (2000), for instance, have
suggested that narrow waisted BPNe (i.e. those with small values of
may also arise
through other means. Soker & Rappaport (2000), for instance, have
suggested that narrow waisted BPNe (i.e. those with small values of  )
result from the prior collimation of high velocity interior winds - those
winds which are interacting with the aspherical AGB envelope, and are
responsible for creating the observed bipolar lobes. It is suggested, in
brief, that separate and smaller accretion disks may be funneling winds
very close to the central emitting sources. Other (broader-waisted)
BPNe are, on the other hand, capable of being formed with more
spherically symmetric interior winds. The trend in Fig. 2 may therefore
reflect the presence of differing formation mechanisms, with sources
deriving from prior collimation of the interior winds appearing to be
characterized by higher values of
)
result from the prior collimation of high velocity interior winds - those
winds which are interacting with the aspherical AGB envelope, and are
responsible for creating the observed bipolar lobes. It is suggested, in
brief, that separate and smaller accretion disks may be funneling winds
very close to the central emitting sources. Other (broader-waisted)
BPNe are, on the other hand, capable of being formed with more
spherically symmetric interior winds. The trend in Fig. 2 may therefore
reflect the presence of differing formation mechanisms, with sources
deriving from prior collimation of the interior winds appearing to be
characterized by higher values of  .
.
Having said this, however, it is apparent that the trend of  with
with  appears to be reasonably continuous - there is no specific value of
appears to be reasonably continuous - there is no specific value of  at
which discontinuities in
at
which discontinuities in  arise. This might, in turn, then require that
central winds display a range of collimations, from very high levels
where
arise. This might, in turn, then require that
central winds display a range of collimations, from very high levels
where  is large, through to more modest levels where
is large, through to more modest levels where  is small.
is small.
We have pointed out that although the evolution in the morphologies of
bipolar nebulae is extremely uncertain, and the province of educated
guesses, one may nevertheless assess the possible evolution of such
shells in a straightforward manner. Specifically, we note that the ratio  between the dimensions of the disks and lobes of BPNe appears to
increase with decreasing 5 GHz brightness temperature
between the dimensions of the disks and lobes of BPNe appears to
increase with decreasing 5 GHz brightness temperature  .
Whilst the
scatter between
.
Whilst the
scatter between  and
and  is far from negligible, the statistical
significance of the trend appears to be high. We therefore conclude that
if older nebulae possess low values of
is far from negligible, the statistical
significance of the trend appears to be high. We therefore conclude that
if older nebulae possess low values of  ,
then the collimating disks
increase in size relative to the lobal extremities - perhaps leading,
eventually, to almost spherical structures such as JnEr 1. This result
appears to conflict with certain models of bipolar expansion, from which
it would be expected that
,
then the collimating disks
increase in size relative to the lobal extremities - perhaps leading,
eventually, to almost spherical structures such as JnEr 1. This result
appears to conflict with certain models of bipolar expansion, from which
it would be expected that
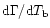 would be constant, or may even be
negative. Various reasons are provided as to why this may arise.
would be constant, or may even be
negative. Various reasons are provided as to why this may arise.
It is also noted that such trends may arise through alternative means. It
is possible, for instance, that smaller values of  derive from
pre-
collimation of the interior winds - that the winds are collimated prior to
their subsequent interaction with the AGB envelope. If this is true, then
our results may suggest a broad continuum of central wind collimations,
rather than there being two specific classes of nebulae, with and without
collimation.
derive from
pre-
collimation of the interior winds - that the winds are collimated prior to
their subsequent interaction with the AGB envelope. If this is true, then
our results may suggest a broad continuum of central wind collimations,
rather than there being two specific classes of nebulae, with and without
collimation.
- Aaquist, A., & Kwok, S. 1990, A&AS, 84, 229
NASA ADS
- Balick, B. 1987, AJ, 94, 671
In the text
NASA ADS
- Balick, B., Icke, V., & Mellema, G. 1997, STScI Press Release PRC97-38
In the text
- Bachiller, R., Planesis, P., Martin-Pintado, J., Bujarrabal, V., & Tafalla, M.
1989, A&A, 210, 366
In the text
NASA ADS
- Cahn, J. H., & Kaler, J. B. 1971, ApJS, 22, 319
In the text
NASA ADS
- Cahn, J. H., Kaler, J. B., & Stanghellini, L. 1992, A&AS, 94, 399
In the text
NASA ADS
- Cahn, J. H., & Rubin, R. H. 1974, AJ, 79, 128
In the text
NASA ADS
- Calabretta, M. R. 1982, MNRAS, 199, 141
In the text
NASA ADS
- Chu, Y. H., Jacoby, G. H., & Arendt, R. 1987, ApJS, 64, 529
In the text
NASA ADS
- Corradi, R. L. M., Livio, M., Balick, B., Munari, U., & Schwarz, H. E. 2001,
ApJ, 553, 211
In the text
NASA ADS
- Corradi, R. L. M., & Schwarz, H. E. 1993a, A&A, 269, 462
In the text
NASA ADS
- Corradi, R. L. M., & Schwarz, H. E. 1993b, A&A, 273, 247
In the text
NASA ADS
- Frank, A., Balick, B., Icke, V., & Mellema, G. 1993, ApJ, 404, L25
In the text
NASA ADS
- Frank, A., & Mellema, G. 1994, ApJ, 430, 800
NASA ADS
- Garcia-Segura, G., Langer, N., Rozyczka, M., & Franco, J. 1999, ApJ, 517,
767
In the text
NASA ADS
- Isaacman, R. 1984, MNRAS, 208, 399
In the text
NASA ADS
- Isobe, T., Feigelsen, E. D., Akritas, M. G., & Jogest Babu, G. 1990, ApJ,
104, 113
- Kaftan-Kassim, M. A. 1969, ApJ, 166, 469
In the text
- Kohoutek, L., & Surdej, J. 1980, A&A, 85, 161
In the text
NASA ADS
- Kwok, S., Purton, C. R., Matthews, H. E., & Spoelstrom, T. A. T. 1985, A&A,
144, 321
In the text
NASA ADS
- Manchado, A., Guerrero, M. A., Stanghellini, L., & Serra-Ricart, M. 1996,
The IAC Morphological Catalog of Northern Planetary nebulae (IAC: Spain)
In the text
- Mellema, G. 1995, MNRAS, 277, 173
In the text
NASA ADS
- Mellema, G. 1997, A&A, 321, L29
In the text
NASA ADS
- Mellema, G., & Frank, A. 1995, MNRAS, 273, 401
NASA ADS
- Milne, D. K. 1979, A&AS, 36, 227
In the text
NASA ADS
- Milne, D. K., & Aller, L. H. 1975, A&A, 38, 183
In the text
NASA ADS
- Milne, D. K., & Aller, L. H. 1982, A&A, 50, 209
In the text
- Perek, L., & Kohoutek, L. 1967, Catalogue of Galactic Planetary Nebulae
(Academia Publishing House: Prague)
In the text
- Phillips, J. P. 1984, A&A, 140, 141
In the text
NASA ADS
- Phillips, J. P. 2001a, PASP, 113, 846
NASA ADS
- Phillips, J. P. 2001b, ApJS, in press
In the text
- Phillips, J. P., & Mampaso, A. 1988, A&A, 190, 237
In the text
NASA ADS
- Pottasch, S. R. 1984, Planetary Nebulae (Dordrecht: Reidel)
- Redman, M. P., O'Connor, J. A., Holloway, A. J., Bryce, M., & Meaburn, J.
2000, MNRAS, 312, L23
In the text
NASA ADS
- Rodriguez, L. F., Garcia-Barreto, J. A., & Gomez, Y. 1985, RMxAA, 11, 109
In the text
NASA ADS
- Sahai, R., Wootten, A., Schwartz, H. E., & Clegg, R. E. S. 1991, A&A, 560,
574
In the text
- Soker, N., & Rappaport, S. 2000, ApJ, 538, 241
In the text
NASA ADS
- Tylenda, R., Acker, A., Stenholm, B. M., & Koppen, J. 1992, A&AS, 95, 337
In the text
NASA ADS
- Van de Steene, G. C., & Zijlstra, A. A. 1994, A&AS, 108, 485
In the text
NASA ADS
- Weedman, D. W. 1968, ApJ, 153, 49
In the text
NASA ADS
- Wilson, O. C. 1958, Rev. Mod. Phys., 30, 1025
In the text
- Zhang, C. Y. 1995, ApJS, 98, 659
In the text
NASA ADS
- Zijlstra, A. A., Pottasch, S. R., & Bignell, C. 1989, A&AS, 79, 329
In the text
NASA ADS
- Zweigle, J., Neri, R., Bachiller, R., Bujarrabal, V., & Grewing, M. 1997,
A&A, 324, 624
In the text
NASA ADS
Copyright ESO 2002
![\begin{table}
{\includegraphics[width=12cm,clip]{table1.eps} }
\end{table}](/articles/aa/full/2002/15/aa2156/img5.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2156f1.eps}\end{figure}](/articles/aa/full/2002/15/aa2156/Timg10.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2156f2.eps}\end{figure}](/articles/aa/full/2002/15/aa2156/Timg14.gif)