A&A 385, 896-899 (2002)
DOI: 10.1051/0004-6361:20020177
Modeling the crossover variability in a differentially rotating star
V. R. Khalack 1,2
1 - Main Astronomical Observatory,
27 Zabolotnogo Str., 03650 Kyiv, Ukraine
2 -
Isaac Newton Institute of Chile, Kiev Branch
Received 12 October 2001 / Accepted 8 January 2002
Abstract
Reconstruction of phase-dependent crossover effect
variations is performed for a differentially rotating star
assuming that point-like magnetic charges are distrubuted under
the stellar surface. Models adopting the solar differential rotation law
and an exponential rotation law are considered and compared to the case
of a rigidly rotating star.
It is shown that neglect of differential stellar rotation
leads to underestimation of the equatorial rotational velocity
by 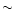 2-5%.
2-5%.
Key words: stars: magnetic fields - stars: rotation - Sun: rotation
Variations of the surface magnetic field with stellar rotation are
observed for the majority of chemically peculiar (CP) stars
(Romanyuk 1997). These variations are thought to be caused by
nonuniformity of the magnetic fields on the surface of CP stars.
Probably, the location of
patches of chemical elements (spots or rings) on the
stellar surface is related to the distribution of the magnetic fields
(Shavrina et al. 2001).
Therefore, it is evident that precise reconstruction of the surface
magnetic field can help provide a comprehensive
element abundance analysis and anomaly mapping.
The last two decades have seen rapid progress in the measurement of the
surface magnetic fields (Mathys 1988, 1991,
1995a, 1995b;
Mathys & Hubrig 1997; Leone & Catanzaro 2001).
First introduced by Mathys (1988),
the moment technique relates the line profile asymmetries
(while measuring the Stokes V parameter) to the mean values
of the longitudinal magnetic field (first moment) and the crossover effect
(second moment) for a given phase of stellar rotation.
Special attention should be paid to
the crossover effect, since it reflects the result of a joint action
of the Zeeman and Doppler effects on the investigated line profile of
the Stokes V parameter (Mathys 1995a).
Such an effect was first detected in HD 125248
and was named a crossover effect by Babcock (1951).
This term comes from the fact that the effect usually achieves its
maximum value when the mean longitudinal magnetic field reverses
its sign, i.e. it crosses zero from one polarity
to another. For example, in the oblique rotator model
(when the magnetic and rotational axes do not coincide) with a
dipolar magnetic field for a rigidly rotating star (Stibbs 1950),
the longitudinal component of the local magnetic field is different
in the two halves of the stellar disk at the surface points with equal
radial velocity of rotation. Apparently, this difference is
maximal at the particular moment when the two magnetic
poles approach the stellar limb, while the mean
longitudinal magnetic field is close to zero.
Recently, Mathys (1995a) proposed a new term,
asymmetry of the longitudinal field, emphasizing the relationship
of the cross-over to the asymmetry in the distribution
of the longitudinal component of the magnetic field,
when considering the two halves of the visible stellar disk
separated by the plane including the line of sight and the
stellar rotational axis. In general, for a differentially
rotating star with a complicated structure of its surface magnetic
field it is not evident that the maximum of the effect
coincides with the moment of sign reversion
of the mean longitudinal magnetic field.
Nevertheless, Babcock's term crossover
effect is usually used to refer to the value that is actually
derived from measurements of the second-order moment of the V
line profile (Mathys 1995a).
As mentioned above, the observable value of the crossover effect
depends on the combined contribution of the Zeeman and Doppler
effects to the line profile asymmetry of the Stokes V parameter
averaged over the visible stellar disk for a given rotation phase.
Therefore, at first it is necessary to model the structure of
the surface magnetic field together with the velocity law for stellar
rotation.
Among the known models the most appropriate one is the oblique rotator model proposed by
Gerth et al. (1997, 1998), especially its
modification (Khalack et al. 2001) that allows one
to reconstruct with high accuracy the geometry of the surface magnetic field
under the given distribution of the point field sources
embedded in the stellar body. In order to simplify the calculations,
let us consider the case of centered symmetric magnetic dipole
with two magnetic charges located close to the stellar centre.
Then the modeled mean longitudinal magnetic field
(directed along Z-axis in Fig. 1)
varies with phase of the stellar rotation in the following way
(Khalack et al. 2001):
![\begin{displaymath}
%
B_{z} \simeq \displaystyle\frac{2aQ}{R^{2}_{\star}} \;
(3\cos{\theta}[A\sin{\theta}+Z\cos{\theta}] - Z),
\end{displaymath}](/articles/aa/full/2002/15/aa1989/img2.gif) |
(1) |
where
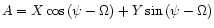 and
and
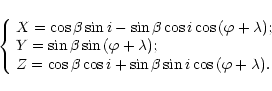 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms1989-fig1.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg5.gif) |
Figure 1:
Geometry of the oblique rotator model with one
point-like magnetic field source. |
| Open with DEXTER |
Here 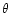 and
and 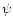 specify an arbitrary point M
on the stellar surface in the spherical reference frame
related to the observer.
The variables
specify an arbitrary point M
on the stellar surface in the spherical reference frame
related to the observer.
The variables 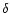 =
=
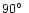 -
-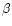 and
and 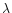 determine
orientation of the dipolar magnetic axis
(defined by location of the magnetic charges)
in the spherical frame related to the star (see Fig. 1).
Angles i and
determine
orientation of the dipolar magnetic axis
(defined by location of the magnetic charges)
in the spherical frame related to the star (see Fig. 1).
Angles i and 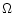 define the inclination of the rotational
axis to the line of sight and its plane-of-sky orientation
relative to the north celestial pole, respectively.
The variables Q and
define the inclination of the rotational
axis to the line of sight and its plane-of-sky orientation
relative to the north celestial pole, respectively.
The variables Q and  determine the modulus of
the magnetic charge and its distance
from the centre of the star, expressed in the units of stellar radius
determine the modulus of
the magnetic charge and its distance
from the centre of the star, expressed in the units of stellar radius
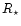 .
From the spherical triangle ZPLj
with the known angles
.
From the spherical triangle ZPLj
with the known angles 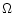 and i, the relation between the two
mentioned spherical frames is derived as (omitting the subscript
j):
and i, the relation between the two
mentioned spherical frames is derived as (omitting the subscript
j):
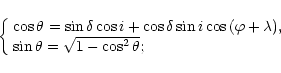 |
(3) |
and
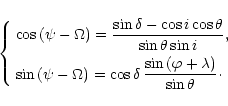 |
(4) |
Stars are expected to rotate differentially
when energy transfer to the surface is dominated by
convection. Let us consider a spherically symmetric star
with a decrease in the angular rotation rate
from equator to pole. Our Sun (if
we neglect its oblation) has the differential rotation law
of the form (Gadun et al. 1985)
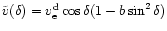 ,
where
,
where 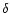 is the
latitude,
is the
latitude,
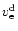 specifies the equatorial velocity
and parameter
specifies the equatorial velocity
and parameter
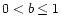 (the case of b=0 corresponds to a rigidly
rotating star). Here we neglect the contribution of turbulence and
meridional circulation to the surface velocity at a given latitude.
Correspondingly, the line-of-sight projection of the
velocity vector at a surface point M(
(the case of b=0 corresponds to a rigidly
rotating star). Here we neglect the contribution of turbulence and
meridional circulation to the surface velocity at a given latitude.
Correspondingly, the line-of-sight projection of the
velocity vector at a surface point M(
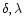 ) is
) is
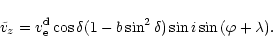 |
(5) |
In the spherical frame related to an observer this
projection can be expressed as (see Fig. 1 and
Eqs. (3), (4)):
![\begin{displaymath}
\tilde{v}_{z} = v_{\rm e}^{\rm d}\sin{i} \sin{(\psi-\Omega)}...
...{\theta}\cos{i}+\sin{\theta}\sin{i}
\cos{(\psi-\Omega)})^{2}].
\end{displaymath}](/articles/aa/full/2002/15/aa1989/img22.gif) |
(6) |
As follows from the definition of the crossover effect (Mathys
1995a), contribution from an arbitrary surface point
M(
 )
is proportional to
)
is proportional to  (1) due to the Zeeman effect, and to
(1) due to the Zeeman effect, and to
 (6) due to the Doppler effect:
(6) due to the Doppler effect:
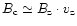 .
Adopting a limb darkening law
for the star in the form
.
Adopting a limb darkening law
for the star in the form
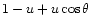 (where
(where
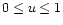 )
and averaging
)
and averaging 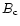 over the visible stellar hemisphere in
accordance with Landolfi et al. (1998), one can obtain the
following theoretical expression for the observed value of the
crossover effect:
over the visible stellar hemisphere in
accordance with Landolfi et al. (1998), one can obtain the
following theoretical expression for the observed value of the
crossover effect:
![\begin{displaymath}
\langle B_{\rm c}\rangle^{\rm d} \; \simeq v_{\rm e}^{\rm d}...
...{1}{2240}\; \{448-168u - b [64-29u + \cos^{2}{i} (128-23u)]\},
\end{displaymath}](/articles/aa/full/2002/15/aa1989/img30.gif) |
(7) |
where
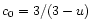 and Y is defined in
(2). For the rigidly rotating star (case b=0)
it transforms into
and Y is defined in
(2). For the rigidly rotating star (case b=0)
it transforms into
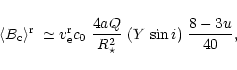 |
(8) |
where
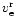 specifies the equatorial velocity.
This expression is in good agreement with the previously obtained
result (Bagnulo et al. 1996) for the model of
an oblique rotator with the centered symmetric magnetic dipole,
where the factor
specifies the equatorial velocity.
This expression is in good agreement with the previously obtained
result (Bagnulo et al. 1996) for the model of
an oblique rotator with the centered symmetric magnetic dipole,
where the factor
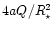 is proportional
to the field magnitude
is proportional
to the field magnitude 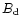 at the magnetic pole.
at the magnetic pole.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1989-fig2.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg36.gif) |
Figure 2:
Shape of the function
f(b=1,u,i)defined by the Eq. (10) for the solar differential rotation law. |
| Open with DEXTER |
In order to simplify the analysis of the obtained results it is useful
to introduce the function f(b,u,i) defined as ratio of
the crossover magnitude in the model of rigidly rotating star
to the crossover magnitude in the differentially rotating model:
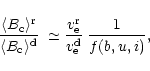 |
(9) |
where (see Eqs. (7), (8))
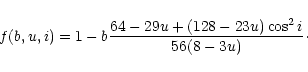 |
(10) |
It is obvious that
f(b,u,i) <1 for an arbitrary value of
the angle i,
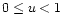 and
and
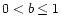 (see, for example, Fig. 2). To
compare two models with different rotation laws let us
postulate
(see, for example, Fig. 2). To
compare two models with different rotation laws let us
postulate
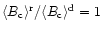 ,
since the same
observations of the crossover effect are employed.
Correspondingly, ratio of the equatorial velocities given
by these two models is (see Eq. (9))
,
since the same
observations of the crossover effect are employed.
Correspondingly, ratio of the equatorial velocities given
by these two models is (see Eq. (9))
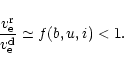 |
(11) |
Thus, adoption of rigid rotation in
modeling of the crossover effect leads to underestimation of
the real equatorial velocity of differentially rotating star.
The plot of function
f(b=1,u,i) (see Eq. (10))
is given in Fig. 2. As follows from this
figure, maximal underestimation
(that corresponds to the minimum of function f(b,u,i))
of the real equatorial velocity in the model of a rigidly
rotating star is about 50% of the velocity estimate
for
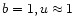 and
and
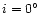 or
or
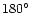 .
For the main sequence stars with
.
For the main sequence stars with
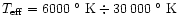 and
and
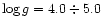 (spectral type B, A and F)
the limb darkening coefficient u is about
(spectral type B, A and F)
the limb darkening coefficient u is about
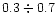 (Diaz-Cordoves et al. 1995).
Accepting the mean inclination of the rotational axis to the line
of sight to be
(Diaz-Cordoves et al. 1995).
Accepting the mean inclination of the rotational axis to the line
of sight to be
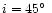 (Landstreet & Mathys 2000)
and assuming
(Landstreet & Mathys 2000)
and assuming
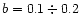 ,
as for the case of the Sun
(Gadun et al. 1985), Eq. (10) leads to
underestimation of the order of 2-5% (see. Fig. 4)
for the real equatorial velocity of the differentially rotating star.
It is of the order of the typical
error bar
,
as for the case of the Sun
(Gadun et al. 1985), Eq. (10) leads to
underestimation of the order of 2-5% (see. Fig. 4)
for the real equatorial velocity of the differentially rotating star.
It is of the order of the typical
error bar
![$\sigma[v_{\rm e}^{\rm r}]$](/articles/aa/full/2002/15/aa1989/img50.gif) in modeling estimates of the rotational velocity
on the stellar equator.
in modeling estimates of the rotational velocity
on the stellar equator.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms1989-fig3.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg51.gif) |
Figure 3:
The same as Fig. 2, but for the differential rotation with an exponential law (14, 15). |
| Open with DEXTER |
In the stability analysis of a magnetized, differentially rotating star
researchers frequently use an exponential law (Uprin 1996)
that significantly simplifies the analytical calculations.
In such a case the rotational velocity depends on the
stellar latitude 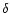 as
as
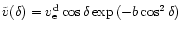 ,
where
,
where
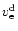 specifies the equatorial velocity, and
the parameter b is restricted as
specifies the equatorial velocity, and
the parameter b is restricted as
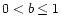 (the case of b=0 corresponds to a rigidly rotating
star). At an arbitrary surface point
M(
(the case of b=0 corresponds to a rigidly rotating
star). At an arbitrary surface point
M(
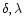 ), projection of the rotational
velocity onto the line of sight is (see Fig. 1)
), projection of the rotational
velocity onto the line of sight is (see Fig. 1)
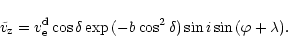 |
(12) |
In order to average the crossover effect
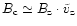 one has to integrate the product of Eqs. (1) and (12)
over the visible stellar hemisphere.
Unfortunately, this integration cannot be done analytically.
As a possible way to
simplify the calculations, the exponent in the velocity expression
(12) can be expanded into a series in
the small parameter b
one has to integrate the product of Eqs. (1) and (12)
over the visible stellar hemisphere.
Unfortunately, this integration cannot be done analytically.
As a possible way to
simplify the calculations, the exponent in the velocity expression
(12) can be expanded into a series in
the small parameter b
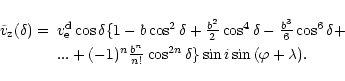 |
(13) |
The resulting series has
an infinite convergence radius. Therefore, it suffices to take
into account only the first few terms to provide an
acceptable accuracy for the final result. Performing the same
calculations as in the previous subsection, one can obtain the
following expression for the function analyzed:
|
f(b,u,i) = 1- b P1 + b2 P2 - b3 P3,
|
(14) |
where
 |
(15) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms1989-fig4.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg57.gif) |
Figure 4:
Dependence of the analyzed function f on the parameter bin the model with the solar differential rotation law (solid line) and in the model with
an exponential law (dotted line). |
| Open with DEXTER |
Only the first four terms in b are taken into account
in the above expression.
For the minimum value of the function f(
![${\rm min}[f(b,u,i)]=0.62$](/articles/aa/full/2002/15/aa1989/img58.gif) at
at
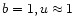 and
and
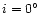 or
or
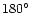 ),
neglect of the rest of the terms leads to an error of 0.002.
The new function (14) depends mainly on u and iin the same manner as the function specified by Eq. (10)
(see Fig. 3). On the other hand, its decrease
with b is comparatively slower than for the function (10)
describing the solar differential rotation law (see Fig. 4).
Consequently, for the star with an exponential law of differential
rotation, the model of a rigidly rotating star gives a relatively
smaller underestimation of errors for the equatorial velocity.
),
neglect of the rest of the terms leads to an error of 0.002.
The new function (14) depends mainly on u and iin the same manner as the function specified by Eq. (10)
(see Fig. 3). On the other hand, its decrease
with b is comparatively slower than for the function (10)
describing the solar differential rotation law (see Fig. 4).
Consequently, for the star with an exponential law of differential
rotation, the model of a rigidly rotating star gives a relatively
smaller underestimation of errors for the equatorial velocity.
This paper is devoted to modeling of the mean crossover effect in
a differentially rotating, spherically symmetric star with a
centered magnetic dipole.
Geometry of the surface magnetic field is derived
for the point field sources with the magnetic
charges embedded in the stellar body. This provides high accuracy
for the field reconstruction (Khalack et al. 2001).
Since the crossover effect is defined by the joint action
of the Zeeman and Doppler effects, the corresponding theoretical
expression (7)
for its mean (averaged over the visible stellar hemisphere)
value is obtained here for the differentially rotating
star with a solar-like rotation law (5).
It is shown that
neglect of the differential character of the stellar rotation leads
to underestimation of the real equatorial velocity up to
2-5%, comparable to the errors
![$\sigma[v_{\rm e}^{\rm r}]$](/articles/aa/full/2002/15/aa1989/img50.gif) in model estimates of the stellar rotation.
Comparatively smaller errors appear in the model
considering the differentially rotating star
with an exponential rotation law for
the same value of the parameter b.
in model estimates of the stellar rotation.
Comparatively smaller errors appear in the model
considering the differentially rotating star
with an exponential rotation law for
the same value of the parameter b.
Nevertheless, the value (10) (related to underestimation of the equatorial velocity)
is very sensitive to the parameter b (see Fig. 4) that
specifies the rate of decrease in the angular rotation of the star
from equator to pole. Thus, in a general case,
for correct modeling of the observable variability
of the values related to the surface magnetic field (the mean
longitudinal magnetic field, the crossover effect, etc.),
the possibility of differential rotation of the star should be
comprehensively considered and then taken into account, if necessary.
Strong differential rotation characterized by
sufficiently large values of bwould induce major distortions in the line profiles, which
are not observed in the majority of CP stars (Mathys 2001).
Therefore, in the case of differential rotation of these stars,
the probable value of b is not very high and the
respective underestimation error of the real equatorial velocity
is of the order of the model uncertainty due to other effects.
Consequently, application of the model with a rigidly rotating
star remains valid.
Acknowledgements
Author is grateful to Prof. Y. Geroyanis, Prof. G. Mathys and
Dr. S. Marchenko for useful advice and fruitful discussion.
- Babcock, H. W. 1951, ApJ, 114, 1
In the text
NASA ADS
- Bagnulo, S., Landolfi, M., & Landi Degl'Innocenti, E. 1996, A&A, 308, 115
In the text
NASA ADS
- Diaz-Cordoves, J., Claret, A., & Gimenez, A. 1995, A&AS, 110, 329
In the text
NASA ADS
- Gadun, A. S., Kostyk, R. I., & Sheminova, V. A. 1985, Kin. & Phys. of Cel. Bodies 15, N6, 53
In the text
- Gerth, E., Glagolevskij, Yu. V., & Scholz, G. 1997, Integral representation of the surface structure of the stellar magnetic field, in Proc. of International Conference Stellar Magnetic Fields, ed. Y. V. Glagolevskij, & I. I. Romanyuk (Special Astrophys. Observ. Press, Moscow), 67
In the text
- Gerth, E., Glagolevskij, Yu. V., & Scholz, G. 1998, Integral representation of the stellar surface structure of the magnetic field, in Proc. of the 26th Meeting and Workshop of the Europian Working Group on CP Stars, ed. P. North, A. Schnell, & J. Ziznovský,
Contr. Astron. Obs. Skalnate Pleso vol. 27, N3, 455
In the text
NASA ADS
- Khalack, V. R., Khalack, Yu. N., Shavrina, A. V., et al. 2001, AZh, 78, N7, 655
In the text
- Landolfi, M., Bagnulo, S., & Landi Degl'Innocenti, E. 1998, A&A, 338, 111
In the text
NASA ADS
- Landstreet, J. D., & Mathys, G. 2000, A&A, 359, 213
In the text
NASA ADS
- Leone, F., & Catanzaro, G. 2001, A&A, 365, 118
In the text
NASA ADS
- Mathys, G. 1988, A&A, 189, 179
In the text
NASA ADS
- Mathys, G. 1991, A&AS, 89, 121
In the text
NASA ADS
- Mathys, G. 1995a, A&A, 293, 733
In the text
NASA ADS
- Mathys, G. 1995b, A&A, 293, 746
In the text
NASA ADS
- Mathys, G. 2001, private communication
In the text
- Mathys, G., & Hubrig, S. 1997, A&AS, 124, 475
In the text
NASA ADS
- Romanyuk, I. I. 1997, The Zeeman effect in stellar spectra, in Proc. of
International Conference Stellar Magnetic Fields, ed. Y. V. Glagolevskij, & I. I. Romanyuk (Special Astrophys. Observ. Press, Moscow), 11
In the text
- Shavrina, A. V., Polosukhina, N. S., Zverko, J., et al. 2001, AZh, 78, N10, 902
In the text
- Smith, M. D. 1994, A&A, 287, 523
NASA ADS
- Stibbs, D. W. N. 1950, MNRAS, 110, 395
In the text
NASA ADS
- Uprin, V. A. 1996, MNRAS, 280, 149
In the text
NASA ADS
Copyright ESO 2002
![\begin{displaymath}
%
B_{z} \simeq \displaystyle\frac{2aQ}{R^{2}_{\star}} \;
(3\cos{\theta}[A\sin{\theta}+Z\cos{\theta}] - Z),
\end{displaymath}](/articles/aa/full/2002/15/aa1989/img2.gif)
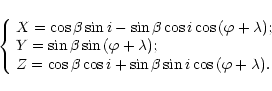
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms1989-fig1.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg5.gif)
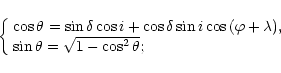
![\begin{displaymath}
\tilde{v}_{z} = v_{\rm e}^{\rm d}\sin{i} \sin{(\psi-\Omega)}...
...{\theta}\cos{i}+\sin{\theta}\sin{i}
\cos{(\psi-\Omega)})^{2}].
\end{displaymath}](/articles/aa/full/2002/15/aa1989/img22.gif)
![\begin{displaymath}
\langle B_{\rm c}\rangle^{\rm d} \; \simeq v_{\rm e}^{\rm d}...
...{1}{2240}\; \{448-168u - b [64-29u + \cos^{2}{i} (128-23u)]\},
\end{displaymath}](/articles/aa/full/2002/15/aa1989/img30.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{ms1989-fig2.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg36.gif)
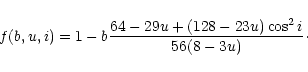
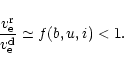
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms1989-fig3.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg51.gif)
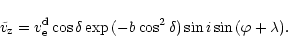
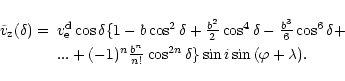

![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{ms1989-fig4.eps}\end{figure}](/articles/aa/full/2002/15/aa1989/Timg57.gif)