A&A 385, 947-950 (2002)
DOI: 10.1051/0004-6361:20020260
T. Harko - K. S. Cheng
Department of Physics, The University of Hong Kong, Pok Fu Lam Road, Hong Kong, PR China
Received 9 August 2001 / Accepted 4 February 2002
Abstract
The Chandrasekhar limit for strange stars described by a linear
equation of state (describing quark matter with density-dependent quark masses) is evaluated.
The maximum mass and radius of the star depend on the fundamental constants
and on the energy density of the quark matter at zero pressure. By comparing the expression for
the mass of the star with the limiting mass formula for a relativistic degenerate
stellar configuration one can obtain an estimate of the mass of the strange quark.
Key words: dense matter - equation of state - stars: fundamental parameters
One of the most important characteristics of compact relativistic
astrophysical objects is their maximum allowed mass. The maximum mass is
crucial for distinguishing between neutron stars and black holes in compact
binaries and in determining the outcome of many astrophysical processes,
including supernova collapse and the merger of binary neutron stars. The
theoretical value of the maximum mass for white dwarfs and neutron stars was
found by Chandrasekhar and Landau and is given by
![]() (Shapiro & Teukolsky 1983), where
(Shapiro & Teukolsky 1983), where ![]() is
the mass of the baryons (in the case of white dwarfs, even pressure comes from
electrons; most of the mass is in baryons). Thus, with the exception of
composition-dependent numerical factors, the maximum mass of a degenerate
star depends only on fundamental physical constants. The radius
is
the mass of the baryons (in the case of white dwarfs, even pressure comes from
electrons; most of the mass is in baryons). Thus, with the exception of
composition-dependent numerical factors, the maximum mass of a degenerate
star depends only on fundamental physical constants. The radius ![]() of the degenerate star obeys the condition
of the degenerate star obeys the condition
![]() ,
with m being the mass of either
electron (white dwarfs) or neutron (neutron stars) (Shapiro & Teukolsky 1983). White dwarfs are supported
against of gravitational collapse by the degeneracy pressure of electrons
whereas for neutron stars this pressure comes mainly from the nuclear force between nucleons (Shapiro & Teukolsky 1983).
For non-rotating neutron stars with the central pressure at their center tending to the
limiting value
,
with m being the mass of either
electron (white dwarfs) or neutron (neutron stars) (Shapiro & Teukolsky 1983). White dwarfs are supported
against of gravitational collapse by the degeneracy pressure of electrons
whereas for neutron stars this pressure comes mainly from the nuclear force between nucleons (Shapiro & Teukolsky 1983).
For non-rotating neutron stars with the central pressure at their center tending to the
limiting value
![]() ,
an upper bound of around
,
an upper bound of around
![]() has been
found (Rhoades & Ruffini 1974).
has been
found (Rhoades & Ruffini 1974).
The quark structure of the nucleons, suggested by quantum cromodynamics, opens the possibility of a hadron-quark phase transition at high densities and/or temperatures, as suggested by Witten (1984). In the theories of strong interaction, quark bag models suppose that breaking of physical vacuum takes place inside hadrons. As a result, vacuum energy densities inside and outside a hadron become essentially different and the vacuum pressure on the bag wall equilibrates the pressure of quarks, thus stabilizing the system. If the hypothesis of the quark matter is true, then some neutron stars could actually be strange stars, built entirely of strange matter (Alcock et al. 1986; Haensel et al. 1986). For a review of strange star properties, see Cheng et al. (1998).
Most of the investigations of quark star properties have been done within
the framework of the so-called MIT bag model. Assuming that interactions of
quarks and gluons are sufficiently small, neglecting quark masses and
supposing that quarks are confined to the bag volume (in the case of a bare
strange star, the boundary of the bag coincides with the stellar surface), the
energy density
![]() and pressure p of a quark-gluon plasma at
temperature T and chemical potential
and pressure p of a quark-gluon plasma at
temperature T and chemical potential
![]() (the subscript f
denotes the various quark flavors u, d, s etc.) are related, in the MIT
bag model, by the equation of state (EOS) (Cheng et al. 1998)
(the subscript f
denotes the various quark flavors u, d, s etc.) are related, in the MIT
bag model, by the equation of state (EOS) (Cheng et al. 1998)
More sophisticated investigations of quark-gluon interactions have shown
that Eq. (1) represents a limiting case of more general equations of
state. For example, MIT bag models with massive strange quarks and lowest-
order QCD interactions lead to some corrections terms in the equation of
state of quark matter. Models incorporating restoration of chiral quark
masses at high densities and giving absolutely stable strange matter can no
longer be accurately described by using Eq. (1). On the other hand, in
models in which quark interaction is described by an interquark potential
originating from gluon exchange and by a density-dependent scalar potential
which restores the chiral symmetry at high densities (Dey et al. 1998), the equation of state
![]() can be well
approximated by a linear function in the energy density
can be well
approximated by a linear function in the energy density ![]() (Gondek-Rosinska et al. 2000).
It is interesting to note that Frieman
& Olinto (1989) and Haensel & Zdunik (1989)
have already mentioned the approximation of the EOS by a linear function (see also
Prakash et al. 1990; Lattimer et al. 1990). Recently
Zdunik (2000) has studied the linear approximation of the
equation of state, obtaining all parameters of the EOS as polynomial
functions of strange quark mass, the QCD coupling constant and bag constant. The
scaling relations have been applied to the determination of the maximum
frequency of a particle in a stable circular orbit around strange stars.
(Gondek-Rosinska et al. 2000).
It is interesting to note that Frieman
& Olinto (1989) and Haensel & Zdunik (1989)
have already mentioned the approximation of the EOS by a linear function (see also
Prakash et al. 1990; Lattimer et al. 1990). Recently
Zdunik (2000) has studied the linear approximation of the
equation of state, obtaining all parameters of the EOS as polynomial
functions of strange quark mass, the QCD coupling constant and bag constant. The
scaling relations have been applied to the determination of the maximum
frequency of a particle in a stable circular orbit around strange stars.
It is the purpose of this paper to obtain, by using a simple phenomenological approach (which is thermodynamical in its essence), the maximum mass and radius (the Chandrasekhar limits) for strange stars obeying a linear equation of state. Of course the maximum mass of compact astrophysical objects is a consequence of General Relativity and not of the character of motion of matter constituents. However, the formulae for maximum mass and radius, due to their simple analytical form, give a better insight into the underlying physics of quark stars, also allowing us to obtain some results which cannot be obtained by numerical methods. For example, from the obtained relations one can find the scaling relations for the maximum mass and radius of strange stars in a natural way.
The present paper is organized as follows. The maximum mass and radius of quark stars with a general linear equation of state is obtained in Sect. 2. In Sect. 3 we discuss our results and conclude the paper.
We assume that the strange star obeys an equation of state
that can be obtained by interpolation with a linear function of density in
the form:
Such an equation of state has been proposed
mainly to describe the strange matter built of u, d and s quarks (Gondek-Rosinska et al. 2000; Zdunik 2000).
The physical consistency of the model requires
![]() .
.
The particle number density and the chemical potential corresponding to EOS (2) are given
respectively by (Zdunik 2000)
The parameters a and ![]() can be calculated, for realistic equations
of state, by using a least squares fit method (Gondek-Rosinska et al. 2000; Zdunik 2000).
For the equations of state incorporating restoration of chiral quark masses at high densities proposed
in Dey et al. (1998) one obtains the values a=0.463,
can be calculated, for realistic equations
of state, by using a least squares fit method (Gondek-Rosinska et al. 2000; Zdunik 2000).
For the equations of state incorporating restoration of chiral quark masses at high densities proposed
in Dey et al. (1998) one obtains the values a=0.463,
![]() g/cm3 and
a=0.455,
g/cm3 and
a=0.455,
![]() g/cm3, respectively (Gondek-Rosinska et al. 2000).
The standard bag model corresponds to a=0.333 and
g/cm3, respectively (Gondek-Rosinska et al. 2000).
The standard bag model corresponds to a=0.333 and
![]() g/cm3 (Cheng et al. 1998).
g/cm3 (Cheng et al. 1998).
From Eqs. (3)-(4) it follows that the particle number and
chemical potential are related by the equation
With the use of Eqs. (2)-(6) one obtains the energy density of
the star in the form
Extremizing the mass with respect to the radius R by means of
![]() gives the relation
gives the relation
The maximum equilibrium radius corresponds to a minimum total
energy of the star (including the gravitational one), for any radius. For
ordinary compact stars, the mass is entirely due to baryons, and the
corresponding (Newtonian) gravitational potential energy is of the order
![]() (
(
![]() for constant density Newtonian
stars). For quark stars, assumed to be formed of massless quarks, the total
mass can be calculated from the total (thermodynamic as well as confinment)
energy in the star. One possibility for the estimation of the gravitational
energy per fermion is to define an effective quark mass incorporating all
the energy contributions (Bannerjee et al. 2000).
for constant density Newtonian
stars). For quark stars, assumed to be formed of massless quarks, the total
mass can be calculated from the total (thermodynamic as well as confinment)
energy in the star. One possibility for the estimation of the gravitational
energy per fermion is to define an effective quark mass incorporating all
the energy contributions (Bannerjee et al. 2000).
The gravitational energy per particle (the strange star is assumed to be
formed from fermions) is
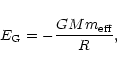 |
(11) |
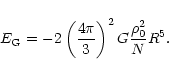 |
(12) |
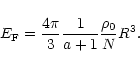 |
(13) |
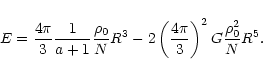 |
(14) |
The maximum radius of the quark star given by Eq. (15) is the radius corresponding
to the maximum mass. On the other hand for the existing models of strange stars,
the configuration with maximum mass has a radius which is lower than the maximum radius.
For example, for strange stars described by the bag model equation of state, the maximum
radius is 11.40 km, while the radius corresponding to the maximum mass is 10.93 km, which is
![]() lower than the maximum radius. This difference is neglected in Eq. (15).
lower than the maximum radius. This difference is neglected in Eq. (15).
The maximum mass and radius of the star are strongly dependent on the numerical value of the coefficient R0 and estimations based on other physical models could lead to different numerical estimates of the limiting values of the basic parameters of the static strange stars.
In the present paper we have shown that there is a maximum mass and radius (the
Chandrasekhar limits) for quark stars whose
equation of state can be approximated by a linear function of
the density. We have also obtained the explicit expressions for ![]() and
and ![]() .
.
With respect to the scaling of
the parameter ![]() of the form
of the form
![]() ,
the
maximum mass and radius have the following scaling behaviors:
,
the
maximum mass and radius have the following scaling behaviors:
A rescaling of the parameter a of the form
![]() ,
with
,
with ![]() unscaled, leads to a transformation of the
radius and mass of the form
unscaled, leads to a transformation of the
radius and mass of the form
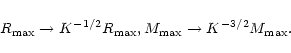 |
(18) |
| (19) |
Generally our formulae (15) and (16) underestimate the maximum values of the mass and radius because we have assumed that the density inside the star is uniform. It is obvious that near the surface the density is much lower than at the center of the compact object. Due to the approximations and simplifications used to derive the basic expressions, reflected mainly in the uncertainties in the exact value of the coefficient R0, Eqs. (15) and (16) cannot provide high precison numerical values of the maximum mass and radius for linear EOS stars, which must be obtained by numerically integrating the gravitational field equations.
For the the linear EOS, ![]() and
and ![]() depend mainly on the
fundamental constants c and G and on the zero pressure density
depend mainly on the
fundamental constants c and G and on the zero pressure density ![]() (the bag constant). The Chandrasekhar expressions for the same
physical parameters involve two more fundamental constants,
(the bag constant). The Chandrasekhar expressions for the same
physical parameters involve two more fundamental constants, ![]() and the mass of the electron or neutron.
and the mass of the electron or neutron.
For quark stars, usually one assume
they are composed of a three-flavour system of massless quarks, confined in
a large bag. Hence the mass of the quark cannot play any role in the mass
formula. But the linear EOS with arbitrary a can describe quark matter
with non-zero quark masses (the mass of the strange quark
![]() MeV), forming a degenerate Fermi gas (Gondek-Rosinska et al. 2000; Zdunik 2000). Therefore
this system should also be described by the same formulae as white dwarfs or
neutron stars, not only by Eqs. (15)-(16). Generally
MeV), forming a degenerate Fermi gas (Gondek-Rosinska et al. 2000; Zdunik 2000). Therefore
this system should also be described by the same formulae as white dwarfs or
neutron stars, not only by Eqs. (15)-(16). Generally ![]() is
a function of the mass of the strange quark, so this mass
implicitly appears in the expression of the maximum mass and radius. But on
the other hand we can assume that the Chandrasekhar limit also applies to
quark stars with the baryon mass substituted by an effective quark mass
is
a function of the mass of the strange quark, so this mass
implicitly appears in the expression of the maximum mass and radius. But on
the other hand we can assume that the Chandrasekhar limit also applies to
quark stars with the baryon mass substituted by an effective quark mass
![]() ,
representing the minimum mass of the quark bubbles composing the
star. Hence we must have
,
representing the minimum mass of the quark bubbles composing the
star. Hence we must have
For
![]() gcm-3 we obtain
gcm-3 we obtain
![]() MeV. For
MeV. For
![]() gcm-3,
Eq. (21)
gives
gcm-3,
Eq. (21)
gives
![]() MeV.
The mass given by Eq. (21) can be considered as the minimum
mass of the stable quark bubble. It is of the same order of magnitude as
the mass
MeV.
The mass given by Eq. (21) can be considered as the minimum
mass of the stable quark bubble. It is of the same order of magnitude as
the mass ![]() of the strange quark. Therefore the Chandrasekhar limit applies
also for quark stars if we take
of the strange quark. Therefore the Chandrasekhar limit applies
also for quark stars if we take
![]() for the mass of the elementary constituent of the star.
for the mass of the elementary constituent of the star.
In the present paper we have considered the maximum mass and radius of strange stars
in the linear approximation of the equation of state and the dependence of these
quantities on the parameter a has been found. We have also pointed out the
existence of scaling relations for the maximum radius of strange stars, an aspect that
has not been mentioned in previous investigations (Witten 1984; Haensel et al. 1986; Bannerjee et al. 2000; Zdunik 2000).
Our formulae also lead to the transformation relations for the maximum mass and
radius of strange stars with respect to separate and simultaneous scaling of the parameters
a and ![]() .
On the other hand the possibility of estimation of the mass of the strange
quark from general astrophysical considerations can perhaps give a better understanding
of the deep connection between micro- and macro-physics.
.
On the other hand the possibility of estimation of the mass of the strange
quark from general astrophysical considerations can perhaps give a better understanding
of the deep connection between micro- and macro-physics.
Acknowledgements
This work is partially supported by a RGC grant of Hong Kong Government and T.H. is supported by a studentship of the University of Hong Kong. The authors are very grateful to the anonymous referee whose comments helped to improve an earlier version of the manuscript.