A&A 385, 572-584 (2002)
DOI: 10.1051/0004-6361:20020137

Influence of non-adiabatic temperature variations on line profile variations of slowly rotating $\beta $ Cephei stars and SPBs[*]

II. Simulations of line profile time series

J. De Ridder 1 - M.-A. Dupret 2 - C. Neuforge 2 - C. Aerts 1


1 - Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200 B, 3001 Heverlee, Belgium
2 - Institut d'Astrophysique et de Géophysique de l'Université de Liège, avenue de Cointe 5, 4000 Liège, Belgium

Received 2 August 2001 / Accepted 23 January 2002

Abstract
We investigate to what extent non-adiabatic temperature variations at the surface of slowly rotating non-radially pulsating $\beta $ Cephei stars and slowly pulsating B stars affect silicon line profile variations. We use the non-adiabatic amplitudes of the effective temperature and gravity variation presented in Dupret et al. (2002), together with a Kurucz intensity grid, to compute time series of line profile variations. Our simulations point out that the line shapes do not change significantly due to temperature variations. We find equivalent width variations of at most two percent of the mean equivalent width. We confront our results with observational equivalent width variations and with photometrically obtained effective temperature variations.

Key words: stars: early-type - stars: variables: $\beta $ Cep - stars: variables: slowly pulsating B stars - line: profiles


1 Introduction

Thirty years ago, Osaki (1971) successfully modeled the basic properties of line profiles of $\beta $ Cephei stars. He showed that assuming only a non-radial velocity field could mimick rather well the variations in position and width of the spectral lines. Later it was discovered that $\beta $ Cephei stars are not the only B stars which show line profile variations (LPVs). The cooler slowly pulsating B stars (SPBs) exhibit similar LPVs but have photospheres which are dominated by transversal motions.

Since the pioneering work of Osaki, there has always been a keen interest in line profile modelling. After all, one can expect that time series of stellar spectra contain more pulsational information than any other observable. Moreover, since the beginning of the 1980s the spectroscopic resolution greatly improved so that LPVs can be studied in much detail. LPVs have been used, for example, to study the influence of rotation on pulsation (e.g. Lee & Saio 1990), to distinguish between non-radial pulsation and spots (e.g. Briquet et al. 2001) or to perform a mode identification via line profile fitting (e.g. Smith & Buta 1979), via the moments of the line profile (e.g. Aerts et al. 1994) or via the Doppler imaging technique (e.g. Telting & Schrijvers 1997). For each of these applications of line profile modelling, it is vital to have a profound understanding of the physics behind the line profile variations. Failing to recognize some of the relevant aspects of LPVs can lead to invalid conclusions.

A problem that is still not satisfactorily settled, is whether temperature variations at the surface of a non-radially pulsating star play an important role in shaping the line profiles. It is well known that, during the pulsation cycle, the temperature and the other thermodynamical quantities like P and $\rho$, are varying with time. This leads to intensity variations both in the continuum and the local line profile. The question is how much this affects the normalized disk integrated flux line profiles. Could, for example, neglecting the temperature variations in the case of line profile fitting, jeopardize a mode identification?

The fact that the effects of temperature variations cannot just be ignored without further investigation, was realized by several authors, be it mainly for rapidly rotating pulsators because the effects are expected to be most pronounced for these stars. Balona (1987) tried to mimick the effects of temperature variations on the moments of a line profile by introducing an artificial extra velocity field. Lee & Saio (1990), using a constant gaussian as local line profile, included a temperature dependent continuum intensity. Lee et al. (1992) extended this work by including equivalent width variations in their model. Schrijvers & Telting (1999) also used in their model a gaussian local line profile with a temperature dependent continuum and equivalent width to see the impact on the performance of the Doppler imaging mode identification technique. Cugier (1993) and Townsend (1997) used a somewhat more advanced temperature dependent local line profile. The essential conclusion of all these authors is basically the same: temperature variations may have a large influence on LPVs. However, the weak point in their investigations is the unknown amplitude of the temperature variation. Often the temperature variations are computed in the adiabatic approach, with an arbitrary free parameter to correct for non-adiabaticity in the photosphere.

In our investigations, we concentrated on $\beta $ Cephei stars and SPBs. Some of them are slow rotators, and are therefore currently the more simple (though still difficult!) cases for mode identification, because the velocity field can be well described by one spherical harmonic $Y_{\ell}^m$. In Dupret et al. (2002, Paper I), non-adiabatic eigenfunctions in the atmospheres of non-rotating non-radially pulsating B stars have been presented. We here present line-profile simulations based on these eigenfunctions. Our main concern was to investigate how local effective temperature variations affect the LPVs of these kinds of stars.

2 Observational evidence

Temperature variations can manifest themselves in at least two obvious ways: photometric colour variations and spectroscopic equivalent width variations.

   
2.1 Effective temperature variation

We used observations in the Geneva photometric system and the $T_{\rm eff}$ calibration by Künzli et al. (1997) to compute the effective temperature as a function of time for some $\beta $ Cephei stars and SPBs. Many targets do not show a clear sinusoidal variation in $T_{\rm eff}(t)$. We therefore estimated the relative $T_{\rm eff}$ variability by computing $\sigma(T_{\rm eff}) / \langle T_{\rm eff}\rangle$, where $\sigma(T_{\rm eff})$ stands for the standard deviation of the set of $T_{\rm eff}$ values and $\langle T_{\rm eff}\rangle$ is the average effective temperature. To obtain reliable values, we only selected stars for which at least 50 measurements (containing all 7 Geneva colours) in the Geneva photometric database were available. The results for 12 SPBs and 15 $\beta $ Cephei stars are shown in Fig. 1.
  \begin{figure} \par\includegraphics[angle=270,width=8.5cm,clip]{3069f1.eps} \end{figure} Figure 1: Relative effective temperature variation as a function of the average effective temperature for SPBs (open circles) and $\beta $ Cephei stars (solid squares) for which at least 50 Geneva photometric measurements are available.
Open with DEXTER

We should be careful with the interpretation of the results presented in Fig. 1: what does an effective temperature mean in the case of a non-radial (and therefore non-spherically symmetric) pulsator? The radiation intensity at the surface of a non-radially pulsating star has an angular dependence due to the pulsation. The disk-integrated flux we observe, is therefore a weighted average, and the derived $T_{\rm eff}$ should also be considered as a weighted average. The amplitudes of the $T_{\rm eff}$ variations of the local atmospheres (see Paper I) are therefore higher. We also recall that the $T_{\rm eff}$ calibration of Künzli et al. (1997) involved computing synthetic photometric colours with static LTE Kurucz models which are subsequently corrected with standard stars to match better the observations. The B stars among these standard stars contained (inevitably) non-radial pulsators.

From Fig. 1 it follows that SPBs appear to have a somewhat lower $T_{\rm eff}$ variability than $\beta $ Cephei stars, but the sample sizes are too small to make this conclusion firm. Figure 2 shows examples of targets for which a clear sinusoidal $T_{\rm eff}$ variation could be found. We include these phase diagrams to show what kind of amplitudes of $T_{\rm eff}$ can be detected if the quality of the data is sufficiently high and if the star has a dominant pulsation mode. We conclude that the $T_{\rm eff}$ can vary by several hundred Kelvin and that this should be considered as a lower limit for the $T_{\rm eff}$ variation of the local atmosphere.

  \begin{figure} \par\includegraphics[angle=270,width=13.5cm,clip]{3069f2.eps} \end{figure} Figure 2: The upper panel shows the real-time variation of the effective temperature $T_{\rm eff}$ of the radially pulsating $\beta $ Cephei star $\delta $ Ceti. All other panels show a phase diagram of the $T_{\rm eff}$ variation. The middle left panel is for the $\beta $ Cephei star HD 147985 where we used a folding frequency of 7.5579 c d-1. The middle right panel is for the same for the $\beta $ Cephei star $\tau ^1$ Lupi, with a folding frequency of 5.445 c d-1. The bottom panels show $T_{\rm eff}$ phase diagrams of two SPBs. The bottom left panel is for the SPB HD 33331 and was folded with the frequency 0.872 c d-1. The bottom right panel is for the SPB HD 181558 and was folded with the frequency 0.8078 c d-1. These data were obtained by researchers of the Institute of Astronomy in Leuven.
Open with DEXTER

2.2 Equivalent width variation

The equivalent width of an absorption line depends on the width of the absorption coefficient, which is a function of thermal and microturbulent velocities, and on the number of absorbers in the proper ionisation and excitation state, which can be computed in LTE with the laws of Saha and Boltzmann. The wings of strong lines also depend on the pressure dependent damping constant (e.g. Gray 1992). The temperature is the most important variable determining the line strength and since the temperature is varying in a pulsating star, we can thus expect to see equivalent width (EW) variations in the spectral lines. In the same way as in the case of the $T_{\rm eff}$, the observed EW variations should be considered as weighted averages of the local EW variations.

In this section, as well as in the remainder of the paper, we will concentrate on silicon lines: the SiII doublet around 413 nm and the SiIII triplet around 456 nm. The former are pronouncedly present in SPBs, the latter in $\beta $ Cephei stars. Being neither too weak nor too strong in almost the entire instability strip where they are used, these Si-lines are often used to study LPVs and identify the modes in pulsating B stars (see e.g. Aerts et al. 1994; Aerts et al. 1999). This spectral line selection criterion implies that their $T_{\rm eff}$dependence is not extremely strong. We will check in this paper whether these lines are sufficiently insensitive to $T_{\rm eff}$ variations to be modeled in slowly rotating pulsators without any incorporation of temperature variations as is done in e.g. the moment method (Aerts et al. 1992)


  \begin{figure} \par\includegraphics[angle=270,width=7.8cm,clip]{3069f3.eps} \end{figure} Figure 3: Relative EW variation as a function of the average effective temperature for SPBs (open circles) and $\beta $ Cephei stars (solid squares). For the SPBs the line SiII (413.0884 nm) was used and for the $\beta $ Cephei stars the line SiIII (455.2622 nm). The solid square with the highest EW variation (around 9%) represents the $\beta $ Cephei star BW Vulpeculae which is known to be a non-linear pulsator with huge LPVs (Aerts et al. 1993).
Open with DEXTER

We obtained observational EW time series of the SiIII 455.2622 nm line of the $\beta $ Cephei stars in the sample of Aerts (1993) and the EW of the SiII 413.0884 nm line of the SPBs in the sample of Aerts et al. (1999). For the majority of cases, the EW phase diagrams showed much scatter. The reason is firstly that the EW is more sensitive to the data reduction proces than e.g. the radial velocity and secondly that many stars are multiperiodic. Similar as for the $T_{\rm eff}$ we computed the relative EW variability with $\sigma(EW) / \langle EW\rangle$, where $\sigma(EW)$ stands for the standard deviation of the set of EW values. The results for 10 $\beta $ Cephei stars and 15 SPBs are shown in Fig. 3. For a small number of targets, it was possible to detect a clear sinusoidal variation in the EW, with the same frequency as in the radial velocity. In Fig. 4 we give as examples: $\delta $ Ceti, which is a monoperiodic radially pulsating $\beta $ Cephei star, $\nu $ Eri which is a non-radial multiperiodically pulsating $\beta $ Cephei with a dominant radial mode (Aerts 1993), the SPB HD 53921, and the SPB HD 181558 which seems to be a monoperiodic g-mode pulsator (De Cat 2001).
  \begin{figure} \par\includegraphics[angle=270,width=12.3cm,clip]{3069f4a.eps}\pa... ...*{3.5mm} \includegraphics[angle=270,width=12.3cm,clip]{3069f4b.eps} \end{figure} Figure 4: EW and radial velocity phase diagrams of the two $\beta $ Cephei stars $\delta $ Ceti and $\nu $ Eri (resp. upper left and upper right panels) and the two SPBs HD 53921 and HD 181558 (resp. lower left and lower right panels). For the $\beta $ Cephei stars the SiIII 455.2622 nm line was used, for HD 53921 the line SiII 412.8053 nm, and for HD 181558 the line SiII 413.0884 nm. The folding frequency was 6.2059 c d-1 for $\delta $ Ceti, 5.76349 c d-1 for $\nu $ Eri, 0.6054 c d-1 for HD 53921 and 0.80780 c d-1 for HD 181558.
Open with DEXTER

We remark that the equivalent width variations of different lines need not be in phase. For example, the EW variation of He lines in an SPB are in antiphase with the EW variations of the SiII doublet (De Cat, private communication). The reason is that, as is well known, the $EW(T_{\rm eff}$) curve has an ascending branch, a top, and a descending branch. For SPBs the SiII doublet is situated in the descending branch of the $EW(T_{\rm eff}$) curve while the He lines are situated in the ascending branch.

Non-adiabatic computations predict a small extra phase shift between the EW and the observed radial velocity $\langle v\rangle$. Observationally however, it is difficult to measure this phase lag because of noise and multiperiodicity.

3 Theoretical modelling

3.1 Basic approach

A C ++ code, named PULSTAR, was implemented to compute time series of spectra. We adopt a one-layer model, and compute a spectrum as follows. The z-axis is taken to be the rotation axis of the star. The integration over the visible surface to obtain the observed flux is made discrete by dividing the surface into many small cells. More precisely, the normalized spectrum $p(\lambda, t)$ at wavelength $\lambda $ and at time t is computed using the following discrete formula:

 \begin{displaymath} p(\lambda, t) = \frac{\displaystyle\sum\limits_{i=1}^{N_{\... ...\varphi_j,t) \;\; I_{\rm c}(\lambda,\theta_i,\varphi_j,t) }, \end{displaymath} (1)

where $N_{\theta}$ and $N_{\varphi}$ are the number of cells in the $\theta$ respectively $\varphi$ direction. zij is a boolean variable which takes the value 1, if the cell $(\theta_i, \varphi_j)$ is visible, and 0 if it is invisible. $\Delta A$ is the to-the-line-of-sight projected area of the cell, and I and $I_{\rm c}$ are respectively the intensity and continuum intensity. In the following subsections we give some more details on the different ingredients of Eq. (1).

3.2 The displacement and velocity field

Currently, PULSTAR assumes a non-radial pulsational displacement field $\vec{\xi}$ in the slow-rotation approximation, with spherical components
 
$\displaystyle \xi_{r}(\theta, \varphi, t)$ = $\displaystyle a \ Y_{\ell}^m(\theta, \varphi) \ {\rm e}^{i\omega t},$  
$\displaystyle \xi_{\theta}(\theta, \varphi, t)$ = $\displaystyle a\ K\ \frac{\partial Y_{\ell}^m(\theta, \varphi)}{\partial\theta} \ {\rm e}^{i\omega t},$ (2)
$\displaystyle \xi_{\varphi}(\theta, \varphi, t)$ = $\displaystyle \frac{a K}{\sin\theta} \frac{\partial Y_{\ell}^m(\theta, \varphi)}{\partial\varphi} \ {\rm e}^{i\omega t},$  

and its corresponding velocity field $\vec{v}_{\rm puls}$. Here, $\omega$ is the pulsational frequency, a is the amplitude of the radial displacement, and a K is the amplitude of the transversal displacement. Concerning the spherical harmonics $Y_{\ell}^m$, we used the definition of Unno et al. (1989). In Paper I, it was shown that the non-adiabatic phase difference between the radial and the transversal components of the displacement vector is negligible. PULSTAR allows the inclusion of an unlimited number of pulsation modes. The program furthermore allows for a uniform rotational velocity $\vec{v}_{\rm rot} = \vec{\Omega} \times \vec{r}$ with $\vec{\Omega} = \Omega \vec{e}_z$ a constant vector and $\vec{r}$ the position vector. Given the observers vector $\vec{k}$, i.e. the unit vector pointing towards the observer, the total velocity projected on the line of sight $v_{\rm tot}$ is simply computed as $v_{\rm tot} = (\vec{v}_{\rm puls} + \vec{v}_{\rm rot})\cdot\vec{k}$.

3.3 Geometrical distortions

Due to the pulsational displacement field, the stellar surface is distorted. PULSTAR is equipped with a subroutine that determines the time-dependent surface normal $\vec{n}_{\scriptscriptstyle\rm S}$ in each point of the stellar surface. We used the Lagrangian expressions for $\vec{n}_{\scriptscriptstyle\rm S}$ derived by Heynderickx et al. (1994). These expressions are not repeated here for the sake of brevity.

The length of the vector $\vec{n}_{\scriptscriptstyle\rm S}$ measures the area of the surface element, so that the projected area $\Delta A$ can be computed from $\Delta A = \vec{n}_{\scriptscriptstyle\rm S} \cdot \vec{k}$. With $\mu \equiv \cos\raisebox{2pt}{\ensuremath{\chi} }$, we denote the cosine of the angle between the local surface normal and the observer's vector: $\mu = (\vec{n}_{\scriptscriptstyle\rm S}/\Vert\vec{n}_{\scriptscriptstyle\rm S}\Vert) \cdot \vec{k}$. The quantity $\mu$ is needed to compute the radiation intensity in the direction of the observer as well as to determine whether a surface element is visible or not. The latter is done by checking the sign of $\mu$: an element is visible when $\mu$ is positive and invisible when $\mu$ is negative.

3.4 Surface intensity

PULSTAR has at its disposal a precomputed 4 dimensional static LTE Kurucz intensity grid $I_{\scriptscriptstyle\rm Kur}(\lambda, \mu, T_{\rm eff}, \log g)$. The microturbulent velocity is fixed at the default value of the Kurucz atmosphere models: 2 km s-1. It is assumed that the surface intensity of the local dynamic atmosphere can be well approximated with the surface intensity of a static atmosphere with parameters $T_{\rm eff}+\delta T_{\rm eff}$ and $\log(g+\delta g)$. The intensity $I(\lambda,\theta_i,\varphi_j,t)$ in Eq. (1) is then computed by

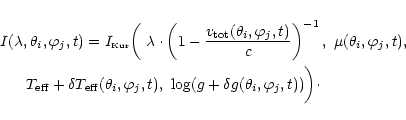
\begin{eqnarray*}& & I(\lambda,\theta_i,\varphi_j,t) = I_{\scriptscriptstyle\rm... ...arphi_j,t), \ \log(g+\delta g(\theta_i,\varphi_j,t)) \bigg)\cdot \end{eqnarray*}


The continuum intensity $I_{\rm c}$ is computed analogously. The factor $(1-v_{\rm tot}/c)$, where c is the speed of light, takes into account that the local intensity spectrum is Doppler shifted because of the local pulsational and rotational velocity of the surface element. PULSTAR computes the intensity at each point of the visible surface by interpolation in its intensity grid $I_{\scriptscriptstyle\rm Kur}$.

The temperature effects on the line-profile variations are taken into account through the variation of the local $\delta T_{\rm eff} / T_{\rm eff}$, and not through the Lagrangian variation of the temperature at the line forming optical depth. As shown in Paper I, it can be argued that at time t the temperature distribution of the perturbed local atmosphere is well approximated by the temperature distribution of an equilibrium model. For the same physical reasons, we assume that the intensity field of the perturbed local atmosphere is also well approximated by the intensity field of an equilibrium atmosphere model. And since for a given metallicity, the latter only depends on the quantities $T_{\rm eff}(t)$ and $\log g(t)$, it is appropriate to use $\delta T_{\rm eff} / T_{\rm eff}$and $\delta g / g$ as variables in our simulations.

   
3.5 The input parameters

As mentioned before, PULSTAR adopts the one-layer model which means that the displacement vector and the velocity vector are computed at one layer only. In what follows we will denote the radius of this layer with R. The quantities a and K in Eq. (2) are to be understood as $\xi_{r}$ and $\xi_{h}/\xi_{r}$ (see Paper I) evaluated at r = R. How this layer was chosen, will be explained later on. Next to a/R and K, the degree $\ell$, the azimuthal number m, the frequency $\nu \equiv \omega / 2\pi$ and the inclination angle i must also be specified. The local non-adiabatic relative effective temperature variation and the relative gravity variation can be related to the relative radial displacement with
  
                         $\displaystyle \frac{\delta T_{\rm eff}}{T_{\rm eff}}$ = $\displaystyle f_{T} \ \frac{\xi_{r}}{R} \ {\rm e}^{i\psi_{T}} = f_{T} \ \frac{a}{R} \ Y_{\ell}^m(\theta,\varphi) \ {\rm e}^{i(\omega t + \psi_{T})},$ (3)
$\displaystyle \frac{\delta g}{g}$ = $\displaystyle f_{g} \ \frac{\xi_{r}}{R} \ {\rm e}^{i\psi_{g}} = f_{g} \ \frac{a}{R} \ Y_{\ell}^m(\theta,\varphi) \ {\rm e}^{i(\omega t + \psi_{g})}$ (4)

which defines the quantities fT, $\psi _{T}$, fg and $\psi _{g}$.

Although, as mentioned earlier, PULSTAR allows to include rotational broadening, the latter was always taken zero in the following sections.

4 The line forming photospheric layers

The contribution of a photospheric layer at depth $x \equiv \log\tau$ to a point of the spectral line at wavelength $\lambda $ is given by the line contribution function (LCF) $C(\lambda,x)$. More information on LCFs can be found in e.g. Albrow & Cottrell (1996) and references therein. There has been a discussion in the literature on how the contribution function of a spectral line should be computed. The results for the calculation of LCFs up to now can be summarized very briefly as follows. Magain (1986) showed convincingly that the contribution function of the intensity I is an inappropriate quantity, and that the contribution function CRof the relative intensity depression $R \equiv (I - I_{\rm c})/ I_{\rm c}$, with $I_{\rm c}$ the continuum intensity, should be considered. However, as we cannot resolve the stellar disk, we need to consider fluxes in stead of intensities. Unfortunately, as shown by Achmad et al. (1991), there is no unique contribution function of the relative flux depression $(F - F_{\rm c})/F_{\rm c}$. Albrow & Cottrell (1996) discovered, however, that there does exist a unique contribution function CU of the absolute flux depression $U \equiv F - F_{\rm c}$. It is the latter LCF that we have used to find the line forming photospheric layers for the Si lines mentioned earlier. In principle, for a non-radially pulsating star, CU is time dependent and should be computed with a non-spherical hydrodynamic atmosphere code. Since such theoretical models are not yet available, we computed CU with a Kurucz (1993) atmosphere model, which is a static plane-parallel stellar atmosphere model computed in LTE. The $T_{\rm eff}$ and the $\log(g)$ of the atmospheres are the same as those of the equilibrium models used in Paper I.

To have an idea about the range of line forming layers, we adopt a new approach. Consider, as an example, the line contribution function $C_{U}(\lambda, x)$ for the SiIII (456.784 nm) line, as shown in Fig. 5.

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{3069f5.eps} \end{figure} Figure 5: The line contribution function CU as a function of the wavelength $\lambda $ and the depth parameter $x \equiv \log\tau_{\rm ross}$, of the SiIII (456.784 nm) line for a stellar atmosphere with parameters $T_{\rm eff} = 22\,643$ K and $\log g = 3.76$.
Open with DEXTER

First, we define the quantity $S_{\alpha }$ with $0 \le \alpha \le 1$ as the smallest connected subset of the $\{\lambda, x\}$ space so that

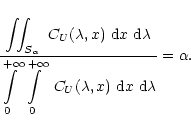\begin{displaymath}\frac{\displaystyle\int\!\!\!\int_{S_{\alpha}} \ C_{U}(\lambd... ... \ C_{U}(\lambda, x) \ {\rm d}x \ {\rm d}\lambda } = \alpha. \end{displaymath} (5)

In other words, $S_{\alpha }$ is the smallest possible region in the $\lambda x$-plane (not necessarily rectangular), so that in that region the volume enclosed between the surface $z = C_{U}(\lambda, x)$ and the z = 0 plane is a fraction $\alpha $ of the total volume enclosed between the surface $z = C_{U}(\lambda, x)$ and the z = 0 plane. Subsequently, we define $x_{\min}$ and $x_{\max}$ with
$\displaystyle x_{\min}(\alpha)$ $\textstyle \,\equiv\,$ $\displaystyle \min\{x \vert x \in S_{\alpha}\},$ (6)
$\displaystyle x_{\max}(\alpha)$ $\textstyle \,\equiv\,$ $\displaystyle \max\{x \vert x \in S_{\alpha}\}.$ (7)

That is, $x_{\min}$ and $x_{\max}$ are the outer points of the region $S_{\alpha }$ in the x-direction. We refer to the range $[x_{\min}, x_{\max}]$ as the line formation range that contributes $\alpha \cdot 100$ percent of the line depression. Although the method described here is applied to the case of line formation in a static photosphere, it can readily be generalized to line formation in a dynamic photosphere.

Our results for the SiIII (456.784 nm) line in the case of the $\beta $ Cephei model and the SiII (412.805 nm) line in the case of the SPB model can be found in Figs. 6 and 7. These figures show that the most contributing layer is $\log\tau = -1.625$ for the SiIII line and $\log\tau = -2.000$ for the SiII line. We used these layers to evaluate the quantities (2), (3) and (4).


  \begin{figure} \par\includegraphics[angle=270,width=8.4cm,clip]{3069f6.eps} \end{figure} Figure 6: Upper and lower end of the line forming range of the SiIII (456.784 nm) line for the $\beta $ Cephei atmosphere model mentioned in Paper I. Given an $\alpha $, the shallowest and the deepest layer of the region $S_{\alpha }$ was computed and plotted. Here $S_{\alpha }$ is the smallest region in $\{\lambda, \log\tau\}$ space so that the line forming contribution of this region is $\alpha \cdot 100$ percent of that of the total line forming contribution. E.g. the 90% contribution range is [-2.875, -0.125]. The stairwise running of the curve is due to discretisation of the computations and should be ignored.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=270,width=8.4cm,clip]{3069f7.eps} \end{figure} Figure 7: Same as in Fig. 6 but for the SiII (412.805 nm) line for the SPB atmosphere model mentioned in Paper I.
Open with DEXTER

One should be aware that we are using the range of line formation computed with CU, as the range of line formation for the relative flux depression. It is unclear how accurate this approximation is. For the Si lines under consideration (in MS B star spectra), we verified whether

  \begin{figure} \par\includegraphics[angle=270,width=8.3cm,clip]{3069f8.eps} \end{figure} Figure 8: The variation of $\xi _{r}/R$ (lower panel) and $\xi _{h}/R$ (upper panel) through the 90% contribution range for the SiIII (456.784 nm) line in the $\beta $ Cephei atmosphere model, as a function of the pulsation frequency, for the modes listed in Table 1. The variation was estimated by computing (s - d)/d where s stands for the value in the shallower end of the range and d for the deeper end of the range. The triangles denote $\ell = 1$, the squares $\ell = 2$, the circles $\ell = 3$ and the crosses $\ell = 4$.
Open with DEXTER


  \begin{figure} \includegraphics[angle=270,width=8.3cm,clip]{3069f9.eps} \end{figure} Figure 9: Same as in Fig. 8 but for the SiII (412.805 nm) line and for the SPB modes listed in Table 2. The triangles denote $\ell = 1$, the squares $\ell = 2$ and the circles $\ell = 3$. The higher the radial order is, the larger the variation of $\xi _{r}/R$ and $\xi _{h}/R$ is. The bottom modes are g20 modes, the top mode is a g60 mode.
Open with DEXTER

the LCF $C_{R}(\lambda,\mu)$ pointed to the same layers of formation as the LCF $C_{Q}(\lambda,\mu)$ of the absolute intensity depression $Q \equiv I - I_{\rm c}$, given a $\mu$. To do so, we rescaled CQ so that its maximum was the same as for CR. It turned out that the rescaled CQ was almost identical to CR.

Although the line forming ranges, given an $\alpha $, are ranges for a static atmosphere, we have a priori no reason to believe that these ranges will be smaller for a dynamic atmosphere. It is therefore interesting to check how much $\xi _{r}/R$and $\xi _{h}/R$ change over the line forming range, in order to see how good the commonly used one-layer model is. From Figs. 6 and 7 one can see that the 90% contribution range in $\log\tau$ is [-2.875, -0.125] for the SiIII line and [-3.625, 0.250] for the SiII line. The variations of $\xi _{r}/R$ and $\xi _{h}/R$ over the line forming range were estimated by computing (s - d)/d where s stands for the value in the shallower end of the range and d for the deeper end of the range. The results for the different pulsation modes listed in Tables 1 and 2 are shown in Figs. 8 and 9. From these figures it can be immediately seen that for some modes, the one-layer approximation is a rather crude one, in the sense that the eigenfunctions $\xi _{r}/R$ and $\xi _{h}/R$ vary quite a lot in the line forming region so that assigning a single value to these quantities may be inappropriate. Remarkable is also that the one-layer approximation is often better for the high-order g-modes of the SPB model than for the low-order p-modes of the $\beta $ Cephei model. It is still unclear, however, how good the one-layer approximation is to compute LPVs. Probably the only way to find out is to compute time series of line profiles with a spectral line synthesis code suitable for the dynamic atmospheres of non-radially pulsating stars. Such an approach, however, is currently beyond our scope. Evaluating the eigenfunctions in a "mean layer'' somehow defined as a weighted average of the line forming layers, would not yield much additional insight since the essential physics (e.g. a different velocity field for the line core than for the line wings) would still not be present. Since the wings are formed deeper in the atmosphere than the core, and because the amplitude of the displacement (and thus the velocity) increases towards the surface, and because the "one'' layer we use is the core-forming layer, we can expect that the Doppler shift of the line wings is overestimated.

It is also interesting to understand the qualitative nature of Figs. 8 and 9. It can be seen that the variation of $\xi _{r}/R$ and $\xi _{h}/R$ increases with increasing frequency for the $\beta $ Cephei star modes, but decreases with increasing frequency for the SPB modes. This is because for p-modes the number of radial nodes of the displacement eigenfunction increases with increasing frequency. As a consequence, for increasing frequency, the "last'' node gets closer to the surface, so that the derivative of $\xi _{r}/R$ and $\xi _{h}/R$ is larger in the atmosphere. For g-modes, as is well known, the number of radial nodes decreases with increasing frequency so that the opposite effect happens. For p-modes, the variation of $\xi _{r}/R$ and $\xi _{h}/R$ for different degrees $\ell$ form one curve, while for g-modes there are clearly three different curves. This can be understood as follows. Close to the surface of the star, the system of equations describing non-adiabatic non-radial oscillations, mainly depend on the degree $\ell$ through the conservation of mass equation (Eq. (21) of Paper I) which contains a term with the factor $\ell (\ell+1)/\omega^2$ associated to the transversal compression. For low-degree p-modes with a relative high frequency, this term is very small. Therefore, for a given frequency, the r-dependent part of the pulsation eigenfunctions does not depend on the degree $\ell$ in the atmosphere in a good approximation. On the other hand, for low-frequency g-modes this term is very significant, so that in the atmosphere the pulsation eigenfunctions of g-modes do depend on the degree $\ell$.

5 Simulation of line profile series

5.1 Setup

Time series of line profiles were computed using non-adiabatic eigenfunctions of the $\beta $ Cephei model and the SPB model presented in Paper I. The equilibrium effective temperature was $T_{\rm eff} = 22\,643$ K for the $\beta $ Cephei model, and $T_{\rm eff} = 15\,190$ K for the SPB model. We chose the equilibrium effective temperatures of these models so that the top of the $EW(T_{\rm eff}$) curve was avoided. A $T_{\rm eff}$ around the top would cause very small EW variations, even if the $T_{\rm eff}$variation would be quite large. The $T_{\rm eff}$ of the SPB model is situated in the descending branch of the $EW(T_{\rm eff}$) curves of the SiII doublet, while the $T_{\rm eff}$ of the $\beta $ Cephei model is situated in the ascending branch of the $EW(T_{\rm eff}$) curves of the SiIII triplet. This way we attempted to evoke large EW variations.

The parameters K, fT, $\psi _{T}$, fg and $\psi _{g}$ are listed in Tables 1 and 2 and were computed, as explained in Paper I, with a non-adiabatic pulsation code with special care for the stellar atmosphere. Since this code was written for non-rotating stars, these parameters are independent of m. The periods of the modes can also be found in Paper I. The azimuthal number m was varied each time from 0 to $\ell$. This resulted in 49 different modes for the $\beta $ Cephei model and 59 different modes for the SPB model.

Next, we turn to the choice of the pulsation amplitude afor each mode. Given a value for fT, the amplitude of $\delta T_{\rm eff} / T_{\rm eff}$ is scaled to the amplitude a of the radial displacement. An unrealistically high value of the latter therefore implies extreme temperature variations, which will undoubtfully show a large but meaningless effect on the LPVs. On the other hand, we should not choose a too small because we wish to know the effect on line profiles in the worst (but still realistic) case. We considered two ways to set the amplitude. One way is to take for each mode a different amplitude a in such a way that the maximum length of the pulsational velocity vector $(\vert\vec{v}_{\rm puls}\vert)_{\rm max}$ is the same for each mode, which is also done by e.g. Townsend (1997). Another way is to take for each mode a different amplitude a in such a way that the maximum length of the relative displacement vector $(\vert\vec{\xi}\vert)_{\rm max} /R$ is the same for each mode. Since the maximum value of $\vert Y_{\ell}^m\vert$ depends on the quantum numbers $(\ell ,m)$, both ways also allow for a better comparison between LPVs coming from different sets of $(\ell ,m)$. Of course, one should avoid amplitudes that would cause shock waves or an unreasonably distorted surface. For this purpose, it seems more natural to fix $(\vert\vec{\xi}\vert)_{\rm max} /R$ for SPBs and to fix $(\vert\vec{v}_{\rm puls}\vert)_{\rm max}$ for $\beta $ Cephei stars, because of the difference in magnitude of their pulsation frequencies. Indeed, for SPBs "reasonable'' velocities can still lead to displacements out of the linear regime while the opposite is true for the $\beta $ Cephei stars. The chosen values of $(\vert\vec{v}_{\rm puls}\vert)_{\rm max}$ or $(\vert\vec{\xi}\vert)_{\rm max} /R$ will be given in the following sections.

A final input parameter that needs discussion is the inclination angle iwhich affects both the line profile variability and the influence of temperature variations on the line profile, because of cancellation effects. For example, the amplitude of the observed radial velocity $\langle v\rangle$ strongly depends on the inclination angle. In fact, as explained in Chadid et al. (2001), for each non-radial mode there exists at least one so-called inclination angle of complete cancellation ( IACC) for which the amplitude of $\langle v\rangle$ is exactly zero. In an analoguous way as in Chadid et al. (2001), one can also compute the inclination angle for which the amplitude of $\langle v\rangle$ reaches its maximum. We call such an angle "inclination angle of least cancellation'' ( IALC). We restrict ourselves in the simulation to inclination angles which are IALCs as the temperature effects are largest for them, and we list them in Table 3. A mode $(\ell ,m)$ can have several IALCs (i.e. several global maxima), but we systematically used the lowest one.

5.2 Results for the $\beta $ Cephei model

For the $\beta $ Cephei model we set the amplitude a by fixing $(\vert\vec{v}_{\rm puls}\vert)_{\rm max}$ to 20 km s-1 for every mode. The amplitudes of the radial velocities $\langle v\rangle$ of the modes with degree $\ell =$ 1, 2, 3, and 4 are then respectively about 11 km s-1, 7 kms-1, 3 km s-1 and 0.5 km s-1. The maximum length of the relative displacement vector, $(\vert\vec{\xi}\vert)_{\rm max} /R$, was always smaller than 1%. Most of the spectroscopically observed non-radially pulsating $\beta $ Cephei stars have an amplitude of $\langle v\rangle$ smaller than 11 km s-1. Some $\beta $ Cephei stars with a radial first mode are known to have a larger $\langle v\rangle$ amplitude, e.g. $\beta $ Cephei, the prototype star itself, shows a radial velocity variation with an amplitude of about 14 kms-1 (Aerts et al. 1994).


 

 
Table 1: The quantities K, fT, $\psi _{T}$, fg and $\psi _{g}$ for the $\beta $ Cephei model (see Paper I) for the spectral line SiIII (456.78 nm) for which we used the layer $\log\tau = -1.625$ as the reference layer.
mode                  K fT $\psi _{T}$ fg $\psi _{g}$

$\ell = 1$     p1		         0.05 2.93 179$^{\circ}$ 21.0 180$^{\circ}$
$\ell = 1$     p2         0.04 3.26 187$^{\circ}$ 26.7 180$^{\circ}$
$\ell = 1$     p3         0.03 3.54 195$^{\circ}$ 33.3 180$^{\circ}$

$\ell = 2$     f		         0.04 3.27 186$^{\circ}$ 26.4 180$^{\circ}$
$\ell = 2$     p1         0.03 3.43 191$^{\circ}$ 30.2 180$^{\circ}$
$\ell = 2$     p2         0.02 3.62 199$^{\circ}$ 36.7 180$^{\circ}$
$\ell = 2$     p3         0.02 3.66 212$^{\circ}$ 47.5 180$^{\circ}$

$\ell = 3$     f		         0.03 3.43 190$^{\circ}$ 29.4 180$^{\circ}$
$\ell = 3$     p1         0.02 3.69 203$^{\circ}$ 39.8 180$^{\circ}$
$\ell = 3$     p2         0.02 3.71 209$^{\circ}$ 45.0 180$^{\circ}$
$\ell = 3$     p3         0.02 3.59 216$^{\circ}$ 51.1 180$^{\circ}$

$\ell = 4$     f		         0.03 3.59 195$^{\circ}$ 33.3 180$^{\circ}$
$\ell = 4$     p1         0.02 3.72 205$^{\circ}$ 42.4 180$^{\circ}$
$\ell = 4$     p2         0.01 3.50 219$^{\circ}$ 53.8 180$^{\circ}$



   
Table 2: The quantities K, fT, $\psi _{T}$, fg and $\psi _{g}$ for the SPB model (see Paper I) for the spectral line SiII (412.81 nm) for which we used the layer $\log\tau = -2.0$ as the reference layer.
mode                  K fT $\psi _{T}$ fg $\psi _{g}$

$\ell = 1$     g20		         17.5 3.62 319$^{\circ}$ 2.00 180$^{\circ}$
$\ell = 1$     g25         24.6 5.68 327$^{\circ}$ 1.95 180$^{\circ}$
$\ell = 1$     g30         36.1 8.54 336$^{\circ}$ 1.89 180$^{\circ}$
$\ell = 1$     g35         50.0 11.2 343$^{\circ}$ 1.86 180$^{\circ}$
$\ell = 1$     g40         66.7 13.6 349$^{\circ}$ 1.79 180$^{\circ}$
$\ell = 1$     g45         86.1 15.4 354$^{\circ}$ 1.73 180$^{\circ}$
$\ell = 1$     g50         108 16.9 357$^{\circ}$ 1.66 180$^{\circ}$

$\ell = 2$     g30		         12.9 6.94 329$^{\circ}$ 1.95 180$^{\circ}$
$\ell = 2$     g35         17.9 9.89 337$^{\circ}$ 1.88 180$^{\circ}$
$\ell = 2$     g40         23.2 12.4 343$^{\circ}$ 1.81 180$^{\circ}$
$\ell = 2$     g45         30.3 14.8 349$^{\circ}$ 1.74 180$^{\circ}$
$\ell = 2$     g50         38.3 16.8 353$^{\circ}$ 1.68 180$^{\circ}$
$\ell = 2$     g55         47.0 18.4 357$^{\circ}$ 1.61 180$^{\circ}$
$\ell = 2$     g60         58.3 19.9 0$^{\circ}$ 1.53 180$^{\circ}$

$\ell = 3$     g40		         11.6 10.7 339$^{\circ}$ 1.87 180$^{\circ}$
$\ell = 3$     g45         15.2 13.5 345$^{\circ}$ 1.79 180$^{\circ}$
$\ell = 3$     g50         19.2 15.8 350$^{\circ}$ 1.71 180$^{\circ}$
$\ell = 3$     g55         23.6 17.8 354$^{\circ}$ 1.63 180$^{\circ}$
$\ell = 3$     g60         29.2 19.6 358$^{\circ}$ 1.55 180$^{\circ}$
$\ell = 3$     g65         35.7 21.2 0$^{\circ}$ 1.45 180$^{\circ}$


 

 
Table 3: Inclination angles of least cancellation which are used in the simulations. These are inclination angles so that the amplitude of the radial velocity $\langle v\rangle$ is largest.
IALC m = 0 m = 1 m = 2 m = 3 m = 4
$\ell = 1$ 0$^{\circ}$ 90$^{\circ}$      
$\ell = 2$ 0$^{\circ}$ 45$^{\circ}$ 90$^{\circ}$    
$\ell = 3$ 0$^{\circ}$ 31.1$^{\circ}$ 54.7$^{\circ}$ 90$^{\circ}$  
$\ell = 4$ 0$^{\circ}$ 23.9$^{\circ}$ 40.9$^{\circ}$ 60$^{\circ}$ 90$^{\circ}$


A first result of the simulations is that - with the realistic amplitudes given above - the non-adiabatic relative temperature variation and the relative gravity variation seem to have very little effect on the line profiles. The relative difference in residual intensity between a line profile computed with and without $T_{\rm eff}$ and $\log g$ variations is always about 1% or less. To visualize for the SiIII (456.784 nm) line this difference in residual intensity for each wavelength in the line and at each phase during the pulsation cycle, we computed for the p1 modes $(\ell ,\,m) = (1,\,0)$ and $(\ell,m) = (1,\,1)$ greyscale plots which are shown in the upper panels of Fig. 10. The abscissa shows the wavelength in nanometer, and the ordinate shows the pulsation phase between 0 and 1. The input parameters are the same as mentioned above, in particular the inclination angle is an IALC. White indicates a positive difference in residual intensity, black a negative difference. The plots can be understood as follows. For the $(\ell,m) = (1,\,0)$ mode, we look pole-on so that we only see the northern hemisphere. The nodal line of the radial displacement coincides with the equator which is the edge of the visible disk. At phase zero, the northern hemisphere is maximally expanded so that the velocity is everywhere zero which is why the spectral line is centered around its laboratory wavelength. At the same time the local $T_{\rm eff}$, and therefore also the local EW, is everywhere lower than the equilibrium value. This results in a spectral line with at each wavelength a higher residual intensity than its counterpart computed without temperature effects. At phase 0.5, the situation is reversed. The northern hemisphere is now maximally compressed so that the local EW is everywhere higher than the equilibrium value which results in a spectral line with a lower residual intensity. For the $(\ell,\,m)$ = (1,1) mode, we look equator-on. At phase zero the nodal line of the radial displacement, and therefore also of $\delta T_{\rm eff}$, coincides with the edge of the disk. The nodal line of the radial component of the pulsational velocity, however, coincides then with the meridian through the center of the disk. Half of the disk is receding from us, half of the disk is approaching towards us. This averages out so that the observed spectral line is centered around its laboratory wavelength. The entire visible disk is in expanded state, so that the local $T_{\rm eff}$, and therefore also the local EW, is everywhere lower than the equilibrium value. As for the $(\ell,\,m)$ = (1,0) this results in a spectral line with a higher residual intensity for each wavelength. At phase 0.5, the situation is exactly the reverse one.

  \begin{figure} \par\mbox{\includegraphics[width=8.8cm,clip]{fig10a.ps}\hspace*{1... ....ps}\hspace*{1.5mm} \includegraphics[width=8.8cm,clip]{fig10d.ps} } \end{figure} Figure 10: Greyscale plots of the difference in residual intensity between the spectra computed with and without temperature, gravity and surface normal variations. White indicates a positive difference, black a negative difference. The upper panels are for the SiIII (456.784 nm) line, for the p1 mode of the $\beta $ Cephei star model. The upper left panel is for the $(\ell ,\,m) = (1,\,0)$ mode, and the upper right panel is for the $(\ell ,\,m) = (1,\,1)$ mode. In both cases, the maximum relative difference in residual intensity is about 0.8%. The lower panels are for the SiII (412.8054 nm) line, for the g40 mode of the SPB star model. The lower left panel is for the $(\ell ,\,m) = (2,\,1)$ mode, and the lower right panel is for the $(\ell ,\,m) = (2,\,2)$ mode. In both cases, the maximum relative difference in residual intensity is about 0.6%.
Open with DEXTER

We fitted the EW curve with a sine function to obtain its amplitude and its phase difference with the $\langle v\rangle$ curve. We found that, in general, a larger degree $\ell$ corresponds to a smaller amplitude of the EW variation, which can be explained with surface cancellation effects. Only the relative EW semi-amplitudes for $\ell = 1$ modes and the relative EW peak-to-peak amplitudes for $\ell = 2$ modes reach values between 1 and 2 percent. The other modes show an EW variability below the current detection treshold, and will therefore be disregarded in this discussion. At first, the values of 1-2 percent seem to be small compared to the corresponding observational values of $\beta $ Cephei stars shown in Fig. 3. However, we reckon that there is a significant contribution of noise and multiperiodicity to the latter values, so that our simulated values are not in contradiction with the observations. For the p1 mode we did extra simulations with the same input parameters as specified before, but for which we varied the inclination angle i from 0$^{\circ}$ to 90$^{\circ}$ in steps of 5$^{\circ}$. The computations were done for $\ell = 1,2$ and $m = 0,\ldots,\ell$. The results are shown in the upper panel of Fig. 11.

  \begin{figure} \par\includegraphics[width=8.6cm,clip]{fig11.ps} \end{figure} Figure 11: The amplitude of the relative equivalent width variation as a function of the inclination angle. The upper panel is for the SiIII (456.784 nm) line and for the p1 mode of the $\beta $ Cephei star model. The lower panel is for the SiII (412.8054 nm) line and for the g40 mode of the SPB star model. Each curve is labeled with its corresponding mode numbers $(\ell ,m)$.
Open with DEXTER

As for the amplitude of the radial velocity $\langle v\rangle$, the inclination dependence of the amplitude of the relative equivalent width variation is clearly described by the associated Legendre polynome $P_{\ell}^{\vert m\vert}(\cos i)$. At inclination angles of complete cancellation, no equivalent width variation is seen, no matter how large the temperature variation is at the surface of the star. Balona (2000) produced a similar figure for $\delta $ Scuti stars. However, the relative difference between the maxima of the relative EW amplitude curves in his figure clearly differ from ours. The reason is that Balona (2000) fixes the amplitude $v_{\rm p} \equiv a \omega$ (instead of $\vert\vec{v}_{\rm puls}\vert _{\rm max}$ as we do), and $v_{\rm p}$ is multiplied by the spherical harmonic normalisation factor $N_{\ell}^m$ which differs from mode to mode.

The causes of the (global) EW variations are in the first place the (local) $T_{\rm eff}$ variations, and in the second place the gravity variation. It was found that the gravity variation has an inhibitive effect on the EW variation, i.e. including both $T_{\rm eff}$ and $\log g$ variations results in a lower amplitude of the EW variation than including only  $T_{\rm eff}$. From Table 1 we see that the importance of the gravity variation increases with increasing radial order, which is a direct consequence of the increasing pulsational acceleration with increasing frequency (see Eq. (23) in Paper I).

Concerning the phase difference $\Delta \psi $ between the $\langle v\rangle$ and the global EW variation, we first recall that the local EW variation depends on both the local $T_{\rm eff}$ and the local $\log g$ variation. $\Delta \psi $ will therefore depend on fT, $\psi _{T}$, fg and $\psi _{g}$. The local gravity variation thus affects $\Delta \psi $ (through its amplitude) despite the fact that $\psi _{g}$ equals the adiabatic value of 180$^{\circ}$. The phase differences $\Delta \psi $ resulting from our simulations can be found in Table 4. Note that $\Delta \psi $ is independent of the value of m. Only fT, $\psi _{T}$, and fg have an effect on $\Delta \psi $, not the geometry.

 

 
Table 4: The phase difference $\Delta \psi $ between the radial velocity variation $\langle v\rangle$ and the EW variation, for the SiIII (456.784 nm) line, for the $\beta $ Cephei model, for those modes with an observationally detectable EW variation.
mode                       $\Delta \psi $

$\ell = 1$     p1		         93$^{\circ}$
$\ell = 1$     p2         77$^{\circ}$
$\ell = 1$     p3         59$^{\circ}$

$\ell = 2$     f		         82$^{\circ}$
$\ell = 2$     p1         72$^{\circ}$
$\ell = 2$     p2         55$^{\circ}$
$\ell = 2$     p3         18$^{\circ}$


The simulations suggest that large deviations from $\Delta\psi = 90^{\circ}$ or $\Delta\psi = 270^{\circ}$ are possible.

We explicitly verified that the variation of the moments of the line profile do not change qualitatively. This means that line profile fitting as well as the moment method are not likely to be confused by temperature and gravity variations as far as mode identification is concerned. Although the moment method assumes a constant equivalent width, Aerts et al. (1992) showed that the method is sufficiently robust to handle EW variations of a few percent.

To have an idea how large the local $T_{\rm eff}$ variation and the local $\log g$ variation is for a particular mode, we systematically kept the largest and the smallest value of $T_{\rm eff}$ and $\log g$ recorded on the visible surface (not necessarily at the same pulsation phase) and made the difference between the two. Effective temperature differences turned out to range from about 750 K to 1100 K depending on the mode. These values are in agreement with the photometrically obtained effective temperatures in Sect. 2.1. The maximum difference between the largest and the smallest recorded value of the the local $\log g$ variation ranges from 0.15 dex up to 0.23 dex, and is larger for larger degree $\ell$.

5.3 Results for the SPB model

For the SPB model, we chose the amplitude a so that the maximum relative displacement $(\vert\vec{\xi}\vert)_{\rm max} /R$ was fixed to 10% for every mode. This led to amplitudes of $\langle v\rangle$ between 1.5 kms-1 and 6.5 km s-1. This can be compared with the largest amplitude of $\langle v\rangle$ ever observed for an SPB: 6.7 kms-1 for HD 181558 (De Cat 2001). The maximum length of the pulsational velocity vector $(\vert\vec{v}_{\rm puls}\vert)_{\rm max}$ ranged from 5 km s-1 to 15 km s-1.

Our conclusions for the SPB model are much the same as our conclusions for the $\beta $ Cephei model. Again, with the amplitudes given above, the non-adiabatic temperature variation and the gravity variation seem to have very little effect on the line profiles. The relative difference between the line profiles computed with and without non-adiabatic effects, are about 1% or less. In the lower panels of Fig. 10, we show greyscale plots similar as the ones shown for the $\beta $ Cephei star model. The plots were computed for the SiII (412.8054 nm) line and for the g40 mode with $(\ell ,\,m) = (2,\,2)$ and $(\ell,\,m)$ = (2,1). The interplay between the different sectors and zones now causes a more complex pattern. Parts of the spectral line have a higher residual intensity while other parts have a lower residual intensity than the corresponding spectral line computed without temperature effects.

As for the $\beta $ Cephei model, only the relative EW semi-amplitudes for $\ell = 1$ modes and the relative EW peak-to-peak amplitudes for $\ell = 2$ modes have values up to 2 percent, even for the higher order modes which have a rather large fT value. The cancellation effects are thus as important for the EW variation as for the $\langle v\rangle$ variation. For the SPBs the gravity variation does not play a role in the EW variation, so that the latter is solely caused by the $T_{\rm eff}$ variation. As a consequence, the non-adiabatic phase shift between the $\langle v\rangle$ and EW curve is the same as the non-adiabatic phase shift between the local $\delta T_{\rm eff} / T_{\rm eff}$ and $\xi _{r}/R$. Table 5, which gives $\Delta \psi $, shows that this is not always exactly the case, but the small deviations can be attributed to the influence of line blending on the EW curve of the SiII lines, which causes an uncertainty of $\Delta \psi $ of a few degrees.

 

 
Table 5: The phase difference $\Delta \psi $ between the radial velocity variation $\langle v\rangle$ and the EW variation, for the SiII (412.8054 nm) line, for the SPB model, for those modes with an observationally detectable EW variation.
mode                       $\Delta \psi $

$\ell = 1$     g20		         128$^{\circ}$
$\ell = 1$     g25         120$^{\circ}$
$\ell = 1$     g30         112$^{\circ}$
$\ell = 1$     g35         106$^{\circ}$
$\ell = 1$     g40         100$^{\circ}$
$\ell = 1$     g45         95$^{\circ}$
$\ell = 1$     g50         92$^{\circ}$

$\ell = 2$     g30		         119$^{\circ}$
$\ell = 2$     g35         111$^{\circ}$
$\ell = 2$     g40         106$^{\circ}$
$\ell = 2$     g45         100$^{\circ}$
$\ell = 2$     g50         97$^{\circ}$
$\ell = 2$     g55         93$^{\circ}$
$\ell = 2$     g60         88$^{\circ}$


We did extra simulations for the g40 mode, for which we varied the inclination angle from 0$^{\circ}$ to 90$^{\circ}$ in steps of 5$^{\circ}$. The results are shown in the bottom panel of Fig. 11, and are very similar to the corresponding figure of the $\beta $ Cephei model. The amplitude of the relative EW variation is maximal at an inclination angle of least cancellation ( IALC) and zero at an inclination angle of complete cancellation ( IACC).

Neither the line profile variations nor the moments of the lines are significantly affected by the inclusion of non-adiabatic temperature variations. Modelling the LPVs of the silicon lines with the velocity field only is therefore also a good approximation for the SPBs.

We conclude this section by mentioning that the local effective temperature perturbation ranged from 500 K to 1300 K, while the local $\log g$ never deviates more than 0.01 dex from its equilibrium value.

6 Summary and conclusions

We investigated to what extend the local non-adiabatic effective temperature variation and the local gravity variation of non-radially pulsating B stars affect the LPVs of silicon lines. A challenging part in this investigation was to find reliable amplitudes of $\delta T_{\rm eff} / T_{\rm eff}$ and $\delta g / g$. To do so, we implemented a non-adiabatic pulsation code which does not use the diffusion approximation in the atmosphere, but assumes instead that the temperature distribution in the local dynamical atmosphere is the same as the one of a Kurucz equilibrium model. For the $\beta $ Cephei model, the amplitude of $\delta T_{\rm eff} / T_{\rm eff}$ turned out to be about 3 to 4 times larger than the amplitude of $\xi_{r}/r$, while the non-adiabatic phase shift between these two quantities ranges from 0 to 40 degrees and increases with increasing degree and radial order. For the (unstable) modes we studied, the amplitude of $\delta g / g$ was about 20 to 50 times larger than the amplitude of $\xi_{r}/r$ while the extra non-adiabatic phase shift between these two quantities was always negligible. For the SPB model, the amplitude of $\delta T_{\rm eff} / T_{\rm eff}$ is between 4 and 20 times larger than the amplitude of $\xi_{r}/r$, which is a much larger ratio than for the $\beta $ Cephei model. The reason is that for SPBs the compression of the gas and thus the temperature variations are mainly caused by the transversal displacements which are much larger than the radial displacements. The extra phase shift for $\delta T_{\rm eff} / T_{\rm eff}$due to non-adiabatic effects ranges still between 0 and 40 degrees but, unlike for the $\beta $ Cephei model, it decreases for increasing radial order.

Finding explicit observational evidence for temperature variations on the surface of non-radially pulsating B stars turned out to be rather difficult. Due to noise and multiperiodicity the phase diagrams of the photometrically obtained $T_{\rm eff}$ and the equivalent width of silicon lines often showed nothing but scatter. Only for a few objects we could find a clear sinusoidal variation with the same frequency as in the radial velocity. These results indicate that EW variations of silicon lines in B stars do not lend themselves to be exploited for purposes of frequency analysis or mode identification.

We simulated line profile series with a code named PULSTAR which uses the amplitudes of $\delta T_{\rm eff} / T_{\rm eff}$ and $\delta g / g$ mentioned above together with a Kurucz intensity grid $I_{\rm Kur}(\lambda, \mu, T_{\rm eff}, \log g)$, and which integrates over the visible stellar surface to compute the normalized flux spectra. We took care to use realistic amplitudes for $\xi_{r}/r$. For the $\beta $ Cephei model as well as for the SPB model we obtained sinusoidal EW variation of a few percent. The exact value depends on the mode $(\ell ,m)$ and the inclination angle i. Balona (2000) found similar results in the case of H$\beta $ lines for $\delta $ Scuti stars. The shape of the line profiles was hardly affected by the temperature variations. Silicon lines are therefore reliable to use for mode identification techniques which neglect the temperature and EW variations. For the $\beta $ Cephei model both the $\delta T_{\rm eff} / T_{\rm eff}$and the $\delta g / g$ variation affected the phase difference between the $\langle v\rangle$ variation and the EW variation, which could deviate quite a lot from the adiabatic value. For the SPB model, the EW variation was caused only by the $\delta T_{\rm eff} / T_{\rm eff}$variation. In all cases, the surface normal variation played only a minor role relative to the velocity, temperature and gravity variations. We also mention that our results remain unchanged when the amplitude is taken smaller.

Given the degree $\ell$ of a $\beta $ Cephei mode, it might be possible to derive the radial order through the phase difference $\Delta \psi $between the $\langle v\rangle$ variation and the EW variation. Table 4 indeed shows that for a given degree $\ell$ the differences in $\Delta \psi $ for different modes are rather large. This would be much more difficult for SPBs, although for these stars, the value of $\Delta \psi $ might still be used to put a constraint on the radial order.

We emphasize that our study concerns only silicon lines in the spectra of slowly rotating B stars. The equivalent widths of weaker spectral lines often have a stronger dependence on the effective temperature, and for these lines temperature and gravity variations on the surface may change the line shape significantly. Such lines, however, are much more subject to noise and are therefore currently less suitable candidate lines for a period and mode analysis. As mentioned by e.g. Balona (1987) rapid rotation can make temperature variations on the surface appear more pronounced in the line profiles, so that for rapidly rotating B stars neglecting temperature variations in line profile modelling may not be justified. To investigate this in a consistent way requires, however, non-adiabatic eigenfunctions computed for a rapidly rotating non-radially pulsating star. Such eigenfunctions are currently not yet available.

Acknowledgements
We would like to thank Dr. P. Magain for sharing with us his expertise on line contribution functions, and an anonymous referee for a critical reading of the manuscript. The authors are members of the Belgian Asteroseismology Group (B.A.G.).

References

 

Copyright ESO 2002