A&A 385, 377-398 (2002)
DOI: 10.1051/0004-6361:20020038
Temporal properties of gamma ray bursts as signatures of jets from the central engine
F. Quilligan1 -
B. McBreen1 -
L. Hanlon1 -
S. McBreen1 -
K. J. Hurley1 -
D. Watson2
1 - Department of Experimental Physics, University College Dublin, Dublin 4, Ireland
2 -
X-Ray Astronomy Group, Department of Physics and Astronomy,
Leicester University, Leicester LE1 7RH, UK
Received 31 July 2001 / Accepted 7 January 2002
Abstract
A comprehensive temporal analysis has been performed
on the 319 brightest GRBs with T90>2 s from the BATSE
current catalog. The GRBs were denoised using wavelets and
subjected to an automatic pulse selection algorithm as an
objective way of identifying pulses and quantifying the effects
of neighbouring pulses. The number of statistically significant
pulses selected from the sample was greater than 3000. The rise
times, fall times, full-widths at half-maximum (FWHM), pulse
amplitudes and pulse areas were measured and the frequency
distributions are presented here. All are consistent with
lognormal distributions provided the pulses are well separated.
The distribution of time intervals between pulses is not random
but compatible with a lognormal distribution when allowance was
made for the 64 ms time resolution and a small excess (5%) of
long duration intervals that is often referred to as a
Pareto-Lévy tail. The time intervals between pulses are most
important because they may be an almost direct measure of the
activity in the central engine. Lognormal distributions of time
intervals also occur in pulsars and SGR sources and therefore
provide indirect evidence that the time intervals between pulses
in GRBs are also generated by rotation powered
systems with super-strong magnetic fields.
A range of correlations are presented on pulse
and burst properties. The rise and fall times, FWHM and area of
the pulses are highly correlated with each other. The pulse
amplitudes are anticorrelated with the FWHM. The time intervals
between pulses and pulse amplitudes of neighbouring pulses are
correlated with each other. It was also found that the number of
pulses, N, in GRBs is strongly correlated with the fluence and
duration and that can explain the well known correlation between
duration and fluence. The GRBs were sorted into three categories
based on N i.e.
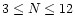 ,
,
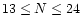 and
and
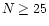 .
The properties of pulses before and after the
strongest pulse were compared for three categories of bursts. No
major differences were found between the distributions of the
pulse properties before and after the strongest pulse in the GRB.
However there is a strong trend for pulses to have slower rise
times and faster fall times in the first half of the burst and
this pattern is strongest for category
.
The properties of pulses before and after the
strongest pulse were compared for three categories of bursts. No
major differences were found between the distributions of the
pulse properties before and after the strongest pulse in the GRB.
However there is a strong trend for pulses to have slower rise
times and faster fall times in the first half of the burst and
this pattern is strongest for category
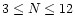 .
This
analysis revealed that the GRBs with large numbers of pulses
have narrower and faster pulses and also larger fluences, longer
durations and higher hardness ratios than the GRBs with smaller
numbers of pulses. These results may be explained by either
homogeneous or inhomogeneous jet models of GRBs. The GRBs with
larger number of pulses are closer to the axis if
.
This
analysis revealed that the GRBs with large numbers of pulses
have narrower and faster pulses and also larger fluences, longer
durations and higher hardness ratios than the GRBs with smaller
numbers of pulses. These results may be explained by either
homogeneous or inhomogeneous jet models of GRBs. The GRBs with
larger number of pulses are closer to the axis if 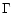 varies
with the opening angle of the jet and the imprint of the jet is
preserved in the pulse structure of the burst. The distribution
of the number of pulses per GRB broadly reflects the beaming by
the jet.
varies
with the opening angle of the jet and the imprint of the jet is
preserved in the pulse structure of the burst. The distribution
of the number of pulses per GRB broadly reflects the beaming by
the jet.
Key words: gamma rays - bursts: gamma rays - observations: methods
- data analysis: methods - statistical
Much of the recent progress in the study of gamma-ray bursts
(GRBs) results from the detection of bursts with good location
accuracy by BeppoSAX that enabled the detection of counterparts at
other wavelengths. The subsequent redshift determination of bursts
have established that these bursts are at cosmological distances
(Costa et al. 1997; van Paradijs et al. 1997). GRBs seem to be connected to
massive stars and become powerful probes of the star formation
history of the universe (Lamb & Reichart 2000; Hanlon et al. 2000; Berger et al. 2001).
However not many redshifts are known and there is still much work
to be done to determine the mechanisms that produce these
enigmatic events.
The most plausible GRB progenitors are expected to be a newly
formed black hole (BH) surrounded by a temporary accretion disk
(Rees 1999; Mészáros 2001; Castro-Tirado 2001; van Putten 2001). The most
popular models include the merger of a neutron star (NS) and a NS
(Eichler et al. 1989; Ruffert & Janka 1999), NS and a BH (Paczynski 1991), BH
white dwarf merger (Fryer et al. 1999) and models of failed
supernovae or collapsars (MacFadyen & Woosley 1999; Paczynski 1998). An
important exception is the model in which the GRB energy is
provided by a newly formed neutron star
(Usov 1992; Thompson 1994). Various explanations have been put
forward for the complicated structure of the light curves. These
range from internal shocks, caused by variations in the velocity
of the outflow (Rees & Mészáros 1994; Piran 1999), to external shocks,
caused by interactions with an external medium
(Mészáros & Rees 1993; Dermer & Mitman 1999). In the internal shock model the
instabilities in the wind leads to shocks which convert a fraction
of the bulk kinetic energy to internal energy remote from the
central engine. A turbulent magnetic field then accelerates
electrons which radiate by synchrotron emission and inverse
Compton scattering, generating the GRB. Many of the observed
features in bursts can be reproduced in the internal shock models
of GRBs
(Sari & Piran 1997; Kobayashi et al. 1997; Daigne & Mochkovitch 1998; Panaitescu et al. 1999; Downes et al. 2001).
A variety of analytical techniques has been applied to the
temporal and spectral profiles of GRBs which place constraints on
the observed distributions which models must satisfy. The
impressive results from these studies include (1) hard to soft
evolution (Golenetskii et al. 1983; Borgonovo & Ryde 2001); (2) the
duration-hardness anticorrelation (Kouveliotou et al. 1993); (3) the
temporal asymmetry of pulses in GRBs (Nemiroff et al. 1993; Link & Epstein 1996);
(4) a bimodal duration distribution of GRBs consistent with two
lognormal distributions (Kouveliotou et al. 1993; McBreen et al. 1994); (5) the
discovery of two different types of pulses in
GRBs (Pendleton et al. 1997); (6) a correlation between
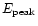 and intensity (Mallozzi et al. 1995); (7) energy dependence of the pulse
duration (Norris et al. 1996); (8) a relationship between the pulse
peak energy,
and intensity (Mallozzi et al. 1995); (7) energy dependence of the pulse
duration (Norris et al. 1996); (8) a relationship between the pulse
peak energy,
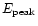 ,
and the photon fluence
(Liang & Kargatis 1996; Crider et al. 1999); (9) lognormal pulse shapes and
time intervals between pulses in long (McBreen et al. 1994; Hurley et al. 1998)
and short GRBs (McBreen et al. 2001); (10) spectra well fit with a
Band function (Band et al. 1993); (11) spectral hardening before a
count rate increase (Bhat et al. 1994); (12) an X-ray excess in
GRB spectra (Strohmayer et al. 1998); (13) a correlation between
complexity and brightness (Stern et al. 1999) and (14) the unique
properties of the pulses and power law relationships between the
pulse properties and durations of GRBs (McBreen et al. 2002).
,
and the photon fluence
(Liang & Kargatis 1996; Crider et al. 1999); (9) lognormal pulse shapes and
time intervals between pulses in long (McBreen et al. 1994; Hurley et al. 1998)
and short GRBs (McBreen et al. 2001); (10) spectra well fit with a
Band function (Band et al. 1993); (11) spectral hardening before a
count rate increase (Bhat et al. 1994); (12) an X-ray excess in
GRB spectra (Strohmayer et al. 1998); (13) a correlation between
complexity and brightness (Stern et al. 1999) and (14) the unique
properties of the pulses and power law relationships between the
pulse properties and durations of GRBs (McBreen et al. 2002).
While GRBs display hard to soft spectral evolution, there is
remarkable constancy of the pulses in GRBs throughout the burst
(Ramirez-Ruiz & Fenimore 2000; Quilligan et al. 1999). The temporal and spectral properties
of a few GRBs with known redshift have yielded two important
results to suggest that GRB properties may be related to their
luminosities. Ramiriz-Ruiz and Fenimore (1999) have shown that
more rapidly variable bursts have higher absolute luminosities.
Norris et al. (2000) have found an anticorrelation between the time
delay in the arrival times of hard and soft photons in pulses and
the luminosity of the GRB.
The light curves of GRBs are irregular and complex. Statistical
studies are necessary to characterise their properties and hence
to identify the physical properties of the emission mechanism. The
statistical methods used for temporal studies can be broadly
divided into four categories: (1) fits to individual pulses in the
GRB using a number of pulse shape parameters
(Norris et al. 1996; Lee et al. 2000b; Lee et al. 2000a); (2) a non-parametric approach
to pulse shapes in GRBs
(McBreen et al. 1994; Hurley et al. 1998; Young et al. 1995; Quilligan et al. 1999); (3) the average
statistical properties of GRBs using a peak-aligned profile
(Stern & Svensson 1996); and (4) the average power spectral density of
GRBs (Belli 1992; Beloborodov et al. 2000; Chang & Yi 2000). One of the first
studies (McBreen et al. 1994) revealed that lognormal distributions
can adequately describe the properties of GRBs. Subsequent
studies (Li & Fenimore 1996; Hurley et al. 1998; Quilligan et al. 1999) have confirmed the
applicability of lognormal distributions in accounting for the
wide range in the observed properties of pulses in GRBs. This
result is not surprising because lognormal distributions arise
from the product of probabilities of a combination of independent
events and such conditions apply to the pulse generation process
in GRBs.
In a different approach (Beloborodov et al. 2000) used Fourier analysis
to study the power spectral density of long GRBs. This approach
revealed that the diversity of GRBs is due to random realisations
of the same process which is self-similar over a range of time
scales (Stern & Svensson 1996). The slope of the PSD was -5/3 suggesting
that GRBs are related to fully developed turbulence. The two
different approaches are quite similar because the lognormal
approach has been used to describe fully developed turbulence
(Arneodo et al. 1999).
The work presented here expands on the earlier analysis
(Quilligan et al. 2000) and provides new insight into the mechanism
which generates GRBs. The aim is to provide a comprehensive
description and understanding of the pulse properties in GRBs and
combine it with other studies of the spectral properties. The
wavelet analysis and the pulse selection algorithm are described
in Sect. 2. The method for comparing the properties of the pulses
before and after the strongest pulse in the GRB is also described
in Sect. 2. The results are presented in Sect. 3, and discussed
in Sect. 4. The conclusions are presented in Sect. 5.
![\begin{figure}
\par\includegraphics[angle=-90,width=13.5cm,clip]{h3056f1.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg17.gif) |
Figure 1:
Illustration of the background subtraction algorithm. The
shaded region indicates the bursting phase of the GRB. |
| Open with DEXTER |
The dataset used was taken from the BATSE current catalogue. The
"discsc'' files are available at
http://www.batse.msfc.nasa.gov/batse/grb/catalog /4b/
(Paciesas et al. 1999). The files contain the data from the four
energy channels, which were combined into a single channel to
maximise the signal to noise ratio. The shapes of GRB pulses
vary little with energy and pulses in different energy channels
can be added together and nearly retain their initial shape. A
subset of the BATSE catalogue was selected based on the criteria
(Norris et al. 1996) that the GRB duration was greater than two
seconds (T90>2 s) and the peak flux
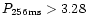 photons cm-2 s-1. In this way a sample of 324 bursts
with good signal to noise and clearly resolved features was
obtained. Five of these bursts could not be analysed properly due
to data gaps, and so our final sample consisted of 319 GRBs. All
319 GRBs were used for the timing analyses. The 250 GRBs that
were summed over only two Large Area Detectors (LADs) were used for all
analyses involving pulse amplitude and area.
photons cm-2 s-1. In this way a sample of 324 bursts
with good signal to noise and clearly resolved features was
obtained. Five of these bursts could not be analysed properly due
to data gaps, and so our final sample consisted of 319 GRBs. All
319 GRBs were used for the timing analyses. The 250 GRBs that
were summed over only two Large Area Detectors (LADs) were used for all
analyses involving pulse amplitude and area.
The first step in the data preparation involved selecting the
appropriate background for subtraction from the GRB. The start and
end times for each burst were identified. A further margin of 10 s was added to both the beginning and end of this chosen
section. Two background sections of duration 30 s were then
selected, one finishing 20 s before the start of the section
containing the burst and the other starting 20 s after the end of
the burst (Fig. 1). These two regions were used to fit a linear
background that was subtracted from the burst section.
One of the difficulties in analysing the time profiles of GRBs is
in overcoming the limitations imposed by the presence of noise in
the signal and the overlap of the individual pulses. The transient
nature of GRBs also means that the usual assumptions for Fourier
transform techniques do not hold (Chang & Yi 2000; Suzuki et al. 2001).
An alternative method of filtering the signal is with wavelets.
Wavelet analysis was pioneered by Daubechies (1992) and others
during the 1980's (Meyer 1993).
Wavelets are specific functions that, when convolved with the signal under
investigation, produce a transformed signal that represents the location and
strength of variations within the original data. The convolution is applied
repeatedly to the data over a range of scales with the convolution function
gradually stretched to coarser and coarser scales, revealing variations at
corresponding scales in the original signal. This iteration with scaling of
the convolved function allows the identification of structure with a variety
of extents both in the spatial and frequency domains.
If the wavelet function is written as 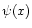 then, more formally,
the transform of f(x) at a particular scale s, can be written as
then, more formally,
the transform of f(x) at a particular scale s, can be written as
where
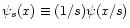 represents the
wavelet dilated by a scale factor s. Let discrete signals be denoted with
the superscript d. At each scale 2j, a
discrete wavelet transform that we denote by Wd2j can be
computed. For the particular choice of scale,
represents the
wavelet dilated by a scale factor s. Let discrete signals be denoted with
the superscript d. At each scale 2j, a
discrete wavelet transform that we denote by Wd2j can be
computed. For the particular choice of scale,
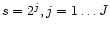 the sequence
the sequence
is called the discrete dyadic wavelet transform of the input
discrete signal
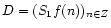 .
The
Wd2j fcomponents provide the detail at each scale, meaning the
response of the (scaled) wavelet function to the detailed
variation of the signal. The coarse signal, Sd2J, provides
the low frequency (slowly varying) component of the signal
remaining at scales larger than 2J. The higher frequency
components can all be recovered from the dyadic wavelet transform
.
The
Wd2j fcomponents provide the detail at each scale, meaning the
response of the (scaled) wavelet function to the detailed
variation of the signal. The coarse signal, Sd2J, provides
the low frequency (slowly varying) component of the signal
remaining at scales larger than 2J. The higher frequency
components can all be recovered from the dyadic wavelet transform
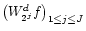 between scales 21and 2J. A fast algorithm for calculating the wavelet transform
of a signal was developed by Mallat & Zhong (1992) and
implementation of this algorithm is at the core of the denoising
procedure used. In Fig. 2, GRB 920513 is shown together with its
dyadic wavelet transform for scales
between scales 21and 2J. A fast algorithm for calculating the wavelet transform
of a signal was developed by Mallat & Zhong (1992) and
implementation of this algorithm is at the core of the denoising
procedure used. In Fig. 2, GRB 920513 is shown together with its
dyadic wavelet transform for scales
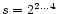 (the lowest
scale, s=21, is not shown because it is dominated by noise).
The transforms at each of the scales are shown (Figs. 2c, d and e), along with the low frequency signal Sd24 containing
the remaining information for scales i>4 (Fig. 2f).
(the lowest
scale, s=21, is not shown because it is dominated by noise).
The transforms at each of the scales are shown (Figs. 2c, d and e), along with the low frequency signal Sd24 containing
the remaining information for scales i>4 (Fig. 2f).
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{h3056f2.eps}\par\vspace*{...
....eps}\par\includegraphics[angle=-90,width=12.5cm,clip]{h3056f4.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg27.gif) |
Figure 2:
The wavelet reconstruction of GRB 920513. a) The GRB profile
and wavelet fit with maxima (identified by the + symbol) and minima
(identified by the x symbol). A total number of 33 pulses were
identified above a threshold of 5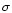 .
b) The residuals between
the wavelet fit and the actual GRB profile. c)-e) The decomposition of GRB 920513
(BATSE trigger 1606) into its component wavelet scales. The wavelet
transform for scales .
b) The residuals between
the wavelet fit and the actual GRB profile. c)-e) The decomposition of GRB 920513
(BATSE trigger 1606) into its component wavelet scales. The wavelet
transform for scales
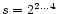 (the finest scale, s=21, is
not shown because it was dominated by noise). f) The low
frequency signal Sd24 containing the remaining information for
scales i>4.
(the finest scale, s=21, is
not shown because it was dominated by noise). f) The low
frequency signal Sd24 containing the remaining information for
scales i>4. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=13.5cm,clip]{h3056f5.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg28.gif) |
Figure 3:
A diagramatic representation of the algorithm for identifying
pulses with appropriate significance. The error bars were calculated
using the count rate in the particular bin, multiplied by the
threshold significance level,
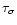 .
The dashed circles
highlight maxima and minima where the error bars overlap. Larger
values of .
The dashed circles
highlight maxima and minima where the error bars overlap. Larger
values of
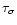 eliminate overlapping regions that were more
widely separated. With a slightly smaller choice of
eliminate overlapping regions that were more
widely separated. With a slightly smaller choice of
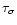 in
this example, pulses 6 and 14 would have been accepted.
in
this example, pulses 6 and 14 would have been accepted. |
| Open with DEXTER |
The function 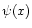 used in the algorithm was chosen so that
the wavelet acts like an edge detector with a delta response
function to a step edge. In fact
Wd2jf is proportional to
the derivative of the original signal smoothed at the scale 2j.
Thus calculating the positions of the modulus maxima of the
transform,
|Wd2J f|, is analogous to locating the sharp
variations in the original signal. Mallat & Zhong (1992) also
developed an algorithm for allowing the reconstruction of a
signal given just the modulus maxima of the wavelet transforms
across a set of scales along with the low frequency signal
remaining at the coarsest scale. This reduced representation can
reconstruct an accurate copy of the original, using an iterative
algorithm that converges quite quickly to acceptable levels.
used in the algorithm was chosen so that
the wavelet acts like an edge detector with a delta response
function to a step edge. In fact
Wd2jf is proportional to
the derivative of the original signal smoothed at the scale 2j.
Thus calculating the positions of the modulus maxima of the
transform,
|Wd2J f|, is analogous to locating the sharp
variations in the original signal. Mallat & Zhong (1992) also
developed an algorithm for allowing the reconstruction of a
signal given just the modulus maxima of the wavelet transforms
across a set of scales along with the low frequency signal
remaining at the coarsest scale. This reduced representation can
reconstruct an accurate copy of the original, using an iterative
algorithm that converges quite quickly to acceptable levels.
A technique for identifying white noise and removing it without
losing any other information was introduced by
Mallat & Hwang (1992). This technique relies on characterising the
behaviour of noise across the various scales in the wavelet
transform using just the information present in the extrema
wavelet representation described in the previous paragraph. The
change in the amplitude of the extrema between scales allows the
number called the Lipschitz exponent to be calculated. More
precisely, each extremum describes a particular curve in
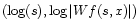 space representing its increase or decay on all
the scales for which Wf(s,x) has been computed. Then the
Lipschitz exponent,
space representing its increase or decay on all
the scales for which Wf(s,x) has been computed. Then the
Lipschitz exponent, 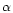 ,
is just the maximum slope of a
straight line that remains above this curve (Young et al. 1995).
Using results from an analysis of white noise
(
,
is just the maximum slope of a
straight line that remains above this curve (Young et al. 1995).
Using results from an analysis of white noise
(
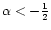 ,
Mallat & Hwang 1992), as well as the
investigation described below, the characteristic distribution of
Lipschitz exponents for the noise present in BATSE GRB profiles
was determined. In general, noise is expected to have a negative
Lipschitz exponent indicating a decreasing amplitude with
increasing scale. Extrema in the wavelet transform which fall in
the range expected for noise can be removed using an algorithm
developed for this purpose.
,
Mallat & Hwang 1992), as well as the
investigation described below, the characteristic distribution of
Lipschitz exponents for the noise present in BATSE GRB profiles
was determined. In general, noise is expected to have a negative
Lipschitz exponent indicating a decreasing amplitude with
increasing scale. Extrema in the wavelet transform which fall in
the range expected for noise can be removed using an algorithm
developed for this purpose.
As an example consider the extremum at around 110 s on the top
(finest) scale of GRB 920513 (Fig. 2c). On the next scale, the
amplitude of this extremum is considerably smaller and by the
following scale it is hardly detectable. It is clear that this
extremum corresponds to a noise feature in the original signal and
visual examination of the transform indicates that the amplitude
of the wavelet transform decays quickly when moving to
progressively coarser scales, as expected for noise. The extremum
at around 95 s corresponds to a pulse with intensity over 25 000
counts per 64 ms. The amplitude of the wavelet maximum increases
on coarser scales, contrary to the behaviour expected for noise.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{3056f4.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg32.gif) |
Figure 4:
The number of pulses selected from the 319 GRBs as a function
of the isolation level
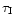 and the threshold
and the threshold
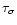 .
The
plot also shows a projection of the data on to the .
The
plot also shows a projection of the data on to the
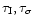 plane and the contour levels are as given in the
legend.
plane and the contour levels are as given in the
legend. |
| Open with DEXTER |
The extrema removal algorithm was combined with a simple
thresholding procedure based on the analysis of a section of the
burst background. For each burst being prepared, a section of the
same burst well separated from the signal was used to generate the
wavelet transform of the background. The standard deviation of the
transform at the scale 22 (the finest scale not dominated by
noise) was combined with a significance level (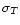 )
to
calculate an amplitude threshold for the wavelet coefficients of
the signal at the same scale. Any extrema in the signal with
amplitudes less than this threshold on scale 22 were assumed to
be due to noise and were removed.
)
to
calculate an amplitude threshold for the wavelet coefficients of
the signal at the same scale. Any extrema in the signal with
amplitudes less than this threshold on scale 22 were assumed to
be due to noise and were removed.
A denoised signal was then reconstructed (e.g. Fig. 2a) using the
algorithm described by Mallat & Zhong (1992). The reconstructed
functions have no spurious oscillations or sharp variations, and
are very similar to the original signal. The residuals between
the background subtracted burst and the reconstructed burst are
shown in Fig. 2b. The residuals were calculated assuming that the
errors in the raw data were Poisson distributed. The variation of
the residuals in the section containing signal do not differ
significantly from a section due to background noise (Fig. 2b).
Each pulse was examined to find minima on each side which were
separated in amplitude from the maximum by more than a chosen
significance level. If the search for minima failed on a pulse it
was rejected and the search for pulses continued. The algorithm
was designed so that the maximum and minima finally selected for a
given pulse were the extreme values in that region of the signal.
The significance level of the maxima and minima was calculated by
multiplying the error on the counts by a scale factor,
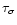 .
Given two data points n1 and n2, where
n1>n2, the points overlap if
.
Given two data points n1 and n2, where
n1>n2, the points overlap if
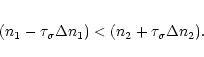
The errors on the counts in the cleaned signal were assumed to be
Poissonian.
The pulse selection process is illustrated in Fig. 3. Starting
with pulse 2, minima 1 and 3 were easily identified. Next, pulse 4
was considered. Pulse 4 overlaps the adjacent minimum 3 (based on
appropriately sized error bars) and both turning points were
rejected and minimum 5 was considered as the true minimum
associated with pulse 2. A minimum, maximum, minimum triplet
consisting of points 1, 2 and 5 was found. At the conclusion of
the analysis the overlapping maxima/minima pairs consisting of
points 6 and 7, 9 and 10 and 13 and 14 were rejected. The
algorithm selected points 2, 8 and 12 as the maxima and identified
associated minima 1, 5, 11 and 15.
The analysis was then extended to allow the identification of
pulses that were well separated from their neighbours such that
the overlap from the surrounding signal did not significantly
affect the profile of the pulse. The fraction of the total height,
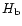 ,
(from pulse to background) which was above the higher
minimum was determined and a threshold was applied to this
fraction, above which pulses were considered isolated. In Fig. 3
the pulses 8 and 12 are not very well separated from their
neighbours whereas pulse 2 is effectively isolated and not
strongly influenced by surrounding signal. The fractional isolated
height of pulse 8 (to which the threshold is applied) was obtained
using (Fig. 3):
,
(from pulse to background) which was above the higher
minimum was determined and a threshold was applied to this
fraction, above which pulses were considered isolated. In Fig. 3
the pulses 8 and 12 are not very well separated from their
neighbours whereas pulse 2 is effectively isolated and not
strongly influenced by surrounding signal. The fractional isolated
height of pulse 8 (to which the threshold is applied) was obtained
using (Fig. 3):
where 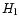 is the height difference between the pulse 8
and the point 5 on the left and
is the height difference between the pulse 8
and the point 5 on the left and 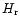 is the height difference
between the pulse 8 and the point 11 on the right.
is the height difference
between the pulse 8 and the point 11 on the right.
For pulse 2 (with point 1 being the higher minimum the smaller
height difference is on the left) the estimate is:
Thus, if the threshold,
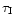 ,
were set above
,
were set above  40% then
pulse 2 would be accepted as isolated and pulse 8 would be
rejected. This method provided an objective way to identify and
quantify pulses that were influenced by neighbouring signals.
40% then
pulse 2 would be accepted as isolated and pulse 8 would be
rejected. This method provided an objective way to identify and
quantify pulses that were influenced by neighbouring signals.
The next task was to characterise the GRB profiles based on the
properties of the constituent pulses. The following
characteristics which had been studied previously
(McBreen et al. 1994; Li & Fenimore 1996; Hurley et al. 1998) were investigated: the
number of pulses per burst, N; the time intervals between
pulses, 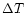 ;
the pulse amplitudes, C; the pulse
area,
;
the pulse amplitudes, C; the pulse
area,
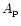 ;
the rise and fall times,
;
the rise and fall times,
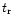 and
and
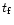 ;
and the pulse durations or full width at half
maximum, FWHM.
;
and the pulse durations or full width at half
maximum, FWHM.
The total number of pulses in the sample of 319 GRBs was
determined for a range of thresholds
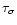 and
varying isolation levels,
and
varying isolation levels,
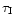 (Fig. 4). The variation
in isolation level has a much larger effect on the sample than the
threshold, and caused a reduction in the number of pulses from
over 3000 at the isolation level of 20% to under 800 at the 80%
level. Figure 4 also shows that the number of pulses falls quite
quickly as
(Fig. 4). The variation
in isolation level has a much larger effect on the sample than the
threshold, and caused a reduction in the number of pulses from
over 3000 at the isolation level of 20% to under 800 at the 80%
level. Figure 4 also shows that the number of pulses falls quite
quickly as
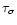 increases from 3 to 5. The
initial rapid reduction in the number of pulses selected may be an
indication of the removal of the small population of noise pulses
remaining after the denoising process. The total number of
pulses is not very sensitive to the threshold level in the region
of 5
increases from 3 to 5. The
initial rapid reduction in the number of pulses selected may be an
indication of the removal of the small population of noise pulses
remaining after the denoising process. The total number of
pulses is not very sensitive to the threshold level in the region
of 5
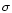 .
The 319 GRBs are listed in Table 1, along with
the total number of pulses above 5
.
The 319 GRBs are listed in Table 1, along with
the total number of pulses above 5
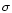 for each burst.
Also included in the table are the number of isolated pulses at
and above the 50% and 75% levels.
for each burst.
Also included in the table are the number of isolated pulses at
and above the 50% and 75% levels.
Table 1:
The BATSE trigger number of the GRBs used in the analysis. N is the total
number of pulses in the GRB, N(50/75) are the numbers of pulses
that are isolated at and above the 50% and 75% levels
respectively.
| GRB |
N |
N(50/75) |
GRB |
N |
N(50/75) |
GRB |
N |
N(50/75) |
GRB |
N |
N(50/75) |
GRB |
N |
N(50/75) |
GRB |
N |
N(50/75) |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 105 |
4 |
3/2 |
1974 |
2 |
0/0 |
2994 |
36 |
20/6 |
3929 |
3 |
2/1 |
6113 |
5 |
3/1 |
7318 |
12 |
5/3 |
| 109 |
19 |
10/2 |
1997 |
13 |
8/2 |
3001 |
3 |
3/2 |
3930 |
19 |
6/1 |
6124 |
30 |
14/5 |
7329 |
3 |
0/0 |
| 130 |
11 |
5/1 |
2037 |
6 |
5/3 |
3035 |
21 |
4/1 |
3936 |
5 |
1/1 |
6168 |
2 |
1/1 |
7343 |
11 |
2/1 |
| 143 |
13 |
6/3 |
2053 |
1 |
1/1 |
3039 |
5 |
3/1 |
3954 |
1 |
1/1 |
6198 |
10 |
1/1 |
7360 |
5 |
4/1 |
| 179 |
4 |
3/2 |
2067 |
8 |
1/1 |
3042 |
19 |
12/6 |
4039 |
33 |
21/7 |
6235 |
6 |
3/1 |
7374 |
1 |
1/1 |
| 219 |
13 |
4/3 |
2080 |
26 |
12/2 |
3057 |
52 |
3/1 |
4048 |
9 |
3/3 |
6242 |
3 |
3/3 |
7429 |
3 |
1/1 |
| 222 |
6 |
0/0 |
2083 |
2 |
2/1 |
3067 |
8 |
4/3 |
4312 |
4 |
2/1 |
6251 |
3 |
3/2 |
7446 |
1 |
1/1 |
| 249 |
21 |
4/1 |
2090 |
15 |
7/2 |
3105 |
30 |
19/9 |
4368 |
12 |
2/2 |
6266 |
9 |
2/1 |
7464 |
3 |
2/1 |
| 394 |
25 |
13/3 |
2110 |
13 |
3/1 |
3110 |
13 |
8/3 |
4556 |
3 |
1/1 |
6274 |
18 |
16/6 |
7475 |
2 |
2/2 |
| 451 |
2 |
2/2 |
2138 |
6 |
2/2 |
3115 |
9 |
6/3 |
4701 |
20 |
8/4 |
6303 |
1 |
1/1 |
7477 |
9 |
3/2 |
| 467 |
3 |
1/1 |
2151 |
3 |
3/3 |
3128 |
36 |
13/1 |
4814 |
2 |
1/1 |
6321 |
3 |
3/3 |
7491 |
40 |
11/1 |
| 469 |
1 |
1/1 |
2156 |
39 |
8/3 |
3138 |
4 |
2/1 |
5080 |
7 |
7/3 |
6329 |
9 |
1/1 |
7503 |
4 |
1/1 |
| 503 |
1 |
1/1 |
2213 |
5 |
5/2 |
3178 |
6 |
3/1 |
5304 |
14 |
0/0 |
6335 |
2 |
2/2 |
7527 |
2 |
2/2 |
| 543 |
3 |
2/1 |
2228 |
28 |
12/5 |
3227 |
17 |
5/3 |
5389 |
13 |
7/3 |
6336 |
3 |
0/0 |
7529 |
1 |
1/1 |
| 647 |
3 |
1/1 |
2232 |
14 |
8/6 |
3241 |
15 |
10/3 |
5417 |
2 |
0/0 |
6397 |
1 |
1/1 |
7530 |
2 |
2/2 |
| 660 |
2 |
2/1 |
2316 |
1 |
1/1 |
3245 |
71 |
24/6 |
5419 |
2 |
1/1 |
6400 |
3 |
3/3 |
7549 |
33 |
6/2 |
| 676 |
4 |
2/1 |
2321 |
11 |
4/1 |
3255 |
12 |
6/3 |
5439 |
4 |
4/3 |
6404 |
13 |
7/2 |
7560 |
12 |
8/6 |
| 678 |
52 |
21/6 |
2329 |
20 |
3/1 |
3269 |
15 |
13/7 |
5447 |
2 |
1/1 |
6413 |
8 |
7/3 |
7575 |
30 |
10/4 |
| 829 |
3 |
0/0 |
2362 |
2 |
2/2 |
3287 |
10 |
6/1 |
5450 |
13 |
5/4 |
6422 |
2 |
0/0 |
7605 |
9 |
9/3 |
| 841 |
6 |
6/3 |
2367 |
3 |
3/2 |
3290 |
6 |
4/3 |
5451 |
2 |
0/0 |
6436 |
3 |
3/3 |
7607 |
8 |
8/3 |
| 869 |
10 |
4/1 |
2371 |
2 |
2/1 |
3306 |
16 |
13/4 |
5470 |
7 |
4/4 |
6451 |
3 |
2/1 |
7678 |
37 |
5/2 |
| 907 |
4 |
3/2 |
2387 |
1 |
1/1 |
3330 |
13 |
5/3 |
5473 |
39 |
27/19 |
6453 |
25 |
5/1 |
7688 |
14 |
9/3 |
| 973 |
3 |
1/1 |
2393 |
2 |
1/1 |
3345 |
4 |
1/1 |
5477 |
12 |
9/5 |
6472 |
47 |
18/5 |
7695 |
27 |
16/5 |
| 999 |
2 |
2/2 |
2431 |
1 |
1/1 |
3351 |
10 |
7/5 |
5486 |
12 |
1/1 |
6525 |
8 |
6/5 |
7711 |
1 |
1/1 |
| 1025 |
4 |
2/1 |
2436 |
11 |
8/2 |
3408 |
44 |
17/5 |
5489 |
16 |
8/4 |
6528 |
8 |
3/1 |
7766 |
22 |
15/6 |
| 1085 |
2 |
0/0 |
2446 |
4 |
3/2 |
3415 |
14 |
8/4 |
5512 |
5 |
1/1 |
6560 |
20 |
16/9 |
7770 |
3 |
2/1 |
| 1122 |
10 |
3/1 |
2450 |
22 |
7/4 |
3436 |
5 |
4/1 |
5523 |
2 |
2/2 |
6576 |
18 |
11/5 |
7775 |
1 |
1/1 |
| 1141 |
9 |
0/0 |
2533 |
49 |
9/1 |
3458 |
8 |
2/2 |
5526 |
34 |
34/14 |
6587 |
28 |
9/4 |
7781 |
4 |
2/2 |
| 1157 |
10 |
8/2 |
2537 |
5 |
2/1 |
3480 |
1 |
1/1 |
5530 |
7 |
5/1 |
6593 |
20 |
13/2 |
7788 |
21 |
14/6 |
| 1159 |
1 |
1/1 |
2586 |
11 |
7/7 |
3481 |
11 |
1/1 |
5548 |
9 |
8/4 |
6621 |
2 |
2/2 |
7845 |
17 |
15/11 |
| 1190 |
4 |
2/2 |
2611 |
3 |
2/2 |
3488 |
6 |
6/5 |
5563 |
1 |
1/1 |
6629 |
6 |
4/3 |
7858 |
5 |
0/0 |
| 1204 |
3 |
3/3 |
2628 |
7 |
5/2 |
3489 |
12 |
2/2 |
5567 |
5 |
1/1 |
6630 |
2 |
1/1 |
7884 |
21 |
15/6 |
| 1385 |
23 |
4/1 |
2700 |
4 |
3/1 |
3491 |
3 |
1/1 |
5568 |
3 |
0/0 |
6665 |
8 |
2/1 |
7906 |
13 |
7/5 |
| 1419 |
3 |
1/1 |
2736 |
1 |
1/1 |
3512 |
1 |
1/1 |
5572 |
3 |
3/3 |
6672 |
4 |
3/1 |
7929 |
6 |
4/1 |
| 1425 |
7 |
5/1 |
2790 |
20 |
10/1 |
3516 |
10 |
7/2 |
5575 |
6 |
2/1 |
6683 |
10 |
10/3 |
7954 |
16 |
14/13 |
| 1440 |
15 |
9/2 |
2793 |
7 |
4/3 |
3523 |
16 |
0/0 |
5591 |
10 |
7/4 |
6694 |
10 |
6/1 |
7969 |
2 |
1/1 |
| 1443 |
2 |
2/2 |
2797 |
3 |
1/1 |
3569 |
4 |
2/2 |
5593 |
1 |
1/1 |
6764 |
8 |
3/1 |
7987 |
6 |
2/1 |
| 1468 |
19 |
17/6 |
2798 |
11 |
1/1 |
3593 |
13 |
6/1 |
5601 |
1 |
1/1 |
6814 |
1 |
1/1 |
7994 |
13 |
1/1 |
| 1533 |
32 |
20/12 |
2799 |
8 |
6/6 |
3598 |
3 |
3/2 |
5614 |
2 |
2/2 |
6816 |
8 |
7/3 |
7998 |
4 |
3/2 |
| 1541 |
33 |
11/1 |
2812 |
15 |
12/9 |
3634 |
7 |
7/3 |
5621 |
6 |
3/1 |
6824 |
2 |
2/2 |
8008 |
6 |
3/3 |
| 1578 |
3 |
0/0 |
2831 |
58 |
12/2 |
3648 |
3 |
3/1 |
5628 |
9 |
4/1 |
6904 |
1 |
1/1 |
8019 |
2 |
2/1 |
| 1606 |
33 |
15/4 |
2852 |
23 |
5/1 |
3649 |
2 |
2/2 |
5644 |
4 |
1/1 |
6930 |
2 |
2/2 |
8022 |
5 |
5/4 |
| 1609 |
8 |
2/1 |
2855 |
13 |
2/1 |
3658 |
4 |
2/1 |
5654 |
5 |
3/2 |
6963 |
17 |
10/2 |
8030 |
7 |
6/3 |
| 1625 |
15 |
2/1 |
2856 |
86 |
19/3 |
3663 |
9 |
7/3 |
5704 |
9 |
8/4 |
7028 |
5 |
3/2 |
8050 |
1 |
1/1 |
| 1652 |
6 |
1/1 |
2889 |
26 |
12/4 |
3765 |
4 |
2/2 |
5711 |
2 |
2/1 |
7113 |
52 |
8/1 |
8063 |
4 |
4/3 |
| 1663 |
16 |
0/0 |
2891 |
18 |
15/4 |
3776 |
7 |
1/1 |
5725 |
13 |
12/6 |
7170 |
16 |
6/2 |
8087 |
8 |
7/3 |
| 1664 |
5 |
1/1 |
2894 |
5 |
1/1 |
3788 |
4 |
3/1 |
5726 |
3 |
3/1 |
7172 |
1 |
1/1 |
8098 |
4 |
2/2 |
| 1676 |
35 |
21/7 |
2913 |
5 |
2/2 |
3860 |
13 |
9/3 |
5773 |
4 |
1/1 |
7185 |
19 |
16/7 |
8099 |
1 |
1/1 |
| 1683 |
6 |
3/1 |
2919 |
3 |
3/2 |
3866 |
1 |
1/1 |
5867 |
7 |
6/3 |
7240 |
4 |
4/4 |
8111 |
2 |
2/1 |
| 1709 |
2 |
0/0 |
2929 |
44 |
16/5 |
3870 |
1 |
1/1 |
5955 |
4 |
2/2 |
7247 |
2 |
1/1 |
|
|
|
| 1711 |
8 |
2/1 |
2953 |
6 |
2/2 |
3891 |
3 |
2/1 |
5989 |
8 |
7/5 |
7255 |
5 |
1/1 |
|
|
|
| 1815 |
10 |
5/2 |
2958 |
2 |
2/2 |
3893 |
3 |
1/1 |
5995 |
7 |
1/1 |
7290 |
1 |
1/1 |
|
|
|
| 1883 |
1 |
1/1 |
2984 |
22 |
16/6 |
3905 |
4 |
4/1 |
6090 |
3 |
1/1 |
7301 |
51 |
13/7 |
|
|
|
| 1886 |
5 |
0/0 |
2988 |
2 |
2/2 |
3912 |
1 |
1/1 |
6100 |
3 |
0/0 |
7305 |
3 |
3/3 |
|
|
|
![\begin{figure}
\par\includegraphics[angle=90,width=12.5cm,clip]{h3056f7.eps} %
\end{figure}](/articles/aa/full/2002/14/aah3056/Timg48.gif) |
Figure 5:
The distribution of the number of pulses (N) per GRB.
The shaded regions highlight the division into four
categories, namely M, N, O and P with
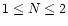 , ,
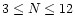 , ,
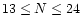 and
and 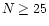 respectively.
respectively. |
| Open with DEXTER |
In the analysis of pulse shapes, non-parametric methods were used
to estimate the various characteristics of the pulse profiles.
This approach was chosen to make the conclusions more robust since
no assumptions were made about the pulse shapes. Also since the
measurements are made on the isolated pulses selected by the
algorithm, the degree of isolation can be varied arbitrarily. If a
particular measurement was sensitive to influence from surrounding
pulses then the threshold
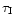 was increased until the
influence was reduced sufficiently, with the proviso that the
number of pulses in the sample remains statistically useful.
was increased until the
influence was reduced sufficiently, with the proviso that the
number of pulses in the sample remains statistically useful.
The classification of pulses into isolated and non-isolated
categories based on the algorithm allowed the measurement of
characteristics of the temporal profile which are affected by
neighbouring signals. The level of interference between pulses and
the surrounding signal is dependent on the threshold at which the
selection of these pulses is made. In fact a broad range of
threshold levels were used to examine the time profiles and
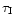 was typically varied from 20% to 80%. It was decided
based on these results to adopt pulses with
was typically varied from 20% to 80%. It was decided
based on these results to adopt pulses with
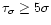 and
and
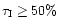 for
the main analysis of the pulse properties.
for
the main analysis of the pulse properties.
The pulse amplitude was measured as the maximum count in a 64 ms
time interval after background subtraction. The pulse area was
measured using the sum of the background subtracted count rates
starting at 5% of the height of the pulse above the left minimum
to 5% of the pulse height above the right minimum on the falling
edge of the profile. The starting point at 5% above the minimum
was chosen to eliminate contributions from background noise for
pulses with minima widely separated from the maximum.
For similar reasons the rise time was measured from 5% of the
height of the pulse above the left minimum to 95% of that height.
The upper value of 95% ensures that the finishing point is robust
against flat topped pulses and noise in the profile near the
maximum. The fall time was measured in a similar way to the rise
times i.e. from 95% to 5% of the pulse height above the right
minimum.
The duration of the individual pulses was measured using the FWHM
of the pulse. This approximation is valid only for well isolated
pulses and tended to give poorer estimates for the true pulse
width as the effect of neighbouring signals increased and the left
and right minima of the pulse rose out of the background.
The frequency distribution of the number of pulses (N) per GRB is
given in Fig. 5. N has a range from 1 to 86 with a peak at a
value of 3, a median of 6 and only 10% of GRBs have 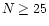 .
For convenience N is divided into four categories (Fig. 5). There
are 34 GRBs in category P and only 7 have N > 50. Many of the
timing studies on GRBs have concentrated on the categories with
large N (e.g. Norris et al. 1996; Li & Fenimore
1996), which means that these
analyses have focussed solely on the tail of the distribution
shown in Fig. 5.
.
For convenience N is divided into four categories (Fig. 5). There
are 34 GRBs in category P and only 7 have N > 50. Many of the
timing studies on GRBs have concentrated on the categories with
large N (e.g. Norris et al. 1996; Li & Fenimore
1996), which means that these
analyses have focussed solely on the tail of the distribution
shown in Fig. 5.
It has been shown previously that the lognormal distribution can
adequately describe the properties of GRBs (Quilligan et al. 1999). The
lognormal distribution is generated by statistical processes
whose results depend on a product of probabilities arising from a
combination of events (Aitchison & Brown 1957). A positive random
variable X is said to be lognormally distributed if 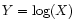 is
normally distributed with mean
is
normally distributed with mean 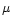 and variance
and variance 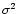 .
The
probability density function is:
.
The
probability density function is:
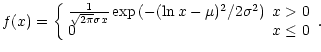 |
|
|
(1) |
The median of the distribution occurs at
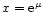 .
Many examples
of lognormal distributions occur in nature, such as the
propagation of a laser beam in a turbulent medium, the size of
cumulus clouds in the atmosphere and terrestrial lightning
(Uman 1987; McBreen et al. 1994). In the case of terrestrial lightning,
the durations, peak currents, intervals between the strokes in the
flashes, and the flash charges are all lognormally distributed.
The statistical properties of strokes in lightning discharges in
the Earths atmosphere have a close resemblance to the statistical
properties of pulses in GRBs. In both cases the result depends on
a multiplicative process arising from a combination of independent
events.
.
Many examples
of lognormal distributions occur in nature, such as the
propagation of a laser beam in a turbulent medium, the size of
cumulus clouds in the atmosphere and terrestrial lightning
(Uman 1987; McBreen et al. 1994). In the case of terrestrial lightning,
the durations, peak currents, intervals between the strokes in the
flashes, and the flash charges are all lognormally distributed.
The statistical properties of strokes in lightning discharges in
the Earths atmosphere have a close resemblance to the statistical
properties of pulses in GRBs. In both cases the result depends on
a multiplicative process arising from a combination of independent
events.
The distribution of the FWHM of the pulses from 319 GRBs and the
best lognormal fit are given in Fig. 6a. Figure 6b shows the same
data plotted as a cumulative percent on logarithmic probability
paper such that a lognormal distribution yields a straight line.
All pulses have
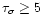 and
and
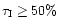 .
The distribution is very broad with a maximum at 0.7 s and half widths at 0.14 s and 3.5 s. The value of the reduced
.
The distribution is very broad with a maximum at 0.7 s and half widths at 0.14 s and 3.5 s. The value of the reduced
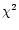 is 0.3 showing the data is well fit by the lognormal
distribution. In obtaining
is 0.3 showing the data is well fit by the lognormal
distribution. In obtaining 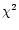 ,
the part of the fit below
0.1 s was not included because of the distortion caused by the
limited time resolution that is apparent in Fig. 6b. The value
of the reduced
,
the part of the fit below
0.1 s was not included because of the distortion caused by the
limited time resolution that is apparent in Fig. 6b. The value
of the reduced 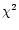 for the best lognormal fit as a
function of
for the best lognormal fit as a
function of
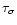 and
and
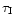 are given
in Figs. 6c an 6d. The fits are acceptable over most of the
range with the largest departures occurring at the lowest values
of
are given
in Figs. 6c an 6d. The fits are acceptable over most of the
range with the largest departures occurring at the lowest values
of
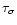 and
and
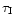 because of the
serious effects of pulse pile up. The lognormal distribution is
a better fit when the effects of the overlapping pulses are
reduced. The parameters of the best lognormal fit for
because of the
serious effects of pulse pile up. The lognormal distribution is
a better fit when the effects of the overlapping pulses are
reduced. The parameters of the best lognormal fit for
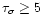 and
and
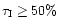 are given in
Table 2.
are given in
Table 2.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{h3056f8.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg55.gif) |
Figure 6:
a) The distribution of the FWHM of pulses with
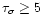 and
and
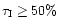 and the best lognormal fit to the data.
b) The same data plotted as a cumulative percent such that a
lognormal distribution yields a straight line. The large
count in the first bin is due to the 64 ms time resolution.
c)-d) The values of reduced
and the best lognormal fit to the data.
b) The same data plotted as a cumulative percent such that a
lognormal distribution yields a straight line. The large
count in the first bin is due to the 64 ms time resolution.
c)-d) The values of reduced 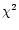 for the best lognormal fit as a
function of
for the best lognormal fit as a
function of
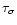 and
and
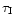 . . |
| Open with DEXTER |
The distribution of the rise times of the pulses and the best
lognormal fit are given in Fig. 7a. Figure 7b shows the same data
plotted as a cumulative percent and the large count in the first
bin is due to the 64 ms resolution of BATSE. The parameters of
the best lognormal fit to the broad distribution are listed in
Table 2. The value of the reduced
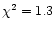 show the data
is compatible with the lognormal distribution.
show the data
is compatible with the lognormal distribution.
![\begin{figure}
\par\psfrag{xlab}[b]{\small$t_{\rm r}$\space (sec)}
\psfrag{ylab}...
...{\small Frequency}
\includegraphics[width=11.2cm,clip]{h3056f10.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg60.gif) |
Figure 7:
a) The distribution of the pulse rise times with
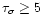 and
and
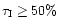 and the best lognormal fit to the data. b) The same
data plotted as a cumulative percent. The large count
in the first bin is due to the 64 ms time resolution.
and the best lognormal fit to the data. b) The same
data plotted as a cumulative percent. The large count
in the first bin is due to the 64 ms time resolution. |
| Open with DEXTER |
![\begin{figure}
\par\psfrag{xlab}[b]{\small$t_{\rm f}$\space (sec)}
\psfrag{ylab}[b]{\small Frequency}
\includegraphics[width=8.8cm,clip]{h3056f11.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg61.gif) |
Figure 8:
The distribution of the fall times of the pulses with
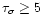 and
and
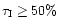 and the best lognormal fit to the data.
and the best lognormal fit to the data. |
| Open with DEXTER |
![\begin{figure}
\par\psfrag{xlab}[b]{\small Pulse Amplitudes (counts)}
\psfrag{y...
...{\small Frequency}
\includegraphics[width=8.8cm,clip]{h3056f12.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg62.gif) |
Figure 9:
The distribution of the pulse amplitudes with
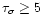 and
and
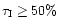 and the best lognormal fit to the data.
and the best lognormal fit to the data. |
| Open with DEXTER |
The distribution of the fall times of the pulses and the best
lognormal fit are given in Fig. 8. The parameters of the best
lognormal fit to the data are given in Table 2. The fall times
are also compatible with the lognormal distribution and have a
wider range with a slightly larger mean than the rise times.
The distributions of the amplitudes and areas of the pulses with
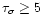 and
and
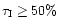 from
250 GRBs, summed over two detectors, and the best lognormal fits
are given in Figs. 9 and 10. The distributions are very broad
and the values of the best lognormal fits to the data are listed
in Table 2. The lognormal distribution is compatible with the
pulse areas and the amplitudes.
from
250 GRBs, summed over two detectors, and the best lognormal fits
are given in Figs. 9 and 10. The distributions are very broad
and the values of the best lognormal fits to the data are listed
in Table 2. The lognormal distribution is compatible with the
pulse areas and the amplitudes.
3.2.4 Time intervals between pulses
The distribution of the time intervals
between the pulses is given in Fig. 11. The peak in the
distribution occurred at about 1.0 s and was truncated at short
time intervals by the 64 ms resolution of the data (Fig. 11a). A
minimum time interval of 128 ms is required because two maxima
must be separated by at least one time bin. There could be a
large additional excess of pulses with separations below the 128 ms resolution of the data that were not resolved. Other studies
using different statistical methods from those employed here
(Panaitescu et al. 1999; Lee et al. 2000a,b; Spada et al. 2000) have also noted a
deficit of time intervals below one second. A parent lognormal
distribution of time intervals with parameters similar to the
observed distribution was simulated and the time intervals
between the pulses recorded with an accuracy of 64 ms. The
resulting distribution is given in Fig. 11a and the values of
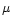 and
and 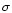 for the parent distribution are given in
Table 2. The measured distribution of time intervals in GRBs is
consistent with the parent lognormal distribution provided a small
(5%) excess of time intervals longer than 15 s is not
included. This excess is clearly visible in Fig. 11a. The time
intervals greater than 15 s are plotted in Fig. 11b. The data is
well fit by a power law of slope -1.2.
for the parent distribution are given in
Table 2. The measured distribution of time intervals in GRBs is
consistent with the parent lognormal distribution provided a small
(5%) excess of time intervals longer than 15 s is not
included. This excess is clearly visible in Fig. 11a. The time
intervals greater than 15 s are plotted in Fig. 11b. The data is
well fit by a power law of slope -1.2.
![\begin{figure}
\par\psfrag{xlab}[b]{\small Pulse Areas (counts)}
\psfrag{ylab}[b]{\small Frequency}
\includegraphics[width=8.8cm,clip]{h3056f13.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg63.gif) |
Figure 10:
The distribution of the pulse areas with
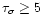 and
and
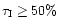 and the best lognormal fit to the data.
and the best lognormal fit to the data. |
| Open with DEXTER |
3.2.5 Peak energies
The values of the peak energy,
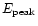 ,
of a large sample of GRBs are given by Preece et al. (2000).
There is an overlap of 77 GRBs with our sample, and the
distribution of the values of
,
of a large sample of GRBs are given by Preece et al. (2000).
There is an overlap of 77 GRBs with our sample, and the
distribution of the values of
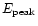 for each section of
these bursts are given in Fig. 12. The distribution was well fit
by a lognormal distribution with a small tail noticeable at low
values of
for each section of
these bursts are given in Fig. 12. The distribution was well fit
by a lognormal distribution with a small tail noticeable at low
values of
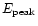 .
The values of
.
The values of 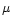 and
and 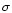 are
given in Table 2. The distribution of
are
given in Table 2. The distribution of
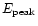 is
noticeably narrower than that of the pulse parameters and spans a
range of about 4 in width.
is
noticeably narrower than that of the pulse parameters and spans a
range of about 4 in width.
![\begin{figure}
\par\includegraphics[angle=-90,width=13.4cm,clip]{h3056f14.eps}\v...
...centage}
\includegraphics[angle=-90,width=13.4cm,clip]{h3056f15.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg64.gif) |
Figure 11:
a) The measured distribution of time intervals between all the
pulses and the best fit lognormal (dashed line) with allowance for the BATSE resolution of 64 ms.
The excess of time intervals >15 s is called the Pareto Lévy tail. b) The Pareto tail of the time
intervals is well fit by a power law (dashed line) of slope 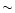 -1.2. -1.2. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=13.5cm,clip]{h3056f16.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg65.gif) |
Figure 12:
The distribution of the peak energies and the best lognormal fit to the data (dashed line). |
| Open with DEXTER |
The major result of this part of the analysis is that the
distributions of the rise times, fall times, FWHM, pulse
amplitudes, pulse areas and the time intervals between the pulses
are all very similar. The frequency distributions are very broad
and cover about three orders of magnitude and all are compatible
with the lognormal distribution. Li & Fenimore (1996) also showed
that the pulse fluences and the time intervals between pulses are
lognormally distributed for individual bursts in a small sample
of bursts with more than 20 pulses. They also scaled the bursts
to the same 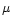 and
and 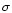 and showed that the summation of
all the peak fluences and time intervals looked lognormal,
although no significance level was given for the result. No
normalisation of pulse properties was applied to the GRBs in this
analysis, because only the brightest 319 bursts which had the
best signal to noise ratio were analysed. From the data available
for those bursts with known redshifts (Atteia et al. 1999), there
does not appear to be any dependable standard by which to scale
the bursts because of the broad range of intrinsic luminosities
and their comparatively small range of distances. Therefore, to
avoid introducing further biases, and to use all of the pulse
information available, the data were analysed without scaling.
However, as a test of this process, the data were also scaled and
the same analysis performed on the scaled data, and no
significant differences were found between the two data sets.
and showed that the summation of
all the peak fluences and time intervals looked lognormal,
although no significance level was given for the result. No
normalisation of pulse properties was applied to the GRBs in this
analysis, because only the brightest 319 bursts which had the
best signal to noise ratio were analysed. From the data available
for those bursts with known redshifts (Atteia et al. 1999), there
does not appear to be any dependable standard by which to scale
the bursts because of the broad range of intrinsic luminosities
and their comparatively small range of distances. Therefore, to
avoid introducing further biases, and to use all of the pulse
information available, the data were analysed without scaling.
However, as a test of this process, the data were also scaled and
the same analysis performed on the scaled data, and no
significant differences were found between the two data sets.
It is important to determine how N relates to the other parameters
of the GRB. In Fig. 13 N is plotted versus burst duration
(T90), total fluence and the median value of
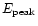 .
Spearman rank order correlation coefficients
.
Spearman rank order correlation coefficients 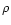 and
associated probabilities were obtained for the quantities in
Fig. 13. The values are listed in Table 3 which also includes an
additional range of burst parameters. The parameter
and
associated probabilities were obtained for the quantities in
Fig. 13. The values are listed in Table 3 which also includes an
additional range of burst parameters. The parameter
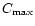 is the maximum value of the peak amplitude in that burst. The high
values of
is the maximum value of the peak amplitude in that burst. The high
values of 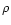 show a strong correlation between N and the total
fluence, T90 and
show a strong correlation between N and the total
fluence, T90 and
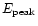 .
.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{3056f13.eps}\par\end{figure}](/articles/aa/full/2002/14/aah3056/Timg67.gif) |
Figure 13:
The number of pulses in a GRB
as a function of a) T90 b) total fluence and c) the
median value of the peak energy of the GRB. Quantisation occurs
in the figures for low values of N. |
| Open with DEXTER |
The values of 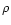 are not always uniformly distributed within
each burst category. T90 versus fluence is much better
correlated for category N than either O or P. N versus
are not always uniformly distributed within
each burst category. T90 versus fluence is much better
correlated for category N than either O or P. N versus
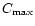 and N versus HR are better correlated for category P than
either N or O.
and N versus HR are better correlated for category P than
either N or O.
The Spearman rank order correlation coefficients and probabilities
were evaluated for isolated pulses with the range of pulse
parameters given in Table 4. The pulse parameters are strongly
correlated with each other. The pulse amplitude is negatively
correlated with the pulse rise and fall times and FWHM. In
general the correlations are stronger for categories M and N than
either O or P. The only significant exception to this trend is
the pulse amplitude versus area which also has the highest values
of 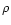 for categories O and P.
for categories O and P.
Spearman rank order correlation coefficients and probabilities
were evaluated for the time intervals between pulses (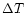 )
with
)
with
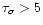 .
The results are presented in Table 5 for two cases (1) the time intervals were not normalised and (2)
the time intervals were normalised to T90. There is a good
correlation between the time intervals in both cases that
declines slowly with increase in the number of time intervals.
The largest values of
.
The results are presented in Table 5 for two cases (1) the time intervals were not normalised and (2)
the time intervals were normalised to T90. There is a good
correlation between the time intervals in both cases that
declines slowly with increase in the number of time intervals.
The largest values of 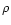 occured in category N.
occured in category N.
The Spearman correlation coefficients were also evaluated between
pulse amplitudes and the results are given in Table 6 for two
cases (1) the amplitudes were not normalised and (2) normalised
to the largest amplitude pulse in the burst. The normalised
pulse amplitudes are less strongly correlated over many pulses
than the time intervals. These results were obtained for all
pulses with
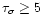 and without satisfying any
selection based on pulse isolation. The role of pulse pile-up has
yet to be investigated.
and without satisfying any
selection based on pulse isolation. The role of pulse pile-up has
yet to be investigated.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{h3056f20.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg94.gif) |
Figure 14:
The median values of a) rise time, b) fall time,
c) FWHM and d) the time intervals between pulses versus the
number of pulses. |
| Open with DEXTER |
It was noticed early in this analysis that pulse properties
depended strongly on N (Quilligan et al. 2000). The median value
of the isolated pulse timing parameters were determined for all
GRBs with the same value of N. The median values of the rise
time, fall time, FWHM and time interval between pulses are plotted
versus N in Fig. 14 (a-d). The largest value usually occurred for
N = 1 or 2 and subsequently declined significantly as Nincreased. There are some values that are well removed from the
general trend but they usually have a small number of pulses. The
median values of the area and amplitude for isolated pulses are
given in Figs. 15a,b. The trend is quite different from Fig. 14. The amplitude is reasonably constant up to 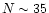 with a clear increase for higher values of N. There is a similar
but weaker trend for the pulse area which has the largest value
at N = 1.
with a clear increase for higher values of N. There is a similar
but weaker trend for the pulse area which has the largest value
at N = 1.
The properties of the four categories of GRBs are summarised in
Table 7. The median values of the pulse timing parameters all
decrease by at least a factor of four from category M to P. In
contrast the median values of T90, total fluence, hardness
ratio and maximum pulse amplitude all increase significantly. The
median variability, is defined as the number of pulses 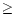 5
5 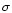 divided by the time the emission is
divided by the time the emission is 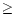 5
5 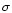 ,
also increases from category M to P.
,
also increases from category M to P.
To study the evolution of the time profile as the GRB
progresses, each GRB was divided into two, to include the pulses
that occur before and after the strongest pulse in the burst.
Only GRBs with more than two pulses are included, resulting in a
reduced total sample of 252. The first half (pre-main pulse) of
the GRB was compared with the second half (post-main pulse). The
bursts are also sub-divided into three categories. A summary of
the properties of the GRBs used is given in Table 8.
The first half/second half analysis was performed on the three
timing parameters of the pulses, time intervals between the
pulses, amplitude, area and the pulse asymmetry ratio which is
defined as the ratio of the pulse rise time to the pulse fall
time. The median values of the distributions in the three
categories in the first half and second half analysis are given in
Table 8 along with the results of the Kolmogorov-Smirnov (KS)
tests. The KS probability is a measure of whether the two
distributions (first/second half) are drawn from the same parent
distribution.
The first result is that the median values of the timing
parameters of the pulses and the time intervals between the pulses
all decrease by an average of 1.8, from the category N to P
including the first half and second half of the GRBs. In the case
of the rise times, the median values of the distributions decrease
from 1.02 to 0.51 in the first half and 0.70 to 0.45 in the second
half. The trend in the median value of the pulse amplitude is in
the opposite direction with larger pulses in category P than
either O or N.
In the first/second half analysis there is a trend in the three
categories for the median rise time to be slower in the first half
of the burst (1.02 versus 0.70 for category N). The difference
could be caused by an additional clearing out effect at the start
of the GRB. There is also a clear indication at the 0.02% level
that the pulse fall time is faster in the first half than the
second for category N (1.09 versus 1.89 for category N) and this
effect weakens for categories O and P. The median values of the
pulse asymmetry ratio also show the most significant differences
for category N where the median values are 1.0 and 0.4 for the
first and second halves. The KS test gives good agreement
between the first half and second half for the FWHM, time
intervals between pulses, the pulse amplitudes and areas. The
median values of the pulse amplitude and areas are however larger
in the first half than the second half for the three categories
of GRBs.
A complete study of the BATSE time profiles of the brightest 319
GRBs has been presented. The statistical analysis of the data
reveal the ubiquitous nature of the lognormal distribution in GRB
time profiles (Figs. 6-10). The means and variances of the best
fit lognormal functions are given in Table 2. The results
presented in Figs. 6-10 are for the isolated pulses from the four
GRB categories. The data in Table 7 and the first half/second
analysis show that the median values of the pulse properties vary
with N. Lognormal distributions also apply to the spectral
properties of GRBs. The BATSE spectroscopic detectors revealed
that the break energies in GRB spectra are compatible with a
lognormal distribution (Preece et al. 2000). The FWHM of the
distributions that describe the pulses are in the range 14-45
(Table 2) whereas the value for
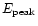 is only
is only 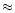 4
and extends from 137 keV to 535 keV. The unexpected narrowness of
the
4
and extends from 137 keV to 535 keV. The unexpected narrowness of
the
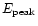 distribution is a major problem in GRBs
(Brainerd 2000). Furthermore, spectral fitting of 41 pulses in
26 GRBs showed that the spectral hardness parameter
distribution is a major problem in GRBs
(Brainerd 2000). Furthermore, spectral fitting of 41 pulses in
26 GRBs showed that the spectral hardness parameter
 decays linearly with energy fluence and that the distribution of
the decay constants is roughly lognormal (Crider et al. 1999).
decays linearly with energy fluence and that the distribution of
the decay constants is roughly lognormal (Crider et al. 1999).
![\begin{figure}
\par\includegraphics[angle=-90,width=12cm,clip]{h3056f21.eps} %
\...
...pace*{2mm}
\includegraphics[angle=-90,width=12cm,clip]{h3056f22.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg104.gif) |
Figure 15:
The median values of a) pulse area and b) pulse
amplitudes versus the number of pulses. |
| Open with DEXTER |
The Spearman rank order correlation coefficients were obtained
for a range of burst parameters (Table 3). There is good
agreement with the results of Lee et al. (2000aa) who used a
different method. N is strongly correlated with total fluence,
T90, HR and
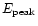 (Fig. 13). N is an important
quantity in determining GRB properties and provides the link
between total fluence and duration since both increase with N.
The correlation coefficients between the parameters that describe
the pulses are given in Table 4. The rise and fall times, FWHM
and area of the pulses are highly correlated. There is a high
probability that a pulse with a fast rise time will also have a
fast fall time and a short FWHM. The pulse amplitude is
negatively correlated with the rise and fall times and FWHM. The
anticorrelation between the pulse amplitude and pulse width has
been observed in other studies (Lee et al. 2000a; Fenimore & Ramirez-Ruiz 2001). The
pulse width is also a function of energy and varies as
E-0.45 (Fenimore et al. 1995) and this effect has been
attributed to synchrotron radiation (Piran 1999). The FWHM
is strongly correlated with the preceding and subsequent time
interval between pulses (Table 4). This result is in agreement
with Nakar & Piran (2001) and the prediction of the internal
shock model. A further comparison of the pulse timing
parameters, the energy dependence and the spectral lag may reveal
further interesting constraints on the emission process
(Norris et al. 2001; Daigne & Mochkovitch 2001). The unique properties of the
pulses in GRBs have been summarised by McBreen et al. (2002).
(Fig. 13). N is an important
quantity in determining GRB properties and provides the link
between total fluence and duration since both increase with N.
The correlation coefficients between the parameters that describe
the pulses are given in Table 4. The rise and fall times, FWHM
and area of the pulses are highly correlated. There is a high
probability that a pulse with a fast rise time will also have a
fast fall time and a short FWHM. The pulse amplitude is
negatively correlated with the rise and fall times and FWHM. The
anticorrelation between the pulse amplitude and pulse width has
been observed in other studies (Lee et al. 2000a; Fenimore & Ramirez-Ruiz 2001). The
pulse width is also a function of energy and varies as
E-0.45 (Fenimore et al. 1995) and this effect has been
attributed to synchrotron radiation (Piran 1999). The FWHM
is strongly correlated with the preceding and subsequent time
interval between pulses (Table 4). This result is in agreement
with Nakar & Piran (2001) and the prediction of the internal
shock model. A further comparison of the pulse timing
parameters, the energy dependence and the spectral lag may reveal
further interesting constraints on the emission process
(Norris et al. 2001; Daigne & Mochkovitch 2001). The unique properties of the
pulses in GRBs have been summarised by McBreen et al. (2002).
The lognormal distribution arises from a statistical process whose
result depends on a product of probabilities arising from a
combination of independent events. It therefore identifies the
statistical process but not the combination of events that lead to
the formation of the pulse shape and the peak energy. In the
internal shock model the main factors contributing to the pulse
shape include (Rees & Mészáros 1994; Piran 1999).
- 1.
- The Lorentz factors, masses and thickness of the
interacting shells.
- 2.
- The distance from the central engine and curvature where
the collisions occur.
- 3.
- The energy conversion in the shock, the nature of the
magnetic field and particle acceleration process.
- 4.
- The synchrotron radiation mechanism possibly modified by
self-absorption and pair production.
- 5.
- The time scale for energy loss by the particles.
The resulting properties of the pulses in GRBs depend on a
combination of many events and hence it is not surprising that the
lognormal distribution gives an elegant description of all their
properties. Random multiplicative processes abound in a variety
of natural phenomena and a good example is the statistical
description of the strokes in flashes of lightning. Almost all
the properties of the strokes in the flashes and the flashes
themselves are well described by lognormal distributions
(Uman 1987; McBreen et al. 1994).
It is often found that distributions that seem to be lognormal
over a wide range change to an inverse power law distribution for
the last few percent. An amplification model has been used to
characterise the transition from a lognormal distribution to a
power law that is often called a Pareto-Lévy tail
(Montroll & Shlesinger 1982). The distribution of time intervals conform
to the lognormal distribution over most of the range with the
exception of about 5% of the time intervals longer than about
15 s (Fig. 11). The Pareto-Lévy tail of time intervals have
an amplification process that is not available to most time
intervals.
The origin of the nonrandom distribution of time intervals between
pulses is an important clue to the GRB process. In the internal
shock model there is almost a one to one correspondence between
the emission of shells and pulses resulting from the collisions of
shells (Kobayashi et al. 1997). Hence the time intervals between pulses
is an almost direct measure of the activity of the central engine.
The temporal behaviour of soft gamma-ray repeaters and young
pulsars provide additional context in which to view the results of
GRB time profiles. The time intervals between about 30
microglitches in the Vela Pulsar are consistent with a lognormal
distribution with a mean of 50 days
(Hurley et al. 1994; Hurley et al. 1995; Cordes et al. 1988). The amount of energy
involved in the microglitches is about 1038 ergs. The
macroglitches in the Vela Pulsar are about a thousand times more
powerful but occur too infrequently to determine the distribution
of time intervals but they have a wide range and do not seem
inconsistent with the lognormal distribution. More energetic
outbursts have been recorded from SGR sources. The two most
energetic events released about
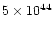 ergs in
ergs in
 -rays from SGR 0526-66 on 5 March 1979 (Mazets et al. 1979)
and about 1043 ergs from SGR 1900+14 on 27 August 1998
(Hurley et al. 1999). The SGR sources also generate a large number of
smaller outbursts, and it has been shown that the time intervals
between outbursts are distributed lognormally
(Hurley et al. 1994; Gögüs et al. 2000). Hence lognormally distributed time
intervals between outbursts and glitches are characteristic
features of SGR sources and neutron star microglitches. It is
widely accepted that these sources are rotating neutron stars with
high magnetic fields. It is not unreasonable to argue that the
coupled effects of rapid rotation and intense magnetic fields
(Kluzniak & Ruderman 1998) are also involved in powering GRBs since the
time intervals between pulses are also consistent with a
lognormal distribution.
-rays from SGR 0526-66 on 5 March 1979 (Mazets et al. 1979)
and about 1043 ergs from SGR 1900+14 on 27 August 1998
(Hurley et al. 1999). The SGR sources also generate a large number of
smaller outbursts, and it has been shown that the time intervals
between outbursts are distributed lognormally
(Hurley et al. 1994; Gögüs et al. 2000). Hence lognormally distributed time
intervals between outbursts and glitches are characteristic
features of SGR sources and neutron star microglitches. It is
widely accepted that these sources are rotating neutron stars with
high magnetic fields. It is not unreasonable to argue that the
coupled effects of rapid rotation and intense magnetic fields
(Kluzniak & Ruderman 1998) are also involved in powering GRBs since the
time intervals between pulses are also consistent with a
lognormal distribution.
The possibility that a rapidly rotating neutron star with a
surface magnetic field of  1015 Gauss could power a GRB
has been suggested (Usov 1992). Once formed such a neutron
star could lose its rotational energy catastrophically on a time
scale of seconds. The rotation of the star decelerates because of
the applied torques. Powerful transient fields may also occur in
the merger of two neutron stars or a neutron star and a black
hole. The energy stored in differential rotation of the collapsed
object would be released in sub-bursts as toroidal magnetic fields
are repeatedly wound up to
1015 Gauss could power a GRB
has been suggested (Usov 1992). Once formed such a neutron
star could lose its rotational energy catastrophically on a time
scale of seconds. The rotation of the star decelerates because of
the applied torques. Powerful transient fields may also occur in
the merger of two neutron stars or a neutron star and a black
hole. The energy stored in differential rotation of the collapsed
object would be released in sub-bursts as toroidal magnetic fields
are repeatedly wound up to 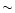 1017 Gauss
(Kluzniak & Ruderman 1998). The emergence of a toroid is accompanied by
huge spin down torques, the reconnection of new surface magnetic
fields and rapid release of a sub-burst of energy of about
1051 ergs. The release of rotational energy in repeated
sub-bursts could power the GRB. If the differentially rotating
compact object forms a torus about a spinning black hole either in
a merger or core collapse of a massive star, energy can be
extracted by the magnetic field that threads the torus and the
black hole (Mészáros 2001). As the torus builds up and ejects
its magnetic toroids, the differential rotation of the torus
could be maintained by the spin of the black hole.The models of
GRBs with the coupled effects of rapid rotation and ultra intense
magnetic fields are particularly attractive because the time
intervals between pulses in GRBs are distributed lognormally and
follow the pattern observed in non-catastrophic events in SGRs
and pulsars.
1017 Gauss
(Kluzniak & Ruderman 1998). The emergence of a toroid is accompanied by
huge spin down torques, the reconnection of new surface magnetic
fields and rapid release of a sub-burst of energy of about
1051 ergs. The release of rotational energy in repeated
sub-bursts could power the GRB. If the differentially rotating
compact object forms a torus about a spinning black hole either in
a merger or core collapse of a massive star, energy can be
extracted by the magnetic field that threads the torus and the
black hole (Mészáros 2001). As the torus builds up and ejects
its magnetic toroids, the differential rotation of the torus
could be maintained by the spin of the black hole.The models of
GRBs with the coupled effects of rapid rotation and ultra intense
magnetic fields are particularly attractive because the time
intervals between pulses in GRBs are distributed lognormally and
follow the pattern observed in non-catastrophic events in SGRs
and pulsars.
The time intervals between the pulses are correlated with each
other and the correlation decreases slowly with increase in the
number of time intervals (Table 5). This effect had previously
been observed in a small sample of GRBs (Nakar & Piran 2001) and
attributed to the internal shock model. In addition the pulse
amplitudes are also correlated with each other and this effect
decreases more rapidly than the time intervals between pulses
(Table 6). Similar correlations have been found between the pulse
amplitudes and also time intervals between pulses in short GRBs
(McBreen et al. 2001). In the internal shock model, these
correlations originate in the central engine and provide strong
constraints on any viable model of GRBs.
GRB models leave open many possibilities to account for the
Pareto-Lévy tail of long time intervals. The excess of long
time intervals have been noted in other studies
(Ramirez-Ruiz & Merloni 2001; Nakar & Piran 2001). The properties of the GRBs with long time
intervals will be covered in a separate publication.
A detailed comparison has been made between the distributions of
the properties of the pulses in the first half and second half for
three categories of GRBs. There are no statistically significant
differences between the median values of the time intervals
between pulses, pulse amplitude, areas and FWHM in the first half
and second half of GRBs (Table 8). There are two trends in the
pulse rise times and fall times that should be noted: 1) the
median rise time is slower in the first half for the three
categories of bursts (Table 8) and 2) the median fall time is
faster in the first half for categories N and O. The combination
of slower rise times and faster fall times gives a pulse
asymmetry ratio with a significant difference between the first
half and second half for category N and at a reduced significance
level for O and P (Table 8). The effect could be caused by a
clearing out process such as additional baryon loading or Compton
drag in the first half of the bursts with small number of
pulses. These results are also compatible with the constancy of
the pulse widths observed by Ramirez-Ruiz & Fenimore (2000) using a peak
aligned profile method on a small sample of GRBs with more than
20 pulses. In the internal shock model, the rapid variability in
GRB time profiles is due to emission from multiple shocks in a
relativistic wind (Piran 1999; Panaitescu et al. 1999; Downes et al. 2001). The
temporal position of the pulse is unconnected to the collision
parameters and in this way the little or no evolution of the
pulses in GRBs can be explained (Fenimore & Ramirez-Ruiz 2001). The rise
time and fall time may be determined by the hydrostatic time
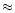 d/c and the angular spreading time
d/c and the angular spreading time 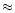 D/c, where dand D are the width and separation of the shells
(Kobayashi et al. 2001). The observed evolution of the pulses requires
the shells to be narrower and farther apart later in the GRB.
This prediction is in agreement with the data because the time
intervals between pulses are longer in the second half of the
burst (Table 8).
D/c, where dand D are the width and separation of the shells
(Kobayashi et al. 2001). The observed evolution of the pulses requires
the shells to be narrower and farther apart later in the GRB.
This prediction is in agreement with the data because the time
intervals between pulses are longer in the second half of the
burst (Table 8).
However, it is evident from Fig. 14 and Tables 7 and 8 that as
the number of pulses in a burst increases, the median values of
the rise and fall times, FWHM and time intervals all decrease and
by about the same amount. The GRBs with more pulses also have on
average significantly longer durations, higher fluences and
hardness ratios (Table 7). The variability index of a GRB was
taken to be the number of pulses 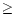
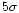 divided by the
time the GRB emission was also
divided by the
time the GRB emission was also 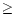
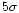 .
The median values
are given in Table 9 for the four GRB categories. The GRBs with
more pulses have a higher variability index. These results
provide an interesting interpretation of the two correlations
that have been reported for GRBs with known redshift: (1) the
more luminous GRBs to be more variable (Fenimore & Ramirez-Ruiz 2001) and (2) there is an anticorrelation between the arrival times of
high energy and low energy pulses in GRBs
(Norris et al. 2000; Salmonson 2000). Recently Schaefer et al. (2001) showed
that there is a relationship between the variability and spectral
lag (Ioka & Nakamura 2001). There is a good correlation between the
values of the variability obtained here and those of
Fenimore & Ramirez-Ruiz (2001). GRBs with higher values of HR have lower
values of
.
The median values
are given in Table 9 for the four GRB categories. The GRBs with
more pulses have a higher variability index. These results
provide an interesting interpretation of the two correlations
that have been reported for GRBs with known redshift: (1) the
more luminous GRBs to be more variable (Fenimore & Ramirez-Ruiz 2001) and (2) there is an anticorrelation between the arrival times of
high energy and low energy pulses in GRBs
(Norris et al. 2000; Salmonson 2000). Recently Schaefer et al. (2001) showed
that there is a relationship between the variability and spectral
lag (Ioka & Nakamura 2001). There is a good correlation between the
values of the variability obtained here and those of
Fenimore & Ramirez-Ruiz (2001). GRBs with higher values of HR have lower
values of
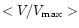 implying they are a more distant
and luminous population (Schmidt 2001).
implying they are a more distant
and luminous population (Schmidt 2001).
Our knowledge on the shape of the emitting region in GRBs is
restricted because, due to relativistic beaming, only a small
portion of angular size 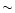
 is visible to the
observer. Thus the observer is unable to distinguish a sphere
from a jet as long as
is visible to the
observer. Thus the observer is unable to distinguish a sphere
from a jet as long as
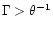 where
where  is
the radius of the opening angle of jet (Rhoads 1997).
However as the source continues its rapid expansion,
is
the radius of the opening angle of jet (Rhoads 1997).
However as the source continues its rapid expansion,  will decrease, and when
will decrease, and when
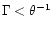 there will be a
marked decrease in the observed flux. The steep time dependence
of the afterglow emission, sometimes with changes in the slope of
the spectrum, and radio emission have been widely interpreted as
evidence for emission from jets
(Castro-Tirado 2001; Mészáros 2001; Frail et al. 2001). The GRBs with more
pulses appear to have higher values of the Lorentz factor
there will be a
marked decrease in the observed flux. The steep time dependence
of the afterglow emission, sometimes with changes in the slope of
the spectrum, and radio emission have been widely interpreted as
evidence for emission from jets
(Castro-Tirado 2001; Mészáros 2001; Frail et al. 2001). The GRBs with more
pulses appear to have higher values of the Lorentz factor
 .
The higher values of
.
The higher values of  may come from a more
efficient and more active central engine. In one variation of
the internal shock model, it was assumed that the degree of
collimation of the jet depended on the mass M at the explosion
(Kobayashi et al. 2001). A wide jet involves a large mass that
results in a flow with a lower
may come from a more
efficient and more active central engine. In one variation of
the internal shock model, it was assumed that the degree of
collimation of the jet depended on the mass M at the explosion
(Kobayashi et al. 2001). A wide jet involves a large mass that
results in a flow with a lower  .
The pulse properties
depend strongly on
.
The pulse properties
depend strongly on
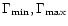 and the
radius of the photosphere
and the
radius of the photosphere 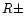 .
GRBs with faster pulses
originate in collisions above
.
GRBs with faster pulses
originate in collisions above 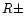 whereas GRBs with slower
pulses have smaller values of
whereas GRBs with slower
pulses have smaller values of  and some collisions below
the photosphere. While this homogeneous model may explain pulse
properties in GRBs, the strong possibility of inhomogeneous jets
with a variable
and some collisions below
the photosphere. While this homogeneous model may explain pulse
properties in GRBs, the strong possibility of inhomogeneous jets
with a variable  should also be examined.
should also be examined.
Baryon loading can be a major problem in GRB models and severely
limit the attainable value of  (Rees 1999; Mészáros et al. 1998; Salmonson 2000). There maybe a broad range of
(Rees 1999; Mészáros et al. 1998; Salmonson 2000). There maybe a broad range of
 's in the outflow with the highest value occurring close
to the rotation axis where the baryon contamination should be at
a minimum. At larger angles from the axis, there may be an
increasing degree of contamination with a corresponding drop in
's in the outflow with the highest value occurring close
to the rotation axis where the baryon contamination should be at
a minimum. At larger angles from the axis, there may be an
increasing degree of contamination with a corresponding drop in
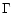 .
The outcome of a collapse in a massive star whose iron
core collapsed to a black hole have been computed
(MacFadyen & Woosley 1999). The resulting jet that drives out through the
star is probably powered by a MHD process which can in principle
convert a large portion of the binding energy at the last stable
orbit into jet energy. The large amount of energy dumped into the
natural funnel-shaped channel creates a highly collimated jet,
focused into a small region of the sky. The largest value of
.
The outcome of a collapse in a massive star whose iron
core collapsed to a black hole have been computed
(MacFadyen & Woosley 1999). The resulting jet that drives out through the
star is probably powered by a MHD process which can in principle
convert a large portion of the binding energy at the last stable
orbit into jet energy. The large amount of energy dumped into the
natural funnel-shaped channel creates a highly collimated jet,
focused into a small region of the sky. The largest value of
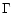 occurs on axis and decreases with increasing
occurs on axis and decreases with increasing 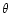 because the material coming at the observer has less energy at
larger angles. The emission is still beamed into an angle
because the material coming at the observer has less energy at
larger angles. The emission is still beamed into an angle
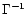 but in this inhomogeneous model the angle varies
across the opening angle of the jet (Rossi et al. 2001). In this
situation the properties of the pulses in GRBs can be influenced
by the jet. The BATSE sample of the brightest GRBs should contain
a range of angles within the jet and hence different values of
but in this inhomogeneous model the angle varies
across the opening angle of the jet (Rossi et al. 2001). In this
situation the properties of the pulses in GRBs can be influenced
by the jet. The BATSE sample of the brightest GRBs should contain
a range of angles within the jet and hence different values of
 .
In this context it is reasonable to identify the
complex GRBs with more pulses and higher values of
.
In this context it is reasonable to identify the
complex GRBs with more pulses and higher values of  with
angles near the axis of jet. The GRBs that are viewed at larger
angles from the jet axis have on average lower values of
with
angles near the axis of jet. The GRBs that are viewed at larger
angles from the jet axis have on average lower values of
 ,
and develop at the greater distances from the central
engine and should have slower pulses.
,
and develop at the greater distances from the central
engine and should have slower pulses.
In this context it is interesting to note that the pulse
evolution consisting of slower rise times and faster fall times in
the first half, is more pronounced for GRBs in category N than
either O or P. In a jet model with a variable  ,
the GRBs
in category N would be on average farther from the axis and more
sensitive to a clearing out effect such as additional baryon
loading or Compton drag (Rees 1999; Ghisellini 2001) in the
initial phase of the GRB.
,
the GRBs
in category N would be on average farther from the axis and more
sensitive to a clearing out effect such as additional baryon
loading or Compton drag (Rees 1999; Ghisellini 2001) in the
initial phase of the GRB.
The steep and variable slope of the decay of GRB afterglows have
been widely interpreted as evidence for jets in GRBs
(Mészáros 2001; Castro-Tirado et al. 2001). If the axis of the jet is pointed
close to the observer, the GRB will be intense and the afterglow
should contain evidence for good alignment. It is interesting
that the two brightest GRBs detected by WFC on BeppoSAX also were
the best aligned. The recent detection of a bright GRB with a
fluence of 10-4 ergs cm-2 also had a very bright
afterglow (Castro-Tirado et al. 2001). However many more GRBs and
afterglows are required to verify the existence of a pattern
between the strongest GRBs and their afterglows
(Frail et al. 2001). The distribution of the number of pulses per
GRB (Fig. 5) may broadly represent the beaming by the jet because
bursts with large numbers of pulses and higher variability
(Table 7) may be close to the axis and bursts with smaller
numbers of pulses and less variability further off-axis.
The properties of the brightest 319 GRBs in the BATSE current
catalogue have been analysed.The automatic pulse selection
process detected more than 3300 pulses. The distributions of
pulse rise and fall times, FWHM, areas, amplitudes and time
intervals between pulses are reasonably consistent with the
lognormal distribution. GRB pulse profiles can be elegantly
described by a small number of parameters that may be very useful
for simulations. The lognormal distribution depends on the
product of probabilities arising from a combination of
independent events and these conditions must therefore apply to
the generation of the temporal and spectral properties of GRB
pulses. A wide range of burst parameters and also pulse
parameters were correlated and the results follow the trend
expected from the internal shock model. The pulse amplitude is
strongly anticorrelated with the other pulse timing parameters.
The time intervals between pulses and pulse amplitudes are
correlated with each other.
A comprehensive analysis has been performed between the first half
and second half of GRBs in three categories defined in terms of N. No major differences were found between the distribution of
pulse properties between the first half and second half of the
GRBs. There is a strong tendency for pulses to have slower rise
times and faster fall times in the first half of the burst. This
trend is stronger in GRBs with small numbers of pulses. The
pulse timing parameters and time intervals all decrease with
increase in N. These results seem to be compatible with jet
models with either a  that varies with the opening angle
or is constant and varies with the mass. If
that varies with the opening angle
or is constant and varies with the mass. If  varies with
the opening angle of the jet, the GRBs with higher values of
varies with
the opening angle of the jet, the GRBs with higher values of
 and greater variability are observed close to the axis of
the jet while GRBs with smaller number of pulses and less
variability are observed at larger angles from the jet. Jets
with values of
and greater variability are observed close to the axis of
the jet while GRBs with smaller number of pulses and less
variability are observed at larger angles from the jet. Jets
with values of  that vary with angle or with mass may
explain the luminosity-variability correlation and the
luminosity-energy lag correlation in GRBs with known redshift.
that vary with angle or with mass may
explain the luminosity-variability correlation and the
luminosity-energy lag correlation in GRBs with known redshift.
This study of the number of pulses in GRBs and their time
structure provides strong evidence for rotation powered systems
with intense magnetic fields and the added complexity of a jet.
These results can be well interpreted by internal shocks in the
framework of theoretical models for the formation of black holes
and subsequent jet formation.
-
Aitchison, J., & Brown, J. A. C. 1957, The Lognormal Distribution (Cambridge,
Cambridge University Press)
In the text
-
Arneodo, A., Manneville, S., Muzy, J. F., & Roux, S. G. 1999, Phil.
Trans. R. Soc. Lond. A, 357, 2415
In the text
-
Atteia, J., Boër, M., & Hurley, K. 1999, A&AS, 138, 421
In the text
NASA ADS
-
Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281
In the text
NASA ADS
-
Belli, B. M. 1992, ApJ, 393, 266
In the text
NASA ADS
-
Beloborodov, A. M., Stern, B. E., & Svensson, R. 2000, ApJ, 535, 158
In the text
NASA ADS
-
Berger, E. A., Kulkarni, S. R., & Frail, D. A. 2001, ApJ, 560, 652
In the text
NASA ADS
-
Bhat, P. N., Fishman, G. J., Meegan, C. A., et al. 1994, ApJ, 426,
604
In the text
NASA ADS
-
Borgonovo, L., & Ryde, F. 2001, ApJ, 548, 770
In the text
NASA ADS
-
Brainerd, J. J. 2000, ApJ, 538, 628
In the text
NASA ADS
-
Castro-Tirado, A. J. 2001 [astro-ph/0102122]
In the text
-
Castro-Tirado, A. J., Sokolov, V. V., Gorosabel, J., et al. 2001,
A&A, 370, 398
In the text
NASA ADS
-
Chang, H., & Yi, I. 2000, ApJ, 542, L17
In the text
NASA ADS
-
Cordes, J. M., Downs, G. S., & Krause-Polstorff, J. 1988, ApJ, 330, 847
In the text
NASA ADS
-
Costa, E., Frontera, F., Heise, J., et al. 1997, Nature, 387, 783
In the text
NASA ADS
-
Crider, A., Liang, E. P., Preece, R. D., et al. 1999, A&AS,
138, 401
In the text
NASA ADS
-
Daigne, F., & Mochkovitch, R. 1998, MNRAS, 296, 275
In the text
NASA ADS
-
Daigne, F., & Mochkovitch, R. 2001, Proceedings of Gamma-Ray Burst and Afterglow Workshop, Woods Hole, November 5-9, in press
In the text
-
Daubechies, I. 1992, Ten Lectures on Wavelets (Philadelphia: Capital City)
In the text
-
Dermer, C. D., & Mitman, K. E. 1999, ApJ, 513, L5
In the text
NASA ADS
-
Downes, T. P., Duffy P., & Komissarov, S. 2001, MNRAS, in press [astro-ph/0102271]
In the text
-
Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340,
126
In the text
NASA ADS
-
Fenimore, E. E., in 't Zand, J. J. M., Norris, J. P., Bonnell, J. T.,
& Nemiroff, R. J. 1995, ApJ, 448, L101
In the text
NASA ADS
-
Fenimore, E. E., & Ramirez-Ruiz, E. 2001, ApJ, submitted
[astro-ph/0004176]
In the text
-
Frail, D. A., Kulkarni, S. R., Sari, R., et al. 2002, ApJ, 562, L55
In the text
NASA ADS
-
Fryer, C. L., Woosley, S. E., Herant, M., & Davies, M. B. 1999, ApJ,
520, 650
In the text
NASA ADS
-
Ghisellini, G. 2001 [astro-ph/0101291]
In the text
-
Gögüs, E., Woods, P. M., Kouveliotou, C., et al. 2000, ApJ, 532, L121
In the text
NASA ADS
-
Golenetskii, S. V., Mazets, E. P., Aptekar, R. L., & Ilinskii, V. N.
1983, Nature, 306, 451
In the text
NASA ADS
-
Hanlon, L., Laureijs, R. J., Metcalfe, L., et al. 2000, A&A, 359,
941
In the text
NASA ADS
-
Hurley, K., Cline, T., Mazets, E., et al. 1999,
Nature, 397, 41
In the text
NASA ADS
-
Hurley, K. J., McBreen, B., Delaney, M., & Britton, A. 1995, Ap&SS,
231, 81
In the text
NASA ADS
-
Hurley, K. J., McBreen, B., Quilligan, F., Delaney, M., & Hanlon, L.
1998, in CP428, Gamma-Ray Bursts, 4th Hunstville Symp., ed. C. A.
Meegan, et al., 191
In the text
-
Hurley, K. J., McBreen, B., Rabbette, M., & Steel, S. 1994, A&A, 288,
L49
In the text
NASA ADS
-
Ioka, K., & Nakamura, T. 2001, ApJ, 554, L163
In the text
NASA ADS
-
Kluzniak, W., & Ruderman, M. 1998, ApJ, 508, L113
In the text
NASA ADS
-
Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92
In the text
NASA ADS
-
Kobayashi, S., Ryde, F., & MacFadyen, A. 2001 [astro-ph/0110080]
In the text
-
Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413,
L101
In the text
NASA ADS
-
Lamb, D. Q., & Reichart 2000, ApJ, 536, 1
In the text
NASA ADS
-
Lee, A., Bloom, E. D., & Petrosian, V. 2000a, ApJS, 131, 21
In the text
NASA ADS
-
Lee, A., Bloom, E. D., & Petrosian, V. 2000b, ApJS, 131, 1
In the text
NASA ADS
-
Li, H., & Fenimore, E. E. 1996, ApJ, 469, L115
In the text
NASA ADS
-
Liang, E., & Kargatis, V. 1996, Nature, 381, 49
In the text
NASA ADS
-
Link, B., & Epstein, R. I. 1996, ApJ, 466, 764
In the text
NASA ADS
-
MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262
In the text
NASA ADS
-
Mallat, S. G., & Hwang, W. L. 1992, IEEE Transactions on Information Theory,
38, 617
In the text
-
Mallat, S. G., & Zhong, S. 1992, IEEE Transactions on Pattern Analysis and
Machine Intelligence, 14, 710
In the text
-
Mallozzi, R. S., Paciesas, W. S., Pendleton, G. N., et al. 1995,
ApJ, 454, 597
In the text
NASA ADS
-
Mazets, E. P., Golentskii, S. V., Ilinskii, V. N., Aptekar, R. L., &
Guryan, I. A. 1979, Nature, 282, 587
In the text
NASA ADS
-
McBreen, B., Hurley, K. J., Long, R., & Metcalfe, L. 1994, MNRAS, 271,
662
In the text
NASA ADS
-
McBreen, S., Quilligan, F., McBreen, B., Hanlon, L., & Watson, D. 2001, A&A, 380, L31
In the text
NASA ADS
-
McBreen, S., McBreen, B., Quilligan, F., & Hanlon, L. 2002, A&AL, in press
In the text
-
Mészáros, P. 2001, Science, 291, 79
In the text
NASA ADS
-
Mészáros, P., & Rees, M. J. 1993, ApJ, 418, L59
In the text
NASA ADS
-
Mészáros, P., Rees, M. J., & Wijers, R. A. M. J. 1998, ApJ,
499, 301
In the text
NASA ADS
-
Meyer, Y. 1993, Wavelets: Algorithms and Applications (Philadelphia: SIAM)
In the text
-
Montroll, E. W., & Shlesinger, M. F. 1982, Proc. Natl. Acad. Sci., USA.,
79, 3380
In the text
-
Nakar, E., & Piran, T. 2001 [astro-ph/0103011]
In the text
-
Nemiroff, R. J., Norris, J. P., Wickramasinghe, W. A. D. T., et al. 1993, ApJ, 414, 36
In the text
NASA ADS
-
Norris, J. P., Nemiroff, R. J., Bonnell, J. T., et al. 1996, ApJ, 459, 393
In the text
NASA ADS
-
Norris, J. P., Marani, G. F., & Bonnell, J. T. 2000, ApJ, 534, 248
In the text
NASA ADS
-
Norris, J. P., Scargle, J. D., & Bonnell, J. T. 2001 [astro-ph/0105052]
In the text
-
Paciesas, W. S., Meegan, C. A., Pendleton, G. N., et al. 1999, ApJS, 122, 465
In the text
NASA ADS
-
Paczynski, B. 1991, Acta Astron., 41, 257
In the text
NASA ADS
-
Paczynski, B. 1998, ApJ, 494, L45
In the text
NASA ADS
-
Panaitescu, A., Spada, M., & Mészáros, P. 1999, ApJ, 522, L105
In the text
NASA ADS
-
Pendleton, G. N., Paciesas, W. S., Briggs, M. S., et al. 1997, ApJ,
489, 175
In the text
NASA ADS
-
Piran, T. 1999, Phys. Rep., 314, 575
In the text
NASA ADS
-
Preece, R. D., Briggs, M. S., Mallozzi, R. S., et al. 2000, ApJS,
126, 19
In the text
NASA ADS
-
Quilligan, F., Hurley, K. J., McBreen, B., Hanlon, L., & Duggan, P.
1999, A&AS, 138, 419
In the text
NASA ADS
-
Quilligan, F., McBreen, B., Hurley, K. J., et al. 2000,
Gamma-Ray Bursts in the Afterglow Era, ed. E. Costa, F. Frontera, & J. Hjorth,
Proceedings of ESO Astrophysics Symposia, XXVI, 78
In the text
-
Ramirez-Ruiz, E., & Fenimore, E. E. 2000, ApJ, 539, 712
In the text
NASA ADS
-
Ramirez-Ruiz, E., & Merloni, A. 2001, MNRAS, 320, L25
In the text
NASA ADS
-
Rees, M. J. 1999, A&AS, 138, 491
In the text
NASA ADS
-
Rees, M. J., & Mészáros, P. 1994, ApJ, 430, L93
In the text
NASA ADS
-
Rhoads, J. E. 1997, ApJ, 487, L1
In the text
NASA ADS
-
Rossi, E. M., Lazzati, D., & Rees, M. J. 2001, Gamma-Ray Burst and Afterglow Workshop, November 5-9, in press
In the text
-
Ruffert, M., & Janka, H.-T. 1999, A&A, 344, 573
In the text
NASA ADS
-
Salmonson, J. D. 2000, ApJ, 544, L115
In the text
NASA ADS
-
Sari, R., & Piran, T. 1997, MNRAS, 287, 110
In the text
NASA ADS
-
Schaefer, B. E., Deng, M., & Band, D. L. 2001, ApJ, 563, L123
In the text
NASA ADS
-
Schmidt, M. 2001, ApJ, 552, 36
In the text
NASA ADS
-
Spada, M., Panaitescu, A., & Mészáros, P. 2000, ApJ, 537, 824
In the text
NASA ADS
-
Stern, B., Poutanen, J., & Svensson, R. 1999, ApJ, 510, 312
In the text
NASA ADS
-
Stern, B. E., & Svensson, R. 1996, ApJ, 469, L109
In the text
NASA ADS
-
Strohmayer, T. E., Fenimore, E. E., Murakami, T., et al. 1998, ApJ,
500, 873
In the text
NASA ADS
-
Suzuki, M., Morikawa, M., & Joichi, I. 2001 [astro-ph/0104232]
In the text
-
Thompson, C. 1994, MNRAS, 270, 480
In the text
NASA ADS
-
Uman, M. 1987, The Lightening Discharge (London: Academic Press)
In the text
-
Usov, V. V. 1992, Nature, 357, 472
In the text
NASA ADS
-
van Paradijs, J., Groot, P. J., Galama, T., et al. 1997, Nature, 386, 686
In the text
NASA ADS
-
van Putten, M. H. P. M. 2001, Phys. Rep., 345, 1
In the text
NASA ADS
-
Young, C. A., Meredith, D. C., & Ryan, J. M. 1995, Ap&SS, 231, 119
In the text
NASA ADS
Copyright ESO 2002
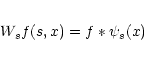
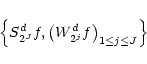
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{h3056f2.eps}\par\vspace*{...
....eps}\par\includegraphics[angle=-90,width=12.5cm,clip]{h3056f4.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg27.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=13.5cm,clip]{h3056f5.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{3056f4.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg32.gif)
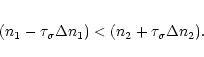
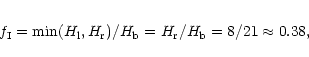
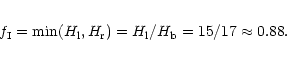
![\begin{figure}
\par\includegraphics[angle=90,width=12.5cm,clip]{h3056f7.eps} %
\end{figure}](/articles/aa/full/2002/14/aah3056/Timg48.gif)
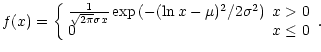
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{h3056f8.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg55.gif)
![\begin{figure}
\par\psfrag{xlab}[b]{\small$t_{\rm r}$\space (sec)}
\psfrag{ylab}...
...{\small Frequency}
\includegraphics[width=11.2cm,clip]{h3056f10.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg60.gif)
![\begin{figure}
\par\psfrag{xlab}[b]{\small$t_{\rm f}$\space (sec)}
\psfrag{ylab}[b]{\small Frequency}
\includegraphics[width=8.8cm,clip]{h3056f11.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg61.gif)
![\begin{figure}
\par\psfrag{xlab}[b]{\small Pulse Amplitudes (counts)}
\psfrag{y...
...{\small Frequency}
\includegraphics[width=8.8cm,clip]{h3056f12.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg62.gif)
![\begin{figure}
\par\psfrag{xlab}[b]{\small Pulse Areas (counts)}
\psfrag{ylab}[b]{\small Frequency}
\includegraphics[width=8.8cm,clip]{h3056f13.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg63.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=13.4cm,clip]{h3056f14.eps}\v...
...centage}
\includegraphics[angle=-90,width=13.4cm,clip]{h3056f15.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg64.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=13.5cm,clip]{h3056f16.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{3056f13.eps}\par\end{figure}](/articles/aa/full/2002/14/aah3056/Timg67.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{h3056f20.eps} \end{figure}](/articles/aa/full/2002/14/aah3056/Timg94.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=12cm,clip]{h3056f21.eps} %
\...
...pace*{2mm}
\includegraphics[angle=-90,width=12cm,clip]{h3056f22.eps}\end{figure}](/articles/aa/full/2002/14/aah3056/Timg104.gif)