A&A 385, 733-742 (2002)
DOI: 10.1051/0004-6361:20020123
J. L. L. Voûte1,2 - M. L. A. Kouwenhoven3 - P. C. van Haren2 - J. J. Langerak2 - B. W. Stappers1,4 - D. Driesens2 - R. Ramachandran1,4 - Th. D. Beijaard2
1 - Astronomical Institute "Anton Pannekoek'', Kruislaan 403,
1098 SJ Amsterdam, The Netherlands
2 -
Instrumentele Groep Fysica, PO Box 80004,
3508 TA Utrecht, The Netherlands
3 -
Astronomical Institute, Utrecht University, PO Box 80000,
3508 TA Utrecht, The Netherlands
4 -
Netherlands Foundation for Research in Astronomy, PO Box 2,
7990 AA Dwingeloo, The Netherlands
Received 16 July 2001 / Accepted 22 January 2002
Abstract
We have designed and constructed PuMa, a pulsar machine that has both
a baseband recording and a digital filterbank mode. Its design is
based on the use of digital signal processors (DSPs). Their operation
is controlled by software, which makes PuMa reconfigurable, flexible
and easy to operate. The maximum number of channels in the digital
filterbank mode is 32768 over a bandwidth of 80 MHz. This makes PuMa
suitable for pulsar observations at low sky frequencies. The maximum
bandwidth in baseband recording mode is two times 10 MHz. The machine
was installed at the Westerbork Synthesis Radio Telescope in The
Netherlands in 1998. We discuss in some detail PuMa's technical
properties and capabilities. Recent observations, a sample of which
are presented here, demonstrate its capabilities and that it
is performing up to its
specifications.
Key words: instrumentation: detectors - instrumentation: miscellaneous - pulsars: general
Pulsars are fast spinning neutron stars with a very strong magnetic field. They emit radiation over almost the entire electromagnetic spectrum and are predominantely studied at radio frequencies, where they are bright and the telescopes are very sensitive. Pulsars are studied to learn about, for instance, their formation (e.g. through the connection with supernova remnants, Frail 1998), their evolution (through population synthesis, e.g. Hartman et al. 1997), the emission mechanism of the pulses (through observations of single and integrated pulses and polarisation, e.g. Deshpande & Rankin 1999) and also to test fundamental physics theories such as general relativity (through the arrival times of the pulses, e.g. Taylor et al. 1992). All these studies require increasingly more sensitive equipment with higher temporal resolution.
For a given radio telescope an observer can improve the signal-to-noise ratio (SNR) of an observation by increasing the duration of the observation and by increasing the bandwidth. Longer observations are not always practical because of observing time constraints, source visibility or source variability. Increasing the bandwidth can also have its drawbacks for pulsar observations. When the broadband pulses traverse the interstellar medium (ISM), the lower frequencies travel more slowly than the higher ones. This effect is called dispersion and is due to the free electrons in the ISM. Dispersion causes the pulse to be smeared since the pulse does not arrive at exactly the same moment in the whole observed radio band. The frequency dependence of dispersion smearing implies that observations at lower frequencies (where pulsars are generally stronger) are more adversely affected. There are two ways to counter the effects of the dispersion smearing, viz. coherent and incoherent dedispersion.
Coherent dedispersion works on the (baseband) sampled voltages of the whole band (Hankins 1971). This can be done in the time and in the frequency domain. In the latter case, the voltage time series is Fourier transformed and the phase of each coefficient is rotated so as to compensate for the differences in arrival time for each frequency. The inverse Fourier transform results in a dispersion-free time series with the same sampling rate as the original time series. This is usually done off-line by a computer after the voltages have been sampled by a baseband recorder (Jenet et al. 1997; Stairs et al. 2000). If the coherent dedispersion is done in the time domain, then the sampled voltage time series is sent through a digital FIR filter (a so-called chirp filter) which gives the correct frequency dependent phase shift, but leaves amplitudes unchanged. This is done in dedicated hardware and can presently only deal with limited bandwidths and dispersion smearing (Backer et al. 1997).
In the incoherent dedispersion method the smearing is reduced by dividing the band into a number of smaller channels. After processing the signals from each channel (detection and integration), the resulting time series are shifted in time to compensate for the different pulse arrival times, and added together. This incoherent dedispersion method has a fundamental limitation with respect to the coherent method: the final time resolution is limited by the dispersion smearing within one channel or the inverse of the bandwidth of the channel. On the other hand, coherent dedispersion is computationally more intensive.
Traditionally, the incoherent method is used and the frequency band is split into channels using banks of analogue filters. These machines have some major drawbacks since the number of channels and usually the channel widths are fixed. This makes it hard, if not impossible, to observe fast pulsars with high dispersion at low sky frequencies. Building filterbanks with a higher number of channels is expensive, since both the number of components and the demands on their quality increase. Also, a large number of channels leads to unnecessary high data rates for many other pulsar observations.
Newer filterbanks, such as the Flexible Filterbank Backend (FFB) at the WSRT (Vasisht 1996; Kouwenhoven et al. 1996), are more versatile, since they have flexible channel widths. However, in the case of the FFB the number of channels is still rather limited (i.e. 32 distributed over 80 MHz). Furthermore its signal processing yields only the power per (linear or circular) polarisation and the total power, from which it is not possible to determine all four Stokes polarisation parameters.
PuMa, short for Pulsar Machine, is a digital pulsar backend, developed in the Netherlands, which was originally intended to serve as a digital filterbank, in which the analogue filters were replaced by Fourier transforms carried out by digital signal processors. Provided that enough computing power and memory is available, the number of frequency channels can be as high as desired, for PuMa the maximum is 32768 channels over 80 MHz. From the resulting time series PuMa can compute all four Stokes parameters. During its development a second observation mode was added which allows PuMa to baseband sample two bands with a width of 10 MHz each.
PuMa was installed at the Westerbork Synthesis Radio Telescope (WSRT) in The Netherlands in 1998. This paper gives a brief outline of WSRT and of the design and functionalities of PuMa. Section 2 describes the boundary conditions for the design of PuMa set by the infrastructure of the observatory. Section 3 discusses some considerations that led to major choices in the design. The signal processing in the machine is described in Sect. 4. The paper concludes with the results of some of the first observations made with PuMa (Sect. 5). Technical details of PuMa's design and operation can be found in van Haren et al. (2000).
The Westerbork Synthesis Radio Telescope (WSRT) is an east-west array of fourteen 25-meter dishes (Baars & Hooghoudt 1974), each equipped with a Multi-Frequency Front-end, covering sky frequencies from 250 MHz to over 8 GHz (Tan 1991; de Bruyn 1996). The typical bandwidth is 80 MHz in both the linear X and Y polarisations. These two signals from each telescope are split into 8 bands, each 10 MHz wide. After sampling, the signals are digitally delayed to compensate for the arrival times at the different telescopes and added coherently to form an analogue signal. This arrangement of the telescopes is called a tied-array and it approximates a single dish of almost one hundred meters diameter.
As the addition and the delays of the signals of all telescopes are fully flexible, the total array can be split into sub-arrays. These sub-arrays can simultaneously observe different radio sources each at their own sky frequency, albeit at a reduced SNR. For pulsar observations this allows for interesting research, such as the simultaneous multi-frequency observation of single pulses.
Signals from two polarisations and eight frequency bands are digitised by PuMa at the 20 MHz Nyquist sampling rate. The required clock signal is derived from a 10 MHz signal from WSRT's MASER. Also derived from the MASER is a pulse at 10-s time intervals, which is used to obtain a well-defined start time for each observation. The MASER's offset with respect to UTC is determined from averaged readings from the Global Positioning System. The present overall inaccuracy in UTC of that start pulse is of order 10 ns; PuMa's own timing inaccuracy is a few nanoseconds.
Particularly at low sky frequencies (a strong feature of WSRT), where the dispersion smearing is most noticeable, channels with narrow bandwidths are required. One of the shortcomings of filterbanks is the limited number of channels, typically several tens. If these channels have a bandwidth of some 10 kHz, then they can only cover several hundreds of kHz, which is far less than the several tens of MHz of bandwidth that is available from the telescopes. At WSRT some 8000 channels would be required to cover the full 80 MHz bandwidth; a number that is clearly outside the range of analogue filterbanks.
In a digital approach, however, the filtering can be done by means of
Fourier transforms, and the need for hardware filterbank channels is
replaced by computing power. With the chosen digital signal
processor![]() (DSP) a Complex Fast Fourier
Transform (CFFT) of 2048 points requires less than 1 ms. Together with
the other computational tasks (computing the four Stokes parameters
and mapping the output data onto n-bit integers for data reduction)
it turned out that 192 of these DSPs could cover the processing of the
incoming 80 MHz band with up to 32768 channels (Sect. 4.3.2).
(DSP) a Complex Fast Fourier
Transform (CFFT) of 2048 points requires less than 1 ms. Together with
the other computational tasks (computing the four Stokes parameters
and mapping the output data onto n-bit integers for data reduction)
it turned out that 192 of these DSPs could cover the processing of the
incoming 80 MHz band with up to 32768 channels (Sect. 4.3.2).
Early on in the project it was realised that the data handling capacity would also allow baseband recording of two times 10 MHz continuously. The DSP computing power, of well over 20 Gflops, can be used to reduce the bandwidth (Sect. 4.3.1).
To facilitate its design and to limit the costs, it was decided to use
commercially available components as much as possible and to use
VME![]() as a means of assembling the digital
modules. The only significant exception was the development of a
(general purpose) printed circuit board that accommodates for 6 DSPs,
together with the necessary hardware to handle the incoming and
outgoing data.
as a means of assembling the digital
modules. The only significant exception was the development of a
(general purpose) printed circuit board that accommodates for 6 DSPs,
together with the necessary hardware to handle the incoming and
outgoing data.
The following sections summarise the various stages of signal handling, data processing and data storage of PuMa. Technical details of its design and construction are described by van Haren et al. (2000), whereas a detailed description of its data processing can be found in PuMa's user manual (Voûte & van Haren 1999). An introduction to PuMa is given by Voûte & van Haren (1998)
PuMa consists of two identical, but independent systems, each capable of processing the X and Y polarisation of four of the eight available WSRT frequency bands. Each system is mounted in a VME-crate, containing a workstation and four identical clusters (of 4 processor boards each) for those frequency bands. PuMa's signals go through a number of hardware modules as shown in Fig. 1.
As the two PuMa halves are independent it is possible to use one half
as a digital filterbank (Sect. 4.3.2) while the other acts
as a baseband recorder (Sect. 4.3.1). Combined with the
ability of WSRT to observe a source at several sky frequencies, PuMa can
record the signals from a given pulsar (in either or both modes)
simultaneously at those frequencies.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3013f1.ps}\end{figure}](/articles/aa/full/2002/14/aah3013/Timg7.gif) |
Figure 1:
PuMa's block scheme. The X and Y polarisations of each of the
8 WSRT frequency bands, labeled A to H, are digitised and routed to a
cluster of 4 processor boards, each board having 6 digital signal
processors. So, PuMa has 2 halves |
| Open with DEXTER | |
| Parameter | Range | |
| General | Observation duration (
|
|
| Clusters to be used | [0, ..., 7] | |
| Mode dependent | ||
| Baseband recording | Bandwidth reduction factor | 1, 2, 4, ..., 32 |
| Polarisations to be stored | [X, Y] | |
| Digital filterbank | Number of channels (
|
16, 32, ..., 4096 |
| Number of samples to add (
|
1, 2, 4, ...,
|
|
| Number of SHARCs to add (
|
1, 2, 3, 6 | |
| Stokes parameters to be stored | [I, Q, U, V] | |
| Mapping | Adjust method | fixed, dynamic |
| Scale value (if fixed) | ||
| Offset value (if fixed) | ||
| Minimum adjust interval | ||
| Mapping range ( |
||
| Number of bits | 1, 2, 4, 8 |
Analog-to-digital converters (ADCs) used in astronomy often have a small dynamic range due to their limited number of bits. Two bits is rather common and in that case it is important that the root-mean-square (rms) of the signal is compatible with the digitiser's threshold levels (Kouwenhoven & Voûte 2001a). The instantaneous rms of the incoming signals can vary considerably during observations, for instance from earth-bound interfering signals. Traditionally these variations in amplitude are controlled by means of an (analogue) automatic gain control (AGC), but these systems have some drawbacks. Unless heavily smeared by dispersion, pulsar signals are periodic increases in the rms of the incoming noise signals, and fast responding AGCs tend to eliminate these variations. This results in a reduction of the strength of the lower harmonics that make-up the pulse profile and hence distorts that profile and adversely affects the signal-to-noise ratio.
This can be avoided by giving the AGCs a slow response, which makes the profile distortion negligible. This advantage, however, is offset by the fact that if the incoming signal has a large (unwanted) deviation in strength of sufficient duration, it takes a relatively long time (typically several times the value of the AGC's time constant) before the signal strength is back to the desired level. During this time the signal is either too strong or too weak for such a digitiser to handle properly and again the signal-to-noise ratio is adversely affected.
In PuMa this problem was circumvented by using a single, commercially available, 12-bit ADC chip. The highest signal level at WSRT is determined by the addition of coherent signals from all 14 telescopes and this level is chosen near full range for the 12 bits. In practice the signal level never drops under the level that requires the lowest 6 converter bits, which makes the distortion (the digitisation noise) of this input ADC negligible. As a consequence, dealing with the maximum range of input signal strengths is passed on to the remainder of PuMa's data processing (Sect. 4.4).
The parameters are given in Table 1 for the two modes of observation, grouped under general parameters, observational mode specific parameters (Sects. 4.3.1 and 4.3.2) and parameters for the mapping of the floating-point data onto n-bit integers (Sect. 4.4).
In this mode PuMa samples the full 10 MHz width of an incoming WSRT
frequency band at the 20 MHz Nyquist frequency. The bandwidth of the
incoming signal can be reduced by factors of 2 to 32 in powers of two.
Digital low-pass filters, so called finite impulse response (FIR)
filters, are used and bandwidth reduction is done in the time domain
rather than in the frequency domain![]() . The filters are
designed to leave the relative phases of all frequencies intact, which
is essential for coherent dedispersion.
. The filters are
designed to leave the relative phases of all frequencies intact, which
is essential for coherent dedispersion.
In this filterbank mode the incoming 10 MHz frequency band is split
into a certain number of channels, i.e. frequency bands with a
correspondingly smaller bandwidth and hence a reduced dispersion
smearing within the channel. Each digital signal processor (DSP)
processes a number of samples that can range from 32 to 8192 in powers
of 2. The X and Y polarisations are processed simultaneously in a
single complex FFT as the real and imaginary inputs. From the
resulting complex spectrum the four Stokes parameters I, Q, U and Vare computed for the resulting 16 to 4096 frequency channels of each
band. At an input sampling rate of 20 MHz, this means that output
samples are produced every 1.6 ![]() s for 16 and 409.6
s for 16 and 409.6 ![]() s for 4096
channels. The bandwidth of these channels is then about 0.6 MHz and
2.4 kHz respectively. With PuMa's ability to process eight WSRT bands
in parallel, the maximum number of frequency channels over the
available 80 MHz is therefore 32768.
s for 4096
channels. The bandwidth of these channels is then about 0.6 MHz and
2.4 kHz respectively. With PuMa's ability to process eight WSRT bands
in parallel, the maximum number of frequency channels over the
available 80 MHz is therefore 32768.
Selecting the number of frequency channels has no effect on the data
rate, as a higher number of channels is compensated by the lower
output-sampling rate. Reduction of the data rate in this mode can be
achieved in two ways. Firstly, it is possible to select which of the
four available Stokes parameters are actually sent over the VME-bus to
storage. Secondly, the user can specify how many consecutive samples
in each frequency channel are accumulated to smooth the data. Further
data reduction is possible by adding the output samples from different
DSPs, which are on the same printed circuit board and can be in
factors 2, 3 or 6.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3013f2.ps}\end{figure}](/articles/aa/full/2002/14/aah3013/Timg13.gif) |
Figure 2:
Number of channels (
|
| Open with DEXTER | |
If
![]() is the number of channels,
is the number of channels,
![]() is the number
of samples that are added within a SHARC DSP and
is the number
of samples that are added within a SHARC DSP and
![]() is the
number of samples that are added from different SHARCs, then the final
sampling time
is the
number of samples that are added from different SHARCs, then the final
sampling time
![]() is:
is:
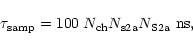 |
(1) |
The dots in Fig. 2 indicate all possible combinations
of
![]() and the product
and the product
![]() .
Combinations of constant
.
Combinations of constant
![]() are indicated with dashed
lines. For a pulsar with a given dispersion measure DM (i.e. the
integral of the electron density along the line of sight in pc cm-3) the dispersion smearing
are indicated with dashed
lines. For a pulsar with a given dispersion measure DM (i.e. the
integral of the electron density along the line of sight in pc cm-3) the dispersion smearing
![]() within one channel
is given by
within one channel
is given by
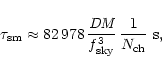 |
(2) |
If an observation is planned, the final time resolution ![]() has to
be set first. The optimal parameters are given by the dot that lies on
the dashed line
has to
be set first. The optimal parameters are given by the dot that lies on
the dashed line
![]() and is the nearest to the right
of the intersection of the dashed line and the solid line
and is the nearest to the right
of the intersection of the dashed line and the solid line
![]() for that observing frequency. Dots on the
dashed line further to the right of the intersection produce the same
time resolution, but have a higher data rate. Dots on the left of the
intersection have a dispersion smearing larger than the sampling time.
If the intersection is below
for that observing frequency. Dots on the
dashed line further to the right of the intersection produce the same
time resolution, but have a higher data rate. Dots on the left of the
intersection have a dispersion smearing larger than the sampling time.
If the intersection is below
![]() ,
than that
resolution can not be obtained with PuMa and WSRT.
,
than that
resolution can not be obtained with PuMa and WSRT.
As mentioned in Sect. 4.2, PuMa's dynamic range of
acceptable input values is more than adequate and the DSPs do their
processing with 32-bit floating-point variables. However, to limit the
amount of data to be stored, the outgoing data f are mapped onto
n-bit integers i according to
![\begin{displaymath}i = {\rm trunc}[ (f-\mathtt{offset}) \cdot \mathtt{scale} ] ,
\end{displaymath}](/articles/aa/full/2002/14/aah3013/img22.gif) |
(3) |
The user can specify the values for offset and scale, but
PuMa can also be instructed to determine the best values for each
outgoing time series dynamically. It does so by determining the mean
and rms of the time series to be mapped over a certain time interval,
which the user can set. With a user specified range (number ![]() of rms values to be mapped on both sides of the mean) the best values
for offset and scale are computed from the mean and rms
and applied in the next interval. PuMa stores the values of scale and offset, which are used over each adjustment interval,
so that (albeit with limited precision) the original time series can
be reconstructed.
of rms values to be mapped on both sides of the mean) the best values
for offset and scale are computed from the mean and rms
and applied in the next interval. PuMa stores the values of scale and offset, which are used over each adjustment interval,
so that (albeit with limited precision) the original time series can
be reconstructed.
Unlike traditional (analogue) automatic gain (and offset) controls, this feed-forward loop does not affect the shape of the pulse and the time to recover from strong interference is limited by the period at which the mapping parameters are updated.
Upon completion of an observation all data are stored on PuMa's hard disks in the raw format in which it was produced by the DSPs. All blocks of data from the DSPs are terminated with a control block, which contains status information of the various hardware modules, and some numerical information that allows consistency checking of the DSP processing. The workstations store the scales and offsets as used by the DSPs in the packing of the output data (Sect. 4.4). Raw data are later formatted into files to facilitate off-line processing and finally stored on tape. These files have a fixed header with all relevant data about the observation parameters, followed by a block which contains the scales and offsets as used by the packing routine and thereafter follow all the observational data. During the preparation of these files data consistency checks are carried out.
When required, PuMa can determine all relevant properties of the incoming signals in a few brief observations before the actual run. The properties in question are the values for the mapping onto the n-bit output samples and the equality of the X and Y polarisation signal strengths. The latter is essential if the four Stokes parameters are to be determined with the highest accuracy. A short baseband recording observation is used to determine the ratio of the individual strengths of the X and Y signals of each cluster. These signal strengths are usually unequal as a result of the normal tolerances of the equipment in the WSRT signal path, including PuMa's ADCs. PuMa uses this ratio to make the two polarisations equal in strength. The best way of achieving this equality is by observing an unpolarised radio source as a calibrator so that the incoming X and Ysignal strengths in each cluster are equal. The packing parameters for the X and Y polarisation signals for baseband recording can best be determined on the intended radio source. In the case where the machine is used as a digital filterbank, the last calibration step is made with a brief filterbank observation to determine the best individual packing parameters for each of the Stokes parameters in each of the clusters in use.
Testing the correct handling, processing and packing of data by PuMa is of prime importance for obtaining reliable results. Along with real data from the telescopes, PuMa can process artificially generated data. We compared the results from the artificial data as processed by PuMa and a "virtual'' PuMa (a Fortran programme on a UNIX workstation). Ignoring rounding-off errors due to the finite precision of the calculations done by each type of processor, the output for all combination of observational parameters and data must be identical. This feature was extremely helpful for testing the correctness of any modifications made in the software of the DSPs or the on-board workstations.
In this section we discuss a few results of observations made with PuMa at the WSRT to demonstrate its capabilities.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{h3013f3.ps}\end{figure}](/articles/aa/full/2002/14/aah3013/Timg23.gif) |
Figure 3:
Pulse profile of PSR B1937+21 observed in the baseband recording
mode (thick line) and the digital filterbankmode (thin line). Also indicated are
the dispersion smearing within one channel of the digital filterbank (
|
| Open with DEXTER | |
We have used an observation of the millisecond pulsar PSR B1937+21 at 328 MHz to show the difference between the baseband recording and the digital filterbank mode. One PuMa half was used in the baseband recording mode. Simultaneously the other half was used in the digital filterbank mode. The observation duration was almost 1000 s.
A band of 10 MHz width was baseband recorded
with 2-bit sampling (
![]() ,
see Kouwenhoven & Voûte
2001a for an explanation for this choice). The data were off-line
coherently dedispersed with DM = 71.037.
The resulting time series was folded using a prediction of the pulse
period
(Backer et al. 1982; Taylor et al. 1993, 1995) and the profile is displayed as a thick line in Fig. 3. Note that this profile is free of any dispersion
smearing. The data were smoothed to a resolution of 6
,
see Kouwenhoven & Voûte
2001a for an explanation for this choice). The data were off-line
coherently dedispersed with DM = 71.037.
The resulting time series was folded using a prediction of the pulse
period
(Backer et al. 1982; Taylor et al. 1993, 1995) and the profile is displayed as a thick line in Fig. 3. Note that this profile is free of any dispersion
smearing. The data were smoothed to a resolution of 6 ![]() s from the
original 50 ns to improve the SNR.
s from the
original 50 ns to improve the SNR.
The digital filterbank was configured with 1024 channels (width ![]() 10 kHz)
and
the square-law detected signals of each channel were 2-bit
sampled without any prior adding of samples (
10 kHz)
and
the square-law detected signals of each channel were 2-bit
sampled without any prior adding of samples (
![]() ,
so
,
so
![]() s) with
s) with
![]() ,
see Kouwenhoven & Voûte 2001b).
The
data were off-line (incoherently) dedispersed with the same dispersion measure
and to the same frequency as the coherently dedispersed data and were
folded using the same ephemeris. The resulting profile is displayed as
the thin line in Fig. 3. Note that the profile has 256 bins (the same number as
in the coherently dedispersed profile) and that the sampling time is about
15 times the binwidth (indicated with
,
see Kouwenhoven & Voûte 2001b).
The
data were off-line (incoherently) dedispersed with the same dispersion measure
and to the same frequency as the coherently dedispersed data and were
folded using the same ephemeris. The resulting profile is displayed as
the thin line in Fig. 3. Note that the profile has 256 bins (the same number as
in the coherently dedispersed profile) and that the sampling time is about
15 times the binwidth (indicated with
![]() ): the profile
is oversampled. This incoherently dedispersed profile does suffer from dispersion
smearing: the (remaining)
smearing within one channel is about 160
): the profile
is oversampled. This incoherently dedispersed profile does suffer from dispersion
smearing: the (remaining)
smearing within one channel is about 160 ![]() s (
s (![]() 27 bins, indicated
with
27 bins, indicated
with
![]() ).
).
The profiles are clearly different. The coherently dedispersed profile is much narrower. The incoherently dedispersed profile is formed by convolving the coherent profile with the dispersion function and the sampling window. Due to this convolution information is lost: e.g. the scattering tail of the profile is clearly visible in the coherent profile but remains hidden in the incoherent profile. A sharper profile will also benefit the determination of the time-of-arrival of the pulses.
The coherent profile contains 16 ![]() 4% less energy than the
incoherent profile. The uncertainty is dominated by the inaccuracy with which
the (off-pulse) baseline of the profile is determined: due to the broad profile
it is hard to determine which
part of the pulse is free of any emission. Since the off-pulse is
so short the baseline has a large error.
4% less energy than the
incoherent profile. The uncertainty is dominated by the inaccuracy with which
the (off-pulse) baseline of the profile is determined: due to the broad profile
it is hard to determine which
part of the pulse is free of any emission. Since the off-pulse is
so short the baseline has a large error.
The difference in energy is partly explained by digitisation losses. The pulses are dispersed over more than a hundred periods within the 10 MHz observation band, which runs from 323 to 333 MHz. Therefore, the baseband recorded data is not amplitude modulated. This data suffers only from loss of accuracy with which the phases of the frequencies in the band are recorded due to the 2-bit digitiser. According to Cooper (1970) the SNR loss in this case is about 12%.
The incoherently dedispersed time series are digitised at a point in the signal path were the channel width is only about 10 kHz. Therefore, these data are amplitude modulated, though with a very small modulation factor. The SNR loss due to 2-bit digitisation is in this case 6% (Kouwenhoven & Voûte 2001a) if the band is assumed to be flat. So, the coherent profile is expected to contain less energy than the incoherent profile, but the observed difference is larger than predicted. This is possibly caused by the deviation of the observed band from a flat one. In that case different channels have different digitisation loss factors. Especially when the pulsar is not equally strong within the band (e.g. due to scintillation) this leads to more (or less) loss of energy.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{h3013f4.ps} \end{figure}](/articles/aa/full/2002/14/aah3013/Timg31.gif) |
Figure 4: Giant pulse of the Crab pulsar (PSR B0531+21) at 1357.5 MHz. The time resolution of the plot is 100 ns. |
| Open with DEXTER | |
The Crab pulsar (PSR B0531+21) is known to emit so-called giant pulses, which can be hundreds of times stronger than an average pulse (Heiles et al. 1970; Staelin & Sutton 1970).
On Nov. 3, 1999 we observed this pulsar with PuMa in the baseband
recording mode, with a band centred at 1357.5 MHz and a width of 5 MHz.
The voltages were 2-bit sampled (
![]() ), stored and
coherently dedispersed off-line with a DM of 56.791 pc cm-3.
The data were detected (i.e. squared) and the samples from both
linear polarisations were added to form the total intensity.
), stored and
coherently dedispersed off-line with a DM of 56.791 pc cm-3.
The data were detected (i.e. squared) and the samples from both
linear polarisations were added to form the total intensity.
Figure 4 shows a giant pulse. Its maximum SNR is
![]() .
This time series is expected to have a
.
This time series is expected to have a ![]() -distribution
with four degrees of freedom (Kouwenhoven & Voûte 2001b). Since
the data have not been smoothed, the SNR shows strong fluctuations.
-distribution
with four degrees of freedom (Kouwenhoven & Voûte 2001b). Since
the data have not been smoothed, the SNR shows strong fluctuations.
At this observing frequency the average receiver temperature is known
to be ![]() K and the sky temperature is 3 K from the background
radiation and about
K and the sky temperature is 3 K from the background
radiation and about
![]() K from the Crab nebula. The
dispersion smearing is about a millisecond, which is a hundred times
longer than the duration of the giant pulse itself. This smearing time
is less than the typical time-constant of the AGC in the WSRT system
for these strong fluctuations, so this AGC does not affect the pulse.
Thirteen telescopes were operational during this observation. The gain
of WSRT in this configuration is
K from the Crab nebula. The
dispersion smearing is about a millisecond, which is a hundred times
longer than the duration of the giant pulse itself. This smearing time
is less than the typical time-constant of the AGC in the WSRT system
for these strong fluctuations, so this AGC does not affect the pulse.
Thirteen telescopes were operational during this observation. The gain
of WSRT in this configuration is
![]() K/Jy. From the
observed SNR the absolute flux density of the pulse can be
calculated (Kouwenhoven & Voûte 2001b). The flux density of the
peak of the giant pulse is
K/Jy. From the
observed SNR the absolute flux density of the pulse can be
calculated (Kouwenhoven & Voûte 2001b). The flux density of the
peak of the giant pulse is
![]() kJy.
kJy.
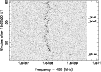 |
Figure 5: Dynamic spectrum of a Mars observation. The frequency resolution is 2.38 Hz, the time resolution is 1.68 s. The dashes on the right indicate the moments that the Mars Polar Lander was supposed to turn on and the moments that the telescope was moved away and back to Mars. Since the signal was not influenced by this movement, it can not originate from Mars. |
| Open with DEXTER | |
The maximum frequency resolution that can be obtained with PuMa in the digital filterbank mode is 10 MHz/ 4096 = 2.4 kHz. Sometimes smaller frequency channels are needed. This was the case when the National Aeronautics and Space Administration (NASA) requested help from the WSRT to try find the missing Mars Polar Lander (MPL). The lander descended on the red planet on December 3, 1999, but after that no signal was detected from the main transmitter of the Lander. The possibility still existed that a second transmitter that was originally intended to communicate with the Mars Global Surveyor (a Mars orbiter) was alive. The Surveyor did not detect the Lander, but this could be due to problems with the Surveyor's receiver. Large telescopes on Earth were requested to look directly for this weak signal from the Lander.
The signal from the Lander consisted of two components separated by 256 kHz, centred at about 401.515 MHz (after Doppler correction for the motion of Mars with respect to the Earth). The width of the signals was only about 1 Hz and it may have been drifting by about 1 Hz/s.
NASA sent instructions to the MPL to turn on its transmitter at 15:30:00 UT on February 4, 2000. This signal was expected to arrive 16 min and 55 s later on Earth.
WSRT observed Mars at that moment and the added signals from all dishes were 4-bit baseband sampled by PuMa with a bandwidth reduction factor of 8, i.e. a sampling time of 400 ns. The data were complex Fourier transformed with an FFT length of 220 on a fast off-line computer and hence, the final frequency resolution was 2.38 Hz. Four consecutive samples were added together to get a time resolution of 1.68 s.
Within one second of the expected arrival time PuMa detected a new
signal at one of the two component frequencies. The signal first
drifted over more than 100 kHz before it started wandering around a
mean frequency of 401.6408 MHz (Fig. 5). However, when
the dishes were moved to point a few degrees away from Mars, the
signal was not affected. No signal was found at the other component
frequency, but a similar signal was detected at about the same
frequency in an earlier observation, when the MPL transmitter was not
turned on and the telescope was pointed to an empty part of the sky.
We therefore concluded that this signal did not originate from the MPL
and was Earth-bound interference.
![\begin{figure}
\par\includegraphics[angle=270,width=17.2cm,clip]{h3013f6.ps} \end{figure}](/articles/aa/full/2002/14/aah3013/Timg40.gif) |
Figure 6:
Dispersion curve of the Crab pulsar (PSR B0531+21). The solid
line is the expected dispersion curve for a DM of 56.791 cm3 pc-1. The grey-scales are four observations made at different
frequencies. To obtain a time resolution of 102.4 |
| Open with DEXTER | |
The flexibility of setting the number of channels and the sampling
time is very useful when observing a pulsar at several frequencies.
To demonstrate this,
we observed the Crab pulsar (PSR B0531+21) for one hour at
328, 382, 840 and 1380 MHz. Due to interference
the bandwidth at the lowest two frequencies was limited to 10 MHz.
To obtain a time resolution of 102.4 ![]() s and minimise the amount
of data, we chose the
combinations of
s and minimise the amount
of data, we chose the
combinations of
![]() and
and
![]() ,
which were
on the dashed line of
,
which were
on the dashed line of
![]() s and the nearest
to the right of the solid line of
s and the nearest
to the right of the solid line of
![]() in
Fig. 2. This was not possible for 328 MHz, for which we
chose the nearest combination at the left of the solid line.
Figure 6 shows the
folded data per channel for each of the four observations.
in
Fig. 2. This was not possible for 328 MHz, for which we
chose the nearest combination at the left of the solid line.
Figure 6 shows the
folded data per channel for each of the four observations.
The majority of the WSRT receivers have dual linear feeds and from
the X and Y signals
the four Stokes parameters can be calculated. To demonstrate the
polarimetric capabilities of PuMa we observed PSR B0329+54
in the filterbank mode for about 600 s. The observation was made
at 1380 MHZ with a bandwidth of 10 MHz (one WSRT frequency band). The
data streams were recorded with 64 frequency channels and with an
effective time resolution of 102.4 ![]() s (
s (
![]() ,
see
Sect. 4.3.2). Each sample was 2-bit digitised.
,
see
Sect. 4.3.2). Each sample was 2-bit digitised.
We calibrated the telescope array for polarisation measurements, following the procedure given by Weiler (1973) and Weiler & Raimond (1976, 1977). After the calibration has been done, the instrumental leakages are small: generally the measured errors are about 1% in all of the eight frequency bands. Therefore, no extra polarimetric correction is applied in post processing.
Off-line the signals in all channels were added after removing the interstellar dispersion delay between the channels. The resulting time series was folded in all Stokes parameters with the rotation period of the pulsar, to construct an average pulse profile (Fig. 7). The solid line gives the total power as a function of pulse phase, the dashed and the dotted line give linear and circular power, respectively. In the bottom panel, the position angle of linear polarisation is drawn. Our profile is in accordance with the one observed by Gould & Lyne (1998).
Our profile is generally in accordance with the ones observed by von Hoensbroech & Xilouris (1997) and by Gould & Lyne (1998), although there are some minor differences. Our ratio of the height of the mean peak and of the side peaks is less than observed by the other authors due to saturation of our 2-bit digitisers (Kouwenhoven & Voûte 2001). Also the linear polarisation and the polarisation angle profile show small differences, but these may be attributed to differences in resolution, observing frequencies and number of integrated pulses.
As was explained in Sect. 2 WSRT allows for simultaneous multifrequency observation of one source by splitting the array into subarrays. The 14 telescopes and the 8 bands are divided over these subarrays. This possibility allows for potentially very interesting studies, mainly of individual pulses.
To test this capability we observed PSR B0329+54 with three subarrays
simultaneously. The telescopes and bands were grouped to obtained
roughly an equal SNR per pulse at each subarray, but it is hard to
predict the SNR of this pulsar because of severe scintillation
effects.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{h3013f7.ps} \end{figure}](/articles/aa/full/2002/14/aah3013/Timg44.gif) |
Figure 7: Pulse profile of PSR B0329+54. In the top panel the total intensity (solid line), the total linear polarisation (dashed line) and the circular polarisation (dotted line) are drawn. The bottom panel shows the polarisation angle |
| Open with DEXTER | |
The left panel of Fig. 8 shows 50 s of observations at three different frequencies: 382, 830 and 1405 MHz. It is clear that the pulse-to-pulse variation of the SNR is correlated over this frequency range. This is an indication that the individual pulses are broadband. Also the individual pulse shapes are correlated over this frequency range. The right panel of Fig. 8 shows an individual pulse, simultaneously observed at three different frequencies. At each frequency the pulse shape consists of the same components at different relative strengths.
 |
Figure 8: Left panel: simultaneous observation of PSR B0329+54 at three different frequencies, viz. 382, 830 and 1405 MHz. Right panel: one individual pulse from this time series. |
| Open with DEXTER | |
Acknowledgements
This work was performed as a joint project of the Anton Pannekoek Institute (University of Amsterdam) and the Astronomical Institute of the Utrecht University with financial support of the Netherlands Foundation for Research in Astronomy. PuMa was built by the Instrumentele Groep Fysica of the Utrecht University. The authors want to dedicate the PuMa project to the late prof. Dr. J. van Paradijs, who strongly supported the project from the very beginning.