A&A 385, 701-715 (2002)
DOI: 10.1051/0004-6361:20020130

The molecular Zeeman effect and diagnostics of solar and stellar magnetic fields

I. Theoretical spectral patterns in the Zeeman regime

S. V. Berdyugina1 - S. K. Solanki2


1 - Astronomy Division, University of Oulu, PO Box 3000, 90401 Oulu, Finland
2 - Max-Planck-Institut für Aeronomie, 37191 Katlenburg-Lindau, Germany

Received 7 September 1991 / Accepted 21 January 2002

Abstract
An overview of the theory of the Zeeman effect in diatomic molecules for the limiting Hund's cases (a) and (b) is given and a numerical approach for the intermediate coupling case (a-b) is developed. In contrast to earlier derivations, which were limited to doublets, this approach is valid for terms of any multiplicity. General properties of the Zeeman effect for the various cases are deduced. Finally, calculated Landé factors for prominent molecular bands in sunspot and cool-star spectra are employed to predict the general behaviour of these bands in the presence of a magnetic field below the Paschen-Back limit. The limiting field strength is calculated and listed.

Key words: molecular processes - Sun: magnetic fields - stars: magnetic fields - techniques: polarimetric


1 Introduction

The spectra of sunspots and of cool stars contain a rich collection of molecular lines (e.g. Wallace et al. 1998). Lines of diatomic molecules observed in sunspot spectra are good temperature and pressure indicators. They are also useful for determining elemental and isotopic abundances. However, little is known about their diagnostic capabilities for magnetic studies. The fact that the effect of the applied magnetic field in molecular lines is smaller and less striking than that observed in the most Zeeman sensitive atomic lines has significantly delayed their use for diagnosing solar and stellar magnetic fields.

With the development of observational facilities, however, reports of puzzling polarization signatures of molecular lines compared to atomic lines have appeared (e.g. Harvey 1973, 1985; Rüedi et al. 1995). These have not yet been understood. This is not surprising in view of the scarcity of theoretical work on the molecular Zeeman and Paschen-Back effects for different coupling and multiplet cases. Contributions made in the physical literature commonly tended to explain level splitting with very high accuracy which is not yet needed in astrophysics, while intensity and polarization patterns of lines were left out of consideration. Also, only a very limited sample of molecules has been studied in laboratories in the presence of a magnetic field. Moreover, the two latest theoretical investigations of the molecular Zeeman effect of spectral lines were separated by five decades (Hill 1929; Schadee 1978).

A review of theoretical and experimental work done before the 1930s was given by Crawford (1934). The major theoretical achievements were understanding the Zeeman effect in multiplet terms for pure Hund's cases (a) and (b) (Kronig 1928) and in doublet terms intermediate between case (a) and case (b) (Hill 1929). However, for the intermediate case, due to Hill's choice of case (b) basis functions, it was difficult to obtain analytical, relatively simple expressions explaining the intensity and polarization of the Zeeman components. Much later, Schadee (1978) repeated Hill's calculations for transitions between doublet states with arbitrary spin-orbit and spin-rotation interactions, but with Hund's case (a) wavefunctions as a basis set. In spite of the major advance which Schadee's work represents, until recently there has been, to our knowledge, only a single attempt to utilize this theory in astrophysics (Illing 1981). This is partly because the problem was solved analytically and only for doublet terms, so that the expressions, although somewhat simpler than those by Hill, remained rather unwieldy and, unfortunately, were published with misprints in the decisive equations (some of them are indicated by Schadee 1980). Nowadays, with considerable computer power at our disposal, the problem of intermediate coupling cases can be solved numerically and, in principle, for terms of any multiplicity.

Here we make use of this possibility to simplify and extend Schadee's description of the Zeeman effect for intermediate cases. The first successful application of this approach has been the first spectral synthesis of molecular Stokes parameters and the first successful fits to molecular Stokes I and V profiles observed in sunspots (Berdyugina et al. 2000). Still missing is a description of the theoretical approach and a thorough investigation of the diagnostic capabilities of Zeeman-split molecular lines and of their applications in studies of solar and stellar magnetic fields.

In the present paper we present details of calculations of the splitting patterns of lines of diatomic molecules observed in spectra of the Sun and other cool stars at weak and moderate magnetic fields, i.e. in the Zeeman regime. In the next paper of this series we investigate the diagnostic capabilities of the Zeeman-split molecular lines typical of solar and stellar spectra, while in still later papers we intend to investigate the molecular Paschen-Back effect. In Sect. 2 of the present paper, we give details of the theory of the molecular Zeeman effect for the two most important spin coupling cases and develop a numerical approach for the intermediate coupling case. In Sect. 3, we present an overview of the diatomic molecular transitions observed in optical and near infrared spectra of the Sun and cool stars and discuss the splitting and Landé factors of a large number of levels and lines.

   
2 The molecular Zeeman effect

The magnetic splitting of energy levels in the case of molecules occurs due to the same fundamental causes as in atoms: if a molecule possesses a non-zero magnetic moment, it interacts with an external magnetic field (Herzberg 1950). The largest contribution to the magnetic moment of a diatomic molecule is due to the magnetic moment associated with the orbital and spin angular momenta of electrons, ${\vec L}$ and ${\vec S}$, respectively, i.e.: ${\bf\mu} = {\mu_{\vec L}} + {\mu_{\vec S}}=\mu_0 ({\vec L}+2{\vec S})$, where $\mu_0$ is the Bohr magneton. If these moments are zero, the contributions from the rotational motion of the molecule and the spins of nuclei need to be taken into account. The energy of the interaction of the magnetic moment ${\bf\mu}$ with the external magnetic field ${\vec H}$ is the scalar product of the vectors:

\begin{displaymath}% \Delta E= - {\bf\mu \cdot {\vec H}}= - \mu_0 ({\vec L}+2{\vec S})\cdot {\vec H}, \end{displaymath} (1)

The energies of magnetic components, therefore, depend on how the electronic angular momenta are coupled to the rotation of the molecule.

  
2.1 Strong spin coupling - Hund's case (a)

In Hund's case (a), the electronic angular momenta, both orbital ${\vec L}$ and spin ${\vec S}$, are strongly coupled to the line joining the nuclei and interact very weakly with the rotation of the nuclei (Herzberg 1950). Therefore, their components along the internuclear axis, denoted by ${\vec \Lambda}$ and ${\vec \Sigma}$, respectively, form ${\vec \Omega}$, the total electronic angular momentum about the internuclear axis, with quantum numbers $\Omega=\vert\Lambda+\Sigma\vert$, where $\Lambda=0,1,2,\dots,L$ and $\Sigma=S,S-1,\dots,-S$. If $\Lambda$ is not equal to zero, there are 2S+1 multiplet components of a given electronic term. States with $\Lambda=0,1,2,3,\dots$ are denoted as $\Sigma, \Pi, \Delta, \Phi$, etc. ${\vec \Omega}$ and the angular momentum of nuclear rotation ${\vec R}$ form the resultant total angular momentum ${\vec J}$ with quantum numbers $J=\Omega,\Omega+1,\Omega+2,\dots$, resulting in the rotational structure of the multiplet subterm for given $\Lambda$ and $\Sigma $ (Fig. 1a). Therefore, in this case, the multiplet splitting of terms is larger than the rotational splitting.


  \begin{figure} \par\includegraphics[width=12.5cm,clip]{ms1893f1.eps}\end{figure} Figure 1: Vector diagrams of a diatomic molecule, denoted by the dumbell shape near the bottom of each frame, in a magnetic field in Hund's case (a) and (b). Solid ellipses indicate the precession of ${\vec J}$ in the magnetic field, ${\vec H}$. At the same time, in Hund's case (a), the much faster precession of ${\vec \Omega}$ about ${\vec J}$ takes place. In Hund's case (b), the nutation of ${\vec \Lambda}$ about ${\vec N}$ is much faster than the precession of ${\vec N}$ and ${\vec S}$ about ${\vec J}$, while the latter is much faster than the precession of ${\vec J}$ in the magnetic field. The faster motions are shown by dashed-line ellipses. ${\vec R}$ is the angular moment of nuclear rotation.
Open with DEXTER

The interaction of the molecular magnetic moment with the external magnetic field causes a precession of the total angular momentum, ${\vec J}$, about the field direction. The space quantization of ${\vec J}$ results in 2J+1 magnetic components ( $M=J,J-1,\dots,-J$) with different energies. If the interaction of the total angular momentum ${\vec J}$ with the external magnetic field ${\vec H}$ is much weaker than the interaction of ${\vec \Omega}$with the rotation, i.e. the magnetic splitting is smaller than the rotational splitting, the Zeeman regime is appropriate. In this case, simple analytical expressions for the Zeeman splitting patterns can be easily determined with the help of the vector diagram shown in Fig. 1a (Herzberg 1950). Since ${\vec L}$ and ${\vec S}$ are strongly coupled to the internuclear axis, the magnetic moment in this direction is equal to $(\Lambda+2\Sigma)\mu_0$. The precession of ${\vec \Omega}$ can be averaged as $\Omega/\sqrt{J(J+1)}$, while the precession of ${\vec J}$ about the magnetic field gives $M/\sqrt{J(J+1)}$. Finally, the magnetic splitting of the level J in Hund's case (a) is expressed as follows:

 \begin{displaymath}% \Delta E=\frac{(\Lambda+2\Sigma)\Omega}{J(J+1)}M\Delta\sigma_{0}=gM\Delta\sigma_{0}, \end{displaymath} (2)

where $\Delta\sigma_0=\mu_0 H$, and g is the analogue of the Landé factor for this case. Thus, the splitting is determined only by the quantum numbers of the transition and is independent of the molecular constants. This behaviour is analogous to the Zeeman effect of atomic lines. Examples of magnetic splitting of rotational levels in the $^2\Pi $ state ( $\Lambda=1, \Sigma=1/2$) in Hund's case (a) are shown in Fig. 2.

The electric dipole selection rules allow the transitions for which $\Delta\Omega\!=\!0,\pm1, \Delta\Lambda\!=\!0,\pm1, \Delta\Sigma\!=\!0, \Delta J\!=\!0,\pm1$, with $\Delta J\!=\!0$ being forbidden for $\Omega\!=\!0\!\rightarrow\!\Omega\!=\!0$ transitions. Note that states with $\Lambda\!=\!0$ always belong to Hund's case (b) and are discussed in Sect. 2.2. The three types of transitions with $\Delta J\!=\!+1,-1,0$ are called, respectively, the R, P and Q rotational branches. For a transition between the upper level $(\Omega',\Sigma',J',M')$ and lower level $(\Omega'',\Sigma'',J'',M'')$, the shift of the Zeeman component from the zero-field position is therefore

 
$\displaystyle % \Delta\sigma=(g'M'-g''M'')\Delta\sigma_{0}.$     (3)


  \begin{figure} \par\includegraphics[width=13.3cm,clip]{ms1893f2.eps}\end{figure} Figure 2: Magnetic splitting of rotational levels with different J in the $^2\Pi $ state ( $\Lambda\!=\!1, \Sigma\!=\!1/2$) for two Hund's cases. While in case (a) the splitting rapidly decreases to zero, in case (b) it becomes almost independent on J and approaches the constant value $\Delta\sigma_0=4.66860 \times 10^{-5}~H$ cm-1 which depends only on the field strength.
Open with DEXTER

Strengths of transitions between Zeeman sublevels are proportional to the squares of the matrix elements of the electric dipole operator (Kronig 1928; Hougen 1970; Schadee 1978):

\begin{displaymath}% \mathcal{S}^{\rm a}=q(\Omega',J',M',\Omega'',J'',M'')^2, \end{displaymath} (4)

which can be split into two parts, the first depending only on $\Omega $ and J, denoted here as $\mathcal{S}_{J'J''}$, and the second on J and M, denoted as $\mathcal{S}_{M'M''}$:

 \begin{displaymath}% \mathcal{S}^{\rm a}=\mathcal{S}_{J'J''}\mathcal{S}_{M'M''}, \end{displaymath} (5)

for which the relatively simple expressions are given in Tables 1 and 2. Note that the $\mathcal{S}_{M'M''}$ are normalized in such a way that their sum over all Zeeman transitions is equal to unity, so that $\mathcal{S}_{J'J''}$represents the line strength in the absence of a magnetic field, i.e. the Hönl-London factor. The normalization of the Hönl-London factors is chosen according to Whiting & Nicholls (1974).


 

 
Table 1: Strengths of transitions between rotational levels for Hund's case (a). In the formulae, $\Omega $ always means the smaller of $\Omega '$ and $\Omega ''$, while $J\!=J'$ for emission and $J\!=\!J''$ for absorption.
$\Delta J$ $\mathcal{S}_{J'J''}$
  $\Delta\Omega=0$ $\Delta\Omega=\pm1$
+1 $\frac{(J+1)^2-\Omega^2}{J+1}$ $\frac{(J\pm\Omega+1)(J\pm\Omega\pm1+1)}{2(J+1)}$
0 $\frac{\Omega^2(2J+1)}{J(J+1)}$ $\frac{(J+\Omega+1)(J-\Omega)(2J+1)}{2J(J+1)}$
-1 $\frac{J^2-\Omega^2}{J}$ $\frac{(J\mp\Omega)(J\mp\Omega\mp1)}{2J}$



 

 
Table 2: Strengths of transitions between Zeeman sublevels normalized in such a way that their sum over all Zeeman transitions for the given J' and J'' is unity. In the formulae, $J\!=\!J'$, $M\!=\!M'$ for emission and $J\!=\!J''$, $M\!=\!M''$ for absorption.
$\Delta J$ $\mathcal{S}_{M'M''}$
  $\Delta M=0$ $\Delta M=\pm 1$
+1 $\frac{(J+1)^2-M^2}{(J+1)(2J+1)(2J+3)}$ $\frac{(J+1\pm M)(J+2\pm M)}{2(J+1)(2J+1)(2J+3)}$
0 $\frac{M^2}{J(J+1)(2J+1)}$ $\frac{(J\mp M)(J+1\pm M)}{2J(J+1)(2J+1)}$
-1 $\frac{J^2-M^2}{J(2J-1)(2J+1)}$ $\frac{(J\mp M)(J-1\mp M)}{2J(2J-1)(2J+1)}$



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms1893f3a.eps}\par\include... ...{ms1893f3b.eps}\par\includegraphics[width=8.8cm,clip]{ms1893f3c.eps}\end{figure} Figure 3: Zeeman patterns of lines in different branches, arising in the electronic transition $^2\Delta-^2\!\Pi$ from the lower rotational level J=6.5, when both upper and lower states are either in Hund's case (a) (top row) or in Hund's case (b) (middle row). The bottom row displays the appearance of the intermediate case when the upper state is in case (a) and the lower state is in case (b). The components with $\Delta M\!=\!-1$ are plotted downward for the sake of clarity. The signs of the effective Landé factors of lines in the P and R branches are always opposite, if $\Delta\Lambda\!\neq\!0$. The splitting of lines of the R and P branches is largest for the intermediate case. Note also that in the Q branches the largest splitting occurs in the $\pi $-components ( $\Delta M=0$).
Open with DEXTER

Knowing the Zeeman shifts and strengths of transitions, we can thus calculate the effective Landé factor:

 \begin{displaymath}% g_{\rm eff}=\sum_{M''}\widetilde{\mathcal{S}}_{M'M''}(g'M'-g''M''), \end{displaymath} (6)

where $\widetilde{S}_{M'M''}$ are strengths normalized as follows:

 \begin{displaymath}% \sum_{\Delta M=k}\widetilde{\mathcal{S}}_{M'M''}=1, \hspace{5mm} k=+1,0,-1. \end{displaymath} (7)

The effective Landé factors are useful for the so-called weak-field approximation, when the magnetic splitting is smaller than the line width broadened by other processes. For most molecular transitions under solar conditions this approximation is acceptable (in the Zeeman regime). With the selection rules, we can obtain expressions for the effective Landé factors of the transitions belonging to the three rotational branches as follows:
 
         $\displaystyle % g_{\rm eff}(R)$ = g'(J'+1)-g''J'',  
$\displaystyle g_{\rm eff}(P)$ = -g'J'+g''(J''+1),  
$\displaystyle g_{\rm eff}(Q)$ = g'+g'', (8)

or, using the expressions for the Landé factors for upper and lower levels,
                        $\displaystyle % g_{\rm eff}(R)$ = $\displaystyle \Delta\Omega\frac{\Omega'+\Omega''+\Sigma}{J''+1}$  
$\displaystyle g_{\rm eff}(P)$ = $\displaystyle -\Delta\Omega\frac{\Omega'+\Omega''+\Sigma}{J''},$ (9)
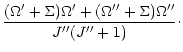$\displaystyle g_{\rm eff}(Q)$ = $\displaystyle \frac{(\Omega'+\Sigma)\Omega'+(\Omega''+\Sigma)\Omega''}{J''(J''+1)}\cdot$  

The Zeeman patterns of lines in different branches are shown in Fig. 3.

From an analysis of the Landé factors, some useful conclusions can be drawn for Hund's case (a).

  
2.2 Weak spin coupling - Hund's case (b)

In Hund's case (b), the orbital angular momentum of the electrons is coupled to the internuclear axis, whereas the spin is either very weakly coupled to the axis or not coupled to it at all (Herzberg 1950). For instance, when $\Lambda=0$, and $S\neq 0$, the spin is not coupled to the axis and, thus, ${\vec \Sigma}$ and ${\vec \Omega}$ are not defined. In Hund's case (b), the orbital angular momentum ${\vec \Lambda}$ and the angular momentum of nuclear rotation form ${\vec N}$, the total angular momentum excluding spin, with quantum numbers $N=\Lambda,\Lambda+1,\Lambda+2,\dots$. If $\Lambda=0$, the angular momentum ${\vec N}$ is identical with the rotational moment. Finally, the angular momenta ${\vec N}$ and ${\vec S}$ form a resultant ${\vec J}$, the total angular momentum including spin, with quantum numbers $J=N+S,N+S-1,\dots,\vert N-S\vert$. Thus, in general, each level with a given N consists of 2S+1 multiplet components. Since the spin is now coupled to rotation, in this case, the rotational splitting of terms is larger than the multiplet splitting.

If the interaction of the total angular momentum ${\vec J}$ with the external magnetic field ${\vec H}$ is much weaker than the interaction of ${\vec S}$ with the rotation, i.e. the magnetic splitting is smaller than the multiplet splitting of rotational levels, the Zeeman regime is appropriate. Then, the energies of the Zeeman patterns can be obtained with the help of the vector diagram for Hund's case (b) (Fig. 1b). Here, the magnetic moment in the direction of ${\vec J}$ is composed of the contribution due to $\Lambda\mu_0$ and $2\sqrt{S(S+1)}\mu_0$ (Herzberg 1950). The nutation of ${\vec \Lambda}$ about ${\vec N}$ averages as $\Lambda/\sqrt{N(N+1)}$, and the precession of ${\vec N}$ about ${\vec J}$ results in $\frac{J(J+1)+N(N+1)-S(S+1)}{2\sqrt{J(J+1)}\sqrt{N(N+1)}}$. The precession of ${\vec S}$ about ${\vec J}$ averages as $\frac{J(J+1)+S(S+1)-N(N+1)}{2\sqrt{J(J+1)}\sqrt{N(N+1)}}$. Finally, the precession of ${\vec J}$ about the magnetic field direction results in the same average as in Hund's case (a), namely $M/\sqrt{J(J+1)}$(see Fig. 1b). Then, the magnetic splitting of the rotational level J is expressed as follows:

 
                      $\displaystyle % \Delta E$ = $\displaystyle \frac{M\Delta\sigma_{0}}{J(J+1)}\Big\{ \frac{\Lambda^2}{2N(N+1)} [J(J+1)+N(N+1)-S(S+1)]$  
    $\displaystyle +J(J+1)-N(N+1)+S(S+1)\, \Big\}$  
  = $\displaystyle gM\Delta\sigma_{0},$ (10)

where g is the Landé factor for this case. As in case (a), the splitting is again determined only by the quantum numbers of the transition and is independent of the molecular constants. Examples of Zeeman splittings of rotational levels with different J are plotted in Fig. 2 (lower panel). Note the difference in behaviour of the Zeeman splitting with increasing J, as compared to Hund's case (a) (upper panel).

The electric dipole selection rules allow transitions for which $\Delta\Lambda\!=\!0,\pm1, \Delta S\!=\!0, \Delta N\!=\!0,\pm1$, $\Delta J\!=\!0,\pm1$ with $\Delta N\!=\!0$ being forbidden for $\Lambda\!=\!0\!\rightarrow\!\Lambda\!=\!0$ transitions. If $\Delta J\!=\!\Delta N$, then the rotational branches R, P and Q with $\Delta J\!=\!+1,-1,0$, respectively, are called main. If $\Delta J\!\neq\!\Delta N$, satellite branches appear, e.g. P$R,\, ^Q$P, etc., where the left superscript denotes the branch type according to the value of $\Delta N$. For a transition between the upper level $(\Lambda',S',N',J',M')$ and lower level $(\Lambda'',S'',N'',J'',M'')$, the shift of the Zeeman component from the zero-field position is calculated according to Eq. (3) with Landé factors given by Eq. (10).

Strengths of transitions between Zeeman sublevels in Hund's case (b) differ from those of case (a), although they can also be represented as a product of two parts, the first depending on $\Lambda$, J and N, denoted here for simplicity as $\mathcal{S}_{N'N''}$, and the second depending on J and M and being the same as in Eq. (5):

 \begin{displaymath}% \mathcal{S}^b=\mathcal{S}_{N'N''}\mathcal{S}_{M'M''}. \end{displaymath} (11)

Here, $\mathcal{S}_{N'N''}$ is the Hönl-London factor for Hund's case (b). When both electronic states involved in the transition are of case (b), expressions of $\mathcal{S}_{N'N''}$ are relatively simple for states of a given multiplicity (see e.g. Schadee 1964).

The effective Landé factors for Hund's case (b) are calculated using Eq. (6) under the normalization given by Eq. (7). As the intensities of the Zeeman components are the same as in Hund's case (a) (see Table 2), the expressions given by Eq. (8) can be used to calculate the effective Landé factors of lines in the main branches. The Zeeman patterns of lines in different branches for Hund's case (b) are shown in Fig. 3.

From the analysis of the effective Landé factors, we can draw some useful conclusions for Hund's case (b) as well.

  
2.3 Intermediate coupling cases

  
2.3.1 Spin uncoupling

It often happens that one of the states or even both are in an intermediate coupling case, i.e. between Hund's cases (a) and (b). Actually, a molecule in slow rotation generally is well described by case (a), whereas for increased rotation case (b) provides a better approximation. Thus, as the molecule gradually passes from a state of slow rotation (with low values of the rotational quantum number J) to one of increased rotation (with higher values of J), the uncoupling of the spin momentum from the molecular axis and its coupling to rotation also takes place gradually. Hence, the Zeeman splitting of levels also gradually changes from Hund's case (a) to (b) as J increases. This transition is treated as a first order perturbation of the pure Hund's cases.

Below we describe the perturbation calculation of the molecular Zeeman effect for the intermediate case (a-b) for terms of any multiplicity. This is in contrast to previous work, which was restricted to doublets.

Consider the effective Hamiltonian consisting of the sum of the spin-orbital, rotational and magnetic energies:

 \begin{displaymath}% \mathcal{H}=\mathcal{H}_{\rm SO}+\mathcal{H}_{\rm rot}+\mathcal{H}^{\rm H} =\mathcal{H}^{\rm ab}+\mathcal{H}^{\rm H} \end{displaymath} (12)

which can be split into two parts, $\mathcal{H}^{\rm ab}$ and $\mathcal{H}^{\rm H}$, the former performing the transformation of the case (a) wavefunctions $\Psi^{\rm a}$ into the intermediate case wavefunctions $\Psi^{\rm ab}$ and the latter describing the interaction with the external magnetic fields. Because of the weak interaction with the magnetic field in the Zeeman regime, the two parts of the Hamiltonian can be treated separately.

The diagonal matrix elements of the Hamiltonian determining the fine and rotational structure of the electronic state with Hund's case (a) wavefunctions as a basis set are given by (Kovàcs 1969):

 
$\displaystyle \mathcal{H}^{\rm ab}(\Lambda,\Sigma;\Lambda,\Sigma) = A_v\Lambda\Sigma +B_v[J(J+1)-\Omega^2+S(S+1)-\Sigma^2],$ (13)

where Av is the constant of the spin-orbit interaction and Bv is the rotational constant for a given vibrational state v. The off-diagonal matrix elements of $\mathcal{H}^{\rm ab}$ are expressed as follows (Kovàcs 1969):
 
$\displaystyle \mathcal{H}^{\rm ab}(\Lambda,\Sigma;\Lambda,\Sigma\pm1) = B_v\sqrt{S(S+1)-\Sigma(\Sigma\pm1)}\sqrt{J(J+1)-\Omega(\Omega\pm1)}.$ (14)

Then, the intermediate case wavefunctions are obtained from the case (a) wavefunctions by the transformation

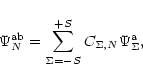\begin{displaymath}% \Psi^{\rm ab}_{N}=\sum_{\Sigma=-S}^{+S}C_{\Sigma,N} \Psi_{\Sigma}^{\rm a}, \end{displaymath} (15)

the coefficients of the linear combination being the elements of the eigenvectors of the perturbation matrix given by Eqs. (13) and (14). These eigenvectors are found numerically.

The second step in the calculation is to find the effect of the external magnetic field on the new wavefunctions $\Psi_N^{\rm ab}$. Matrix elements of the perturbation $\mathcal{H}^{\rm H}$ due to the interaction with the magnetic field are given by (e.g. Schadee 1978):

 
                                     $\displaystyle \mathcal{H}^{\rm H}(\Lambda,\Sigma; \Lambda,\Sigma) = \frac{(\Lambda+2\Sigma)\Omega}{J(J+1)}M\Delta\sigma_0,$  
    $\displaystyle \mathcal{H}^{\rm H}(\Lambda,\Sigma; \Lambda,\Sigma\pm1) = \frac{M\Delta\sigma_0}{J(J+1)}\sqrt{S(S+1)-\Sigma(\Sigma\pm1)}$  
    $\displaystyle \qquad\times\sqrt{J(J+1)-\Omega(\Omega\pm1)}.$ (16)

Then, the Zeeman shifts of the energy levels are obtained as follows:

 \begin{displaymath}% \Delta E=\sum_{\Sigma_k}\sum_{\Sigma_j} C_{\Sigma_k,N} C_{\... ...{\mathcal{H}^{\rm H}}_{\Sigma_k\Sigma_j} = gM\Delta\sigma_{0}, \end{displaymath} (17)

where ${\mathcal{H}^{\rm H}}_{\Sigma_k\Sigma_j}$ are the elements of the perturbation matrix given by Eq. (16) and the Landé factor g is now a linear combination of the perturbation matrix elements divided by $M\Delta\sigma_0$. It is obvious that even for doublet terms the analytical expressions of the intermediate Landé factors are rather complicated, while for terms of higher multiplicity they become extremely unwieldy. For this reason we restricted ourselves to numerical calculations of the intermediate case Landé factors for the terms of our interest (which are discussed in Sect. 3).

The elements $C_{\Sigma,N}$ and, thus, the Landé factors depend on the spin-orbit coupling and rotational constants. The ratio $Y\!=\!A_v/B_v$characterizes how close the coupling is to the limiting cases. For $Y\!\gg\!J(J+1)$ the Landé factor takes the form of case (a) given by Eq. (2); for $Y\!\ll\!J(J+1)$ it approaches case (b) given by Eq. (10).

Strengths of transitions between Zeeman sublevels in the intermediate case can be expressed with the help of the elements of the transformation matrix (Kovàcs 1969):

 
$\displaystyle \mathcal{S}^{\rm ab} = \mathcal{S}_{N'N''}^{J'J''}\mathcal{S}_{M'M''}$  
$\displaystyle \mathcal{S}_{N'N''}^{J'J''} = \vert\sum_{\Sigma=-S}^{+S} C_{\Sigma,N'}\sqrt{\mathcal{S}_{J'J''}}C_{\Sigma,N''}\vert^2.$ (18)

Here, $\mathcal{S}_{N'N''}^{J'J''}$ and $\mathcal{S}_{J'J''}$ are the Hönl-London factors for the intermediate Hund's case (a-b) and pure case (a), respectively. The latter have been introduced in Eq. (5) and are tabulated in Table 1. $\mathcal{S}_{M'M''}$ is the normalized strength of the Zeeman component (cf. Eqs. (5) and (11)), it is tabulated in Table 2. The transformation matrix coefficients $C_{\Sigma,N'}$ and $C_{\Sigma,N''}$ are calculated for the upper and lower states involved in the transitions.

The analytical expressions of the matrix elements $C_{\Sigma,N}$ and Hönl-London factors $\mathcal{S}_{N'N''}^{J'J''}$ for various multiplet states are given by Kovàcs (1969), although they can be easily calculated numerically as described above. The intermediate case Hönl-London factors are to be normalized according to the sum rule given by Whiting & Nicholls (1974).

The most important conclusions for the intermediate case (a-b) are the following.

2.3.2 Orbital momentum uncoupling

Rotational levels of states with $\Lambda\neq0$ are usually doubly degenerate, since the projection of the orbital angular momentum onto the internuclear axis can have two values: $+\Lambda$ and $-\Lambda$. The degeneracy is removed if the interaction of the orbital momentum with the rotation of the nuclei is taken into account (e.g. Herzberg 1950; Kovàcs 1969). If both states have $\Lambda\neq0$, rotational lines appear as doublets arising due to transitions between the rotational sublevels of different symmetry. This phenomenon is called $\Lambda$-type doubling.

The two sublevels arising due to the possible projections become energetically non-equivalent because of the interaction of the orbital angular momentum with the rotation and consequent uncoupling of the former from the internuclear axis. The case of complete uncoupling of the orbital angular momentum from the internuclear axis is classified as Hund's case (d). It can therefore be stated that $\Lambda$-type doubling reflects an early stage of the gradual transition from case (a) or case (b) to case (d). Taking into account the orbit-rotation interaction in the perturbation calculations should alter the relative intensities and magnetic splitting of lines of the $\Lambda$-doublets, which are assumed to be equal without such interaction. Although it is in principle possible to include this effect in our approach, here we neglect this perturbation as its effect is an order of magnitude smaller than the perturbation considered in Sect. 2.3.1 (e.g. Radford 1962). Therefore, by neglecting perturbations due to ${\vec L}$ uncoupling we introduce an error that is only of the order of 10-3 for the Landé factor of a given level. For astronomical purposes this accuracy is quite adequate.

  
3 Molecules observed in solar and stellar spectra

In the visible part of sunspot spectra, lines of about 10 diatomic molecules have been identified. They arise due to electronic-vibration-rotational transitions. These transitions are observed in spectra of cool stars as well. In Table 3 we present a list of the transitions of interest. In order to identify Hund's case, for each electronic state we give minimum multiplet and rotational splittings. Recall that the state belongs to Hund's case (a) if its multiplet splitting is larger than the rotational one, and to case (b) if it is vice versa. If the two kinds of splitting are of a comparable size or their relation changes when J increases, the states are classified as intermediate between the two cases. As multiplet splitting increases rapidly with the number of electrons (Herzberg 1950), lighter molecules have normally states described by Hund's case (b) or intermediate, while heavier molecules tend to have states in Hund's case (a).


   
Table 3: Diatomic molecules having transitions in the optical and near IR that are present in sunspot spectra.
    Mult. Rot. Mag. Hund's
  State split.(1) split.(1) field(2) case
    (cm-1) (cm-1) (G)  
TiO $X^3\Delta$ 96 2.2 $4.7\,\times10^4$ a
  $A^3\Phi$ 170 3.1 $6.6\,\times10^4$ a
  $B^3\Pi$ 16 1.0 $2.1\,\times10^4$ a-b(3)
  $C^3\Delta$ 90 2.0 $4.3\,\times10^4$ a
  $a^1\Delta$ - 3.2 $6.9\,\times10^4$ a
  $b^1\Pi$ - 2.0 $4.3\,\times10^4$ a
  $c^1\Phi$ - 4.2 $9.0\,\times10^4$ a
C2 $a^3\Pi$ 15.3 3.3 $7.1\,\times10^4$ a-b
  $d^3\Pi$ 16.9 3.5 $7.5\,\times10^4$ a-b
CH $X^2\Pi $ 27.9 57.6 $6.0\,\times10^5$ b
  $A^2\Delta$ 2.0 89.4 $4.3\,\times10^4$ b
OH $X^2\Pi $ 139 56.7 $1.2\,\times10^6$ a-b
  $A^2\Sigma$ 0.1 34.8 2100 b
CN $X^2\Sigma$ 0.0036 3.8 77 b
  $A^2\Pi$ 52.6 26.1 $5.6\,\times10^5$ a-b
  $B^2\Sigma$ 0.0078 3.9 167 b
MgH $X^2\Sigma$ 0.013 11.6 280 b
  $A^2\Pi$ 35.3 7.8 $1.7\,\times10^5$ a-b
  $B'^2\Sigma$ $\dots^{(4)}$ 12.4 $\dots^{(4)}$ b
CaH $X^2\Sigma$ 0.022 8.6 470 b
  $A^2\Pi$ 79 12.9 $2.8\,\times10^5$ a-b
  $B^2\Sigma$ 0.0069 8.6 148 b
FeH $^4\Delta$ 191 19.5 $4.1\,\times10^5$ a-b
  $^4\Delta$ 214 17.5 $3.7\,\times10^5$ a-b

(1) Multiplet and rotational splittings are given for the closest levels, i.e. they represent minimum splittings in a given state.
(2) The equivalent magnetic field strength is calculated for the smallest splitting in the state. It represents an estimate of the field
strength at which the Zeeman regime is no longer valid and the Paschen-Back effect has to be taken into account.
(3) Hund's case changes from (a) to (b) as J increases.
(4) Multiplet splitting was not resolved (Balfour & Cartwright 1976).


As discussed in Sect. 2, for the Zeeman regime to be valid, the magnetic splitting of molecular levels must be smaller than their multiplet or rotational splitting, depending on Hund's case. For the molecules of interest, we list in Table 3 the magnetic field strength which produces a Zeeman splitting equal to the smallest splitting of the electronic state, be it multiplet or rotational. The tabulated field strengths represent estimates below which the Zeeman regime is appropriate. One can see that all $\Sigma $ states, which are always in case (b), can be treated in the Zeeman regime only at very weak fields, generally below 500G. This happens because the spin-rotational coupling is usually so weak that these two angular momenta are uncoupled even by a small field. This is the molecular analogue of the atomic Paschen-Back effect. In a forthcoming paper we will discuss this effect and review the states suffering from it. All other states, in both Hund's cases, can be treated in the Zeeman regime with high confidence up to at least 10kG. Such strong fields are normally not observed on the Sun and other cool stars. Transitions within or between such states can be described by the formalism outlined in this paper. Exceptions to this rule may be cool magnetic white dwarfs, which can have strong fields.


  \begin{figure} \par\includegraphics[width=15.8cm,clip]{ms1893f4a.eps}\par\includ... ...ms1893f4b.eps}\par\includegraphics[width=15.8cm,clip]{ms1893f4c.eps}\end{figure} Figure 4: Landé factors for the triplet states of TiO calculated for pure Hund's cases (a) and (b) - solid lines, and for the intermediate (a-b) case - dashed lines.
Open with DEXTER

When studying magnetic fields in sunspots or on K- and M-type stars, molecular lines often are a source of great irritation. Such analyses generally only employ profiles of atomic lines, most of which are blended by molecular lines in sunspot spectra and in the spectra of cool stars. In order to compensate for these blends, the Zeeman-split molecular line profiles must be synthesized. An important example are the OH lines blending the Fe I 15652.9 Å line in sunspot umbrae (Berdyugina et al. 2002; Lagg et al., in preparation). On the other hand, the stronger and more magnetically sensitive molecular lines can provide a powerful diagnostic tool for studying solar and stellar magnetic fields. Therefore, we calculated Landé factors for the states listed in Table 3 and the effective Landé factors of the transitions between these states. These Landé factors are valid within the Zeeman regime, i.e. for field strengths below those listed in Table 3. Below we summarize the magnetic properties of the molecular states listed in Table 3 and transitions between or within them. Calculations for pure cases (a) and (b) are valid for any vibrational band in a given electronic system. The perturbation calculations for the intermediate case are always made for the (0, 0) band, if not mentioned otherwise.

3.1 TiO

The triplet states of TiO are under strong spin-orbit coupling, except probably the $B^3\Pi$ state. Recently we showed that the Zeeman splitting of the $\alpha\,(C^3\Delta-X^3\Delta)$ and $\gamma\,(A^3\Phi-X^3\Delta)$ systems calculated for pure Hund's case (a) reproduced the Stokes V profiles observed in sunspots very well (Berdyugina et al. 2000). Therefore, the case (a) effective Landé factors for these systems should generally be adequate, especially for transitions between lower rotational levels.

In order to estimate deviations from case (a), we carried out perturbation calculations as described in Sect. 2.3.1. For the coupling constant Y we used values close to: 96 ($X^3\Delta$), 116 ($A^3\Phi$), 42 ($B^3\Pi$), and 99 ($C^3\Delta$), respectively (Ram et al. 1999; Phillips 1973). These values imply that deviations from case (a) are to be expected for rotational levels with J larger than 10, 11, 6, and 10, respectively. Indeed, as the perturbation calculations show, some deviations appear starting from around these levels (see Fig. 4), although case (a) remains a very good approximation for all states except $B^3\Pi$. As shown in Fig. 4, the $B^3\Pi_2$ state represents a very good example of the gradual spin uncoupling as J increases, so that for lower rotational levels (J<5) the case (a) Landé factors are a good approximation, while for higher levels (J>25) the case (b) Landé factors are better. It is interesting that the case (a) and (b) Landé factors of the states with the spin projection zero ( $X^3\Delta_2$, $A^3\Phi_3$, $B^3\Pi_1$, $C^3\Delta_2$) are not very different (the second row in Fig. 4), so that the perturbation calculation does not alter very much the effective Landé factors of the R2, P2 and Q2 branches.

It is remarkable also that levels that are magnetically insensitive when described in case (a) become split because of the applied perturbation. This is the case for the $X^3\Delta_1$, $B^3\Pi_0$ and $C^3\Delta_1$ states (see the first row in Fig. 4). Since in these states $(\Lambda+2\Sigma)\Omega=0$, the case (a) Landé factors are zero as well. The small spin uncoupling, however, removes the degeneracy of the levels.

  \begin{figure} \par\includegraphics[width=13.2cm,clip]{ms1893f5.eps}\end{figure} Figure 5: The effective Landé factors for the TiO $\alpha $-system calculated in the Zeeman regime for case (a) - left panel, and deviations from them due to the perturbation caused by spin uncoupling - right panel. R, Q and P branches are represented by solid, dashed and dashed-dotted lines, respectively. In case (a) $g_{\rm eff}$ of all R and P branches as well as of the Q1 branch are zero.
Open with DEXTER


  \begin{figure}\includegraphics[width=13.4cm,clip]{ms1893f6.eps}\end{figure} Figure 6: The same as Fig. 5 for the $\gamma $-system. All lines of the system are magnetically sensitive, especially those in the P3 and R3 branches.
Open with DEXTER


  \begin{figure}\includegraphics[width=13.4cm,clip]{ms1893f7.eps}\end{figure} Figure 7: The same as Fig. 5 for the $\gamma '$-system. In case (a) (left panel) the $g_{\rm eff}$ of the R1, P1 and Q1 branches are zero. With the perturbation taken into account, the magnetic sensitivity of the P1, P3 and R1, R3 branches increases with J, while that of the other branches is only slightly modified.
Open with DEXTER

Turning now from the splitting of individual levels to the Zeeman effect of transitions we find that the $\alpha (C^3\Delta-X^3\Delta)$ system has, among others, the lowest magnetic sensitivity: the $g_{\rm eff}$ of its P and R branches are exactly zero in case (a), since $\Delta\Omega=0$ (Fig. 5). Also, as noted above, the first multiplet substates $\Delta_1$ are not Zeeman sensitive in case (a), since $\Lambda+2\Sigma=0$ (see Eq. (2)), which results in zero effective Landé factors of the Q1 branch as well. Lines of the Q2 and Q3 branches exhibit a Zeeman triplet splitting for small J numbers, but the strengths of lines are very small and decrease rapidly as J increases. The perturbation does not modify significantly the magnetic sensitivity of the branches whose effective Landé factors are still close to zero (Fig. 5).

The $\gamma $-system $(A^3\Phi-X^3\Delta)$ is one of the most magnetically sensitive systems, especially the P3 and R3 branches with $\vert g_{\rm eff}\vert\leq2.1$ (Fig. 6). The deviations because of the perturbation are small for small J numbers but become significant for larger J. This results in a gradual increase of $\vert g_{\rm eff}\vert$ as a function of J, so that $\vert g_{\rm eff}\vert$ approach 0.3-0.5 at $J\!=\!30$ for the P and R branches. Lines of all Q as well as the P2 and R2 branches are the least perturbed.


  \begin{figure} \par\includegraphics[width=13.5cm,clip]{ms1893f8.eps}\end{figure} Figure 8: The effective Landé factors for the TiO singlet band systems calculated in the Zeeman regime. R, Q and P branches are represented by solid, dashed and dashed-dotted lines.
Open with DEXTER

The most significant deviations due to the perturbation are seen for the $B^3\Pi$ state. This alters significantly the effective Landé factors of lines of the $\gamma '$-system $(B^3\Pi-X^3\Delta)$. The spin coupling in the upper electronic state is completely transformed from case (a) into case (b) over a rather small range of J values (see Fig. 4). Because of this, the $\vert g_{\rm eff}\vert$ of the P1, P3 and R1, R3 branches increase and take values between 2 and 1, even for large J numbers (Fig. 7). Landé factors of lines of the other branches are not significantly perturbed, which is typical for all the TiO triplet systems.

For singlet states the total spin $S\!=\!0$. Then, there is no difference between pure Hund's cases (a) and (b), and the expressions for Landé factors given by Eqs. (2) and (10) are reduced to the same formula. Thus, the effective Landé factors of the $\beta\,(c^1\Phi-a^1\Delta)$ and $\delta\,(b^1\Pi-a^1\Delta$) systems calculated with no perturbations are correct in the first order approximation. These are presented in Fig. 8. The systems show moderate magnetic sensitivity with $\vert g_{\rm eff}\vert\leq1.6$, which rapidly decreases as J increases.

On the basis our Landé-factor calculations we conclude that most TiO lines with $J\leq12$ and also larger J for the $\gamma '$-system observed in spectra of sunspots and cool stars are potentially good indicators of surface magnetic fields.

3.2 CH


  \begin{figure} \par\includegraphics[width=13.8cm,clip]{ms1893f9.eps}\end{figure} Figure 9: The effective Landé factors for the CH A-X system calculated in the Zeeman regime for case (b) - left panel, and deviations from them due to the perturbation caused by incomplete spin uncoupling - right panel. R, Q and P branches are represented by solid, dashed and dashed-dotted lines.
Open with DEXTER

Lines of the $A^2\Delta\!-\!X^2\Pi$ system are responsible for the spectral feature called the G-band, which plays a key role in stellar spectral classification. When the Sun is imaged in G-band radiation, it reveals the presence of the so-called G-band bright points, which correspond to small-scale magnetic structures within intergranular lanes (cf. Berger & Title 2001 and references therein). However, the relationship between the G-band bright points and the magnetic field is not entirely straightforward and in need of clarification, in particular since the bright points are a subject of intensive study. Therefore, the magnetic properties of the CH lines, which provide a major contribution to the G-band, are of great importance.

Because of small values of the spin coupling constants (Y'=-0.075 and Y''=2, Bembenek et al. 1990) both electronic states of the system are of pure case (b). The deviations due to incomplete spin uncoupling are rather small (Fig. 9) and occur only for the very first lines of the R1, R2 and Q2  rotational branches. The magnetic sensitivity of transitions at low J is quite high, especially for lines of the R1, P2 and Q1 branches, for which maximum perturbed $g_{\rm eff}$ values of 2.0, -1.1 and 1.4 are respectively reached. This makes the most Zeeman sensitive CH lines of the A-X system an attractive indicator of solar and stellar magnetic fields.

3.3 C2


  \begin{figure} \par\includegraphics[width=13.5cm,clip]{ms1893f10.eps}\end{figure} Figure 10: The same as Fig. 9 for the C2 Swan system. The Q branches are very weak in this system and, therefore, are not plotted here.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=14cm,clip]{ms1893f11.eps}\end{figure} Figure 11: The same as Fig. 9 for the OH vibration-rotational transitions between the levels in the ground state $X^2\Pi $.
Open with DEXTER

Both upper and lower electronic states of the Swan system $(d^3\Pi-a^3\Pi)$ are under intermediate spin coupling, as their coupling constants Y are relatively small, -9.7 and -9.4, respectively (Huber & Herzberg 1979). However, deviations from pure case (b) due to incomplete spin uncoupling are seen only for small J(Fig. 10), while lines with $J\geq10$ are well described by case (b). In general, the magnetic sensitivity of lines from this system is not very large as compared to other molecular band systems at similar wavelengths in the visible.

  
3.4 OH


  \begin{figure} \par\includegraphics[width=13.8cm,clip]{ms1893f12.eps}\end{figure} Figure 12: The same as Fig. 9 for the OH A-X system.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=18cm,clip]{ms1893f13.eps}\end{figure} Figure 13: The same as Fig. 9 for the CN, MgH and CaH A-X systems. The pure case (b) $g_{\rm eff}$ values are identical for all three molecules and are given in the leftmost panel, while the deviation due to a partial uncoupling of the spin are different and are plotted individually for the three molecules in the three right-hand panels.
Open with DEXTER

The ground state $X^2\Pi $ needs to be described by intermediate case coupling which rapidly approaches pure case (b) as J increases, since Y = -7.5 (Abrams et al. 1994). Vibration-rotational bands of the Meinel system arising due to transitions between the levels of the ground state are observed in the infrared. Lines of the R and P branches show moderate splitting: $\vert g_{\rm eff}\vert\leq0.33$ (Fig. 11), while lines of the Q branches are too weak to be useful. The perturbation calculations are found to be important only for transitions with small J numbers. The effective Landé factors are larger for bands of the $\Delta v=2$ sequence as compared with those of the $\Delta v=1$ sequence. In Fig. 11 the perturbation calculations are shown for the (2, 0) band. Lines of different multiplet transitions in this system have effective Landé factors of opposite sign. This explains the puzzling observation of the Zeeman-split opposite-polarity OH lines from the (2, 0) band in sunspot spectra published by Harvey (1985). Using the present calculations we recently performed the first successful fit to Stokes I and V profiles of these lines (Berdyugina & Solanki 2001) and also OH lines from the (3, 1) band blending the strongly magnetically sensitive Fe I 15652.9Å line in sunspot umbrae (Berdyugina et al. 2002; Lagg et al., in preparation).

The first excited electronic state $A^2\Sigma$ is of pure case (b), as $\Lambda=0$ and the spin is not coupled to the internuclear axis at all. Therefore, magnetic properties of lines of the A-X system observed in the ultraviolet are well described by case (b), with relatively small deviations due to perturbations in the ground state (Fig. 12). Lines of the Q branches are more magnetically sensitive and less perturbed. Lines of the R1 and P2 branches show the smallest effective Landé factors.

As mentioned at the beginning of the present section, because of the weak spin-rotational coupling in $\Sigma $ states, the Zeeman regime calculations for them are limited to rather small magnetic field strengths. For the OH $A^2\Sigma$ state, the limit is about 2kG (see Table 3). Already at this field strength and certainly above it the Paschen-Back effect needs to be taken into account. This implies that in order to use the ultraviolet OH lines to study sunspot umbrae and cool stars, whose magnetic field strengths can reach larger values, the calculations must be done in the Paschen-Back regime.

3.5 CN, MgH, CaH

The ground and first excited electronic states of CN, MgH and CaH are of two kinds: $^2\Sigma$ and $^2\Pi $, which result in two band systems $A^2\Pi-X^2\Sigma$ and $B^2\Sigma -X^2\Sigma $ for each molecule. The magnetic properties of the $^2\Sigma$ states in the Zeeman regime are the same as discussed for the OH $A^2\Sigma$ state (Sect. 3.4), namely they are of pure case (b) and suffer from the Paschen-Back effect at very weak magnetic field strengths (see Table 3). The $A^2\Pi$ states of the three molecules are of the intermediate case (a-b) with somewhat different spin-orbit coupling constants: $Y({\rm CN})=-31$, $Y({\rm MgH})=5.7$, $Y({\rm CaH})=18$ (Cerny et al. 1978; Bernath et al. 1985; Berg & Klynning 1974). As a result, the deviations from pure case (b) for the three molecules are of different amounts (Fig. 13), the MgH A-X system being the closest to case (b). Recall that these calculations are valid only for the Zeeman regime, which is strongly limited in application, but can be useful, for instance, for the interpretation of the Hanle effect in MgH lines discovered in the Sun by Stenflo & Keller (1997). With the properly accounted Paschen-Back effect, the A-X systems of CN, MgH and CaH would be sensitive tools for solar and stellar magnetic studies; see our earlier results for MgH, presented by Berdyugina et al. (2000), where, however, perturbations to pure case (a) were combined with the Paschen-Back effect in the multiplet structure.

The $B^2\Sigma -X^2\Sigma $ systems of the three molecules are certainly of pure case (b), and the only perturbation which should be taken into account is the uncoupling of the spin from the rotation because of the Paschen-Back effect, which is the subject of a forthcoming paper. Here, in Fig. 14, we present calculations for the Zeeman regime only, which is applicable for very weak fields (see Table 3). Since $\Lambda=0$ and S=1/2 in both states, the magnetic sensitivity of the systems is rather low: $\vert g_{\rm eff}\vert\leq0.4$. This is critical for the CN B-X system, whose lines are observed in the near ultraviolet. Therefore, it cannot be considered as a useful indicator of solar and stellar magnetic fields. Generally, the A-X systems are much more magnetically sensitive than the B-X systems of these molecules.


  \begin{figure} \par\includegraphics[width=7cm,clip]{ms1893f14.eps} \end{figure} Figure 14: The same as Fig. 9 for the $B^2\Sigma -X^2\Sigma $ systems of CN, MgH, CaH. As $\Sigma $-states are always in pure case (b), no perturbation calculation is needed for the Zeeman regime.
Open with DEXTER

3.6 FeH

The $^4\Delta-^4\!\Delta$ system is produced by transitions between two electronic states with couplings of the angular momenta that are intermediate between the limiting cases (a) and (b) (Phillips et al. 1987), although the perturbation analysis has not been yet done and the spin-orbit coupling constants were not determined. This makes it difficult to predict values of the effective Landé factors for FeH lines for the intermediate case. In Fig. 15 we present only calculations for Hund's case (a). In this case, $g_{\rm eff}$ of the R and P branches are zero, and only lines of the Q branches are magnetically sensitive, which appear as simple Zeeman triplets with $\vert g_{\rm eff}\vert\leq2.2$.

The perturbations due to spin uncoupling are expected to be large for the R and P branches. The behaviour of the perturbed Landé factors appears to be similar to that of the TiO $\gamma '$-system shown in the right panel of Fig. 7. Namely, absolute values of the $g_{\rm eff}$of lines in the R and P branches will increase as J increases. Qualitatively, this is just what was observed by Wallace et al. (1998) in sunspots. Lines of the Q branches are expected to be less perturbed (see Fig. 7) and, thus, they will keep their high magnetic sensitivity for $J\leq10.5$. This is confirmed by our preliminary case (a) calculation of the most sensitive line Q7/2,7/2(3.5) ( $g_{\rm eff}\!=\!2.2$) which fits perfectly the sunspot observations (Berdyugina et al. 2001).

We conclude that FeH lines of this system represent a powerful tool for solar and stellar magnetic field studies, but are currently limited in usefulness due to the unknown spin-coupling constants. As soon as the spin-coupling constants are measured, the perturbed Landé factors can be calculated. Note also that in principle our perturbation calculation of the Zeeman effect can itself be used as a tool for determining the spin-coupling constants if appropriate Stokes I and V observations are available.


  \begin{figure} \par\includegraphics[width=7cm,clip]{ms1893f15.eps}\end{figure} Figure 15: The same as Fig. 5 for the FeH $^4\Delta-^4\!\Delta$ system. The multiple Q sub-branches are identified by the corresponding $\Omega $values. The perturbations from case (a) are expected to be similar to those shown in the right panel of Fig. 7 for the TiO $\gamma '$-system.
Open with DEXTER

4 Summary

The theory of the molecular Zeeman effect has, in contrast to the atomic effect, been largely neglected. With improved observations, the need for improvements in the theory has increased. We present here an approach that allows, in addition to the limiting Hund's cases (a) and (b), to compute the splittings and strengths of the Zeeman components in the intermediate case (a-b) for terms of any multiplicity.

Already this step enables some general conclusions to be drawn regarding the influence of the magnetic field on bands of transitions of interest for the study of solar and stellar magnetism. Thus, we can say which molecular transitions observed in the visible are magnetically sensitive and can be useful diagnostics (if the lines are sufficiently strong and unblended). In the Zeeman regime the spectral lines have a symmetric splitting pattern regardless of the spin coupling case. For the pure Hund's cases the splitting is largest for small J values and rapidly decreases as J increases. However, within a band, some transitions can belong to one case while others belong to an intermediate case. This alters significantly the dependence of the effective Landé factors of lines on J, so that they can increase as J increases. This applies in particular to the TiO $\gamma '$ $(B^3\Pi-X^3\Delta)$ and FeH $^4\Delta-^4\!\Delta$ systems. Furthermore, the splitting of transitions in the intermediate case is in general larger than for pure Hund's cases (the other parameters ${\vec L}$, ${\vec S}$, etc. being equal). One important finding is Landé factors of negative sign are quite common for molecular levels and lines. Moreover, the sign of effective Landé factors can change within a band because of gradual spin decoupling, i.e. in the intermediate Hund's case (a-b). We have calculated effective Landé factors in the pure and intermediate cases for a sample of astrophysically important molecules and have drawn conclusions for individual bands in Sect. 3 which are not repeated here.

It is clear, however, that the present paper is only one step of many that need to be undertaken before the full power of the molecular Zeeman effect can be applied to solar and stellar studies. In a next step we intend to explore the diagnostic capabilities of various magnetic transitions within the Zeeman regime, followed by a comparison with observations (which have already been initiated by Berdyugina et al. 2000). Particularly interesting cases, such as FeH will be studied separately. Finally, we plan to turn to the molecular Paschen-Back effect. As can be seen from Table 3 it is potentially important for all the listed molecules except FeH and TiO (if we restrict ourselves to transitions in the visible).

Acknowledgements
We are grateful to Dr. P. Braun for very useful discussions and an anonymous referee for valuable comments.

References

 

Copyright ESO 2002