

Up: Detecting low amplitude periodicities HIPPARCOS
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1709f1.eps} \end{figure}](/articles/aa/full/2002/14/aa1709/Timg4.gif) |
Figure 1:
The photometry (upper left panel) of the A2 V star HIP50191 (HD88955, 3.85mag( V)) with 173 data points has a noise level of 0.54mmag
in the amplitude spectrum (middle left panel), which is the lowest in our sample of stars. The photometry (upper right panel) of the F5 V star
HIP114789
(HD219269, 10.29mag( V)) with 83 data points has a noise level of 10.3mmag in the amplitude spectrum (middle right panel), which is the highest in our sample of stars. The spectral windows of the data are given in lower two panels. |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{ms1709f2.eps} \end{figure}](/articles/aa/full/2002/14/aa1709/Timg5.gif) |
Figure 2:
The histrogram illustrates the incidence of frequencies determined in amplitude spectra of light curves of presumably constant stars with an amplitude exceeding a
given S/N ratio. The numbers are normalised to a uniform distribution from 0 to 36
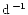 .
It is split into a low- and high-frequency
domain and uses different binnings. .
It is split into a low- and high-frequency
domain and uses different binnings. |
During the HIPPARCOS mission an individual star was observed up to 350 times
over the whole mission lifetime, depending on the position on the sky.
The temporal distribution and density of photometric data can be very different from star to star (Figs. 1).
It is an overlap of a 20min to 108min and
a 3 to 5 week cycle (Eyer & Grenon 2000; van Leeuwen 1997). For our sample of stars we found light curves with up to 339 data points.
To analyse the large amount of data sets in a reasonable time we wrote a Fortran 90 program based on the DFT
(Discrete Fourier analysis; Deeming 1975). The software tool computes the mean (noise) level in the
amplitude spectrum
from 0 to 34.9
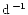 with a frequency resolution of
with a frequency resolution of
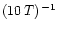 ,
where T is the total time span of a dataset.
The noise level and the up to 4 highest
peaks in the amplitude spectrum, with a signal to noise ratio ( S/N ratio) exceeding 3.25 and an arbitrarily selected minimum distance
of 1
,
where T is the total time span of a dataset.
The noise level and the up to 4 highest
peaks in the amplitude spectrum, with a signal to noise ratio ( S/N ratio) exceeding 3.25 and an arbitrarily selected minimum distance
of 1
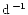 ,
were stored in an individual file.
,
were stored in an individual file.
In Figs. 1 we show amplitude spectra of the
two extreme cases with the lowest (HIP50191, 3.85mag(V)) and highest (HIP114789, 10.27mag(V)) noise level encountered
in our investigation. Both stars have no significant peak in the amplitude spectra. A PDM algorithm basically gives similar results but is more computer time consuming. Hence
DFT was given preference.
Due to the instrumental design of HIPPARCOS, one would expect to find a priori some characteristic frequencies which are listed
in Table 1 when analysing real data. The frequency which corresponds to the rotation of HIPPARCOS
(
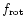 ), and the harmonics are prime candidates. Indeed they are found in all spectral windows (see also
Fig. 1, lower panels). The optical axes of the system which images the sky
onto the focal plane include an angle of 58
), and the harmonics are prime candidates. Indeed they are found in all spectral windows (see also
Fig. 1, lower panels). The optical axes of the system which images the sky
onto the focal plane include an angle of 58 .
Hence, when a star is in the field of view of one system,
it will appear in the other after 20.6min due to the satellite rotation. This is the shortest possible time interval for consecutive observations and
can be taken as the clocking interval for HIPPARCOS. The frequency of 34.9
.
Hence, when a star is in the field of view of one system,
it will appear in the other after 20.6min due to the satellite rotation. This is the shortest possible time interval for consecutive observations and
can be taken as the clocking interval for HIPPARCOS. The frequency of 34.9
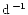 ,
relative
to which the spectral window appears to be symmetric, corresponds to the Nyquist frequency for
evenly spaced data, and corresponds to twice the shortest possible sampling interval of 20.6min. Although, at a first
glance, the HIPPARCOS data do not appear to be evenly spaced, this concept obviously still is applicable, because of the
nearly constant rotation rate of the spacecraft. Due to the operation of HIPPARCOS, data gaps can be very large, which
increases significantly the amplitude of sidelobes and hence the noise level in the amplitude spectrum.
,
relative
to which the spectral window appears to be symmetric, corresponds to the Nyquist frequency for
evenly spaced data, and corresponds to twice the shortest possible sampling interval of 20.6min. Although, at a first
glance, the HIPPARCOS data do not appear to be evenly spaced, this concept obviously still is applicable, because of the
nearly constant rotation rate of the spacecraft. Due to the operation of HIPPARCOS, data gaps can be very large, which
increases significantly the amplitude of sidelobes and hence the noise level in the amplitude spectrum.


Up: Detecting low amplitude periodicities HIPPARCOS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1709f1.eps} \end{figure}](/articles/aa/full/2002/14/aa1709/Timg4.gif)
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{ms1709f2.eps} \end{figure}](/articles/aa/full/2002/14/aa1709/Timg5.gif)