A&A 385, 724-732 (2002)
DOI: 10.1051/0004-6361:20020148

Measurement of lifetimes by laser-induced fluorescence and determination of transition probabilities of astrophysical interest in Nd III

Z. G. Zhang¹ - S. Svanberg¹ - P. Palmeri² - P. Quinet^2,3 - E. Biémont^2,3

1 - Department of Physics, Lund Institute of Technology, PO Box 118, 22100 Lund, Sweden
2 - Astrophysique et Spectroscopie, Université de Mons-Hainaut, 7000 Mons, Belgium
3 - IPNAS, Bât. B15, Université de Liège, Sart Tilman, 4000 Liège, Belgium

Received 04 July 2001 / Accepted 20 December 2001

Abstract
Selective lifetime measurements by time-resolved laser-induced fluorescence spectroscopy for 5 levels belonging to the 4f³5d configuration of doubly ionized neodymium provide a first and useful experimental test of the relativistic Hartree-Fock calculations in this ion of astrophysical interest. As a consequence, the accuracy of the transition probabilities deduced in the present work is well assessed. These new data are expected to help astrophysicists in the future to refine the analysis of the composition of chemically peculiar stars which frequently show large overabundances of lanthanides when compared to the solar system standards.

Key words: atomic data - atomic processes - stars: chemically peculiar

1 Introduction

Natural neodymium appears in the form of seven stable isotopes. According to nucleosynthesis theories, the isotopes 143 (12.2%), 144 (23.8%), 145 (8.3%) and 146 (17.2%) are produced either by the r or s process while the isotope 142 (27.1%) results from the s process and the isotopes 148 (5.8%) and 150 (5.6%) are formed by a pure r process.

Singly-ionized neodymium (Nd II) is frequently observed in astrophysical spectra (Merril 1956; Jaschek & Jaschek 1995): it has been identified in M and MS stars e.g. by Smith & Lambert (1985) and in Bp stars e.g. by Cowley & Crosswhite (1978). Some Nd II lines appear very strongly in the stars of the Cr-Eu-Sr subgroup (Adelman 1973) or in Am stars (Smith 1973, 1974). The analysis of Nd II lines leads to strong overabundances in Ba stars (Lambert 1985) or in S-type stars (Bidelman 1953). Nd II is also observed in the solar photospheric spectrum (Anders & Grevesse 1989).

Doubly ionized neodymium (Nd III), which is expected to be the dominant species in hotter stars, has been identified in the spectra of some CP stars like HR 465, HD 51418 and HD 200311 (Cowley 1976; Aikman et al. 1979; Bidelman et al. 1995) and in the spectrum of HD 192913 and HD 43819, Bp stars of the Si subgroup (Cowley & Crosswhite 1978; Ryabchikova et al. 1990). Some Nd III lines have also been found in the spectrum of HD 101065, a rapidly oscillating star also known as Przybylski's star (Cowley et al. 1998, 2000). However, the difficulty of analyzing the third spectrum of most rare earth elements (REE), including Nd III, in low resolution IUE spectra has been discussed by Cowley & Greenberg (1988) in relation to the uncertainties affecting the solar model and in relation to the lack of reliable gf-values. The new high-resolution, high signal-to-noise HST spectra now available (Leckrone et al. 1999) allow the identification of many features belonging to the doubly ionized lanthanides that emphasize the need for accurate radiative parameters for all the REE. These data are particularly important for the study of CP stars that frequently show large overabundances of lanthanides when compared to the solar system values (see e.g. Cowley 1984) and for the metal-poor galactic halo stars in relation to the early history of the galaxy (see e.g. Sneden et al. 1996).

Doubly ionized neodymium (Nd III, Z=60) belongs to the Ce I isoelectronic sequence and has [Xe]4f^{4 5}I₄ as the ground state. Up to now, according to the NIST compilation (Martin et al. 1978; http://physics.nist.gov/cgi-bin/AtData), only 29 levels of this ion have been experimentally determined. They belong to the 4f⁴ and to the 4f³(⁴I$^{\circ}$, ⁴F$^{\circ}$)5d configurations. They were deduced from the 9500 lines observed between 181.0 and 871.5 nm by Crosswhite (1975, 1976). This spectrum is thus very poorly known and in need of completion.

Previous transition probability calculations in Nd III are extremely scarse. To our knowledge, the only available data have been obtained by Cowley & Bord (1998) who calculated gf-values for the analysis of the spectra of $\gamma$Equulei and HR 6870, and by Bord (2000) who performed HFR calculations having in mind the analysis of the chemically peculiar stars HD 122970 and HD 101065. No experimental measurements (lifetimes or transition probabilities) are available so far for Nd III. In view of the complexity of the configurations involved in the REE, experimental transition probabilities or radiative lifetimes are however indispensable to test the validity of the theoretical models.

The above considerations concerning the need for and the lack of radiative atomic data for the Nd²⁺ ion justify the present effort to improve the situation. In fact, to meet our objectives, i.e. the determination of a large number of transition probabilities of astrophysical interest as accurately as possible, we have compared laser lifetime measurements for 5 levels with theoretical values resulting from configuration interaction calculations. Although the theoretical approach used was similar to that considered by Bord (2000), the present calculation considers configuration interactions (that are vital in the complex spectrum considered here) in a more detailed way, with the consequence that the deduced transition probabilities are expected to be more accurate.

The present work is part of an extensive program of lifetime measurements in doubly ionized REE carried out at the Lund Laser Centre (LLC) in Sweden and of transition probability calculations at the Liège and Mons universities. So far, the results obtained concern about 50000 transitions of the following ions: La III (Li & Jiang 1999), La III - Lu III (Biémont et al. 1999), Ce III (Li et al. 2000), Gd III (Zhang et al. 2000), Er III (Biémont et al. 2001a), Pr III (Palmeri et al. 2001; Biémont et al. 2001b), Tm III (Li et al. 2001), Yb III (Biémont et al. 2001c), Ho III (Biémont et al. 2001d) and Eu III (Zhang et al. 2001). These new atomic data are progressively incorporated in a database of astrophysical interest, D.R.E.A.M., which is available on a web site at the address: http://www.umh.ac.be/~astro/dream.shtml and is also accessible directly through anonymous ftp at the address: umhsp02.umh.ac.be/pub/ftp_astro/dream.

2 Experimental measurements

The five levels of Nd III, considered in the present experiment, belong to the configuration 4f³5d and their lifetimes were measured using two-step excitation time-resolved laser-induced fluorescence technique. The experimental schemes followed for the measurements are summarized in Table 1.

 

 

Table 1: Nd III levels measured and the corresponding excitation schemes.

Levels $^{{\rm a}}$	Lower level	Upper level	Excitation	Laser	Observed
	(cm-1)	(cm-1)	$\lambda_{\rm air}$ (nm)	mode $^{{\rm b}}$	$\lambda_{\rm air}$ (nm)
4f3(4F$^{\circ}$)5d  5H $_3^{\circ}$	0.0	27788.2	359.762	$2\omega+S$	359.8
4f3(4F$^{\circ}$)5d  5H $_4^{\circ}$	1137.8	28745.3	362.117	$2\omega+S$	362.1
4f3(4F$^{\circ}$)5d  5H $_5^{\circ}$	2387.6	30232.3	359.032	$2\omega+S$	359.0
4f3(4F$^{\circ}$)5d  5H $_6^{\circ}$	3714.9	31394.6	361.173	$2\omega+S$	361.2
4f3(4F$^{\circ}$)5d  5H $_7^{\circ}$	5093.3	32832.6	360.397	$2\omega+S$	360.4

$^{{\rm a}}$

From Martin et al. (1978).

$^{{\rm b}}$

2$\omega$ means frequency-doubling and S is written for Stokes component.

The experimental set-up used in the present experiment is illustrated in Fig. 1. Nd²⁺ ions were produced in a laser-induced plasma using 532 nm wavelength laser pulses emitted with a 10 Hz repetition rate and 10 ns duration Nd:YAG laser (laser B) (Continuum surelite) with variable pulse energy (0-50 mJ). In order to obtain the suitable excitation, 8 ns pulses emitted by another Nd:YAG laser (laser A) (Continuum NY-82) were sent to a stimulated Brillouin scattering (SBS) compressor to shorten the pulses down to 1 ns. The laser was used to pump a dye laser (Continuum Nd-60). DCM dye was used in the experiments, and the frequency-doubling of the dye laser and further stimulated Raman scattering were obtained using a KDP crystal and a hydrogen cell.

	Figure 1: Experimental set-up used for the lifetime measurements for Nd III.
Open with DEXTER

The lasers were triggered by a digital delay generator (Stanford Research System, Model 535) and the delay between the ablation and excitation pulses was adjusted. After the ions were produced through perpendicularly focusing the B laser onto the surface of a Nd foil rotated in a vacuum chamber, the ions were excited selectively by the excitation laser crossing the plasma horizontally. The fluorescence decay was imaged by two CaF₂ lenses and concentrated on the entrance slit of a vacuum monochromator. A Hamamatsu R3809U-58 photomultiplier was used for the detection.

The time-resolved signal was averaged with a digital transient recorder (Tektronix model DSA 602) and the fluorescence decay curve was sent to a personal computer for lifetime determination. The lifetime evaluation was performed by fitting the fluorescence decay signal curve with an exponential function with adjustable parameters. For each level, more than 20 curves were averaged. The five lifetimes measured are reported in Table 2.

In order to be sure that the Nd²⁺ lines of interest were considered, the modification of the fluorescence signal as a function of the delay time was investigated. Possible flight-out-of-view effects are carefully avoided by enlarging the slit of the monochromator and choosing a suitable delay time.

As a further refinement, a magnetic field of about 60 Gauss was added in the plasma zone by a pair of Helmholtz coils in order to eliminate possible Zeeman quantum beat effects but also to weaken the background associated with the ablation laser and the plasma recombination processes.

In order to obtain a sufficiently high signal-to-noise ratio, a decay curve was obtained by averaging fluorescence photons from more than 2000 pulses. A typical decay curve is shown in Fig. 2.

	Figure 2: A typical experimental time-resolved fluorescence signal from the level at 31394.6 cm-1 of Nd III. The lifetime deduced from the fit was 70 ns. The departure from the straight line for values larger than 300 ns is due to the increasing importance of noise.
Open with DEXTER

3 Theoretical approach

It has been shown in many previous papers (see e.g. the references quoted at the end of Sect. 1) that, for heavy ions such as singly or doubly ionized REE, the consideration of both intravalence and core-valence correlation is essential for atomic structure calculations. The detailed consideration of configuration interaction effects in complex configurations with an open f shell severely limits the choice of a theoretical method for performing the calculations for the 4f⁴-4f³5d transitions in Nd III. In particular, the use of a fully ab initio relativistic approach like the MCDF method must be ruled out in view of the huge number of relativistic states involved and in view of the unrealistic amount of computer time needed for the calculations. In fact, up to now, the various attempts to use the MCDF method for complex situations such as the one considered here have failed. A versatile alternative, which has appeared usable and leads to accurate results (i.e. generally in agreement within a few percent with experimental data obtained with laser techniques) in many different situations, is the relativistic Hartree-Fock technique (HFR) as described and coded by Cowan (1981) but modified for the inclusion of core-polarization effects (see e.g. Palmeri et al. 2000). The lack of convergence problems and the reasonable computer time needed has led us to adopt this approach here.

Detailed comparisons between theoretical calculations and experiment in Er III (Biémont et al. 2001a) and Tm III (Li et al. 2001) have emphasized the fact that the 4f-5d transitions deserve special attention in lanthanides in relation to the fact that 4f electrons are deeply imbedded inside the 5s²5p⁶ closed shells of the xenon core. A difficulty arises because the analytical core-polarization and core-penetration corrections to the dipole operator are no longer valid (see e.g. Quinet et al. 1999). A possible solution is to apply an empirical scaling factor to the uncorrected <4f|r|5d> radial matrix element. Although this semi-empirical approach could be useful, it was not followed in the present work. Instead, we have preferred to introduce in the model explicit interactions between the configurations of interest (i.e. 4f⁴ and 4f³5d) and some higher configurations with three, two or one electron(s) in the 4f subshell. More precisely, configuration interaction was explicitly retained among the configurations 4f⁴ + 4f³6p + 4f³5f + 4f³6f + 4f²5d² + 4f²6s² + 4f²6p² + 4f²5d6s and 4f³5d + 4f³6d + 4f³6s + 4f²5d6p + 4f²6s6p + 4f5d³ + 4f5d²6s + 4f5d6s². These configuration lists extend considerably those considered by Bord (2000) (i.e. 4f⁴+ 4f²5d² + 4f²5d6s + 4f³6p and 4f³5d + 4f³6s) and are expected to include the most important effects due to intravalence and core-valence correlation. The core-core correlation could a priori be tested by considering the one- and two-electron excitations from the 5s and 5p subshells to 4f but this was prevented, in the present work, by the computer limitations.

  

Table 2: Calculated and experimental lifetimes (in ns) obtained in the present work for selected 4f³5d levels in Nd III.

The HFR method was combined with a least-squares optimization routine minimizing the discrepancies between observed and calculated energy levels. More precisely, the average energy ( $E_{\rm av}$) and the spin-orbit integral ($\zeta$$_{\rm 4f}$) were adjusted using the five 4f⁴ levels within the ⁵I multiplet. The average energy ( $E_{\rm av}$), the Slater parameters ($F^{\rm k}$, $G^{\rm k}$) and the spin-orbit integrals ($\zeta$$_{\rm 4f}$, $\zeta$$_{\rm 5d}$) were optimized using the twenty-four experimental 4f³5d levels taken from the NIST compilation (Martin et al. 1978). The effective interaction operators ($\alpha$, $\beta$ and $\gamma$) could not be included in the fitting procedure of 4f³5d levels because of the lack of experimental level values in this configuration. The radial parameters adopted in the present calculations are reported in Table 3. For the other configurations (for which no experimental levels are available), a scaling factor of 0.85 was applied to the $F^{\rm k}$, $G^{\rm k}$ and $R^{\rm k}$ integrals in order to partly take into account interaction with distant configurations not included explicitly in the physical model, according to a well-established procedure. In addition, the average energies were adjusted to reproduce the energies predicted by Brewer (1971) for the lowest level of each configuration, i.e. 4f³6p ⁵K₅ ( $E = 61\,000\pm 2000$ cm^-1), 4f²5d^{2 5}L₆( $E = 72\,000\pm 5000$ cm^-1), 4f²5d6s ⁵K₅ ( $E = 96\,000\pm 5000$ cm^-1), 4f²6s^{2 3}H₄ ( $E = 122\,000\pm 7000$ cm^-1), 4f²6p^{2 5}I₄( $E = 186\,000\pm 9000$ cm^-1), 4f³6s ⁵I $_4^{\circ}$ ( $E = 30\,500\pm 2000$ cm^-1), 4f²5d6p ⁵L $_6^{\circ}$ ( $E = 126\,000\pm 4000$ cm^-1) and 4f²6s6p ⁵I $_4^{\circ}$( $E = 154\,000\pm 7000$ cm^-1).

The calculated energy levels are compared with experiments, when available, in Table 4 for odd-parity levels below 33000 cm^-1. In view of the very good agreement between theory and experiment (the mean deviation is 0.23%), the new calculated levels are expected to be reliable to a few tens of percent and, consequently, can be used to support future analysis and identification work. We report also in Table 4 the calculated Landé g-factors. They agree well with the values calculated by Bord (2000): $\Delta = 0.014 \pm 0.023$for 34 odd levels, the largest discrepancies appearing, as expected, for the strongly perturbed levels: $E = 27\,569.8$, 27788.2 and 29397.3 cm^-1. There are no other g-factors available for comparison.

 

 

Table 3: Radial parameters adopted in the present calculations for the 4f⁴and 4f³5d configurations in Nd III.

Config.	Parameter	Ab initio	Fit	Fit/ab initio
		(cm-1)	(cm-1)
4f4	$E_{\rm av}$		35392
	F2(4f,4f)	92635	78740	0.850 $^{{\rm *}}$
	F4(4f,4f)	57680	49028	0.850 $^{{\rm *}}$
	F6(4f,4f)	41373	35167	0.850 $^{{\rm *}}$
	$\zeta_{\rm 4f}$	849	780	0.919
4f35d	$E_{\rm av}$		43230
	F2(4f,4f)	101378	64485	0.636
	F4(4f,4f)	63552	65286	1.027
	F6(4f,4f)	54705	28855	0.631
	$\zeta_{\rm 4f}$	947	898	0.948
	$\zeta_{\rm 5d}$	831	755	0.909
	F2(4f,5d)	26408	16541	0.626
	F4(4f,5d)	13021	8809	0.677
	G1(4f,5d)	12823	9161	0.714
	G3(4f,5d)	10202	4251	0.417
	G5(4f,5d)	7735	9805	1.268

$^{{\rm *}}$

Fixed value.

 

 

Table 4: Low-lying odd energy levels (E < 33000 cm^-1) of Nd III.

Config.	J	$E_{\exp}^{{\rm a}}$	$E_{\rm calc}^{{\rm b}}$	$\Delta E^{{\rm c}}$	$g_{\rm calc}^{{\rm d}}$	Eigenvector composition $^{{\rm e}}$
		(cm-1)	(cm-1)	(cm-1)
4f35d	6		15290		0.724	93% (4I$^{\circ}$)5d  5L$^{\circ}$
4f35d	5	15262.2	15322	-60	0.683	90% (4I$^{\circ}$)5d  5K$^{\circ}$ + 6% (4I$^{\circ}$)5d  3I$^{\circ}$
4f35d	6	16938.1	16944	-6	0.910	95% (4I$^{\circ}$)5d  5K$^{\circ}$
4f35d	7		17077		0.915	96% (4I$^{\circ}$)5d  5L$^{\circ}$
4f35d	7	18656.3	18628	28	1.053	97% (4I$^{\circ}$)5d  5K$^{\circ}$
4f35d	4	18883.7	18819	65	0.625	88% (4I$^{\circ}$)5d  5I$^{\circ}$ + 9% (4I$^{\circ}$)5d  3H$^{\circ}$
4f35d	8		18980		1.043	98% (4I$^{\circ}$)5d  5L$^{\circ}$
4f35d	3	19211.0	19271	-60	0.547	77% (4I$^{\circ}$)5d  5H$^{\circ}$ + 10% (4I$^{\circ}$)5d  3G$^{\circ}$ + 7% (4F$^{\circ}$)5d  5H$^{\circ}$
4f35d	5		19740		0.887	40% (4I$^{\circ}$)5d  3I$^{\circ}$ + 36% (4I$^{\circ}$)5d  5I$^{\circ}$ + 6% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	4	20144.3	20082	62	0.871	64% (4I$^{\circ}$)5d  5H$^{\circ}$ + 18% (4I$^{\circ}$)5d  3H$^{\circ}$
4f35d	2		20218		0.343	94% (4I$^{\circ}$)5d  5G$^{\circ}$
4f35d	8	20410.9	20373	38	1.149	96% (4I$^{\circ}$)5d  5K$^{\circ}$
4f35d	5	20388.9	20388	1	0.936	56% (4I$^{\circ}$)5d  5I$^{\circ}$ + 15% (4I$^{\circ}$)5d  3H$^{\circ}$ + 12% (4I$^{\circ}$)5d  3I$^{\circ}$
4f35d	3		20560		0.870	77% (4I$^{\circ}$)5d  5G$^{\circ}$ + 10% (4I$^{\circ}$)5d  3G$^{\circ}$ + 7% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	6		20822		1.029	33% (4I$^{\circ}$)5d  5I$^{\circ}$ + 32% (4I$^{\circ}$)5d  3I$^{\circ}$ + 14% (4I$^{\circ}$)5d  3K$^{\circ}$
4f35d	9		20975		1.133	99% (4I$^{\circ}$)5d  5L$^{\circ}$
4f35d	4		21183		1.034	51% (4I$^{\circ}$)5d  5G$^{\circ}$ + 15% (4I$^{\circ}$)5d  3G$^{\circ}$ + 13% (4I$^{\circ}$)5d  3H$^{\circ}$
4f35d	5	21886.8	21878	9	1.021	61% (4I$^{\circ}$)5d  5H$^{\circ}$ + 22% (4I$^{\circ}$)5d  3I$^{\circ}$
4f35d	6	22047.8	22048	0	1.088	60% (4I$^{\circ}$)5d  5I$^{\circ}$ + 12% (4I$^{\circ}$)5d  5H$^{\circ}$ + 10% (4I$^{\circ}$)5d  3I$^{\circ}$
4f35d	9	22197.0	22171	26	1.217	95% (4I$^{\circ}$)5d  5K$^{\circ}$
4f35d	4		22438		0.934	39% (4I$^{\circ}$)5d  3H$^{\circ}$ + 34% (4I$^{\circ}$)5d  5G$^{\circ}$ + 11% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	7	22702.9	22665	37	1.151	61% (4I$^{\circ}$)5d  5I$^{\circ}$ + 17% (4I$^{\circ}$)5d  3I$^{\circ}$ + 13% (4I$^{\circ}$)5d  3K$^{\circ}$
4f35d	5		22787		1.215	71% (4I$^{\circ}$)5d  5G$^{\circ}$ + 7% (4I$^{\circ}$)5d  3G$^{\circ}$ + 7% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	6		22918		0.991	47% (4I$^{\circ}$)5d  3K$^{\circ}$ + 28% (4I$^{\circ}$)5d  5H$^{\circ}$ + 6% (2H$^{\circ}$)5d  3K$^{\circ}$
4f35d	10		23041		1.199	99% (4I$^{\circ}$)5d  5L$^{\circ}$
4f35d	7		23694		0.891	82% (4I$^{\circ}$)5d  3L$^{\circ}$ + 7% (2K$^{\circ}$)5d  3L$^{\circ}$
4f35d	6	23819.3	23953	-134	1.075	38% (4I$^{\circ}$)5d  5H$^{\circ}$ + 34% (4I$^{\circ}$)5d  3I$^{\circ}$ + 13% (4I$^{\circ}$)5d  3K$^{\circ}$
4f35d	3		24034		0.771	72% (4I$^{\circ}$)5d  3G$^{\circ}$ + 16% (4I$^{\circ}$)5d  5G$^{\circ}$ + 6% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	7	24003.2	24093	-90	1.196	33% (4I$^{\circ}$)5d  5H$^{\circ}$ + 30% (4I$^{\circ}$)5d  5I$^{\circ}$ + 23% (4I$^{\circ}$)5d  3I$^{\circ}$
4f35d	6		24481		1.295	79% (4I$^{\circ}$)5d  5G$^{\circ}$ + 7% (4I$^{\circ}$)5d  3H$^{\circ}$
4f35d	8	24686.4	24605	81	1.230	84% (4I$^{\circ}$)5d  5I$^{\circ}$ + 12% (4I$^{\circ}$)5d  3K$^{\circ}$
4f35d	5		24653		1.067	51% (4I$^{\circ}$)5d  3H$^{\circ}$ + 18% (4I$^{\circ}$)5d  5G$^{\circ}$ + 7% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	7		25039		1.123	45% (4I$^{\circ}$)5d  3K$^{\circ}$ + 31% (4I$^{\circ}$)5d  5H$^{\circ}$ + 8% (4I$^{\circ}$)5d  5I$^{\circ}$
4f35d	0		25883			33% (4F$^{\circ}$)5d  5D$^{\circ}$ + 25% (4S$^{\circ}$)5d  5D$^{\circ}$ + 20% (4F$^{\circ}$)5d  3P$^{\circ}$
4f35d	8		25894		1.020	84% (4I$^{\circ}$)5d  3L$^{\circ}$ + 8% (2K$^{\circ}$)5d  3L$^{\circ}$
4f35d	7		26120		1.139	43% (4I$^{\circ}$)5d  3I$^{\circ}$ + 22% (4I$^{\circ}$)5d  3K$^{\circ}$ + 20% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	6	26503.2	26564	-61	1.178	48% (4I$^{\circ}$)5d  3H$^{\circ}$ + 14% (4I$^{\circ}$)5d  5G$^{\circ}$ + 8% (4G$^{\circ}$)5d  3H$^{\circ}$
4f35d	4		26608		1.049	79% (4I$^{\circ}$)5d  3G$^{\circ}$ + 10% (4I$^{\circ}$)5d  5G$^{\circ}$
4f35d	1		26787		1.489	42% (4F$^{\circ}$)5d  5D$^{\circ}$ + 39% (4S$^{\circ}$)5d  5D$^{\circ}$ + 7% (4F$^{\circ}$)5d  3P$^{\circ}$
4f35d	2		27295		1.446	41% (4S$^{\circ}$)5d  5D$^{\circ}$ + 40% (4F$^{\circ}$)5d  5D$^{\circ}$
4f35d	8	27391.4	27300	91	1.138	71% (4I$^{\circ}$)5d  3K$^{\circ}$ + 12% (4I$^{\circ}$)5d  5I$^{\circ}$ + 10% (2H$^{\circ}$)5d  3K$^{\circ}$
4f35d	3	27569.8	27433	137	1.085	26% (4F$^{\circ}$)5d  5H$^{\circ}$ + 21% (4S$^{\circ}$)5d  5D$^{\circ}$ + 19% (4F$^{\circ}$)5d  5D$^{\circ}$
4f35d	2		27525		0.395	83% (4F$^{\circ}$)5d  5G$^{\circ}$
4f35d	3	27788.2	27749	39	0.873	53% (4F$^{\circ}$)5d  5H$^{\circ}$ + 15% (4S$^{\circ}$)5d  5D$^{\circ}$ + 14% (4F$^{\circ}$)5d  5D$^{\circ}$
4f35d	9		28109		1.114	83% (4I$^{\circ}$)5d  3L$^{\circ}$ + 7% (2K$^{\circ}$)5d  3L$^{\circ}$
4f35d	3		28532		0.921	85% (4F$^{\circ}$)5d  5G$^{\circ}$
4f35d	4		28657		1.249	29% (4F$^{\circ}$)5d  5H$^{\circ}$ + 25% (4S$^{\circ}$)5d  5D$^{\circ}$ + 22% (4F$^{\circ}$)5d  5D$^{\circ}$
4f35d	4	28745.3	28839	-94	1.102	56% (4F$^{\circ}$)5d  5H$^{\circ}$ + 16% (4S$^{\circ}$)5d  5D$^{\circ}$ + 14% (4F$^{\circ}$)5d  5D$^{\circ}$
4f35d	5		29204		1.194	84% (4I$^{\circ}$)5d  3G$^{\circ}$
4f35d	0		29361			43% (4F$^{\circ}$)5d  3P$^{\circ}$ + 29% (4S$^{\circ}$)5d  5D$^{\circ}$ + 9% (2D$^{\circ}$)5d  1S$^{\circ}$
4f35d	4		29440		1.132	78% (4F$^{\circ}$)5d  5G$^{\circ}$
4f35d	5	29397.3	29519	-122	1.036	31% (4F$^{\circ}$)5d  5H$^{\circ}$ + 14% (2H$^{\circ}$)5d  3I$^{\circ}$ + 12% (4F$^{\circ}$)5d  5G$^{\circ}$
4f35d	6		29626		1.018	23% (2H$^{\circ}$)5d  3K$^{\circ}$ + 12% (4I$^{\circ}$)5d  3K$^{\circ}$ + 9% (2H$^{\circ}$)5d  1I$^{\circ}$
4f35d	1		29840		1.273	29% (4F$^{\circ}$)5d  5P$^{\circ}$ + 24% (4F$^{\circ}$)5d  3P$^{\circ}$ + 23% (4F$^{\circ}$)5d  5F$^{\circ}$
4f35d	2		29991		1.191	20% (4F$^{\circ}$)5d  3D$^{\circ}$ + 19% (4F$^{\circ}$)5d  5P$^{\circ}$ + 11% (4F$^{\circ}$)5d  3F$^{\circ}$
4f35d	5	30232.3	30198	34	1.142	49% (4F$^{\circ}$)5d  5H$^{\circ}$ + 30% (4F$^{\circ}$)5d  5G$^{\circ}$
4f35d	1		30298		1.057	51% (4F$^{\circ}$)5d  5F$^{\circ}$ + 38% (4F$^{\circ}$)5d  5P$^{\circ}$
4f36s	4		30431		0.611	92% (4I$^{\circ}$)6s  5I$^{\circ}$

 

 

Table 4: continued.

Config.	J	$E_{\exp}^{{\rm a}}$	$E_{\rm calc}^{{\rm b}}$	$\Delta E^{{\rm c}}$	$g_{\rm calc}^{{\rm d}}$	Eigenvector composition $^{{\rm e}}$
		(cm-1)	(cm-1)	(cm-1)
4f35d	3		30702		1.116	13% (4S$^{\circ}$)5d  5D$^{\circ}$ + 12% (2H$^{\circ}$)5d  3G$^{\circ}$ + 9% (4F$^{\circ}$)5d  3F$^{\circ}$
4f35d	1		30768		1.420	28% (4F$^{\circ}$)5d  3P$^{\circ}$ + 25% (4F$^{\circ}$)5d  5P$^{\circ}$ + 12% (4F$^{\circ}$)5d  5F$^{\circ}$
4f35d	2		30860		1.118	75% (4F$^{\circ}$)5d  5F$^{\circ}$ + 14% (4F$^{\circ}$)5d  5P$^{\circ}$
4f35d	5		30898		1.009	30% (4F$^{\circ}$)5d  5G$^{\circ}$ + 17% (2H$^{\circ}$)5d  3I$^{\circ}$ + 16% (4I$^{\circ}$)6s  5I$^{\circ}$
4f35d	4		30918		0.884	31% (4F$^{\circ}$)5d  3H$^{\circ}$ + 15% (2H$^{\circ}$)5d  3H$^{\circ}$ + 10% (4F$^{\circ}$)5d  5G$^{\circ}$
4f35d	2		30921		1.336	49% (4F$^{\circ}$)5d  5P$^{\circ}$ + 16% (4F$^{\circ}$)5d  3F$^{\circ}$ + 10% (4G$^{\circ}$)5d  3F$^{\circ}$
4f35d	6		30931		1.069	38% (2H$^{\circ}$)5d  3K$^{\circ}$ + 28% (4F$^{\circ}$)5d  5G$^{\circ}$ + 6% (4F$^{\circ}$)5d  5H$^{\circ}$
4f35d	3		30989		1.329	38% (4F$^{\circ}$)5d  5P$^{\circ}$ + 13% (2H$^{\circ}$)5d  3F$^{\circ}$ + 11% (4F$^{\circ}$)5d  3F$^{\circ}$
4f36s	5		31268		0.924	46% (4I$^{\circ}$)6s  5I$^{\circ}$ + 18% (4I$^{\circ}$)6s  3I$^{\circ}$ + 12% (2H$^{\circ}$)5d  3I$^{\circ}$
4f35d	3		31371		1.247	33% (4F$^{\circ}$)5d  5F$^{\circ}$ + 20% (4F$^{\circ}$)5d  5P$^{\circ}$
4f35d	6	31394.6	31378	17	1.211	70% (4F$^{\circ}$)5d  5H$^{\circ}$ + 12% (4F$^{\circ}$)5d  5G$^{\circ}$ + 7% (4I$^{\circ}$)5d  5H$^{\circ}$
4f35d	2		31639		1.053	17% (4S$^{\circ}$)5d  3D$^{\circ}$ + 13% (4F$^{\circ}$)5d  3F$^{\circ}$ + 13% (4F$^{\circ}$)5d  3P$^{\circ}$
4f35d	3		31733		1.220	53% (4F$^{\circ}$)5d  5F$^{\circ}$ + 9% (4S$^{\circ}$)5d  3D$^{\circ}$
4f35d	7		31860		1.125	36% (2H$^{\circ}$)5d  3K$^{\circ}$ + 28% (4F$^{\circ}$)5d  5H$^{\circ}$ + 7% (2G$^{\circ}$)5d  3I$^{\circ}$
4f35d	4		31866		0.907	27% (4G$^{\circ}$)5d  5I$^{\circ}$ + 14% (2H$^{\circ}$)5d  3G$^{\circ}$ + 11% (2H$^{\circ}$)5d  1G$^{\circ}$
4f35d	1		31924		1.083	35% (4S$^{\circ}$)5d  5D$^{\circ}$ + 18% (4F$^{\circ}$)5d  3D$^{\circ}$ + 16% (4F$^{\circ}$)5d  5D$^{\circ}$
4f35d	4		32137		0.798	51% (4G$^{\circ}$)5d  5I$^{\circ}$ + 14% (2H$^{\circ}$)5d  3G$^{\circ}$ + 6% (4F$^{\circ}$)5d  3G$^{\circ}$
4f35d	0		32178			45% (4F$^{\circ}$)5d  5D$^{\circ}$ + 39% (4S$^{\circ}$)5d  5D$^{\circ}$ + 7% (2P$^{\circ}$)5d  3P$^{\circ}$
4f35d	3		32218		1.180	26% (4F$^{\circ}$)5d  5P$^{\circ}$ + 18% (2H$^{\circ}$)5d  3G$^{\circ}$ + 9% (4F$^{\circ}$)5d  3F$^{\circ}$
4f35d	2		32323		1.266	28% (4S$^{\circ}$)5d  5D$^{\circ}$ + 20% (4F$^{\circ}$)5d  5D$^{\circ}$ + 9% (4F$^{\circ}$)5d  3P$^{\circ}$
4f35d	5		32330		1.147	23% (4F$^{\circ}$)5d  5F$^{\circ}$ + 14% (4F$^{\circ}$)5d  3H$^{\circ}$ + 9% (2G$^{\circ}$)5d  3G$^{\circ}$
4f35d	4		32336		1.199	64% (4F$^{\circ}$)5d  5F$^{\circ}$ + 12% (4G$^{\circ}$)5d  5I$^{\circ}$ + 7% (4F$^{\circ}$)5d  3G$^{\circ}$
4f35d	6		32444		1.109	36% (2H$^{\circ}$)5d  1I$^{\circ}$ + 35% (4F$^{\circ}$)5d  5G$^{\circ}$ + 11% (2H$^{\circ}$)5d  3K$^{\circ}$
4f35d	2		32589		1.015	39% (2H$^{\circ}$)5d  3F$^{\circ}$ + 15% (4F$^{\circ}$)5d  5D$^{\circ}$ + 13% (4S$^{\circ}$)5d  5D$^{\circ}$
4f36s	6		32792		1.060	64% (4I$^{\circ}$)6s  5I$^{\circ}$ + 18% (4I$^{\circ}$)6s  3I$^{\circ}$ + 7% (2H$^{\circ}$)5d  3I$^{\circ}$
4f35d	7	32832.6	32818	15	1.178	53% (4F$^{\circ}$)5d  5H$^{\circ}$ + 28% (2H$^{\circ}$)5d  3K$^{\circ}$
4f35d	1		32830		1.121	26% (4F$^{\circ}$)5d  5D$^{\circ}$ + 19% (4S$^{\circ}$)5d  3D$^{\circ}$
4f35d	4		32848		1.217	40% (4F$^{\circ}$)5d  3F$^{\circ}$ + 19% (4G$^{\circ}$)5d  3F$^{\circ}$
4f36s	5		32959		0.962	34% (4I$^{\circ}$)6s  3I$^{\circ}$ + 17% (4I$^{\circ}$)6s  5I$^{\circ}$ + 13% (4G$^{\circ}$)5d  5I$^{\circ}$

 

 

Table 5: Calculated oscillator strengths (log gf) and transition probabilities (gA) for 4f⁴-4f³5d transitions of Nd III. Only transitions for which log gf > -4.0are given in the table. Wavelengths in air are deduced from the experimental energy levels compiled by Martin et al. (1978). For each level, we give the energy (cm^-1), the parity (o: odd; e: even) and the J value.

$\lambda$ (nm)		Lower level				Upper level				log gf		gA(1)		gA(2)
328.367		2387.6	(e)	6.0		32832.6	(o)	7.0		-3.25		3.50E+05		3.94E+05
330.409		1137.8	(e)	5.0		31394.6	(o)	6.0		-3.30		3.06E+05		3.54E+05
330.677		0.0	(e)	4.0		30232.3	(o)	5.0		-3.35		2.70E+05		2.78E+05
343.335		3714.9	(e)	7.0		32832.6	(o)	7.0		-1.65		1.28E+07		1.44E+07
343.609		1137.8	(e)	5.0		30232.3	(o)	5.0		-1.64		1.30E+07		1.34E+07
344.646		2387.6	(e)	6.0		31394.6	(o)	6.0		-1.64		1.29E+07		1.49E+07
347.783		0.0	(e)	4.0		28745.3	(o)	4.0		-1.97		6.00E+06		3.81E+06
353.762		1137.8	(e)	5.0		29397.3	(o)	5.0		-2.65		1.22E+06
359.032		2387.6	(e)	6.0		30232.3	(o)	5.0		-0.77		8.74E+07		8.99E+07
359.762		0.0	(e)	4.0		27788.2	(o)	3.0		-0.91		6.35E+07		6.35E+07
360.397		5093.3	(e)	8.0		32832.6	(o)	7.0		-0.62		1.24E+08		1.40E+08
361.173		3714.9	(e)	7.0		31394.6	(o)	6.0		-0.54		1.46E+08		1.69E+08
362.117		1137.8	(e)	5.0		28745.3	(o)	4.0		-0.82		7.68E+07		4.88E+07
362.612		0.0	(e)	4.0		27569.8	(o)	3.0		-1.20		3.16E+07
370.132		2387.6	(e)	6.0		29397.3	(o)	5.0		-1.05		4.38E+07
394.126		1137.8	(e)	5.0		26503.2	(o)	6.0		-3.75		7.60E+04
414.552		2387.6	(e)	6.0		26503.2	(o)	6.0		-2.70		7.83E+05
422.241		3714.9	(e)	7.0		27391.4	(o)	8.0		-2.74		6.83E+05
438.698		3714.9	(e)	7.0		26503.2	(o)	6.0		-2.38		1.46E+06
440.764		1137.8	(e)	5.0		23819.3	(o)	6.0		-3.62		8.29E+04
448.343		5093.3	(e)	8.0		27391.4	(o)	8.0		--1.34		1.51E+07
456.768		0.0	(e)	4.0		21886.8	(o)	5.0		-3.28		1.66E+05
462.499		2387.6	(e)	6.0		24003.2	(o)	7.0		-1.98		3.33E+06
466.468		2387.6	(e)	6.0		23819.3	(o)	6.0		-3.28		1.62E+05
476.704		3714.9	(e)	7.0		24686.4	(o)	8.0		-1.71		5.65E+06
478.106		1137.8	(e)	5.0		22047.8	(o)	6.0		-1.69		6.03E+06
490.326		0.0	(e)	4.0		20388.9	(o)	5.0		-1.83		4.13E+06
492.102		2387.6	(e)	6.0		22702.9	(o)	7.0		-1.77		4.66E+06
492.757		3714.9	(e)	7.0		24003.2	(o)	7.0		-0.83		4.08E+07
496.280		0.0	(e)	4.0		20144.3	(o)	4.0		-3.45		9.53E+04
497.265		3714.9	(e)	7.0		23819.3	(o)	6.0		-1.26		1.52E+07
508.500		2387.6	(e)	6.0		22047.8	(o)	6.0		-0.66		5.71E+07
510.242		5093.3	(e)	8.0		24686.4	(o)	8.0		-0.38		1.05E+08
512.699		2387.6	(e)	6.0		21886.8	(o)	5.0		-1.08		2.11E+07
519.306		1137.8	(e)	5.0		20388.9	(o)	5.0		-0.75		4.42E+07
520.390		0.0	(e)	4.0		19211.0	(o)	3.0		-1.19		1.60E+07
525.989		1137.8	(e)	5.0		20144.3	(o)	4.0		-1.12		1.83E+07
526.502		3714.9	(e)	7.0		22702.9	(o)	7.0		-0.66		5.30E+07
528.676		5093.3	(e)	8.0		24003.2	(o)	7.0		-1.51		7.41E+06
529.410		0.0	(e)	4.0		18883.7	(o)	4.0		-0.65		5.23E+07
545.316		3714.9	(e)	7.0		22047.8	(o)	6.0		-3.85		3.19E+04
563.354		1137.8	(e)	5.0		18883.7	(o)	4.0		-2.06		1.82E+06
567.715		5093.3	(e)	8.0		22702.9	(o)	7.0		-1.41		8.02E+06
584.507		5093.3	(e)	8.0		22197.0	(o)	9.0		-1.13		1.44E+07
598.780		3714.9	(e)	7.0		20410.9	(o)	8.0		-1.22		1.13E+07
614.507		2387.6	(e)	6.0		18656.3	(o)	7.0		-1.29		9.05E+06
632.724		1137.8	(e)	5.0		16938.1	(o)	6.0		-1.36		7.31E+06
652.664		5093.3	(e)	8.0		20410.9	(o)	8.0		-2.36		6.77E+05
655.033		0.0	(e)	4.0		15262.2	(o)	5.0		-1.44		5.73E+06
669.097		3714.9	(e)	7.0		18656.3	(o)	7.0		-2.31		7.21E+05
687.072		2387.6	(e)	6.0		16938.1	(o)	6.0		-2.44		5.13E+05
707.799		1137.8	(e)	5.0		15262.2	(o)	5.0		-2.73		2.53E+05

gA(1):

Weighted HFR transition probabilities (this work).

gA(2):

Weighted HFR transition probabilities normalized with the laser measurements of the present work.

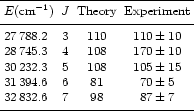
Experimental and theoretical radiative lifetimes obtained in the present work are compared in Table 2. As seen from the table, the agreement between both sets of values is very good, the average percentage error being 7.7% without the 28745.3 cm^-1 level, and 13.5% with it. For this level, the calculated lifetime ( $\tau_{\rm calc} = 108$ ns) is a factor of 1.6 shorter than the measurement ( $\tau_{\exp} = 170\pm 10$ ns). There is no clear reason for this discrepancy. It could possibly be attributed to a wrong intermediate coupling representation of the calculated eigenvector, the level appearing strongly mixed (see Table 4). However, some of the levels, for which the agreement with experiment is good, also appear strongly mixed.

The computed oscillator strengths (log gf) and transition probabilities (gA) are listed in Table 5 alongside the lower and upper experimental energy levels of the transitions and the air wavelengths in nm. These wavelengths were derived from the Nd III experimental levels compiled by Martin et al. (1978). Only transitions with log gf > -4.0 are reported in Table 5. We give in Table 5 both the HFR gA-values calculated as above described and also the weighted transition probabilities normalized according to the new laser lifetime measurements. The comparison between our gf-values and the results published by Bord (2000) is illustrated in Fig. 3. As seen from this figure, the general agreement between both sets of values is very gratifying (as expected because two different versions of the same code were used). Exceptions occur for the lines at 353.7622, 370.1320, 496.2798 and 545.3159 nm. For these transitions, our log gf-values are equal to -2.65, -1.05, -3.45 and -3.85, respectively while the Bord's results are -3.29, -2.29, -6.08 and -7.52. However, for the latter two lines (496.2798 and 545.3159 nm), the discrepancies are obviously related to the fact that the line strengths are affected by severe cancellation effects. Indeed, the cancellation factor (CF), as defined by Cowan (1981), is generally smaller than 0.01 in both calculations for these two transitions. For the lines at 353.7622 and 370.1320 nm, the discrepancies between our calculated oscillator strengths and Bord's results could be due to the fact that the upper 4f³5d level, situated at 29397.3 cm^-1, is strongly mixed (31% (⁴F$^{\circ}$)5d ⁵H$^{\circ}$ + 14% (²H$^{\circ}$)5d ³I$^{\circ}$ + 12% (⁴F$^{\circ}$)5d ⁵G$^{\circ}$ in our calculation) and is probably very sensitive to small differences in the eigenvector compositions.

For the reasons stated above, the present set of transition probabilities is expected to be the most accurate presently available. The detailed results are available in the database mentioned at the end of Sect. 1.

	Figure 3: Comparison of the HFR oscillator strengths obtained in this work with those published by Bord (2000).
Open with DEXTER

4 Nd III in stellar spectra

The information concerning the occurence of the third spectra of the REE in stellar sources is rather scarse and scattered through the literature although the presence of these ions in stellar spectra has long been recognized (Swings 1944; Adelman 1974; Cowley 1976). Some systematic searches have nevertheless been undertaken (see e.g. Cowley & Greenberg 1988) and, more recently, the satellite spectra have stimulated new investigations of these ions: Copernicus spectra of $\alpha$²CVn or BUSS spectra of the same star have been investigated by Leckrone (1976) and by Hensberge et al. (1986), respectively. IUE spectra of HD 51418 have been considered by Adelman & Shore (1981).

Although Nd II is expected to be the dominant species in cold CP stars, it is important to compare the abundances derived from this ion to those obtained from the consideration of Nd III lines in order to get information on eventual non-LTE effects or on possible element stratification in the stellar atmospheres (Proffitt et al. 1999). In addition, the lines of doubly ionized REE are expected to be stronger in hotter stars where the doubly ionized elements could be dominant but the identification of the lines and the abundance work, in many cases, has been performed in the past or is still prevented by the lack of reliable atomic data.

As pointed out in the introduction, Nd III has been identified or mentioned as possibly present in a number of stars: HR 465, HD 51418, HD 200311 (Cowley 1976; Aikman et al. 1979; Bidelman et al. 1995), HD 192913 (Cowley & Crosswhite 1978; Ryabchikova et al. 1990), HD 101065 (Cowley et al. 1998) but the identification can be complicated by problems of different types. The identification of lanthanides in stars showing strong Si II lines is made difficult by the fact that only a few stars are known which show very sharp lines. According to Cowley (1976), Nd III is strong in the spectrum of HR 465 but, in $\beta$CrB, the coincidences are indicated as marginally significant, the author insisting however upon the fact that the strong Nd III lines appear shortward of the Balmer jump and, consequently, that his study is not well suited for the detection of this ion.

For HD 101065, Bord (2000) has deduced an abundance of neodymium 5000 larger than the solar result, a value similar to that deduced from an analysis of Nd II lines; this result has to be reduced by 0.7-0.8 dex if the surface magnetic field is taken into account. The analysis by Ryabchikova et al. (2000) of the cool roAp star HD 122970, based on the gf-values of Bord (2000), leads to an overabundance of Nd by a factor of about 275 relative to the solar abundance. We did not try to correct the results of these two analyses on the basis of the new gf-values obtained in the present work because the detailed list of the transitions considered is not available in the corresponding papers. Nevertheless, on the basis of the general agreement of the two sets of data observed in Fig. 1, the general conclusions of Bord (2000) remain valid. The main improvement due to the present work is the fact that these results are now firmly established on the basis of the laser experimental results.

In conclusion, as an extrapolation of the present work, it is expected that, in the future, the new transition probabilities now available for Nd III will make possible more reliable quantitative analysis of stellar spectra of CP stars.

Acknowledgements

This work was financially supported by the Swedish Natural Science Research Council and by the EU-TMR access to Large-Scale facility programme (contract HPRI-CT-1999-00041). Financial support from the Belgian FNRS is acknowledged by E.B., P.P. and P.Q.

References

 

• Adelman, S. J. 1973, ApJS, 26, 1 In the text NASA ADS  
• Adelman, S. J. 1974, ApJS, 28, 51 In the text NASA ADS  
• Adelman, S. J., & Shore, S. N. 1981, PASP, 93, 85 In the text NASA ADS  
• Aikman, G. C. L., Cowley, C. R., & Crosswhite, H. 1979, ApJ, 232, 812 In the text NASA ADS  
• Anders, E., & Grevesse, N. 1989, Geoch. Cosmochim. Acta, 53, 197 In the text NASA ADS  
• Bidelman, W. P. 1953, ApJ, 117, 377 In the text NASA ADS  
• Bidelman, W. P., Cowley, C. R., & Iler, A. L. 1995, Publ. Obs. Univ. Michigan, 12, 77 In the text  
• Biémont, E., Li, Z. S., Palmeri, P., & Quinet, P. 1999, J. Phys. B, 32, 3409 In the text NASA ADS  
• Biémont, E., Garnir, H. P., Bastin, T., et al. 2001a, MNRAS, 321, 481 In the text NASA ADS  
• Biémont, E., Garnir, H. P., Palmeri, P., et al. 2001b, Phys. Rev., 64, 022503 In the text  
• Biémont, E., Garnir, H. P., Li, Z. S., et al. 2001c, J. Phys. B, 34, 1869 In the text  
• Biémont, E., Palmeri, P., Quinet, P., et al. 2001d, MNRAS, 328, 1085 In the text NASA ADS  
• Bord, D. J. 2000, A&A, 144, 517 In the text  
• Brewer, J. 1971, JOSA, 59, 2083 In the text  
• Cowan, R. D. 1981, The theory of Atomic Structure and Spectra (University of California Press, Berkeley, CA, USA) In the text  
• Cowley, C. R. 1976, ApJS, 32, 631 In the text NASA ADS  
• Cowley, C. R. 1984, Phys. Scr., T8, 28 In the text  
• Cowley, C. R., & Bord, D. J. 1998, The Third Spectrum of Neodymium: Application to HR 6870 and $\gamma$Equulei, in The Scientific Impact of the Goddard High Resolution Spectrograph, ed. J. C. Brandt, T. B. Ake III, C. C. Petersen, ASP Conf. Ser., 143, 346 In the text  
• Cowley, C. R., & Crosswhite, H. M. 1978, PASP, 90, 108 In the text NASA ADS  
• Cowley, C. R., Bidelman, W. P., & Mathys, G. 1998, BAAS, 30, 1317  
• Cowley, C. R., & Greenberg, M. 1988, MNRAS, 232, 763 In the text NASA ADS  
• Cowley, C. R., Ryabchikova, T., Kupka, F., et al. 2000, MNRAS, 317, 299 In the text NASA ADS  
• Crosswhite, H. 1975, 1976, unpublished work, quoted by Martin et al. (1978) In the text  
• Hensberge, H., Van Santvoort, J., Van der Hucht, K. A., & Morgan, T. H. 1986, A&A, 158, 113 In the text NASA ADS  
• Jaschek, C., & Jaschek, M. 1995, The Behavior of Chemical Elements in Stars Cambridge University Press) In the text  
• Lambert, D. L. 1985, in Cool Stars with Excesses of Heavy Elements, ed. M. Jaschek, & P. C. Keenan (Reidel), 191 In the text  
• Leckrone, D. S. 1976, in The Physics of Ap Stars, IAU Colloq. 32, ed. W. W. Weiss, H. Jenkner, & J. J. Wood, Universitätssterwarte Wien, Vienna In the text  
• Leckrone, D. S., Proffitt, C. R., Wahlgren, G. M., Johansson, S. G., & Brage, T. 1999, AJ., 117, 1454 In the text NASA ADS  
• Li, Z. S., Lundberg, H., Wahlgren ,G. M., & Sikström, C. M. 2000, Phys. Rev. A, 62, Electronic version Ref. No. 032505 In the text  
• Li, Z. S., Zhang, Z. G., Lokhnygin, V., et al. 2001, J. Phys. B, 34, 1349 In the text  
• Li, Z. S., & Jiang, Z. K. 1999, Phys. Scr., 60, 414 In the text  
• Martin, W. C., Zalubas, R., & Hagan, L. 1978, Atomic Energy Levels, The Rare-Earth Elements, Nat. Bur. Stand. Ref. Data Ser. 60, Washington D.C., USA In the text  
• Merrill P.W. 1956, Lines of the Chemical Elements in Astronomical Spectra, Carnegie Institute of Washington, Publ., 610  
• Palmeri, P., Quinet, P., Frémat, Y., Wyart, J.-F., & Biémont, E. 2000, ApJS, 129, 367 In the text NASA ADS  
• Proffitt, C. R., Brage, T., Leckrone, D. S., et al. 1999, ApJ, 512, 942 In the text NASA ADS  
• Quinet, P., Palmeri, P., Biémont, E., et al. 1999, MNRAS, 307, 934 In the text NASA ADS  
• Ryabchikova, T. A., Davidova, E. S., & Adelman, S. J. 1990, PASP, 102, 581 In the text NASA ADS  
• Ryabchikova, T. A., Savanov, I. S., Hatzes, A. P., Weiss, W. W., & Handler, G. 2000, A&A, 357, 981 In the text NASA ADS  
• Smith, M. A. 1973, ApJS, 25, 277 In the text NASA ADS  
• Smith, M. A. 1974, ApJ, 189, 101 In the text NASA ADS  
• Sneden, C., McWilliam, A., Preston, G. W., et al. 1996, ApJ, 467, 819 In the text NASA ADS  
• Smith, V. V., & Lambert, D. L. 1985, ApJ, 294, 326 In the text NASA ADS  
• Swings, P. 1944, ApJ, 100, 132 In the text NASA ADS  
• Zhang, Z. G., Li, Z. S., Lundberg, H., et al. 2000, J. Phys. B, 33, 521 In the text NASA ADS  
• Zhang, Z. G., Persson, A., Li, Z. S., Svanberg, S., & Jiang, Z. K. 2001, Eur. Phys. J. D, 13, 301 In the text NASA ADS