A rectified echelle spectrum of WR46 by Hamann et al. (1995b) is shown in Paper I (their Fig.14). We note that according to Smith et al. (1996) the N IV 3480 emission line is only faintly present, while a spectrum by Massey & Conti (1983) does show this line on the edge of their spectrum with a intensity of 0.2 in continuum units. Crowther et al. (1995, hereafter CSH) showed the spectrum to be similar to other weak-lined early-type WN stars, e.g. WR128 (WN4(h)) and WR152 (WN3(h)) (spectral types of Smith et al. 1996). The differences are that WR46 shows no sign of any hydrogen, the N V (resp. He II) lines are stronger (resp. weaker) and the wings are somewhat broader as a result of a faster wind. CSH modeled the observed triangular line profiles assuming a spherical, low-density WR stellar wind. We note that the spectrum of WR3 (HD9974, WN3) is very similar to that of WR46 (Marchenko priv. comm.), except for the O VI 3811/34 emission lines, which are absent in WR3, but very prominent in WR46. The discussion of this feature is deferred to Sect. 5.2.
To illustrate the variable behaviour of the spectral lines we present a gallery of grey-scale figures of various lines observed in different years. These figures show either the same line on different nights (Fig.1), different lines of different elements during a single night (Fig.2), the same element and ionization (Fig.3) during subsequent nights, or both (Fig.4). We discuss the characteristic behaviour of WR46 in the N V 4944 emission line. This line shows both an obvious radial-velocity curve (e.g., the second night in 1998 (Fig.4), or the fourth night in 1995 (top panel of Fig.3)), and, a stand-still with, or without, a change of flux (e.g., second night in 1995, Fig.4).
We introduce a new variable, the so-called continuum-corrected equivalent
width
![]() ,
which measures the line flux relative to the continuum
of a specific spectrum, which was chosen to have truly simultaneous photometry
available (V0 with
,
which measures the line flux relative to the continuum
of a specific spectrum, which was chosen to have truly simultaneous photometry
available (V0 with
![]() min) near the mean brightness.
First, the different lines with adjacent continuum are extracted and
rectified using a first- or second-order polynomial. Then, we measure the
standard equivalent width relative to the continuum of the spectrum itself.
Since the emission lines contribute only <10% to the broad-band
photometry, the EW of all the lines can be transformed to
min) near the mean brightness.
First, the different lines with adjacent continuum are extracted and
rectified using a first- or second-order polynomial. Then, we measure the
standard equivalent width relative to the continuum of the spectrum itself.
Since the emission lines contribute only <10% to the broad-band
photometry, the EW of all the lines can be transformed to
![]() ,
according to:
,
according to:
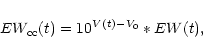 |
(1) |
| emission | 1989 | 1990 | 1991 | 1995a | 1998 |
| W | 1.03 | 1.047 | |||
| U | 1.047 | ||||
|
|
|||||
| L | (1.0) | 1.048 | |||
| B | 1.04 | 1.060 | |||
| V | 1.05 | 1.069 | |||
| O VI 5290 | 1.22 | 1.37 | |||
| O VI 3811/34 | 1.54 | 1.39 | |||
| N V 4944 | 1.36 | 1.43 | 1.47 | 1.51 | 1.29 |
| N V 4604/20 | 1.66 | 1.71 | 1.38 | 1.37 | |
| He II 4859 | 1.78 | 1.77 | 1.38 | 2.25 | 1.17a |
| He II 5412 | 1.33 | 1.53 | 1.26 | 1.20 | 1.27 |
| He II 6560 | 1.26 | 1.45 | 1.17 | 1.23 | |
| He II 4686 | 1.25 | 1.33 | 1.16 | 1.21 |
![\begin{figure}
\par\includegraphics[width=17.2cm,clip]{specdayart90.ps}
\end{figure}](/articles/aa/full/2002/14/aa10242/Timg23.gif) |
Figure 6: As in Fig.5, but for the 1990 data. |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{specdayart91.ps}
\end{figure}](/articles/aa/full/2002/14/aa10242/Timg24.gif) |
Figure 7: As in Fig.5, but for the 1991 data. |
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{specdayart95.ps}
\end{figure}](/articles/aa/full/2002/14/aa10242/Timg25.gif) |
Figure 8: As in Fig.5, but for the 1995 data. Note that the nights are not presented as a time sequence. |
We determine the ratios of the maximum over the minimum flux-level of the continuum and the main emission lines for each observing run and the results are listed in Table2. Because of the low number of cycles (2-3) observed per season, the determinations can only serve as a relative measure, since all lines (and continuum) are observed simultaneously. The table is ordered from the inner to the outer layers of the atmosphere and shows as trend that the amplitude increases when going outwards, out to the formation region of either the spectral line He II 4859, or, in 1991, O VI 3811/34. Further out, the ratio of the line fluxes decreases, presumably, as the effect of the variable source wears out due to a larger distance. In Paper III, this change of amplitude dependent on the height in the atmosphere is interpreted as a change of the distortion of the (line- and continuum-) emission-forming layers. The measurements of these ratios are translated into a graphical representation in Fig.1 of Paper III.
We measure the bisector (i.e., the line center for each line) at three different intensities above the continuum, namely at 20, 50 and 85% of the maximum line intensity. A similar method was applied to WR6 by Robert et al.(1992). We check the stability of the wavelength calibration by measuring also the interstellar and atmospheric lines. A systematic offset was notable only a few times, which we subsequently corrected. The square root of the variance of these measurements (after correction) may be considered as error estimates for each data set: 30-50 kms-1 in 1989-91 and 3-5 kms-1 in 1995 and 1998.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{specdayart98.ps}
\end{figure}](/articles/aa/full/2002/14/aa10242/Timg26.gif) |
Figure 9: As in Fig.5, but for the 1998 data. Time is measured as HJD-2450000. |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{phaseallP_bisart.ps}
\end{figure}](/articles/aa/full/2002/14/aa10242/Timg28.gif) |
Figure 11:
Bisector at 50%-level of N V 4944 in
kms-1 for all seasons folded with the various periods. From left to
right we applied phasing with |
We conclude that the radial-velocity amplitude for most emission lines is in the range K = 50-100 kms-1. We assume that the lines formed closer to the WR star give a better indication than the N V 4604/20 line complex, which results in an outstandingly high amplitude of 250-300 kms-1. Such a large amplitude for this line-complex has also been observed by Niemela et al. (1995). Discussion of this phenomenon is deferred to Sect. 5.2.
Copyright ESO 2002