A&A 385, 264-272 (2002)
DOI: 10.1051/0004-6361:20020081

Weak magnetic flux features on the Sun

B. Hartje - F. Kneer

Universitäts-Sternwarte, Geismarlandstraße 11, 37083 Göttingen, Germany

Received 16 November 2001 / Accepted 15 January 2002

Abstract
We observed weak magnetic flux in enhanced CaK network and in its surroundings at various positions on the solar disc ( $\cos\theta=1.0\dots0.1$). The Gregory Coudé Telescope at the Observatorio del Teide on Tenerife was used together with an image scanner and a Stokes V polarimeter. ${1\over2}(I_\lambda\pm V_\lambda)$ spectrograms in the 6302Å region were taken. A second order flat fielding and smoothing brought the polarimetric sensitivity to a detection limit of 0.001 $I_{\rm c}$ (with $I_{\rm c}$ = continuum intensity) for exposure times of 300 ms in pixels corresponding to 0 $.\!\!^{\prime\prime}$$5\times$0 $.\!\!^{\prime\prime}$19 ($\widehat=$ slit width $\times $ pixel size of detector). We present correlations between continuum intensity, line center intensity, and magnetic flux and discuss Stokes V profiles. The V amplitude asymmetry from areas with strong flux decreases towards the limb, a change of sign is not identified. The magnetic fields are ordered around strong flux centers with decreasing mean field strength outwards from the centers. In the range of $1\times 10^{16}$Mx to $5\times 10^{16}$Mx (in one pixel of $5\times 10^{14}$cm2) the probability distribution of the magnetic flux is $\sim$ $\vert\Phi\vert^{-q}$ with $q\approx3$, different from a Gaussian distribution. From this we derive tentativily a radial dependence from the flux centers of the form $\Phi(r)\sim1/r$. For the probability distributions a significant center-to-limb variation is not detected. Together with the center-to-limb behaviour of the asymmetries, we interpret this tentatively as an isotropic orientation of the weak magnetic flux elements and of the gas flows. A vertical orientation of the magnetic fields is also compatible with the measurements, though.

Key words: Sun: photosphere - magnetic fields - techniques: polarimetric


1 Introduction

Small-scale magnetic fields on the Sun and their dynamics and interaction with the solar atmosphere and the convective subphotospheric gas represent a lively field of research. We refer the reader to recent conference proceedings (Sigwarth 2001) and to the review by Hurlbert et al. (2000).

Many observational results, with high polarimetric accuracy, from weak flux structures on the Sun are contained in the works of Sigwarth et al. (1999) and Sánchez Almeida & Lites (2000). The magnetic network possesses Stokes V amplitudes of typically 4% of the continuum intensity. Outside the network the amplitudes are 1% or even much below this value and the V profiles are often very asymmetric (more precisely: far from anti-symmetric) and show often double structures or are only one-sided.

There exist several possible explanations for the strong asymmetries. Steiner (2000) proposes magnetopauses, i.e. interfaces which separate two regimes of different flow and magnetic fields from a field-free plasma. He considers also temperature inversions leading to tow-humped V profiles. Additionally to these types of canopy, Grossmann-Doerth et al. (2000) model oblique magnetic flux sheets embedded in non-magnetic gas above and below the magnetic structure. The authors admit that mixed polarity configurations, i.e. both magnetic polarities within the resolution element, combined with appropriate velocities can as well produce the observed V asymmetries. An extreme picture of such mixed polarities was put forward by Sánchez Almeida et al. (1996) and Sánchez Almeida & Lites (2000) with the MIcro-Structured Magnetic Atmospheres (MISMA). MISMAs are km-sized magnetic tubes with a dominant polarity and a minority contribution of opposite polarity. They too are imbedded in a non-magnetized atmosphere and possess various gas velocities. The inversion of the observed, asymmetric Stokes V profiles gives field strengths in the kGauss range. Sánchez Almeida (2000) suggests that, due to the strong magnetic fields, the flux tubes are very much evacuated with the consequence that a large part of the magnetic flux in the solar atmosphere is elusive, invisible.

The present work deals with observations and their analysis of weak magnetic flux signals in the surroundings of small CaK faculae, with good spatial resolution and polarimetric sensitivity. We shall describe results relevant to weak activity which possibly feeds, by injection of magnetic flux bundels, the granular magneto-convection process.

2 Observations

The observations for this contribution were obtained on 1. September 1998 with the Gregory Coudé Telescope and its Czerny Turner spectrograph at the Observatorio del Teide/Tenerife. By means of slit-jaw video imaging we selected weakly active regions and enhanced CaK network regions at various positions of the solar disc ranging from $\mu = \cos\theta$ = 1.0 to $\mu $ = 0.1.

Spectrograms around 6302 Å were taken with a Stokes Vpolarimeter. The wavelength region contains the two Fe I lines 6301.5Å (Landé factor $g_{\rm eff} = 1.67$) and 6302.5Å (g = 2.5) and the two telluric H2O lines at 6302.00Å and 6302.76Å.

The V polarimeter is mounted behind the spectrograph's entrance slit and consists of a $\lambda$/4 retarder plate followed by two crossed calcites. It thus splits the light beam into two beams of circularly polarized light ${1\over2}(I+V)$ and ${1\over2}(I-V)$. They are focussed onto two different parts of a Thompson TH 7863 FT CCD detector (384$\times $286 pixels) at the spectrograph exit. The pixel size corresponds to 0 $.\!\!^{\prime\prime}$192 along the spatial direction and to 5.83mÅ in wavelength. The slit width was chosen to 60$\mu $ ($\widehat=$ 0 $.\!\!^{\prime\prime}$5) and the exposure time was 300ms.

We used the image scanner described by Stolpe & Kneer (1998) and a Bowen compensator (Koschinsky & Kneer 1996) which corrects for the instrumental polarization upon the reflections at the mirrors of the scanner. The $Q/U \rightarrow V$crosstalk was below 0.05. Small fields of view of 30 $.\!\!^{\prime\prime}$9 (along the slit) $\times $ 14 $.\!\!^{\prime\prime}$2 (in the scan direction) were recorded with 30 scanner positions separated by 0 $.\!\!^{\prime\prime}$48. The duration of such scans was approximately 12 s. The fields of view included the enhanced CaK networks.

For the data analysis, dark frames, flat fields (by moving the telescope pointing during exposure), and frames with a fixed pattern mounted at the spectrograph slit were also taken.

3 Data analysis

3.1 General data reduction

The spectrograms were corrected in the usual way for their dark offset and for the recording imperfections (vignetting, dust on the CCD, inhomogeneities of the spectrograph slit, ...) by means of the flat field data. Small differential distortions of the two ${1\over2}(I\pm V)$spectrograms due to their different paths through the spectrograph were reduced as much as possible using the above mentioned fixed pattern exposures (distortions along the slit direction) and using the spectral lines themselves for a best overlap of the two spectrograms in wavelength direction. It was noticed e.g. by Keller et al. (1994) that imaging the two ${1\over2}(I\pm V)$spectrograms onto different parts of the detector limits the polarimetric sensitivity due to limited knowledge of the gain table. We could substantially meloriate the sensitivity by applying the second order flat fielding recommended by Sánchez Almeida & Martínez Pillet (1994).

From the Stokes I spectrograms we then obtained maps of the continuum intensity, of the line center intensity, and of the velocity. The latter two were determined from fourth order polynomials fitted to the line cores of the Fe I 6302.5 profiles. The minimum position of the 6302.5 line averaged over the field of view was adopted as reference wavelength, i.e. with velocity v = 0.

To reduce the noise in the V spectrograms we averaged the Vprofiles of the two Fe I lines and then applied a boxcar smoothing over 87.5mÅ in the wavelength direction and over 0 $.\!\!^{\prime\prime}$575 ($\widehat=$ 3 pixels) in the spatial direction. From these smoothings we arrive at a rms of the noise in the V spectrograms of approximately 0.001$I_{\rm c}$, where $I_{\rm c}$ represents the continuum intensity (see next sections for examples of the remaining noise). We used the maximum amplitude of $\vert V\vert/I_{\rm c}$ = 0.003 as the lower limit for the further analysis of the V profiles.

From the V profiles we derived two-dimensional maps of the magnetic flux, of the V asymmetry and of the velocity in the magnetized plasma from the zero crossings $v_{\rm zc}$ of the V profiles.

3.2 Calibration of magnetic flux


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3304F1.eps} \end{figure} Figure 1: Calibration of magnetic flux; Stokes V profiles calculated by shifting the intensity profiles of the Fe I 6301.5 and 6302.5 lines from the Fourier Transform Spectrometer Atlas (Neckel 1999) by the amount according to their Zeeman pattern from a constant 1000 Gauss field along the line of sight. Dotted: stokes V profile of 6302.5; dashed: after boxcar smoothing over 87.5 mÅ; dash-dotted and dot-dot-dot-dashed: the same for 6301.5; solid: average of the two smoothed V profiles.
Open with DEXTER


  \begin{figure} \includegraphics[width=12cm,clip]{H3304F2.eps} \end{figure} Figure 2:  Stokes V spectrograms; from left to right: Fe I 6301.5 Å, Fe I 6302.5 Å, average of the two former, smoothed in wavelength direction over 87.5mÅ, and smoothed in spatial direction over 0 $.\!\!^{\prime\prime}$575 (3 pixels on the CCD detector). The spectrum is from the position as indicated by horizontal short lines in the magnetogram of Fig. 4. and the amplitudes are limited to $\vert V\vert/I_{\rm c} = 0.015$ in the representation. The left and right tickmarks are at 1 $^{\prime \prime }$ distance.
Open with DEXTER

To estimate the magnetic flux in the observed areas on the Sun we proceeded as follows: the spectral range around 6302Å was copied from the high resolution Fourier Transform Spectrometer (FTS) Atlas by Brault and Neckel (quoted by Neckel 1999). A constant magnetic field of 1000 Gauss along the line of sight was applied to the FTS profiles of the two Fe I lines. The ${1\over2}(I_\lambda\pm V_\lambda)$ spectra are thus shifted according to their Zeeman pattern. From these the $V_{\lambda}$ profiles are obtained. The ratio of the V amplitudes of the 6301.5 and 6302.5 lines is 0.674, very close to the ratio of the Landé factors (=0.667). Smoothing and averaging as in the observations allows to relate the magnetic flux from 1000 Gauss (along the line of sight, area filling factor 1.0) in one pixel to an observable V amplitude. Figure 1 depicts the result. The solid $V_{\lambda}$ profile has an amplitude of $V_{\lambda}/I_{\rm c}\approx0.20$.

The area of one pixel (= projection of slit width $\times $ projection of CCD pixel size onto the sky) is $0\hbox{$.\!\!^{\prime\prime}$ }5\times0\hbox{$.\!\!^{\prime\prime}$ }192\times$ $(725\times10^{5})^2$ cm $^2\approx5\times 10^{14}$ cm2. (We note that the above pixel size is not the spatial resolution of the data which is given by the telescope with its spectrograph, by the smoothing process, and by the seeing.) The magnetic flux through this area from a 1000 Gauss field is $5\times 10^{17}$Mx. Thus, the applied lower limit $\vert V\vert/I_{\rm c} = 0.003$corresponds to $7.5\times 10^{15}$Mx and the mean flux density |B|(averaged over the pixel area) amounts to 15 Gauss.

The achieved polarimetric sensitivity leads to very much the same lower limit of detected magnetic flux (in one pixel) as the one obtained by Wang et al. (1995) in deep magnetograms. They give a lower limit for the field strength of 2 Gauss in a 1 $^{\prime \prime }$$\times $1 $^{\prime \prime }$ area which corresponds to 1016Mx.

A word of caution is appropriate. Admittedly, our above "calibration'' cannot be accurate, especially since the applied 1000 Gauss are chosen constant and belong to the weak field limit which must not be correct. Another calibration method would be the synthesis of the V profiles from standard model atmospheres. This would require an adjustment of some atmospheric parameters (like micro- and macro-turbulence) to reproduce the observed Stokes I profiles. The V profiles calculated from such an atmosphere with a constant magnetic field along the line of sight should be very similar to those in Fig. 1. Obviously, sophisticated inversion techniques (e.g. Bellot Rubio et al. 2000a,2000b; Sánchez Almeida 1997) can lead to a preciser information about the magnetic field strengths. The numbers for the fluxes given in the following sections are thus to be taken with this caution in mind.

4 Results and discussion

4.1 Stokes V profiles

Figure 2 gives an example of the V spectrograms obtained after the data analysis and noise reduction. This spectrogram is taken from near disc center. Its position in the corresponding scan is indicated by the short horizontal marks in the magnetogram of Fig. 4, which will be discussed below.

We show in Fig. 2 from left to right: V spectrogram in 6301.5, the same in 6302.5, the average of the two, after boxcar smoothing over 87.5 mÅ, and finally after boxcar smoothing over three pixels in spatial direction. The wavelength zero position was defined as the zero crossing of the average of those V profiles in the field of view with $\vert V\vert _{\rm max}/I_{\rm c}\ge 0.02$. The suppression of noise from left to right in Fig. 2 is substantial. V profiles not recognizable in the two spectrograms to the left appear with a high definition in the one to the right.

  \begin{figure} \par\includegraphics[width=8.6cm,clip]{H3304F3.eps} \end{figure} Figure 3: Several Stokes V profiles taken from the positions marked in Fig. 2 (the numbers - top to bottom - there correspond to the same numbers here). The first four profiles in the upper panel show the typical asymmetry of weak flux profiles, the fifth profile represents one below the above limit of $\vert V\vert/I_{\rm c} = 0.003$. The middle panel depicts noise, from left to right: in 6301.5, in 6302.5, their average, then smoothed over 87.5mÅ, finally smoothed over 0 $.\!\!^{\prime\prime}$575. The bottom panel gives a strong, albeit still asymmetric V profile (from left to right as in the middle panel).
Open with DEXTER

Figure 3 depicts V profiles, separated by vertical dotted lines. They stem from the spectrogram of Fig. 2, i.e. from the positions there with the short horizontal marks. The profiles are labeled with the same numbers as in Fig. 2. The first four V profiles show the strong asymmetry of the signals from solar areas with low magnetic flux. The fifth profile (upper right in Fig. 3) represents one just below the lower limit adopted above.

The middle panel in Fig. 3 shows noise in (from left to right) 6301.5, 6302.5, their average, smoothed in wavelength, and smoothed in spatial direction. The two original "profiles'' possess peak to peak amplitudes of $\vert V\vert/I_{\rm c}\approx0.01$, that is a rms noise of 0.003. Averaging and smoothing suppresses further the noise below 0.001.

The bottom panel of Fig. 3 gives profiles with strong amplitude, albeit still asymmetric. The presentation from left to right is in the same manner as for the noise above and in Fig. 2. It is important to note that the amplitudes in the two Fe I lines are very similar. This is an indication for strong, kGauss magnetic fields. In the weak field limit one would expect a ratio of the amplitudes close to the ratio of the Landé factors. (The two lines possess very similar slopes in the wings of their intensity profiles, see also Sect. 3.2 and Fig. 1.) Socas Navarro & Sánchez Almeida (2001) find for a large range of V amplitudes ( $0.001<V_{\rm max}<0.1$) of the same lines that the ratio of these amplitudes is larger than in the weak field limit, indicative for strong, kGauss fields, even for the weakest detectable V signals. We cannot follow their analysis with the present data since the signals from each of the two lines alone are too noisy at weak amplitudes.

4.2 Maps, correlations, and centers of magnetic flux

In this subsection we describe and discuss the intensity - velocity - magnetic field relations.

Figure 4 shows an example with data from near disc center. We present, from left to right and starting with the upper row: continuum intensity, line center intensity, velocity from the shift of the I profile, magnetic flux, V amplitude asymmetry, and velocity from V zero crossing. For the magnetogram, the extrema of the V profiles were taken. The asymmetry for this presentation is defined as the difference between the blue and the red extremum of the V profile, i.e. the non-normalized value $\delta a=\vert V\vert _{\rm blue,max}-\vert V\vert _{\rm red,max}$.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3304F4.eps} \end{figure} Figure 4: Several maps obtained from the I and V profiles; from left to right starting with the uppermost row: continuum intensity, line center intensity, velocity measured from displacement of minimum of I profile, magnetic flux (representation limited to 0.015 $\ge \vert V\vert/I_{\rm c} >$ 0.003, bright and dark shading for positive and negative polarity, respectively), asymmetry, and velocity from the zero crossing $v_{\rm zc}$ of the V profiles. The field of view is 30 $.\!\!^{\prime\prime}$9$\times $14 $.\!\!^{\prime\prime}$2 (distance of tickmarks 1 $^{\prime \prime }$), and the data are from disc center.
Open with DEXTER

The continuum intensity fluctuation amounts to $\Delta I_{\rm c,rms}/I_{\rm c,av}=0.035$, that of the line center is $\Delta I_{\rm lc,rms}/I_{\rm lc,av}=0.089$. The line of sight velocity fluctuation from the I profile is $v_{\rm lc,rms}=345$ms-1. Continuum and line center intensity fluctuations are clearly anticorrelated, their correlation coefficient being -0.58. This is interpreted as penetration of convection into a stably stratified atmosphere (Holweger & Kneer 1989; Balthasar et al. 1990; Gadun et al. 2000 and references in the latter work). At disc center, blue V amplitude asymmetry (brighter than average in Fig. 4) dominates.

The velocities from the V zero crossing, $v_{\rm zc}$, are meaningful only when the V profiles are firstly well above noise and secondly not too asymmetric, e.g. one-sided only or more like Stokes Q profiles like the ones shown in the top row of Fig. 3. Since we are interested in the weak V signals, which tend to be asymmetric (see below), we shall not deal furtheron with the $v_{\rm zc}$ values. The velocities in the solar areas which produce the asymmetric V profiles need an investigation by means of theoretical modelling (e.g. Steiner et al. 1998; Cattaneo 1999a,1999b; Emonet & Cattaneo 2001; Stein & Nordlund 2000) and by inversion techniques (Bellot Rubio et al. 2000a,2000b; Sánchez Almeida 1997).

Further inspection of Fig. 4 shows that only the areas with strongest magnetic flux appear in the line center image as brightenings in this example from disc center. A drawing of their relationship (not shown) clearly demonstrates that the line center intensity is enhanced in areas of strong flux, which is known as the line gap phenomenon (cf., e.g., Chapman & Sheeley 1968; Kneer & von Uexküll 1991 and references therein). Yet it is important to notice that weak flux is not correlated with the line center intensity.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3304F5.eps} \end{figure} Figure 5: Various V amplitudes; clockwise from upper left: |V|/Ic > 0.017, $0.017 \ge \vert V\vert/I_c > 0.009$, 0.009 $\ge $ |V|/Ic > 0.005, $0.005 \ge \vert V\vert/I_c > 0.003$; same region as in Fig. 4.
Open with DEXTER

We have devided the flux of the magnetogram of Fig. 4 into four V amplitude ranges. The result is seen in Fig. 5. Obviously, there exist centers of "strong'' flux, and the V amplitudes decrease with increasing distance from the centers. Even the pixels with weakest (detectable) flux, $0.005 \ge\vert V\vert/I_{\rm c} > 0.003$, are not randomly distributed but are located at the outskirts of the magnetic patches, at 3 $^{\prime \prime }$-5 $^{\prime \prime }$ distance from the flux centers. Further out, the fluxes fall below the detection limit and partly mix with fluxes of opposite polarity. This is important by itself and shows in addition that our imposed lower limit is well above noise.

4.3 Asymmetries

We use here the common expression for the relative amplitude asymmetry

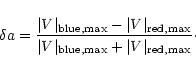\begin{displaymath}\delta a= {\vert V\vert _{\rm blue,max}-\vert V\vert _{\rm re... ...\vert V\vert _{\rm blue,max}+\vert V\vert _{\rm red,max}}\cdot \end{displaymath} (1)


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3304F6.eps} \end{figure} Figure 6: Relative amplitude asymmetries of the Stokes V profiles at various positions on the solar disc. The numbers in the graphs indicate the $\cos\theta$ value.
Open with DEXTER

Figure 6 shows the asymmetries in the fields of view at various positions on the solar disc, the numbers in the graphs indicating the $\cos\theta$ value. We note:

1.
Below $\vert V\vert _{\lambda,{\rm max}}/I_{\rm c}\approx0.01$ ( $\widehat=\,50$Gauss mean flux density) strong positive as well as negative asymmetries occur. Values of $\pm1.0$ do occur frequently from the single-sided V profiles. (We remind from Fig. 3, that relative amplitudes of 0.01 are well detected in our data.)

2.
Above this $\vert V\vert _{\lambda,{\rm max}}/I_{\rm c}$ value the asymmetries are concentrated around a certain value, which is approximately +0.15 at $\cos\theta$ = 1.0 and decreases towards the limb to approximately 0. The data do not show a change of sign of the asymmetry near the limb. This confirms the earlier finding by Stenflo et al. (1987) who measured a change of sign for the area asymmetry, but not for the amplitude asymmetry. Martínez Pillet et al. (1997), however, found a change of sign towards the limb for both the area and the amplitude asymmetry in plage regions, with a large scatter about the average asymmetry, though.

4.4 Distributions

4.4.1 Solar data

We ask for the occurrence of (unsigned) magnetic flux values through one pixel in our observations. The fluxes were calculated from the $\vert V\vert _{\lambda,{\rm max}}$ values in the spectrograms by means of the calibration described above (Sect. 3.2). In Fig. 7 the distribution from the data near disc center is shown ( $\ast \ast \ast $). Plotted there are the numbers $\Delta N$ of pixels, relative to the total pixel number, in a certain interval of $\Delta^{10}\log\vert\Phi\vert$ (= 0.07918), that is the distribution

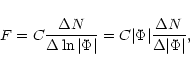\begin{displaymath}F = C{\Delta N\over\Delta\ln\vert\Phi\vert} = C\vert\Phi\vert{\Delta N\over\Delta\vert\Phi\vert}, \end{displaymath} (2)

where C is a constant.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3304F7.eps} \end{figure} Figure 7: Area coverage vs. magnetic flux in one pixel ($\approx $ $5\times 10^{14}$cm2) from the observations at $\mu = \cos\theta$ = 1.0 ( $\ast \ast \ast $, total coverage 55%) and from Gaussian noise with standard deviation as the noise in the data (+, very few values above limit) and larger by a factor 4.0 ( $\diamond \diamond \diamond $).
Open with DEXTER

The slope of the straight line in Fig. 6 on the double-logarithmic drawing is $-1.93\approx-2.0$. This gives

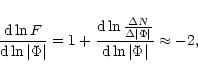\begin{displaymath}{{\rm d}\ln F\over {\rm d}\ln\vert\Phi\vert} = 1 + {{\rm d}\l... ...elta\vert\Phi\vert}\over {\rm d}\ln\vert\Phi\vert} \approx -2, \end{displaymath} (3)

or

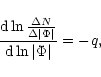\begin{displaymath}{{\rm d}\ln{\Delta N\over\Delta\vert\Phi\vert}\over \rm d\ln\vert\Phi\vert}= -q, \end{displaymath} (4)

with $q\approx3$, and

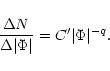\begin{displaymath}{\Delta N\over\Delta\vert\Phi\vert}= C^\prime\vert\Phi\vert^{-q}. \end{displaymath} (5)

The probability $W(\vert\Phi\vert)$ for the occurrence of a flux in the interval $[\vert\Phi\vert,\vert\Phi\vert+\Delta\vert\Phi\vert]$, in the range indicated in Fig. 7, is thus

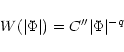\begin{displaymath}W(\vert\Phi\vert) = C^{\prime\prime}\vert\Phi\vert^{-q}\, \end{displaymath} (6)

with a constant $C^{\prime\prime}$ and $q\approx3.0$. This steep dependence as well as the distribution in Fig. 7 show that much of the magnetic flux in the considered region (enhanced network) comes from the areas with the dimmest signals, which supports the findings by Sáchez Almeida & Lites (2000) and Socas Navarro & Sáchez Almeida (2001). A caveat is appropriate. The power law distribution of Eq. (6) must break down at very low flux values. Otherwise the total (unsigned) flux would diverge and the area coverage would be >100%.

We recall from Fig. 5 the geometric distributions about flux centers and derive tentatively a simple dependence on the distance r of the fluxes from the flux centers of the form

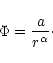\begin{displaymath}\Phi = {a\over r^\alpha}\cdot \end{displaymath} (7)

Using

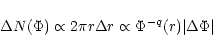\begin{displaymath}\Delta N(\Phi)\propto2\pi r\Delta r\propto\Phi^{-q}(r)\vert\Delta\Phi\vert \end{displaymath} (8)

and replacing $\vert\Delta\Phi\vert$ by $\Delta r$ by means of Eq. (7) we arrive at the relation

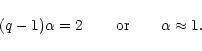\begin{displaymath}(q-1)\alpha=2\,~~~~~~{\rm or}~~~~~~\alpha\approx1. \end{displaymath} (9)

We consider this a weak radial dependence, valid only for the range 20Gauss to 100Gauss (mean flux density), as indicated in Fig. 7. It is a consequence of the steep probability distribution, $W(\vert\Phi\vert)\propto\vert\Phi\vert^{-3}$.

We have tested the influence of seeing on the geometric and the probability distributions. For this we constructed a radially symmetric function $\vert V\vert _{\rm max}\propto b/r^2$, but with a smooth top at r=0. We then smeared it with normalized Gaussian seeing functions $\propto\exp[-r^2/(2\sigma^2)]$ with various standard deviations $\sigma$, $0\hbox{$.\!\!^{\prime\prime}$ }75\le\sigma\le 1\hbox{$.\!\!^{\prime\prime}$ }5$. The result is that seeing flattens the probability distribution somewhat, but does not steepen it.

Wang et al. (1995) obtained a different power law for intra-network magnetic fields, $W(\vert\Phi\vert)\approx C^{\prime\prime\prime}\vert\Phi\vert^{-2}$. These authors measured entire patches of weak fluxes, while we use here the pixel size as the relevant area, irrespectively of the flux through neighbouring pixels. Moreover, as a consequence of counting isolated "elements'', in the Wang et al. investigation, the power law distribution holds for fluxes > $2\times 10^{17}$Mx, and their distribution possesses a maximum at $6\times 10^{17}$Mx and then decreases towards lower flux values.

We do not know the state of evolution of the observed area. We refrain from speculating whether this kind of distribution reflects a diffusion process or advection of small flux to the centers seen in Fig. 4 in the upper left magnetogram. Investigations of the temporal evolutions of intra-network fields were undertaken e.g. by Wang et al. (1996) and Zhang et al. (1998a,1998b). Following these works the intra-network fields appear as clusters within the network cells and disappear by diffusion below the detection limit and by coalescence with elements of the same or of the opposite polarity, while they are moving essentially towards the network boundaries. Since our observations were already taken from close to the network we assume that the weak fluxes studied here have a different state of evolution than the intra-network fields.

From the distribution, we can calculate the average energy density $e_{\rm mag} = B^2/(8\pi)$ contained in the magnetized plasma. We assume vertical magnetic fields, i.e. directed along the line of sight or opposite to it and no cancellation of V signals due to mixed polarity. For isotropically oriented fields the numbers below would be a factor of three larger. In the case of mixed polarity fields within one pixel the numbers below would represent lower limits of the magnetic energy density. We adopt two extreme possibilities for averaging the contribution from each pixel (with flux above our detection limit) to the magnetic energy density:

1.
We take the (average) magnetic flux densities |B| in Fig. 7 at face value, i.e. as varying between 15 Gauss and 200 Gauss. This gives
$e_{\rm mag} \approx25$ergcm-3,
which refers to a layer where the V extrema are formed.

2.
We assume that we deal always with magnetic fields of 1000 Gauss at continuum forming layers in the non-magnetic surrounding. We recall, however, that Keller et al. (1994) estimated from Stokes V observations of intra-network magnetic fields in the two Fe I 5247 and 5250 lines an upper limit of 500 Gauss. Similarly, Stolpe & Kneer (2000) argued from the appearance of weak flux in both granules and intergranular spaces that the corresponding magnetic field strengths should not be larger than approximately 550 Gauss. From the magnetic flux distribution we obtain the corresponding filling factors which give an intrinsic field strength of 1000 Gauss and obtain
$e_{\rm mag} \approx6\times 10^2$ergcm-3.

These values have to be compared with the thermal energy density $e_{\rm th}={3\over2}nk{T}\approx1.6\times 10^5$ergcm-3 or the convective energy $e_{\rm conv}=(\rho/2)v^2=3\dots5\times 10^3$ergcm-3. For the latter two estimates we took the data for the total particle density n, the temperature T, and the mass density $\rho$ of the quiet Sun atmospheric model VALC (Vernazza et al. 1981) and a velocity of the granular convection v of 1.5...2.0kms-1 at $\tau_{5000}=1$. In other words, if the magnetic fields are of kGauss strength their energy density becomes comparable to that of the convective flow. This agrees with the result of the turbulent dynamo simulations by Emonet & Cattaneo (2001).

4.4.2 Gaussian noise

To study how the observations compare with pure noise we have tested random, normally distributed numbers instead of the observed V spectrograms. The standard deviation of the flux $\Phi_0$ was chosen such that the rms of the V spectrograms was the same as in the observations, i.e. $\approx $ $0.003I_{\rm c}$. These noise spectrograms were then treated in the same manner as the observations, by taking the average of the two Fe lines, .... The "distribution'' is shown also in Fig. 7 (+, just one interval in $\Delta^{10}\log\vert\Phi\vert$). Only very few noise V profiles reach the limit of $0.003I_{\rm c}$. When we increase the standard deviation by a factor of 4 the noise distribution becomes clearly visible ( $\diamond \diamond \diamond $ in Fig. 7). Yet its shape is completely different from that of the observed data. The solar distribution is neither dominated by observational noise nor does it possess intrinsically Gaussian properties.

Taking a Gaussian probability distribution

\begin{displaymath}{\Delta N\over\Delta\vert\Phi\vert}= A\exp\left[-\vert\Phi\vert^2/\left(2\Phi_0^2\right)\right] \end{displaymath} (10)

with a constant A, the representation as in Fig. 7 would be the function G:

\begin{displaymath}G = A^\prime\vert\Phi\vert\exp\left[-\vert\Phi\vert^2/\left(2\Phi_0^2\right)\right]\cdot \end{displaymath} (11)

Its double-logarithmic slope is

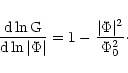\begin{displaymath}{\rm d\ln G\over \rm d\ln\vert\Phi\vert} = 1 -{\vert\Phi\vert^2\over\Phi_0^2}\cdot \end{displaymath} (12)

The latter has the forms
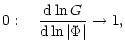$\displaystyle \vert\Phi\vert$ $\textstyle \rightarrow$ $\displaystyle 0:~~~{{\rm d}\ln G\over \rm d\ln\vert\Phi\vert} \rightarrow 1,$ (13)
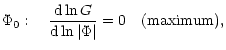$\displaystyle \vert\Phi\vert$ = $\displaystyle \Phi_0:~~~{{\rm d}\ln G\over \rm d\ln\vert\Phi\vert} = 0~~~({\rm maximum}),$ (14)
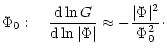$\displaystyle \vert\Phi\vert$ $\textstyle \gg$ $\displaystyle \Phi_0:~~~{{\rm d}\ln G\over \rm d\ln\vert\Phi\vert} \approx -{\vert\Phi\vert^2\over\Phi_0^2}\cdot$ (15)

This is reflected in the distribution in Fig. 7 ( $\diamond \diamond \diamond $).

4.4.3 Center-to-limb variation

We present in Fig. 8 the distributions obtained from positions of $\cos\theta$ = 1.0 to 0.1. We note that the area coverages with magnetic flux in our pixels lie between 44% and 88% of the total fields of view. We consider this a large amount.


  \begin{figure} \par\includegraphics[width=8.7cm,clip]{H3304F8.eps} \end{figure} Figure 8: Area coverage vs. magnetic flux in one pixel, center-to-limb variation. Upper panel: $\ast \ast \ast $: $\mu = \cos\theta$ = 1.0 (total coverage 55%); $\diamond \diamond \diamond $: $\mu $ = 0.6 (57%); $\bigtriangleup \bigtriangleup \bigtriangleup $: $\mu $ = 0.4 (72%); $\times \times \times $: $\mu $ = 0.1 (82%); lower panel: $\ast \ast \ast $: $\mu $ = 1.0 (other region, 44%); $\diamond \diamond \diamond $: $\mu $ = 0.8 (86%); $\bigtriangleup \bigtriangleup \bigtriangleup $: $\mu $ = 0.2 (63%).
Open with DEXTER

The distributions in the upper panel of Fig. 8 ressemble each other, apart from the total area coverage. They all have similar slopes ${\rm d}\ln F/\rm d\ln\vert\Phi\vert$ in the range of 20 Gauss to 100 Gauss. The distribution from $\cos\theta = 0.1$ ( $\times \times \times $) is somewhat different, it shows a decline at 20 Gauss towards lower field strengths.

The lower panel of Fig. 8 gives additional information about possible flux distributions. The functions at $\mu=1.0$ (other region than discussed above) and $\mu=0.2$ exhibit a bump at "large'' fluxes, as if these large flux centers are more extended than in the regions for the data of the upper panel. Inspection of images similar as those in Fig. 5 (not shown) confirm this impression. (The distribution of the fluxes from $\cos\theta = 0.4$ in the upper panel exhibits a similar behaviour.) But at flux densities below approximately 60 Gauss the two distributions have again the same slope close to -2.0.

The data from $\cos\theta = 0.8$ ( $\diamond \diamond \diamond $ in the lower panel of Fig. 8) are very different. Here we observed obviously a region with extended strong fluxes and only few small fluxes in their surroundings. Very likely, this was a region in a different evolutionary state than the other regions.

Again, as found for the asymmetry, we do not see a significant center-to-limb variation of the (line of sight) magnetic flux distributions, neither in the slopes nor in the flux amplitudes. On the one hand, this is, at first reasonning, compatible with an isotropic orientation of the magnetic fields. Assume that, in addition, the velocities, and their gradients which are needed to produce the V asymmetries, are oriented isotropically as well. Then one would understand the lack of a center-to-limb variation of both the asymmetry from weak flux elements and of the flux distribution.

On the other hand, an interpretation as magnetic fields standing out vertically in the solar atmosphere is also possible: the reduction of the line of sight component of the flux towards the limb is compensated by the increase of the area observed in one pixel due to foreshortening. Such a scenario requires that patches of magnetic flux, from which the distributions are derived, be geometrically much more extended than the pixel size. Otherwise, the foreshortening would reduce the observed magnetic flux through one pixel.

Radiative transfer effects, i.e. the different $V_{\lambda}$ formation heights when observing at different angles, may also play a rôle.

5 Conclusions

The Gregory Coudé Telesope at the Observatorio del Teide was successfully used to investigate weak flux magnetic fields on sub-arcsecond scales The polarimetric sensitivity of $\vert V_\lambda\vert/I_{\rm c}<0.003$ on small areas corresponding to 0 $.\!\!^{\prime\prime}$5$\times $0 $.\!\!^{\prime\prime}$19 ($\widehat=$ slit width$\times $pixel size of the detector) allowed us to confirm earlier findings in one part and to arrive at new detections in other parts. The essential results are summarized as follows:

1.
We find a high anticorrelation between the fluctuations of the continuum and line center intensity fluctuations in Fe I 6302.5Å, confirming the work e.g. by Gadun et al. (2000 and references therein).

2.
Small magnetic flux features with $\vert\Phi\vert\le2.5\times 10^{16}$Mx (through one pixel of the above size) exhibit very asymmetric V profiles at all positions on the solar disc. Stronger fluxes show a relative amplitude asymmetry near disc center of approximately +0.15, i.e. a blue asymmetry. This decreases towards the limb. A change of sign is not seen (cf. Stenflo et al. 1987 and Martínez Pillet et al. 1997).

3.
We identified magnetic flux centers near enhanced CaK network regions. With increasing distance r from these centers the flux decreases with the approximate dependence $\propto1/r$. It falls below our detection limit at distances of 3 $^{\prime \prime }$-5 $^{\prime \prime }$.

4.
Our main results are the probabilities of the occurrence of magnetic flux. The observed regions of 30 $.\!\!^{\prime\prime}$9$\times $14 $.\!\!^{\prime\prime}$2 about enhanced network possess an area coverage of magnetic flux of 44%-88%. In the range of $1\times 10^{16}$Mx to $5\times 10^{16}$Mx we find a flux dependence of the probability $W(\vert\Phi\vert)\propto\vert\Phi\vert^{-q}$ with $q\approx3$. This is very different from a Gaussian distribution. With few exceptions of strong flux centers, this behaviour does not change from center to limb on the solar disc, neither in the flux amplitudes nor in the slopes of their probabilites.

The probability distribution found by Wang et al. (1995) for intra-network fields is different, $W(\vert\Phi\vert)\propto\vert\Phi\vert^{-2}$. In this latter work, the magnetic fluxes of entire, isolated patches were measured, while we take the area as the pixel size and measure the flux through this pixel irrespectively of the flux through neighbouring areas. We have tested that smoothing (by telescope and seeing) does not steepen the probability, it flattens it somewhat, but not too much, such that $q\approx3$ should be considered as a lower limit.

Our observations were not an experimentum crucis to decide on the correctness of either the magnetopause model by Steiner (2000) to produce the asymmetries or the MISMA model by Sánchez Almeida et al. (1996) and Sánchez Almeida & Lites (2000). However, in view of the increasing asymmetries towards the low flux end the picture of mixed polarities within the resolution element becomes highly probable.

A further step should be the observation of the temporal evolution of such flux centers, and their ambient area, for which constantly high-quality observing conditions are needed. This should include accurate polarimetric probing of the solar atmosphere with various spectral lines, especially at those regions where weak fluxes of different polarities mix, such as in the lower left image of Fig. 5 above. Time series would elucidate the interaction of weak flux structures with granular convection which is intensively studied via numerical simulations e.g. by the Chicago group (Cattaneo 1999a,1999b; Emonet & Cattaneo 2001) and by Stein & Nordlund (2000).

The investigation of features, i.e. different flux centers, with different magnetic strength such as above in our analyis of the $\cos\theta = 0.8$ observations, and of their evolution is also of interest. The polarimetric sensitivity, on small spatial scales and with a low noise level, must also be increased to study the small-flux elements, their interaction with the gas flow and with neighbouring magnetic structures, and to extend the flux distributions to the lower end. Low noise observations are also a prerequisite to feed inversion codes with tractable data. Future new telescopes with large apertures and with Adaptive Optics combined with image restoration techniques (e.g. Koschinsky et al. 2001) will certainly bring new insight into the nature and the dynamics of the magnetic fields on small scales. This includes many magnetic phenomena on the Sun, from weak intra-network flux elements to strong plages and sunspot finestructures.

Acknowledgements
We are very grateful to Dr. J. Sánchez Almeida for stimulating discussions and to the referee for valuable suggestions. The Gregory Coudé Telescope is operated by the Universitäts-Sternwarte Göttingen at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias.

References

 

Copyright ESO 2002