The aim of this study is to measure the various physical
parameters, including effective temperature (T
![]() ), surface
gravity (log g), chemical composition and, for binary stars, the
radius ratio directly from optical and near-infrared spectra.
This is achieved by finding the
best-fit model spectra within a grid of theoretical models
using the method of
), surface
gravity (log g), chemical composition and, for binary stars, the
radius ratio directly from optical and near-infrared spectra.
This is achieved by finding the
best-fit model spectra within a grid of theoretical models
using the method of ![]() minimization.
minimization.
The methods for hot single stars have been described in detail (Jeffery et al. 2001), including the generation of model atmospheres (STERNE), the synthesis of model spectra (SPECTRUM) and the least-squares minimization ( SFIT). These techniques have been extended to model binary stars which consist of both a hot and a cool component. Although they have already been introduced (Jeffery & Aznar Cuadrado 2001), the method is described more formally here.
The fundamental assumption is that both cool and
hot absorption sources are primarily stellar.
We consider the observed normalized spectrum
![]() .
Our aim is to reconstruct the best-fit model spectrum
.
Our aim is to reconstruct the best-fit model spectrum
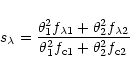
The principal free parameters which govern the measured spectrum are thus:
The model atmospheres and flux distributions used to analyse the hot star were computed with the line-blanketed plane-parallel LTE code STERNE. The high-resolution spectra were calculated with the LTE code SPECTRUM (see Jeffery et al. 2001).
The model atmospheres were calculated on a
three-dimensional rectangular grid defined
by
![]() ,
,
![]() ,
and composition
,
and composition ![]() = 1 -
= 1 -
![]() ,
,
![]() and
and
![]() = 0.
The larger value of
= 0.
The larger value of ![]() or
or
![]() is reduced to compensate for trace
elements.
is reduced to compensate for trace
elements.
Synthetic spectra were calculated on wavelength intervals
3800-5020 Å
(blue) and
8450-8670 Å (CaT). Linelists comprising some 142
absorption lines of hydrogen, helium, carbon, magnesium and silicon
were taken from the list of assessed data for hot stars LTE_LINES
(Jeffery 1991).
Microturbulent velocity
![]() and solar abundances for
all elements other than hydrogen and helium were assumed (see above).
and solar abundances for
all elements other than hydrogen and helium were assumed (see above).
Model atmospheres and flux distributions used to analyse the cool star
were taken from the Kurucz' standard grid of ATLAS models
(Kurucz 1993a), for
![]() ,
,
![]() ,
,
![]() ,
-0.3, 0.0 and
,
-0.3, 0.0 and
![]() .
.
Grids of high resolution spectra were calculated in the same spectral
regions as for the hot star using Kurucz' code SYNTHE
(Kurucz 1993b; Jeffery et al. 1996) assuming a microturbulent velocity
![]() .
.
For a given observation, an optimum fit
was obtained by minimizing ![]() ,
,
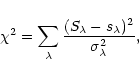 |
(1) |
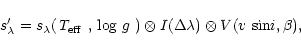 |
(2) |
In the construction of ![]() ,
each wavelength point was given a weight
,
each wavelength point was given a weight
![]() ,
the inverse of the standard deviation
of the mean normalized flux in line-free regions. In our spectra
,
the inverse of the standard deviation
of the mean normalized flux in line-free regions. In our spectra
![]() .
Some spectral regions needed to be excluded
from the fit (e.g. bad columns or strong lines missing from the
theoretical spectrum). In SFIT, such defects are masked by increasing
.
Some spectral regions needed to be excluded
from the fit (e.g. bad columns or strong lines missing from the
theoretical spectrum). In SFIT, such defects are masked by increasing
![]() in appropriate wavelength intervals. We used
in appropriate wavelength intervals. We used
![]() = 0.1.
= 0.1.
In any such fitting procedure, the normalization of the observed spectrum can be of crucial importance (Jeffery 1998). The problem is to normalize the observed spectrum correctly without, for example, compromising the wings of broad absorption lines. This is particularly difficult when there is an unknown contribution to the line opacity from metal lines in a cool star companion, so that there may be no "true'' continuum anywhere in the observed spectrum.
| Star | T
|
log g | y | Reference |
| PG0004+133 | 4.97 |
0.01 |
SFIT | |
| (Fig. 1) | 25025 |
Paper I | ||
| 24700 |
4.5 |
0.028 | Moehler et al. (1990a) | |
| PG0229+064 | 18000 |
4.35 |
0.33 |
SFIT |
| 20100 |
Paper I | |||
| 19000 |
4.55 |
0.16 | Ramspeck et al. (2001) | |
| 22000 |
4.65 |
0.137 | Heber et al. (1999) | |
| PG0240+046 | 36200 |
6.25 |
1.94 |
SFIT |
| 34800 |
Paper I | |||
| 37000 |
5.3 |
1.222 | Thejll et al. (1994) | |
| PG0342+026 | 24000 |
5.17 |
0.01 |
SFIT |
| 27900 |
Paper I | |||
| 24000 |
4.90 |
0.003 | Heber et al. (1999) | |
| 25000 |
5.25 |
0.000 | Theissen et al. (1995) | |
| 26220 |
5.67 |
0.004 | Saffer et al. (1994) | |
| 22300 |
5.00 |
0.000 | Lamontagne et al. (1987) | |
| PG0839+399 | 37300 |
6.02 |
<0.01 |
SFIT |
| 35600 |
Paper I | |||
| 36100 |
5.91 |
0.002 | Saffer et al. (1994) | |
| PG1233+426 | 25560 |
5.52 |
<0.01 |
SFIT |
| 28750 |
Paper I | |||
| 26500 |
5.60 |
0.005 | Saffer et al. (1994) | |
| 26200 |
5.30 |
0.000 | Lamontagne et al. (1985) | |
| PG2259+134 | 28500 |
5.93 |
0.02 |
SFIT |
| 28350 |
Paper I | |||
| 22500 |
5.00 |
0.000 | Theissen et al. (1995) | |
| 28500 |
5.30 |
0.022 | Theissen et al. (1993) | |
|
|
||||
The initial normalization was performed by fitting a low-order spline function
to a series of pseudo-continuum points, usually the highest points in the
spectrum. SFIT includes two re-normalization algorithms which may be used
to optimize the fit (cf. Jeffery et al. 1998). One computes a low-order polynomial
fit to the residual, the other applies a low-pass Gaussian filter. A second
order polynomial was used to renormalize the spectrum in wavelength ranges
4200-4650 Å and 8000-8850 Å while a third order polynomial was
used in the region of high order Balmer lines (H9, H8,
H
![]() ,
etc.). Because low-order polynomials are used, individual line
profiles are unaffected.
,
etc.). Because low-order polynomials are used, individual line
profiles are unaffected.
In principle and for suitable data with negligible noise, SFIT can solve
simultaneously for as many parameters as required. In practice, it is
necessary to restrict the free solution to between two and three parameters at
a time, keeping others fixed, and to iterate until the optimum solution is
obtained. SFIT requires a set of initial estimates for the free
parameters. Results from the flux distribution analysis (Paper I) were
used for
![]() and the radius ratio. Standard values were assumed
for
and the radius ratio. Standard values were assumed
for
![]() and y1.
and y1.
Table 4 presents the results of the spectral analysis of single sdB stars (labeled SFIT), together with the results of the flux distribution analysis (Paper I) and results from literature.
The radius ratio R2/R1 is directly related to the effective temperatures
of both components, so must be a "free'' parameter whenever either T
![]() is free. The contribution of the cool companion in the blue spectrum is
reflected in the presence and strength of some metallic lines, being good
indicators of the temperature of the cool star and the radius ratio of the
system. Therefore, the blue spectrum is also used to fix
is free. The contribution of the cool companion in the blue spectrum is
reflected in the presence and strength of some metallic lines, being good
indicators of the temperature of the cool star and the radius ratio of the
system. Therefore, the blue spectrum is also used to fix
![]() and
R2/R1. It was frequently difficult to find a solution for
and
R2/R1. It was frequently difficult to find a solution for
![]() ,
,
![]() and R2/R1 consistent with the flux distribution analysis
(Paper I). In cases of conflict, we attempted to keep R2/R1
consistent between the two studies, although even this was not always
possible (Table 5).
and R2/R1 consistent with the flux distribution analysis
(Paper I). In cases of conflict, we attempted to keep R2/R1
consistent between the two studies, although even this was not always
possible (Table 5).
| Star |
|
|
y1 |
|
|
R2/R1 | Ref. |
| PG0110+262 | 21000 |
5.17 |
<0.01 |
5250 |
4.53 |
3.2 |
SFIT |
| 21050 |
5485 |
4.2 |
1 | ||||
| 21000 |
<
|
5000 |
6.0 | 2 | |||
| 22000 |
<
|
5500 |
4.4 | 3 | |||
| 22000 |
4500 |
7.8 | 4 | ||||
| PG0749+658 | 25400 |
5.70 |
<0.01 |
5000 |
4.58 |
3.5 |
SFIT |
| 25050 |
5600 |
3.9 |
1 | ||||
| 24600 |
5.54 |
0.004 | 5 |
||||
| 23500 |
4125 |
6.3 | 4 | ||||
| PG1104+243 | 32850 |
5.40 |
0.01 |
6400 |
4.30 |
5.9 |
SFIT |
| 28000 |
5735 |
6.1 |
1 | ||||
| 27500 |
4300 |
10.6 | 4 | ||||
| 27200 |
5.50 |
6 | |||||
| 28000 |
4600 |
9.8 | 7 | ||||
| PG1701+359 | 32500 |
5.75 |
<0.01 |
6000 |
4.60 |
2.7 |
SFIT |
| 36075 |
6450 |
4.8 |
1 | ||||
| 30000 |
5.00 |
0.000 | 8 | ||||
| 28500 |
4000 |
6.2 | 4 | ||||
| 26250 |
5.80 |
9 | |||||
| PG1718+519 | 29000 |
6.00 |
<0.01 |
5200 |
4.55 |
4.8 |
SFIT |
| 29950 |
5925 |
8.2 |
1 | ||||
| 30000 |
5.00 |
0.000 | 5125 |
8 | |||
| 25000 |
4300 |
10.7 | 4 | ||||
| 23300 |
4.25 |
9 | |||||
| PG2110+127 | 26500 |
5.20 |
<0.01 |
5400 |
4.40 |
4.7 |
SFIT |
| (Fig. 2) | 24900 |
5500 |
5.5 |
1 | |||
| 30000 |
5.00 |
0.000 | 5375 |
8 | |||
| 33700 |
5.33 |
0.004 | 5 | ||||
| 26000 |
4500 |
10.4 | 4 | ||||
| PG2135+045 | 28400 |
4.80 |
<0.01 |
5000 |
4.40 |
3.1 |
SFIT |
| 26325 |
4375 |
4.7 |
1 | ||||
| 32100 |
4.79 |
0.016 | 5 |
||||
| 27000 |
4400 |
6.5 | 4 | ||||
| PG2148+095 | 30000 |
4.90 |
<0.01 |
5700 |
4.40 |
3.0 |
SFIT |
| (Fig. 4) | 22950 |
4375 |
5.0 |
1 | |||
| 25000 |
<
|
5000 |
6.0 | 2 | |||
| 26000 |
4300 |
7.9 | 4 | ||||
|
|
|||||||
| 5 = Saffer et al. (1994); 6 = Lamontagne et al. (1987); 7 = Ferguson et al. (1984); 8 = Theissen et al. (1995); | |||||||
| 9 = Theissen et al. (1993). | |||||||
In the initial analysis of the blue spectrum, the cool companion is assumed
to have
![]() (cf. Paper I). Applying SFIT gives new
values, first for y1, then for
(cf. Paper I). Applying SFIT gives new
values, first for y1, then for
![]() ,
,
![]() ,
,
![]() and
R2/R1.
and
R2/R1.
With these improved estimates for the sdB star properties, the red spectrum
is analyzed. In particular,
![]() is determined by fitting the calcium
triplet.
is determined by fitting the calcium
triplet.
A second analysis is now performed in the blue in order to refine the fit to the hot star spectrum, using the new parameters for the cool star. The above procedure is repeated until the solutions converge.
Table 5 presents the results for composite spectrum sdB stars,
together with previous results from the literature. Solar metallicity
was adopted for all stars except PG1104+243, for which we adopted
![]() .
The
instrumental profile is large compared with any rotational broadening
except in the cases of PG1701+359 and PG1718+519, where
.
The
instrumental profile is large compared with any rotational broadening
except in the cases of PG1701+359 and PG1718+519, where
![]() and 10
and 10
![]() ,
respectively, were adopted.
,
respectively, were adopted.
Table 5 includes values for R2/R1 for some previous papers. These have been computed from cited flux ratios at 5500 Å, effective temperatures and/or spectral types and an appropriate bolometric correction.
The formal errors associated with the best fit parameters xi are given by
the diagonal elements
![]() of the inverse of the
covariance matrix
of the inverse of the
covariance matrix ![]() ,
whose elements are given by
,
whose elements are given by
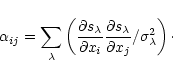 |
(3) |
For a single-star spectrum, only the derivatives between T
![]() ,
log g and y
need to be calculated. In the case of a binary system, the derivatives between
the physical parameters of both components of the system are required. These
have to be evaluated numerically, e.g.
,
log g and y
need to be calculated. In the case of a binary system, the derivatives between
the physical parameters of both components of the system are required. These
have to be evaluated numerically, e.g.
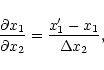 |
(4) |
The errors given in Tables 4 and 5 are total errors.
For example the total error ![]() in
in
![]() is given by
is given by
| = | 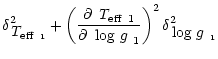 |
||
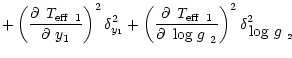 |
|||
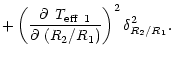 |
(5) |
There are also systematic differences between the methods used to obtain
R2/R1 in this paper and in Paper I. To compare these methods we
have constructed a simple test. The energy distribution and normalized
spectrum of a binary system containing a typical sdB star and a main-sequence
star were computed. These were resampled to mimic the observational data
available to us in each investigation. The data were then analyzed using
BINFIT (to fit the flux distribution, Paper I) and SFIT
independently. The model parameters and the results of the ![]() analysis
are shown in Table 6.
analysis
are shown in Table 6.
| Parameter | Model | BINFIT | SFIT |
|
|
24000 | 24060 |
24190 |
|
|
6.0 | 6.02 |
|
| y1 | 0.10 | 0.11 |
|
|
|
4500 | 4550 |
4500 |
|
|
4.5 | 4.54 |
|
| R2/R1 | 6.29 | 5.90 |
6.27 |
Copyright ESO 2002