A&A 385, 131-142 (2002)
DOI: 10.1051/0004-6361:20020099

Physical parameters for subdwarf B stars
with composite spectra[*]

R. Aznar Cuadrado - C. S. Jeffery

Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland

Received 5 November 2001 / Accepted 16 January 2002

Abstract
New intermediate-resolution spectra have been obtained for a number of subdwarf B stars having both single and composite spectra. Physical parameters have been determined for the sdB stars and, in composite-spectrum systems, their cool companions. For these binaries, we have developed a method which uses the blue-optical spectrum to determine the effective temperatures of both stars, the surface gravity of the hot stars and the radius ratio of the system. The surface gravity of the cool star is measured using the infrared calcium triplet. The surface gravities of these cool companions identify them as main-sequence stars with masses in the range 0.8-1.2$M_\odot $, confirming a previous energy distribution analysis. There is also evidence that the composite-spectrum sdBs are more helium-poor than single-spectrum sdBs.

Key words: stars: formation - stars: early-type - stars: subdwarfs - stars: fundamental parameters - stars: binaries: spectroscopic


1 Introduction

Subdwarf B (sdB) stars are the most extreme of horizontal branch stars, being predominantly helium stars of approximately half a solar mass overlaid by a hydrogen-rich veneer (Heber 1986). Common in both our own galaxy (Green et al. 1986) and in giant ellipticals (Brown et al. 1997), they present a problem for stellar evolution theory: how does a red giant star dispose of its entire hydrogen-rich envelope prior to core helium ignition?

From an initial supposition that sdB stars were predominantly single, models including enhanced mass-loss rates (e.g. D'Cruz et al. 1996), and white dwarf mergers (Iben 1990; Saio & Jeffery 2000) have been investigated. However a significant fraction of sdB stars are known to have composite spectra (Ferguson et al. 1984; Allard et al. 1994; Jeffery & Pollacco 1998), leading to suggestions of a binary fraction between 50% and 100%. Recent radial velocity studies (Saffer et al. 2001) have identified three distinct groups: 1) single-spectrum sdBs with small or negligible velocity variations, 2) single-spectrum sdBs with large velocity variations and likely periods of hours to days and 3) composite-spectrum sdBs with small velocity variations and relatively long periods. Another recent investigation finds that the second group comprises some $60\pm8\%$ of all sdBs (Maxted et al. 2001). The clear conclusion is that binary evolution plays a significant rôle in the formation of sdB stars.

For the group (2) sdBs, the binary companion is invisible. Radial velocity and, in some cases, light curve studies will yield vital clues about the overall dimensions of these binary systems, and hence about their previous evolution. For group (3), dynamical information is less accessible - although very careful observations over a long time base will be an important tool in this endeavour. Fortunately and by definition, the binary companion in a composite spectrum can be seen.


 

 
Table 1: Instrumental configurations.
Dates Telesc. Spec. Grating Dichroic Slit Detector R $\lambda$/Å
1997 Sep. 4 INT IDS R1200R - 1.6'' TEK3 5000 8000-8800
1997 Sep. 12,13 WHT ISIS R1200B 5700 1.2'' TEK1 4000 4200-4650
      R600R 5700 1.2'' TEK2 4300 8000-8850
1998 Oct. 3,4 WHT ISIS R1200B 5300 1.2'' TEK1 4000 4200-4650
1999 Mar. 26,27 INT IDS R1200B - 1.2'' TEK5 2500 3800-4700
      R1200R - 1.2'' TEK5 5000 8000-8850


We have already examined the flux distributions for a number of binaries (Aznar Cuadrado & Jeffery 2001: Paper I) and concluded that the companions are main sequence stars. This contradicted previous analyses (Allard et al. 1994; Jeffery & Pollacco 1998) which suggested that the companions were overluminous. Therefore it is important to verify the results spectroscopically. Such an approach carries an additional bonus. The near-infrared triplet lines of ionized calcium are very strong in late-type stars and provide a sensitive diagnostic of surface gravity, providing the effective temperature and metallicity are known (Cohen 1979; Jones et al. 1984; Smith & Drake 1987; J$\o$rgensen et al. 1992). If both surface gravities and the radius ratio can be measured, the mass ratio can be determined directly and provides a very important tool for exploring the previous evolution of this group of sdB stars.

In this paper we introduce the methods used to analyse the spectra of composite-spectrum sdB stars, and present results for an initial sample. The methods are tested by providing independent analyses for a number of single-spectrum sdB stars.

2 Observations and data reduction

The observations used in this analysis have been collected from the William Herschel (4.2 m) and the Isaac Newton (2.5 m) Telescopes at the Roque de los Muchachos Observatory on La Palma between 1997 and 1999. Instrumental setups for each observing run are given in Table 1.

The stars in the current analysis were all selected because they had been observed with IUE and their flux distributions were well understood (Aznar Cuadrado 2001). The possibility that composite spectrum systems might be chance alignments has also been examined for these stars (ibid.). The sample included a number of stars known to have composite spectra or to have an infrared colour excess, as well as a comparable number considered to be "single-spectrum'' systems. The log of observations is given in Table 2.

   
Table 2: Spectroscopic observations of single and composite sdB stars.
Star Telesc. HJD $\lambda_{\rm cen}$ exp S/N
    (-2450000) (Å) (s)  
           
           
PG0004+133 WHT  705.704 4400 1200  80
PG0110+262 WHT  704.639 4400 1800  92
  WHT  705.733 8400 1800  74
PG0229+064 WHT 1091.702 4400  200 140
PG0240+046 WHT 1091.721 4400  850 140
PG0342+026 WHT  705.748 4400  900  93
PG0749+658 INT 1264.399 4250  300  70
  INT 1264.538 8400  600  48
PG0839+399 INT 1265.387 4250  600  50
PG1104+243 INT 1265.667 4250  300  52
  INT 1264.596 8400  300  65
PG1233+427 INT 1265.591 4250  150  60
PG1701+359 WHT  704.359 4400  900 150
  WHT  704.359 8400  900  73
PG1718+519 WHT  705.377 4400 1200  80
  WHT  705.378 8400 1200  60
PG2110+127 WHT  704.399 4400 1200 100
  INT  696.543 8400  900  90
PG2135+045 WHT 1090.366 4400  900  70
  INT  696.580 8400 1800  35
PG2148+095 WHT  705.427 4400 1200 170
  WHT  705.426 8400 1200 100
PG2259+134 WHT  704.454 4400 1800  65

All stellar spectra were bias subtracted, flat-fielded, sky subtracted and one-dimensional spectra were extracted using standard IRAF packages. Copper-argon-neon comparison spectra were used to provide a wavelength calibration corresponding to each stellar observation. Spectra were normalized with respect to the local continuum.

The blue spectra are dominated by the hydrogen Balmer series, which are both temperature and gravity sensitive. Other prominent features present in both single and composite-spectrum subdwarfs are the He I$\lambda$4388Å and He I$\lambda$4471Å lines, the magnesium doublet at $\lambda$4481 Å, the silicon triplet at $\lambda\lambda$ 4553, 4568 and 4575 Å, and the C II$\lambda$4267Å doublet, amongst others. The near-infrared spectra of composite sdBs are dominated by the calcium triplet at $\lambda\lambda$ 8498, 8542 and 8662 Å. There are many weaker unidentified features. Several broad hydrogen Paschen lines come from the hot subdwarf. These are effectively invisible because the subdwarf spectrum is swamped by the cool star. However, they have the effect of depressing the apparent continuum in this spectral range.

3 Radial velocities

The spectra in our sample included both single and composite systems. Their radial velocities were measured by cross-correlation with theoretical models for both hot and cool star spectra.

This process includes the subtraction of the continuum and the conversion of the wavelength scale to logarithmic units, before calculating the cross-correlation function (ccf). Several spectral regions were excluded from the ccf, including wavelengths corresponding to bad CCD columns, cool-star features in composite systems (e.g. the G-band at $\lambda$ 4200 Å), broad Balmer lines, or strong lines from the observed spectrum that didn't appear in the synthetic spectrum. The ccf was then converted to velocity units and the position of its peak was measured by fitting a Gaussian.

The cross-correlation templates used for measuring the radial velocities $v_{\rm rad}$ of each observed spectrum were taken to be the best-fit model spectrum for the total system as described below. Hence, for single spectrum sdBs, we obtain a single radial velocity. For composite systems, the blue spectrum is dominated by lines from the hot star and so provides the sdB star velocity. The red spectrum is dominated by calcium lines from the cool companion and hence gives the cool star velocity. The heliocentric velocities measured from each observation are given in Table 3.

 

 
Table 3: Heliocentric radial velocity measurements of single and composite sdB stars.
Star HJD sdB K star  
  (-2450000) v v $\delta v$
Single        
PG0004+133  705.704 -20.6 $\pm$ 4    
PG0229+064 1091.702   7.6 $\pm$ 4    
PG0240+046 1091.721  63.4 $\pm$ 2    
PG0342+026  705.748  13.4 $\pm$ 8    
PG0839+399 1265.387  25.7 $\pm$ 8    
PG1233+427 1265.591  65.5 $\pm$ 8    
PG2259+134  704.454 -14.4 $\pm$ 6    
Composite        
PG0110+262  704.639    1.0 $\pm$ 6 --- 35.9
   705.733 ---   36.9 $\pm$ 2  
PG0749+658 1264.399  -21.0 $\pm$ 7 ---  0.2
  1264.538 ---  -21.2 $\pm$ 2  
PG1104+243 1265.667    -4.6 $\pm$ 8 ---  8.4
  1264.596 ---  -13.0 $\pm$ 4  
PG1701+359  704.359 -121.9 $\pm$ 3 --- 13.9
   704.359 --- -135.8 $\pm$ 2  
PG1718+519  705.377  -63.3 $\pm$ 3 --- 14.7
   705.378 ---  -48.6 $\pm$ 1  
PG2110+127  704.399   27.0 $\pm$ 1 ---  1.1
   696.543 ---   25.9 $\pm$ 1  
PG2135+045 1090.365  -30.0 $\pm$ 1 ---  2.0
   696.580 ---  -28.0 $\pm$ 2  
PG2148+095  705.427 -152.7 $\pm$ 1 --- 34.8
   705.426 --- -117.9 $\pm$ 2  


Errors on individual velocities are the formal errors given by the least squares Gaussian fit to the ccf peaks. The actual errors are probably much larger, but difficult to determine quantitatively (the typical ccf width is 200-400  $\mbox{km}\,\mbox{s}^{-1}$). The standard deviation about the mean ($\sim$14  $\mbox{km}\,\mbox{s}^{-1}$) may be a better indication.

In composite systems, the difference $\delta v$ between the two component radial velocities would be a measure of the lower limit to the orbital velocity of the sdB star. Systems with large velocity differences between hot and cool components could be short-period systems, i.e. PG0110+262, PG1701+359, PG1718+519 and PG2148+095.

In the interim, other groups have used radial velocity studies to detect binary sdB stars (Maxted et al. 2001; Saffer et al. 2001). From our sample, the single-spectrum sdB PG0839+399 is a radial velocity binary (Maxted et al. 2001), while the composite-spectrum sdBs PG0749+658 and PG1701+359 do not show detectable velocity variations (ibid.). Consequently, our conclusions may be subject to unidentified systematic errors. In the case of PG0229+064 heliocentric radial velocities of $+8\pm2$ and $+8\pm3$  $\mbox{km}\,\mbox{s}^{-1}$ measured on 1998 July 20 and September 13 respectively (Ramspeck et al. 2001) are essentially identical with our own measurement. Additional velocities for PG1233+427 ($53\pm2$  $\mbox{km}\,\mbox{s}^{-1}$: 2000 January 30 and 31), PG0342+026 ($15\pm2$  $\mbox{km}\,\mbox{s}^{-1}$: 1998 Sep. 11, $14\pm2$  $\mbox{km}\,\mbox{s}^{-1}$: 2000 Jan. 30) and PG0749+658 ($-11\pm2$ $\mbox{km}\,\mbox{s}^{-1}$: 2000 Jan. 31) have also been communicated to us (Edelmann & Heber, private communication). These are not sufficiently different from our own measurements to make us suspect that any are short-period spectroscopic binaries.

Prior to analysis, the wavelengths of the observed spectra were corrected to the laboratory rest frame by applying these measured radial velocity shifts.

4 Spectral analysis

The aim of this study is to measure the various physical parameters, including effective temperature (T $_{\rm eff}$), surface gravity (log g), chemical composition and, for binary stars, the radius ratio directly from optical and near-infrared spectra. This is achieved by finding the best-fit model spectra within a grid of theoretical models using the method of $\chi^2$ minimization.

The methods for hot single stars have been described in detail (Jeffery et al. 2001), including the generation of model atmospheres (STERNE), the synthesis of model spectra (SPECTRUM) and the least-squares minimization ( SFIT). These techniques have been extended to model binary stars which consist of both a hot and a cool component. Although they have already been introduced (Jeffery & Aznar Cuadrado 2001), the method is described more formally here.

The fundamental assumption is that both cool and hot absorption sources are primarily stellar. We consider the observed normalized spectrum $S_{\lambda}$. Our aim is to reconstruct the best-fit model spectrum

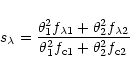
\begin{displaymath}s_{\lambda} = \frac{\theta_1^2 f_{\lambda 1} + \theta_2^2 f_{\lambda 2}} {\theta_1^2 f_{\rm c 1} + \theta_2^2 f_{\rm c 2} } \end{displaymath}

where $\theta$ are the stellar angular diameters, $f_{\lambda}$ is the theoretical emergent flux, $f_{\rm c}$ is the continuum flux and subscripts 1 and 2 refer to the individual stellar components. The fluxes are functions of each star's properties: $f_1 = f_1 (\mbox{\it T$_{\rm eff}$ }_1, \mbox{\,log $g$ }_1, \ldots)$ and $f_2 = f_2 (\mbox{\it T$_{\rm eff}$ }_2, \mbox{\,log $g$ }_2, \ldots)$. The angular diameters cannot be solved for explicitly from S, but their ratio gives $R_2/R_1 = \theta_2/\theta_1$.

The principal free parameters which govern the measured spectrum are thus:

The radial velocities have already been discussed. Ideally, stellar composition entails many more free parameters than metallicity and helium abundance alone, but requires high-resolution spectroscopy to measure, as does the microturbulent velocity. Helium abundance cannot be measured directly for cool sources. Tests showed that $\mbox{${\rm [Fe/H]}$ }_2$ cannot be uniquely determined from the given data. Similarly, given the magnitude of errors in $\mbox{\it T$_{\rm eff}$ }_1$, it is not practical to measure $\mbox{${\rm [Fe/H]}$ }_1$ in detail. Thus the following assumptions are made. The abundances of all elements other than hydrogen and helium are in proportion to their cosmic abundances, with $\mbox{${\rm [Fe/H]}$ }_1 = \mbox{${\rm [Fe/H]}$ }_2 = 0$. The helium abundance of the cool star is normal: $y_2 = y_\odot$. The adopted microturbulent velocities are typical for early-type stars $\mbox{\,$v_{\rm t}$ }_1=5\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$ and main-sequence late-type stars $\mbox{\,$v_{\rm t}$ }_2=2\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$. The latter assumption is very important as it affects both the metallicity $\mbox{${\rm [Fe/H]}$ }_2$ (see above) and the derived radius ratio R2/R1. We have adopted $\mbox{\,$v_{\rm t}$ }_2=2\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$ in order that the latter quantity as derived from spectral fitting be as consistent as possible with $\theta_2/\theta_1$ derived from spectrophotometry (Paper I) where we used cool star models computed with $\mbox{\,$v_{\rm t}$ }_2=2\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$. Secondary effects on $\mbox{\it T$_{\rm eff}$ }_2$ and $\mbox{\,log $g$ }_2$ are not significant here.

4.1 Model grids

The model atmospheres and flux distributions used to analyse the hot star were computed with the line-blanketed plane-parallel LTE code STERNE. The high-resolution spectra were calculated with the LTE code SPECTRUM (see Jeffery et al. 2001).

The model atmospheres were calculated on a three-dimensional rectangular grid defined by $\mbox{\it T$_{\rm eff}$ }= 18\,000 (2000) 40\,000 \,\mbox{K}$, $\mbox{\,log $g$ }= 4.5 (0.5) 7.0$, and composition $n_{\rm H}$ = 1  - $n_{\rm He}$, $\mbox{\,$n_{\rm He}$ }= 0.01, 0.10 (0.10) 0.60$ and ${\rm [Fe/H]}$ = 0. The larger value of $n_{\rm H}$ or $n_{\rm He}$ is reduced to compensate for trace elements.

Synthetic spectra were calculated on wavelength intervals 3800-5020 Å (blue) and 8450-8670 Å (CaT). Linelists comprising some 142 absorption lines of hydrogen, helium, carbon, magnesium and silicon were taken from the list of assessed data for hot stars LTE_LINES (Jeffery 1991). Microturbulent velocity $\mbox{\,$v_{\rm t}$ }=5.0\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$ and solar abundances for all elements other than hydrogen and helium were assumed (see above).

Model atmospheres and flux distributions used to analyse the cool star were taken from the Kurucz' standard grid of ATLAS models (Kurucz 1993a), for $\mbox{\it T$_{\rm eff}$ }=3500 (500) 8000$, $\mbox{\,log $g$ }=2.0 (0.5) 4.5$, $\mbox{${\rm [Fe/H]}$ }=-0.5$, -0.3, 0.0 and $\mbox{\,$v_{\rm t}$ }=2.0\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$.

Grids of high resolution spectra were calculated in the same spectral regions as for the hot star using Kurucz' code SYNTHE (Kurucz 1993b; Jeffery et al. 1996) assuming a microturbulent velocity $\mbox{\,$v_{\rm t}$ }=2~\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$.

4.2 SFIT

For a given observation, an optimum fit was obtained by minimizing $\chi^2$,

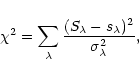\begin{displaymath}\chi^2 = \sum_{\lambda} { (S_{\lambda} - s_{\lambda})^2 \over \sigma^2_{\lambda}}, \end{displaymath} (1)

the weighted square residual between the normalized observed spectrum, $S_{\lambda}$, and the theoretical spectrum,

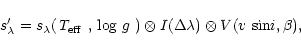\begin{displaymath}s'_{\lambda} = s_{\lambda}(\mbox{\it T$_{\rm eff}$ }, \mbox{\... ... })\otimes I(\Delta \lambda) \otimes V(v~{\rm sin} i, \beta), \end{displaymath} (2)

where $I(\Delta \lambda)$ and $V(v~{\rm sin} i, \beta)$ represent the instrumental and rotational broadening, respectively. Instrumental broadening is measured from the width of the emission lines in the copper-argon comparison lamp. The $\chi^2$ minimization was carried out using a variant of the algorithm AMOEBA (Press et al. 1989; Jeffery et al. 2001).

In the construction of $\chi^2$, each wavelength point was given a weight $w_{\lambda} = 1 / \sigma_{\lambda}$, the inverse of the standard deviation of the mean normalized flux in line-free regions. In our spectra $\sigma_{\lambda} \sim 0.01$. Some spectral regions needed to be excluded from the fit (e.g. bad columns or strong lines missing from the theoretical spectrum). In SFIT, such defects are masked by increasing $\sigma$ in appropriate wavelength intervals. We used $\sigma_{\lambda}$ = 0.1.

In any such fitting procedure, the normalization of the observed spectrum can be of crucial importance (Jeffery 1998). The problem is to normalize the observed spectrum correctly without, for example, compromising the wings of broad absorption lines. This is particularly difficult when there is an unknown contribution to the line opacity from metal lines in a cool star companion, so that there may be no "true'' continuum anywhere in the observed spectrum.


 

 
Table 4: Atmospheric properties of single-spectrum sdB stars measured spectroscopically using SFIT and previously.
Star T $_{\rm eff}$ log g y Reference
PG0004+133 $^\dagger$25025 $\pm$ 400 4.97 $\pm$ 0.10 0.01 $\pm$ 0.01 SFIT
(Fig. 1) 25025 $\pm$ 400     Paper I
  24700 $\pm$ 1300 4.5 $\pm$ 0.2 0.028 Moehler et al. (1990a)
PG0229+064 18000 $\pm$ 1025 4.35 $\pm$ 0.10 0.33 $\pm$ 0.01 SFIT
  20100 $\pm$ 400     Paper I
  19000 $\pm$ 950 4.55 $\pm$ 0.10 0.16 Ramspeck et al. (2001)
  22000 $\pm$ 1000 4.65 $\pm$ 0.15 0.137 Heber et al. (1999)
PG0240+046 36200 $\pm$ 400 6.25 $\pm$ 0.10 1.94 $\pm$ 0.02 SFIT
  34800 $\pm$ 1850     Paper I
  37000 $\pm$ 2000 5.3 $\pm$ 0.3 1.222 Thejll et al. (1994)
PG0342+026 24000 $\pm$ 375 5.17 $\pm$ 0.10 0.01 $\pm$ 0.01 SFIT
  27900 $\pm$ 975     Paper I
  24000 $\pm$ 1200 4.90 $\pm$ 0.20 0.003 Heber et al. (1999)
  25000 $\pm$ 2500 5.25 $\pm$ 0.20 0.000 Theissen et al. (1995)
  26220 $\pm$ 1000 5.67 $\pm$ 0.15 0.004 Saffer et al. (1994)
  22300 $\pm$ 1000 5.00 $\pm$ 0.30 0.000 Lamontagne et al. (1987)
PG0839+399 37300 $\pm$ 500 6.02 $\pm$ 0.10 <0.01 $\pm$ 0.01 SFIT
  35600 $\pm$ 1800     Paper I
  36100 $\pm$ 1000 5.91 $\pm$ 0.15 0.002 Saffer et al. (1994)
PG1233+426 25560 $\pm$ 550 5.52 $\pm$ 0.10 <0.01 $\pm$ 0.01 SFIT
  28750 $\pm$ 900     Paper I
  26500 $\pm$ 1000 5.60 $\pm$ 0.15 0.005 Saffer et al. (1994)
  26200 $\pm$ 1500 5.30 $\pm$ 0.30 0.000 Lamontagne et al. (1985)
PG2259+134 28500 $\pm$ 600 5.93 $\pm$ 0.10 0.02 $\pm$ 0.01 SFIT
  28350 $\pm$ 750     Paper I
  22500 $\pm$ 2500 5.00 $\pm$ 0.20 0.000 Theissen et al. (1995)
  28500 $\pm$ 1600 5.30 $\pm$ 0.20 0.022 Theissen et al. (1993)

$^\dagger$ T $_{\rm eff}$ assumed from Paper I.


The initial normalization was performed by fitting a low-order spline function to a series of pseudo-continuum points, usually the highest points in the spectrum. SFIT includes two re-normalization algorithms which may be used to optimize the fit (cf. Jeffery et al. 1998). One computes a low-order polynomial fit to the residual, the other applies a low-pass Gaussian filter. A second order polynomial was used to renormalize the spectrum in wavelength ranges 4200-4650 Å and 8000-8850 Å while a third order polynomial was used in the region of high order Balmer lines (H9, H8, H $_{\epsilon}$, etc.). Because low-order polynomials are used, individual line profiles are unaffected.

In principle and for suitable data with negligible noise, SFIT can solve simultaneously for as many parameters as required. In practice, it is necessary to restrict the free solution to between two and three parameters at a time, keeping others fixed, and to iterate until the optimum solution is obtained. SFIT requires a set of initial estimates for the free parameters. Results from the flux distribution analysis (Paper I) were used for $\mbox{\it T$_{\rm eff}$ }_1, \mbox{\it T$_{\rm eff}$ }_2$ and the radius ratio. Standard values were assumed for $\mbox{\,log $g$ }_1, \mbox{\,log $g$ }_2$ and y1.

4.3 Analysis: single stars

For single sdB stars, SFIT was applied to the blue spectra. The first parameter derived was the composition y of the sdB star. Within the T $_{\rm eff}$ range of sdB stars, the strength of helium lines depends far more on helium abundance than T $_{\rm eff}$ or log g. T $_{\rm eff}$ and log g were found next by finding the best fit to the Balmer lines. Rotational broadening is small compared with the instrumental profiles in these spectra.

Table 4 presents the results of the spectral analysis of single sdB stars (labeled SFIT), together with the results of the flux distribution analysis (Paper I) and results from literature.

4.4 Analysis: binary stars

For composite sdB stars, SFIT was applied separately to both blue and red spectra. Again, the first parameter to be fixed from the analysis of the blue spectrum is the composition of the sdB star, i.e. y1. Afterwards, $\mbox{\it T$_{\rm eff}$ }_1$, $\mbox{\,log $g$ }_1$ of the sdB star and R2/R1 are found by fitting the observed Balmer lines. The lower limit of the model grid was occasionally too large to fit the observed helium lines. In these cases only an upper limit to y1 can be given.

The radius ratio R2/R1 is directly related to the effective temperatures of both components, so must be a "free'' parameter whenever either T $_{\rm eff}$ is free. The contribution of the cool companion in the blue spectrum is reflected in the presence and strength of some metallic lines, being good indicators of the temperature of the cool star and the radius ratio of the system. Therefore, the blue spectrum is also used to fix $\mbox{\it T$_{\rm eff}$ }_2$ and R2/R1. It was frequently difficult to find a solution for $\mbox{\it T$_{\rm eff}$ }_1$, $\mbox{\it T$_{\rm eff}$ }_2$ and R2/R1 consistent with the flux distribution analysis (Paper I). In cases of conflict, we attempted to keep R2/R1 consistent between the two studies, although even this was not always possible (Table 5).

 

 
Table 5: Atmospheric properties of composite sdB stars measured spectroscopically using SFIT and previously. Subscript 1 refers to the hot subdwarf, subscript 2 refers to the cool companion.
Star $\mbox{\it T$_{\rm eff}$ }_1$ $\mbox{\,log $g$ }_1$ y1 $\mbox{\it T$_{\rm eff}$ }_2$ $\mbox{\,log $g$ }_2$ R2/R1 Ref.$^\dagger$
PG0110+262 21000 $\pm$ 750 5.17 $\pm$ 0.17 <0.01 $\pm$ 0.01 5250 $\pm$ 800 4.53 $\pm$ 0.21 3.2 $\pm$ 1.9 SFIT
  21050 $\pm$ 575     5485 $\pm$ 200   4.2 $\pm$ 0.2 1
  21000 $\pm$ 1000 < $5.90\pm 0.10$   5000 $\pm$ 500   6.0 2
  22000 $\pm$ 1000 < $5.50\pm 0.10$   5500 $\pm$ 500   4.4 3
  22000 $\pm$ 1500     4500 $\pm$ 500   7.8 4
PG0749+658 25400 $\pm$ 500 5.70 $\pm$ 0.11 <0.01 $\pm$ 0.02 5000 $\pm$ 500 4.58 $\pm$ 0.24 3.5 $\pm$ 1.2 SFIT
  25050 $\pm$ 675     5600 $\pm$ 300   3.9 $\pm$ 0.3 1
  24600 $\pm$ 1000 5.54 $\pm$ 0.15 0.004       5$^\ast$
  23500 $\pm$ 1500     4125 $\pm$ 500   6.3 4
PG1104+243 32850 $\pm$ 1550 5.40 $\pm$ 0.12 0.01 $\pm$ 0.02 6400 $\pm$ 1000 4.30 $\pm$ 0.31 5.9 $\pm$ 1.1 SFIT
  28000 $\pm$ 875     5735 $\pm$ 150   6.1 $\pm$ 0.2 1
  27500 $\pm$ 1500     4300 $\pm$ 500   10.6 4
  27200 $\pm$ 1500 5.50 $\pm$ 0.30         6
  28000 $\pm$ 5000     4600 $\pm$ 1000   9.8 7
PG1701+359 32500 $\pm$ 1325 5.75 $\pm$ 0.12 <0.01 $\pm$ 0.01 6000 $\pm$ 1000 4.60 $\pm$ 0.23 2.7 $\pm$ 1.8 SFIT
  36075 $\pm$ 700     6450 $\pm$ 230   4.8 $\pm$ 0.2 1
  30000 $\pm$ 2500 5.00 $\pm$ 0.20 0.000       8
  28500 $\pm$ 1500     4000 $\pm$ 500   6.2 4
  26250 $\pm$ 1250 5.80 $\pm$ 0.20         9
PG1718+519 29000 $\pm$ 1550 6.00 $\pm$ 0.14 <0.01 $\pm$ 0.01 5200 $\pm$ 400 4.55 $\pm$ 0.23 4.8 $\pm$ 1.6 SFIT
  29950 $\pm$ 1100     5925 $\pm$ 70   8.2 $\pm$ 0.3 1
  30000 $\pm$ 2500 5.00 $\pm$ 0.20 0.000 5125 $\pm$ 500     8
  25000 $\pm$ 1500     4300 $\pm$ 500   10.7 4
  23300 $\pm$ 1000 4.25 $\pm$ 0.20         9
PG2110+127 26500 $\pm$ 1700 5.20 $\pm$ 0.18 <0.01 $\pm$ 0.06 5400 $\pm$ 400 4.40 $\pm$ 0.24 4.7 $\pm$ 1.1 SFIT
(Fig. 2) 24900 $\pm$ 6500     5500 $\pm$ 575   5.5 $\pm$ 0.3 1
  30000 $\pm$ 2500 5.00 $\pm$ 0.20 0.000 5375 $\pm$ 500     8
  33700 $\pm$ 1000 5.33 $\pm$ 0.15 0.004       5
  26000 $\pm$ 1500     4500 $\pm$ 500   10.4 4
PG2135+045 28400 $\pm$ 800 4.80 $\pm$ 0.22 <0.01 $\pm$ 0.01 5000 $\pm$ 500 4.40 $\pm$ 0.30 3.1 $\pm$ 0.5 SFIT
  26325 $\pm$ 9950     4375 $\pm$ 1790   4.7 $\pm$ 0.6 1
  32100 $\pm$ 1000 4.79 $\pm$ 0.15 0.016       5$^\ast$
  27000 $\pm$ 1500     4400 $\pm$ 500   6.5 4
PG2148+095 30000 $\pm$ 860 4.90 $\pm$ 0.16 <0.01 $\pm$ 0.01 5700 $\pm$ 400 4.40 $\pm$ 0.31 3.0 $\pm$ 0.8 SFIT
(Fig. 4) 22950 $\pm$ 825     4375 $\pm$ 200   5.0 $\pm$ 0.2 1
  25000 $\pm$ 1000 < $5.80\pm 0.10$   5000 $\pm$ 500   6.0 2
  26000 $\pm$ 1500     4300 $\pm$ 500   7.9 4

$^\dagger$References: 1 = Paper I; 2 = Ulla & Thejll (1998); 3 = Thejll et al. (1995); 4 = Allard et al. (1994);
5 = Saffer et al. (1994); 6 = Lamontagne et al. (1987); 7 = Ferguson et al. (1984); 8 = Theissen et al. (1995);
9 = Theissen et al. (1993).
$^\ast$ Saffer et al. (1994) did not recognise the composite nature of these stars.


In the initial analysis of the blue spectrum, the cool companion is assumed to have $\mbox{\,log $g$ }_2 = 4.5$ (cf. Paper I). Applying SFIT gives new values, first for y1, then for $\mbox{\it T$_{\rm eff}$ }_1$, $\mbox{\,log $g$ }_1$, $\mbox{\it T$_{\rm eff}$ }_2$ and R2/R1.

With these improved estimates for the sdB star properties, the red spectrum is analyzed. In particular, $\mbox{\,log $g$ }_2$ is determined by fitting the calcium triplet.

A second analysis is now performed in the blue in order to refine the fit to the hot star spectrum, using the new parameters for the cool star. The above procedure is repeated until the solutions converge.

Table 5 presents the results for composite spectrum sdB stars, together with previous results from the literature. Solar metallicity was adopted for all stars except PG1104+243, for which we adopted $\mbox{${\rm [Fe/H]}$ }_2=-0.5$. The instrumental profile is large compared with any rotational broadening except in the cases of PG1701+359 and PG1718+519, where $\mbox{\,$v\,\sin i$ }=5$ and 10  $\,\mbox{$\mbox{km}\,\mbox{s}^{-1}$ }$, respectively, were adopted.

Table 5 includes values for R2/R1 for some previous papers. These have been computed from cited flux ratios at 5500 Å, effective temperatures and/or spectral types and an appropriate bolometric correction.

4.5 Errors

The formal errors associated with the best fit parameters xi are given by the diagonal elements $\delta_i = (\alpha^{-1})_{ii}$ of the inverse of the covariance matrix $\alpha$, whose elements are given by

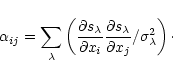\begin{displaymath}\alpha_{ij} = \sum_{\lambda} \left( {{\partial s_{\lambda}}... ...} \over {\partial x_{j}}} / \sigma^{2}_{\lambda}\right)\cdot \end{displaymath} (3)

Since SFIT is never run with all parameters free, the full covariance matrix is never computed. Thus the total errors $\sigma_i$ need to be obtained from a careful analysis of the partial errors $\delta_i$.

For a single-star spectrum, only the derivatives between T $_{\rm eff}$, log g and y need to be calculated. In the case of a binary system, the derivatives between the physical parameters of both components of the system are required. These have to be evaluated numerically, e.g.

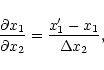\begin{displaymath}{\partial x_{1} \over \partial x_{2}} = {{x'_{1} - x_{1}} \over \Delta x_{2}}, \end{displaymath} (4)

where x1 represents parameters of the sdB star and x2 represents parameters of the cool star. $\Delta x_{2}$ is an increment used to compute a change in x1, usually 1$\%$ of x2. x'1 are parameters derived when using $x_{2}+\Delta x_{2}$ as input to the fit.

The errors given in Tables 4 and 5 are total errors. For example the total error $\sigma$ in $\mbox{\it T$_{\rm eff}$ }_{\rm 1}$ is given by

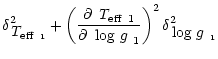$\displaystyle \sigma^2_{\mbox{\it T$_{\rm eff}$ }_{1}}$ = $\displaystyle \delta^2_{\mbox{\it T$_{\rm eff}$ }_{1}} + \left({\partial ~\mbox... ...over \partial ~\mbox{\,log $g$ }_{1}}\right)^2 \delta^2_{\mbox{\,log $g$ }_{1}}$  
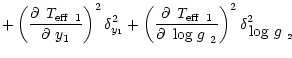    $\displaystyle + \left({\partial ~\mbox{\it T$_{\rm eff}$ }_{1} \over \partial ~... ...over \partial ~\mbox{\,log $g$ }_{2}}\right)^2 \delta^2_{\mbox{\,log $g$ }_{2}}$  
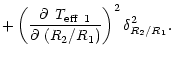    $\displaystyle + \left({\partial ~\mbox{\it T$_{\rm eff}$ }_{1} \over \partial ~(R_2/R_1)}\right)^2 \delta^2_{R_2/R_{1}}.$ (5)

In addition to the formal errors cited, there are additional systematic errors. Principal amongst these are in the metallicity of the cool star, $\mbox{${\rm [Fe/H]}$ }_2$. This has a strong influence on the measurement of $\mbox{\,log $g$ }_2$ from the calcium triplet, and hence on the radius ratio R2/R1 because the latter is primarily fixed by the strength of the metal-lines relative to Balmer lines in the blue spectrum. High-resolution spectra will be required to address this problem.

There are also systematic differences between the methods used to obtain R2/R1 in this paper and in Paper I. To compare these methods we have constructed a simple test. The energy distribution and normalized spectrum of a binary system containing a typical sdB star and a main-sequence star were computed. These were resampled to mimic the observational data available to us in each investigation. The data were then analyzed using BINFIT (to fit the flux distribution, Paper I) and SFIT independently. The model parameters and the results of the $\chi^2$ analysis are shown in Table 6.

 

 
Table 6: Comparison of BINFIT and SFIT for a test binary.
Parameter Model BINFIT SFIT
$\mbox{\it T$_{\rm eff}$ }_1$ (K) 24000 24060 $\pm$ 260 24190 $\pm$ 300
$\mbox{\,log $g$ }_1$ 6.0   6.02 $\pm$ 0.05
y1 0.10   0.11 $\pm$ 0.01
$\mbox{\it T$_{\rm eff}$ }_2$ (K) 4500 4550 $\pm$ 150 4500 $\pm$ 200
$\mbox{\,log $g$ }_2$ 4.5   4.54 $\pm$ 0.05
R2/R1 6.29 5.90 $\pm$ 0.16 6.27 $\pm$ 0.20


The results are all consistent with the test model except the value of R2/R1 given by BINFIT. The errors associated with this parameter are possibly underestimated, since they are only derived from the formal error in the angular diameters.

5 Results

5.1 Single-star spectra

Figure 1 shows the best fit model for the single sdB star PG0004+133.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3269F1.PS}\end{figure} Figure 1: Normalized blue spectrum of the single sdB star PG0004+133 (histogram) together with the best fit model spectrum (polyline). The symbol $\times $ marks a CCD defect.
Open with DEXTER

In addition to results reported in Table 4, the following individual remarks are noted. PG0004+133: since only the H$\gamma$ line is available, we have assumed T $_{\rm eff}$ from Paper I.

PG0229+064: with y=0.33, this is a helium-rich sdB star (Heber et al. 1999). The metal lines imply a higher metal abundance than assumed in the model. This has also been found by Ramspeck et al. (2001) who, in particular, find C and N overabundant by nearly one dex.

PG0240+046: an even more helium-rich sdB star with 66$\%$ of He abundance, consistent with a previous abundance of 55$\%$ Thejll et al. (1994).

PG0342+026: C, Si and Mg appear to be underabundant relative to the assumed solar composition.

PG0839+399 and PG1233+426: the helium abundance is below the measurement threshold, and metals are underabundant.

PG2259+134: C appears to be underabundant.

5.2 Composite spectra

Results for sdB stars with composite spectra are shown in Table 5. Figures 2 and 3 show best fits for the composite sdB star, PG2110+127.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3269F2.PS}\end{figure} Figure 2: Normalized blue spectrum of the composite PG2110+127 a) together with the best fit composite model spectrum b) formed by adding models with c)  $\mbox{\it T$_{\rm eff}$ }_{1}=26\,500$ K, $\mbox{\,log $g$ }_{1}=5.20$, y=0.01, $\mbox{\,$v_{\rm t}$ }_1=5$  $\mbox{km}\,\mbox{s}^{-1}$ and d) $\mbox{\it T$_{\rm eff}$ }_{2}=5400$ K, $\mbox{\,log $g$ }_{2}=4.40$, $\mbox{${\rm [Fe/H]}$ }=0.00$, $\mbox{\,$v_{\rm t}$ }_2=2$  $\mbox{km}\,\mbox{s}^{-1}$ with radius ratio R2/R1=4.7. The model spectra have been velocity shifted and degraded to match the observations. The symbol $\times $ marks a CCD defect.
Open with DEXTER

The radius ratios (R2/R1) and hence, by implication, the radii of the cool stars (R2) are all smaller than measured previously.

In nearly all cases, the Hei lines are weaker than predicted by models with $\mbox{\,$n_{\rm He}$ }_1=0.01$, implying hot star He abundances below this value. In addition, metal lines from the hot star, (e.g. silicon, carbon and magnesium), appear to be too strong in the model compared with the observations. Since we assumed $\mbox{${\rm [Fe/H]}$ }_1=0.0$, this implies that metals are generally underabundant in the sdB stars in our sample. This requires confirmation from high-resolution spectroscopy. In addition to results reported in Table 5, the following individual remarks are noted.

PG0110+262 and PG0749+658: C underabundant


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3269F3.PS}\end{figure} Figure 3: Normalized red spectrum of the composite PG2110+127 around the infrared calcium triplet (histogram) together with the best fit model spectrum (polyline).
Open with DEXTER

PG1104+243: with $y=0.01\pm0.01$, this is the most helium-rich composite sdB in our sample. The strength of the Ca K line and other metallic lines in the blue spectrum indicates $\mbox{\it T$_{\rm eff}$ }_2 = 6400 \,\mbox{K}$, $\log g_2=4.3$, and $R_2/R_1 \sim 6$. However, assuming the same radius ratio and $\mbox{${\rm [Fe/H]}$ }_2=0.0$, the red spectrum gives $\mbox{\it T$_{\rm eff}$ }_2 = 4500 \,\mbox{K}$ and $\log g_2=4.6$. Since the blue spectrum provides very strong constraints on $\mbox{\it T$_{\rm eff}$ }_2$ and R2/R1, it was necessary to adopt a reduced value for $\mbox{${\rm [Fe/H]}$ }_2=-0.5$ to maintain consistency with Paper I.

PG1701+359 and PG1718+519: C, Mg and Si underabundant. R2/R1 significantly smaller than in Paper I. This could be due to the adoption of too high metallicity $\mbox{${\rm [Fe/H]}$ }_2$.

PG2110+127: C, Mg and Si underabundant.

PG2135+045: C, Mg and Si underabundant. R2/R1 significantly smaller than in Paper I. This is probably due to the absence of IUE LW and JHK photometry which led to particularly large errors in the Paper I $\mbox{\it T$_{\rm eff}$ }$ measurements.

PG2148+095: C, Mg and Si underabundant. R2/R1 significantly smaller than in Paper I probably due to significant differences in $\mbox{\it T$_{\rm eff}$ }$. The latter are probably due to the absence of an IUE LW spectrum and a possible anomaly in the J-band photometry.

Significant differences between the results of the spectroscopic ( SFIT) and photometric (Paper I) analyses have been discussed above. Tables 4 and 5 also include the results of earlier photometric and spectroscopic analyses. The current results agree well with previous spectroscopic analyses (Moehler et al. 1990a; Saffer et al. 1994; Heber et al. 1999) in the cases of PG0342+026, PG0839+399, PG1233+426 and PG0749+658. They do not agree well in the cases of PG0004+133, PG0229+064, PG2110+127 and PG2135+045.

The high helium abundance may contribute to the $\mbox{\it T$_{\rm eff}$ }$ discrepancy in PG0229+064, a cool He-rich subdwarf with a relatively low surface gravity. Saffer et al. (1994) did not recognize the composite nature of PG0749+658 and PG2135+045, and it is not clear how they modelled the spectrum of PG2110+127. When deriving the sdB parameters, Theissen et al. (1993, 1995) corrected for the continuum light of the cool companions, but not the (weaker) Balmer lines from the cool stars. Therefore these results may not be fully reliable.

5.3 (logg-T $_\mathsfsl{eff}$) diagram and helium abundances

Figure 5 compares the sdB stars analysed here with an homogeneous sample of sdB stars (Moehler, private communication) and the location of the helium main sequence (He-MS) and zero-age extreme horizontal branch (ZAEHB) (Moehler et al. 1990a).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3269F4.PS}\end{figure} Figure 4: As in Fig. 1 but for the composite sdB star PG2148+095.
Open with DEXTER

The surface gravities of hot stars in composite sdBs lie in the range $ 4.80 \le \log g \le 6.00$, while our sample of single sdB stars have $4.35 \le \log g \le 6.25$. Although both log g and T $_{\rm eff}$ ranges for composite sdBs are slightly smaller than for the single-spectrum stars, there is essentially no difference between their distribution in the log g-T $_{\rm eff}$ diagram and that of larger samples of sdB stars analyzed previously.

A striking result of this study is that the majority of single-spectrum sdB stars have helium abundances of y=0.01 or higher, while the composite stars have y<0.01 (the minimum currently available in our model grid).

Low surface He abundances are expected in sdB stars because of the competition between gravitational settling and radiative levitation acting on different ions. The same diffusive processes may be responsible for the apparently low abundances of carbon, silicon and magnesium in our sample (cf. Bergeron et al. 1988).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3269F5.PS}\end{figure} Figure 5: Position of single sdB stars (filled circles) and composite sdB stars (filled triangles) in the ( $\mbox{\,log $g$ }_1$- $\mbox{\it T$_{\rm eff}$ }_1$) diagram as derived from the spectral analysis SFIT. Open circles represent the position of an homogeneous sample of sdB stars (Maxted et al. 2001). The position of the He-MS and ZAEHB are represented as solid and dash-dotted lines, respectively (Moehler et al. 1990a).
Open with DEXTER

It has already been noted that sdB stars with composite spectra and, hence, F-, G- or K-type companions form a distinct group from those with no or unseen companions (Saffer et al. 2001). With a separate evolutionary history, a distinct surface abundance might be anticipated, but remains to be explained.

Two single-spectrum sdB stars (PG0229+064 and PG0240+046) have $y\gg 0.01$. It is interesting that these particular examples lie at the extremities of our sample. Recalling the three groups of sdBs introduced earlier (Saffer et al. 2001), such helium-rich sdBs may form a completely separate subgroup. They were identified in the PG survey (Green et al. 1986: spectral classes sdB-O, sdOA and sdOD) and subsequently (Moehler et al. 1990a: HesdB, Saffer et al. 1994). The latter found most of the He-rich sdBs to have $\mbox{\it T$_{\rm eff}$ }>30\,000\,\mbox{K}$, and commented that it was difficult to reconcile these stars with time-dependent diffusion calculations.

We do not currently know whether any He-rich sdB stars are members of short-period binary systems. The latter is particularly important - one scenario for the production of sdBs is the merger of two helium-white dwarfs (Iben 1990; Saio & Jeffery 2000). The surface layers of the product may be so helium-rich that diffusive processes could not completely remove the surface helium. A significant number of He-rich binary sdBs would demand an alternative explanation.

5.4 Composite sdB companions in the HR diagram

The cool companions in binary sdB stars have surface gravities in the range $4.30 \le \log g_2 \le 4.58$. Figure 6 shows the position of the cool companion in binary sdB stars in the (log g-T $_{\rm eff}$) diagram as derived from SFIT together with the location of the ZAMS and TAMS from stellar models with solar composition (Girardi et al. 2000).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{H3269F6.PS}\end{figure} Figure 6: Position of the cool companion in composite sdB stars in the ( $\mbox{\,log $g$ }_2$- $\mbox{\it T$_{\rm eff}$ }_2$) diagram as derived from the spectral analysis. The position of the ZAMS and TAMS from stellar models with solar composition (Girardi et al. 2000) are plotted as dash-dotted and dashed lines, respectively. Labels refer to identification numbers in Table 7.
Open with DEXTER

The observations are consistent with surface gravities of main-sequence stars. This comparison may be taken further by assuming a canonical 0.5$M_\odot $ for the masses of the sdB stars. Using the sdB surface gravities and the measured radius ratios, the luminosities of both components can be calculated (Table 7).
   
Table 7: Spectroscopically determined luminosities and masses for composite sdB star companions compared with the photometric analysis (Paper I). The luminosities assume 0.5 $M_\odot $ for the sdB stars (Heber et al. 1984; Heber 1986).
Star SFIT Paper I
  $L_2/\mbox{\,$L_{\odot}$ }$ $\mbox{\it T$_{\rm eff}$ }_2/\,\mbox{K}$ $L_2/\mbox{\,$L_{\odot}$ }$ $\mbox{\it T$_{\rm eff}$ }_2/\,\mbox{K}$
1 PG0110+262 $0.64\pm0.40$ $5250\pm~800$ $0.19\pm0.04$ $5485\pm~200$
2 PG0749+658 $0.19\pm0.08$ $5000\pm~500$ $0.18\pm0.07$ $5600\pm~300$
3 PG1104+243 $2.85\pm1.78$ $6400\pm1000$ $4.90\pm0.77$ $5735\pm~150$
4 PG1701+359 $0.21\pm0.14$ $6000\pm1000$ $0.48\pm0.10$ $6450\pm~230$
5 PG1718+519 $0.21\pm0.06$ $5200\pm~400$ $1.02\pm0.15$ $5925\pm~~70$
6 PG2110+127 $1.45\pm0.44$ $5400\pm~400$ $0.03\pm0.02$ $5500\pm~575$
7 PG2135+045 $1.17\pm0.48$ $5000\pm~500$ $0.31\pm0.54$ $4375\pm1790$
8 PG2148+095 $1.47\pm0.44$ $5700\pm~400$ $0.11\pm0.03$ $4375\pm~200$

Table 7 presents the luminosities, effective temperature and masses of the cool companions of composite sdB stars. These results reinforce our conclusion (Paper I) that the cool companions in composite sdB systems are main-sequence stars with $M \sim 1.0\pm0.1 \mbox{\,$M_{\odot}$ }$.

5.5 Mass ratios in composite sdB systems

The mass ratio of a binary system containing a hot sdB star and a cool companion is given by q = M2/M1. From g = (G M)/R2 and the radius ratio R2/R1, the mass ratio can be expressed as

 
q = (R2/R1)2 (g1/g2). (6)

This method of measuring q is subject to the normally quite large errors in measuring $\log g$. Mass ratios for composite systems analysed by us lie in the range 0.52 < q < 3.83.

Assuming the cool companions in our sample to be main-sequence stars with effective temperatures $ 4500 < \mbox{\it T$_{\rm eff}$ }_2/\,\mbox{K} < 6500$, then their masses should be in the range $0.75\le M / \mbox{\,$M_{\odot}$ }\le1.32$ (Gray 1992). Hence, assuming that the hot components of the binary systems are sdB stars with typical masses of $\sim$ $ 0.5 ~M_{\odot}$ (Heber et al. 1984; Heber 1986), then the mass ratios should be in the range $1.50 \le q \le 2.65$. Clearly, the surface gravity ratio method is not yet sufficiently sensitive to yield the mass ratio directly.

6 Discussion

Green et al. (2001) have discussed the evolutionary origin of subdwarf B stars in view of findings regarding the distribution of binary periods and companions found in other surveys (Saffer et al. 2001). They deduce that sdB stars with spectral lines from a cooler companion invariably have periods longer than a year, while very short-period sdBs have essentially invisible companions. The deduction is that both groups are produced by Roche lobe overflow/mass transfer from low-mass stars near the tip of the red giant branch. If the initial binary is sufficiently wide and the secondary is sufficiently massive and able to accept the dynamic mass transfer of the first couple of tenths of a solar mass without filling its Roche lobe, then the initial mass ratio may be reduced sufficiently to allow stable mass transfer and avoid a common-envelope phase. In this case the orbital period would remain long, and the secondary would increase in mass, becoming a blue straggler (BS) with $\mathrel{\raise1.16pt\hbox{$>$ }\kern-7.0pt \lower3.06pt\hbox{{$\scriptstyle \sim$ }}}$ $1\mbox{\,$M_{\odot}$ }$, as observed by ourselves. An important question will be to determine accurately the upper and lower limits on both masses and periods for such sdB+BS binaries. Green $\&$ Liebert (2001) suggest that binaries with less massive secondaries would form a common-envelope and end up either merging or as short-period sdB+MS systems.

The division of sdBs into long- and short-period binaries suggests a reason for the difference in helium abundance between the two samples. While low-helium (and -metal) abundances are known to be a result of atmospheric diffusion in high-gravity stars within a certain temperature range, external forces may partially disrupt these. Tidal interaction due to a binary companion will be much stronger in a short-period than in a long-period system. Unless the sdB star is rotating completely synchronously, tidal effects will operate on timescales shorter than diffusion ($\sim$105 years) and may dilute the chemical separation. Extremely low-hydrogen abundances would therefore be seen preferentially in long-period sdB binaries.

The presence of sdBs within the sample with helium abundances significantly greater than normal (e.g. PG0229+064, PG0240+046) may be a consequence of their belonging to sdB group (1) - apparently single stars (Saffer et al. 2001). It is interesting that no sdB star with y>0.03 is known to be a short-period binary (Maxted et al. 2001). Since sdB stars are known with extremely high helium abundances (cf. Jeffery et al. 1987), we suggest that these could have an entirely separate origin, being the products of helium plus helium white dwarf mergers (Iben 1990). Evidence for such a conclusion is provided by the extreme helium star V652Her (Jeffery et al. 2001), considered to be strong evidence for such a merger product evolving to become an isolated helium main-sequence star (Saio & Jeffery 2000). When it becomes a subdwarf, diffusion will inevitably modify the initially helium-rich atmosphere. However, with a much more limited reservoir of hydrogen, extremely low helium abundances will be difficult to achieve. Consequently sdBs produced by mergers could be expected to show a very wide range of helium abundances.

7 Conclusions

We have analysed representative samples of sdB stars having apparently single or composite spectra. The atmospheric properties of the sdB stars were measured by comparing moderate-resolution blue spectra with theoretical models. In the case of sdBs with composite spectra, the atmospheric properties of the cool companions were measured from the blue spectra and from near-infrared spectra, where the infrared calcium triplet provides an invaluable surface gravity indicator.

Both samples covered a similarly wide range in T $_{\rm eff}$ and log g. However the composite sdB stars invariably have lower helium abundances in their atmospheres than the single-spectrum sdBs. Although we cannot entirely explain this phenomenon, we suggest that it may be due to tidal effects disrupting diffusive separation in short-period systems more than in long-period systems. Some of the composite sdB stars also showed depletions of metals including silicon, carbon and magnesium.

Assuming a typical surface luminosity representing all subdwarf B stars of log $(L_{\rm sdB}/\mbox{\,$L_{\odot}$ }) = 1.40 \pm 0.13$, the majority of the companions of composite sdBs have luminosities in the range $0.4 \le L_{\rm cool}/\mbox{\,$L_{\odot}$ }\le 2.6$, consistent with being main-sequence stars of about $1\pm0.2 \mbox{\,$M_{\odot}$ }$. This supports the hypothesis that composite sdB stars are the result of Roche lobe overflow near the red-giant tip in a low-mass binary with nearly equal initial masses (Green et al. 2001).

This is the first time that an attempt has been made to model accurately the spectra of composite subdwarf B stars and to measure the cool star luminosity using the infrared calcium triplet. Although successfully executed, higher resolution spectra will be needed to measure the metallicity of the cool star and hence the radius ratios with greater accuracy.

Acknowledgements
This research is supported by a grant to the Armagh Observatory from the Northern Ireland Department of Culture, Arts and Leisure and by the UK Particle Physics and Astronomy Research Council through the award of telescope time and travel grants. We are particularly grateful to Prof Philip Dufton and Drs Sabine Moehler and Betsy Green for helpful discussions and to Dr Don Pollacco for obtaining some of the observations.

References

 
Copyright ESO 2002