

Up: The origin of the
According to observational data (Davidson & Humphreys 1997),
the Weigelt blobs (Weigelt & Ebersberger 1986) close to 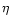 Car
(for example, blob B) are
compact gas condensations (low-intensity compact ejecta with a high
hydrogen concentration
Car
(for example, blob B) are
compact gas condensations (low-intensity compact ejecta with a high
hydrogen concentration
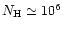 cm-3 and a Fe concentration of
cm-3 and a Fe concentration of
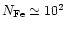 cm-3).
cm-3).
The blob diameter is
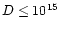 cm, and the distance from the central star is
cm, and the distance from the central star is
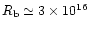 cm. The diameter of the photosphere of the central star is
cm. The diameter of the photosphere of the central star is
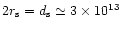 cm, and its effective temperature is
cm, and its effective temperature is
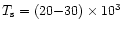 K. These parameter values are preliminary. For
example, according to recent HST/STIS observations (T. Gull, private communication, April 2001), the distance
K. These parameter values are preliminary. For
example, according to recent HST/STIS observations (T. Gull, private communication, April 2001), the distance 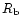 between the blob B and the central star is around
between the blob B and the central star is around
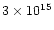 cm, i.e. an order of magnitude smaller than derived from previous data.
The fact that the blob is located close enough to the central star is of importance for
our model. The dilution factor of the radiation from
cm, i.e. an order of magnitude smaller than derived from previous data.
The fact that the blob is located close enough to the central star is of importance for
our model. The dilution factor of the radiation from 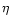 Car,
Car,
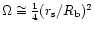 ,
is around
10-6 - 10-5,
which is many orders of magnitude greater than that for a typical planetary nebula. For illustration, we present in Fig. 1 a schematic picture of a gas condensation having a spherical shape with an average diameter D (as judged from density) and an average volume concentration
,
is around
10-6 - 10-5,
which is many orders of magnitude greater than that for a typical planetary nebula. For illustration, we present in Fig. 1 a schematic picture of a gas condensation having a spherical shape with an average diameter D (as judged from density) and an average volume concentration 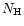 of hydrogen atoms and ions and being located at the distance
of hydrogen atoms and ions and being located at the distance
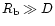 from the star.
from the star.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{Fig1.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg34.gif) |
Figure 1:
Model geometry of the compact gas condensation (blob) in the vicinity of
the central star of  Carinae.
Carinae. |
The most intense part of the stellar radiation with h
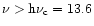 eV is absorbed almost completely by neutral hydrogen having a concentration of
eV is absorbed almost completely by neutral hydrogen having a concentration of
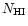 (
(
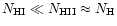 ), provided that the optical density
), provided that the optical density
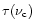 of the Lyman-continuum is high enough, i.e.,
of the Lyman-continuum is high enough, i.e.,
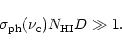 |
(1) |
Condition (1) is satisfied if the hydrogen density 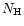 exceeds some
critical value
exceeds some
critical value
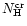 :
:
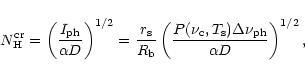 |
(2) |
where  is the rate coefficient of the HII
is the rate coefficient of the HII
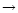 HI recombination process, and
HI recombination process, and
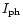 is the effective intensity of the radiation incident on the blob surface and ionizing hydrogen.
As an estimate we use, as in our previous paper (Johansson & Letokhov 2001b), average values of the blackbody radiation intensity
is the effective intensity of the radiation incident on the blob surface and ionizing hydrogen.
As an estimate we use, as in our previous paper (Johansson & Letokhov 2001b), average values of the blackbody radiation intensity
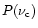 and photoionization cross section
and photoionization cross section
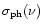 in the effective frequency interval
in the effective frequency interval
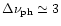 eV above
eV above
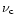 ,
where
,
where 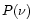 and
and
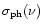 are sufficiently large. Condition (1) means that the local Strömgren boundary separating the HII and HI regions is inside the gas condensation being considered, as shown in Fig. 1. For blob B near
are sufficiently large. Condition (1) means that the local Strömgren boundary separating the HII and HI regions is inside the gas condensation being considered, as shown in Fig. 1. For blob B near 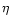 Carinae at
Carinae at
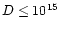 cm and
cm and
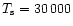 K, the critical density
K, the critical density
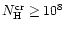 cm-3.
cm-3.
The physical depth
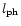 at which the photoionization state of hydrogen is sustained at
at which the photoionization state of hydrogen is sustained at
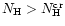 is defined by the expression
is defined by the expression
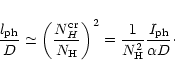 |
(3) |
At
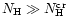 ,
the depth
,
the depth
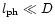 ,
i.e. there is a thin front layer of the blob facing the central star (Fig. 1).
,
i.e. there is a thin front layer of the blob facing the central star (Fig. 1).
At
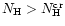 the neutral component HI absorbs almost
all of the power
the neutral component HI absorbs almost
all of the power 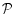 (in photons/s) of the Lyman-continuum radiation coming from the star:
(in photons/s) of the Lyman-continuum radiation coming from the star:
where
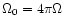 is the solid angle and
is the solid angle and
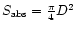 is the disc area of the blob absorbing the incident radiation from the central star. Most of the absorbed energy is reemitted due to radiative recombination of the hydrogen ions formed. The major proportion (
is the disc area of the blob absorbing the incident radiation from the central star. Most of the absorbed energy is reemitted due to radiative recombination of the hydrogen ions formed. The major proportion (
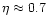 )
of the absorbed energy is emitted in the resonance line HI Ly
)
of the absorbed energy is emitted in the resonance line HI Ly .
The maximum value of the optical density
.
The maximum value of the optical density 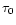 (Ly
(Ly )
with reference to the center of Ly
)
with reference to the center of Ly in the HII region is
in the HII region is
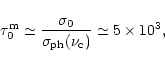 |
(5) |
where we have set
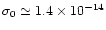 cm2 and
cm2 and
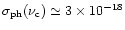 cm2 (average value) in the frequency interval (
cm2 (average value) in the frequency interval (
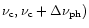 .
For illustration, we show in Fig. 2 the qualitative distribution of the average concentrations of HII and HI inside the blob, as well as the evolution of the Ly
.
For illustration, we show in Fig. 2 the qualitative distribution of the average concentrations of HII and HI inside the blob, as well as the evolution of the Ly radiation spectrum in various zones of the blob.
radiation spectrum in various zones of the blob.
![\begin{figure}
\par\includegraphics[%
width=16cm,clip]{Fig2rev4.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg68.gif) |
Figure 2:
Radial profiles of the ionized (
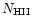 )
and neutral hydrogen ( )
and neutral hydrogen (
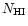 )
concentrations and a qualitative evolution of the spectral shape of the Ly )
concentrations and a qualitative evolution of the spectral shape of the Ly radiation in the active HII region, the Strömgren boundary region, and the passive
fluorescence region relative to the FeII absorption profile.
radiation in the active HII region, the Strömgren boundary region, and the passive
fluorescence region relative to the FeII absorption profile. |
The Ly radiation proves to be trapped in the HII region, but the diffusion confinement time is limited by the fact that the number of scattering events is limited because of the Doppler frequency redistribution of the scattered Ly
radiation proves to be trapped in the HII region, but the diffusion confinement time is limited by the fact that the number of scattering events is limited because of the Doppler frequency redistribution of the scattered Ly photons. This redistribution makes them leave the trapping region relatively fast via the wings of the Doppler profile (Osterbrock 1967). Since the optical density
photons. This redistribution makes them leave the trapping region relatively fast via the wings of the Doppler profile (Osterbrock 1967). Since the optical density 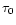 is limited to
is limited to
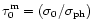 ,
and the damping factor for Ly
,
and the damping factor for Ly is
is
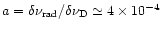 ,
the optical density in the Lorentz wings is
,
the optical density in the Lorentz wings is
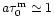 ,
where we assume the Doppler spectral width to be
,
where we assume the Doppler spectral width to be
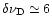 cm-1 and the natural spectral width,
cm-1 and the natural spectral width,
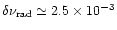 cm-1. Therefore, the Ly
cm-1. Therefore, the Ly photons leave the HII region by diffusion while suffering an increase in the Doppler width
photons leave the HII region by diffusion while suffering an increase in the Doppler width
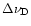 by a factor of
by a factor of
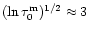 ,
so that the total power emitted by the surface of the blob into Ly
,
so that the total power emitted by the surface of the blob into Ly is
is
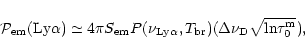 |
(6) |
where
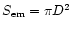 is the area of the emitting surface of the spherical
blob and
is the area of the emitting surface of the spherical
blob and
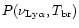 is the average spectral intensity of Ly
is the average spectral intensity of Ly on the blob surface, given by the Planck distribution at a frequency of
on the blob surface, given by the Planck distribution at a frequency of
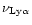 and a spectral brightness temperature of
and a spectral brightness temperature of
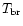 ,
account being taken of the spectral line broadening due to trapping. In the steady-state case where the absorption of the trapped Ly
,
account being taken of the spectral line broadening due to trapping. In the steady-state case where the absorption of the trapped Ly in the HII region of the blob is negligible, we have
in the HII region of the blob is negligible, we have
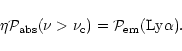 |
(7) |
It follows from (7) that the brightness temperature
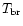 of the Ly
of the Ly radiation on the open surface of the blob can be estimated by the expression
radiation on the open surface of the blob can be estimated by the expression
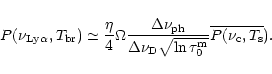 |
(8) |
It can be seen that the dilution factor 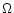 can largely be compensated for by the
effect of the spectral compression of the absorbed energy into the relatively narrow
Ly
can largely be compensated for by the
effect of the spectral compression of the absorbed energy into the relatively narrow
Ly radiation. Note that the intensity of the Ly
radiation. Note that the intensity of the Ly radiation inside the HII
region of the blob is higher than that on the blob surface,
radiation inside the HII
region of the blob is higher than that on the blob surface,
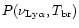 ,
by a factor of
,
by a factor of
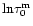 due to diffusion
confinement. Therefore, to determine the brightness temperature
due to diffusion
confinement. Therefore, to determine the brightness temperature
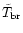 of the radiation incident on the boundary between the HII and HI regions inside the blob
(the Strömgren boundary in Fig. 1), the right-hand side of expression (7)
should be increased by
of the radiation incident on the boundary between the HII and HI regions inside the blob
(the Strömgren boundary in Fig. 1), the right-hand side of expression (7)
should be increased by
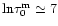 times, which is
equivalent to the same increase in
times, which is
equivalent to the same increase in 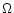 :
:
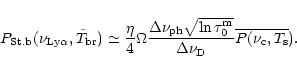 |
(9) |
The temperature
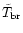 is fairly close to the temperature of the blackbody radiation of the central star's photosphere (for
is fairly close to the temperature of the blackbody radiation of the central star's photosphere (for
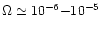 ,
the temperature
,
the temperature
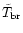 is
is
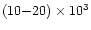 K), but the spectral width of the line radiation leaving the active HII region is still insufficient to compensate for the difference in wavelength between the Ly
K), but the spectral width of the line radiation leaving the active HII region is still insufficient to compensate for the difference in wavelength between the Ly emission and the FeII absorption lines (see the top part of Fig. 2). This radiation suffers further spectral diffusion both in the HII/HI transition region (the Strömgren boundary), which is optically denser for Ly
emission and the FeII absorption lines (see the top part of Fig. 2). This radiation suffers further spectral diffusion both in the HII/HI transition region (the Strömgren boundary), which is optically denser for Ly ,
and mainly in the passive, weakly ionized HI region.
,
and mainly in the passive, weakly ionized HI region.
The physical depth
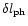 of the HII/HI transition region is shallow:
of the HII/HI transition region is shallow:
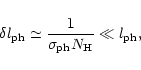 |
(10) |
in comparison with the physical length
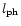 of the photoionization depth (the physical depth of the active HII part of blob B):
of the photoionization depth (the physical depth of the active HII part of blob B):
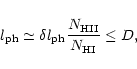 |
(11) |
defined by expression (3). Note that, for the reader's convenience, we present here these well-known expressions (Mihalas 1978) in order to give explanations to the designations used. The optical thickness of the HII/HI transition layer with physical width
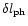 can be estimated as:
can be estimated as:
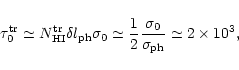 |
(12) |
where
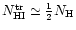 is the average concentration of HI in the transition layer,
and
is the average concentration of HI in the transition layer,
and
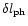 is determined by Eq. (10).
The high density of HI compensates the small width of this layer and as a result the
optical thickness of the transient layer
is determined by Eq. (10).
The high density of HI compensates the small width of this layer and as a result the
optical thickness of the transient layer
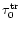 is almost equal to
the optical thickness
is almost equal to
the optical thickness
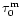 of the whole active zone.
Nevertheless, these values of
of the whole active zone.
Nevertheless, these values of 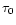 are much smaller than the magnitude required for the Ly
are much smaller than the magnitude required for the Ly excitation of FeII:
excitation of FeII:
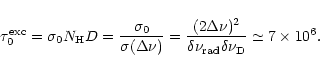 |
(13) |
However, the remaining, dissipating (passive) volume of the blob is also large enough to provide for
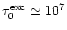 and the appropriate broadening of the Ly
and the appropriate broadening of the Ly line as a result of the Doppler frequency diffusion of the radiation on the Lorentz wing of the Ly
line as a result of the Doppler frequency diffusion of the radiation on the Lorentz wing of the Ly resonance line.
resonance line.
The physical depth
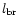 of the passive HI region, at which the diffusion spectrum broadening necessary for the excitation of FeII is reached, is defined by the expression
of the passive HI region, at which the diffusion spectrum broadening necessary for the excitation of FeII is reached, is defined by the expression
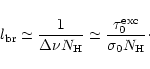 |
(14) |
The depth
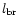 (see Figs. 1 and 2) can be compared with the depth
(see Figs. 1 and 2) can be compared with the depth
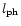 of the photoionization region. Their ratio is given by
of the photoionization region. Their ratio is given by
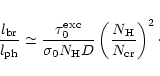 |
(15) |
At
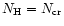 the depth
the depth
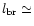 (0.01 to 0.1)
(0.01 to 0.1)
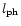 ,
so that the transition region fully provides for the necessary diffusion broadening of Ly
,
so that the transition region fully provides for the necessary diffusion broadening of Ly .
At
.
At
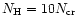 ,
the depth
,
the depth
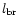 increases to (0.1 to 1)
increases to (0.1 to 1)
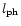 .
Finally,
.
Finally,
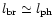 at a hydrogen concentration in the gas condensation defined as
at a hydrogen concentration in the gas condensation defined as
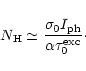 |
(16) |
For example, for blob B in the vicinity of 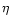 Car, this regime is reached at
Car, this regime is reached at
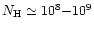 cm-3.
cm-3.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{Fig3.EPS}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg108.gif) |
Figure 3:
Energy levels and quantum transitions in FeII relevant to the anomalous
UV FeII spectral lines. |
The following two well-known processes take place in the passive HI region where the Ly radiation is transferred in a medium with
radiation is transferred in a medium with
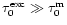 .
At first, a more effective increase of the radiation spectral width (in proportion to
.
At first, a more effective increase of the radiation spectral width (in proportion to
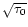 )
occurs as a result of the Doppler frequency redistribution in the Lorentz wings, which compensates, according to (12),
for the frequency difference
)
occurs as a result of the Doppler frequency redistribution in the Lorentz wings, which compensates, according to (12),
for the frequency difference
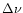 between the Ly
between the Ly and the FeII absorption lines. The diffusion broadening of the Ly
and the FeII absorption lines. The diffusion broadening of the Ly radiation spectrum in the HI region of the blob is limited exactly by the photoselective absorption of this radiation by FeII at
radiation spectrum in the HI region of the blob is limited exactly by the photoselective absorption of this radiation by FeII at
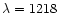 Å and intensity transformation in the blue wing of Ly
Å and intensity transformation in the blue wing of Ly into an intense UV fluorescence of FeII (see the bottom right-hand part of Fig. 2). Secondly, a more effective diffusive confinement of the Ly
into an intense UV fluorescence of FeII (see the bottom right-hand part of Fig. 2). Secondly, a more effective diffusive confinement of the Ly radiation takes place, resulting in a substantial increase, by at least
radiation takes place, resulting in a substantial increase, by at least
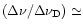 50 times, of its spectrum-integrated intensity. However, to carry out a quantitative analysis of the radiation transfer in the HI-to-HII boundary region, in which the HI and HII concentrations change sharply over a short distance of
50 times, of its spectrum-integrated intensity. However, to carry out a quantitative analysis of the radiation transfer in the HI-to-HII boundary region, in which the HI and HII concentrations change sharply over a short distance of
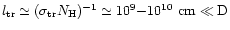 requires a special computer modeling, and this will be the subject of a special publication. So, in the case of blob B near
requires a special computer modeling, and this will be the subject of a special publication. So, in the case of blob B near 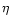 Car, the extreme spectral brightness of the Ly
Car, the extreme spectral brightness of the Ly radiation causes a very strong excitation of FeII ions contained in the blob matter as a result of the Ly
radiation causes a very strong excitation of FeII ions contained in the blob matter as a result of the Ly quasi-coincidence (
quasi-coincidence (
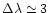 Å) with the absorption line of FeII in a low-lying metastable state. The subsequent extremely bright fluorescence on UV FeII lines ensures an effective radiative cooling of the blob.
Å) with the absorption line of FeII in a low-lying metastable state. The subsequent extremely bright fluorescence on UV FeII lines ensures an effective radiative cooling of the blob.
To conclude this brief consideration of the evolution of the spectrum and intensity of
the Ly radiation, let us emphasize that Ly
radiation, let us emphasize that Ly has a very high optical
density, so that one should take into account the diffusive frequency redistribution
far in the Lorentz wings. At the same time the transfer of the UV FeII radiation
(considered in Sect. 5 below) takes place at a more moderate optical density
has a very high optical
density, so that one should take into account the diffusive frequency redistribution
far in the Lorentz wings. At the same time the transfer of the UV FeII radiation
(considered in Sect. 5 below) takes place at a more moderate optical density
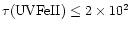 ,
so that the Lorentz wings take
no part in the evolution of the intensity and spectrum of UV FeII. This remark is
specially made to avoid confusion between similar designations for the two different
spectral lines, because in both cases (for the Ly
,
so that the Lorentz wings take
no part in the evolution of the intensity and spectrum of UV FeII. This remark is
specially made to avoid confusion between similar designations for the two different
spectral lines, because in both cases (for the Ly and the UV FeII line) the
transfer of radiation in an optically dense medium plays an important part.
and the UV FeII line) the
transfer of radiation in an optically dense medium plays an important part.


Up: The origin of the
Copyright ESO 2002
![]() Car
(for example, blob B) are
compact gas condensations (low-intensity compact ejecta with a high
hydrogen concentration
Car
(for example, blob B) are
compact gas condensations (low-intensity compact ejecta with a high
hydrogen concentration
![]() cm-3 and a Fe concentration of
cm-3 and a Fe concentration of
![]() cm-3).
cm-3).
![]() cm, and the distance from the central star is
cm, and the distance from the central star is
![]() cm. The diameter of the photosphere of the central star is
cm. The diameter of the photosphere of the central star is
![]() cm, and its effective temperature is
cm, and its effective temperature is
![]() K. These parameter values are preliminary. For
example, according to recent HST/STIS observations (T. Gull, private communication, April 2001), the distance
K. These parameter values are preliminary. For
example, according to recent HST/STIS observations (T. Gull, private communication, April 2001), the distance ![]() between the blob B and the central star is around
between the blob B and the central star is around
![]() cm, i.e. an order of magnitude smaller than derived from previous data.
The fact that the blob is located close enough to the central star is of importance for
our model. The dilution factor of the radiation from
cm, i.e. an order of magnitude smaller than derived from previous data.
The fact that the blob is located close enough to the central star is of importance for
our model. The dilution factor of the radiation from ![]() Car,
Car,
![]() ,
is around
10-6 - 10-5,
which is many orders of magnitude greater than that for a typical planetary nebula. For illustration, we present in Fig. 1 a schematic picture of a gas condensation having a spherical shape with an average diameter D (as judged from density) and an average volume concentration
,
is around
10-6 - 10-5,
which is many orders of magnitude greater than that for a typical planetary nebula. For illustration, we present in Fig. 1 a schematic picture of a gas condensation having a spherical shape with an average diameter D (as judged from density) and an average volume concentration ![]() of hydrogen atoms and ions and being located at the distance
of hydrogen atoms and ions and being located at the distance
![]() from the star.
from the star.
![\begin{figure}
\par\includegraphics[angle=-90,width=16cm,clip]{Fig1.eps}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg34.gif)
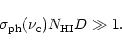
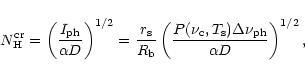
![]() at which the photoionization state of hydrogen is sustained at
at which the photoionization state of hydrogen is sustained at
![]() is defined by the expression
is defined by the expression
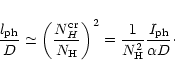
![]() the neutral component HI absorbs almost
all of the power
the neutral component HI absorbs almost
all of the power ![]() (in photons/s) of the Lyman-continuum radiation coming from the star:
(in photons/s) of the Lyman-continuum radiation coming from the star:
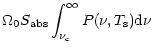
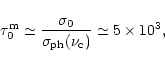
![]() radiation proves to be trapped in the HII region, but the diffusion confinement time is limited by the fact that the number of scattering events is limited because of the Doppler frequency redistribution of the scattered Ly
radiation proves to be trapped in the HII region, but the diffusion confinement time is limited by the fact that the number of scattering events is limited because of the Doppler frequency redistribution of the scattered Ly![]() photons. This redistribution makes them leave the trapping region relatively fast via the wings of the Doppler profile (Osterbrock 1967). Since the optical density
photons. This redistribution makes them leave the trapping region relatively fast via the wings of the Doppler profile (Osterbrock 1967). Since the optical density ![]() is limited to
is limited to
![]() ,
and the damping factor for Ly
,
and the damping factor for Ly![]() is
is
![]() ,
the optical density in the Lorentz wings is
,
the optical density in the Lorentz wings is
![]() ,
where we assume the Doppler spectral width to be
,
where we assume the Doppler spectral width to be
![]() cm-1 and the natural spectral width,
cm-1 and the natural spectral width,
![]() cm-1. Therefore, the Ly
cm-1. Therefore, the Ly![]() photons leave the HII region by diffusion while suffering an increase in the Doppler width
photons leave the HII region by diffusion while suffering an increase in the Doppler width
![]() by a factor of
by a factor of
![]() ,
so that the total power emitted by the surface of the blob into Ly
,
so that the total power emitted by the surface of the blob into Ly![]() is
is
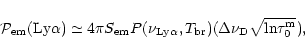
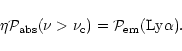
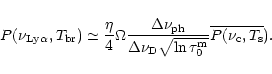
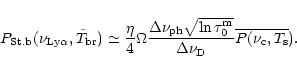
![]() of the HII/HI transition region is shallow:
of the HII/HI transition region is shallow:
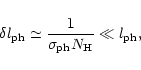
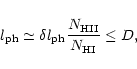
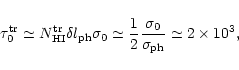
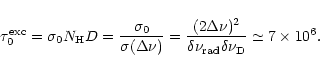
![]() of the passive HI region, at which the diffusion spectrum broadening necessary for the excitation of FeII is reached, is defined by the expression
of the passive HI region, at which the diffusion spectrum broadening necessary for the excitation of FeII is reached, is defined by the expression
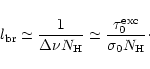
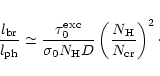
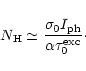
![\begin{figure}
\par\includegraphics[width=14cm,clip]{Fig3.EPS}\end{figure}](/articles/aa/full/2002/13/aah3002/Timg108.gif)
![]() radiation is transferred in a medium with
radiation is transferred in a medium with
![]() .
At first, a more effective increase of the radiation spectral width (in proportion to
.
At first, a more effective increase of the radiation spectral width (in proportion to
![]() )
occurs as a result of the Doppler frequency redistribution in the Lorentz wings, which compensates, according to (12),
for the frequency difference
)
occurs as a result of the Doppler frequency redistribution in the Lorentz wings, which compensates, according to (12),
for the frequency difference
![]() between the Ly
between the Ly![]() and the FeII absorption lines. The diffusion broadening of the Ly
and the FeII absorption lines. The diffusion broadening of the Ly![]() radiation spectrum in the HI region of the blob is limited exactly by the photoselective absorption of this radiation by FeII at
radiation spectrum in the HI region of the blob is limited exactly by the photoselective absorption of this radiation by FeII at
![]() Å and intensity transformation in the blue wing of Ly
Å and intensity transformation in the blue wing of Ly![]() into an intense UV fluorescence of FeII (see the bottom right-hand part of Fig. 2). Secondly, a more effective diffusive confinement of the Ly
into an intense UV fluorescence of FeII (see the bottom right-hand part of Fig. 2). Secondly, a more effective diffusive confinement of the Ly![]() radiation takes place, resulting in a substantial increase, by at least
radiation takes place, resulting in a substantial increase, by at least
![]() 50 times, of its spectrum-integrated intensity. However, to carry out a quantitative analysis of the radiation transfer in the HI-to-HII boundary region, in which the HI and HII concentrations change sharply over a short distance of
50 times, of its spectrum-integrated intensity. However, to carry out a quantitative analysis of the radiation transfer in the HI-to-HII boundary region, in which the HI and HII concentrations change sharply over a short distance of
![]() requires a special computer modeling, and this will be the subject of a special publication. So, in the case of blob B near
requires a special computer modeling, and this will be the subject of a special publication. So, in the case of blob B near ![]() Car, the extreme spectral brightness of the Ly
Car, the extreme spectral brightness of the Ly![]() radiation causes a very strong excitation of FeII ions contained in the blob matter as a result of the Ly
radiation causes a very strong excitation of FeII ions contained in the blob matter as a result of the Ly![]() quasi-coincidence (
quasi-coincidence (
![]() Å) with the absorption line of FeII in a low-lying metastable state. The subsequent extremely bright fluorescence on UV FeII lines ensures an effective radiative cooling of the blob.
Å) with the absorption line of FeII in a low-lying metastable state. The subsequent extremely bright fluorescence on UV FeII lines ensures an effective radiative cooling of the blob.
![]() radiation, let us emphasize that Ly
radiation, let us emphasize that Ly![]() has a very high optical
density, so that one should take into account the diffusive frequency redistribution
far in the Lorentz wings. At the same time the transfer of the UV FeII radiation
(considered in Sect. 5 below) takes place at a more moderate optical density
has a very high optical
density, so that one should take into account the diffusive frequency redistribution
far in the Lorentz wings. At the same time the transfer of the UV FeII radiation
(considered in Sect. 5 below) takes place at a more moderate optical density
![]() ,
so that the Lorentz wings take
no part in the evolution of the intensity and spectrum of UV FeII. This remark is
specially made to avoid confusion between similar designations for the two different
spectral lines, because in both cases (for the Ly
,
so that the Lorentz wings take
no part in the evolution of the intensity and spectrum of UV FeII. This remark is
specially made to avoid confusion between similar designations for the two different
spectral lines, because in both cases (for the Ly![]() and the UV FeII line) the
transfer of radiation in an optically dense medium plays an important part.
and the UV FeII line) the
transfer of radiation in an optically dense medium plays an important part.