A&A 385, 289-300 (2002)
DOI: 10.1051/0004-6361:20011818
X. Cao1,2 - H. C. Spruit2
1 - Shanghai Astronomical Observatory, Chinese Academy of
Sciences, 80 Nandan Road, Shanghai 200030, China,
and National Astronomical Observatories,
Chinese Academy of Sciences, China
2 -
Max-Planck-Institut für Astrophysik,
Postfach 1317, 85741
Garching bei München, Germany
Received 2 August 2000 / Accepted 18 December 2001
Abstract
We present a linear analysis of the stability of accretion
disks in which angular momentum is removed by the magnetic torque
exerted by a centrifugally driven wind. The effects of the dependence
of the wind torque on field strength and inclination, the
sub-Keplerian rotation due to magnetic forces, and the compression of
the disk by the field are included. A WKB dispersion relation
is derived for the stability problem. We find that the disk is
always unstable if the wind torque is strong. The
growth time scale of the instability can be as short as the orbital
time scale. The instability is mainly the result of the
sensitivity of the mass flux to changes in the inclination of the field
at the disk surface. Magnetic diffusion in the disk stabilizes if the
wind torque is small.
Key words: accretion, accretion disks - ISM: jets and outflows - magnetohydrodynamics (MHD)
Magnetically driven winds can remove angular momentum from the disk. The wind acceleration is sensitive to the inclination of magnetic field at the disk surface (Blandford & Payne 1982). If the magnetic field is advected inwards by the accreted matter, the field inclination at the disk surface is mainly determined by radial velocity of the matter in the disk. A small perturbation increasing the radial velocity causes the poloidal field to be bent closer to the disk surface, so that it gives rise to a higher mass loss. By the increased angular momentum loss, the radial velocity continues to increase. Thus an instability arises (LPP).
A number of factors have to be included in the analysis. If the magnetic field strength increases inward in the disk, it exerts an outward radial force providing partial support against gravity, so that the rotation of accretion flow is sub-Keplerian. The height of the disk is compressed by both the vertical component of gravitational force and the vertical pressure of the radial magnetic field component.
In principle, one can numerically calculate the disk structure and the magnetic field configuration in the disk simultaneously (Ogilvie & Livio 1998). For simplicity, in this work we use an approximate field configuration to estimate the scale-height of an isothermal disk compressed by the field.
We assume that the accreting matter is corotating with
magnetic field lines in the disk. This is an appropriate limit,
if the field is sufficiently strong (e.g. Ogilvie & Livio 2001).
The matter at the disk surface is centrifugally accelerated
along the magnetic field line anchored at the disk surface. The matter
corotates with the magnetic field line roughly till it approaches
Alfvén point. Beyond the Alfvén radius, the magnetic field exerts no
further torque on the escaping wind matter. The magnetic torque can be
estimated if the mass loss rate in the wind and the Alfvén radius are
known. The mass loss rate in the wind is governed by the position of slow
sonic point in the wind. The slow sonic speed is close to the sound
speed, if the Alfvén radius
![]() .
To avoid solving
the equation of radiative transfer in vertical direction of the disk,
we approximate the temperature of the disk to be a constant along the
vertical direction. The sonic point occurs roughly at
the maximum of the effective potential, if the temperature is not very
high.
.
To avoid solving
the equation of radiative transfer in vertical direction of the disk,
we approximate the temperature of the disk to be a constant along the
vertical direction. The sonic point occurs roughly at
the maximum of the effective potential, if the temperature is not very
high.
A fair assumption is that the pressure distribution in z direction, as measured along a field line, is hydrostatic between the footpoint and the sonic point. This provides an estimate of the density at the sonic point, and hence the mass loss rate.
For most of the stability analysis, a local approximation can be made
involving the values of physical quantities near the foot point of a
field line. The analysis, however, involves the magnetic torque in
an essential way, hence the value of the Alfvén radius ![]() for the field
line must be known. Since the Alfvén radius depends on the global field
configuration, not only on the field strength at the base of the field line,
it can be regarded as an external parameter for the stability analysis.
To minimize the number of additional parameters in the analysis, we assume
the field at the Alfvén surface to be roughly self-similar, varying as a
power of distance from the axis. The value of
for the field
line must be known. Since the Alfvén radius depends on the global field
configuration, not only on the field strength at the base of the field line,
it can be regarded as an external parameter for the stability analysis.
To minimize the number of additional parameters in the analysis, we assume
the field at the Alfvén surface to be roughly self-similar, varying as a
power of distance from the axis. The value of ![]() can then be
determined and we can evaluate the torque exerted by the wind on the
disk. It depends on the mass flux along the field line, which depends on the
density at the sonic point. This in turn depends sensitively on both the
temperature of the disk and on the inclination and strength of the field near
the disk.
can then be
determined and we can evaluate the torque exerted by the wind on the
disk. It depends on the mass flux along the field line, which depends on the
density at the sonic point. This in turn depends sensitively on both the
temperature of the disk and on the inclination and strength of the field near
the disk.
Changes in torque exterted cause the mass distribution in the disk to change. This in turn causes changes in the distribution of the field lines anchored in the disk. Since the mass and angular momentum loss rate on a field line depends sensitively on the field configuration (in particular the inclination), there is a strong intrinsic feedback, and it is the purpose of our investigation to see under which conditions this feedback leads to instability of the type proposed by LPP.
The stability problem is in principle global in nature, but we have localized it by a WKB approximation in a short wavelength limit, and the dispersion relation is then derived for the stability problem.
A further simplification we make is that the magnetic torque in a steady wind can also be applied in the perturbations. This assumption is valid if the time scale of the instability is much longer than the disk-wind coupling time scale. We discuss this further in the last section.
Since our focus is on the instability caused by the wind torque, we leave out angular momentum transported by the usual disk viscosity, so that viscous modes are also absent in stability analyses. The radial pressure gradient in the momentum equation is neglected for similar reasons, to avoid the presence of an acoustic mode. The circular motion of the disk in equilibrium is given by the balance between the gravity and radial magnetic force. We assume the magnetic field above the disk to be a potential field. The magnetic field configuration above the disk is determined from the values of the normal component of the field at the disk surface.
For the distribution of mass with distance above the midplane we assume the Gaussian distribution valid for an isothermal disk, but also include the effect of vertical confinement by the magnetic pressure on the disk thickness.
We assume the magnetic field above the disk to be a potential field. The magnetic field configuration above the disk is determined from the values of the normal component of the field at the disk surface. Strictly speaking, the presence of a magnetic torque will lead to an azimuthal component of the field. However, the azimuthal field component at the disk surface is always small compared with the radial component for any wind models as long as the Alfvén radius is far from the radius of the field footpoint at the disk mid-plane (see further discussion in Sect. 3.2). If the magnetic field strength inside the disk is suffiently weak, differential rotation acting on the r- and z-components will produce a time-dependent azimuthal field. Such a nonstationary state will lead to magnetic turbulence such as found in numerical simulations of an initially weak field (Hawley et al. 1995). The field we consider here, on the other hand, is a systematic poloidal field (i.e. crossing the disk plane), and sufficiently strong that Balbus-Hawley instability is suppressed. At this strength, the field is also sufficiently strong to enforce "isorotation'': constancy of the rotation rate along field lines. Though the origin of such fields is not as clear as the turbulent fields that evolve from initially weak seed fields, they are by far the most logical configurations for producing systematic outflows from accretion disks. Spruit et al. (1995), Stehle (1997) and Stehle & Spruit (2001) have shown that even surprisingly strong poloidal fields, approaching (a fraction of) equipartition with orbital kinetic energy, can still be stably anchored in a disk. These analyses did not include instabilities associated with magnetically driven outflows however, which are the subject of the present study.
From standard magnetic wind theory, we know that the
angular momentum flux along a field line is given by
![]() ,
where r is the
cylindrical radial coordinate,
,
where r is the
cylindrical radial coordinate, ![]() the Alfvén radius,
the Alfvén radius,
![]() the mass loss rate, and
the mass loss rate, and ![]() the rotation rate of the
footpoint at radius
the rotation rate of the
footpoint at radius ![]() on the disk. This is the total angular
momentum flux, including both the magnetic torque and the flux carried
by the mass itself. For the effect on the disk, only the magnetic torque
on the disk. This is the total angular
momentum flux, including both the magnetic torque and the flux carried
by the mass itself. For the effect on the disk, only the magnetic torque
![]() is consequential; evaluating it at the disk surface, and
counting both surfaces, we have
is consequential; evaluating it at the disk surface, and
counting both surfaces, we have
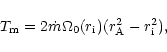 |
(1) |
The mass loss rate in the wind is governed by the position of the sonic
point:
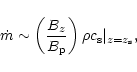 |
(2) |
As discussed in Sect. 2, the mass loss rate of wind from an
isothermal disk is estimated as
![\begin{displaymath}\dot m \sim \left({\frac {B_z}{B_{\rm p}}} \right)
\rho_{0}c_{\rm s}\exp[-(\Psi_{\rm es}-\Psi_{\rm ei})/c_{\rm s}^2],
\end{displaymath}](/articles/aa/full/2002/13/aah2372/img28.gif) |
(3) |
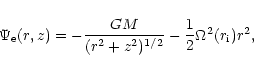 |
(4) |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{torq1.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg33.gif) |
Figure 1:
The magnetic torque as functions of the dimensionless
angular velocity of the disk and the magnetic inclination
|
| Open with DEXTER | |
The position of the sonic point can be estimated, if we know the shape
of the magnetic field lines between the footpoint and the sonic point.
In principle, the field line shape is computable by solving the
radial and vertical momentum equations together with suitable boundary
conditions. Analytic solutions are available only for two
extreme cases, the weak and strong field extremes.
We find that the
field line shapes are slightly different in these two extreme cases.
In the strong field case, the disk is compressed mainly by the
vertical component of magnetic force, and the shape is similar to
the Kippenhahn-Schlüter model (KS) (Kippenhahn & Schlüter 1957), valid for
an isothermal sheet suspended against gravity by a magnetic field.
The exact shape of the field lines depends on the thermal structure of the
disk. For our purposes an isothermal layer would be a sufficient model, and
the KS model applicable. Its analytic form is still a
bit too cumbersome however, so we have approximated it by the following
expression:
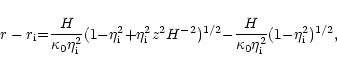 |
(5) |
We approximate the position of the sonic point
as the maximum of the effective potential along the magnetic field line.
The height above the disk of the sonic point at radius r0 of the disk
is then from using the potential (4) and the magnetic field line shape (5):
![$\displaystyle z_{\rm s}\simeq
{H\over {\eta_{\rm i}} }\Bigg\{\left[ {\frac
{\ka...
...^2H
{-}\kappa_0^2\eta_{\rm i}^2H}}\right ]^2{-}1{+}\eta_{\rm i}^2\Bigg\}^{1/2},$](/articles/aa/full/2002/13/aah2372/img38.gif) |
(6) |
To complete the estimate, we need the value of the scale height of
the disk H, which can be calculated from the vertical component
of momentum equation
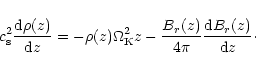 |
(7) |
![\begin{figure}
\par\includegraphics[width=7.8cm,height=7.8cm,clip]{torq2.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg42.gif) |
Figure 2: Same as Fig. 1, but for H/r=0.001. |
| Open with DEXTER | |
As a result of the magnetic
forces the distribution is not exactly the Gaussian distribution
of an isothermal disk.
In this case, we define the disk scale height H as
![]() ,
the disk scale height H can then be
evaluated numerically.
From these numerical values, we have constructed
a fitting formula used in the rest of the calculations
to represent the parameter dependence of the scale height H:
,
the disk scale height H can then be
evaluated numerically.
From these numerical values, we have constructed
a fitting formula used in the rest of the calculations
to represent the parameter dependence of the scale height H:
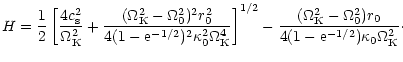 |
(8) |
![$\displaystyle \Delta\Psi_{\rm e} = \Psi_{\rm es}-\Psi_{\rm ei}
={1\over 2}\Omeg...
...i}^2+\eta_{\rm i}^2z_{\rm s}^2H^{-2})^{1/2}
-(1-\eta_{\rm i}^2)^{1/2}\right]^2.$](/articles/aa/full/2002/13/aah2372/img47.gif) |
(9) |
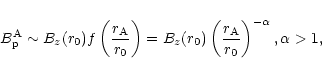 |
(10) |
At the Alfvén point, the Alfvén velocity is
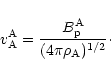 |
(11) |
Mass and magnetic flux conservation along a magnetic field line
requires
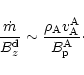 |
(12) |
![\begin{displaymath}r_{\rm A}\simeq \left[ {\frac { {B_{z}^{\rm d}}^2} {4\pi\dot ...
...
\right]^
{\frac {1}{\alpha+1}}r_0^{\frac {\alpha}{\alpha+1}}.
\end{displaymath}](/articles/aa/full/2002/13/aah2372/img54.gif) |
(13) |
We define dimensionless quantities by
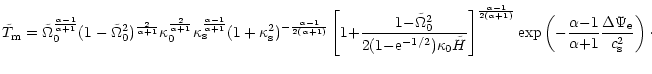 |
(15) |
With increasing field strength, the rotation of the disk becomes
more sub-Keplerian. Though the increasing field strength itself
increases the torque through the increasing Alfvén radius
(second factor in Eq. (15)), the lower rotation of the footpoints
also increases the potential barrier that the wind has to overcome
(last factor). In many cases of interest, an increasing field strength
will reduce the magnetic torque (e.g. Shu 1991; Ogilvie &
Livio 1998, 2001). In the following, we use the rotation rate relative to Keplerian,
![]() ,
as measure of the field strength. Figures 1 and 2
show expression (15) for the cases
,
as measure of the field strength. Figures 1 and 2
show expression (15) for the cases
![]() and
and
![]() .
.
The magnetic torque ![]() exerted on the unit surface
area of the disk is given by
exerted on the unit surface
area of the disk is given by
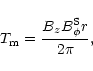 |
(16) |
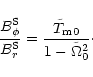 |
(17) |
As discussed in Sect. 2, we neglect the usual disk viscosity
in the problem. Torques due to the magnetic wind are therefore the only
source of angular momentum loss of the disk material, and in their absence
the mass flux through the disk vanishes. The mass conservation and angular
momentum equations for the disk are then
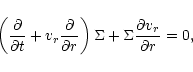 |
(18) |
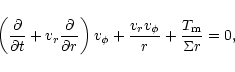 |
(19) |
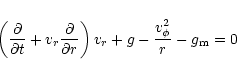 |
(20) |
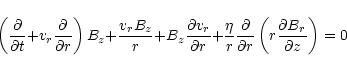 |
(21) |
As discussed in Sect. 2, a potential field above the disk is
assumed, so that the stream function of the field satisfies
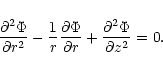 |
(22) |
As discussed in Sect. 2, the problem can be localized by
a WKB approximation in a short wavelength limit.
The perturbed stream function is still given by Eq. (22):
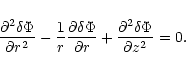 |
(23) |
Equation (23) has separable solutions
![]() ,
where F(r) satisfies
,
where F(r) satisfies
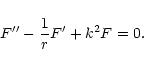 |
(24) |
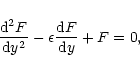 |
(25) |
Denote Eulerian perturbations of a quantity q by ![]() ,
Lagrangian
perturbations by an index 1, and the equilibrium state by an index 0.
The perturbed fraction of the stream function is:
,
Lagrangian
perturbations by an index 1, and the equilibrium state by an index 0.
The perturbed fraction of the stream function is:
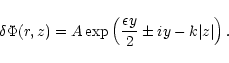 |
(26) |
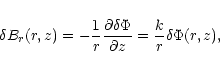 |
(27) |
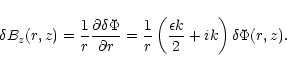 |
(28) |
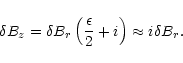 |
(29) |
| + | (30) | ||
| + | (31) |
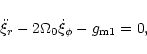 |
(32) |
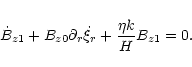 |
(33) |
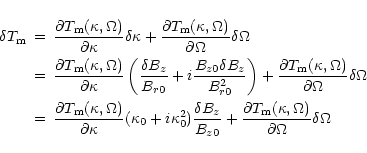
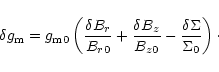 |
(34) |
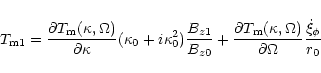 |
(35) |
![\begin{displaymath}g_{\rm m1}= g_{\rm m0}\left[(1-i\kappa_0){{B_{z1}}\over {B_{z0}}}
+\partial_r\xi_r\right],
\end{displaymath}](/articles/aa/full/2002/13/aah2372/img102.gif) |
(36) |
| + | 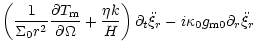 |
||
| + | ![$\displaystyle \left[2\Omega_{0}(2\Omega_{0}+S)
+{\frac {\eta k} {\Sigma_0r^2H} } {\frac {\partial T_{\rm m}}{\partial\Omega}}
\right]\ddot\xi_{r}$](/articles/aa/full/2002/13/aah2372/img105.gif) |
||
| - | 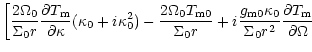 |
||
| + | ![$\displaystyle \left.{\frac {\eta k g_{\rm m0}} {H}}\right]\partial_r\dot\xi_r
+{\frac {2\eta k\Omega_0} {H}}(2\Omega_0+S)\dot\xi_r$](/articles/aa/full/2002/13/aah2372/img107.gif) |
||
| - | 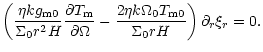 |
(37) |
We write the perturbed quantities as
![\begin{displaymath}\xi_{r} \sim \exp[i(\omega t+kr)].
\end{displaymath}](/articles/aa/full/2002/13/aah2372/img109.gif)
| - | 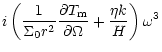 |
||
| - | ![$\displaystyle \left[\kappa_{0}g_{\rm m0}k+2\Omega_{0}(2\Omega_{0}+S)
+{\frac {\...
...k}{\Sigma_0r^2H}} {\frac {\partial T_{\rm m}}{\partial \Omega}}
\right]\omega^2$](/articles/aa/full/2002/13/aah2372/img112.gif) |
||
| + | 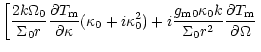 |
||
| - | ![$\displaystyle \left.{2k\Omega_{0}{T_{\rm m0}}\over {\Sigma_{0}r}}
+{\frac {\eta k^2 g_{m0}}{H}}
+i{\frac {2\eta k\Omega_0}{H}}(2\Omega_0
+S)\right]\omega$](/articles/aa/full/2002/13/aah2372/img114.gif) |
||
| - | 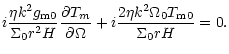 |
(38) |
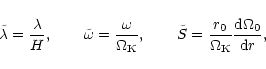
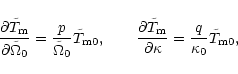
Equation (38) becomes
| - | 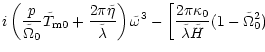 |
||
| + | 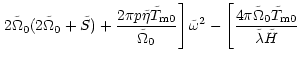 |
||
| - | 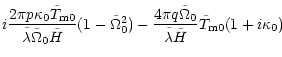 |
||
| - | ![$\displaystyle \left.{\frac {4\pi^2\tilde\eta}{\tilde\lambda^2\tilde H}}
(1-\til...
...a \tilde\Omega_0}{\tilde\lambda}}
(2\tilde\Omega_0+\tilde S)\right]\tilde\omega$](/articles/aa/full/2002/13/aah2372/img123.gif) |
||
| - | 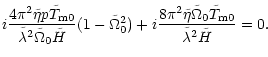 |
(40) |
The dispersion relation contains several small parameters, since
a number of conditions have to be satisfied for consistence with the
assumptions made. For a local approximation to be valid, we must have
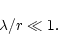 |
(41) |
| (42) |
The nature of the unstable modes can be explored by looking
at limiting cases. We can look at the
case where the magnetic torque is weak,
![]() .
Assuming
.
Assuming
![]() and
and
![]() to be the same order
and ignoring quadratic and higher terms, the last two terms
in Eq. (40) containing
to be the same order
and ignoring quadratic and higher terms, the last two terms
in Eq. (40) containing
![]() can be omitted. The dispersion relation reduces to
a third-order equation. Let
can be omitted. The dispersion relation reduces to
a third-order equation. Let
![]() ,
it can then
be separated into two equations:
,
it can then
be separated into two equations:
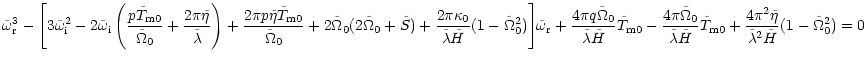 |
(43) |
| - | 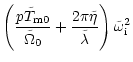 |
||
| - | ![$\displaystyle \left[ 3\tilde\omega_{\rm r}^2
{-}2\tilde\Omega_0(2\tilde\Omega_0...
...2\pi p\tilde\eta\tilde T_{\rm m0}}
{\tilde\Omega_0}}\right]\tilde\omega_{\rm i}$](/articles/aa/full/2002/13/aah2372/img139.gif) |
||
| + | 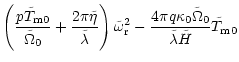 |
||
| - | 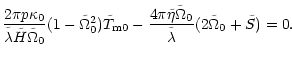 |
(44) |
We now analyze the marginal stability, i.e.,
![]() .
In the absence of the magnetic torque (
.
In the absence of the magnetic torque (
![]() ),
Eqs. (43) and (44) reduce to
),
Eqs. (43) and (44) reduce to
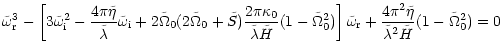 |
(45) |
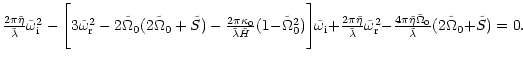 |
(46) |
![\begin{displaymath}\tilde\omega_{\rm r}=\pm
\left[2\tilde\Omega_0(2\tilde\Omega_0+\tilde S)\right]^{1/2},
\end{displaymath}](/articles/aa/full/2002/13/aah2372/img150.gif) |
(47) |
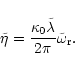 |
(48) |
Further progress can be made if we assume that the diffusivity is small, and
by looking at conditions near marginal stability. Treating
![]() it
as a small quantity of the same order as the other small quantities, i.e.
it
as a small quantity of the same order as the other small quantities, i.e.
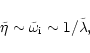
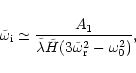 |
(49) |
| (50) | |
| A1= |
(51) |
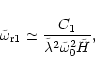 |
(52) |
 |
(53) |
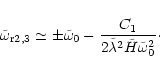 |
(54) |
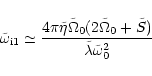 |
(55) |
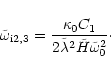 |
(56) |
The stability condition
for the inward traveling wave mode is
![\begin{displaymath}\tilde\eta<{\frac {\kappa_0\tilde\lambda}{2\pi}}
[2\tilde\Omega_0(2\tilde\Omega_0+\tilde S)]^{1/2}.
\end{displaymath}](/articles/aa/full/2002/13/aah2372/img168.gif) | (57) |
We now include the magnetic torque. In this section we treat it
as a small quantity of same order as the other small quantities in the
problem. In the absence of the magnetic diffusion (
![]() ),
Eqs. (43) and (44) reduce to
),
Eqs. (43) and (44) reduce to
| - | 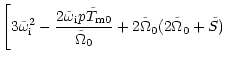 |
||
| + | 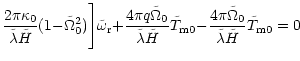 |
(58) |
| - | ![$\displaystyle {\frac {p\tilde T_{\rm m0}}{\tilde\Omega_0}}
\tilde\omega_{\rm i}...
...\over{\tilde\lambda\tilde H}}(1{-}\tilde\Omega_0^2)
\right]\tilde\omega_{\rm i}$](/articles/aa/full/2002/13/aah2372/img177.gif) |
||
| + | 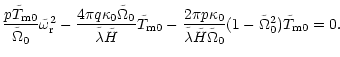 |
(59) |
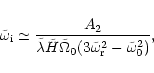 |
(60) |
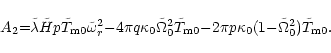 |
(61) |
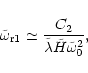 |
(62) |
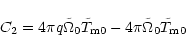 |
(63) |
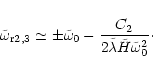 |
(64) |
The first mode, ![]() ,
can be understood by setting the magnetic
torque to zero. Equations (52) and (55) show that the wave frequency and
the damping rate are then proportional to the diffusivity
,
can be understood by setting the magnetic
torque to zero. Equations (52) and (55) show that the wave frequency and
the damping rate are then proportional to the diffusivity ![]() .
This mode is stabilized by the magnetic diffusion.
.
This mode is stabilized by the magnetic diffusion.
In the limit of
![]() and
and
![]() ,
the pair of modes 2, 3 has the same frequency (cf. Eqs. (54) & (64))
,
the pair of modes 2, 3 has the same frequency (cf. Eqs. (54) & (64))
![\begin{displaymath}\tilde\omega_{\rm r2,3}\simeq \pm
\left [2\tilde\Omega_0(2\ti...
...\Omega_0^2){{2\pi\kappa_0}\over{\tilde\lambda}}
\right]^{1/2}.
\end{displaymath}](/articles/aa/full/2002/13/aah2372/img188.gif) |
(67) |
The growth rates of the three modes (65, 66) are all
proportional to the magnetic torque. Hence they all qualify as instabilities
caused by the coupling between the disk and the outflow, if their
![]() are
negative. The dependence of the torque on the rotation rate is positive (p>0),
while the quantity q is negative (torque decreases as field inclination
with respect to the disk plane increases).
If the magnetic field strength in the disk is not strong enough to signifiantly
affect the rotation rate
are
negative. The dependence of the torque on the rotation rate is positive (p>0),
while the quantity q is negative (torque decreases as field inclination
with respect to the disk plane increases).
If the magnetic field strength in the disk is not strong enough to signifiantly
affect the rotation rate ![]() ,
the second term in (65) is small,
and the sign of
,
the second term in (65) is small,
and the sign of
![]() is determined by the first term, involving q.
Since q<0,
is determined by the first term, involving q.
Since q<0,
![]() ,
so this mode tends to be
unstable except perhaps when magnetic support of the disk becomes
significant. Its actual stability depends on the values of the other
parameters. In the following, we analyze this mode more quantitatively.
The two oscillatory modes
,
so this mode tends to be
unstable except perhaps when magnetic support of the disk becomes
significant. Its actual stability depends on the values of the other
parameters. In the following, we analyze this mode more quantitatively.
The two oscillatory modes
![]() ,
which represent
traveling waves, are stable. These two modes are not specifically related
to the magnetic wind torque, and we will not discuss them further.
,
which represent
traveling waves, are stable. These two modes are not specifically related
to the magnetic wind torque, and we will not discuss them further.
We obtain growth rate of the instabilities by solving Eq. (40)
numerically. For the shear rate ![]() we take the Keplerian value
S=-3/2.
we take the Keplerian value
S=-3/2.
The problem is described by the dimensionless
disk scale-height ![]() ,
the angular velocity of accretion flow
,
the angular velocity of accretion flow
![]() which is a measure of the magnetic field strength,
the inclination of magnetic field
which is a measure of the magnetic field strength,
the inclination of magnetic field
![]() at the disk surface, and the dimensionless
magnetic diffusivity
at the disk surface, and the dimensionless
magnetic diffusivity
![]() .
The magnetic torque is sensitive to the inclination of magnetic
field
.
The magnetic torque is sensitive to the inclination of magnetic
field ![]() and the angular velocity of accretion flow
and the angular velocity of accretion flow
![]() ,
which depends on the field strength
through its contribution to support of the disk against gravity.
We take the self-similar index
,
which depends on the field strength
through its contribution to support of the disk against gravity.
We take the self-similar index ![]() of the
magnetic field shape to be 4 in the following.
In Figs. 1 and 2, the magnetic torque as functions
of
of the
magnetic field shape to be 4 in the following.
In Figs. 1 and 2, the magnetic torque as functions
of ![]() and
and
![]() is plotted for different
values of the dimensionless disk scale-height
is plotted for different
values of the dimensionless disk scale-height ![]() .
For small disk scale-height, i.e., if the
temperature of gas in accretion disk is low, a magnetic torque is
present only if the angular velocity is close to Keplerian velocity
and the magnetic field inclination angle to the disk surface is low
(low
.
For small disk scale-height, i.e., if the
temperature of gas in accretion disk is low, a magnetic torque is
present only if the angular velocity is close to Keplerian velocity
and the magnetic field inclination angle to the disk surface is low
(low ![]() ,
see Fig. 2).
The numerically determined stability boundaries for the neutral
wave mode are plotted in Figs. 3 and 4.
,
see Fig. 2).
The numerically determined stability boundaries for the neutral
wave mode are plotted in Figs. 3 and 4.
Examples of the growth rate of the neutral wave mode
for different parameter values are shown in Figs. 5-11.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{mist1.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg201.gif) |
Figure 3:
The stability condition of the neutral wave mode,
for disk thickness H/r=0.01
and wavelength
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{mist2.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg202.gif) |
Figure 4: Same as Fig. 3, but for H/r=0.001. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{ist1.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg204.gif) |
Figure 5:
The growth rate of the instability as functions of
magnetic field inclination |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{ist2.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg205.gif) |
Figure 6:
Same as Fig. 5, but for different value of angularvelocity:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{ist3.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg206.gif) |
Figure 7:
Same as Fig. 5, but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{ist4.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg207.gif) |
Figure 8:
Same as Fig. 5, but for
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{ist5.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg208.gif) |
Figure 9: Same as Fig. 6, but for H/r=0.001. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{ist6.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg209.gif) |
Figure 10:
Same as Fig. 6, but without magnetic diffusion, i.e.,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,height=8cm,clip]{ist7.ps}\par\end{figure}](/articles/aa/full/2002/13/aah2372/Timg210.gif) |
Figure 11:
Same as Fig. 8, but without magnetic diffusion,
|
| Open with DEXTER | |
We have presented a linear stability analysis of disks with magnetically driven winds, and confirm the instability by the mechanism proposed by LPP.
In the presence of a strong magnetic field, the disk is compressed by the vertical component of gravitational force as well as vertical magnetic pressure, and the vertical structure of the disk is significantly altered, which affects the position of sonic point and the wind torque. In this strong field case, the angular velocity of accretion flow significantly deviates from the Keplerian velocity due to the radial magnetic force, and the magnetic torque is then negligible for any magnetic field inclination angle (see Figs. 1 and 2, see also Ogilvie & Livio 1998). We have taken these effects into account in present investigation.
The system of equations analyzed has four modes. In the absence of a magnetic field, two are a neutral displacements. One of these two is not specifically related to the magnetic wind torque, and we have excluded it from quantitative analysis. The other has a frequency proportional to the magnetic torque (real and imaginary parts of the frequency are of the same order of magnitude), it can become unstable.
The final two modes represent an inward and an outward traveling wave. The restoring force in the wave is a combination of the coriolis force (epicyclic motion) and the magnetic forces. Both inward and outward traveling waves are stable in the range of validity of our assumptions.
In Fig. 5, the
growth rate of the instability is plotted for angular velocity
very close to Keplerian velocity (
![]() ), which may
approximate the case considered in LPP.
The disk becomes more unstable if the angular velocity of the flow is
close to Keplerian (see Figs. 5-8).
For high inclination angles of magnetic field line with respect
to the surface of the disk (large
), which may
approximate the case considered in LPP.
The disk becomes more unstable if the angular velocity of the flow is
close to Keplerian (see Figs. 5-8).
For high inclination angles of magnetic field line with respect
to the surface of the disk (large ![]() ), the magnetic torque is
very small. Instability is then suppressed by magnetic diffusion.
), the magnetic torque is
very small. Instability is then suppressed by magnetic diffusion.
The magnetic torque makes
the disk unstable, while magnetic diffusion has a stabilizing effect,
suppressing instability at low
![]() and/or high
and/or high ![]() (see Figs. 3 and 4). Comparing Figs. 6 and 9, we see that the disk
is less unstable in low temperature case (
(see Figs. 3 and 4). Comparing Figs. 6 and 9, we see that the disk
is less unstable in low temperature case (
![]() )
while
the instability occurs for lower values of
)
while
the instability occurs for lower values of ![]() .
.
To see the effect of magnetic diffusion, Figs. 10 and
11 show the growth rates for the cases with
![]() .
In the
absence of magnetic diffusion, the disk is always unstable, though
the growth rates can be very small.
.
In the
absence of magnetic diffusion, the disk is always unstable, though
the growth rates can be very small.
The physical reason for the instability found here has been described in LPP (see discussion in Sect. 2). A perturbation increasing vr causes the poloidal field to be bent close to the disk plane, as the field is advected inwards by the accreting matter. This tends to increase the mass flow along the field. There is also an opposing effect, however. As the poloidal magnetic field is bent towards the disk plane, the radial curvature force on the disk (opposite to gravitational force increases). Due to this increased support against gravity, the rotation rate of the field line decreases. As a result, the "potential barrier'' for mass flowing along the field line is larger, decreasing the mass flux and magnetic torque. The instability decreases with increasing field strength through its effect on the rotation rate, since the instability is driven by the magnetic torques. We find that the inclination of the magnetic field still has the strongest influence on the magnetic torque, and dominates over the change in the potential barrier.
Since the instability is caused by the magnetic torque by the
centrifugally driven wind from the disk, the
instability disappears as the magnetic torque vanishes
(compare the instability growth rate with the magnetic torque in
Figs. 1 and 2). The disk is stable
without a magnetic torque. The modes are oscillations damped
by magnetic diffusion, if the magnetic torque is small.
If the magnetic torque is large, the instability time scale is comparable
with the dynamical time scale of the disk, and the instability is not
much affected by magnetic diffusion (compare Figs. 6 and 10).
From the marginal stability condition shown in Figs. 3 and 4,
one sees that the disk is generally stabilized by diffusion
in the lower right corner of the ![]() -
-
![]() space, i.e. corresponding to low magnetic torques.
We find that the instability is insensitive to the
perturbation wavelength.
space, i.e. corresponding to low magnetic torques.
We find that the instability is insensitive to the
perturbation wavelength.
Associated with the perturbations in the disk are changes of the field configuration above the disk. These affect the acceleration of the wind, and hence the wind torque. In our analysis, we have taken the response of the wind torque to these changes to be instantaneous. This is motivated by the fact that the magnetic torque acts on the disk surface, and changes as soon as the azimuthal field component at the surface changes. This is perhaps somewhat contrary to the impression that one might have based on the steady wind model. In the steady wind model, the torque is often pictured as "effectively acting'' at the Alfvén surface. In reality, the torque is constant along the field line, hence acts equally at the disk surface. When changes due to motions in the disk take place, changes in the torque travel up at the Alfvén speed and are first felt in disk itself.
The actual propagation of these torque changes has not
been considered here, since its time scale is short, of the order of the
Alfvén travel time over the disk thickness. The time scale
![]() for an Alfvén wave to travel over the scale-height is of the order
for an Alfvén wave to travel over the scale-height is of the order
![]() ,
which is short except
for weak fields. The time scale for Alfvén wave traveling from
the disk surface to the Alfvén point in the wind is in fact shorter than
this,
,
which is short except
for weak fields. The time scale for Alfvén wave traveling from
the disk surface to the Alfvén point in the wind is in fact shorter than
this, ![]()
![]() .
The disk-wind coupling time scale is therefore of
the order of the disk dynamical time (Wardle & Königl 1993; Königl &
Wardle 1996).
The present analyses are valid if the instability growth time scale is much
longer than the disk-wind coupling time scale. This is the case since for
weak fields, where the coupling time is long, the growth time of the
instability itself is also long.
.
The disk-wind coupling time scale is therefore of
the order of the disk dynamical time (Wardle & Königl 1993; Königl &
Wardle 1996).
The present analyses are valid if the instability growth time scale is much
longer than the disk-wind coupling time scale. This is the case since for
weak fields, where the coupling time is long, the growth time of the
instability itself is also long.
In order to check on the effect of finite Alfvén travel times in the
disk-wind coupling process on the
instability properties of the disk, we have done a test calculation
with a simplified description of this effect. In this calculation,
we manually induce a time delay
of the dynamical time scale of the disk on the wind torque:
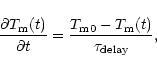 |
(68) |
The nonlinear evolution of the instability analyzed gas to be studied by numerical simulations. Some such simulations have already been reported by Agapitou & Papaloizou (2001, in preparation).
Acknowledgements
This work was done in the context of the TMR Network "accretion onto black holes'' (European Commission grant ERBFMRX-CT98-0195). XC thanks for support from the MPG-CAS exchange program, the NSFC under grant Nos. 19703002, 10173016, the NKBRSF (No. G1999075403), and the Pandeng Project.