

Up: Atmospheric circulation and tides
Here we explore the implications of day-night temperature
variations on the abundances of a condensing species. Suppose
that on the day side, a
given condensate (e.g. iron) condenses at a pressure level
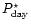 and a corresponding temperature
and a corresponding temperature
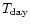 .
If the temperature
on the night side
.
If the temperature
on the night side
 is smaller, at what pressure
is smaller, at what pressure
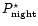 will condensation take place?
will condensation take place?
Assuming an ideal gas, we write the Clausius-Clapeyron
equation as
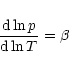 |
(A.1) |
where p is the partial pressure of saturation of the condensing
species and
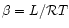 is the ratio of the latent
heat of condensation L to the thermal energy
is the ratio of the latent
heat of condensation L to the thermal energy 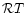 .
For most
condensing species of significance here,
.
For most
condensing species of significance here,
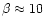 .
We
furthermore assume that
.
We
furthermore assume that 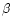 is independent of T and P, which
introduces only a slight error in our estimates.
is independent of T and P, which
introduces only a slight error in our estimates.
By definition, on the day side, the saturation abundance of the
condensing species, x=p/P is maximal and equal to 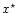 at
at
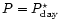 .
On the other hand, the night side temperature is
lower and the abundance becomes:
.
On the other hand, the night side temperature is
lower and the abundance becomes:
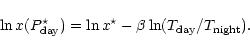 |
(A.2) |
In order to reach condensation, i.e. 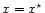 ,
one has to penetrate
deeper into the atmosphere. Equation (A.1) implies that
,
one has to penetrate
deeper into the atmosphere. Equation (A.1) implies that
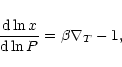 |
(A.3) |
and hence, on the night side,
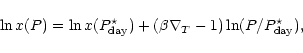 |
(A.4) |
assuming that 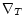 is constant.
Using Eq. (A.2), one obtains the condensation pressure
on the night side:
is constant.
Using Eq. (A.2), one obtains the condensation pressure
on the night side:
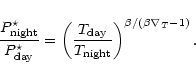 |
(A.5) |
Using
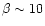 ,
,
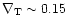 and
and
 ,
one finds
,
one finds
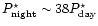 ,
a very significant
variation of the condensation pressure. This implies that air flowing
on constant pressure levels around the planet would lead to a rapid
depletion of any condensing species on the day side, compared to what
would be predicted from chemical equilibrium calculations. This can
potentially also remove important absorbing gases from the day side,
as in the case of TiO, which can be removed by CaTiO3 condensation,
or Na, removed by Na2S condensation (Lodders 1999).
Of course, most of the variation depends on the exponential factor
,
a very significant
variation of the condensation pressure. This implies that air flowing
on constant pressure levels around the planet would lead to a rapid
depletion of any condensing species on the day side, compared to what
would be predicted from chemical equilibrium calculations. This can
potentially also remove important absorbing gases from the day side,
as in the case of TiO, which can be removed by CaTiO3 condensation,
or Na, removed by Na2S condensation (Lodders 1999).
Of course, most of the variation depends on the exponential factor
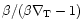 ,
which is infinite in the limit when the
atmospheric temperature profile and the condensation profile are
parallel to each other.
,
which is infinite in the limit when the
atmospheric temperature profile and the condensation profile are
parallel to each other.
In the discussion, we implicitly assumed
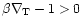 ;
however,
when the atmosphere is close to an isotherm, this factor can become
negative. In this case the day/night effect is even more severe, as
the condensing species is entirely removed from this quasi-isothermal
region.
;
however,
when the atmosphere is close to an isotherm, this factor can become
negative. In this case the day/night effect is even more severe, as
the condensing species is entirely removed from this quasi-isothermal
region.


Up: Atmospheric circulation and tides
Copyright ESO 2002
![]() and a corresponding temperature
and a corresponding temperature
![]() .
If the temperature
on the night side
.
If the temperature
on the night side
![]() is smaller, at what pressure
is smaller, at what pressure
![]() will condensation take place?
will condensation take place?
![]() at
at
![]() .
On the other hand, the night side temperature is
lower and the abundance becomes:
.
On the other hand, the night side temperature is
lower and the abundance becomes:
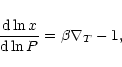
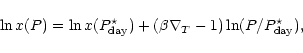
![]() ;
however,
when the atmosphere is close to an isotherm, this factor can become
negative. In this case the day/night effect is even more severe, as
the condensing species is entirely removed from this quasi-isothermal
region.
;
however,
when the atmosphere is close to an isotherm, this factor can become
negative. In this case the day/night effect is even more severe, as
the condensing species is entirely removed from this quasi-isothermal
region.