A&A 385, 55-61 (2002)
DOI: 10.1051/0004-6361:20020145

Analysis of the long-term polarization behaviour of BL Lac[*]

V. A. Hagen-Thorn1,2 - E. G. Larionova1 - S. G. Jorstad1,3 - C.-I. Björnsson4 - V. M. Larionov1,2


1 - Astronomical Institute of St. Petersburg State University, Universitetsky pr. 28, 198504 St. Petersburg, Russia
2 - Isaac Newton Institute of Chile, St. Petersburg Branch, Russia
3 - Institute for Astrophysical Research, Boston University, 725 Commonwealth Ave., Boston, MA 02215, USA
4 - Stockholm Observatory, 13336 Saltsjöbaden, Sweden

Received 29 August 2001 / Accepted 22 January 2002

Abstract
An analysis is performed of polarimetric and photometric observations of BL Lac carried out in 1969-1991 at the Astronomical Institute of St. Petersburg State University. The distribution of polarization directions certainly points to the existence of the preferred direction of polarization ( $\theta= 22\hbox{$^\circ$ }$) close to the direction of the jet observed by VLBI. High polarization degree and colorimetric data are evidence of the synchrotron nature of the variable source. The relative Stokes parameters are distributed normally over some mean value. The correlations between different parameters characterizing the flux density and polarization of the central point source allow us to consider that in BL Lac there is a continually acting source of polarized radiation on which the sources with randomly distributed polarization directions are superimposed.

Key words: BL Lac objects: individual: BL Lac - techniques: polarimetric


1 Introduction

Polarization variability is one of the main properties of blazars. The variations occur on different time scales: from dozens of years to hours and even minutes. The nature of these variations may be diverse. Usually, long-term photometric variability is explained as arising in jets in synchrotron sources. Then polarization variability may give information on the variations of the magnetic field in the jet and other properties of these sources. Rapid variability could be caused by flares in an accretion disk near the central engine. In this case the flares would most likely be of thermal origin and the polarization due to scattering. The polarization variability (if it exists) would then provide information on the geometric parameters of the scattering matter. However, a synchrotron nature of the emission in flares is not excluded. In either case an investigation of the optical polarization variability is very important tool for studying of properties of active galactic nuclei (AGNs) in the regions close to the central engine.

BL Lac is one of the most well-studied blazars. Several international campaigns (e.g. Moore et al. 1982; Brindle et al. 1985) have been organized to investigate its variability. However, polarization data were obtained only in a few of these. It is essential to note that such campaigns give information about variability on short time scales but are less useful for studying the long-term behaviour.

At the Astronomical Institute of St. Petersburg State University polarimetric observations of BL Lac were begun in 1969. The prolonged series of such observations include data for 1969-1991. The results have been published in two papers (Hagen-Thorn et al. 1984, 1994). The preliminary results of the analysis of part of these data may be found in two other papers (Hagen-Thorn et al. 1985, 1986). Here we analyze the entire mass of observational data that include the results of polarimetric observations on 517 dates.

2 Observational data and their processing

All polarimetric data were obtained with a photoelectric polarimeter at the 48-cm reflecting telescope of the Byurakan station of the Astronomical Institute. A photomultiplier with a multialkaline cathode was used in all observations, usually performed without filters. More details may be found in Hagen-Thorn et al. (1984).


  \begin{figure} \psfig{figure=ms1853f1.eps,width=120mm,clip=}\end{figure} Figure 1:  The variations with time of several intensity and polarization parameters for point source; the mean values of some of these are shown by dotted lines.
Open with DEXTER

The value of polarimetric observations strongly increases when these are accompanied by photometric data. Unfortunately, we have very few simultaneous photoelectric estimations of the brightness of BL Lac; however, the object was intensively observed in our photographic monitoring program of AGNs in B band (Johnson system) with typically 3-5 photographic estimates of BL Lac's brightness per night. The data have been published in a series of papers in Contributions of the Astronomical Observatory of St. Petersburg University (see Hagen-Thorn et al. 1991 and references therein). These data, as well as data taken from the literature, allow us to construct the combined light curve of BL Lac that we use below.

At this point we make some important remarks:

(i)
Though the galactic latitude of BL Lac is low ( $b = - 12\hbox{$^\circ$ }$) and it lies behind a diffuse molecular cloud (Marscher et al. 1991), the interstellar polarization along the line of sight is less than 0.8% (Moore et al. 1982). We ignore this since the observed polarization is usually much higher;
(ii)
Polarimetric observations were made without filters over a wide spectral band. Because the wavelength dependence of polarization is small and the effective wavelength in observations without filters (0.51$\mu$) is sufficiently close to the effective wavelength of B band (0.43$\mu$), we consider that the observed polarization represents that in the B band;
(iii)
Because of aberrations of the telescope, seeing, scattering in the emulsion, etc., we consider that the photographic data represent the brightness of the object within a circle of diameter $\sim$7 $^{\prime\prime}$. Photoelectric data were obtained with diaphragms of 19 $^{\prime\prime}$ and 27 $^{\prime\prime}$. Therefore, fluxes (we use this term henceforth for brevity instead of "flux densities'') within these diaphragms are slightly higher than fluxes found from photographic magnitudes. (To transform magnitudes to fluxes we use the absolute calibration of Mead et al. 1990.) According to Kinman (1975), because of contamination by the light of the underlying galaxy, the difference in fluxes between diaphragms 7 $^{\prime\prime}$ and 19 $^{\prime\prime}$ (or 27 $^{\prime\prime}$) is 0.18 mJy (or 0.26 mJy). Hence, these corrections were applied when finding absolute Stokes parameters ( $Q_{\rm obs}, U_{\rm obs}$);
(iv)
We assume that only the point-like source is responsible for the polarization; therefore the absolute Stokes parameters found $Q_{\rm obs}$ and $U_{\rm obs}$ are those for the point source ( $Q_{\rm p} = Q_{\rm obs}, U_{\rm p} = U_{\rm obs}$);
(v)
To find the values of the B-band point-source flux density $I_{\rm p}$ we reduced photographically observed fluxes by 0.30 mJy to correct for the estimated flux of the host galaxy within the 7 $^{\prime\prime}$ diaphragm (see Hagen-Thorn et al. 1985, although we use an update value for this correction). These corrected flux values $I_{\rm p}$ were used for the calculation of the relative Stokes parameters $p_{x,\rm p}, p_{y,\rm p}$ and then of the degree of polarization of the point source. Table 1 contains all the data for the point source of BL Lac. Figure 1 summarizes the variations with time of several intensity and polarization parameters. Henceforth, we drop the subscript "p'' - "point'' since, with the exception of the next section, we shall deal only with the data for the point source.

3 Distribution of polarization angles

The histogram for observed directions of polarization (the preferred direction of the electric vector) $\theta$ is presented in Fig. 2a. Here we use the data for all 517 nights of the polarimetric observations (the number of nights with simultaneous estimates of the total intensity and polarization parameters is reduced to 451 because the brightness estimates are not available for some nights). We see that the bulk of data lies near $\theta\approx 20\hbox{$^\circ$ }$. Comparison with Fig. 1 shows that this is not due to uneven temporal spacing of the observations. Therefore, we assert that BL Lac has a preferred direction of polarization in the optical region.


  \begin{figure} \psfig{figure=ms1853f2.eps,width=88mm,clip=}\end{figure} Figure 2: The distributions of observed polarization directions a) and relative Stokes parameters b), c).
Open with DEXTER

The histogram of observed values of $\theta$ has a narrow maximum near $\theta= 20\hbox{$^\circ$ }$ and wings reaching to $\theta= 20\hbox{$^\circ$ }\pm 90\hbox{$^\circ$ }$. Figures 2b,c give the histograms of the relative Stokes parameters $p_{x,\rm obs}$, $p_{y,\rm obs}$. Use of the $\chi^2$-test reveals that both distributions may be represented (at a significance level of 5%) by normal distributions (these are also given in Figs. 2b,c). The parameters of the normal distributions are as follows: $\overline{p_{x,\rm obs}} = 4.33\%$, $\sigma_{p_{x,\rm obs}} = 5.10\%$; $\overline{p_{y,\rm obs}} = 4.32\%$, $\sigma_{p_{y,\rm obs}} = 5.73\%$ $(\overline{p_{\rm obs}} = 6.1\%$, $\overline{\theta_{\rm obs}} = 22\hbox{$^\circ$ })$.

We have verified whether the results are similar for the central point source only. Again the $\chi^2$-test shows that the distributions are normal with parameters $\overline{p_x} = 6.21\%$, $\sigma_{p_x} = 7.47\%$, $\overline{p_ y} = 6.79\%$, $\sigma_{p_y}= 7.73\%$, ( $\overline{p} = 9.2\%, \overline{\theta}=24\hbox{$^\circ$ })$. The location of all 451 points for the central source in the plane $\{{p_x, p_y}\}$is shown in Fig. 3 (dots). The point ( $\overline {p_x}, \overline {p_y}$) is indicated by the black square. The errors in the relative Stokes parameters are less than 2% (the cross in the upper-left corner). The strong polarization variability is stressed by the fact that the dispersion is much higher than the errors.


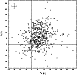  \begin{figure} \psfig{figure=ms1853f3.eps,width=88mm,clip=}\end{figure} Figure 3: The plane $\{{p_x, p_y}\}$ for the point source; the characteristic errors in relative Stokes parameters are shown by cross, the point ( $\overline {p_x}, \overline {p_y}$) is indicated by the black square.
Open with DEXTER

4 The general properties of the point source

The first panel of Fig. 1 shows that flux variations are characterized by numerous outbursts. The time scales of these outbursts are different: from an entire season to several days, the minimum timescale to which our observations are sensitive. Such behaviour in the flux variations of BL Lac has been described many times (e.g., Webb et al. 1988; Hagen-Thorn et al. 1997).

Visual inspection of panels 2 and 3 of Fig. 1 shows that contrary to the behaviour of the parameter I, the Stokes parameters Q and U that describe the polarization behaviour are much less variable. With the exception of several points, all others lie near the median level. The relationship between these absolute Stokes parameters is shown in Fig. 4. Here the dotted lines give the mean values of the parameters Q ( $\bar Q = 0.084$) and U ($\bar U$ = 0.090), and the solid lines represent the results of the least square fits. The slopes of the lines are $\alpha_{\rm Q} = -0.005\pm0.006$, $\alpha_{\rm U} = -0.012\pm0.006$. Their distinctions with respect to the 0-slope are not significant. Therefore, on average the Stokes parameters Q and U are independent of I.


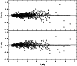  \begin{figure} \psfig{figure=ms1853f4.eps,width=88mm,clip=}\end{figure} Figure 4: The connection between the absolute Stokes parameters for the entire data.
Open with DEXTER

One can see that the scatter of the values Q and U relative to mean is higher for high values of I. This is due primarily to the fact that I is included as a factor when finding Q and U from an observation. Hence, the same errors in the observed polarization parameters lead to higher scatter when I is higher.

Since the variations of the parameters Q and U are small while the total flux I is strongly variable, the degree of polarization should depend on the total flux. Figure 5 confirms this: the highest degree of polarization occurs at lower flux levels, although this is only an average tendency. For example, in four cases (out of six) when $I \ge 5$ mJy the degree of polarization is quite high (between 12% and 20%). As expected, the same behaviour as in Fig. 5 is seen in the dependence of the relative Stokes parameters px and py on I (Fig. 6).

  \begin{figure} \psfig{figure=ms1853f5.eps,width=88mm,clip=}\end{figure} Figure 5: The dependence of the degree of polarization on flux.
Open with DEXTER


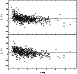  \begin{figure} \psfig{figure=ms1853f6.eps,width=88mm,clip=}\end{figure} Figure 6: The dependencies of the relative Stokes parameters on flux. Dotted lines give the mean values of the Stokes parameters.
Open with DEXTER

It is evident from Fig. 3 that there must be a dependence between the degree of polarization and its direction: the strongest polarization has to occur when the position angle is near the preferred value. Figure 7 shows that this is indeed the case: the distribution of degree of polarization is almost symmetric with respect to the preferred direction of $\theta= 24\hbox{$^\circ$ }$. (Note that some points for $\theta< 24\hbox{$^\circ$ }- 90\hbox{$^\circ$ }= - 66\hbox{$^\circ$ }$ may be transported to the right in the region of $\theta> 90\hbox{$^\circ$ }$ by adding $180\hbox{$^\circ$ }$).

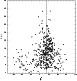  \begin{figure} \psfig{figure=ms1853f7.eps,width=88mm,clip=}\end{figure} Figure 7: The connection between the degree and direction of polarization.
Open with DEXTER


  \begin{figure} \psfig{figure=ms1853f8.eps,width=88mm,clip=}\end{figure} Figure 8: The connection between the direction of polarization and total flux.
Open with DEXTER

The last dependence which we consider in this section is that between the polarization direction and total flux (Fig. 8). Although there is considerable scatter, one can see that the points corresponding to lower fluxes group more closely around the preferred direction than do the higher flux points. To illustrate this we construct the distributions of $\theta$ for two intensity intervals: $1 \div 2$ mJy and $3 \div 4$  mJy (Fig. 9). The difference in the shape of the distributions is evident.

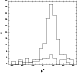  \begin{figure} \psfig{figure=ms1853f9.eps,width=88mm,clip=}\end{figure} Figure 9: The difference in the shape of the distributions of position angle for two intervals of flux.
Open with DEXTER

5 The behaviour during individual observational seasons

In previous section we discussed the gross variability properties of the BL Lac's central point source. In this section we consider the behaviour on shorter time scales. As is apparent in Fig. 1, the behaviour of the variable source is different for different observational seasons. For example the difference between the seasons of 1989 and 1990 is striking. In the first one the flare in I is accompanied by variations in the parameters Q and U, in the second there are no noticeable variations in Q and U while a flare in total flux is evident. Sometimes we see correlated variations between the absolute Stokes parameters: in 1973 (JD 2441860-2442014) there is a visible correlation between I and Q, and in 1975 (JD 2442626-2442723) - between I and U. The absolute Stokes parameters for these seasons are compared in Figs. 10a,b.

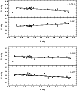  \begin{figure} \psfig{figure=ms1853f10.eps,width=88mm,clip=}\end{figure} Figure 10: The dependencies of Q and U on I for two seasons: 1973 a) and 1975 b); r - correlation coefficients, the lines are drawn by least squares method.
Open with DEXTER

The correlation coefficients and the best straight-line fit to the data (found by least squares method) are given in Fig. 10. The equations of the straight lines are as follows:

Q=$\displaystyle (-0.124\pm0.025)I + (0.181\pm0.049),$  
U=$\displaystyle (0.088\pm0.023)I +(0.002\pm0.044)$ (1)

for 1973 and
Q=$\displaystyle (-0.047\pm0.022)I + (0.007\pm0.044),$  
U=$\displaystyle (-0.123\pm0.032)I + (0.226\pm0.064)$ (2)

for 1975.

There are seasons when no correlation exists between the parameters I and Q or U. As an example, in Fig. 11 the data are given for 1980 (JD 2444456-2444583). Here we see the same behaviour as found in the previous section for all the data: when the flux increases the degree of polarization becomes lower while the parameters Q and U, on average, do not change. The equations of the best-fit straight lines are as follows:

Q=$\displaystyle (-0.008\pm0.025)I + (0.122\pm0.054),$  
U=$\displaystyle (0.005\pm0.026)I + (0.142\pm0.057).$ (3)

The slopes of the lines are very close to 0.


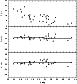  \begin{figure} \psfig{figure=ms1853f11.eps,width=88mm,clip=}\end{figure} Figure 11: The same as in Fig. 10 but for 1980 (two lower panels); additionally the dependence of the degree of polarization on the total flux is given (upper panel).
Open with DEXTER

6 Discussion and conclusions

The rapid optical variability, power-law spectrum, (Hagen-Thorn et al. 1992, 2000), strong and highly variable optical polarization of BL Lac point to synchrotron nature of the variable sources. In this case the presence of a preferred direction of polarization indicates a preferred direction of the underlying magnetic field in the region where the radiation comes into existence. For BL Lac this direction ( $\theta = 114\hbox{$^\circ$ }$) is nearly orthogonal to the direction of the movement of VLBI components in the 1980s, $188\hbox{$^\circ$ }- 196\hbox{$^\circ$ }$(Mutel et al. 1990). Furthermore, the magnetic field is even closer to perpendicular to the jet axis on 1-2 milliarsecond scales of $195\hbox{$^\circ$ }{-} 206\hbox{$^\circ$ }$ (Denn et al. 2000) as one can expect if the optical radiation arises in shocks in the jet relatively close to the central engine (Marscher & Gear 1985).

Such behaviour of the polarization at radio wavelengths is not unusual and can be explained by models involving transverse shocks moving along the jet (Hughes et al. 1985). For example, Aller et al. (1996) report a preferred direction of polarization for BL Lac at centimeter wavelengths of about $20\hbox{$^\circ$ }$ in 1980's and note, however, considerable variations of the direction of polarization which they explain by oblique shock model. In general, the behaviour of polarization in the optical and centimeter wavelengths is similar though the data are perhaps related to the different regions of the jet. On the other hand, this similarity shows that the underlying magnetic field is stable, on average, on large scales.

Figures 2 b,c and 3 formally allow one to explain the variability of polarization direction for BL Lac by a model in which components with randomly distributed polarization directions are superimposed on a long-lived underlying source of polarized radiation with $p = 9.2\%, \theta= 24\hbox{$^\circ$ }$. Such a model has been suggested by Hagen-Thorn (1980) to explain polarization variability of the blazar OJ 287.

In this model the general photometric and polarization behaviour depends on the number and properties of superimposed components. The analysis of the short-term variability (not considered in this paper) shows that as many as tens of variable components may act simultaneously (Brindle et al. 1985) and that the degree of polarization of some of these may be as high as 50%, with different polarization directions (Hagen-Thorn et al. 1986).

A consideration of the observed dependencies between flux level, degree of polarization and its direction confirms the reality of the model and allow us to specify some properties of the underlying source.

The concentration of polarization angles near the preferred direction ( $\theta= 24\hbox{$^\circ$ }$) at low and moderate brightness levels (Figs. 8, 9) reveals a significant contribution of the underlying source to the total flux compared with that of variable components. The underlying source dominates at low brightness levels (I<1 mJy), as indicated by the small scatter of the position angle of polarization near $\theta= 24\hbox{$^\circ$ }$.

At low brightness levels (corresponding to a small number of variable components), the appearance of a new, highly polarized component with $\theta\sim 24\hbox{$^\circ$ }$ results in higher observed polarization along the preferred direction (the highest degrees of polarization in Figs. 5, 7). On the other hand, a new polarized component with position angle of polarization perpendicular to the preferred direction cancels the polarization of the underlying source, causing low observed polarization. This explains why Fig. 5 shows a significant scatter of the degree of polarization when the flux is low.

A large number of randomly polarized components with similar fluxes result in moderate (even low) variability of the polarized flux, since polarizations with different position angles cancel each other. The brightness, in contrast, can vary more widely due to the linear dependence on the number of components (panels 1-3 in Fig. 1, Fig. 4). Newly born polarized components can cause a decrease in the observed polarization despite the rise in total flux. Such an inverse dependence of the degree of polarization on the flux is apparent in Fig. 5. When the number of randomly polarized components is large the contribution of the underlying source weakens and the shape of the distribution of the position angle of polarizaton changes relative to that at low brightness levels (see Figs. 8, 9).

At high brightness levels (I>3 mJy), Fig. 8 shows uniform scattering of $\theta$ within $180\hbox{$^\circ$ }$. Therefore, one expects the brightness variability of underlying source to be moderate such that the source can not dominate when the flux is high. It is most likely that a newly born bright component is responsible for the photopolarimetric behaviour of the object at high brightness levels.

As was shown previously (for details see Hagen-Thorn & Marchenko 1999), when the variability is due to a single dominant component with constant relative Stokes parameters and variable flux, the dependence of the absolute Stokes parameters Q and U on I must be linear with the slope of the dependence giving the relative Stokes parameters of the variable component. Figure 10 shows the dependence of Q and U on I for two seasons. Though the correlation coefficients are not very high, the straight lines represent the dependence sufficiently well. One may conclude that the general behaviour of the object can be represented by the existence of components with the relative Stokes parameters determined by the slopes of the corresponding dependence. For seasons 1973 and 1975 we obtain from (1) and (2), respectively, $p_x = - 12.4\%$, $p_y = 8.8\%$, $P = 15.2\%$, $\theta= 73\hbox{$^\circ$ }$ and $p_x = - 4.7\%$, $p_y = - 12.3\%$, $P = 13.2\%$, $\theta = 125\hbox{$^\circ$ }$. Note that in both cases the polarization direction does not coincide with the preferred angle. However, these values must be considered only as average ones since in reality the behaviour at each moment is determined by the combined action of several short-lived variable components. These must be very high polarized because the combined polarization is quite high (more than 10%).

In conclusion, the model of a continually acting, underlying source of polarized radiation plus components with randomly distributed polarization directions and high degrees of polarization explains quite well the observational data. Future combined high-frequency VLBI polarimetric imaging and optical-IR polarization monitoring will allow a closer examination of the relationship between the relativistic jet and the magnetic field in the most compact regions of blazars.

In the near future we plan to analyse the temporal behaviour of BL Lac on time scales shorter than those considered in present work.

Acknowledgements
This work was supported by Federal Program "Integration'' (grants A0007 & K0232) and Russian Fund of the Basic Researches (grant 98-02-16609). V.A.H.-Th. thanks the Stockholm Observatory for hospitality. S.G.J. was supported by US National Science Foundation grant AST-9802941. The authors thank Alan Marscher for a constructive discussion.

References

 

Copyright ESO 2002