A&A 385, 94-110 (2002)
DOI: 10.1051/0004-6361:20020115
J. Bergeat - A. Knapik - B. Rutily
Centre de Recherche Astronomique de Lyon (UMR 5574 du CNRS),
Observatoire de Lyon,
9 avenue Charles André, 69561 St-Genis-Laval Cedex,
France
Received 7 June 2001 / Accepted 7 January 2002
Abstract
Making use of the HIPPARCOS data and refining a previous study of the space distribution of the
carbon-rich giant stars located in the vicinity of the Sun (Paper I), we fully investigate
their space distributions and space velocities on the basis of our photometric grouping
(CVi i.e. carbon variable stars with i=1 to 7; HCj i.e. hot carbon stars with j=0 to 5). As
expected, the CH stars (a subset of the HC stars delineated on the grounds of
spectroscopic criteria) need to be considered separately. We also used groupings according to
variability classes.
The various biases affecting the use of the data are taken into account as far as possible.
The mean distance to the Galactic plane of the faint
![]() HC-stars amounts to 0.5 kpc compared to
0.15 kpc for the bright
HC-stars amounts to 0.5 kpc compared to
0.15 kpc for the bright
![]() CV-stars.
Exponentially decreasing distributions are fit with distance scales of
CV-stars.
Exponentially decreasing distributions are fit with distance scales of
![]() kpc
and 0.19 kpc respectively, and a normalization factor of 5.2% to 7.3% for the former component,
compatible with a thick disk and thin disk respectively. Projected surface densities on the
Plane are given with a total of about
kpc
and 0.19 kpc respectively, and a normalization factor of 5.2% to 7.3% for the former component,
compatible with a thick disk and thin disk respectively. Projected surface densities on the
Plane are given with a total of about
![]() ,
including 6% of CH stars and at
least 18% for the other HC-stars (namely the HC'-sample).
While halo-type velocities are found for CH stars with a substantial drift of
,
including 6% of CH stars and at
least 18% for the other HC-stars (namely the HC'-sample).
While halo-type velocities are found for CH stars with a substantial drift of
![]() ,
the solar reflex velocities and residual-velocity dispersions for the
HC'-sample are about twice those of the CV-sample, close to thick disk and thin disk values
respectively.
In summary, we identify the HC-sample as a component of the thick disk contaminated by the CH
stars which are a spheroidal contribution, and possibly by CV-stars at HC5. As expected,
the CV-sample is a component of the old (thin) disk, dated from AVR,
,
the solar reflex velocities and residual-velocity dispersions for the
HC'-sample are about twice those of the CV-sample, close to thick disk and thin disk values
respectively.
In summary, we identify the HC-sample as a component of the thick disk contaminated by the CH
stars which are a spheroidal contribution, and possibly by CV-stars at HC5. As expected,
the CV-sample is a component of the old (thin) disk, dated from AVR,
![]() on average, but with a likely spread
from a few
on average, but with a likely spread
from a few
![]() up to
up to
![]() While the former (HC) represents
very old low mass stars (initial masses less than
While the former (HC) represents
very old low mass stars (initial masses less than
![]() but subject to
mass-loss), the latter (CV) are younger stars with higher initial masses on average (up to a few
solar masses). The high frequency of HC'-stars rules out models requiring rare events.
Better modeling of mixing events in low mass stars on the RGB and AGB could help. Less dragged
up carbon is needed to transform the low-mass stars with a low O/H ratio into carbon giants.
but subject to
mass-loss), the latter (CV) are younger stars with higher initial masses on average (up to a few
solar masses). The high frequency of HC'-stars rules out models requiring rare events.
Better modeling of mixing events in low mass stars on the RGB and AGB could help. Less dragged
up carbon is needed to transform the low-mass stars with a low O/H ratio into carbon giants.
Key words: stars: AGB and post-AGB - stars: carbon - stars: late-type - stars: variables: general - stars: kinematics
The carbon-rich giant stars occupy a special place in the realm of stellar evolution. They are stars of low and intermediate initial masses evolved far from the main sequence up to the red giant branch and asymptotic branch where they experience thermal pulses (TPAGB; Wallerstein & Knapp 1998; Busso et al. 1999). Alternatively, anomalous surface abundances may result from mass exchange in a binary system, with a TP-AGB companion that became a white dwarf (Han et al. 1995 and references therein). This is the model accepted for BaII stars, many of them having proved to be binary members (Mc Clure et al. 1980; Jorissen & Boffin 1992). The low-luminosity carbon stars classified into the R-types however fail to show any evidence of binarity, and Mc Clure (1997a) considered they could be the product of coalescence of components.
With the
existence of carbon dwarfs (Dahn et al. 1977; Green et al. 1991;
Bothun et al. 1991), some carbon giants may be evolved from carbon dwarfs,
exactly like dwarf BaII stars (e.g. Bergeat & Knapik 1997) that are
potential precursors for some future BaII subgiants and giants. Those carbon dwarfs
are likely members of binary systems (Liebert et al. 1994; Green & Margon
1994) and their velocities of several hundreds of
![]() relative
to the Sun are typical of a spheroidal population (halo).
relative
to the Sun are typical of a spheroidal population (halo).
We investigate the space distributions and space velocities from HIPPARCOS data, of a sample
of about 300 carbon giants first
analyzed by Knapik et al. (1998, hereafter Paper I). They proposed a model of
the distribution of observed parallaxes, making use of the cumulative distribution of
HIPPARCOS proper motions which are very accurate when compared with those previously
available. The HIPPARCOS carbon stars are close to the Sun. They only show some
concentration towards the Galactic plane while the 5987 stars in Stephenson's
(1989) catalogue exhibit, in addition, a positive galactocentric gradient towards
Galactic anticenter
(Fuenmayor 1981), and clumps correlated with the local spiral arms
(Cygnus-Perseus and Sagittarius-Carinae: Stephenson's Fig. 2). Having described and
taken into account the biases which affect the mean values from HIPPARCOS data, Knapik
et al. (Paper I) adopted a flat subsystem or slab. They found their data to be roughly
consistent with uniform density in star number. Part of the present paper is intended to
refine this picture, especially concerning the frequency distribution vs.
height (i.e. distance to galactic plane
![]() ).
).
Classical analyses of velocity data include the determination of the solar reflex velocity, and then the evaluation of the maximal dispersions along the three ellipsoid axes (see e.g. Delhaye 1965 for a summary of early results). They make use of radial velocities and/or proper motions. A better constraint of the kinematic solution is obtained when individual parallaxes are available (Mihalas & Binney 1981, Sects. 6 and 7). For carbon stars, it was impracticable before HIPPARCOS since no reliable parallaxes were available.
The early studies on late-type giants are summarized in Blanco (1965) and on
variables by Plaut (1965). The solar motions and velocity ellipsoids
for early R stars (Vandervort 1958; Mc Leod
1947) seem similar to those of G and K dwarfs. The most extensive study was by Dean
(1976), which included 427 stars, mainly classified N or late-R. The author
concluded that the obtained kinematic solution is close to the one obtained for F5 dwarfs.
Among the R stars, the CH stars (Keenan 1942; Bidelman 1956) are on
average high velocity stars with respect to the Sun. They are believed to be members of binary
systems (McClure 1997b) but the eventual orbital velocities should be small on
average (0-15
![]() )
when compared to the high velocities observed
with respect to the Sun. Hartwick & Cowley
(1985) studied 51 confirmed and probable CH stars. They concluded that they are
halo tracers. A majority of carbon giants and related objects are variables of various types
in the General Catalogue of Variable Stars (GCVS, Kholopov et al. 1985), namely
Lb (irregulars), SR (semi-regulars a or b) and M (Miras). The oxygen-rich long period
variables (LPVs) show specific kinematic solutions with large solar reflex
velocities and larger dispersions at shorter periods (e.g. Delhaye
1965; Mihalas & Binney 1981). A
question is whether the carbon-rich LPVs display a similar behavior.
)
when compared to the high velocities observed
with respect to the Sun. Hartwick & Cowley
(1985) studied 51 confirmed and probable CH stars. They concluded that they are
halo tracers. A majority of carbon giants and related objects are variables of various types
in the General Catalogue of Variable Stars (GCVS, Kholopov et al. 1985), namely
Lb (irregulars), SR (semi-regulars a or b) and M (Miras). The oxygen-rich long period
variables (LPVs) show specific kinematic solutions with large solar reflex
velocities and larger dispersions at shorter periods (e.g. Delhaye
1965; Mihalas & Binney 1981). A
question is whether the carbon-rich LPVs display a similar behavior.
Apart from the CH stars which are associated with the spheroidal component, the carbon giants are mainly disk objects. It is especially interesting to explore the connection of those stars with the old (thin) disk and with the recently discovered thick disk (e.g. Freeman 1987a). These structures deserve their many recent studies (e.g. Buser et al. 1999; Schwarzkopf & Dettmar 2000; Chiba & Beers 2000; Prochaska et al. 2000; Kerber et al. 2001; Ojha 2001).
The first classification of the carbon-rich giants in discrete photometric groups (13 groups named HCi and CVj with i=0 to 5 and j=1 to 7, and the fourteenth SCV as a transition to S stars), was established by Knapik & Bergeat (1997), Bergeat et al. (1999) and Knapik et al. (1999). The new effective temperatures proposed for carbon-rich giants and related objects by Bergeat et al. (2001) rely on spectral energy distributions (SEDs), model atmospheres and measured angular diameters. The classification and the homogeneous temperature scale obtained proved to be tightly correlated. It was concluded that the main parameter of this photometric classification is effective temperature (Bergeat et al. 2001). This is the first classification to achieve this, providing a sound basis for further model atmosphere analysis. A good correlation is also found with luminosities (Knapik et al. 2001 and Table 3 hereafter). Sampling according to our photometric classification is thus preferred to that making use of spectral classification, even in its refreshed version (Keenan 1993).
The statistical biases affecting parallaxes and deduced quantities were studied in Paper I.
They are re-examined in Sect. 2 with special attention paid to differences between the
HC and CV-groups. The mean distances
![]() to the Galactic plane
are investigated in Sect. 3, while the influence of the Malmquist bias is estimated in
Sect. 4. After correction for selection effects in sampled cylinders, the distributions of
HC- and CV-stars with distances
to the Galactic plane
are investigated in Sect. 3, while the influence of the Malmquist bias is estimated in
Sect. 4. After correction for selection effects in sampled cylinders, the distributions of
HC- and CV-stars with distances
![]() to the Plane are investigated in Sect. 5,
and local space densities derived. The projected surface densities of carbon giants according
to photometric groups (Sect. 6) and effective temperatures (Sect. 7) are presented. A first
crude analysis of kinematic data is then performed, making use of mean radial and tangential
velocities with respect to the Sun (Sect. 8). Finally the reflex solar velocities (Sect. 9) and
stellar residual-velocity ellipsoids (Sect. 11) are derived, the former for variability
classes as well (Sect. 10). The results are discussed (Sect. 12) in terms of two
distinct populations: the CV-stars associated with the old (thin) disk and most of the HC-stars
(HC'-sample, i.e. non-CH HC-stars) with the thick disk. The CH stars
are confirmed as a halo component.
to the Plane are investigated in Sect. 5,
and local space densities derived. The projected surface densities of carbon giants according
to photometric groups (Sect. 6) and effective temperatures (Sect. 7) are presented. A first
crude analysis of kinematic data is then performed, making use of mean radial and tangential
velocities with respect to the Sun (Sect. 8). Finally the reflex solar velocities (Sect. 9) and
stellar residual-velocity ellipsoids (Sect. 11) are derived, the former for variability
classes as well (Sect. 10). The results are discussed (Sect. 12) in terms of two
distinct populations: the CV-stars associated with the old (thin) disk and most of the HC-stars
(HC'-sample, i.e. non-CH HC-stars) with the thick disk. The CH stars
are confirmed as a halo component.
Knapik et al. (Paper I) studied the space distribution of the nearly 300 carbon-rich giant
stars observed by the satellite HIPPARCOS (ESA 1997). No appreciable correlation
with interstellar extinction, galactocentric distance and/or spiral arms structures was
detected in this sample of nearby stars (Sect. 2 of Paper I). Due to the limited accuracy
of the observed parallaxes
![]() ,
the statistical use of parallaxes, distances,
absolute magnitudes etc. is hampered by statistical biases.
The bias investigated by Lutz & Kelker (1973, hereafter LK) is twofold
,
the statistical use of parallaxes, distances,
absolute magnitudes etc. is hampered by statistical biases.
The bias investigated by Lutz & Kelker (1973, hereafter LK) is twofold
The relative accuracies of the HIPPARCOS proper motions are far higher than those of the
corresponding observed parallaxes in the catalogue (ESA 1997). In addition, no
appreciable bias is expected on the former data. Adopting a model by Hanson
(1979) on the cumulative distribution of proper motions, Knapik et al. (Paper I)
established a simple power law
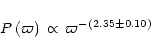 |
(1) |
The hot carbon stars (HC-stars; Bergeat et al. 1999) appear less concentrated
toward the Galactic plane (Paper I) than the cool carbon variables
(CV-stars; Knapik & Bergeat 1997 and Knapik et al. 1999). This
assumption based on galactic latitudes (Stephenson 1989) was
confirmed by the HIPPARCOS data. Since the HIPPARCOS sample and Paper I model are dominated
by about 195 CV-stars, we focus here on the case of the subsample of 104 HC-stars, repeating the
analysis of the cumulative distribution of proper motions (Sect. 3 of Paper I).
This more dispersed diagram led us to an exponent of
![]() which is not
significantly different from that in Eq. (1). Finally, we adopt the latter for the whole sample
of carbon stars, including peculiar objects.
which is not
significantly different from that in Eq. (1). Finally, we adopt the latter for the whole sample
of carbon stars, including peculiar objects.
The distribution of Eq. (1) results from the Malmquist bias on the magnitude-limited HIPPARCOS
sample. The limiting visual apparent magnitude
![]() was adopted in Paper I for the whole sample, leading to the absolute visual magnitudes
was adopted in Paper I for the whole sample, leading to the absolute visual magnitudes
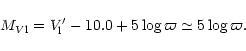 |
(2) |
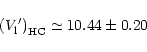 |
(3) |
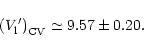 |
(4) |
| 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.70 | 0.80 | 0.90 | 1.0 | 1.122 | 1.259 | 1.50 | 2.00 | |
|
|
4.321 | 3.103 | 2.423 | 2.000 | 1.738 | 1.554 | 1.329 | 1.204 | 1.131 | 1.086 | 1.052 | 1.031 | 1.013 | 1.0023 |
Making use of Eq. (2) for the whole sample, the distribution
![\begin{displaymath}N\left(M_{{V}}\right)\simeq 50.68 \exp \left[-\left(M_{{V}}+1.5\right)^{2}/
2\left(1.06\right)^{2}\right]
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img50.gif) |
(5) |
![\begin{displaymath}f\left(\varpi \right)={\left[\,\int_{-\infty}^{x_{\rm {l}}}{\...
...{-1/2}\,
\exp\left(-{x}^{2}/2\right)\,{\rm d}x\,\right]}^{-1}.
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img52.gif) |
(6) |
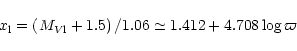 |
(7) |
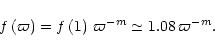 |
(8) |
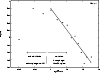 |
Figure 1: The distribution of the HIPPARCOS carbon stars as a function of the estimated true parallax. Power law (10) is shown as a dashed line. Beyond 1 kpc, the increasing influence of incompleteness of the sample is clearly seen. |
| Open with DEXTER | |
As stated in Paper I, roughly correcting the distribution of Eq. (1), we obtain
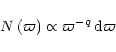 |
(9) |
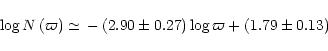 |
(10) |
| G | n |
|
|
|
|
|
|
|
|
|
|
| n.d. | mas | n.d. | kpc | kpc | kpc | n.d. | mas | kpc | kpc | kpc | |
| HC0 | 4 |
|
1.07: | 1.11: | 1.04: | 1.06 | 0.98: |
|
0.201: | 0.20: | 0.19: |
| HC1 | 25 |
|
1.28 | 1.07 | 0.84 | 0.92 | 0.91 |
|
0.377 | 0.55 | 0.43 |
| HC2 | 27 |
|
1.23 | 1.19 | 0.97 | 0.96 | 1.01 |
|
0.077 | 0.71 | 0.58 |
| HC3 | 17 |
|
1.24 | 1.61 | 1.30 | 1.48 | 0.88 |
|
0.004 | 0.62 | 0.50 |
| HC4 | 13 |
|
1.22 | 1.41 | 1.16 | 1.26 | 0.92 |
|
0.292 | 0.67 | 0.55 |
| HC5 | 18 |
|
1.06 | 1.24 | 1.17 | 1.17 | 1.02 |
|
0.240 | 0.48 | 0.46 |
| CV1 | 31 |
|
1.25 | 1.06 | 0.85 | 0.83 | 1.02 |
|
0.015 | 0.18 | 0.15 |
| CV2 | 43 |
|
1.28 | 0.91 | 0.71 | 0.75 | 0.95 |
|
0.048 | 0.17 | 0.16 |
| CV3 | 32 |
|
0.97: | 1.11 | 1.14: | 0.84 | 1.36: |
|
0.085 | 0.20 | 0.20 |
| CV3* | 31 |
|
1.27 | 1.14 | 0.90 | 0.97 | 0.93 |
|
0.078 | 0.20 | 0.16 |
| CV4 | 28 |
|
1.28 | 0.97 | 0.76 | 0.79 | 0.96 |
|
0.003 | 0.17 | 0.13 |
| CV5 | 28 |
|
1.29 | 0.81 | 0.63 | 0.68 | 0.93 |
|
0.027 | 0.18 | 0.14 |
| CV6 | 25 |
|
1.28 | 0.88 | 0.69 | 0.69 | 1.00 |
|
0.008 | 0.23 | 0.18 |
| CV7 | 6 |
|
1.08: | 1.09: | 1.01 | 1.04: | 0.97: |
|
0.128: | 0.33: | 0.30: |
| SCV | 3 |
|
1.15: | 1.11: | 0.97 | 1.05: | 0.92: |
|
0.111: | 0.14: | 0.13: |
Following the analysis of the HIPPARCOS data on carbon stars,
a simplified model of a uniformly-populated slab or flat cylinder was proposed in
Sect. 8 of Paper I. Its theoretical distribution was
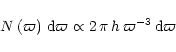 |
(11) |
The true parallaxes as estimated in Sect. 5 of Paper I can, at least to a first approximation,
be used to derive mean parallaxes (
![]() )
free of the Lutz & Kelker
(1973) bias. The pdf of the "observed'' distance (as compared to the "true'' distance D) is
)
free of the Lutz & Kelker
(1973) bias. The pdf of the "observed'' distance (as compared to the "true'' distance D) is
![\begin{displaymath}f\left(D_{0} \right)=\exp\left[ - \left(1/D_{0}-1/D\right)^{2...
...sigma}^{2}\right]
/{\left(2\pi\right)}^{1/2}\sigma {D_{0}}^{2}
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img122.gif) |
(12) |
![\begin{displaymath}\langle D_{0} \rangle = \frac{1}{{\left(2\pi\right)}^{1/2}\si...
...^{2}/2{\sigma}^{2}\right]}{{\varpi}_{0}}
\,\rm {d}{\varpi}_{0}
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img124.gif) |
(13) |
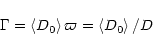 |
(14) |
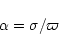 |
(15) |
The relation between pdfs
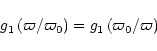 |
(16) |
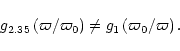 |
(17) |
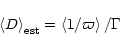 |
(18) |
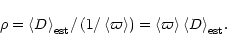 |
(19) |
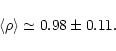 |
(20) |
| (21) |
| (22) |
Considering the distances from the Galactic plane
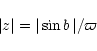 |
(23) |
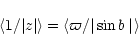 |
(24) |
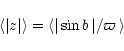 |
(25) |
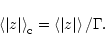 |
(26) |
We observe that the values for the HC-groups are much larger than those of the CV-groups.
We find respectively
![\begin{displaymath}\left[ \, \left< \vert z \vert \, \right>_{\rm {c}} \right]_{\rm {HC}} \simeq \left( 0.50
\pm 0.06 \right)\,\rm {kpc}
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img156.gif) |
(27) |
![\begin{displaymath}\left[ \, \left< \vert z \vert \, \right>_{\rm {c}} \right]_{\rm {CV}} \simeq \left( 0.16
\pm 0.03 \right)\,\rm {kpc}.
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img157.gif) |
(28) |
![\begin{displaymath}\left[ \, \left< \vert z \vert \, \right>_{\rm {c}} \right]_{\rm {CV}} \simeq \left( 0.15
\pm 0.02 \right)\,\rm {kpc}.
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img158.gif) |
(29) |
![\begin{displaymath}\left[ \, \left< \vert z \vert \, \right>_{\rm {c}} \right]_{...
...t>_{\rm {c}} \right]_{\rm {CV}} \simeq 3.13 \;\rm {or}
\;3.33
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img159.gif) |
(30) |
The CV-stars are, on average, about three times more concentrated towards the Plane than the HC-ones. A clear-cut jump between both regimes appears at HC5-CV1 two groups which are however close to each other in terms of mean effective temperatures (Bergeat et al. 2001), and also on the grounds of mean absolute magnitudes (Col. 2 of Table 3 and Knapik et al. 2001). We emphasize that those results were quite unexpected when the definitions of our photometric groups were adopted, precisely on the basis of photometric criteria only. In Table 2, the values quoted for HC0, SCV and CV7 are only indicative.
In Sect. 7.4 of Paper I, we concluded that the subset of the bright N-variables
(CV-stars) in the HIPPARCOS sample is little affected by the Malmquist bias, while the
opposite situation prevails for the faint hotter R-type stars (HC-stars).
This statement applies to the evaluation of mean absolute magnitudes for the HC and CV-groups,
and thus to mean luminosities. Despite the differences between those two categories, only
a Gaussian curve could successfully be fitted to the distribution of the visual absolute
magnitudes, namely Eq. (5). Along the sequence of the thirteen HC and CV-groups (HC0 to HC5
and then CV1 to CV7) which is also an effective temperature sequence (Bergeat et al.
2001), the mean absolute visual magnitude hardly changes,
contrary to its bolometric counterpart. The latter displays a much wider range
(Table 3 with results from Knapik et al. 2001).
Mean bolometric corrections were computed (Col. 5 of Table 3), and then mean
absolute visual magnitudes (Col. 6) from
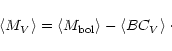 |
(31) |
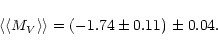 |
(32) |
| G |
|
|
(inf; sup) |
|
|
| HC0 | -1.71 | -0.92; -2.98 | -0.13 | -1.58 | |
| HC0(a) | -1.32 | -0.92; -1.81 | -0.13 | -1.19 | |
| HC1 | -1.06 | -0.35; -2.11 | -0.60 | -0.46 | |
| HC1(c) | -0.74 | -0.00; -1.80 | -0.60 | -0.14 | |
| HC2 | -1.22 | -0.58; -2.15 | -0.60 | -0.62 | |
| HC2(c) | -1.02 | -0.30; -2.00 | -0.60 | -0.42 | |
| HC3 | -1.99 | -1.15; -3.36 | -0.88 | -1.11 | |
| HC4 | -3.00 | -2.11; -4.54 | -1.16 | -1.84 | |
| HC5 | -3.37 | -2.81; -4.12 | -1.70 | -1.67 | |
| CV1 | -3.72 | -3.62 | -3.01; -4.79 | -2.07 | -1.65 |
| CV2 | -4.34 | -4.24 | -3.65; -5.35 | -2.42 | -1.92 |
| CV3 | -4.39 | -4.29 | -3.74; -5.32 | -2.64 | -1.75 |
| CV4 | -4.66 | -4.56 | -3.91; -5.80 | -2.83 | -1.83 |
| CV5 | -4.82 | -4.72 | -4.24; -5.60 | -3.17 | -1.65 |
| CV6 | -5.05 | -4.95 | -4.49; -5.79 | -3.43 | -1.62 |
| CV7 | -5.43 | -4.60; -6.80 | -4.62 | -0.81 | |
| CV7(b) | -5.81 | -5.20; -6.70 | -4.62 | -1.19 | |
| SCV | -5.77 | -5.51; -6.06 |
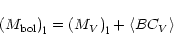 |
(33) |
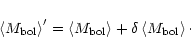 |
(34) |
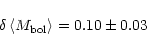 |
(35) |
 |
Figure 2: The influence of the Malmquist bias on the HIPPARCOS sample of HC2-stars. |
| Open with DEXTER | |
We conclude that the corrections on mean absolute magnitudes due to the Malmquist bias are small (and could have been neglected) when compared to the large ranges (inf; sup) in Table 3. The intrinsic dispersions of the absolute bolometric magnitudes in a given group are enlarged by substantial errors on parallaxes.
We plotted diagrams of
![]() vs.
vs.
![]() for every group,
and then, globally, for the HC- and CV-stars respectively. Having found no
marked difference between both Galactic hemispheres, we finally used
for every group,
and then, globally, for the HC- and CV-stars respectively. Having found no
marked difference between both Galactic hemispheres, we finally used
![]() -coordinates in diagrams. Rectangular domains of widths such as
-coordinates in diagrams. Rectangular domains of widths such as
![]() to 1.8 kpc, are populated. Their heights are
to 1.8 kpc, are populated. Their heights are
![]() kpc for
the HC-stars and
kpc for
the HC-stars and
![]() to 0.6 kpc for the CV-stars (a ratio of about 3: Eq. (30)).
to 0.6 kpc for the CV-stars (a ratio of about 3: Eq. (30)).
The influence of the Malmquist bias was roughly compensated at by applying Eq. (6) with
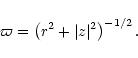 |
(36) |
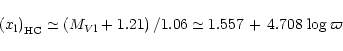 |
(37) |
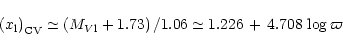 |
(38) |
 |
Figure 3: The influence of the Malmquist bias on the HIPPARCOS sample of CV4-stars. |
| Open with DEXTER | |
| Groups | n |
|
1/z0 | N0/2 | z0 | z0N0 | NF | N'0/2 |
|
NF' | Population | ||
| kpc | kpc-1 | kpc-3 | kpc | kpc-2 | kpc-3 | kpc-2 | |||||||
| HC | 104 | 1.28 | 3.065 | 1.05 | 1.00 | 10.6 | 0.95 | 20.4 | 0.073 | 0.067 | Thick disk+Halo | ||
| HC' | 81 | 2.81 | 8.3 | 15.9 | 0.057 | 0.052 | Thick disk | ||||||
| CV | 195 | 0.8 | 5.592 | 5.33 | 0.95 | 134 | 0.188 | 50.3 | 0.927 | 147 | 55.3 | 0.933 | Thin disk |
| +SCV |
We denote by N the space density of stars in
![]() corrected for the Malmquist bias
(Sect. 5.1). An exponential decrease of the space density with
corrected for the Malmquist bias
(Sect. 5.1). An exponential decrease of the space density with
![]() is usually derived for various stars (Gilmore & Reid 1983; Freeman 1987a,
1987b; Gould et al. 1996). Hence we studied diagrams (not shown here) of
is usually derived for various stars (Gilmore & Reid 1983; Freeman 1987a,
1987b; Gould et al. 1996). Hence we studied diagrams (not shown here) of
![]() vs.
vs.
![]() according to
according to
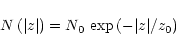 |
(39) |
The high accuracy of the CV fit is due to the first three points at 0.08, 0.24 and 0.4 kpc,
which have very high weights (95.5% of the total). It is probably accidental.
Increasing the radius of the sampled cylinder to 0.96 kpc leads to the same
slope within 1% and to a reduction of 17% of
![]() For the HC-sample, which is about half
the CV-one in star number, the accuracy is lower. Varying the cylinder radius from 1.28 kpc to
1.6 kpc increases the slope from
For the HC-sample, which is about half
the CV-one in star number, the accuracy is lower. Varying the cylinder radius from 1.28 kpc to
1.6 kpc increases the slope from
![]() to
to
![]() with
with
![]() .
Unacceptable scatter is obtained when adopting 0.96 kpc (Poisson error bars). Finally,
the adopted solutions are those given in Table 4, i.e. for 0.8 kpc (CV-sample)
and 1.28 kpc (HC-sample) respectively. Both coefficients of determination are very high.
The projected densities (on the Plane)
.
Unacceptable scatter is obtained when adopting 0.96 kpc (Poisson error bars). Finally,
the adopted solutions are those given in Table 4, i.e. for 0.8 kpc (CV-sample)
and 1.28 kpc (HC-sample) respectively. Both coefficients of determination are very high.
The projected densities (on the Plane)
![]() and space densities in the
Plane N0/2 are also quoted for both samples. The ratio (CV to HC) of the latter is about
12.6 while that of the former is only 2.5. This is a direct consequence of the distance scales
z0 differing from one another, with a ratio of nearly 0.2.
and space densities in the
Plane N0/2 are also quoted for both samples. The ratio (CV to HC) of the latter is about
12.6 while that of the former is only 2.5. This is a direct consequence of the distance scales
z0 differing from one another, with a ratio of nearly 0.2.
The vertical distance scale
![]() kpc falls in the
middle of the 0.6-1.45 kpc range of values published for the thick disk.
It is in excellent agreement with recently
published values such as
kpc falls in the
middle of the 0.6-1.45 kpc range of values published for the thick disk.
It is in excellent agreement with recently
published values such as
![]() kpc by Ojha (2001) or
kpc by Ojha (2001) or
![]() kpc
by Kerber et al. (2001). This disk represents a structure much thicker than the
classical thin disk to which our
kpc
by Kerber et al. (2001). This disk represents a structure much thicker than the
classical thin disk to which our
![]() kpc corresponds well.
The latter value is close to that of Kerschbaum & Hron (1992) for C-rich SRbs and
Miras, viz. 0.18 kpc. Claussen et al. (1987) and Groenewegen et al. (1992)
found 0.2 kpc for various samples of carbon giants. Van Eck & Jorissen (2000) derived
0.22 kpc for (bright) intrinsic-S stars and 0.58 kpc for (faint) extrinsic-S stars which
are brighter (
kpc corresponds well.
The latter value is close to that of Kerschbaum & Hron (1992) for C-rich SRbs and
Miras, viz. 0.18 kpc. Claussen et al. (1987) and Groenewegen et al. (1992)
found 0.2 kpc for various samples of carbon giants. Van Eck & Jorissen (2000) derived
0.22 kpc for (bright) intrinsic-S stars and 0.58 kpc for (faint) extrinsic-S stars which
are brighter (
![]() )
than the HC-stars
(
)
than the HC-stars
(
![]() ).
).
The population of the thick disk was also named "Intermediate Population II'' (IPII; e.g. Majewski 1993 for a review). Not all spiral galaxies exhibit such a structure and its (dynamical) origin is unknown: various theories like violent thin disk heating by satellite accretion (model 6 in Table 1 of Majewski's paper) were proposed. Here we take advantage of the natural separation of carbon giants on the grounds of their SEDs, into two categories (HC and CV), whose space distributions differ markedly (i.e. thick disk and thin disk respectively). Of course, mutual contamination of both samples is likely at HC5-CV1, and halo CH stars are also involved. There is no such separation for faint oxygen-rich stars and the studies of the thick disk are difficult. Gilmore & Reid (1983) modeled the distribution of the faintest M-dwarfs with two exponentials of distance scales 0.3 kpc and 1.45 kpc, and a normalization factor (NF) of 2% for the thick disk population. Making use of HST data, Gould et al. (1996) found 0.323 kpc and 0.656 kpc, and 20%. The numbers for carbon giants (Table 4) are 0.19 kpc and 0.95 kpc, and a NF of 7.3% for the thick disk + halo (5.7% for thick disk).
We conclude that the distribution of the HC-stars is typical of a thick disc component contaminated by a true spheroidal contribution, to which the 23 hot HC-stars classified as CH stars belong. The CV-stars are found as a component of the (old) thin disk. Since the CV6-CV7 objects with thick circumstellar dust shells and the SCV-stars are almost absent from the HIPPARCOS sample, we propose a tentative 10% correction to the CV-densities in Cols. 11-12 of Table 4. Then the normalization factors (NF') should be 6.7% and 93.3% for the thick disk + halo and thin disk respectively (5.2% for thick disk).
There were 567 carbon stars (597 SEDs) successfully studied in our previous papers, including
The corresponding projected densities in the Plane are given in
Table 5 (calibration from Table 4). The value
for the CV7-group is certainly underestimated by a factor of typically two.
The average frequency is about 40.5 stars per group, but the distribution is quite non-uniform.
Two peaks are observed at nearly HC1-HC2 and CV5-CV6 respectively, with a minimum at HC3-HC4.
This is consistent with the mean true parallaxes quoted in Col. 3 of Table 2:
they show a minimum in the same range. Those rarer HC3 to HC5 stars are observed farther from Sun
on average. We also notice a minimum at CV4. It can be considered an artifact of our
classification which is tighter in effective temperatures
at CV4-CV5 than it is at CV3-CV4 or CV5-CV6 (Bergeat et al. 2001). If only one
group (CV4-5) was adopted instead, it would have been the most populated one in the
whole diagram. This interpretation will be confirmed in Sect. 7.
| HC0 | HC1 | HC2 | HC3 | HC4 | HC5 | CV1 | CV2 | CV3 | CV4 | CV5 | CV6 | CV7 | SCV |
| 0.6 | 4.9 | 4.6 | 3.3 | 3.2 | 3.8 | 5.8 | 7.7 | 8.2 | 5.7 | 10.1 | 12.6 | 3.6:
|
1.6 |
|
|
3.84 | 3.81 | 3.78 | 3.75 | 3.72 | 3.69 | 3.66 | 3.63 | 3.60 | 3.57 | 3.54 |
|
|
3.81 | 3.78 | 3.75 | 3.72 | 3.69 | 3.66 | 3.63 | 3.60 | 3.57 | 3.54 | 3.51 |
|
|
0.70 | 0.35 | 1.40 | 0.53 | 2.28 | 3.33 | 3.15 | 4.90 | 3.15 | 3.15 | 6.48 |
|
|
|||||||||||
|
|
3.51 | 3.48 | 3.45 | 3.42 | 3.39 | 3.36 | 3.33 | 3.30 | 3.27 | 3.24 | |
|
|
3.48 | 3.45 | 3.42 | 3.39 | 3.36 | 3.33 | 3.30 | 3.27 | 3.24 | 3.21 | |
|
|
5.96 | 13.7 | 11.4 | 5.78 | 4.38 | 0.70:
|
1.93:
|
1.40:
|
0.70:
|
0.35:
|
|
|
|
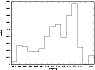 |
Figure 4: The distribution of the 567 studied carbon stars in the fourteen groups. The scale is normalized for a total of unity. |
| Open with DEXTER | |
The present statistics relies on a sample about twice the HIPPARCOS one. The existence is confirmed of two great families in those samples (HC and CV+SCV), made of distinct stellar populations (Sect. 5).
The sequence of the HC- and CV-groups correlates well with that of decreasing effective
temperatures from Bergeat et al. (2001) for 432 SEDs. The values are distributed in
the range
| (40) |
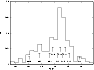 |
Figure 5: The distribution of the 432 SEDs of carbon stars with effective temperatures (arrows point to mean values). |
| Open with DEXTER | |
The maximum of Fig. 5 is located near
![]() centered
at 2820 K, i.e. at nearly CV4
centered
at 2820 K, i.e. at nearly CV4
![]() The minimum of Fig. 4 at CV4 has no counterpart here. It is thus an artifact of the
classification which is tighter in effective temperatures at CV4-CV5. A relative minimum is
hardly noticed in the range
The minimum of Fig. 4 at CV4 has no counterpart here. It is thus an artifact of the
classification which is tighter in effective temperatures at CV4-CV5. A relative minimum is
hardly noticed in the range
![]() or
or
![]() that is near HC5-HC3, which corresponds
to the minimum in Fig. 4. The asymmetric distribution is still compatible with
the existence of the two families (HC and CV). An additional minimum is observed at
that is near HC5-HC3, which corresponds
to the minimum in Fig. 4. The asymmetric distribution is still compatible with
the existence of the two families (HC and CV). An additional minimum is observed at
![]() (2140-2290 K) since few CV6 or CV7 stars fall in this
range. The calibration of effective temperatures is difficult here
(Bergeat et al. 2001). Also part of the CV7-stars are missing.
The reality and meaning of this latter minimum is questionable.
A systematic underestimate of nearly 100 K in the calibration of the CV7 stars
cannot be ruled out. Alternatively, a true jump in
(2140-2290 K) since few CV6 or CV7 stars fall in this
range. The calibration of effective temperatures is difficult here
(Bergeat et al. 2001). Also part of the CV7-stars are missing.
The reality and meaning of this latter minimum is questionable.
A systematic underestimate of nearly 100 K in the calibration of the CV7 stars
cannot be ruled out. Alternatively, a true jump in
![]() can intervene at the
CV6-CV7 junction, as induced by substantial photospheric opacities from circumstellar
dust at
can intervene at the
CV6-CV7 junction, as induced by substantial photospheric opacities from circumstellar
dust at
![]()
| Type | n |
|
|
|
|
|
|
|
|
|
| mas | mas | km s-1 | kpc | kpc | km s-1 | km s-1 | K | |||
| CV | 195 |
|
|
|
|
|
|
|
2720 | -4.6 |
| (+SCV) | ||||||||||
| HC | 104 |
|
|
|
|
|
|
|
4350 | -1.8 |
| HC | 81 |
|
|
|
|
|
|
|
4300 | -1.7 |
| (1) | ||||||||||
| HC | 12 |
|
|
|
|
|
|
|
5400 | -1.8 |
| (2) | ||||||||||
| HC | 23 |
|
|
|
|
|
|
|
4170 | -1.6 |
| (3) |
Prior to a detailed analysis of the velocities, we derive the mean values of the radial
components
![]() and those of the tangential ones from proper motions
and parallaxes i.e.
and those of the tangential ones from proper motions
and parallaxes i.e.
![\begin{displaymath}V_{\rm {t}}\simeq 4.738\left[ \left(\mu_{\alpha}\cos \delta \...
...a}^{2}
\right] ^{1/2}/\,\varpi \simeq 4.738 \, \mu /\, \varpi.
\end{displaymath}](/articles/aa/full/2002/13/aa1555/img306.gif) |
(41) |
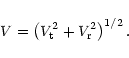 |
(42) |
It is remarkable that all confirmed CH stars on the one hand and the HdC stars on the other hand,
are all contained in the HC photometric groups (specifically the "hot carbon stars''
with
![]() Bergeat et al. 2001). Conversely the
13C-rich stars or J-stars, are found in both the HC and CV-groups. Mean values and
dispersions are quoted in Table 7 for five samples
Bergeat et al. 2001). Conversely the
13C-rich stars or J-stars, are found in both the HC and CV-groups. Mean values and
dispersions are quoted in Table 7 for five samples
 |
(43) |
Concerning velocities, marked differences are observed. The CV-stars display the smallest mean
proper motions and velocities
(with
![]() )
and
consistently, a mean distance to the Galactic plane less than those of the HC-stars. For
the HC-stars, the mean proper motions and radial velocities are 2-3 times the respective values
for the CV-stars. The velocities of the HC(1)-sample (CH stars omitted) are twice those of the
CV-sample. Finally, the CH stars (HC(3) sample) do have mean velocities which are twice the
overall mean for the HC-sample they strongly affect.
The mean distances to the Galactic plane are however similar for the three samples as
found for mean true parallaxes. Conversely, the HdC and RCB stars (sample HC(2)) display
simultaneously smaller mean velocities and a stronger concentration to the Plane than stars of
the whole HC-sample. Those latter two subsamples are however very small (n=23 and 12
respectively) and the conclusions are only provisional.
)
and
consistently, a mean distance to the Galactic plane less than those of the HC-stars. For
the HC-stars, the mean proper motions and radial velocities are 2-3 times the respective values
for the CV-stars. The velocities of the HC(1)-sample (CH stars omitted) are twice those of the
CV-sample. Finally, the CH stars (HC(3) sample) do have mean velocities which are twice the
overall mean for the HC-sample they strongly affect.
The mean distances to the Galactic plane are however similar for the three samples as
found for mean true parallaxes. Conversely, the HdC and RCB stars (sample HC(2)) display
simultaneously smaller mean velocities and a stronger concentration to the Plane than stars of
the whole HC-sample. Those latter two subsamples are however very small (n=23 and 12
respectively) and the conclusions are only provisional.
The HC and CV-stars clearly belong to two
distinct populations on kinematic grounds, as was the case for locations (Sect. 5).
The differences are very large when the CH stars are included (HC in
Table 7), and remain marked when they are rejected (sample HC(1)).
We have noticed that
![]() for the
CV-stars located on orbits close to the Galactic plane. This is also the case for the
HC(1)-sample which is supposed to be free of CH stars. Conversely, it is observed that
for the
CV-stars located on orbits close to the Galactic plane. This is also the case for the
HC(1)-sample which is supposed to be free of CH stars. Conversely, it is observed that
![]() for the
HC- and HC(3)-samples. The causes for those differences appear in the detailed analyses
of Sects. 9 and 11.
for the
HC- and HC(3)-samples. The causes for those differences appear in the detailed analyses
of Sects. 9 and 11.
Mean effective temperatures from Bergeat et al. (2001) and mean absolute bolometric
magnitudes (Knapik et al. 2001) freed from the bias described by Smith & Eichhorn
(1996), and corrected for the influence of the Malmquist bias as described in
Sect. 4, are quoted in Table 7. It is confirmed that the HdC and RCB stars
are found in the high effective temperatures fringe of the HC-stars. No such trend is seen
for the CH stars. No significant difference is found between the
![]() -values of the three HC subsamples which are surprisingly close to
one another.
-values of the three HC subsamples which are surprisingly close to
one another.
The basic considerations of the present section can be found in Mihalas & Binney (1981, Sect. 6) and the used equations are given in Appendix A. We have adopted for the velocity components, the following usual frame: the U-axis towards the Galactic anticenter, the V-axis towards the direction of Galactic rotation, both axes lying in the Galactic plane, and the W-axis pointing towards the North Galactic Pole.
Calculating the mean values
![]() and
and
![]() from Eqs. (A5) to (A7), we meet the same bias
as described in Sect. 3.1. It originates from the very fact that the
components are not linear functions of the true parallax
from Eqs. (A5) to (A7), we meet the same bias
as described in Sect. 3.1. It originates from the very fact that the
components are not linear functions of the true parallax ![]() .
We use angular velocities
instead, which are linear in
.
We use angular velocities
instead, which are linear in ![]() viz.
viz.
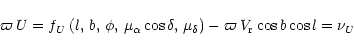 |
(44) |
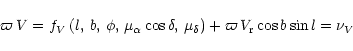 |
(45) |
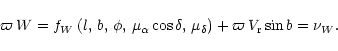 |
(46) |
| = | |||
| = | (47) |
We have however conducted various tests, such as the diagrams of U, V and W vs.
![]() where the "rule of thumb'' was applied and least square regressions as well. The former
method may help in detecting possible failures in the latter one. No significant correlation was
found.
where the "rule of thumb'' was applied and least square regressions as well. The former
method may help in detecting possible failures in the latter one. No significant correlation was
found.
Making use of Eqs. (A8), (A11) and (A12), the solar velocities were derived for four
samples (Table 8), (1) the CV-stars, (2) the HC-stars, (3) the HC-stars not
confirmed as CH stars (HC'), and (4) the confirmed CH stars. Error estimates are also given.
The latter were evaluated in a rough way, for various accuracies of estimated true parallaxes
as quoted in Paper I, quoted errors on observed proper motion components (ESA 1997),
and errors or quality quotation (a, b...) of observed radial velocities. The influence of
relative errors on proper motions proves negligible. The influence of estimated true
parallaxes is usually larger than that of radial velocities. When inaccurate, the latter may
occasionally play a role. The degree of correlation, usually small, of the various terms in the
Appendix equations, is difficult to estimate, especially for small samples corresponding to
individual photometric groups.
| S | n |
|
|
|
|
|||
| CV | 180 | -2.3 | 5.85 | -0.6 | 4.3 | 7.6 | 68 | 34 |
| HC | 90 | -16.3 | 30.5 | -25.3 | 6.5 | 35.2 | 62 | 11 |
| HC' | 70 | -14.6 | 11.0 | -5.7 | 3.8 | 18.65 | 37 | 12 |
| CH | 20 | -29 | 117 | -112 | 21 | 122 | 76 | 10 |
| C | 427 | -9.6 | 11.7 | -6.5 | 4.6 | 15.8 | 51 | 17 |
| CH | 51 | -1 | 147 | -142 | 9 | 147 | 90 | 3.5 |
| SSM | -10.4 | 14.8 | -9.6 | 7.3 | 19.5 | 56 | 23 | |
| BSM | -9 | 11 | -5.75 | 6 | 15.4 | 51 | 23 | |
| PSV | -9 | 12 | -6.75 | 7 | 16.5 | 53 | 25 | |
| SLS | -10.0 | 5.25 | 0.0 | 7.17 | 13.4 | 28 | 32 | |
The results are compared to the values derived by Dean (1976) from a sample (C)
of 427 radial velocities. The majority of Dean's stars are CV-stars but some HC-stars were
included as well, which probably explain why his data seem intermediate between ours for the
CV- and HC-samples respectively. Its mean value of the distance to the Galactic plane is however
![]() which is practically our value
which is practically our value
![]() for the CV-stars (Table 7). The same is true for the stellar
residual-velocities distributions (see Sect. 11 and Table 11), except for the
component perpendicular to the Galactic plane which is slightly smaller than ours for the
CV-sample.
for the CV-stars (Table 7). The same is true for the stellar
residual-velocities distributions (see Sect. 11 and Table 11), except for the
component perpendicular to the Galactic plane which is slightly smaller than ours for the
CV-sample.
We have added in Table 8 the results for the standard solar motion (SSM)
and for the basic solar motion (BSM) as given by Mihalas & Binney (1981, p. 398).
The components of the peculiar velocity of the Sun relative to the LSR (namely PSV) from Mihalas
& Binney (1981, p. 400) are also given. We however adopt the values
![]()
| (48) |
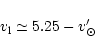 |
(49) |
The same lag is responsible for
![]() for the HC-group,
while
for the HC-group,
while
![]() for the HC'-group is close to the values for SSM
and BSM. The apex coordinates are roughly consistent for the five groups considered. The values
of
for the HC'-group is close to the values for SSM
and BSM. The apex coordinates are roughly consistent for the five groups considered. The values
of
![]() and
and ![]() for CV-stars are all small ones. There is
no appreciable lag or leading of the CV-sample with respect to the Sun. These results confirm
the CV-groups belonging to a classic disk population (or thin disk). The HC-groups seem again
representative of an older kinematic population (thick disk). It is contaminated by a
spheroidal component, the CH stars, which is similar to the sample of Hartwick & Cowley
(1985).
for CV-stars are all small ones. There is
no appreciable lag or leading of the CV-sample with respect to the Sun. These results confirm
the CV-groups belonging to a classic disk population (or thin disk). The HC-groups seem again
representative of an older kinematic population (thick disk). It is contaminated by a
spheroidal component, the CH stars, which is similar to the sample of Hartwick & Cowley
(1985).
Bergeat et al. (2001) have shown that the sequence of photometric groups from HC0 to HC5 and then from CV1 to CV7 is a sequence of decreasing effective temperatures. It is also a sequence of increasing luminosities as shown by Knapik (1999) and Knapik et al. (2001). The mean values displayed in Table 3 illustrate this result. The analysis of the kinematic trends along this sequence is thus tempting, but limited by low accuracy.
The average solar velocities and apex coordinates as obtained for 11 of
the 14 photometric groups are given in Table 9.
A clear-cut dichotomy between the HC- and CV-groups, is confirmed.
The solar space velocity drops from more than
![]() to
to
![]() and the jump seems to occur between HC5 and CV1.
and the jump seems to occur between HC5 and CV1.
| G | i | n |
|
|
|
|||
| HC1 | 1 | 23 | 6 | 28 | 27 | 39 | -78 | 43 |
| HC1* | 1 | 18 | -7 | 25 | 14 | 30 | 75 | 28 |
| HC2 | 2 | 25 | -43 | 69 | 2 | 82 | 58 | 1.4 |
| HC2* | 2 | 18 | -27 | 24 | 0.9 | 36 | 42 | 1.4 |
| HC3 | 3 | 14 | -18 | -11 | -13 | 25 | -33 | -31 |
| HC3* | 3 | 12 | -18 | -15 | -6 | 24 | -41 | -14 |
| HC4 | 4 | 12 | -6 | 24 | 31 | 39 | 77 | 51 |
| HC4* | 4 | 7 | -15 | 0.1 | 22 | 27 | 0.2 | 56 |
| HC5 | 5 | 16 | -13 | 29 | -17 | 36 | 66 | 28 |
| HC5* | 5 | 15 | -6 | 4 | -6 | 9 | 33 | 36 |
| CV1 | 6 | 29 | -6 | 9 | -6 | 13 | 56 | 27 |
| CV2 | 7 | 43 | -0.4 | 7 | 3 | 7 | 86 | 22 |
| CV3 | 8 | 30 | -9 | 6 | 12 | 16 | 33 | 48 |
| CV4 | 9 | 28 | -6 | 2 | 2 | 7 | 19 | 15 |
| CV5 | 10 | 27 | 2 | 8 | 5 | 9 | -74 | 30 |
| CV6 | 11 | 24 | 7 | 2 | 12 | 14 | -15 | 57 |
| HC1* | 1.5 | 36 | -17 | 25 | 7 | 31 | 56 | 14 |
| +HC2* | ||||||||
| HC3* | 3.4 | 19 | -17 | -10 | 4 | 20 | -30 | 13 |
| +HC4* |
Since the CH stars are considered as halo tracers, we also computed the solar velocities in new
HC-samples without the confirmed CH stars (star-symbols in Table 9). No
confirmed CH star was found in the CV-groups. The most outstanding result is that the
HC-like velocity data of HC5 is entirely due to one star, namely
![]() ,
and that the
HC5*-results are seemingly CV-like. A ratio of 2.7 however remains between the mean solar
velocities of the HC1*- to HC4*-groups
,
and that the
HC5*-results are seemingly CV-like. A ratio of 2.7 however remains between the mean solar
velocities of the HC1*- to HC4*-groups
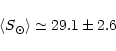 |
(50) |
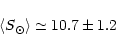 |
(51) |
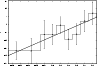 |
Figure 6:
The |
| Open with DEXTER | |
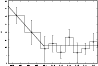 |
Figure 7:
The |
| Open with DEXTER | |
Revisiting the data on mean distances to the Galactic plane, we could see that despite
the HC5 high value
![]() (see Table 2), the poorly-documented distribution
(see Table 2), the poorly-documented distribution
![]() seems finally CV-like. Removing V Ari only reduces
seems finally CV-like. Removing V Ari only reduces
![]() to 0.44. We conclude that the
space distribution and the kinematics of HC5* are typically CV-like, but that the populated
galactic volume (i.e. the galactic scale above the plane) is rather HC-like.
Between mean values, a difference was found at
to 0.44. We conclude that the
space distribution and the kinematics of HC5* are typically CV-like, but that the populated
galactic volume (i.e. the galactic scale above the plane) is rather HC-like.
Between mean values, a difference was found at ![]() ,
on the first coordinate,
with for the HC1* to HC4* sample
,
on the first coordinate,
with for the HC1* to HC4* sample
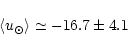 |
(52) |
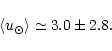 |
(53) |
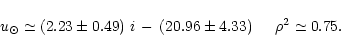 |
(54) |
| (55) |
The solar reflex velocities toward the Galactic anticenter
![]() increase along the HC-CV sequence of photometric groups, from negative values (i.e. directed
towards Galactic center) to slightly positive ones. From radial velocity measurements of 179
carbon stars towards the Galactic anticenter, Metzger & Schechter (1994) already
found that their sample is moving radially outward with respect to the LSR at a velocity of
increase along the HC-CV sequence of photometric groups, from negative values (i.e. directed
towards Galactic center) to slightly positive ones. From radial velocity measurements of 179
carbon stars towards the Galactic anticenter, Metzger & Schechter (1994) already
found that their sample is moving radially outward with respect to the LSR at a velocity of
![]() i.e. corresponding to
i.e. corresponding to
![]() which is very close to our average
which is very close to our average
![]() for 270 carbon stars.
There is actually no reason to favor linear relations
and curved fits might prove better for
for 270 carbon stars.
There is actually no reason to favor linear relations
and curved fits might prove better for ![]() and
and ![]() when more accurate data
will be available. Clearly more data is needed before a firm conclusion can
be reached. Intruders from the halo may well remain in the HC*-samples.
when more accurate data
will be available. Clearly more data is needed before a firm conclusion can
be reached. Intruders from the halo may well remain in the HC*-samples.
Dehnen (2000) studied the HIPPARCOS data for 3527 main-sequence stars with
![]() and 2491 mainly late-type non-main-sequence stars, high velocity stars excluded.
In a
and 2491 mainly late-type non-main-sequence stars, high velocity stars excluded.
In a
![]() -diagram (velocities relative to LSR and u-axis towards Galactic
center: his Fig. 9, p. 809), he found a bimodal distribution he attributed to the effect of
the second Lindblad resonance. Our data (after subtraction
of the solar motion relative to LSR of Dehnen & Binney 1998) coincide
with his principal mode (essentially his sample of early-type stars, including the Sun).
No coincidence was found with his secondary mode (intermediate velocities) mainly populated by
late-type stars.
-diagram (velocities relative to LSR and u-axis towards Galactic
center: his Fig. 9, p. 809), he found a bimodal distribution he attributed to the effect of
the second Lindblad resonance. Our data (after subtraction
of the solar motion relative to LSR of Dehnen & Binney 1998) coincide
with his principal mode (essentially his sample of early-type stars, including the Sun).
No coincidence was found with his secondary mode (intermediate velocities) mainly populated by
late-type stars.
| G | n |
|
|
|
|
|||
| Lb | 86 | -0.2 | 14 | -8.7 | -1.0 | 14 | 89 | -4 |
| SRb | 77 | -4.9 | 3.5 | 1.8 | 6.8 | 9.0 | 35 | 49 |
| Miras | 29 | 1.9 | 5.2 | 0.0 | 9.0 | 11 | -71 | 58 |
| M+SRa | 43 | 1.0 | 2.7 | 2.5 | 7.9 | 8.5 | -71 | 70 |
| LPV 1 | 56 | -6.0 | 2.9 | 2.3 | 5.7 | 8.8 | 26 | 41 |
| LPV 2 | 54 | 1.3 | 3.7 | 1.6 | 12 | 13 | -71 | 73 |
| Cst | 61 | -18 | 42 | -37 | 13 | 48 | 67 | 15 |
| Cst* | 42 | -11 | 24 | -19 | 6.9 | 27 | 66 | 15 |
We have considered samples delineated according to the classification scheme of the GCVS catalog of Kholopov et al. (1985). Again the components of the reflex solar velocity were derived from the method used in Sect. 9. The results are quoted in Table 10. The distribution of the carbon stars in terms of photometric groups is shown in Fig. 8 for every variability class (M for carbon Miras, SRa for large amplitude semi-regular variables, SRb for smaller amplitude semi-regulars, Lb for irregular variables and Cst for constant stars). It appears that the constant stars are also HC-stars while most of the variable carbon stars are found in the CV-groups as first-intended. Also, the Lb-variables are predominantly HC5 to CV3, which makes them intermediate. Then, the SRb-variables are abundant from HC5 to CV6, while the SRa-variables and Miras appear as more concentrated between CV4 and CV7. There is a statistical correlation between the sequence of increasing variability "Cst, Lb, SRb, SRa and Miras" and the sequence of photometric groups "HC1 to CV7''. This point will be further discussed in Knapik et al. (2001), together with mean luminosities.
The sample of the irregular (Lb) variables is the largest one. It displays a slight lag in
![]() which makes it again intermediate between the other variables on one hand and the
constant stars on the other hand. While the former have practically no lag like the CV-stars,
the latter show an appreciable lag like the HC-stars (Table 8 and
Table 10). The compositions of variability classes as shown in
Fig. 8, explain those results. The Lb- and SRb-samples contain 2 and 3 CH stars
respectively. Removing them does not change appreciably the results of
Table 10). Conversely, a Cst*-sample is
considered from which 19 CH stars were rejected. The lag
which makes it again intermediate between the other variables on one hand and the
constant stars on the other hand. While the former have practically no lag like the CV-stars,
the latter show an appreciable lag like the HC-stars (Table 8 and
Table 10). The compositions of variability classes as shown in
Fig. 8, explain those results. The Lb- and SRb-samples contain 2 and 3 CH stars
respectively. Removing them does not change appreciably the results of
Table 10). Conversely, a Cst*-sample is
considered from which 19 CH stars were rejected. The lag
![]() and the spatial velocity
and the spatial velocity
![]() are almost halved in this latter sample.
are almost halved in this latter sample.
We also considered two subsamples, namely LPV 1
with
![]() and LPV 2 with
and LPV 2 with
![]() The latter is dominated by Miras and
SRas and the solution found is consistent.
The solar velocity for the LPV 1 sample is close to the result
for the SRb-sample. The trend to larger components of the solar
reflex velocity for shorter periods, as shown by oxygen-rich LPVs (e.g. Delhaye
1965; Mihalas & Binney 1981, Table 6.3 p. 396), is not found here.
Those latter giants presumably correspond to the second mode (Sect. 9) of Dehnen
(2000).
The latter is dominated by Miras and
SRas and the solution found is consistent.
The solar velocity for the LPV 1 sample is close to the result
for the SRb-sample. The trend to larger components of the solar
reflex velocity for shorter periods, as shown by oxygen-rich LPVs (e.g. Delhaye
1965; Mihalas & Binney 1981, Table 6.3 p. 396), is not found here.
Those latter giants presumably correspond to the second mode (Sect. 9) of Dehnen
(2000).
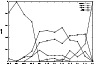 |
Figure 8: The distribution of the 276 HIPPARCOS carbon stars with variability class amongst the photometric groups, normalized to unity. |
| Open with DEXTER | |
We finally study the stellar residual-velocity distributions, determining their axes and maximal dispersions, and then the dispersions along the three galactic axes. We make use of a method adapted from Charlier (1926), already adopted by Bergeat et al. (1978). An account of Charlier's method can be found in Atanasijevic (1971).
We abandoned the idea of a detailed study of the residual-velocity distributions in each
photometric group, due to small samples and low accuracy.
The results are summarized in Table 11, where the dispersions
are significantly higher for the HC-sample than for the CV-sample. The ratio ranges from
2.3 (third axis) to about 4 (first and second axes which are nearly in the Galactic plane).
Removing the confirmed CH stars, we obtain the HC'-sample whose velocity dispersions are about
twice those
of the CV-sample, whichever axis is considered. Those results again point to two distinct
populations, the HC one being contaminated by a contribution from halo (CH stars). The vertical
dispersion of 42 to
![]() observed for the HC'- and HC-samples, is typical of
the thick disk (
observed for the HC'- and HC-samples, is typical of
the thick disk (
![]() ,
Freeman 1987a; Gilmore 1989)
while the value of
,
Freeman 1987a; Gilmore 1989)
while the value of
![]() for the CV-sample is representative of the old (thin)
disk (
for the CV-sample is representative of the old (thin)
disk (
![]() ;
Gilmore 1989).
More specifically, the three velocity components usually adopted for the thick disk from
Norris (1999) and for the old disk from Freeman (1987a) are given
for comparison with the values for the HC'- and CV-samples respectively. The agreement is
excellent in both cases. As usual,
it is found that the third axis (smallest extreme dispersion) of the velocity ellipsoid
is oriented nearly perpendicular to the Galactic plane, and the other two axes lie
approximately in the Plane. Usually, the direction of the largest velocity dispersion is
nearly toward the Galactic center. This is very nearly the case of the CV-sample.
;
Gilmore 1989).
More specifically, the three velocity components usually adopted for the thick disk from
Norris (1999) and for the old disk from Freeman (1987a) are given
for comparison with the values for the HC'- and CV-samples respectively. The agreement is
excellent in both cases. As usual,
it is found that the third axis (smallest extreme dispersion) of the velocity ellipsoid
is oriented nearly perpendicular to the Galactic plane, and the other two axes lie
approximately in the Plane. Usually, the direction of the largest velocity dispersion is
nearly toward the Galactic center. This is very nearly the case of the CV-sample.
| S | n | j | Lj | Bj |
|
|
|
|
|
CV
|
180 | 1 | 5.3 | 1.9 | 30.2 | 30.1 | 22.2 | 23.4 |
| 2 | 93.8 | 38.3 | 22.1 | |||||
| 3 | 277.7 | 51.6 | 23.4 | |||||
| C
|
427 | 29.8 | 19.8 | 14.0 | ||||
| OD
|
40 | 25 | 20 | |||||
|
HC
|
90 | 1 | 74.0 | 15.0 | 106.0 | 85.4 | 104.3 | 54.4 |
| 2 | 343.2 | -2.9 | 83.3 | |||||
| 3 | 62.4 | -74.7 | 54.4 | |||||
| HC'
|
70 | 1 | 328.5 | 15.4 | 59.6 | 59.0 | 57.8 | 42.1 |
| 2 | 56.4 | 8.0 | 57.0 | |||||
| 3 | 300.5 | -72.7 | 42.3 | |||||
| TD
|
65 | 54 | 38 | |||||
|
CH
|
20 | 1 | 756 | 17 | 281 | 163 | 277 | 85 |
| 2 | 349 | 12 | 156 | |||||
| 3 | 293 | 68 | 86 | |||||
| CH
|
51 | ? | 161 | 125 |
Making use of the age versus velocity (AVR) relation of Wielen et al. (1992), the
![]() obtained for the space velocities of CV-stars of
Table 11 would correspond to an average of
obtained for the space velocities of CV-stars of
Table 11 would correspond to an average of
![]() Within the uncertainties,
the AVR of Carlberg et al. (1985) would yield
Within the uncertainties,
the AVR of Carlberg et al. (1985) would yield
![]() The two relations actually differ. From an analysis of the HR diagram and pulsation masses
(Knapik et al. 2001), we favor the former age but there is probably a
considerable spread in individual values from a few 102 Myr up to 8-12 Gyr.
The values for the HC-groups fell completely outside the AVRs published in both papers.
It is clear again that the
HC-stars are a distinct older population with large velocity dispersions. The various lags
of CH stars along the v-axis
influence the dispersions in the Galactic plane, and deviate the vertex axis.
The two relations actually differ. From an analysis of the HR diagram and pulsation masses
(Knapik et al. 2001), we favor the former age but there is probably a
considerable spread in individual values from a few 102 Myr up to 8-12 Gyr.
The values for the HC-groups fell completely outside the AVRs published in both papers.
It is clear again that the
HC-stars are a distinct older population with large velocity dispersions. The various lags
of CH stars along the v-axis
influence the dispersions in the Galactic plane, and deviate the vertex axis.
The space distribution and velocity data of HIPPARCOS carbon-rich giants were studied in
detail. The biases (Lutz-Kelker, Smith-Eichhorn and Malmquist) were investigated, refining the
analysis of Paper I. While the Lutz-Kelker bias (1973) is accounted for in our
estimated true parallaxes, the bias described by Smith & Eichhorn (1996) is avoided,
as far as possible, by averaging on quantities which are linear functions of parallaxes.
Corrections for mean distances and absolute magnitudes were proposed to account for the
Malmquist bias (1924, 1936). They prove to be small here. The exponent
in the frequency distribution of true parallaxes is however increased from -2.9 or
![]() (uniform slab) to
(uniform slab) to
![]() by the Malmquist bias. The HIPPARCOS sample
seems almost complete up to a distance of nearly 1 kpc from the sun. It was shown that the
average height above the Plane is
by the Malmquist bias. The HIPPARCOS sample
seems almost complete up to a distance of nearly 1 kpc from the sun. It was shown that the
average height above the Plane is
![]() for the HC-stars, about
three times that of the CV-stars, viz.
for the HC-stars, about
three times that of the CV-stars, viz.
![]() .
.
The vertical space distributions are described in terms of a simple exponential law with a
distance
scale for HC-stars much larger (
![]() thick disk) than that for the CV-stars
(
thick disk) than that for the CV-stars
(
![]() thin disk). The local densities in the Plane and projected surface
densities were deduced, with an estimated total of nearly
thin disk). The local densities in the Plane and projected surface
densities were deduced, with an estimated total of nearly
![]() among which
29% are HC-stars. If the HC5-stars (whose case is not clear) are rejected, this percentage falls
to 24% with 18% attributed to thick disk HC-stars and 6% to halo CH stars. Detailed densities
were established in terms of photometric groups and effective temperatures, confirming asymmetric
and bimodal distributions (HC- and CV-zones).
among which
29% are HC-stars. If the HC5-stars (whose case is not clear) are rejected, this percentage falls
to 24% with 18% attributed to thick disk HC-stars and 6% to halo CH stars. Detailed densities
were established in terms of photometric groups and effective temperatures, confirming asymmetric
and bimodal distributions (HC- and CV-zones).
The mean radial and tangential velocities with respect to the Sun turn out to be about
![]() for 195 CV-stars and about
for 195 CV-stars and about
![]() for 81 non-CH
HC-stars, that is an unambiguous ratio of 2, suggestive of distinct kinematic populations.
Those average velocities are much higher for 23 confirmed CH stars, in excess of
for 81 non-CH
HC-stars, that is an unambiguous ratio of 2, suggestive of distinct kinematic populations.
Those average velocities are much higher for 23 confirmed CH stars, in excess of
![]() The reflex solar velocity with respect to our groups was then
calculated and compared to reference motions. Also they are quite consistent with previous
results for carbon stars. While the CH stars show halo velocities with a
substantial drift of
The reflex solar velocity with respect to our groups was then
calculated and compared to reference motions. Also they are quite consistent with previous
results for carbon stars. While the CH stars show halo velocities with a
substantial drift of
![]() in the v-velocity, typical of a slowly
rotating system (Hartwick & Cowley found
in the v-velocity, typical of a slowly
rotating system (Hartwick & Cowley found
![]() ), the contaminated
HC-sample shows only
), the contaminated
HC-sample shows only
![]() In the case of the HC'-sample, it is even
smaller (
In the case of the HC'-sample, it is even
smaller (
![]() ), i.e. in the low-range drift velocity of thick disk
tracers (Majewski 1993) with median distances from plane of about 0.5 kpc.
No appreciable lag is found for the CV-stars (
), i.e. in the low-range drift velocity of thick disk
tracers (Majewski 1993) with median distances from plane of about 0.5 kpc.
No appreciable lag is found for the CV-stars (
![]() ), whose space
distributions and velocities are typical of the thin disk, most of them being younger and
more massive than the Sun. Large velocities perpendicular to the Plane are observed mostly
for the CH stars. The
), whose space
distributions and velocities are typical of the thin disk, most of them being younger and
more massive than the Sun. Large velocities perpendicular to the Plane are observed mostly
for the CH stars. The ![]() -component increases
along the sequence of photometric groups. Correspondingly, the space velocity
-component increases
along the sequence of photometric groups. Correspondingly, the space velocity ![]() appears
as 2.7 times larger for HC*-stars than it is for CV-stars.
appears
as 2.7 times larger for HC*-stars than it is for CV-stars.
The analyses according to variability classes illustrate the fact that variables are essentially in the CV-groups while constant stars are found in the HC-groups. Amongst the carbon variables, the irregular variables (Lb-class) exhibit kinematic data (lag and space velocity), intermediate between the other variables and the constant stars.
Finally, the ellipsoids of the residual velocities of HC- and CV-stars were investigated.
The dispersions of the HC sample range from 2.3 to 4 times higher than those of the CV-sample.
The ratio still amounts to about 2 when the non-CH HC stars (i.e. the HC'-sample) are
considered. Their dispersions are remarkably close to the values quoted by Norris
(1999) for the bulk thick disk stars. The
![]() value is characteristic of the thick disk
population at the solar distance from the Galactic center (Freeman 1987a, p. 612).
The dispersions of the CV-sample are very close to the values usually quoted for the old disk
(Freeman 1987a).
Making use of the age vs. velocity relations (AVR) of Wielen et al. (1992), we
obtained 3 Gyr as a typical average age of the CV-sample, and 6 Gyr from the relation of
Carlberg et al. (1985), which seems less likely. The individual values
probably range from a few hundred million years up to 8-12 Gyr. The HC and HC'-samples clearly
fall outside those relations, and low-mass stars with ages in excess of 10 Gyr are indicated.
value is characteristic of the thick disk
population at the solar distance from the Galactic center (Freeman 1987a, p. 612).
The dispersions of the CV-sample are very close to the values usually quoted for the old disk
(Freeman 1987a).
Making use of the age vs. velocity relations (AVR) of Wielen et al. (1992), we
obtained 3 Gyr as a typical average age of the CV-sample, and 6 Gyr from the relation of
Carlberg et al. (1985), which seems less likely. The individual values
probably range from a few hundred million years up to 8-12 Gyr. The HC and HC'-samples clearly
fall outside those relations, and low-mass stars with ages in excess of 10 Gyr are indicated.
We conclude that the CV-sample is a component of the old (thin) disk. Most HC-stars are members of the thick disk with contaminations from halo CH stars and a few CV-stars. Conversely, the Mira V CrB (CV7) might be a halo intruder on the basis of its high velocities, especially perpendicular to Plane. The thick-disk membership on the basis of space distribution and velocities, and the high space density of HC-stars, are certainly important clues in the investigation of the true nature of the mysterious hot carbon stars, which have lower metallicities on average (e.g. Wallerstein & Knapp 1998). Less dragged-up carbon is needed to make a carbon star from a star with low initial O/H ratio, and low mass stars do have smaller hydrogen-rich envelopes to enrich of only a few tenths of one solar mass. Possible correlations of kinematics and metallicities need be investigated (see Prochaska et al. 2000 for stellar abundances in the thick disk).
The HC-stars are relatively low-luminosity objects with
![]() (Tables 3 & 7). The third Dredge-up process of carbon
and (eventually) s-process elements in TP-AGB stars (Iben & Renzini 1983) occurs
only for
(Tables 3 & 7). The third Dredge-up process of carbon
and (eventually) s-process elements in TP-AGB stars (Iben & Renzini 1983) occurs
only for
![]() depending on details of the models and codes used
(e.g. Marigo et al. 1999). Those models fail to explain the HC-stars. Full
discussion of this topic is postponed to a future paper (Knapik et al. 2001). For
the time being, we emphasize the point that the high frequency of the thick disk HC'-stars
depending on details of the models and codes used
(e.g. Marigo et al. 1999). Those models fail to explain the HC-stars. Full
discussion of this topic is postponed to a future paper (Knapik et al. 2001). For
the time being, we emphasize the point that the high frequency of the thick disk HC'-stars
![]() is a strong argument against theories necessitating
rare events. The binary model itself, for which no evidence was found in the observations
of HC'-stars (McClure 1997a), seems unlikely. The discrepancy possibly originates in
insufficient knowledge of mixing processes in low-mass stars evolving along RGB and AGB or at
He-flash, prior to TP-AGB (Busso et al. 1999).
is a strong argument against theories necessitating
rare events. The binary model itself, for which no evidence was found in the observations
of HC'-stars (McClure 1997a), seems unlikely. The discrepancy possibly originates in
insufficient knowledge of mixing processes in low-mass stars evolving along RGB and AGB or at
He-flash, prior to TP-AGB (Busso et al. 1999).
Suntzeff et al. (1993) have studied a sample of stars in the Large Magellanic Cloud
(LMC), suspected to be CH stars, which are very luminous
![]() Our CH stars are actually much fainter (-1.8). If confirmed, the existence of such
bright CH stars should probably be explained in terms of evolutive tracks for LMC metallicity
Our CH stars are actually much fainter (-1.8). If confirmed, the existence of such
bright CH stars should probably be explained in terms of evolutive tracks for LMC metallicity
![]() shifted towards higher effective temperatures with respect to
tracks for solar abundances
shifted towards higher effective temperatures with respect to
tracks for solar abundances
![]() The carbon stars Azzopardi et al.
(1991) and Westerlund et al. (1991) ascribed to the Galactic bulge
(spheroidal region extending about 3 kpc from
the Galactic center) are finally much closer to our HC-stars. Westerlund et al.
(1995) published the HR diagram of 20 bulge C-stars. Their locus corresponds
to
The carbon stars Azzopardi et al.
(1991) and Westerlund et al. (1991) ascribed to the Galactic bulge
(spheroidal region extending about 3 kpc from
the Galactic center) are finally much closer to our HC-stars. Westerlund et al.
(1995) published the HR diagram of 20 bulge C-stars. Their locus corresponds
to
![]() and
and
![]() with
with
![]() and
and
![]() which corresponds well to the content of Table 7 for
the HC-stars. The mean metallicity higher in the bulge than outside it, is possibly responsible
for the mean value
which corresponds well to the content of Table 7 for
the HC-stars. The mean metallicity higher in the bulge than outside it, is possibly responsible
for the mean value
![]() slightly lower than
those quoted in
Table 7. Ng (1998) suggested that the stars of Azzopardi et al. are
not intrinsic bulge stars, but Tyson & Rich (1991) found that their kinematics are
the same as those of bulge K and M stars. It is possible that the bulge and the thick disk
are parts of the same dynamical component, at least in systems with small bulges, like the Galaxy
(Freeman 1987a).
slightly lower than
those quoted in
Table 7. Ng (1998) suggested that the stars of Azzopardi et al. are
not intrinsic bulge stars, but Tyson & Rich (1991) found that their kinematics are
the same as those of bulge K and M stars. It is possible that the bulge and the thick disk
are parts of the same dynamical component, at least in systems with small bulges, like the Galaxy
(Freeman 1987a).
Graff et al. (2000) analyzed the velocity residuals of 551 carbon stars in the LMC.
They found two different populations (20% of stars with
![]() and 80% with
and 80% with
![]() ),
and identify them with young disk and old disk populations respectively. The former, which does
exhibit a slightly higher metallicity, has no counterpart in our HIPPARCOS sample. It should
probably be searched for beyond the HIPPARCOS range, in the local structures of spiral arms.
There is however no hot faint carbon giants in the LMC (i.e. no low-luminosity R-type stars of
our HC'-sample)
which could correspond to the thick disk population. Conversely, the faint-end of the C star
luminosity function is at about
),
and identify them with young disk and old disk populations respectively. The former, which does
exhibit a slightly higher metallicity, has no counterpart in our HIPPARCOS sample. It should
probably be searched for beyond the HIPPARCOS range, in the local structures of spiral arms.
There is however no hot faint carbon giants in the LMC (i.e. no low-luminosity R-type stars of
our HC'-sample)
which could correspond to the thick disk population. Conversely, the faint-end of the C star
luminosity function is at about
![]() in the Small Magellanic Cloud (SMC),
and at
in the Small Magellanic Cloud (SMC),
and at
![]() in the Fornax dwarf galaxy (Azzopardi 1999).
Those
numbers are in very good agreement with our mean values for early HC-stars in
Table 3.
in the Fornax dwarf galaxy (Azzopardi 1999).
Those
numbers are in very good agreement with our mean values for early HC-stars in
Table 3.
Acknowledgements
We thank Dr. Alain Jorissen who suggested part of this study. Valuable suggestions from an anonymous referee are gratefully acknowledged.
Introducing the galactic proper motion components
| (A.1) |
| (A.2) |
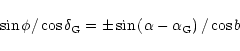 |
(A.3) |
| (A.4) |
| U= |
|||
| (A.5) | |||
| V= |
|||
| (A.6) | |||
| W= | (A.7) |
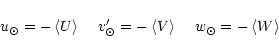 |
(A.8) |
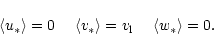 |
(A.9) |
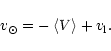 |
(A.10) |
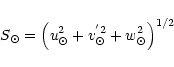 |
(A.11) |
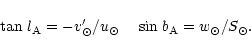 |
(A.12) |