A&A 384, L27-L30 (2002)
DOI: 10.1051/0004-6361:20020207
T. A. Enßlin - S. Heinz
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, Postfach 1317, 85741 Garching, Germany
Received 18 January 2002 / Accepted 5 February 2002
Abstract
The Chandra X-ray Observatory is finding a surprisingly
large number of cavities in the X-ray emitting intracluster medium (ICM),
produced by the release of radio plasma from active galactic nuclei. In
this letter, we present simple analytic formulae for the evolution of the
X-ray deficit and for the radio spectrum of a buoyantly rising bubble. The
aim of this work is to provide a theoretical framework for the planning and
the analysis of X-ray and radio observations of galaxy clusters. We show
that the cluster volume tested for the presence of cavities by X-ray
observations is a strongly rising function of the sensitivity.
Key words: radiation mechanisms: thermal - radiation mechanism: non-thermal - galaxies: active - intergalactic medium - galaxies: cluster: general - radio continuum: general
While the early phase of radio galaxy evolution is characterized by
supersonic expansion into the surrounding medium, the radio lobes
quickly settle into pressure equilibrium with the ICM after the AGN
has shut off. Our description sets in at this moment t1, where the
bubble is located at a cluster radius r1 with volume
![]() and pressure
and pressure
![]() .
The bubble will then quickly
approach a terminal velocity
.
The bubble will then quickly
approach a terminal velocity
![]() ,
governed by the balance
of buoyancy and drag forces. During its rise, the bubble volume
changes according to the adiabatic law
,
governed by the balance
of buoyancy and drag forces. During its rise, the bubble volume
changes according to the adiabatic law
![]() ,
where the adiabatic index
,
where the adiabatic index
![]() is
close to 4/3, which we will take as our fiducial value for numerical
examples. The magnetic field strength should evolve according to
is
close to 4/3, which we will take as our fiducial value for numerical
examples. The magnetic field strength should evolve according to
![]() ,
if the expansion of the bubble
is isotropic. For simplicity, we only consider spherical bubbles with
radius
,
if the expansion of the bubble
is isotropic. For simplicity, we only consider spherical bubbles with
radius ![]() ,
which gives sufficiently accurate estimates for most
applications. If the bubble becomes highly deformed or even
disintegrates, more sophisticated models than ours will have to be
used. We further assume, that entrainment of environmental gas into
the bubble is dynamically insignificant on the considered time-scales,
implying that the bubble is X-ray dark. Numerical simulations
(e.g., Reynolds et al. 2001) support the latter.
,
which gives sufficiently accurate estimates for most
applications. If the bubble becomes highly deformed or even
disintegrates, more sophisticated models than ours will have to be
used. We further assume, that entrainment of environmental gas into
the bubble is dynamically insignificant on the considered time-scales,
implying that the bubble is X-ray dark. Numerical simulations
(e.g., Reynolds et al. 2001) support the latter.
It is often convenient to express physical quantities like the bubble
volume and the magnetic field strength in terms of the values they
would have if the bubble were adiabatically moved to the cluster
center. We denote these by the subscript 0 (e.g.,
![]() ). As our working
example, we will investigate a cluster described by an isothermal
). As our working
example, we will investigate a cluster described by an isothermal
![]() -profile with a density profile of
-profile with a density profile of
![]() ,
pressure
,
pressure
![]() ,
and constant sound speed
,
and constant sound speed
![]() .
.
We define the origin of the cluster coordinate system at the cluster
center, with the x and y axis defining the image plane and the
z-axis the line of sight to the observer, and the coordinate system
oriented so that the bubble center is located in the x-z plane at
![]() .
Its projected distance
from the cluster center is
.
Its projected distance
from the cluster center is
![]() ,
where
,
where
![]() .
The
angle
.
The
angle ![]() should be roughly conserved along the bubble's
trajectory in a spherical cluster atmosphere.
should be roughly conserved along the bubble's
trajectory in a spherical cluster atmosphere.
The buoyancy speed of the bubble can be estimated from the balance of
buoyancy and drag forces. The buoyancy force
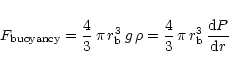 |
(1) |
![\begin{displaymath}t(r_1,r_2) = \frac{\tau}{2}\, \left[{\rm B}_{\frac{x^2}{1+x^2...
...}-\frac{3}{4} \right)
\right]_{r_1/r_{\rm c}}^{r_2/r_{\rm c}},
\end{displaymath}](/articles/aa/full/2002/12/aaea182/img40.gif) |
(5) |
If the initial bubble is large compared to the cluster core
Eq. (3) can give supersonic rise velocities. In such a case
Eq. (2) is no longer valid. Instead, strongly increased
dissipation will limit the rise velocity to the subsonic regime. In
such a case one will adopt
![]() ,
with
,
with
![]() .
.
The X-ray emissivity at cluster radius r and for a given density
and pressure profile is
![]() ,
where n is the electron number density and
,
where n is the electron number density and
![]() is the plasma cooling function.
is the plasma cooling function.
In the following we will assume that the gas surrounding the bubble has essentially settled back into hydrostatic equilibrium in the dark matter potential, which is unperturbed by the radio galaxy activity.
In general, the surface brightness integral must be solved
numerically, but in the case of a ![]() -model atmosphere, it can be
expressed in closed form. For an undisturbed line of sight (i.e., not
intersecting a bubble) the observed surface brightness (neglecting
cosmological corrections) is given by
-model atmosphere, it can be
expressed in closed form. For an undisturbed line of sight (i.e., not
intersecting a bubble) the observed surface brightness (neglecting
cosmological corrections) is given by
For a line of sight intersecting the surface of a bubble, the intersection
points are located at
![]() ,
with
,
with
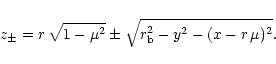 |
(7) |
![$\displaystyle I_{{\rm X,{\rm b}}}(x,y) = I_{\rm X,{\rm cl}}(x,y) -{I_0}\, \left...
...frac{1}{2})}{{\rm B}(3\beta - \frac{1}{2}, \frac{1}{2})}\right]_{z_{-}}^{z_{+}}$](/articles/aa/full/2002/12/aaea182/img53.gif) |
(8) |
Another important diagnostic is the number of missing counts
![]() from the cavities, i.e., the photons emitted from a
spherical region of radius
from the cavities, i.e., the photons emitted from a
spherical region of radius ![]() at distance r from the center
in an unperturbed cluster atmosphere during the exposure interval
at distance r from the center
in an unperturbed cluster atmosphere during the exposure interval
![]() .
For a detector with effective area
.
For a detector with effective area ![]() and a
source distance of D we define
and a
source distance of D we define
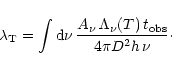 |
(9) |
![\begin{displaymath}\Delta N_{\rm X} = \frac{\pi \lambda_{\rm T} n_0^2 r_{\rm
c}...
...^{2-3\beta}\,r_{\rm c}}{(3\beta-2)\,r} \right]_{v_{-}}^{v_{+}}
\end{displaymath}](/articles/aa/full/2002/12/aaea182/img59.gif) |
(10) |
| |
Figure 1:
Contours of the X-ray deficit
significance
|
| Open with DEXTER | |
In order to design searches for cavities in promising cluster
candidates, it is useful to estimate the expected signal to noise
ratio (
![]() )
of a potential observation. The
signal is the expected number of missing photons from the volume
occupied by the bubble,
)
of a potential observation. The
signal is the expected number of missing photons from the volume
occupied by the bubble,
![]() .
The
background, on top of which the missing photons have to be detected,
is the expected number of photons
.
The
background, on top of which the missing photons have to be detected,
is the expected number of photons
![]() from the area on the
sky subtended by the cavity, assuming there were no cavity. This
assumes that the instrument point spread function is not more extended
than the cavity. The noise is then given by the fluctuation in this
photon number, which is
from the area on the
sky subtended by the cavity, assuming there were no cavity. This
assumes that the instrument point spread function is not more extended
than the cavity. The noise is then given by the fluctuation in this
photon number, which is
![]() .
.
The signal-to-noise ratio of a small bubble (so that the cluster density
does not vary significantly across its diameter,
![]() ), in an isothermal
), in an isothermal ![]() -model is well
approximated by
-model is well
approximated by
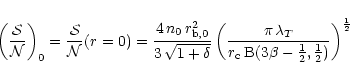 |
(12) |
If the question of interest is the detectability of cavities of a given
fixed size at all cluster radii one can use the incompressible limit
![]() of Eqs. (11) and (13). This case is also displayed in
Figs. 1 and 2.
of Eqs. (11) and (13). This case is also displayed in
Figs. 1 and 2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Ea182_f2.ps}
\end{figure}](/articles/aa/full/2002/12/aaea182/Timg81.gif) |
Figure 2:
Volume of the cluster [in units of
|
| Open with DEXTER | |
Synchrotron, inverse Compton, and adiabatic losses cool an electron with
initial dimensionless momentum
![]() down
to
down
to
![]() ,
where
,
where
If a bubble is rising with a constant velocity ![]() (e.g. because it approaches the sound velocity) the following parameters
give the correct q value:
(e.g. because it approaches the sound velocity) the following parameters
give the correct q value:
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
.
An initially relativistic power-law electron spectrum
![]() for
for
![]() becomes
becomes
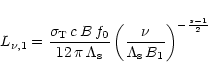 |
(19) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{Ea182_f3.ps}
\end{figure}](/articles/aa/full/2002/12/aaea182/Timg112.gif) |
Figure 3:
Bubble's central X-ray contrast
(compared to the undisturbed cluster) for various angles between plane of
sky and Bubble's trajectory, its radio flux, and its rising time
as a function of the (unprojected) radial position. Adopted
parameters:
|
| Open with DEXTER | |
As an aid and stimulus for future observations we provided simple analytic formulae of X-ray and radio properties of rising buoyant bubbles of radio plasma in galaxy clusters. The detectability of a bubble decreases with its cluster radius. The X-ray contrast of a bubble moving in the plane of the sky decreases slowly until the X-ray background dominates, then it drops rapidly. The contrast of a bubble moving along the line of sight declines quickly outside the cluster core. Similarly, the radio luminosity of the bubble at a given frequency declines rapidly with increasing cluster radius and suddenly vanishes when cooling has removed the emitting electrons. After that point, only a weak flux of synchrotron-self Comptonized emission remains (Enßlin & Sunyaev 2002). Figure 3 illustrates these dependencies for an example with parameters similar to Perseus A.
Acknowledgements
We acknowledge useful comments by Eugene Churazov, Federica Govoni, Daniel E. Harris, Gopal-Krishna, Brian R. McNamara, and the referee Paul E. J. Nulsen.