A&A 384, 1107-1118 (2002)
DOI: 10.1051/0004-6361:20020086
Turbulent radial mixing in the solar nebula
as the source of crystalline silicates in comets
D. Bockelée-Morvan1 - D. Gautier1 -
F. Hersant
1 -
J.-M. Huré1,2 -
F. Robert 3
1 - Observatoire de Paris, 5 place Jules Janssen, 92195 Meudon,
France
2 -
Université de Paris 7, 2 place Jussieu, 75251,
Paris Cedex 05, France
3 -
Laboratoire de Minéralogie, Muséum d'Histoire Naturelle,
61 rue Buffon, 75005 Paris, France
Received 3 October 2001 / Accepted 9 January 2002
Abstract
There is much debate about the origin of crystalline silicates in
comets. Silicates in the protosolar cloud were likely amorphous,
however the
temperature of the outer solar nebula was too cold
to allow their formation in this region by thermal annealing or
direct condensation. This paper investigates the formation of crystalline
silicates
in the inner hot regions of the solar nebula, and their diffusive
transport out to the comet formation zone, using a turbulent
evolutionary model of the solar nebula. The model
uses time-dependent temperature and surface density
profiles generated from the 2-D 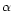 -disk model
of Hersant et al. (2001). It is shown that
turbulent diffusion is an efficient process to carry crystalline silicates
from inner to outer disk regions within timescales of a few
104 yr.
The warmest solar nebula models which reproduce the D/H ratios measured
in meteorites, comets, Uranus and Neptune (Hersant et al. 2001)
provide a mass fraction of crystalline silicates in
the Jupiter-Neptune region in agreement with that measured in comet Hale-Bopp.
-disk model
of Hersant et al. (2001). It is shown that
turbulent diffusion is an efficient process to carry crystalline silicates
from inner to outer disk regions within timescales of a few
104 yr.
The warmest solar nebula models which reproduce the D/H ratios measured
in meteorites, comets, Uranus and Neptune (Hersant et al. 2001)
provide a mass fraction of crystalline silicates in
the Jupiter-Neptune region in agreement with that measured in comet Hale-Bopp.
Key words: solar system: formation -
comets: general - comets: individual: C/1995 O1 (Hale-Bopp) - planetary systems: fonction - planetary systems: protoplanetary disks
The origin of cometary silicates is controversial. Infrared spectra
obtained from ground-based telescopes and the Infrared Space Observatory (ISO)
have shown that Mg-rich olivines and
pyroxenes are present in cometary grains in both amorphous and
crystalline form (Hanner et al. 1994; Hayward et al. 2000;
Crovisier et al. 1997, 2000;
Wooden et al. 1999). Since the formation of crystalline
silicates requires high temperatures, in
contrast to the amorphous variety, the puzzling question is how comets could
have incorporated both high- and low temperature materials, including ices.
Crystalline silicates are encountered in various environments.
They are found in interplanetary dust particles (IDPs), sometimes
coexisting with the amorphous form in the aggregate IDPs thought to be
of cometary origin (Bradley et al. 1992, 1999). Silicates in
chondritic meteorites,
formed in the inner hot solar nebula, are entirely crystalline. Crystalline
silicates have been detected in disks around pre-main-sequence
Herbig Ae/Be stars (e.g., Malfait et al. 1998;
Bouwman et al. 2001). These disks, surrounding intermediate-mass
stars (2-20 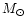 ), are believed to be similar to the
primitive solar nebula from which the Solar System was formed.
Crystalline silicates are also found in the debris disks present around
young main sequence stars as, e.g.,
), are believed to be similar to the
primitive solar nebula from which the Solar System was formed.
Crystalline silicates are also found in the debris disks present around
young main sequence stars as, e.g., 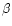 -Pic (Knacke et al. 1993).
On the other hand, there is no spectral evidence for their presence
in the diffuse interstellar medium or molecular clouds, nor in young
stellar objects (Demyk et al. 1999; Hanner et al. 1998). It
is thus likely that the crystalline
silicates present in cometary grains were produced during or after the
collapse of the presolar cloud. Crystalline silicates can form at high
temperature by direct condensation or thermal annealing of amorphous
silicates. This latter process requires temperatures of at least 800 K
(e.g., Gail 1998). The detection of silica SiO2 in Herbig Ae/Be systems
and comets is consistent with compositional changes associated to
thermal annealing of amorphous grains (Bouwman et al. 2001).
-Pic (Knacke et al. 1993).
On the other hand, there is no spectral evidence for their presence
in the diffuse interstellar medium or molecular clouds, nor in young
stellar objects (Demyk et al. 1999; Hanner et al. 1998). It
is thus likely that the crystalline
silicates present in cometary grains were produced during or after the
collapse of the presolar cloud. Crystalline silicates can form at high
temperature by direct condensation or thermal annealing of amorphous
silicates. This latter process requires temperatures of at least 800 K
(e.g., Gail 1998). The detection of silica SiO2 in Herbig Ae/Be systems
and comets is consistent with compositional changes associated to
thermal annealing of amorphous grains (Bouwman et al. 2001).
We follow the current opinion that silicates infalling from the
presolar cloud onto the nebula discoid were all amorphous. Chick &
Cassen (1997) studied the thermal processing of silicates
during the collapse of the presolar cloud in order to assess their
survivability. Combining results of envelope radiative heating with
heating in the
accretion shock above the disk (Neufeld & Hollenback 1994), they
show that grains of silicates infalling at distances larger than
1 AU from the Sun escaped vaporization. From the temperature radial
profiles they compute, we can deduce that, during this
stage, the formation of crystalline silicates by annealing of
amorphous silicates was inefficient at distances greater than 2-3 AU.
Gail (1998) improved the analysis of the problem.
Assuming that the nebula was
already formed, he studied the fate of amorphous silicates radially infalling
onto the Sun. Using a stationary model of the nebula, he showed that
the annealing of amorphous silicates was
inefficient at heliocentric distances greater than 1.5 AU. In other words,
the temperature was too cold in the outer nebula where comets are
currently supposed to have been formed, for the
interstellar silicate grains to be thermally processed prior to
their incorporation to comets. Therefore, either crystallization was
initiated by a low temperature process, as proposed for disks around evolved
stars (Molster et al. 1999),
or there was a
significant radial mixing between the warm and cold parts of the solar
nebula. However, Gail (1998) did not take into account in his
calculations any mixing process. More recently, Gail (2001)
studied mixing by turbulent diffusion in a stationary Keplerian
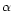 -disk.
-disk.
We investigate here the thermal annealing of
amorphous silicates in the hot regions of the solar nebula and their
diffusive transport out to the comet formation zone by using a turbulent
evolutionary model of the nebula. In fact, large-scale
radial mixing in the nebula has previously been shown
to be a requisite in order to fit measurements of the D/H ratio in water
in LL3 meteorites and Oort cloud comets (Drouart et al. 1999;
Mousis et al. 2000). While these authors used a 1-D turbulent model,
we take advantage here of
the recent 2-D evolutionary model of Hersant et al. (2001)
which provides an improved description of the nebula. The model
generates time-dependent temperature, density, and pressures profiles
throughout the nebula. Hersant et al. further studied
the radial distribution and
time evolution of the deuterium enrichment in water
in the solar nebula due to isotopic
exchange with H2 (the main reservoir of deuterium)
and diffusive turbulent transport. Using the D/H values measured
in LL3 meteorites and Oort cloud comets, they constrained the parameters
of the nebula, namely its initial accretion rate 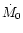 ,
initial
outer radius
,
initial
outer radius
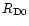 ,
and the coefficient of turbulent viscosity
,
and the coefficient of turbulent viscosity 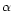 (Shakura & Sunyaev 1973).
(Shakura & Sunyaev 1973).
The goal of the present paper is to investigate whether the solar nebula
models selected by Hersant et al. (2001), which fit
the D/H ratio in comets,
are also able to explain the amount of crystalline silicates detected in
these objects. Section 2 summarizes observational constraints obtained
on the nature of silicates in comets. The model is presented in Sect. 3
and the results are discussed in Sect. 4.
Table 1:
Relative mass fractions of silicates in comet C/1995 O1 (Hale-Bopp).
| Date |
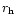 [AU]
[AU] |
Cry Ol |
Cry Pyr |
Am Ol |
Am Pyr |
Cry Tota |
Reference |
| 7 Oct. 1996 |
2.8 |
0.22 |
0.08 |
-b |
0.72 |
0.30 |
Crovisier et al. (2000) |
| |
|
0.50 |
-b |
0.10 |
0.40 |
0.50 |
Colangeli et al. (1999)c |
| 11 Apr. 1997 |
0.93 |
0.33 |
0.20 |
0.31 |
0.13 |
0.54 |
Wooden et al. (1999) |
| |
|
0.08 |
0.80d |
0.08 |
0.03 |
0.88 |
Wooden et al. (1999)e |
| 28 Dec. 1997 |
3.9 |
0.22 |
0.14 |
-b |
0.64 |
0.56 |
Crovisier et al. (2000) |
a Relative mass fraction of silicates in crystalline form, to be
directly compared to model calculations of 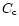 . .
b Silicate component not considered in the fit of the spectrum.
c Spectral fit includes amorphous carbon. Silicate mass fractions have
been here renormalized.
d Sum of ortho- and clino-pyroxene contributions. Ortho-pyroxene
contribution is dominant.
e In contrast to other spectral analyses, crystalline pyroxenes are
assumed to be cooler than other silicates.
|
Measurements concerning cometary silicates are reviewed in detail by
Hanner et al. (1997) and Hanner (1999). A summary is given
here.
The nature of cometary silicates was mainly investigated from
their Si-O stretching bands falling around 10 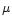 m. Low resolution
8-13
m. Low resolution
8-13 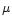 m spectra have been acquired for a dozen
comets (see Hanner et al. 1994; Hanner 1999 and
references therein). Strong structured
emission features were observed for half of them. The detection of a peak
at 11.2-11.3
m spectra have been acquired for a dozen
comets (see Hanner et al. 1994; Hanner 1999 and
references therein). Strong structured
emission features were observed for half of them. The detection of a peak
at 11.2-11.3 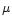 m in 1P/Halley and some of the later observed comets
pointed out the presence of Mg-rich crystalline olivines
mixed with Fe-bearing amorphous olivines and pyroxenes
(Hanner et al. 1994; Wooden et al. 1999).
m in 1P/Halley and some of the later observed comets
pointed out the presence of Mg-rich crystalline olivines
mixed with Fe-bearing amorphous olivines and pyroxenes
(Hanner et al. 1994; Wooden et al. 1999).
Observations of comet C/1995 O1 (Hale-Bopp) provided new insights on silicate mineralogy
(Hanner et al. 1997; Hayward et al. 2000;
Wooden et al. 1999; Crovisier et al. 1997, 2000).
The 10-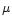 m spectra exhibit several discrete peaks, which have
been attributed to the presence of at least five different Mg-rich silicates
in cometary dust: amorphous
pyroxene, amorphous olivine, crystalline ortho-pyroxene, crystalline
clino-pyroxene, and crystalline olivine (Wooden et al. 1999).
ISO observations of the full 2-45
m spectra exhibit several discrete peaks, which have
been attributed to the presence of at least five different Mg-rich silicates
in cometary dust: amorphous
pyroxene, amorphous olivine, crystalline ortho-pyroxene, crystalline
clino-pyroxene, and crystalline olivine (Wooden et al. 1999).
ISO observations of the full 2-45 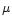 m spectra of comet Hale-Bopp
showed several broad emission features longward 16
m spectra of comet Hale-Bopp
showed several broad emission features longward 16 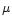 m, all attributed
to bending mode vibrations of Mg-rich crystalline olivine
(Crovisier et al. 1997, 2000; Brucato et al. 1999a;
Colangeli et al. 1999).
m, all attributed
to bending mode vibrations of Mg-rich crystalline olivine
(Crovisier et al. 1997, 2000; Brucato et al. 1999a;
Colangeli et al. 1999).
All interpretations of Hale-Bopp spectra agree on the presence of
olivines
and pyroxenes in both amorphous and crystalline form.
However, they differ quantitatively. A summary of inferred relative
abundances is given in
Table 1. The relative mass fraction of silicates in crystalline
form inferred from Hale-Bopp spectra varies from 30 to 90%. Not included
in Table 1 is the estimation made by Hayward et al.
(2000) of 20% of
crystalline silicates . As explained by Hanner (1999), it is
difficult
to determine accurately the relative abundances of minerals in cometary dust from their
infrared spectra. With respect to other results, Wooden et al. (1999)
suggest a much higher mass fraction of crystalline
pyroxenes (Table 1). In contrast to other studies, they
attribute the 9.3 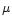 m peak to crystalline pyroxene. In order to
reproduce the
relative strength of this feature observed at various heliocentric
distances with a similar relative mass fraction of crystalline pyroxenes
with respect to the other dust components, they argue
that crystalline pyroxenes must be cooler than other silicate components,
hence the different result.
As discussed by Wooden et al., this requires that pyroxene crystals are
separate particles in the Hale-Bopp's coma. This doesn't fit with
current views of cometary dust as porous aggregate particles mixing
silicates and carbonaceous material, and might deserve further studies
(see the discussion of Hayward et al. 2000).
m peak to crystalline pyroxene. In order to
reproduce the
relative strength of this feature observed at various heliocentric
distances with a similar relative mass fraction of crystalline pyroxenes
with respect to the other dust components, they argue
that crystalline pyroxenes must be cooler than other silicate components,
hence the different result.
As discussed by Wooden et al., this requires that pyroxene crystals are
separate particles in the Hale-Bopp's coma. This doesn't fit with
current views of cometary dust as porous aggregate particles mixing
silicates and carbonaceous material, and might deserve further studies
(see the discussion of Hayward et al. 2000).
10-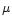 m spectra obtained in other long-period comets indicate a silicate
mineralogy in these comets similar to that in comet Hale-Bopp (Wooden et
al. 1999). However, significant spectral differences are seen between comets.
Colangeli et al. (1995, 1996) attribute these differences to
variations in the relative amounts of the various silicates or
in the Mg/Fe ratio.
Hayward et al. (2000) argue that they might rather
reflect variations in the dust size distribution and temperature.
m spectra obtained in other long-period comets indicate a silicate
mineralogy in these comets similar to that in comet Hale-Bopp (Wooden et
al. 1999). However, significant spectral differences are seen between comets.
Colangeli et al. (1995, 1996) attribute these differences to
variations in the relative amounts of the various silicates or
in the Mg/Fe ratio.
Hayward et al. (2000) argue that they might rather
reflect variations in the dust size distribution and temperature.
Data on
short-period comets, presumably formed in the Kuiper Belt, are very sparse.
They usually exhibit weak and broad featureless 10 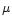 m emission,
presumably due to their deficiency in small particles
(Hanner et al. 1994). However, crystalline olivines might be
present in short-period comets as well, as suggested by the ISO spectrum
of comet 103P/Hartley 2 which shows the presence of a peak at 11.3
m emission,
presumably due to their deficiency in small particles
(Hanner et al. 1994). However, crystalline olivines might be
present in short-period comets as well, as suggested by the ISO spectrum
of comet 103P/Hartley 2 which shows the presence of a peak at 11.3 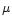 m
(Crovisier et al. 1999, 2000).
m
(Crovisier et al. 1999, 2000).
The goal of our modelling is to investigate whether crystalline silicates
formed in the inner warm regions of the solar nebula can be efficiently
transported by turbulent diffusion to the outermost cold regions where
comets presumably formed. This model treats both the amorphous-to-crystalline
phase transition of small silicate particles and their diffusive transport
throughout the nebula as a function of time.
We use a simplistic approach in which only two dust
components are considered, regardless of their mineralogy: amorphous and
crystalline silicates. The amorphous-to-crystalline transition by thermal
heating can be treated thanks to recent laboratory measurements (Sect. 3.3).
The model solves time-dependent equations which describe the diffusive
transport of small dust particles
in a turbulent accretion disk (Morfill & Völk 1984). Defining
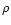 as the mass density of the disk (dominated by H2 and He),
and
as the mass density of the disk (dominated by H2 and He),
and 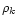 as the mass density of dust particles of chemical index k,
we have:
as the mass density of dust particles of chemical index k,
we have:
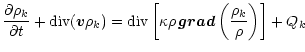 |
|
|
(1) |
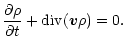 |
|
|
(2) |
The second term in the left part of Eqs. (1) and (2) is the
advection term
describing inward mass transport towards the central object at
the velocity 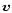 .
We assume that the dust particles are well mixed with the gas
(Dubrulle et al. 1995), so that their radial velocity
.
We assume that the dust particles are well mixed with the gas
(Dubrulle et al. 1995), so that their radial velocity 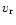 is
the same as that of the gas.
In the case of a thin Keplerian disk,
is
the same as that of the gas.
In the case of a thin Keplerian disk, 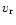 is equal to -3
is equal to -3
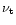 /2r, where
/2r, where
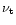 is the turbulent viscosity and r is the radial distance. The
effect of the turbulence in the
solar nebula is to smooth out any concentration gradient. This diffusion is
represented by the first term in the right part of Eq. (1): the turbulent
diffusivity
is the turbulent viscosity and r is the radial distance. The
effect of the turbulence in the
solar nebula is to smooth out any concentration gradient. This diffusion is
represented by the first term in the right part of Eq. (1): the turbulent
diffusivity 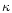 is set to the ratio of
turbulent viscosity
is set to the ratio of
turbulent viscosity
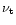 to the Prandtl number
to the Prandtl number 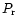 .
For reasons
discussed in Hersant et al. (2001),
.
For reasons
discussed in Hersant et al. (2001), 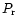 is taken equal to 0.7.
Qk is a source or sink term
which describes local production and destruction processes. Equation (2)
is the equation of continuity of the total mass flow.
is taken equal to 0.7.
Qk is a source or sink term
which describes local production and destruction processes. Equation (2)
is the equation of continuity of the total mass flow.
Using Eqs. (1) and (2), it can be shown that, in the midplane of
the disk,
the relative concentration
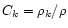 follows the diffusion
equation:
follows the diffusion
equation:
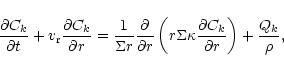 |
(3) |
where 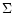 is the surface density of the disk.
is the surface density of the disk.
The annealing process of amorphous
silicates and the diffusive transport of crystalline silicates in the
outer regions of the solar nebula can be investigated by solving two
diffusion equations which are coupled by source and sink terms:
The indices "a'' and "c'' refer to amorphous and crystalline silicates,
respectively, and Q is the coupling term representing the annealing
process. If
 is the characteristic timescale for annealing
(Sect. 3.3), then
is the characteristic timescale for annealing
(Sect. 3.3), then
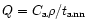 and we have:
and we have:
Equations (6) and (7) do not include sublimation and condensation terms.
Sublimation is taken into account
in the boundary conditions by setting
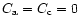 at the distance rwhere the temperature of the nebula is high enough to allow efficient
sublimation (Sects. 3.2 and 3.3). We do not consider the
re-formation of silicates which subsequently occurs as the
hot gas is cooling down (see the discussion in Sect. 4).
Solving Eqs. (6) and (7) requires an evolutionary solar nebula
model giving surface density and temperature radial profiles in the
midplane of the disk as a function of time.
at the distance rwhere the temperature of the nebula is high enough to allow efficient
sublimation (Sects. 3.2 and 3.3). We do not consider the
re-formation of silicates which subsequently occurs as the
hot gas is cooling down (see the discussion in Sect. 4).
Solving Eqs. (6) and (7) requires an evolutionary solar nebula
model giving surface density and temperature radial profiles in the
midplane of the disk as a function of time.
We sum up here the solar nebula model that we use, and which is
described in length by Hersant et al. (2001). The temporal
evolution of the solar nebula is
modelled by a sequence of
stationary solutions provided by the 2-D accretion disk model of
Huré (2000), where the
vertical stratification of the physical quantities is explicitly calculated.
In a 2-D model, the midplane temperature,
pressure, and volumetric density are generally slightly higher than in a
1-D model where
a vertically homogeneous disk is assumed (Huré & Galliano 2001).
This model uses the well known 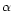 prescription of Shakura &
Sunyaev (1973), which permits modellers to parameterize
the effects of small scale turbulence. The prescription
consists of writing the turbulent viscosity as
prescription of Shakura &
Sunyaev (1973), which permits modellers to parameterize
the effects of small scale turbulence. The prescription
consists of writing the turbulent viscosity as
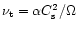 ,
where
,
where 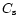 is the sound velocity and
is the sound velocity and 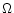 is the
Keplerian angular velocity.
is the
Keplerian angular velocity.
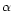 is a non-dimensional parameter whose value depends on the nature
of the turbulence and is usually taken, for simplicity, as constant with
respect to the heliocentric distance in the disk and time.
is a non-dimensional parameter whose value depends on the nature
of the turbulence and is usually taken, for simplicity, as constant with
respect to the heliocentric distance in the disk and time.
The 2-D model is calculated for a given
accretion rate 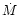 which governs the inflow of matter from the disk
onto the proto-Sun. As the disk evolves and
cools down, the turbulence is less and less efficient, and this accretion
rate
which governs the inflow of matter from the disk
onto the proto-Sun. As the disk evolves and
cools down, the turbulence is less and less efficient, and this accretion
rate 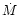 diminishes. The evolutionary model
begins when the formation of the Sun
is almost complete. The subsequent evolution of the nebula is obtained
by calculating
2-D models for a temporal sequence of accretion rates following the
prescription of Makalkin & Dorofeyeva (1991). These authors
have shown that the
evolution of
diminishes. The evolutionary model
begins when the formation of the Sun
is almost complete. The subsequent evolution of the nebula is obtained
by calculating
2-D models for a temporal sequence of accretion rates following the
prescription of Makalkin & Dorofeyeva (1991). These authors
have shown that the
evolution of 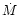 as a function of time can be described
by a simple power law which depends upon the accretion rate and
the outer radius of the nebula
as a function of time can be described
by a simple power law which depends upon the accretion rate and
the outer radius of the nebula
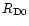 at t = 0 according to:
at t = 0 according to:
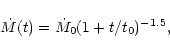 |
(8) |
with
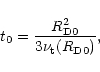 |
(9) |
where
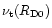 is the coefficient for turbulent viscosity
at the initial outer radius
of the nebula. Such evolution agrees with the numerical evolutionary
models of Ruden & Lin (1986) or Ruden & Pollack (1991).
It is
also consistent with the decrease of the mass accretion rate with increasing
age observed in T Tauri stars (Hartmann et al. 1998).
is the coefficient for turbulent viscosity
at the initial outer radius
of the nebula. Such evolution agrees with the numerical evolutionary
models of Ruden & Lin (1986) or Ruden & Pollack (1991).
It is
also consistent with the decrease of the mass accretion rate with increasing
age observed in T Tauri stars (Hartmann et al. 1998).
The model takes also into account that, under the action of turbulence,
the nebula spreads out viscously with time. It is assumed that
the evolution of its outer radius 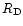 follows:
follows:
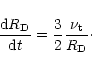 |
(10) |
The model input parameters are finally
the initial radius
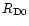 and accretion rate
and accretion rate 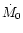 of the nebula,
and
of the nebula,
and 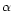 .
.
With this solar nebula model, Hersant et al. studied the radial
distribution and time evolution of the
deuterium enrichment in water in the solar nebula due to isotopic
exchange with H2 and diffusive turbulent transport. Assuming that the
highly D-enriched component measured in LL3 meteorites
(D/H = (73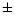 12
12
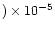 )
is representative of
the grains in the presolar cloud (Drouart et al. 1999;
Mousis et al. 2000), Hersant et al. were able to explain
the D/H value of
)
is representative of
the grains in the presolar cloud (Drouart et al. 1999;
Mousis et al. 2000), Hersant et al. were able to explain
the D/H value of 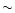
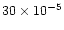 measured in cometary water
as due to some mixing between water vapor reprocessed in the inner regions
of the solar nebula by isotopic exchange with H2, and the unprocessed
component of its outer regions.
measured in cometary water
as due to some mixing between water vapor reprocessed in the inner regions
of the solar nebula by isotopic exchange with H2, and the unprocessed
component of its outer regions.
Hersant et al. (2001) showed that the three
parameters defining the nebula can be constrained by the deuterium enrichments
measured in LL3 meteorites, comets, proto-Uranian and proto-Neptunian
ices, taking into account a few other
physical constraints, namely: 1) the mass of the nebula cannot exceed
0.3 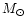 in order to maintain the stability
of the disk (Shu et al. 1990); 2) the angular momentum must have
been transported outward to Neptune by turbulence in
in order to maintain the stability
of the disk (Shu et al. 1990); 2) the angular momentum must have
been transported outward to Neptune by turbulence in
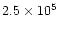 yr;
3) the
initial temperature of the nebula was higher than 1000 K inside 3 AU to
secure the crystallization of silicates in the inner regions.
Hersant et al. concluded that
yr;
3) the
initial temperature of the nebula was higher than 1000 K inside 3 AU to
secure the crystallization of silicates in the inner regions.
Hersant et al. concluded that 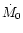 was in between
was in between
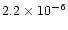 and 10-5
and 10-5 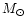 yr-1,
yr-1,
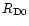 between
12.8 and
39 AU, and
between
12.8 and
39 AU, and 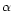 between 0.006 and 0.02. For the purpose
of this paper in which the temperature of the
nebula is crucial for determining where and when the conversion of
amorphous silicates into the crystalline variety occurred, they selected
among all nebulae fitting observational constraints one of the coldest and one
of the hottest nebulae, named cold nebula and warm nebula, respectively.
Their parameters are given in Table 2.
They also selected a nebula intermediate between the cold and
warm nebulae, called nominal nebula (Table 2).
Radial profiles of
between 0.006 and 0.02. For the purpose
of this paper in which the temperature of the
nebula is crucial for determining where and when the conversion of
amorphous silicates into the crystalline variety occurred, they selected
among all nebulae fitting observational constraints one of the coldest and one
of the hottest nebulae, named cold nebula and warm nebula, respectively.
Their parameters are given in Table 2.
They also selected a nebula intermediate between the cold and
warm nebulae, called nominal nebula (Table 2).
Radial profiles of 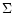 and T as
a function of time are shown in Fig. 1 for these three nebulae.
Adiabats (P,T) of the nominal solar nebula at various epochs are
shown in Fig. 2.
and T as
a function of time are shown in Fig. 1 for these three nebulae.
Adiabats (P,T) of the nominal solar nebula at various epochs are
shown in Fig. 2.
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{MS1967f1.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg54.gif) |
Figure 1:
Surface density (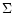 )
and temperature (T)
radial profiles as a function of time for the three nebulae defined in
Table 2. Plain lines are for times 103, 104, 105,
and 106 years. Dotted lines are for times )
and temperature (T)
radial profiles as a function of time for the three nebulae defined in
Table 2. Plain lines are for times 103, 104, 105,
and 106 years. Dotted lines are for times
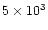 , ,
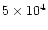 ,
and ,
and
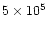 years. years. |
| Open with DEXTER |
Solving Eqs. (6) and (7) requires, in addition to a
solar nebula model, data on silicates crystallization and sublimation.
The thermally induced amorphous-to-crystalline transition has been studied
both theoretically (see Gail 1998 and references therein) and in the
laboratory (e.g. Ashworth et al. 1984; Nuth & Donn
1982; Hallenbeck et al. 1998;
Brucato et al. 1999b; Fabian et al. 2000).
The crystallization process corresponds, on
a microscopic scale, to the movement of oxygen and silicon atoms to new
locations characterized by deeper local energy minima. The characteristic
timescale for the amorphous-crystalline transition can be expressed as:
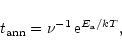 |
(11) |
where 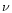 is a characteristic vibrational frequency and
is a characteristic vibrational frequency and 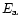 acts as an
activation energy (Lenzuni et al. 1995). In
experimental determinations of
acts as an
activation energy (Lenzuni et al. 1995). In
experimental determinations of 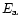 ,
,
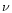 is set to 2-2.5
is set to 2-2.5  1013 s-1, the average value between
the
frequencies of the stretching and bending modes of the SiO4 tetrahedron
(Lenzuni et al. 1995; Gail 1998). From thermal annealing
experiments
made at
1013 s-1, the average value between
the
frequencies of the stretching and bending modes of the SiO4 tetrahedron
(Lenzuni et al. 1995; Gail 1998). From thermal annealing
experiments
made at  1100 and 1300 K on
1100 and 1300 K on  20-nm sized smoke particles,
Brucato et al. (1999b) estimated
an activation temperature
20-nm sized smoke particles,
Brucato et al. (1999b) estimated
an activation temperature
 of 47500 K for amorphous Mg-rich
pyroxenes (hereafter referred to as MgSiO3, enstatite).
Brucato et al. (1999b) derived a temperature of 45500 K from
the annealing experiment
of Hallenbeck et al. (1998).
Experiments made at 1000 K by Fabian et al. (2000)
on nanometre-sized
smoke particles of Mg-rich pyroxene and Mg-rich olivine
(Mg2SiO4, forsterite) give activation temperatures of
42040 and 39100 K, respectively.
The difference in the measured activation energies for Mg-rich pyroxene
between Brucato et al. (1999b)
and Fabian et al. (2000) comes from a different definition of the
annealing time. Both studies monitored the evolution of IR spectra of
silicates undergoing
annealing. While Fabian et al. define the annealing time as the
time when the first crystalline IR features appear,
Brucato et al.
define it as the time when crystalline IR features no longer evolve.
Between these two stages, Hallenbeck et al. (1998) observed a stall
phase in the spectra before the features sharpened due to the crystal
becoming more ordered.
of 47500 K for amorphous Mg-rich
pyroxenes (hereafter referred to as MgSiO3, enstatite).
Brucato et al. (1999b) derived a temperature of 45500 K from
the annealing experiment
of Hallenbeck et al. (1998).
Experiments made at 1000 K by Fabian et al. (2000)
on nanometre-sized
smoke particles of Mg-rich pyroxene and Mg-rich olivine
(Mg2SiO4, forsterite) give activation temperatures of
42040 and 39100 K, respectively.
The difference in the measured activation energies for Mg-rich pyroxene
between Brucato et al. (1999b)
and Fabian et al. (2000) comes from a different definition of the
annealing time. Both studies monitored the evolution of IR spectra of
silicates undergoing
annealing. While Fabian et al. define the annealing time as the
time when the first crystalline IR features appear,
Brucato et al.
define it as the time when crystalline IR features no longer evolve.
Between these two stages, Hallenbeck et al. (1998) observed a stall
phase in the spectra before the features sharpened due to the crystal
becoming more ordered.
Experiments revealed a significant distinction in the
amorphous-to-crystalline transition between micrometre-sized glass and smoke
particles (Fabian et al. 2000). This is something interesting
to consider, especially given the large size
of interstellar dust (typically 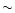 0.1
0.1 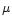 m) compared to that of
the laboratory smokes.
First, the timescale at 1000 K for
crystallization of MgSiO3 glass particles exceeds that of MgSiO3
smoke particles. In addition, the activation temperature determined for
these micrometre particles with
m) compared to that of
the laboratory smokes.
First, the timescale at 1000 K for
crystallization of MgSiO3 glass particles exceeds that of MgSiO3
smoke particles. In addition, the activation temperature determined for
these micrometre particles with 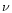 = 2
= 2 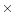 1013 s-1
decreases with increasing annealing temperature
(Fabian et al. 2000). We performed a least-square fit to the
annealing times measured for temperatures
between 1030 K and 1121 K (median values of Table 3 in Fabian et al.
2000), which shows that the measurements can be fitted by an
exponential law (Eq. (11)) with
1013 s-1
decreases with increasing annealing temperature
(Fabian et al. 2000). We performed a least-square fit to the
annealing times measured for temperatures
between 1030 K and 1121 K (median values of Table 3 in Fabian et al.
2000), which shows that the measurements can be fitted by an
exponential law (Eq. (11)) with
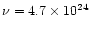 s-1 and
s-1 and
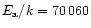 K (note that the uncertainties on
K (note that the uncertainties on 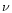 and
and
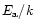 are
large: respectively at least
are
large: respectively at least 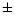 2 orders of magnitude and
2 orders of magnitude and 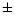 5000 K,
taking the range of estimated annealing times as the uncertainty on the
measurements). Although this law may not apply over a large temperature
range, it permits us to investigate larger timescales for
crystallization with respect to those derived for nanometre smoke particles.
Table 3 gives the laws for
5000 K,
taking the range of estimated annealing times as the uncertainty on the
measurements). Although this law may not apply over a large temperature
range, it permits us to investigate larger timescales for
crystallization with respect to those derived for nanometre smoke particles.
Table 3 gives the laws for
 considered in this paper and
considered in this paper and
 values at T = 1000 K.
The laws (1) to (3) come from the
mentioned experiments on smoke particles. Law numbered (4) is that
derived in the paragraph above, from measurements on micrometre grains.
The law numbered (5) (
values at T = 1000 K.
The laws (1) to (3) come from the
mentioned experiments on smoke particles. Law numbered (4) is that
derived in the paragraph above, from measurements on micrometre grains.
The law numbered (5) (
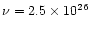 s-1 and
s-1 and
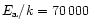 K) is possibly more appropriate for 0.1
K) is possibly more appropriate for 0.1 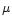 m sized particles. It was derived from law (4), assuming the linear
grain size dependence suggested
by annealing experiments made on silicate glassy sheets
(Fabian et al. 2000).
m sized particles. It was derived from law (4), assuming the linear
grain size dependence suggested
by annealing experiments made on silicate glassy sheets
(Fabian et al. 2000).
The annealing timescales we use are those determined for nearly pure
magnesium silicates. It can be objected that these
measurements are not fully appropriate for our purpose, since amorphous
silicates in the protosolar cloud contained some iron. Demyk et al.
(1999) studied the infrared signatures of the silicates
around two massive protostellar objects and showed that they can be well
reproduced with Mg-Fe pyroxenes amorphous grains with a Fe/Mg ratio of
about 0.5. It would be thus interesting to use annealing timescales
characteristic of such compounds. Annealing experiments have been
made for pure iron-silicate and magnesium-iron silicates (Hallenbeck et al.
1998), but the activation temperatures required for our model
are not available. Hallenbeck et al. (1998) found that
annealing timescales are much larger for iron silicates than for
magnesium silicates. On the other hand, the evolution of mixed magnesium-iron
silicates resembles that of magnesium silicate samples (Hallenbeck et al.
1998).
Table 3:
Laws for annealing timescales.
| Lawa |
Compound |
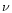 |
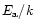 |
 |
| |
|
[s-1] |
[K] |
1000 K [s] |
| (1) |
Mg2SiO4 smoke |
2  1013
1013 |
39100 |
4.8  104
104 |
| (2) |
MgSiO3 smoke |
2 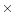 1013
1013 |
42040 |
9.1 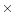 104
104 |
| (3) |
MgSiO3 smoke |
2.5 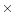 1013
1013 |
47500 |
1.7 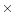 107
107 |
| (4) |
MgSiO3 glass |
5 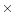 1024
1024 |
70000 |
5.0 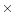 105
105 |
| (5) |
MgSiO3 glass |
2.5 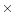 1026
1026 |
70000 |
1.0 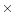 104 104 |
a Timescale laws for crystallization parameterized by
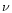
and
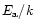
:
(1) Mg
2SiO
4 smoke,
Fabian et al. (2000); (2) MgSiO
3
smoke,
Fabian et al. (2000); (3) MgSiO
3 smoke,
Brucato et al.
(1999b); (4) MgSiO
3 glass, Fabian et al. (2000), see text;
(5) MgSiO
3, 0.1
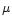
m glass, see text.
The stability of Mg-rich silicates against vaporization has been studied
by Duschl et al. (1996). It is shown that silicates decompose in a near
equilibrium process with the gas phase and gradually disappear over
a finite temperature interval of 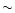 300 K. We have considered the
(
300 K. We have considered the
(
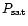 ,
T) equilibrium curve with f = 0.9 given in Fig. 4 of
this paper,
which corresponds to the situation where a fraction f = 0.9 of the Si
is still bound into grains. This curve is plotted in Fig. 2 over
the (P, T) adiabat of the solar nebula. The last grains
disappear at a
temperature
,
T) equilibrium curve with f = 0.9 given in Fig. 4 of
this paper,
which corresponds to the situation where a fraction f = 0.9 of the Si
is still bound into grains. This curve is plotted in Fig. 2 over
the (P, T) adiabat of the solar nebula. The last grains
disappear at a
temperature 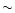 100 K higher (Duschl et al. 1996). Taking the
(
100 K higher (Duschl et al. 1996). Taking the
(
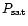 ,
T) equilibrium curve with f = 0 that corresponds to the full
disappearance of silicate grains would not change significantly our
results, keeping in mind that sublimation curves depend somewhat on the
silicate composition.
,
T) equilibrium curve with f = 0 that corresponds to the full
disappearance of silicate grains would not change significantly our
results, keeping in mind that sublimation curves depend somewhat on the
silicate composition.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{MS1967f2.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg64.gif) |
Figure 2:
Adiabat (P, T) of the nominal nebula as a function
of time. Curves from top to bottom correspond to increasing times.
Plain lines are for times 103, 104, 105,
and 106 years. Dotted lines are for times
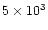 , ,
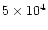 ,
and ,
and
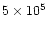 years. The dashed line shows
the equilibrium curve against vaporization of silicates taken
from Duschl et al. (1996). This equilibrium curve intersects the
nebula adiabat at years. The dashed line shows
the equilibrium curve against vaporization of silicates taken
from Duschl et al. (1996). This equilibrium curve intersects the
nebula adiabat at
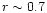 ,
0.6, 0.4, 0.3, and 0.1 AU for times of
103, 104, ,
0.6, 0.4, 0.3, and 0.1 AU for times of
103, 104,
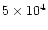 ,
105, and ,
105, and
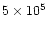 years,
respectively. years,
respectively. |
| Open with DEXTER |
Numerical integration of the coupled partial differential Eqs. (6)
and (7) requires initial
conditions and boundary conditions at the inner r0 and outer 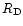 radii at
any time. This is a classical
radii at
any time. This is a classical
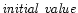 problem which can be
solved by finite differencing, given a r-grid and time step.
problem which can be
solved by finite differencing, given a r-grid and time step.
Equations (6) and (7) mix advective and diffusion terms, each
of them
requiring a specific differencing scheme to avoid numerical dissipation
and stability problems. Therefore, we used the "operator splitting'' method
and computed separately, and successively within one time step,
the time evolution of 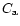 and
and 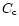 due to the advective and
diffusion terms. The time evolutions resulting from the chemical and
diffusion terms were treated together.
due to the advective and
diffusion terms. The time evolutions resulting from the chemical and
diffusion terms were treated together.
For the transport term, we used the explicit spatial differencing scheme
suggested
by Hawley et al. (1984) (Sect. II.c.ii) which mixes the second-order
(in space) averaging scheme of Wilson (1978) and the first-order
upwind scheme.
For treating the diffusion, we used the Crank-Nicholson differencing scheme
which is second-order in both space and time (see Drouart et al. 1999).
The r-grid has been defined between
r0 = 0.1 AU and 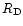 with
logarithmic steps such that
with
logarithmic steps such that
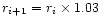 .
The time step
has been set
to
.
The time step
has been set
to
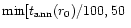 yr
yr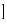 .
For minimizing the
computer time,
.
For minimizing the
computer time,
 values less than 50 yr (5 yr for the cold nebula)
were set to 50 yr (5 yr for the cold nebula).
values less than 50 yr (5 yr for the cold nebula)
were set to 50 yr (5 yr for the cold nebula).
As initial condition, we took
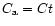 and
and
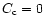 at any r, where
Ct is a constant setting the relative mass concentration of silicates with
respect to H2. Since Eqs. (6) and (7) are linear in Ct and
we are interested in the relative fraction of crystalline versus amorphous
silicates, we took Ct = 1.
at any r, where
Ct is a constant setting the relative mass concentration of silicates with
respect to H2. Since Eqs. (6) and (7) are linear in Ct and
we are interested in the relative fraction of crystalline versus amorphous
silicates, we took Ct = 1. 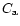 and
and 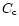 then provides directly the
relative mass fractions of amorphous and
crystalline silicates, respectively. With this initial condition,
we assume that the silicates are
only in amorphous form throughout the nebula at t = 0. Due to hot
temperatures
at small r, the initial concentrations are in fact determined by the thermal
radial profile of the nebula at t = 0.
Figure 3 shows that silicates
are essentially amorphous at distances larger than 10 AU for the
considered nebulae. These initial conditions are
valid, providing that the grains outside 10 AU were not thermally processed
in the preceding stages of solar nebula formation and evolution. As
discussed in Sects. 1 and 4.1, silicates suffered little processing
during the collapse phase (Chick & Cassen 1997).
then provides directly the
relative mass fractions of amorphous and
crystalline silicates, respectively. With this initial condition,
we assume that the silicates are
only in amorphous form throughout the nebula at t = 0. Due to hot
temperatures
at small r, the initial concentrations are in fact determined by the thermal
radial profile of the nebula at t = 0.
Figure 3 shows that silicates
are essentially amorphous at distances larger than 10 AU for the
considered nebulae. These initial conditions are
valid, providing that the grains outside 10 AU were not thermally processed
in the preceding stages of solar nebula formation and evolution. As
discussed in Sects. 1 and 4.1, silicates suffered little processing
during the collapse phase (Chick & Cassen 1997).
The boundary spatial condition
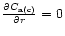 was taken at
was taken at
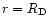 .
This implies that we neglect radial influx
of material from the outside.
When the sublimation boundary
.
This implies that we neglect radial influx
of material from the outside.
When the sublimation boundary
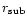 extends
farther than r0 = 0.1 AU, the inner spatial boundary condition is
extends
farther than r0 = 0.1 AU, the inner spatial boundary condition is
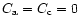 at
at
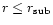 .
When this is not the case
(for the considered
nebulae, this happens only at
.
When this is not the case
(for the considered
nebulae, this happens only at
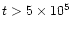 yr, Fig. 3),
we assumed, for
simplicity,
yr, Fig. 3),
we assumed, for
simplicity,
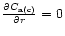 .
.
The temporal and radial evolution of the relative mass fraction of crystalline
silicates 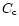 is shown in Fig. 3, for the three considered nebulae.
In Fig. 4 is plotted the mass fraction of crystalline silicates
integrated over the whole nebula
is shown in Fig. 3, for the three considered nebulae.
In Fig. 4 is plotted the mass fraction of crystalline silicates
integrated over the whole nebula
 as a function of time:
as a function of time:
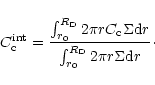 |
(12) |
The calculations shown in Figs. 3-4 refer to the
annealing timescales
 computed with the law (1) at the top of Table 3,
namely
computed with the law (1) at the top of Table 3,
namely
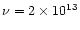 s-1 and
s-1 and
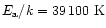 (Fabian et al. 2000). The calculations
made with the other
laws given in Table 3 provide qualitatively the same results.
(Fabian et al. 2000). The calculations
made with the other
laws given in Table 3 provide qualitatively the same results.
At time slightly above 0 yr, silicate grains are vaporized or
are in crystalline form within some distance which depends
on the initial thermal structure of the nebula. This distance, that
we call the crystalline front, is 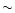 5 to 7 AU for the considered
nebulae. As time goes on, amorphous silicates, present in the outer regions,
are transported towards the inner regions by advection and turbulent
diffusion, and
then thermally
annealed. This radial inward flux of amorphous material inside the
region where crystallization takes place balances the loss
of crystalline silicates by advective transport within the evaporation
zone. As shown in Fig. 4, the integrated mass fraction of crystalline
silicates is maintained
to a value that slightly exceeds the value acquired at
5 to 7 AU for the considered
nebulae. As time goes on, amorphous silicates, present in the outer regions,
are transported towards the inner regions by advection and turbulent
diffusion, and
then thermally
annealed. This radial inward flux of amorphous material inside the
region where crystallization takes place balances the loss
of crystalline silicates by advective transport within the evaporation
zone. As shown in Fig. 4, the integrated mass fraction of crystalline
silicates is maintained
to a value that slightly exceeds the value acquired at
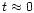 up to times
up to times
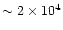 yr due to on-going crystallization.
When mass input from crystallization no longer balances
loss by evaporation, the integrated mass fraction of crystalline silicates
then decreases to reach a plateau value. The ratio between
this long term plateau value and the crystalline mass fraction at
t
yr due to on-going crystallization.
When mass input from crystallization no longer balances
loss by evaporation, the integrated mass fraction of crystalline silicates
then decreases to reach a plateau value. The ratio between
this long term plateau value and the crystalline mass fraction at
t 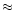 0 is
more than 25% for the nebulae considered here (Fig. 4). This shows
that
turbulent diffusion of both amorphous and crystalline silicates is an
efficient process for maintaining a high proportion
of crystalline silicates in the solar nebula, as it is cooling down.
0 is
more than 25% for the nebulae considered here (Fig. 4). This shows
that
turbulent diffusion of both amorphous and crystalline silicates is an
efficient process for maintaining a high proportion
of crystalline silicates in the solar nebula, as it is cooling down.
The effects of turbulent diffusion are seen on the radial profiles of
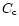 shown in Figs. 3A-C. Crystalline silicates are
progressively mixed with the
amorphous grains
present in the outer regions, so that
shown in Figs. 3A-C. Crystalline silicates are
progressively mixed with the
amorphous grains
present in the outer regions, so that 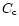 continuously increases in the
outer regions to finally reach a plateau equal to the
continuously increases in the
outer regions to finally reach a plateau equal to the
 plateau value mentioned above. In turn, the crystalline front
moves towards the Sun, as the nebula cools with time.
plateau value mentioned above. In turn, the crystalline front
moves towards the Sun, as the nebula cools with time.
The characteristic timescale for radial mixing is approximately given by the
accretion rate timescale t0 defined by Eq. (9) and equal
to 
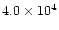 ,
,
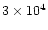 and
and
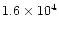 yr for the cold, nominal and warm nebulae,
respectively (Hersant et al. 2001).
Figure 3 shows that, indeed, the plateau is reached faster for the
warm
nebula than for the nominal nebula, and faster for the nominal nebula than for
the cold nebula. For example, at t = 104 yr,
the value of
yr for the cold, nominal and warm nebulae,
respectively (Hersant et al. 2001).
Figure 3 shows that, indeed, the plateau is reached faster for the
warm
nebula than for the nominal nebula, and faster for the nominal nebula than for
the cold nebula. For example, at t = 104 yr,
the value of 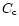 at r = 15 AU is
at r = 15 AU is  80% the plateau value for the warm nebula, while,
at the outermost
distances of the cold nebula, the silicates are still essentially amorphous.
At times larger than
80% the plateau value for the warm nebula, while,
at the outermost
distances of the cold nebula, the silicates are still essentially amorphous.
At times larger than 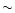 5-
5-
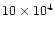 yr, the mass
fraction of crystalline silicates at r > 10 AU no longer evolves for the
three nebulae considered here. The timescale for radial mixing is
governed by the diffusion timescale
yr, the mass
fraction of crystalline silicates at r > 10 AU no longer evolves for the
three nebulae considered here. The timescale for radial mixing is
governed by the diffusion timescale
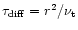 ,
which
increases rapidly with increasing distance, and also increases
significantly with
increasing time, due to decreasing temperature and disk thickness with time
(Fig. 5).
,
which
increases rapidly with increasing distance, and also increases
significantly with
increasing time, due to decreasing temperature and disk thickness with time
(Fig. 5).
Table 4:
Crystalline mass fraction in the outer solar nebula
at infinite time.
| Lawa |
Compound |
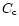 |
| |
|
Solar nebula |
| |
|
cold |
nominal |
warm |
| (1) |
Mg2SiO4 smoke |
0.022 |
0.123 |
0.58 |
| (2) |
MgSiO3 smoke |
0.018 |
0.094 |
0.44 |
| (3) |
MgSiO3 smoke |
0.013 |
0.064 |
0.29 |
| (4) |
MgSiO3 glass |
0.013 |
0.066 |
0.30 |
| (5) |
MgSiO3, 0.1 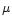 m glass m glass |
0.015 |
0.076 |
0.35 |
a Timescale laws for silicate crystallization labelled according to Table 3.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{MS1967f3a.eps}\\...
...\\ [4mm]
\includegraphics[angle=270,width=8.5cm,clip]{MS1967f3c.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg87.gif) |
Figure 3:
Mass fraction of crystalline silicates as a function of
radius and time in the solar nebula. Thermal annealing is modelled
using law (1) of Table 3 (
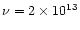 s-1 and s-1 and
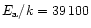 K; Fabian et al. 2000). A) cold nebula. B) nominal nebula. C) warm nebula. K; Fabian et al. 2000). A) cold nebula. B) nominal nebula. C) warm nebula. |
| Open with DEXTER |
The mass fraction of crystalline silicates in the plateau is, as expected,
strongly dependent on the thermal structure of the early nebula.
The cold and warm nebulae considered here are extreme, so that the
crystalline fraction varies from
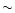 0.02 to 0.6 for the annealing timescales considered in the calculations
shown in Fig. 3. Table 4 shows that, in contrast, the
degree of
crystallinity reached in the plateau is not very sensitive to the
0.02 to 0.6 for the annealing timescales considered in the calculations
shown in Fig. 3. Table 4 shows that, in contrast, the
degree of
crystallinity reached in the plateau is not very sensitive to the
 law. Comparing results obtained for laws (1) and
(2), the
model predicts similar (within 30%) degrees of crystallinity for
olivine and pyroxene grains. The degree of crystallinity is lower for
Mg-rich pyroxene grains than for olivine, due to their slightly higher
activation temperature
law. Comparing results obtained for laws (1) and
(2), the
model predicts similar (within 30%) degrees of crystallinity for
olivine and pyroxene grains. The degree of crystallinity is lower for
Mg-rich pyroxene grains than for olivine, due to their slightly higher
activation temperature
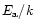 .
The
.
The
 laws used for modelling the
annealing of MgSiO3 glass particles (laws (4) and (5))
provide results
not very different (within 40%) from those derived using experimental data
on smoke MgSiO3 particles (law (2)).
laws used for modelling the
annealing of MgSiO3 glass particles (laws (4) and (5))
provide results
not very different (within 40%) from those derived using experimental data
on smoke MgSiO3 particles (law (2)).
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{MS1967f4.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg88.gif) |
Figure 4:
Mass fraction of crystalline silicates integrated over the
whole nebula
 (Eq. (12)) as a function of time.
Thermal annealing is modelled using law (1) of Table 3.
Calculations for
the three nebulae are shown.
(Eq. (12)) as a function of time.
Thermal annealing is modelled using law (1) of Table 3.
Calculations for
the three nebulae are shown. |
| Open with DEXTER |
The present work is based on the assumption that crystalline
silicates were formed from the annealing of amorphous silicates
moving radially in the disk equatorial plane towards the inner hot regions.
Another mechanism for the formation of crystalline silicates may result from
the re-condensation of silicates. Silicates infalling onto the
disk underwent heating in the collapsing presolar cloud or during
the shock when arriving onto the disk. Chick & Cassen (1997) have
investigated the temperatures experienced by
infalling interstellar grains during this early stage of Solar System
formation and conclude that silicates evaporate within 1 AU. Both
theoretical considerations and compositional constraints from meteorites
argue that the thermal regime experienced in the midplane of the
accretion disk
was more severe and controlled the vaporization distances of refractory
grains (Chick & Cassen 1997). In the solar nebula models
investigated
here, the vaporization distance of silicates is 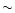 1 AU, a value
less than the value
1 AU, a value
less than the value
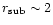 AU required to explain the relative
abundances of moderately volatile elements of carbonaceous meteorites
(Cassen 1996, 2001).
AU required to explain the relative
abundances of moderately volatile elements of carbonaceous meteorites
(Cassen 1996, 2001).
We do not take into account in our model the condensation of silicates
in the vapor phase which takes place near the Sun when the nebula cools
down.
This would require a kinetic treatment
of the chemical surface reactions during grain growth for
which data are lacking (Gail 1998; Gail & Sedlmayr 1999),
and would demand a coupling of the
dust and gas diffusion
equations. Should the condensation of silicates actually produce the
crystalline form, as is expected, neglecting this process leads
to an underestimation of
the relative fraction of crystalline silicates with respect to the amorphous
variety. Since the mass of material located within the sublimation
region is much smaller than the mass
located outside (<10% for the selected nebulae; see Fig. 14
of Hersant et al. 2001), we believe that
neglecting the contribution of crystalline silicates condensed from
the vapor phase does not significantly affect our results. There are
however presumptions that vapour phase condensates are present in
cometary grains. A class of very porous interplanetary dust
particles called CP, and suspected to be of cometary origin, shows
Mg-rich pyroxene crystals with whisker and platelet morphologies
(Bradley et al. 1983). These micro-structures are expected to
grow by
condensation from a relatively low-pressure vapour phase.
Silicates in meteorites are all in crystalline form. However, crystalline
silicates in meteorites were not necessarily produced by the annealing
process investigated in the present work. Therefore, we cannot
discuss the crystallinity of meteorites only in the
context of our model, although there is no apparent conflict, since
Fig. 3 shows that silicates within 3 AU remain essentially
crystalline at times less than 105 yr.
Most meteorites - stony, stony-iron and iron - record melting events
related to the metamorphism and magmatism of at least, seventy small
parent bodies (Scott 1991). In addition, a large number of asteroids
seem differentiated. Although the mechanism that yielded this increase
in temperature of the asteroidal parent body is still largely debated, no
amorphous interstellar
silicates present in the protosolar nebula would have
survived such thermal stress linked to the planetesimal formation and
evolution. Therefore, in the inner zone of the solar system, all solid
bodies appear crystalline.
Among the classes of meteorites that could have preserved a partial
record of the crystalline state of their amorphous silicate precursors,
are the carbonaceous and the unequilibrated type 3 chondrites
(especially the type LL3.0). These meteorites consists of chondrules
and matrix.
Chondrules are 100 to 1000 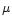 m size spheroidal silicates, mainly
made of olivine and pyroxene, which constitute the dominant fraction
(up to 70%) of chondrites. They are the products of partial melting of
precursor silicates - possibly the amorphous interstellar dust - with
negligible contribution of sulphides, oxides and iron. Although the
conditions of formation of chondrules are not totally understood,
experimental simulations have allowed a precise reconstruction of their
thermal history. (1) Their heating time during which sub-melting was
taking place varied from 100 s (Tsuchiyama & Nagahara 1981) to 20
h (Lofgren & Russell 1988). (2) Essentially based on the
distribution of the chemical elements between the different
mineralogical phases coexisting in chondrules (as for example the
Fe/Mg partitioning coefficients) cooling rates were estimated to lie
between 100 to 2000
m size spheroidal silicates, mainly
made of olivine and pyroxene, which constitute the dominant fraction
(up to 70%) of chondrites. They are the products of partial melting of
precursor silicates - possibly the amorphous interstellar dust - with
negligible contribution of sulphides, oxides and iron. Although the
conditions of formation of chondrules are not totally understood,
experimental simulations have allowed a precise reconstruction of their
thermal history. (1) Their heating time during which sub-melting was
taking place varied from 100 s (Tsuchiyama & Nagahara 1981) to 20
h (Lofgren & Russell 1988). (2) Essentially based on the
distribution of the chemical elements between the different
mineralogical phases coexisting in chondrules (as for example the
Fe/Mg partitioning coefficients) cooling rates were estimated to lie
between 100 to 2000 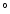 C/hr (Radomsky & Hewins 1990). (3)
The range of
heating temperature depends almost exclusively on the Mg-Al-Si chemical
proportions of the chondrules and ranges from 1200 to 1700
C/hr (Radomsky & Hewins 1990). (3)
The range of
heating temperature depends almost exclusively on the Mg-Al-Si chemical
proportions of the chondrules and ranges from 1200 to 1700 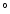 C. The
occurrence of the three common textures (granular in Mg-rich olivine
chondrules, pophyritic in Fe-rich olivine chondrules, radiating in
pyroxene chondrules) are experimentally reproduced by heating the
precursor silicates to near-liquidus temperature (1300-1800
C. The
occurrence of the three common textures (granular in Mg-rich olivine
chondrules, pophyritic in Fe-rich olivine chondrules, radiating in
pyroxene chondrules) are experimentally reproduced by heating the
precursor silicates to near-liquidus temperature (1300-1800 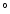 C) but not
higher (Hewins & Radomsky 1990).
C) but not
higher (Hewins & Radomsky 1990).
These short heating and cooling times associated with these high
silicate melting temperatures are consistent with the idea that
chondrules formed by transient heating phenomena (as those involved in
electric discharges) in the dust-rich regions of the protosolar nebula.
These conditions are not
accounted for in the present model.
It is clear that amorphous precursors of chondrules, if
any, would not have survived through such a violent thermal history.
As far as the matrix is concerned, its origin is poorly documented
mainly because of its very fine grain structure. The matrix is
essentially composed of broken fragments of chondrules, of clay
minerals and sub-micronic silicates and sulfides which are also found
as relic grains in chondrules. Matrix lumps are sometimes enclosed in
chondrule rims and therefore the formation of the matrix post-date the
chondrule formation. The fact that amorphous mineral are extremely rare
in the matrix cannot be taken as an evidence that the dust
was entirely crystalline at the time and location of the matrix
formation. Indeed, an intense circulation of water in the parent body
meteorites is attested by the presence of low temperature
phyllosilicates (such as smectite) essentially located in the matrix.
For a given chemical composition, the formation rate of clay
minerals is enhanced for amorphous compared to crystalline silicates.
Although the alteration rates of amorphous silicate has not been
experimentally measured, it seems possible that all the pre-existing
interstellar amorphous silicates - if any - would have been transformed
in clays during mild hydrothermal events.
To summarize this discussion on silicates in meteorites, the post-formation
geological processes have likely erased the amorphous structures of
interstellar precursors.
We discuss now the model results in the context of the amount of crystalline
silicates present in the dust of long-period comets such as Hale-Bopp.
Dynamical considerations suggest that these comets formed mainly in the
Uranus-Neptune zone. Our model shows that microscopic grains made of
crystalline silicates present in the inner regions of the solar nebula are
efficiently transported outwards to the comet formation zone by
turbulence in timescales of a few 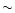 104 yr.
104 yr.
The mass fraction of crystalline silicates in the dust of comet Hale-Bopp
is estimated between 0.3-0.5 to 0.9 (Table 1). Comparing with model
results obtained in the outer regions (Table 4), we see that our
model well explains the low range of measured values in the case of the warm
nebula, regardless the crystallization law
 adopted. On the other
hand, the interpretation of the high degree of crystallinity
adopted. On the other
hand, the interpretation of the high degree of crystallinity
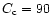 %
inferred by Wooden et al. (1999) would require a still warmer nebula.
%
inferred by Wooden et al. (1999) would require a still warmer nebula.
Radial mixing by turbulence is efficient as long as the grains are coupled to
the gas. The decoupling occurs when particles agglomerate and grow up to
sufficiently large sizes. There is no general consensus
on the critical size for decoupling: it is about 1 m according to
Weidenschilling (1997) and Supulver & Lin (2000), while
Stepinski & Valageas (1996) advocate for centimetre, or even smaller,
sizes. To be valid, our proposed scenario requires that timescales for
grain growth from micrometre sizes to centimetre or metre sizes are not
too short with respect to the diffusion timescale for radial mixing.
Dust coagulation in protoplanetary disks is a complex problem, which is
not yet well understood (see the review of Beckwith et al. 2000).
The sticking process depends both on the chemical and physical properties of
the grains, and on their relative velocity induced by thermal and
turbulent motions, gas drag and sedimentation. Theoretical calculations
predict that particle growth from sub-micron to metre sizes is very rapid
and occurs in timescales of typically a thousand orbital revolutions, that is
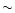 10 3 to
10 3 to 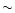 10 4 yr from 1 to 10 AU (Weidenschilling &
Cuzzi 1993; Stepinski & Valageas 1996; see also
Weidenschilling 1997,
for results obtained at 30 AU). Such short coagulation timescales
are in conflict
with observational evidence that disks around T Tauri and Herbig Ae/Be
stars of ages
10 4 yr from 1 to 10 AU (Weidenschilling &
Cuzzi 1993; Stepinski & Valageas 1996; see also
Weidenschilling 1997,
for results obtained at 30 AU). Such short coagulation timescales
are in conflict
with observational evidence that disks around T Tauri and Herbig Ae/Be
stars of ages 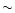 105-107 years are still dominated in mass by
millimetre grains (see the review of Natta et al. 2000).
On the other hand, fast coagulation seems a requisite to explain the
presence of planets in the Solar System (Stepinski & Valageas
1996).
The coagulation timescales given above can be compared to our diffusion
timescales. These latter are plotted
as a function of radial distance and time in Fig. 5, for the warm nebula
parameters
which fit cometary silicate measurements.
Coagulation timescales are somewhat lower, but by a factor of 5 at most,
than the diffusion
timescales computed at t < 105 yr. Therefore, given
actual uncertainties on grain growth, destruction processes by
collisions (Benz 2000), and transport through turbulent eddies,
we conclude that turbulent radial mixing of dust grains in the solar
nebula is a plausible mechanism for explaining the large amount
of crystalline silicates in comets.
105-107 years are still dominated in mass by
millimetre grains (see the review of Natta et al. 2000).
On the other hand, fast coagulation seems a requisite to explain the
presence of planets in the Solar System (Stepinski & Valageas
1996).
The coagulation timescales given above can be compared to our diffusion
timescales. These latter are plotted
as a function of radial distance and time in Fig. 5, for the warm nebula
parameters
which fit cometary silicate measurements.
Coagulation timescales are somewhat lower, but by a factor of 5 at most,
than the diffusion
timescales computed at t < 105 yr. Therefore, given
actual uncertainties on grain growth, destruction processes by
collisions (Benz 2000), and transport through turbulent eddies,
we conclude that turbulent radial mixing of dust grains in the solar
nebula is a plausible mechanism for explaining the large amount
of crystalline silicates in comets.
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm,clip]{MS1967f5.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg92.gif) |
Figure 5:
Diffusion timescale
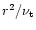 in the warm nebula as a
function of time. Curves from bottom to top correspond to increasing times.
Plain lines are for times 103, 104, 105,
and 106 years. Dotted lines are for times
in the warm nebula as a
function of time. Curves from bottom to top correspond to increasing times.
Plain lines are for times 103, 104, 105,
and 106 years. Dotted lines are for times
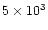 , ,
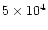 ,
and ,
and
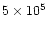 years.
years. |
| Open with DEXTER |
In order to explain the D/H ratios in cometary H2O and HCN,
Hersant et al. (2001) concluded that microscopic grains of H2O
and HCN ices, which subsequently accreted into cometesimals, condensed
and were mixed together in the 10-20 AU range at times
of typically 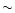 105 yr. Interestingly enough, this is also
the time when the crystalline mass fraction in this heliocentric
range has reached the plateau value (Fig. 3). In other words, at times
of
105 yr. Interestingly enough, this is also
the time when the crystalline mass fraction in this heliocentric
range has reached the plateau value (Fig. 3). In other words, at times
of 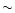 105 yr, silicates and icy particles with observed cometary
properties were available in the comet formation zone. Their sticking
and coagulation into kilometre-sized bodies could have then proceeded rapidly.
With a vertical 1-D model run at r = 30 AU which does not include
turbulence, Weidenschilling (1997) shows that the formation of comets
could have been completed in about
105 yr, silicates and icy particles with observed cometary
properties were available in the comet formation zone. Their sticking
and coagulation into kilometre-sized bodies could have then proceeded rapidly.
With a vertical 1-D model run at r = 30 AU which does not include
turbulence, Weidenschilling (1997) shows that the formation of comets
could have been completed in about
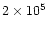 yr. To conclude,
our nebula model permits us to consistently explain both siliceous
and deuterium cometary composition by large scale turbulent radial
mixing in the solar nebula. In turn, the amount of
crystalline silicates in comets
provides us with additional constraints on the parameters of the
2-D model of Hersant et al. (2001).
yr. To conclude,
our nebula model permits us to consistently explain both siliceous
and deuterium cometary composition by large scale turbulent radial
mixing in the solar nebula. In turn, the amount of
crystalline silicates in comets
provides us with additional constraints on the parameters of the
2-D model of Hersant et al. (2001).
One of our primary goals was to investigate whether solar
nebulae models which fit deuterium enrichments in primitive Solar System
bodies (Hersant et al. 2001), would be able to explain the
amount of crystalline silicates measured in cometary dust. In fact, the
present
analysis based on three selected nebulae shows
that producing the amount of cometary crystalline silicates
requires the warm nebula.
Since a number of other warm nebulae fitting deuterium enrichments can be
generated by the 2-D model, the relative proportion of
crystalline silicates in comets can be used as an additional constraint to the
selection of nebulae. Based on the observational data (Table 1),
we adopted the value of
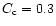 for this constraint.
A number of
nebulae were then calculated, as in Hersant et al., each one
defined
by the initial accretion rate
for this constraint.
A number of
nebulae were then calculated, as in Hersant et al., each one
defined
by the initial accretion rate 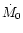 and radius
and radius
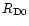 of the nebula,
and the coefficient
of turbulent viscosity
of the nebula,
and the coefficient
of turbulent viscosity 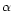 .
The equations of diffusion 6
and 7
were then integrated as a function of radial distance and time, using the
surface
density and temperature radial profiles of these nebulae. Nebulae which do
not provide adopted constraints were rejected. The ranges of
acceptable nebula parameters fitting both D/H and
.
The equations of diffusion 6
and 7
were then integrated as a function of radial distance and time, using the
surface
density and temperature radial profiles of these nebulae. Nebulae which do
not provide adopted constraints were rejected. The ranges of
acceptable nebula parameters fitting both D/H and 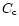 measurements are
substantially reduced with respect to those obtained by Hersant et al. (2001).
They are:
measurements are
substantially reduced with respect to those obtained by Hersant et al. (2001).
They are:
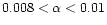 ,
,
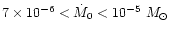 yr-1, and
yr-1, and
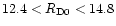 AU.
AU.
The derived ranges of acceptable 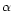 ,
,
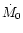 and
and
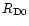 values are very small and should not be taken too seriously.
First, the adopted physical and chemical constraints might not be
fully appropriate. Indeed, there are still large uncertainties on D/H values
and silicate composition in comets. More important, among
physical constraints adopted by Hersant et al. (2001), the
initial mass
of the solar nebula was limited to masses smaller than 0.3
values are very small and should not be taken too seriously.
First, the adopted physical and chemical constraints might not be
fully appropriate. Indeed, there are still large uncertainties on D/H values
and silicate composition in comets. More important, among
physical constraints adopted by Hersant et al. (2001), the
initial mass
of the solar nebula was limited to masses smaller than 0.3 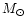 ,
in
order to satisfy the criterion of gravitational stability of the disk, and
the radius of the solar nebula was forced to reach Neptune distance in the
first
,
in
order to satisfy the criterion of gravitational stability of the disk, and
the radius of the solar nebula was forced to reach Neptune distance in the
first
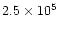 yr. These assumptions, which could be
certainly somewhat relaxed, result in the rejection
of nebulae with warm temperatures in their early life and constrain the
initial radius of the nebula to a small range. The second point to consider
is that the results are model dependent and obtained under several assumptions.
Among these, the value of the Prandtl number, which is not well known, has
a strong influence on the derived
yr. These assumptions, which could be
certainly somewhat relaxed, result in the rejection
of nebulae with warm temperatures in their early life and constrain the
initial radius of the nebula to a small range. The second point to consider
is that the results are model dependent and obtained under several assumptions.
Among these, the value of the Prandtl number, which is not well known, has
a strong influence on the derived 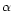 ,
,
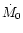 and
and
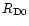 ranges
(Hersant et al. 2001). The uncertainties on the timescales for
isotopic exchanges and thermal annealing are significant.
Finally, the validity of the disk model may be
also questioned. Standard
ranges
(Hersant et al. 2001). The uncertainties on the timescales for
isotopic exchanges and thermal annealing are significant.
Finally, the validity of the disk model may be
also questioned. Standard 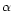 -disks are known to be not extended and
warm enough
to explain observations of circumstellar disks. Many alternative
and controversial solutions have been proposed and are beyond
the scope of the present paper. The initial high accretion
rate of
-disks are known to be not extended and
warm enough
to explain observations of circumstellar disks. Many alternative
and controversial solutions have been proposed and are beyond
the scope of the present paper. The initial high accretion
rate of 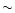 10-5
10-5 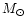 yr-1 that we derived
would correspond to that of Class 0 protostars when mass infall from
the envelope is feeding the disk (André et al. 2000).
Admittedly, this stage of the early
nebula is not well treated in our model and might affect the initial
and boundary conditions
of our transport equations. However, we must point out that
time-dependent models describing the early stages of the solar nebula
when most of its chemical evolution occurs, are not yet available.
yr-1 that we derived
would correspond to that of Class 0 protostars when mass infall from
the envelope is feeding the disk (André et al. 2000).
Admittedly, this stage of the early
nebula is not well treated in our model and might affect the initial
and boundary conditions
of our transport equations. However, we must point out that
time-dependent models describing the early stages of the solar nebula
when most of its chemical evolution occurs, are not yet available.
This paper presents a model to explain the presence of a high
amount of crystalline silicates in comets. The proposed scenario
is that crystalline silicates formed in the inner warm regions
of the solar nebula by the thermal annealing of amorphous silicates.
They were then transported out to the comet formation zone by turbulent
diffusion. This paper follows those of Drouart et al. (1999),
Mousis et al. (2000) and Hersant et al. (2001), which
interpret the
variety of deuterium enrichments observed in primitive objects of
the Solar System by isotopic exchange in the solar nebula and turbulent
radial mixing.
Our study makes use of the 2-D evolutionary solar nebula model
developed by Hersant et al. (2001). It takes into
account the rapid evolution of temperatures and pressures during disk
evolution. Such an approach is necessary to investigate quantitatively
whether the proposed scenario is plausible, since both thermal annealing
and turbulent mixing processes are strongly temperature dependent.
Using solar nebula parameters which fit D/H ratios in comets, we show that
turbulent diffusion is an efficient mechanism for
mixing amorphous and crystalline grains in the comet formation
zone. The timescale required for radial mixing is typically
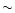
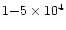 yr, depending on the solar nebula model. These
values are comparable, within a factor of a few, to
theoretical expectations concerning the characteristic timescales for
particle growth in the solar nebula. It is also well below the
time needed to form kilometer-sized comets from a population of
microscopic grains (Weidenschilling 1997). Therefore, given actual
uncertainties on grain growth in the solar nebula, it seems likely that
fast dust coagulation did not preclude large-scale radial mixing,
allowing the transport of crystalline silicates from inner to outer regions.
yr, depending on the solar nebula model. These
values are comparable, within a factor of a few, to
theoretical expectations concerning the characteristic timescales for
particle growth in the solar nebula. It is also well below the
time needed to form kilometer-sized comets from a population of
microscopic grains (Weidenschilling 1997). Therefore, given actual
uncertainties on grain growth in the solar nebula, it seems likely that
fast dust coagulation did not preclude large-scale radial mixing,
allowing the transport of crystalline silicates from inner to outer regions.
One of the aims of our modelling was to investigate whether the solar nebulae
selected by Hersant et al. (2001) to fit cometary D/H ratios would
also explain quantitatively
the high amount of crystalline silicates. Our calculations show
that fitting both observational constraints is possible, provided that we
use model parameters which generate warm nebulae. Using the mass fraction
of crystalline silicates estimated in comet Hale-Bopp as an additional
constraint to the model of Hersant et al. (2001), we derived the
ranges of
nebula parameters 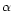 ,
,
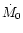 and
and
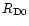 which fit both
cometary and silicate composition. The ranges of acceptable parameters
are small and may not represent the number of uncertainties and
assumptions in our model. However, this study qualitatively
demonstrates the need of
high temperatures in an extended zone of the solar nebula, to explain
both D/H and the properties of cometary silicates. In addition, it
shows that, in essence, the amount of crystalline silicates in comets
should permit us to check the validity of any model of the solar
nebula in which the temperature distribution is calculated.
More conclusive studies will have to await for the availability of
more realistic time-dependent models for solar nebula early evolution.
which fit both
cometary and silicate composition. The ranges of acceptable parameters
are small and may not represent the number of uncertainties and
assumptions in our model. However, this study qualitatively
demonstrates the need of
high temperatures in an extended zone of the solar nebula, to explain
both D/H and the properties of cometary silicates. In addition, it
shows that, in essence, the amount of crystalline silicates in comets
should permit us to check the validity of any model of the solar
nebula in which the temperature distribution is calculated.
More conclusive studies will have to await for the availability of
more realistic time-dependent models for solar nebula early evolution.
Our model predicts that, in a few 104 yr, the crystalline/amorphous
silicates ratio reaches the same value in almost the whole
nebula, except in the innermost regions. This might imply that
all comets formed in the turbulent part of the
solar nebula could have the same crystalline/amorphous silicates ratio,
a result not in conflict with available data on long-period comets
(Sect. 2). However, firm conclusions should await for more
detailed models which include grain coagulation, since
this process affects the efficiency of radial mixing by turbulence.
In addition, measurements of the crystalline/amorphous silicates ratio in
comets are still too sparse to allow detailed comparison with
model predictions. Data on Jupiter family comets
coming
from the Kuiper Belt are specifically required. They may
reveal a lower content of crystalline silicates, if they were
formed in a non-turbulent part of the outer nebula.
Acknowledgements
We thank D. Fabian, for providing us with laboratory results before
publication, and P. Michel and J. R. Brucato for enlightening discussions.
This work was supported by the Programme national de planétologie de
l'Institut national des sciences de l'univers (INSU) and the
Centre de la recherche scientifique (CNRS).
-
André, P., Ward-Thompson, D., & Barsony, M. 2000, in
Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russel
(The University of Arizona Press, Tucson), 59
In the text
-
Ashworth, J. R., Mallinson, L. G., Hutchinson, R., & Biggar, G. M. 1984,
Nature, 308, 259
In the text
NASA ADS
-
Beckwith, S. V. W., Henning, T., & Nakagawa, Y. 2000, in
Protostars and Planets IV, ed. V. Mannings, A. P. Boss, & S. S. Russel
(The University of Arizona Press, Tucson), 553
In the text
-
Benz, W. 2000. Space Sci. Rev., 92, 279
In the text
NASA ADS
-
Bouwman, J., Meeus, G., de Koter, A., et al. 2001, A&A, 375, 950
In the text
NASA ADS
-
Bradley, J. P., Brownlee, D. E., & Veblen, D. R. 1983, Nature, 301, 473
In the text
NASA ADS
-
Bradley, J. P., Humecki, H. J., & Germani, M. S. 1992,
ApJ, 394, 643
In the text
NASA ADS
-
Bradley, J. P., Keller, L. P., Snow, T., et al. 1999, Science, 285, 1716
In the text
NASA ADS
-
Brucato, J. R., Colangeli, L., Mennela, V., Palumbo, P., & Bussoletti, E.
1999a, P&SS, 47, 773
In the text
NASA ADS
-
Brucato, J. R., Colangeli, L., Mennela, V., Palumbo, P., & Bussoletti, E.
1999b, A&A, 348, 1012
In the text
NASA ADS
-
Cassen, P. 1996, Meteoritics & Planetary Science, 31, 793
In the text
-
Cassen, P. 2001, Meteoritics & Planetary Science, 36, 671
In the text
-
Chick, K. M., & Cassen, P. 1997, ApJ, 477, 398
In the text
NASA ADS
-
Colangeli, L., Brucato, J. R., Ferrini, et al. 1999, Adv. Space Res., 23, 1243
In the text
NASA ADS
-
Colangeli, L., Mennela, V., Rotundi, A., Palumbo, P., & Bussoletti, E.
1995, A&A, 293, 927
In the text
NASA ADS
-
Colangeli, L., Mennela, V., Rotundi, A., Palumbo, P., & Bussoletti, E.
1996, A&A, 312, 643
In the text
NASA ADS
-
Crovisier, J., Brooke, T. Y., Leech, K., et al. 2000, in Thermal emission
spectroscopy and analysis of dust disks, and regoliths, ed. M. L. Sitko,
A. L. Sprague, & D. K. Lynch, Astron. Soc. Pac. Conf. Ser., 196, 109
In the text
-
Crovisier, J., Encrenaz, T., Lellouch, E., et al. 1999,
in The Universe seen by ISO, ed. P. Cox, & M. F.
Kessler, ESA SP-427, 161
In the text
-
Crovisier, J., Leech, K., Bockelée-Morvan, D., et al. 1997, Science,
275, 1904
In the text
NASA ADS
-
Demyk, K., Jones, A. P., Dartois, E., Cox, P., & d'Hendecourt, L. 1999, A&A, 349, 267
In the text
NASA ADS
-
Drouart, A., Dubrulle, B., Gautier, D., & Robert, F. 1999, Icarus, 140, 129
In the text
NASA ADS
-
Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237
In the text
NASA ADS
-
Duschl, W. J., Gail, H.-P., & Tscharnuter, W. M. 1996, A&A, 312, 624
In the text
NASA ADS
-
Fabian, D., Jäger, C., Henning, Th., Dorschner, J., & Mutschke, H.
2000, A&A, 364, 282
In the text
NASA ADS
-
Gail., H.-P. 1998, A&A, 332, 1099
In the text
NASA ADS
-
Gail., H.-P. 2001, Radial mixing in protoplanetary accretion disks. I.
Stationary disc models with annealing and carbon combustion, A&A, 378, 192
In the text
NASA ADS
-
Gail., H.-P., & Sedlmayr, E. 1999, A&A, 347, 594
In the text
NASA ADS
-
Hallenbeck, S. L., Nuth, J. A., & Daukantas, P. L. 1998, Icarus, 131, 198
In the text
NASA ADS
-
Hanner, M. S. 1999, Space Sci. Rev., 90, 99
In the text
NASA ADS
-
Hanner, M. S., Brooke, T. Y., & Tokunaga, A. T. 1998, ApJ, 502, 871
In the text
NASA ADS
-
Hanner, M. S., Gehrz, R. D., Harker, D. E., et al. 1997, Earth, Moon, and
Planets, 79, 247
In the text
NASA ADS
-
Hanner, M. S., Lynch, D. K., & Russel, R. W. 1994, ApJ, 425, 274
In the text
NASA ADS
-
Hartmann, L., Calvet, N., Gullbring, E., & D'Alessio, P. 1998, ApJ, 495,
385
In the text
NASA ADS
-
Hawley, J. F., Smarr, L. L., & Wilson, J. R. 1984, ApJ, 55, 211
In the text
-
Hayward, T. L., Hanner, M. S., & Sekanina, Z. 2000, ApJ, 538, 428
In the text
NASA ADS
-
Hersant, F., Gautier, D., & Huré, J.-M. 2001, ApJ, 554, 391
In the text
NASA ADS
-
Hewins, R. H. 1997, Ann. Rev. Earth. Planet. Sci., 25, 61
-
Hewins R. H., & Radomsky, P. M. 1990, Meteoritics, 25, 309
In the text
NASA ADS
-
Huré, J.-M. 2000, A&A, 358, 378
In the text
NASA ADS
-
Huré, J.-M., & Galliano, F. 2001, A&A, 366, 359
In the text
NASA ADS
-
Knacke, R. F., Fajardo-Acosta, S. B., Tedesco, C. M., et al. 1993, ApJ, 418,
440
In the text
NASA ADS
-
Lenzuni, P., Gail, H.-P., & Henning, Th. 1995, ApJ, 447, 848
In the text
NASA ADS
-
Lofgren, G. E., & Russell, W. J. 1988, Geochim. Cosmochim. Acta, 50, 1715
In the text
-
Makalkin, A. B., & Dorofeyeva, V. A. 1991, Izv. Earth
Phys., 27, 650
In the text
-
Malfait, K., Waelkens, C., Waters, L. B. F. M., et al. 1998, A&A, 332, L25
In the text
NASA ADS
-
Molster, F. J., Yamamura, I., Waters, L. B. F. M., et al. 1999, Nature, 401, 563
In the text
NASA ADS
-
Morfill, G. E., & Völk, H. J. 1984, ApJ, 287, 371
In the text
NASA ADS
-
Mousis, O., Gautier, D., Bockelée-Morvan, D., Robert, F., &
Dubrulle, B. 2000, Icarus, 148, 513
In the text
NASA ADS
-
Natta, A., Grinin, V. P., & Mannings, V. 2000, in Protostars and Planets
IV, ed. V. Mannings, A. P. Boss, & S. S. Russel
(The University of Arizona Press, Tucson), 559
In the text
-
Neufeld, D. A., & Hollenbach, D. J. 1994, ApJ, 428, 170
In the text
NASA ADS
-
Nuth, J. A., & Donn, B. 1982, ApJ, 257, L103
In the text
NASA ADS
-
Radomsky, P. M., & Hewins, R. H. 1990, Geochim. Cosmochim.
Acta, 54, 3475
In the text
NASA ADS
-
Ruden, S. P., & Lin, D. N. C. 1986, ApJ, 308, 883
In the text
NASA ADS
-
Ruden, S. P., & Pollack, J. B. 1991, ApJ, 375, 740
In the text
NASA ADS
-
Scott, E. R. D. 1979, Mineral. Mag., 43, 415
In the text
-
Shakura, N. L., & Sunyaev, R. A. 1973, A&A, 24, 337
In the text
NASA ADS
-
Shu, F. H., Tremaine, S., Adams, F. C., & Ruden, S. P. 1990, ApJ, 358
In the text
-
Stepinski, T. F., & Valageas, P. 1996, A&A, 309, 301
In the text
NASA ADS
-
Supulver, K. D., & Lin, D. N. C. 2000, Icarus, 146, 525
In the text
NASA ADS
-
Wilson, J. R. 1978, in Source of Gravitational
Radiation, ed. L. Smarr (Cambridge University Press, Cambridge), 423
In the text
-
Tsuchiyama, A., & Nagahara, H. 1981, in Proceedings of the 6th symposium
on Antartic Meteorites, ed. T. Nagata, Mem. Nat. Inst. Polar Res.,
Spec. Issue, 20, 175
In the text
-
Weidenschilling, S. J. 1997, Icarus, 127, 290
In the text
NASA ADS
-
Weidenschilling, S. J., & Cuzzi, J. N. 1993, in Protostars and Planets III,
ed. E. H. Levy, & J. I. Lunine (The University of Arizona Press, Tucson),
1031
In the text
-
Wooden, D. H., Harker, D. E., Woodward, C. E., et al. 1999, ApJ, 517, 1034
In the text
NASA ADS
Copyright ESO 2002
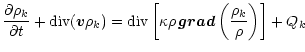
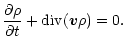
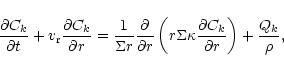
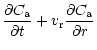
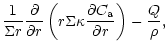
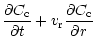
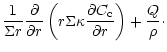
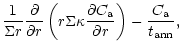
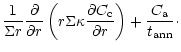
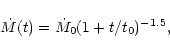
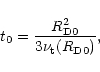
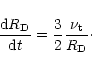
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{MS1967f1.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg54.gif)
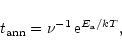
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{MS1967f2.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg64.gif)
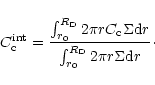
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{MS1967f3a.eps}\\...
...\\ [4mm]
\includegraphics[angle=270,width=8.5cm,clip]{MS1967f3c.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg87.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{MS1967f4.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg88.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.7cm,clip]{MS1967f5.eps}\end{figure}](/articles/aa/full/2002/12/aa1967/Timg92.gif)