4 Results

4.1 Integrated photometric parameters

The morphological classification, based on the galaxy colors, and the calculated magnitudes and colors for the objects in the sample are listed in Table 3. The magnitudes were derived by two independent methods. The first one is the integration of the intensity pixels in a series of diaphragms with increasing radius until the sum converges. The second method consisted of the integration of the luminosity profile (see Sect. 4.2). The results following the two methods are in very good agreement. However, the comparison with the magnitudes listed in The Third Reference Catalog of Bright Galaxies (de Vaucouleurs et al. 1991; hereafter RC3), are in a reasonable agreement only for ESO602-G 031, ESO025-G002, 1H1934-063, 1H2107-097, and CTSF10.01. The remaining objects show differences up to 0.5 mag. This is the case for MRK509 for which the RC3 lists $m_{\rm b} = 13.0$ while our value is $m_{\rm b} = 13.50$. Moreover, Kotilainen & Ward (1994; hereafter KW94) obtained for the same galaxy $m_{\rm b} = 14.06$. We attribute the discrepancies to variability of the AGN.

  

Table 3: Morphologies, magnitudes and colors derived for the galaxy sample.

The luminosity for the objects in the sample ranges from -18.7 to -22.3 with an average $M_{\rm b} = -20.7$. This value is rather similar to that found by Yee (1983), $M_{\rm b} = -20.4$, for a sample of Seyfert galaxies, but somewhat higher when compared to $M_{\rm b} = -20.0$ found by KW94 for a sample of Seyfert 1 galaxies. On the other hand, Christensen (1975) found that for a sample of normal spiral galaxies $M_{\rm B} = -19.7$. Note that $M_{\rm b}$ values given by the other authors have been recalculated using H₀ = 75 km s^-1 Mpc^-1.

   
4.2 Luminosity profiles

Since our sample is composed of both elliptical and spiral galaxies, we have used two different methods in order to obtain surface brightness profiles. For elliptical galaxies, profiles were obtained using the ELLIPSE routine within STSDAS (Jedrezejewski 1987). Basically the task starts from a first guess elliptical isophote defined by approximate values for the center coordinates, ellipticity and position angle. With these initial values the image is sampled along an elliptical path producing an intensity distribution as a function of the position angle. Then the harmonic content of this distribution is analyzed by least-squares. The harmonic amplitudes, together with the local image radial gradient, are related to a specific ellipse geometric parameter and give information on how much the current parameter value deviates from the true one. The parameter is then modified by the calculated value and the process continues until convergence is reached.

The approach was different for spiral galaxies because the ELLIPSE algorithm does not converge due to the clumpy structure present in the spiral arms. In this case we have used the equivalent profile m versus $r_{\rm eq}$, where $r_{\rm eq} = (S/\pi)^{1/2}$ being S(m) proportional to the area projected on the image (in square arcsecs) subtended by all those points of the galaxy for which the intensity I(m') = 10^-0.4m satisfies the condition I(m')> I(m) (Sérsic 1982). It is worth noting that this last profile and that used for an elliptical galaxy show exactly the same behavior for an E0 galaxy.

The B, V and I profiles were then decomposed into 3 assumed components: Gaussian (due to the stellar-like profile of the AGN), bulge and disk. In three cases we noted the presence of other components such as bars, arms or lens. These structures have not been taken into account in the fit because their contribution to the total luminosity of the galaxy were not greater than 5%. The functional form adopted for each of the fitting component is as follows:

$$% I(r)=I_0 \exp(-2.71*(r/fw)^2)$$ (1)

for the Gaussian;

$$% I(r)=I_{\rm e} \exp(-7.688*((r/r_{\rm eff})^{.25}-1))$$ (2)

for the bulge;

$$% I(r)=I_{\rm d} \exp(-r/d_{\rm l}-(h_{\rm d}/r)^3)$$ (3)

for the disk component.

In the above expressions I₀ is the peak of the Gaussian profile at r=0 and fw the full width at half maximum (FWHM). The quantity $I_{\rm e}$ is the intensity at $r_{\rm eff}$, the radius that encloses half of the total luminosity of the bulge (also known as the effective radius). Finally, $I_{\rm d}$ is the central intensity, $d_{\rm l}$ the length scale and $h_{\rm d}$ the radius of central cutoff of the disk component.

In order to obtain the above parameters we followed the method described by Shombert & Bothum (1987) using the NFIT routine implemented in STSDAS. This routine must be provided with appropriate initial parameters in order to begin the fit. Disk parameters can be guessed directly through the profile since the disk is not seriously contaminated by the bulge in the outermost region of the galaxy profile. However, it is necessary to have photometric data at large radii in order to avoid contamination from other more central components (Prieto et al. 1992). The main difficulty was to perform the fit to the Gaussian and bulge components since they completely overlap each other. This problem was solved by performing an initial fit considering only the innermost region data, generally the first 4-5 $\hbox{$^{\prime\prime}$ }$. During this process we fixed the disk guessed parameters and the fw value that was initially calculated using field stars. Task converges rapidly at this step and calculated parameters do not significantly depend on the initial adopted values. Finally, the calculated parameters for the Gaussian and bulge components together with those of the disk were used as initial values to perform the fit over the whole range of the luminosity profile, omitting those points affected by additional structures. Uncertainties in the parameters were calculated by doing small variations on the initial adopted values prior to the fitting. We found that the differences were never greater than 20%. We have also checked how seeing influences the calculated parameters by deconvolving the images. The most seriously affected parameters are those of the bulge (I₀ tends to be higher and $r_{\rm e}$ tends to be smaller) but the variations were never greater than 10-15%. Moreover, as deconvolution is a conservative process, the luminosity ratios within the components remain unchanged between the errors.

From the derived photometric parameters we were then able to calculate the total luminosity for each of the 3 components by integrating Eqs. (1)-(3) as follows:

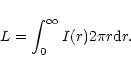$$% L=\int_0^{\infty}I(r)2\pi r {\rm d}r.$$ (4)

This integration leads to the following results:

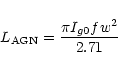$$% L_{\rm AGN}= \frac {\pi I_{g0} fw^2}{2.71}$$ (5)

for the Gaussian

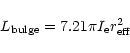$$% L_{\rm bulge}=7.21\pi I_{\rm e} r_{\rm eff}^2$$ (6)

for the bulge

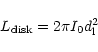$$% L_{\rm disk}=2\pi I_0 d_{\rm l}^2$$ (7)

for the disk component when $h_{\rm d}=0$.

For the case $h_{\rm d} \neq 0$, the above integral has no analytic solution, so a numerical integration was adopted. Total magnitudes obtained using the above procedure are, on average, 0.10 mag brighter than those calculated through the integration of the image intensity pixels, as was explained in Sect. 4.1. This systematic difference is not surprising since now the luminosity profile integration is made up to $r=\infty$.

  

Table 4: Photometric parameters derived for the galaxy sample.

  

Table 5: Luminosity ratios between components.

Figures 2a-j present the observed luminosity profiles and the fit applied to each galaxy. Color profiles have been obtained directly from the fitted profiles. Decomposition in the three components is only shown for the B data. Table 4 lists the photometric parameters calculated from the decomposition technique and Table 5 lists the bulge to disk, bulge to Gaussian and Gaussian to total luminosity ratios in the B, V and I filters. Note that in Table 4, $g_0=-2.5 \log(I_0$), $m_{\rm e}=-2.5 \log(I_{\rm e}$) and $b_0=-2.5 \log(I_{\rm d}$). These quantities are expressed in mag arcsec^-2.

A very interesting result was obtained from the decomposition profiles: In six out of eight disk galaxies it was necesary to truncate the exponential profile in order to get an adecuate fit. In fact, the radius of the central cutoff $h_{\rm d}$ ranged from 3 kpc for CTS A08.12 and 1H 2107-097, up to 10 kpc as is the case of ESO 602-G031. Moreover, for each galaxy the cutoff radius corresponds to a reddened region that is well identified in the B-V color map. We have obtained very similar colors for these regions, $(B-V)\sim1.2$. Color maps for three galaxies of the sample are presented in Sect. 5.

4.3 Color diagram and gradients

The dominant stellar population of the individual galaxies is inferred from the integrated colors. This information, together with the luminosity profiles, can be used to derive the morphological type of the host galaxies. Figure 3 illustrates the color-color diagram (B-V) vs. (V-I) for the galaxies listed in Table 3. We have compared our data with those obtained from Hunt et al. (1999) for a sample of Seyfert 1 galaxies. The colors of both samples show a similar behavior. We have also plotted in that figure the integrated averaged colors of normal galaxies, taken from Table 2 of de Jong et al. (1996), for two different morphological types as well as Stellar population models for E galaxies with ages between 12 and 15 Gyr computed by Tantalo et al. (1998).

From the color-color diagram we conclude that: a) 40% of the sample (ESO602-G031, 1H1934-063, 1H2107-097, and CTSF10.01) has a stellar population typical of Seyfert galaxies hosted by a spiral galaxy; b) CTSC16.16 and CTSA08.12 are early-type galaxies; c) The integrated (B-V) color of MRK509 is bluer than that expected for any morphological type. However, it should be stressed that nearly half the luminosity of MRK509 comes from its AGN.

Figure 2: Luminosity B (empty squares), V (empty circles), I (filled squares) and color B-V and V-I profiles of the sample galaxies. Solid line is the best fit to the data. Decomposition in a Gauss (points) bulge (short dashed) and disk components (long dashed) is only shown for the B data. Color B-V and V-I profiles were calculated using the obtained fitted functions. a) CTC C16.16, b) CTS G03.04, c) CTS A08.12, d) ESO 602- G031, e) ESO 025- G 002, f) 1H 1934-063, g) 1H 2107-097, h) ESO 354- G 004, i) MRK 0509, j) CTS F10.01.

Figure 2: continued.

Figure 3: Color-color diagram for the sample galaxies (filled squares). Stars represent the Hunt et al. (1999) sample. Upper and lower crosses show the average color for normal galaxies with 0<T<2 and 6<T<8 respectively. The small box show color models for elliptical galaxies with ages between 12 and 15 Gyr taken from Tantalo et al. (1998).

A quick inspection of the color profiles in Figs. 2a-j shows that almost all galaxies present color gradients. In 1H1934-063, 1H2107-097, MRK509 and CTSF10.01, their B-V and V-I colors become monotonically redder with increasing distance to the galaxy center. In addition, the Seyfert nucleus leaves a clear signature in the color profiles: in the central 3 $\hbox{$^{\prime\prime}$ }$ colors are, on average, 0.3 mag bluer than those of the external parts of the galaxy. However, ESO602-G031 and ESO354-G004 show redder B-V color gradients towards the center but their V-I color profiles are almost constant along the galaxy radius. It is worth noting that 1H 2107-097 has a V-I color profile abnormally red ( $V-I \sim 1.8$) at large radius.

Color profiles can be interpreted in terms of the spectral energy distribution of a given galaxy. Our sample is composed of nine Seyfert 1 galaxies and one Narrow-Line Seyfert 1 galaxy. These type of galaxies have strong emission lines and a continuum which can be accounted for by a combination of stellar population and a non-thermal spectrum. A significant difference in line intensity ratios and in the optical spectral index is observed among Seyfert 1 and Narrow Line Seyfert 1 galaxies (RPD2000). Seyfert 1s, like CTS C16.16, A08.12, CTS F10.01 and CTS G03.04 have continua steeper to the blue (RPD2000), which is consistent with the observed color profiles. The galaxy 1H 2107-097, has a flat continumm (Fig. 1c in RPD2000) and it is the only galaxy in our sample that shows peculiar color profiles. The B-V profile is very blue in the galaxy center while the V-I is abnormally red.

4.4 H$\alpha$ images

It is surprising to see that only one out of the 6 (16%) imaged galaxies shows H$\alpha$ emission beyond the nucleus. In fact, we detected disk emission in ESO 025-G002, as can be seen from the continuum subtracted $\rm H\alpha + [NII]$ image presented in Fig. 4. From this image we can appreciate that emission is extended up to a distance of 8 kpc from the nucleus.

The previous result is different from that reported by Pogge (1989) (hereafter P89) who found that 3 out of 9 (33%) of the Seyfert 1 galaxies showed extended emission within the inner 1 kpc. Moreover, P89 results contrast with those found by GD97 that report that 8 out of 13 (61%) Seyfert 1 galaxies showed extended emission. However, we must note that the mean distance for our sample is $vz = 10\,500$ km s^-1, leading to a scale length of 0.7 kpc arcsec^-1. This is well below the resolution of both P89 and GD97 works, for which the mean distance of the samples is $vz \sim 2000$ km s^-1 that leads to a scale length of 0.1 kpc arcsec^-1.

On the other hand, another important issue to have in mind is how these samples were defined. In principle, the P89 and GD97 samples are similar, but while GD97 do not use interaction as a selecting criterion, P89 excludes interacting galaxies. Similarly, P89 does not limit the sample by inclination angle while GD97 do. None of these selecting critera was used to define our sample.