A&A 384, 899-907 (2002)
DOI: 10.1051/0004-6361:20020133
P. D. Morley1 - I. Schmidt2
1 - Development Systems Group B301, Veridian Systems
Division, 14700 Lee Road, Chantilly, VA 20151, USA
2 -
Departamento de Física, Universidad
Técnica Federico Santa María, Casilla 110-V, Valparaíso, Chile
Received 14 May 2001 / Accepted 16 November 2001
Abstract
We employ an effective gravitational stellar final
collapse model which contains the relevant physics involved in
this complex phenomena: spherical radical infall in the
Schwarzschild metric of the homogeneous core of an advanced star,
giant magnetic dipole moment, magnetohydrodynamic material
response and realistic equations of state (EOS). The
electromagnetic pulse is computed both for medium size cores
undergoing hydrodynamic bounce and large size cores undergoing
black hole formation. We clearly show that there must exist two
classes of neutron stars, separated by maximum allowable masses:
those that collapsed as solitary stars (dynamical mass limit) and
those that collapsed in binary systems allowing mass accretion
(static neutron star mass). Our results show that the
electromagnetic pulse spectrum associated with black hole
formation is a universal signature, independent of the nuclear
EOS. Our results also predict that there must exist black holes
whose masses are less than the static neutron star stability
limit.
Key words: pulsars: general - radiation mechanisms: general
What is the measurable signal for gravitational collapse? It certainly produces gravitational waves, but unfortunately these have shown to be undetectable so far. However, there is another signal. Since the star has a sizable magnetic field, and since we expect this field to get quenched very rapidly during gravitational collapse, a massive electromagnetic pulse (MEMP) is created. We further show that the power spectrum is unlike any other naturally occurring phenomena: a wave packet whose wavetrain lasts only 2 milliseconds and whose characteristic power spectrum is a square block.
We present a simulation, within an effective model, of the iron-core collapse of massive stars which produce type II supernova. Depending on the core's mass, either a hydrodynamic bounce occurs above nuclear densities or the collapse races unhindered into the formulation of a stellar size black hole. Either case produces a MEMP. Our main contribution in this paper is the calculation of the energy spectrum of the MEMP. In cases where the collapsing core has mass greater than the dynamical neutron star mass limit (discussed herein), a hydrodynamic bounce cannot occur and no visible supernova results. In such cases, the MEMP is the only electromagnetic signal associated with the gravitational collapse.
One of the unexpected secondary results is the finding that, in general, there exist two classes of neutron stars: the first class is made up of solitary neutron stars which do not have the opportunity to accrete matter from a binary companion, and therefore have original masses coming from the collapse process. This mass is bounded by the ability of the nuclear equation of state to produce a hydrodynamic bounce. An unexpected secondary finding is that this imposes an heretofore unappreciated constraint on candidate nuclear equations of state. The maximum mass of the neutron star in this class is the dynamical mass, being the largest core mass that can undergo a hydrodynamic bounce. We will see that this dynamical mass limit is considerably less than the static mass limit, so the bounce does indeed save the core from further collapse due to its own self-gravity. The second class of neutron stars are those that can accrete matter from a binary companion and so their maximum mass is constrained by the requirement of static stability: the maximum static neutron star mass. In general, we find that the maximum static mass can exceed the dynamic mass by as large as 100%.
A current review of the status of gravitational collapse is given
in Joshi (2000), who discusses spherically symmetric collapse.
Fryer & Heger (2000) discuss core collapse from the viewpoint of
creating type II supernova from the hydrodynamic bounce. The
remnant size cores found by Fryer and Heger are close to the sizes
in this paper, though they do not investigate the remnant size
versus the nuclear equation of state. In the present paper, we
consider spherical radial infall and stop the simulation if bounce
occurs; continuing on would require incorporating shock physics.
As shown in the work of Bocquet et al. (1995), only gigantic
magnetic fields
B > 1010
![]() (
(
![]() Gauss,
Gauss,
![]() T) cause stellar deformation. Since the
magnetic fields considered in this paper fall far below this large
critical field, the star is not deformed by its magnetic field. An
interesting followup to the research presented here, is to apply
the effective gravitational collapse model to stars having
non-negligible rotation.
T) cause stellar deformation. Since the
magnetic fields considered in this paper fall far below this large
critical field, the star is not deformed by its magnetic field. An
interesting followup to the research presented here, is to apply
the effective gravitational collapse model to stars having
non-negligible rotation.
In general, there are three sources for electromagnetic and gravitational radiation associated with stellar collapse: the direct radiation phase emitted by the stellar object before the formation of a black hole, the so-called damped oscillations known as quasi-normal ringing (Iyer 1987) that are the vibrations of a black hole shaking off its non-zero multipole charge moments, and the late-time power-law tail (Price 1972; Cunningham 1978; Leaver 1986; Hod 1999, 2000a,b) underneath the damped oscillations. Because of the gravitational redshift, essentially the only energy that survives to infinity comes from the direct radiation phase, before the black hole forms. In this paper, we calculate the direct phase electromagnetic energy radiated by stellar objects that bounce and become stable neutron stars, and stellar objects so massive that they become black holes.
In order to calculate the electromagnetic radiation produced by the gravitational collapse, our strategy is the following. During the collapse the infall kinetic energy decreases while the system does mechanical work against the internal star pressure. This pressure has, in general, two components: material (nuclear) pressure and electromagnetic pressure. However, all published nuclear equations of state have the property that the nuclear pressure is orders of magnitude larger than the electromagnetic pressure; indeed, only for magnetic fields greater than 1018 Gauss does the electromagnetic pressure approach parity with the nuclear pressure. Using conservation of energy, the continuity equation and the material equation of state, we can calculate how the star radius changes with time. If we further assume that the stellar magnetic field can be approximated by a dipole field, and that the lines of magnetic field are frozen in the material and carried along with it, we can relate the change in the star's radius with time to the change in its effective magnetic moment. The usual dipole radiation formula then gives the energy spectrum of the radiation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms1471f1r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg9.gif) |
Figure 1: Difference between proper and Schwarzschild times. |
| Open with DEXTER | |
We simulate the collapse to the hydrodynamic bounce, or to twice
the gravitational radius,
![]() ,
if no bounce occurs.
In the former case, the bounce cuts off the MEMP, while in the
latter case, final black hole formation at radius =
,
if no bounce occurs.
In the former case, the bounce cuts off the MEMP, while in the
latter case, final black hole formation at radius = ![]() occurs
almost instantaneously later after the simulation ends. Because of
the gravitational redshift, the final stellar trajectory from
2
occurs
almost instantaneously later after the simulation ends. Because of
the gravitational redshift, the final stellar trajectory from
2![]() to
to ![]() adds little to the observable energy at
infinity. Thus the MEMP calculated is expected to be an accurate
profile. The reason why we stop at 2
adds little to the observable energy at
infinity. Thus the MEMP calculated is expected to be an accurate
profile. The reason why we stop at 2![]() is because, while the
Schwarzschild metric is the exterior metric during gravitational
collapse and as such, is the clock time in the effective collapse
model, the radiation process must be calculated in proper time. In
Fig. 1, we plot the difference between proper time and
Schwarzschild time. Only when the core radius becomes less than
3
is because, while the
Schwarzschild metric is the exterior metric during gravitational
collapse and as such, is the clock time in the effective collapse
model, the radiation process must be calculated in proper time. In
Fig. 1, we plot the difference between proper time and
Schwarzschild time. Only when the core radius becomes less than
3![]() is there a difference in the two clocks. By stopping the
simulation at 2
is there a difference in the two clocks. By stopping the
simulation at 2![]() ,
we can still reliably calculate the core
surface as a function of proper time, by using the Taylor
expansion employing the Schwarzschild time solution of the
collapse model. Indeed, one can calculate from this figure that
the time error is 8.364 microseconds
,
we can still reliably calculate the core
surface as a function of proper time, by using the Taylor
expansion employing the Schwarzschild time solution of the
collapse model. Indeed, one can calculate from this figure that
the time error is 8.364 microseconds ![]() ,
where
,
where
![]() ,
with
,
with ![]() being the core mass. At
the same time, we fold in the gravitational and Doppler redshift,
since the difference between the Schwarzschild time and proper
time leads to a gravitational redshift of the produced radiation.
being the core mass. At
the same time, we fold in the gravitational and Doppler redshift,
since the difference between the Schwarzschild time and proper
time leads to a gravitational redshift of the produced radiation.
The collapse process from the initial starting configuration of
the iron-core mass density (![]() )
of
)
of
![]() gm/cm3 and inward speed
gm/cm3 and inward speed
![]() to
either hydrodynamic bounce or twice
to
either hydrodynamic bounce or twice ![]() takes less than 3
milliseconds. In contrast, the characteristic time scale for
neutrino diffusion out of the core is
takes less than 3
milliseconds. In contrast, the characteristic time scale for
neutrino diffusion out of the core is ![]()
![]() s. This 103 times larger neutrino diffusion scale means
that these particles cannot influence the bounce or the MEMP. The
role of the neutrinos is not to carry away the binding energy of
the collapsing matter, as it sometimes is erroneously stated.
Rather, the collapsing matter must do work against the equation of
state and this energy is stored as internal energy, entirely
analogous to a weight compressing a spring. This stored energy is
not lost, but remains primarily as elevated Fermi levels of
electrons and nucleons. Thus the energy the neutrinos actually
carry away is the energy from nuclear beta decay, relaxed elastic
energy and thermal heat energy. The difference in the time scales
for neutrino diffusion and hydrodynamic infall means that the
iron-core collapse is adiabatic, allowing a concise formulation
for the conservation of energy. Previous work, Morley
(2000), showed that neutrino transport in the iron-core was
due to elastic scattering and typically
s. This 103 times larger neutrino diffusion scale means
that these particles cannot influence the bounce or the MEMP. The
role of the neutrinos is not to carry away the binding energy of
the collapsing matter, as it sometimes is erroneously stated.
Rather, the collapsing matter must do work against the equation of
state and this energy is stored as internal energy, entirely
analogous to a weight compressing a spring. This stored energy is
not lost, but remains primarily as elevated Fermi levels of
electrons and nucleons. Thus the energy the neutrinos actually
carry away is the energy from nuclear beta decay, relaxed elastic
energy and thermal heat energy. The difference in the time scales
for neutrino diffusion and hydrodynamic infall means that the
iron-core collapse is adiabatic, allowing a concise formulation
for the conservation of energy. Previous work, Morley
(2000), showed that neutrino transport in the iron-core was
due to elastic scattering and typically ![]() 1000 collisions
occurred before escape. Our collapse code in the present paper
shows beyond a doubt, that if no hydrodynamic bounce occurs, these
diffusing neutrinos are trapped in the infalling nuclear material
and are carried into the resulting black hole. Thus observation of
neutrinos associated with particular supernova proves that the
initial infall did not form a black hole.
1000 collisions
occurred before escape. Our collapse code in the present paper
shows beyond a doubt, that if no hydrodynamic bounce occurs, these
diffusing neutrinos are trapped in the infalling nuclear material
and are carried into the resulting black hole. Thus observation of
neutrinos associated with particular supernova proves that the
initial infall did not form a black hole.
Another physical insight into the problem is the recognition that
the iron-cores have flat density profiles. In Fig. 2, we show the
neutron star density profile using the Friedman-Pandharipande
equation of state, Straumann (1992). Thus the
approximation that the star collapses homogeneously is excellent
(t = Schwarzschild time):
![]() .
In this
paper, we treat spherical radial infall. As mentioned earlier, a
very interesting follow-on to this research is to remove this
constraint and allow core rotation in the effective collapse
model.
.
In this
paper, we treat spherical radial infall. As mentioned earlier, a
very interesting follow-on to this research is to remove this
constraint and allow core rotation in the effective collapse
model.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{ms1471f2r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg21.gif) |
Figure 2: Neutron star density profile using the Friedman-Pandharipande equation of state, Straumann (1992). |
| Open with DEXTER | |
Further
simplifications can be achieved by using the fact that the
electrical conductivity of the iron-core is very high, nearly
infinite. This allows the magnetohydrodynamic approximation: the
lines of magnetic force are frozen into the material and are
carried along with it. In this paper, we approximate the iron-core
stellar magnetic field by a magnetic dipole of moment ![]() .
We use the model of a uniformly magnetized sphere of magnetization
per unit volume
.
We use the model of a uniformly magnetized sphere of magnetization
per unit volume ![]() .
The relation of
.
The relation of ![]() to
to ![]() is
is
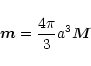 |
(1) |
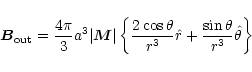 |
(2) |
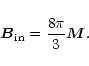 |
(3) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms1471f3r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg28.gif) |
Figure 3: Stellar magnetic dipole field. |
| Open with DEXTER | |
This is shown in Fig. 3. In general, a = a(t) and
![]() .
The magnetohydrodynamic material response is
the constancy of the magnetic flux through the polar region, Fig. 4
.
The magnetohydrodynamic material response is
the constancy of the magnetic flux through the polar region, Fig. 4
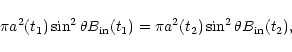 |
(4) |
(where
![]() ), giving
), giving
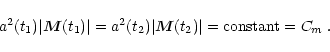 |
(5) |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{ms1471f4r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg33.gif) |
Figure 4: Constancy of the magnetic flux through the polar region. |
| Open with DEXTER | |
Therefore
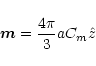 |
(6) |
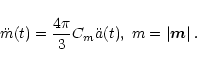 |
(7) |
Thus we have obtained a relation between the second order time derivative of the stellar effective magnetic moment and the star's surface acceleration, which will allow us to obtain the power radiated once we know the acceleration. This will be obtained by a numerical simulation, whose ingredients we explain in the next sections.
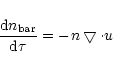 |
(8) |
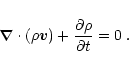 |
(9) |
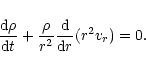 |
(10) |
| (12) |
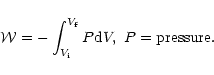 |
(13) |
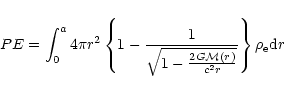 |
(15) |
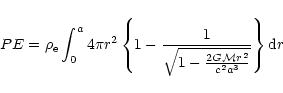 |
(16) |
To order O(
vr2/c2), the instantaneous kinetic energy is
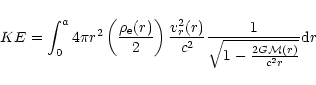 |
(19) |
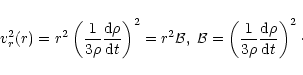 |
(20) |
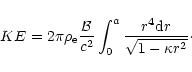 |
(21) |
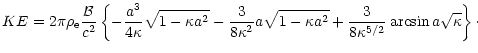 |
(22) |
![$\displaystyle KE = \int_{0}^{a}4\pi r^{2}\left(\frac{\rho_{\rm e}(r)}{2}\right)...
...{c^{4}} \right]
{1 \over \sqrt{1 - \frac{2G{\cal M}(r)}{c^{2}r}}} {\rm d}r\cdot$](/articles/aa/full/2002/12/aa1471/img78.gif) |
(23) |
| Class | Property | Applicability |
| normal matter |
|
atomic nuclei |
| iron-core |
|
proto-neutron star |
| neutronic | cold neutron star |
The different regimes for the nuclear EOS are listed in Table 1.
In this paper, two different nuclear EOS were used in the collapse calculations: the "Argonne AV14 + UVII" (Wiringa 1988) and the QCD (Kislinger 1978).
Perturbation theory in quantum chromodynamics (QCD) breaks down at
![]() twice nuclear density, where it must be joined to phenomenological
EOS. Both EOS used here are joined to the Baym EOS, as mentioned earlier. At
some time in the future, the nuclear EOS will be known accurately, and then
collapse calculations will lead to predictions with less error.
twice nuclear density, where it must be joined to phenomenological
EOS. Both EOS used here are joined to the Baym EOS, as mentioned earlier. At
some time in the future, the nuclear EOS will be known accurately, and then
collapse calculations will lead to predictions with less error.
Now we have all the ingredients for the numerical simulation. Once
the initial stellar radius, surface velocity, mass and density are
given, we can compute
![]() using the continuity Eq. (11), and therefore the new density and potential energy
(Eq. (17)) in the next
using the continuity Eq. (11), and therefore the new density and potential energy
(Eq. (17)) in the next ![]() step. Then we
calculate the work necessary to reach this new density using the
corresponding EOS, and check whether the bounce condition given in
Eq. (14) is met. If it is, which means that the new
kinetic energy vanishes, there is a bounce and we stop the
simulation. If it is not, we continue by checking also whether we
have reached twice
step. Then we
calculate the work necessary to reach this new density using the
corresponding EOS, and check whether the bounce condition given in
Eq. (14) is met. If it is, which means that the new
kinetic energy vanishes, there is a bounce and we stop the
simulation. If it is not, we continue by checking also whether we
have reached twice ![]() ,
in which case we also stop. If we have
not reached that radius we compute the new kinetic energy (18), which allows us in turn to get the new surface
velocity solving Eq. (24) and then use the continuity
equation again, and so on. This logic is described in Fig. 5. Notice that the desired quantity, the surface
acceleration, is obtained directly from the continuity Eq. (11), as
,
in which case we also stop. If we have
not reached that radius we compute the new kinetic energy (18), which allows us in turn to get the new surface
velocity solving Eq. (24) and then use the continuity
equation again, and so on. This logic is described in Fig. 5. Notice that the desired quantity, the surface
acceleration, is obtained directly from the continuity Eq. (11), as
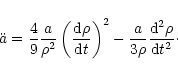 |
(25) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms1471f5r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg93.gif) |
Figure 5: Code logic. |
| Open with DEXTER | |
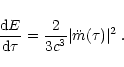 |
(26) |
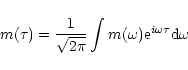 |
(27) |
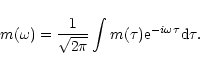 |
(28) |
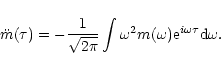 |
(29) |
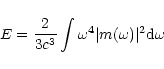 |
(30) |
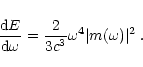 |
(31) |
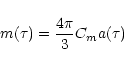 |
(32) |
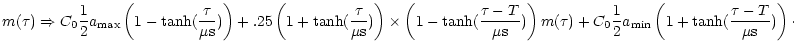 |
(33) |
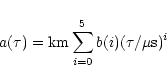 |
(34) |
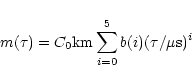 |
(35) |
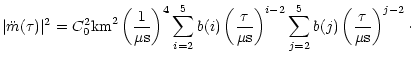 |
(36) |
E =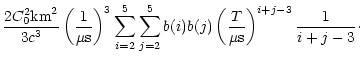 |
(37) |
When the collapse extends below 3 ![]() ,
we need to use multiple RORO
functions to separate out the contribution of each surface to the radiation
spectrum, since each surface has a different gravitational redshift
and Doppler shift. Then the energy radiated from each surface radius
can be corrected by the correct attenuation factor, as perceived from
an observer far away.
,
we need to use multiple RORO
functions to separate out the contribution of each surface to the radiation
spectrum, since each surface has a different gravitational redshift
and Doppler shift. Then the energy radiated from each surface radius
can be corrected by the correct attenuation factor, as perceived from
an observer far away.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ms1471f6r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg115.gif) |
Figure 6: Integration contour. |
| Open with DEXTER | |
We must compute ![]() where
where ![]() is given by Eq. (28).
Letting
is given by Eq. (28).
Letting
![]() ,
,
![]() and
and
![]() ,
we have
,
we have
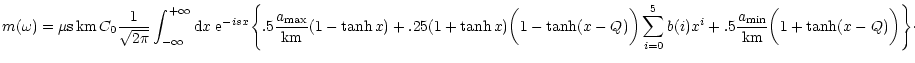 |
(38) |
![$\displaystyle m(\omega) = \frac{\mu {\rm s \; km} \; C_{0}}
{\sqrt{2 \pi}} (-2 ...
...h Q}\sum_{j=0}^{5}b(j)
\Bigg(-i \pi \left(\frac{2N+1}{2}\right)\Bigg)^{j}\Bigg]$](/articles/aa/full/2002/12/aa1471/img122.gif) |
|||
![$\displaystyle + \sum_{N=0}^{\infty}{\rm e}^{-isQ -s \pi(\frac{2N+1}{2})} \Bigg[...
...ft(\frac{2N+1}{2}\right)\Bigg)^{j}
+.5(a_{\rm min}/{\rm km})\Bigg] \Bigg\}\cdot$](/articles/aa/full/2002/12/aa1471/img123.gif) |
(39) |
![\begin{figure}
\par\includegraphics[width=6cm]{ms1471f7r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg129.gif) |
Figure 7: Radii time trajectory, for core masses of 1.5 and 5 solar masses, for the initial conditions stated in the text. Also, an acceleration profile of a core bounce in the Argonne EOS, for a 0.75 solar mass core. |
| Open with DEXTER | |
In the collapse studies, whenever a star goes below three times
![]() ,
we solve for the radius as a function of proper time by
means of the Taylor expansion
,
we solve for the radius as a function of proper time by
means of the Taylor expansion
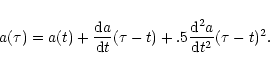 |
(40) |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{ms1471f8r.eps}
\end{figure}](/articles/aa/full/2002/12/aa1471/Timg131.gif) |
Figure 8: Spectrum of the radiated energy, for the Argonne (for a core of 1.0825 solar masses) and QCD (for a core of 1.3806 solar masses) equations of state, and for a core mass of 1.5 and 5 solar masses, for the initial conditions mentioned in the text. |
| Open with DEXTER | |
It is also of interest to see the kinetics of black hole
formation. Unexpectedly, we find that once the maximum core mass
allowing hydrodynamic bounce is exceeded, the black hole is formed
independently of the nuclear EOS. Thus, for example, the radius
function a(![]() ), infall speed vr(a), and acceleration
function acc(
), infall speed vr(a), and acceleration
function acc(![]() )
are all identical for a 1.5 solar mass core
collapse, whatever nuclear EOS is used. Thus the MEMP of black
hole formation is a universal signature. Though this has been
derived in an effective gravitational collapse model, we believe
this is a true theorem in physics. It is of interest then, whether
the introduction of stellar rotation also reintroduces nuclear EOS
dependence for black hole MEMP. It is probably true that once the
core mass exceeds the neutron star dynamical mass, whether it is
rotating or not, the black hole MEMP is a universal function. In
Fig. 7, we give the kinetics of a 1.5 solar mass core collapse and
a 5.0 solar mass core collapse, along with an example of a core
bounce.
)
are all identical for a 1.5 solar mass core
collapse, whatever nuclear EOS is used. Thus the MEMP of black
hole formation is a universal signature. Though this has been
derived in an effective gravitational collapse model, we believe
this is a true theorem in physics. It is of interest then, whether
the introduction of stellar rotation also reintroduces nuclear EOS
dependence for black hole MEMP. It is probably true that once the
core mass exceeds the neutron star dynamical mass, whether it is
rotating or not, the black hole MEMP is a universal function. In
Fig. 7, we give the kinetics of a 1.5 solar mass core collapse and
a 5.0 solar mass core collapse, along with an example of a core
bounce.
| Core | bounce | Init. rad. | Fin. dens. | Fin. rad. | Time |
| 0.75 | yes | 70.88 | 6.40 (14) | 8.21 | 2175 |
| 1.00 | yes | 78.01 | 7.80 (14) | 8.48 | 2145 |
| 1.38 | barely | 86.87 | 7.64 (14) | 9.50 | 2110 |
| Core | Emitted Energy | Received Energy |
| QCD 0.75 | 1.07 (43) | 1.07 (43) |
| QCD 1.00 | 1.47 (43) | 1.47 (43) |
| QCD 1.3806 | 2.05 (43) | 1.98 (43) |
| ARG 0.75 | 1.27 (43) | 1.27 (43) |
| ARG 1.0825 | 1.82 (43) | 1.76 (43) |
| Core | bounce | Init. rad. | Fin. dens. | Fin. rad. | Time |
| 0.75 | yes | 70.88 | 1.60 (15) | 6.05 | 2195 |
| 1.08 | barely | 80.10 | 1.29 (15) | 7.36 | 2144 |
| Core | Initial rad. | Time | Rad energy |
| 1.5 | 89.3 | 2142 | 2.66 (43) |
| 5 | 133.40 | 2001 | 7.60 (43) |
The code logic is given in Fig. 5. Following Arnett
(1977), the iron core begins collapse with a fairly uniform
density of 1012 gm/cm3 and initial infall speed
![]() .
After choosing the mass of the
core, the initial radius is determined.
.
After choosing the mass of the
core, the initial radius is determined.
In Fig. 7, we present the results we obtained for the stellar surface for core masses of 1.5 and 5.0 solar masses, and in Fig. 8 the results for the energy spectrum of the emitted electromagnetic radiation, for the Argonne EOS (for a core of 1.0825 solar masses) and QCD (for a core of 1.3806 solar masses) EOS cases, and for core masses of 1.5 and 5.0 solar masses (independent of EOS).
The main result of the paper is the calculation of the MEMP from
the collapse. Both the total energy and its spectral
characteristics are derived. In cases where the core collapse is
greater than the dynamical neutron star mass, the MEMP is the only
electromagnetic experimental signature. It is hoped that this will
spur activity to develop a suitable experimental
receiver![]() . To answer the question as to
whether the surrounding material from the collapsing object will
quench or change an observational signal is clearly complicated,
and it requires a detailed calculation in transport theory using
information on the supernova models that vary tremendously on
their precursor environment, which is beyond the scope of the
present paper.
. To answer the question as to
whether the surrounding material from the collapsing object will
quench or change an observational signal is clearly complicated,
and it requires a detailed calculation in transport theory using
information on the supernova models that vary tremendously on
their precursor environment, which is beyond the scope of the
present paper.
The existence of two classes of neutron star masses leads to the situation where a stellar core greater than the dynamical mass, but less than the static mass, collapses to form a black hole, thus producing black holes less massive than the mass limit of neutron star stability. For example, a black hole of 1.6 solar masses can exist. This possibility sheds light on one of the most perplexing problems of astrophysics: how do black holes of stellar masses form? As envisioned here, a core more massive than the dynamical mass collapses and forms a black hole. It may now accrete the remaining outlying surface matter to produce a whole continuum of stellar mass size black holes.
After this paper was submitted for publication, we were informed of the work of Hanami (1997). This author attempted to explain gamma-ray bursts using the change in the magnetic field of a collapsing stellar object. Unfortunately, there are several problems associated with this work. Hanami did not consider the fact that the star radiates continuously throughout the collapse trajectory and his numerical solution violates Maxwell's equations. He used a zero pressure EOS, which will not give the correct surface acceleration and core remnant. In order to compute the total energy, the gravitational redshift must be properly included. The calculation of the gravitational redshift is a very difficult problem as explained in the present paper, because, as the star collapses and radiates, each instantaneous stellar configuration has a different redshift. In order to do this, one needs to employ multiple Roll-on-roll-off mathematical functions in the complex energy plane, correct for the gravitational redshift and add the spectrums incoherently. Hanami did not consider this and simply calculated the redshifted power at the initial collapse configuration, to obtain his result. At the bottom of page 688 and top of page 689, Hanami (1997) alludes to the fact that his solution is the quasi-normal ringing (QNR), but his eigenfrequency is incorrect (QNR have precise discrete eigenfrequencies). Also his time dependence does not correspond to any known quasi-normal mode damping.