A&A 384, 908-911 (2002)
DOI: 10.1051/0004-6361:20020108
On the orbital period changes of two W-type overcontact binaries:
RW Comae Berenices and CE Leonis
Qian Shengbang
Yunnan Observatory, Chinese Academy of Sciences,
PO Box 110, 650011 Kunming, PR China
National Astronomical Observatories, Chinese
Academy of Science (NAOCAS)
United Laboratory of Optical Astronomy, Chinese
Academy of Science (ULOAC)
Received 14 May 2001 / Accepted 30 November 2001
Abstract
O-C diagrams of two very short-period W-type overcontact binaries,
RW Com and CE Leo, are formed by considering the general trends
of their O-C curves and the natures of the period changes are analyzed.
For RW Com, its period shows a secular decrease with a
rate of
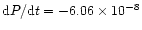 days/year. Weak evidence indicates
that a small-amplitude oscillation is superimposed on the secular decrease.
For CE Leo its period is increasing at rate of
days/year. Weak evidence indicates
that a small-amplitude oscillation is superimposed on the secular decrease.
For CE Leo its period is increasing at rate of
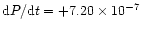 days/year. The masses of the primary
components of the two W UMa stars are nearly the same and the main
difference between the two systems is that they have a different mass
ratio (q=0.34 for RW Com and 0.50 for CE Leo respectively). The different
type of period changes may be the result of
their different mass ratio. These findings are in agreement with Qian's (2001)
conclusion that W-type stars with high-mass ratio (q>0.4) usually
show a increasing period, while the periods of low-mass ratio
systems (q<0.4) are decreasing. The period oscillation of RW Com
may be caused either by the presence of an unseen third body or by
magnetic activity cycles. The secular period changes of the two binary stars
can be explained by the combination of the thermal relaxation oscillation
(TRO) and the variable angular momentum loss (AML) via the change of
depth of overcontact.
days/year. The masses of the primary
components of the two W UMa stars are nearly the same and the main
difference between the two systems is that they have a different mass
ratio (q=0.34 for RW Com and 0.50 for CE Leo respectively). The different
type of period changes may be the result of
their different mass ratio. These findings are in agreement with Qian's (2001)
conclusion that W-type stars with high-mass ratio (q>0.4) usually
show a increasing period, while the periods of low-mass ratio
systems (q<0.4) are decreasing. The period oscillation of RW Com
may be caused either by the presence of an unseen third body or by
magnetic activity cycles. The secular period changes of the two binary stars
can be explained by the combination of the thermal relaxation oscillation
(TRO) and the variable angular momentum loss (AML) via the change of
depth of overcontact.
Key words: stars: binaries: close -
stars: individual: RW Com -
stars: individual: CE Leo -
stars: evolution
RW Com was discovered to be a W UMa type star by Jordan (1923).
It was later studied by others (for references see
Milone et al. 1980). A series of works by Milone et al. (1980, 1985, 1987) showed that RW Com is an W-type
overcontact binary with a mass ratio of q=0.34.
The light variation of CE Leo was
discovered by Hoffmeister (1963) who classified the variable
as RRc-type. Wenzel & Zeigler (1966) identified the system
as a W UMa-type binary and published the first ephemeris:
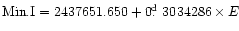 .
Later, CE Leo
was observed photoelectrically by Hoffmann (1983) and by
Samec & Bookmyer (1987). Recently, Samec et al. (1993)
published complete light curves in BVRI and a photometric
analysis of their observations based on the WD (Wilson-Devinney)
method. It was shown that CE Leo is a W-type overcontact binary with
a mass ratio of 0.51. The physical parameters of the two W UMa stars,
given by Maceroni and van't Veer (1996), are listed in Table 1 in
solar units.
.
Later, CE Leo
was observed photoelectrically by Hoffmann (1983) and by
Samec & Bookmyer (1987). Recently, Samec et al. (1993)
published complete light curves in BVRI and a photometric
analysis of their observations based on the WD (Wilson-Devinney)
method. It was shown that CE Leo is a W-type overcontact binary with
a mass ratio of 0.51. The physical parameters of the two W UMa stars,
given by Maceroni and van't Veer (1996), are listed in Table 1 in
solar units.
Table 1:
Physical properties of two overcontact binaries.
|
star name |
M1 |
M2 |
R1 |
R2 |
P |
i |
f |
q |
|
RW Com |
0.92 |
0.31 |
0.84 |
0.52 |
0.237 |
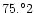 |
17 |
0.34 |
| CE Leo |
0.94 |
0.47 |
0.94 |
0.68 |
0.303 |
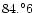 |
3 |
0.50 |
Epochs and orbital periods of RW Com have been given by
several authors (for references see Srivastava 1987). The
period change of the system was first noticed by Milone et al. (1980) who gave a period decrease rate of
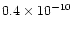 day per
day, but did not present an O-C diagram. Many times of light minimum of
RW Com were collected by
Srivastava (1987) and after his collection some visual
or photographic timings were
compiled in the Eclipsing Binaries Minima Database (EBMD)
(available at http://www.oa.uj.edu.pl/ktt/krttk_dn.html) and two
photoelectric timings have been published by Ogloza (1997).
The O-C diagram calculated with the ephemeris (Beljawsky 1924):
day per
day, but did not present an O-C diagram. Many times of light minimum of
RW Com were collected by
Srivastava (1987) and after his collection some visual
or photographic timings were
compiled in the Eclipsing Binaries Minima Database (EBMD)
(available at http://www.oa.uj.edu.pl/ktt/krttk_dn.html) and two
photoelectric timings have been published by Ogloza (1997).
The O-C diagram calculated with the ephemeris (Beljawsky 1924):
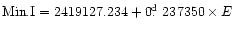 is presented in Fig. 1. It has been split into several portions by
Srivastava (1987) who proposed that several period jumps have occurred
around points B, C and D. However, these jumps were mainly based on
two visual timings and from points C to D the O-C values suddenly increase
is presented in Fig. 1. It has been split into several portions by
Srivastava (1987) who proposed that several period jumps have occurred
around points B, C and D. However, these jumps were mainly based on
two visual timings and from points C to D the O-C values suddenly increase
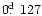 in a short time interval (about 6700 days).
Before and after the jump, the general O-C trend shows
secular decrease. These facts indicate that the O-C jumps
may be caused by the miscalculation of the O-C values of timings
after HJD2438000.
in a short time interval (about 6700 days).
Before and after the jump, the general O-C trend shows
secular decrease. These facts indicate that the O-C jumps
may be caused by the miscalculation of the O-C values of timings
after HJD2438000.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{fig1.EPS}\end{figure}](/articles/aa/full/2002/12/aa1467/Timg9.gif) |
Figure 1:
O-C diagram of RW Com. Solid dots refer to mean O-C values of
some visual or photographic data, solid squares to photoelectric observations,
and two open circles to individual visual timings. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{fig2.EPS}\end{figure}](/articles/aa/full/2002/12/aa1467/Timg10.gif) |
Figure 2:
O-C curve of RW Com formed by considering the general O-C trend. |
| Open with DEXTER |
The new
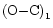 curve formed is displayed in Fig. 2 which may
show a roughly parabolic variation indicating a secular decrease
in the period. Srivastava (1987) pointed out that the data in the
time interval 1967-1986 showed a sinusoidal variation. In order to check
this, a sinusoidal term is added to a quadratic ephemeris to get a good fit
to the observations (solid line in Fig. 2):
curve formed is displayed in Fig. 2 which may
show a roughly parabolic variation indicating a secular decrease
in the period. Srivastava (1987) pointed out that the data in the
time interval 1967-1986 showed a sinusoidal variation. In order to check
this, a sinusoidal term is added to a quadratic ephemeris to get a good fit
to the observations (solid line in Fig. 2):
During the least-squares solution, the two individual visual timings
are not used. With the coefficient of the square term, a
continuous period decrease rate
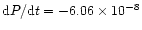 days/year is determined.
days/year is determined.
The residuals of the timings after HJD2438000 based on the quadratic
part of Eq. (1), are presented in Fig. 3 where two points showing
large deviations are discarded. Although they show slightly
large scatters, the general trend of those residuals may indicate a
cyclic variation. With the periodic part of Eq. (1), a cyclic
variation with a period of about T=13.3years and an amplitude of
about
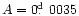 is determined which can be explained by the light
time effect via the presence of a third body. If the orbital plane of the
third body is parallel to the visual line, its mass
should be:
M3=0.133
is determined which can be explained by the light
time effect via the presence of a third body. If the orbital plane of the
third body is parallel to the visual line, its mass
should be:
M3=0.133 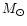 .
On the other
hand, RW Com contains two late-type stars which possess strong magnetic
activity. The period oscillation may be caused by magnetic activity cycles
in the components.
.
On the other
hand, RW Com contains two late-type stars which possess strong magnetic
activity. The period oscillation may be caused by magnetic activity cycles
in the components.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig3.EPS}\end{figure}](/articles/aa/full/2002/12/aa1467/Timg18.gif) |
Figure 3:
Residuals of timings after HJD2438000
calculated with the quadratic part of Eq. (1) |
| Open with DEXTER |
Many times of light minimum of CE Leo were tabulated in the paper of Samec
et al. (1993). After their collection, some timings have been reported
in the EBMD and three CCD times have been published by Safar
& Zejda (2000). The O-C values calculated with the
ephemeris of Samec et al. (1993):
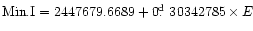 are shown in Fig. 4. In order to understand the nature of the
period change of CE Leo easily, 10 visual timings published in earlier
BBSAG bulletins Nos. 9-37 have been omitted by Samec et al. (1993)
and they proposed that the period showed an abrupt or a continuous
decrease. However, the O-C
values (
are shown in Fig. 4. In order to understand the nature of the
period change of CE Leo easily, 10 visual timings published in earlier
BBSAG bulletins Nos. 9-37 have been omitted by Samec et al. (1993)
and they proposed that the period showed an abrupt or a continuous
decrease. However, the O-C
values (
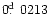 ,
,
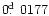 ,
and
,
and
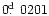 )
of the three CCD timings
show that recently the period of CE Leo has been increasing.
)
of the three CCD timings
show that recently the period of CE Leo has been increasing.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{fig4.EPS}\special{psfile=fig4.eps angle=0 hoffset=100 voffset=0 vscale=38 hscale=38}
\end{figure}](/articles/aa/full/2002/12/aa1467/Timg23.gif) |
Figure 4:
O-C curve of CE Leo where open circles refer to visual or
photographic observations and solid dots to photoelectric or CCD data. |
| Open with DEXTER |
As we can see from Fig. 4, the general O-C trend after HJD2441000
suggests that the orbital period of CE Leo may show secular increase.
By considering this general trend, O-C values of Meinunger & Wenzell's
(1968) timings are recalculated and are shown in Fig. 4 as
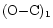 .
With weight 1 for visual or photographic data and weight 8 for
photoelectric or CCD observations, a weighted least-squares solution leads
to the following ephemeris:
.
With weight 1 for visual or photographic data and weight 8 for
photoelectric or CCD observations, a weighted least-squares solution leads
to the following ephemeris:
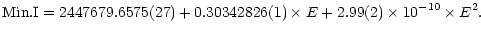 |
|
|
(2) |
The coefficient of the square term reveals a continuous period increase rate
of
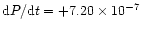 days/year.
If only the photoelectric and CCD data are used, we can obtain:
days/year.
If only the photoelectric and CCD data are used, we can obtain:
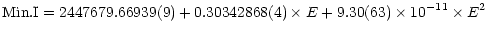 |
|
|
(3) |
and a period increase rate of
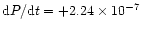 days/year.
Although the rate is smaller than that derived using all timings, the
general trends of both are the same.
days/year.
Although the rate is smaller than that derived using all timings, the
general trends of both are the same.
If the secular period changes of the two W UMa stars are caused by a
conservative mass transfer (MT) between the components, then the mass
transfer rates would be:
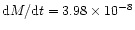 and
and
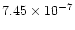
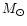 /year but with different directions.
The masses of the primary components of RW Com and CE Leo are almost
equal. Why do their periods show different changes? One is decreasing,
while the other is increasing. As shown in Table 1, the main difference
in the two systems is the slightly larger mass ratio. This
suggests that the different mass ratios may result in the different kind
of period changes. Recently, based on period changes of 30 W-type
overcontact binaries, Qian (2001) has found that there may exist a
correlation between the period change and the mass ratio. The high-mass ratio
systems (q>0.4) usually show secular period increase, while the orbital
periods of low-mass ratio systems (q<0.4) vary with a long-time decrease.
The period changes of the two W-type systems are in agreement with this
conclusion.
/year but with different directions.
The masses of the primary components of RW Com and CE Leo are almost
equal. Why do their periods show different changes? One is decreasing,
while the other is increasing. As shown in Table 1, the main difference
in the two systems is the slightly larger mass ratio. This
suggests that the different mass ratios may result in the different kind
of period changes. Recently, based on period changes of 30 W-type
overcontact binaries, Qian (2001) has found that there may exist a
correlation between the period change and the mass ratio. The high-mass ratio
systems (q>0.4) usually show secular period increase, while the orbital
periods of low-mass ratio systems (q<0.4) vary with a long-time decrease.
The period changes of the two W-type systems are in agreement with this
conclusion.
Secular period variations for W UMa stars, especially
decreases, are usually explained by angular momentum
loss (AML) via magnetic stellar wind. However, for
RW Com and CE Leo, the timescales of the period changes are
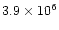 and
and
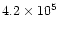 years respectively
that are much shorter than the timescale of the AML (about 108-1010years). How can the AML cause the secular period
change? In order to explain this, Qian (2001) proposed an artificial
scenario in which the rate of AML is changed by the variation of the depth
of overcontact. For a given W UMa star, the period decrease
means the reduction of separation between the components and
the increasing depth of overcontact. This will cause increased mixing
in the CCE which tends to bury the strong
surface magnetic field. Thus, the magnetic braking is weakened,
leading to a decreased AML rate (Vilhu 1981;
Smith 1984). As the rate of AML is less than the critical
loss rate of Rahunen (1981), the calculations of Rahunen
(1981) have shown that the evolution of the system is mainly
controlled by thermal relaxation oscillation (TRO) (Lucy 1976;
Flannery 1976; Robertson & Eggleton 1977). The period
will increase and then decrease the depth of overcontact. Then, the
decreased mixing in the CCE may result in a rather strong magnetic
field which causes a large AML (larger than the critical
value of Rahunen 1981). In this case, the evolution of the
system is mainly controlled by AML, and finally, the period will
decrease again. The different period changes of the two systems
may suggest they are at different evolutionary stages, i.e.,
RW Com is on the AML-controlled stage, while CE Leo is on the
TRO-Controlled stage.
years respectively
that are much shorter than the timescale of the AML (about 108-1010years). How can the AML cause the secular period
change? In order to explain this, Qian (2001) proposed an artificial
scenario in which the rate of AML is changed by the variation of the depth
of overcontact. For a given W UMa star, the period decrease
means the reduction of separation between the components and
the increasing depth of overcontact. This will cause increased mixing
in the CCE which tends to bury the strong
surface magnetic field. Thus, the magnetic braking is weakened,
leading to a decreased AML rate (Vilhu 1981;
Smith 1984). As the rate of AML is less than the critical
loss rate of Rahunen (1981), the calculations of Rahunen
(1981) have shown that the evolution of the system is mainly
controlled by thermal relaxation oscillation (TRO) (Lucy 1976;
Flannery 1976; Robertson & Eggleton 1977). The period
will increase and then decrease the depth of overcontact. Then, the
decreased mixing in the CCE may result in a rather strong magnetic
field which causes a large AML (larger than the critical
value of Rahunen 1981). In this case, the evolution of the
system is mainly controlled by AML, and finally, the period will
decrease again. The different period changes of the two systems
may suggest they are at different evolutionary stages, i.e.,
RW Com is on the AML-controlled stage, while CE Leo is on the
TRO-Controlled stage.
Acknowledgements
This work was supported by the Chinese Natural Science
Foundation (No. 10003004) and by the National Key Fundamental Research
Project through grant G1999075405. Many thanks are given to the referee
for his/her useful suggestions and comments and to the copy-editor for
improving the author's English writing.
- Beljawsky, S. 1924, Astr. Nach., 221, 139
In the text
- Flannery, B. P. 1976, APJ, 205, 217
In the text
NASA ADS
- Hoffmann, M. 1983, IBVS, 2344
In the text
- Hoffmeister, C. 1963, AN, 287, 169
In the text
NASA ADS
- Jordan, F. C. 1923, AJ, 35, 44
In the text
NASA ADS
- Lucy, L. B. 1976, ApJ, 205, 217
In the text
- Maceroni, C., & van't Veer, F. 1996, A&A, 311, 523
NASA ADS
- Meinunger, L., & Wenzel, W. 1968, VSS(4), 430
In the text
- Milone, E. F., Chia, T. T., Castle, K. G., Robb, R. M., & Merrill,
J. E. 1980, ApJS, 43, 339
In the text
NASA ADS
- Milone, E. F., Hrivnak, B. J., Hill, G., & Fisher, W. A. 1985, AJ,
90, 109
In the text
NASA ADS
- Milone, E. F., Wilson, R. E., & Hrivnak, B. J. 1985, ApJ, 319, 325
NASA ADS
- Ogloza, W. 1997, IBVS, 4534
In the text
- Qian, S. B. 2001, MNRAS, 328, 635
In the text
NASA ADS
- Rahunen, T. 1981, A&A, 102, 81
In the text
NASA ADS
- Robertson, J. A., & Eggleton, P. P. 1977, MNRAS, 179, 359
In the text
NASA ADS
- Safar, J., & Zejda, M. 2000, IBVS, 4888
In the text
- Samec, R. G., & Bookmyer, B. B. 1987, IBVS, 3053
In the text
- Samec, R. G., Wen Su, Terrell, D., & Hube, D. P. 1993, AJ, 106, 318
In the text
NASA ADS
- Smith, R. C. 1984, Q. Jl R. Astro. Soc., 25, 405
In the text
NASA ADS
- Srivastava, R. K. 1987, Ap&SS, 139, 373
In the text
NASA ADS
- Vilhu, O. 1981, Ap&SS, 78, 401
In the text
NASA ADS
- Wenzel, W., & Zeigler, E. 1966, MVS, 4(2), 20
In the text
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{fig1.EPS}\end{figure}](/articles/aa/full/2002/12/aa1467/Timg9.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{fig2.EPS}\end{figure}](/articles/aa/full/2002/12/aa1467/Timg10.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig3.EPS}\end{figure}](/articles/aa/full/2002/12/aa1467/Timg18.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{fig4.EPS}\special{psfile=fig4.eps angle=0 hoffset=100 voffset=0 vscale=38 hscale=38}
\end{figure}](/articles/aa/full/2002/12/aa1467/Timg23.gif)