A&A 384, 925-936 (2002)
DOI: 10.1051/0004-6361:20020084
Mira kinematics in the post-Hipparcos era
N. Kharchenko1 - E. Kilpio2 - O. Malkov2 -
E. Schilbach3
1 - Main Astronomical Observatory, Golosiiv,
Kiev - 127 03680, Ukraine
2 - Institute of Astronomy of the Russian Acad. Sci.,
48 Pyatnitskaya St., Moscow 109017, Russia
3 - Astronomisches Rechen-Institut Heidelberg,
Mönchhofstraße 12-14, 69120 Heidelberg, Germany
Received 11 July 2000 / Accepted 19 December 2001
Abstract
The complete data set of Mira variables from the 4th edition of the
General Catalog of Variable Stars was analyzed and supplemented by the
proper motions and radial velocities presently available for Miras.
The resulting sample of 724 Miras with periods between 78 and 612 days
contains proper motions reduced to the Hipparcos system, radial velocities and
V magnitudes. For each of 10 subgroups of Miras divided according to their
periods and spectral types, statistical parallaxes were determined by
application of five different methods. The mean absolute magnitudes,
the spatial velocities and their dispersions as well as the elements of
the Galactic orbits were computed as functions of the periods. The
(
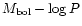 )
relation obtained was found to be considerably steeper than
the PLR usually assumed for LMC Miras. For Miras in the period range
145- 200 days, no significant net motion radially outwards in the Galaxy
as suggested by Feast & Whitelock (2000) was found.
The predicted frequency of Miras
was computed as a function of the visual magnitude.
)
relation obtained was found to be considerably steeper than
the PLR usually assumed for LMC Miras. For Miras in the period range
145- 200 days, no significant net motion radially outwards in the Galaxy
as suggested by Feast & Whitelock (2000) was found.
The predicted frequency of Miras
was computed as a function of the visual magnitude.
Key words: stars: fundamental parameters - stars: variables: general
Miras are the most numerous variables among bright pulsating
stars. They are classified as red giants located at the top of the
giant branch. At maximum, their absolute visual
magnitude can rise above
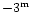 and, therefore, they can be found at
large distances from the Sun. The ages of the Miras range from 109to 1010 years, thus they reach ages comparable to the age of the
Galaxy.
and, therefore, they can be found at
large distances from the Sun. The ages of the Miras range from 109to 1010 years, thus they reach ages comparable to the age of the
Galaxy.
Although a well-defined period-luminosity relation (PLR) has been observed
for Miras in the Large Magellanic Cloud (Feast et al. 1989), there is still
a problem in using these variables as universal distance indicators
inside and outside the Galaxy.
The main difficulty consists of the fact that according to the Mira pulsation
theory, this relation is not applicable to all Long Period Variables (LPVs),
but must be considered in context with the star formation history of
the stellar system to which they belong.
This requires a knowledge of the chemical composition and present
mass distribution, i.e. on parameters that are usually poorly determined
(e.g., Feast & Whitelock 1999; Barthès & Luri 2001).
Another problem is the dependence of the PLR
on the pulsation mode of Mira variables.
From theoretical works (Barthès
1998), the PLRs for Miras of solar mass and solar metallicity and pulsating
with the same period but in
different modes may yield absolute magnitude differences of more than 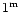 .
According to the analysis of available data on Mira luminosities,
a majority of the Miras pulsates probably in the same mode, although other
modes may be valid for a significant fraction of these variables (e.g.,
Feast 1999).
.
According to the analysis of available data on Mira luminosities,
a majority of the Miras pulsates probably in the same mode, although other
modes may be valid for a significant fraction of these variables (e.g.,
Feast 1999).
A reliable study of the Mira PLRs and a proof of the theory of
pulsation for the Miras would require accurate data on luminosities and
the linear diameters of Mira variables pulsating in different
modes and within a wide range of periods. However, due to the relatively
large distances of the Mira variables, their direct
luminosity calibration via trigonometric parallaxes is still extremely
difficult. Determining the trigonometric parallaxes of 18 Miras with a
relative accuracy better than 33%, Hipparcos improved the existing
situation (e.g., Alvarez et al. 1997; Bedding & Zijlstra 1998; van
Leeuwen et al. 1997) but did not solve the problem which, probably,
must be delayed to the future when accurate distances of numerous Mira
variables will become available. At present, statistical methods provide
the only possibility to estimate the absolute magnitudes of a
larger number of Mira variables. Nevertheless, as long as no clear
approach has been found how a mass and metallicity effect on the PLR
can be taken into
account and how Miras can be separated according to their mode of pulsation,
we can derive only a general tendency of the Mira PLR
which may vary depending on the proportion of stars of given
properties in a considered sample.
Investigating a sample of 154 Miras and 203 Semiregulars from the Hipparcos
Catalogue, Barthès et al. (1999) found that these stars could be
divided into four groups differing by their kinematics.
The method is based on a maximum-likelihood algorithm and the usage of
Hipparcos parallaxes and proper motions as well as radial velocities,
photometry,
periods etc. For each of the groups, the authors also obtained the
spatial distribution and the distribution of luminosity, period and color.
Although Miras fall in each of the four groups, the majority (66%) was
found to belong to one group.
Recently, a series of three papers (Whitelock et al. 2000; Whitelock &
Feast 2000; Feast & Whitelock 2000) was published dealing with Miras
observed by Hipparcos. From infrared photometry and Hipparcos parallaxes,
an infrared (K) PLR was obtained for Miras in the Solar neighbourhood.
The Mira kinematics was investigated on the basis of Hipparcos proper
motions and published radial velocities. It was found that Miras in
the period range 145-200 days show a net radial motion outwards in the Galaxy.
The PLR for Mira variables in the V-band based on the method of
statistical parallaxes was derived by Osvald & Risley (1961), Clayton
& Feast (1969), Kharchenko (1994). In recent years, new and accurate
kinematic data were published for Mira variables such as the
Hipparcos (ESA 1997) and Tycho-2 (Høg et al. 2000) catalogues for
proper motions and the compilation of Barbier-Brossat & Figon (2000)
for radial velocities. Therefore, a revision of the previous results
by the use of new data can be a timely and useful task.
We checked the complete data set of Mira variables listed in the 4th
edition of the General Catalog of Variable Stars, estimated the
completeness of the catalogue with respect to Miras and supplemented
the data with the proper motions and radial velocities available for
the Miras at present. The results of the analysis are described in
Sects. 2 and 3. Based on the final sample of 724 Miras, we determine
the statistical parallaxes and mean absolute magnitudes and compare
the resulting PLR with theoretical predictions in Sect. 4. We
present the kinematic parameters and predictions of the frequency of
Mira variables in Sect. 5. Finally, the conclusions are given in
Sect. 6.
The 4th edition of the General Catalog of Variable Stars, hereafter
referred to as the GCVS-4 (Kholopov et al. 1985-1998), and
the New Catalogue of Suspected Variable Stars (Kukarkin et al. 1982) contain
6166
long-period variables of the Mira type. For 1110 of them, periods are
missing in the catalogues, for other 14 stars no estimates of their
brightness are given. Therefore, we excluded these stars from
further analysis.
Photometric data in the GCVS-4 are extremely heterogeneous, and for a wide
majority of the Miras only photographic magnitudes (P in Table 1) are
known. In order to convert the GCVS magnitudes to the Johnson
V-band, we used in a first step the intrinsic color indices
from Straizys (1992) for red giants of M5III type which corresponds
to the mean
spectral type of the Mira variables in the sample considered. Then,
a correction P=B-0.11 (Allen 1973) was introduced for the
stars with photographic magnitudes. The corresponding color indices
are given in Table 1 together with the numbers of the GCVS
stars in each subgroup. Finally, the reddening was taken into account
by a statistical approach (see Chapter 4 below).
Since the magnitudes at maximum are the most complete and accurate
photometric data in the catalogue, we used this indicator of brightness
(hereafter marked simply as V) as the basic input parameter to
obtain the results presented in the following sections.
Table 1:
Photometric reduction.
| Photometric |
(V-x) color |
Number of |
| band, x |
[mag] |
stars |
| P |
-1.45 |
4098 |
| B |
-1.56 |
62 |
| V |
0.00 |
545 |
| R |
+2.13 |
10 |
| I |
+4.06 |
289 |
| J |
+4.96 |
1 |
| H |
+5.90 |
1 |
| K |
+6.20 |
36 |
Usually, the completeness of a catalogue is defined by a magnitude
where the observed frequency function
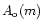 of the apparent magnitudes stops
growing. This approach neglects, however, selection effects and gives,
as a rule, an overestimation. In order to determine the
completeness of the GCVS-4 with respect to Miras, we used a method
applied already by Kharchenko (1994) to find the completeness of the
GCVS-3 (Kukarkin et al. 1969). The method is based on a comparison
between the numbers of Miras predicted by a model and those actually found
in the catalogue. We assumed the spatial distribution of Miras as
being consistent with a Galactic model including a spheroid and set of disk
subsystems. The frequencyfunction
of the apparent magnitudes stops
growing. This approach neglects, however, selection effects and gives,
as a rule, an overestimation. In order to determine the
completeness of the GCVS-4 with respect to Miras, we used a method
applied already by Kharchenko (1994) to find the completeness of the
GCVS-3 (Kukarkin et al. 1969). The method is based on a comparison
between the numbers of Miras predicted by a model and those actually found
in the catalogue. We assumed the spatial distribution of Miras as
being consistent with a Galactic model including a spheroid and set of disk
subsystems. The frequencyfunction
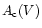 of the Mira variables
divided into j subgroups in accordance with their periods is:
of the Mira variables
divided into j subgroups in accordance with their periods is:
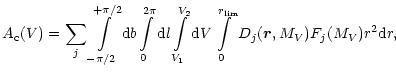 |
|
|
(1) |
where l, b are galactic coordinates, r is the distance from the
Sun (
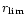 ranges from 10 to 50 kpc depending on the
direction of integration l, b),
ranges from 10 to 50 kpc depending on the
direction of integration l, b),
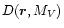 is the density distribution proposed by Bahcall
& Soneira (1980) and F(MV) is the luminosity function as
determined in present paper (see Chapter 5 below). A similar equation
can be also written for the frequency function of the periods:
is the density distribution proposed by Bahcall
& Soneira (1980) and F(MV) is the luminosity function as
determined in present paper (see Chapter 5 below). A similar equation
can be also written for the frequency function of the periods:
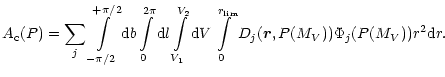 |
|
|
(2) |
The results of the comparison are shown in Fig. 1. Even if
the GCVS-4 contains about 2000 Miras more than the GCVS-3, we must
conclude that both catalogues are complete up to magnitude
at maximum
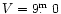 .
According to
Figs. 1 and 2, the Miras added in the GCVS-4 are
mostly faint stars located in a few sky areas.
.
According to
Figs. 1 and 2, the Miras added in the GCVS-4 are
mostly faint stars located in a few sky areas.
![\begin{figure}
\par\includegraphics[angle=270,width=7.1cm,clip]{10095f1.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg26.gif) |
Figure 1:
Numbers of Miras predicted (curves) and listed in the GCVS-4
(histograms) plotted as a function of the period for the following two groups:
Miras with magnitudes at maximum
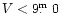 a) and a) and
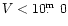 b). The lower panel shows the distribution of
Miras in the GCVS-4 (histogram, solid curve) and in the GCVS-3 (histogram,
dashed curve) versus magnitude at maximum V. The solid curve
indicates the predicted distribution.
b). The lower panel shows the distribution of
Miras in the GCVS-4 (histogram, solid curve) and in the GCVS-3 (histogram,
dashed curve) versus magnitude at maximum V. The solid curve
indicates the predicted distribution. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=7.1cm,clip]{10095f2.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg27.gif) |
Figure 2:
Distribution of Mira variables from the GCVS-4 on the sky
(in equatorial coordinates) for different magnitude ranges. |
| Open with DEXTER |
The proper motion data for the Mira variables are relatively rare and
rather heterogeneous. Analysing the data available before the end of
eighties,
Kharchenko (1992) reduced proper motions of 303 Miras to a common
reference system. During the last decade, a number of new catalogues
containing proper motions of Mira variables was published. These
catalogues are: PPM (Röser & Bastian 1991;
Bastian & Röser 1993a,b),
Hipparcos and Tycho-1 (ESA 1997), ACT RC (Urban et al. 1998),
TRC (Høg et al. 1998), CMC11 (1999) and Tycho-2 (Høg et al. 2000).
The numbers of Miras in the catalogues
are listed in Table 2.
Table 2:
Sources for the proper motion data.
| Catalogue |
Number of Miras |
| Hipparcos |
239 |
| Tycho-2 |
780 |
| Tycho-1 |
452 |
| ACT RC |
534 |
| TRC |
382 |
| CMC11 |
323 |
| PPM |
247 |
| Kharchenko (1992) |
303 |
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{10095f3.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg28.gif) |
Figure 3:
Proper motion differences in mas/year between the compiled
catalogue and original astrometric catalogues as a function of magnitude. |
| Open with DEXTER |
The proper motions from these catalogues were reduced to the Hipparcos
reference system which gives, at present, the best realization of
an inertial system in the optical. Using stars in common, we
compared the Hipparcos proper motions
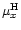 ,
,
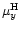 with the
corresponding data
with the
corresponding data  ,
,
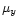 in each catalogue and derived
corrections for different zero points
in each catalogue and derived
corrections for different zero points
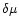 and precession
terms
and precession
terms 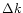 ,
,
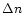 as
as
Finally, the mean weighted proper motions and the corresponding rms
errors were computed for each star. The weight for a star in each
catalogue was set in accordance with the individual proper motion
error given for this star in the original catalogue.
Figure 3 shows the proper motion differences between the
final catalogue and the original catalogues.
In total, for 1041 Mira variables, proper motions in the Hipparcos system
were determined.
We checked various catalogues and lists containing radial velocities.
In nine of them the relevant data for Mira variables were found.
It is a well-known fact that the radial velocity 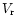 can be derived
from absorption
and/or from emission lines. In the case of Mira variables, the
essential information on radial velocity, i.e. on the radial component
of the space velocity, is obtained from absorption lines: they refer
to the atmosphere of a given star and so describe its true radial
velocity. On the contrary, emission lines reflect the state of star's
envelope and include an additional velocity component resulting from
stellar winds. Therefore, we introduced a correction in
can be derived
from absorption
and/or from emission lines. In the case of Mira variables, the
essential information on radial velocity, i.e. on the radial component
of the space velocity, is obtained from absorption lines: they refer
to the atmosphere of a given star and so describe its true radial
velocity. On the contrary, emission lines reflect the state of star's
envelope and include an additional velocity component resulting from
stellar winds. Therefore, we introduced a correction in 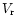 computed from emission lines making use of the relation (Ikaunieks
1971):
computed from emission lines making use of the relation (Ikaunieks
1971):
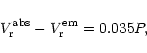 |
(5) |
where P is the period.
For stars included in more than one catalogue, the 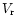 values were
averaged. The resulting list contains
values were
averaged. The resulting list contains 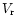 for 786 stars.
Table 3 gives the references for the data on radial
velocities and numbers of Mira variables considered in each catalogue.
for 786 stars.
Table 3 gives the references for the data on radial
velocities and numbers of Mira variables considered in each catalogue.
Table 3:
Sources for the radial velocity data.
| Reference |
Number of Miras |
| Feast (1963) |
403 |
| Smak & Preston (1965) |
271 |
| Perry & Bidelman (1965) |
11 |
| Feast (1966) |
52 |
| Feast et al. (1972) |
3 |
| Dean (1976) |
19 |
| Barnes & Fekel (1977) |
2 |
| Feast et al. (1980) |
19 |
| Barbier-Brossat & Figon (2000) |
58 |
The typical accuracy of a radial velocity of a Mira variable is
estimated to be a few kilometers per second. The main uncertainties
contributing to the resulting error are: the error of measurements,
the error due to the phase and/or intrinsic variations, and the error
due to dispersion in the relation between velocities from emission
lines and radial velocities (Eq. (5)). For example, in their
determinations of radial velocities, Smak & Preston (1965) estimated
these errors as 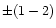 km s-1,
km s-1, 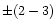 km s-1, and
km s-1, and 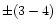 km s-1,
respectively. In the following, we assumed the mean error of radial
velocity obtained from a single spectrogram of an average quality to
be
km s-1,
respectively. In the following, we assumed the mean error of radial
velocity obtained from a single spectrogram of an average quality to
be 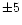 km s-1.
km s-1.
In total, our list contains 1103 Mira variables with proper motions in the
Hipparcos system and/or radial velocities. For 724 of them
both proper motions and radial velocities are available. According to the
GCVS-4, 753 Miras in our list are stars of spectral types K or M, 53 of
type C, R or N and 41 of S. These Miras were classified as
titanium or oxygen-rich (M), carbon (C) and zirconium (S) stars,
respectively. For the remaining 256 Miras, the spectral type is not known
and so we assume them to be oxygen-rich stars.
Figure 4 shows the distribution of radial velocities and
proper motions (
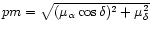 )
of the Miras from our sample versus V-magnitudes
and period.
)
of the Miras from our sample versus V-magnitudes
and period.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10095f4.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg47.gif) |
Figure 4:
Distribution of proper motions and radial velocities of Mira
variables in our sample versus V-magnitude and period. The small,
medium and large circles indicate 43 Miras whose trigonometric
parallaxes were determined by Hipparcos with a relative error better
than 50%, 33% and 15%, respectively. |
| Open with DEXTER |
For the majority of the Mira variables, equatorial coordinates were
taken from the astrometric catalogues listed in
Table 2 in accordance with their priority: Hipparcos
(239 stars), Tycho-2 (623 stars), Tycho-1 (38 stars), CMC11 (90 stars),
PPM (8 stars). The coordinates of the remaining 105 stars were taken from
the GCVS-4 and transformed to the equinox 2000.0.
Figure 5 shows that our kinematic sample represents the complete
period range covered by the GCVS-4. Its distribution over the period is
consistent with the distribution of Miras brighter than V = 12 which
is the limiting magnitude of the kinematic sample. The mean and median
periods of the kinematic sample agree sufficiently with those of the
whole GCVS-4 sample.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10095f5.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg48.gif) |
Figure 5:
Distribution of Mira variables versus period. The lines
from top to bottom correspond to: all Miras listed in the GCVS-4, Miras
with magnitudes at maximum V < 12 and 724 Miras with
both proper motions and radial velocities. |
| Open with DEXTER |
At relatively small distances from the Sun, there are only a few Miras known.
Therefore, Hipparcos could achieve rather moderate accuracy in
trigonometric parallaxes for this type of star: from 239 Miras
observed by Hipparcos, only 43, 18 and 4 Miras have parallaxes with a
relative accuracy better than 50%, 33% and 15%,
respectively. According to Fig. 4, these stars do not
cover the complete range of periods and represent poorly the
kinematic properties of Miras, as well.
In this paper we applied the method of statistical parallaxes to estimate
the average distances and hence the mean absolute magnitudes of Miras
selected within a given range of periods and visual magnitudes.
The method is based on the assumption that the peculiar
motions of stars in such a group
are randomly distributed, and their kinematic data,
on average, reflect the solar motion. For 724 Mira variables in
our sample, the proper motions in the Hipparcos system and radial
velocities are available. According to their period distribution,
the oxygen-rich Miras were divided into 8 groups (see Table 4).
For each group, the statistical parallax method works
correctly if a sample includes a sufficient number of randomly moving
stars distributed homogeneously all over the sky and chosen within a small
range of magnitudes (and, consequently, distances). In order to satisfy
these conditions sufficiently well,
we first determined statistical parallaxes for 388 Miras selected
from the basic sample in a range of magnitudes at maximum
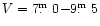 .
Following the
.
Following the 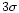 criterion, we excluded 6 stars due to
the relatively large proper motions and/or radial velocities.
criterion, we excluded 6 stars due to
the relatively large proper motions and/or radial velocities.
For each star we computed proper motion components
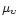 ,
,
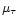 assuming the galactic coordinates of the solar apex
to be
assuming the galactic coordinates of the solar apex
to be
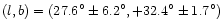 which corresponds to the solar velocity with respect to the LSR derived
by Dehnen & Binney (1998) from the Hipparcos data (see also Chapter 5).
The solar velocity
which corresponds to the solar velocity with respect to the LSR derived
by Dehnen & Binney (1998) from the Hipparcos data (see also Chapter 5).
The solar velocity 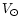 relative to the
Miras was derived from the radial velocities for each group, separately.
All velocity components were corrected for Galactic rotation with
relative to the
Miras was derived from the radial velocities for each group, separately.
All velocity components were corrected for Galactic rotation with
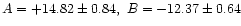 km s-1/kpc (Feast & Whitelock 1997). These values
are based on the Hipparcos proper motions and, therefore, could be considered
as the most reliable estimates of the Oort constants. Since in each group,
the distribution of Miras over the sky is sufficiently uniform, uncertainties
in the values of the Oort constants should not affect considerably the resulting
statistical parallaxes. Indeed, changing the values of the Oort constants
within reasonable limits we did not find any significant change in the
results (even in a case of A = B = 0 the corresponding
statistical parallaxes differ less than 11% from the values computed with
the Oort constants of Feast & Whitelock 1997).
km s-1/kpc (Feast & Whitelock 1997). These values
are based on the Hipparcos proper motions and, therefore, could be considered
as the most reliable estimates of the Oort constants. Since in each group,
the distribution of Miras over the sky is sufficiently uniform, uncertainties
in the values of the Oort constants should not affect considerably the resulting
statistical parallaxes. Indeed, changing the values of the Oort constants
within reasonable limits we did not find any significant change in the
results (even in a case of A = B = 0 the corresponding
statistical parallaxes differ less than 11% from the values computed with
the Oort constants of Feast & Whitelock 1997).
For each group, the statistical parallaxes were
computed in five different approaches:
 the classical upsilon component method based on the
relation between the proper motion component
the classical upsilon component method based on the
relation between the proper motion component
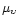 and the
solar velocity
and the
solar velocity 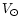
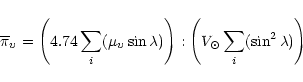 |
(6) |
where 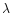 is the angular distance between a star and the
standard solar apex;
is the angular distance between a star and the
standard solar apex;
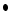 the classical tau component method based on the
relation between the proper motion components
the classical tau component method based on the
relation between the proper motion components
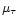 and the
radial velocities
and the
radial velocities 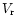
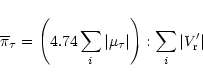 |
(7) |
where
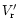 is the radial velocity corrected for the solar
motion;
is the radial velocity corrected for the solar
motion;
 the relation between the solar motion with respect to the
stars in a given group, computed from proper motions and radial
velocities. This approach does not use any preliminary assumption on
apex coordinates
the relation between the solar motion with respect to the
stars in a given group, computed from proper motions and radial
velocities. This approach does not use any preliminary assumption on
apex coordinates
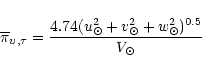 |
(8) |
where the solar motion components
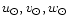 were derived from
were derived from
Here
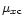 and
and
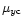 are the proper motion components corrected
for the Galactic rotation;
are the proper motion components corrected
for the Galactic rotation;
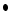 the relation between the upsilon component dispersion
and radial velocity dispersion
the relation between the upsilon component dispersion
and radial velocity dispersion
 |
(11) |
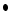 the relation between the tau component dispersion and
radial velocity dispersion
the relation between the tau component dispersion and
radial velocity dispersion
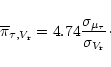 |
(12) |
For each group and each method, the rms errors of the results were
estimated from
the propagation of the mean errors of the input data. In each case,
the scatter of parallaxes was obtained to be less than 2 mas.
The statistical parallaxes and their rms errors computed for each group
by the different methods do not differ considerably and thus were averaged.
The results are given in Table 4.
Based on the statistical parallaxes, the corresponding mean absolute
magnitudes at maximum were derived for each group by iteration
of the equations:
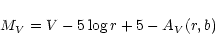 |
(13) |
![\begin{displaymath}%
A_V(r,b) = a_V\,h_{\rm Za} [1 - \exp( - r \vert\sin b\vert / h_{\rm Za})] / \vert\sin b\vert
\end{displaymath}](/articles/aa/full/2002/12/aa10095/img111.gif) |
(14) |
where b is the galactic latitude and AV (r,b) is the total
interstellar extinction at a distance r from the Sun.
The corresponding reddening is
EB-V = AV/3.1.
After a critical analysis of different interstellar extinction models
(Kilpio & Malkov 1997), the extinction in the Galactic plane
per 1 kpc, aV, and the scale height of the extinction layer,
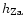 ,
were taken from Sharov (1963) where they are given in
dependence of the direction and the limiting distance. For larger
distances, the mean values
,
were taken from Sharov (1963) where they are given in
dependence of the direction and the limiting distance. For larger
distances, the mean values
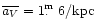 and
and
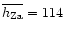 pc were assumed.
pc were assumed.
In general, from 5 to 10 iterations were needed to obtain convergent
solutions
of (13) and (14) for different groups. The corresponding PLR based on
330 oxygen-rich Miras with magnitudes at maximum V between 7.0 and 9.5
is presented in Fig. 6 and
Table 4. The errors given for
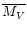 are the
rms errors of the mean absolute magnitudes at maximum obtained
for each group. We have to emphasize
that two important factors, uncertainties in the total interstellar
extinction AV (r,b) and in the apparent magnitudes at maximum V, are not
explicitly
included in the error estimation of absolute magnitudes since, generally
speaking, they are not known for each Mira. By the determination of the mean
absolute magnitude from a large sample of homogeneous and uniformly
distributed stars, we can expect that, to a certain extent, these factors
compensate for themselves.
On the other hand, errors in AV (r,b) and V (among other uncertainties)
fully contribute
to a scatter of estimated individual absolute magnitudes and, consequently,
to the rms errors of the mean absolute magnitudes
in Fig. 6 and Table 4.
are the
rms errors of the mean absolute magnitudes at maximum obtained
for each group. We have to emphasize
that two important factors, uncertainties in the total interstellar
extinction AV (r,b) and in the apparent magnitudes at maximum V, are not
explicitly
included in the error estimation of absolute magnitudes since, generally
speaking, they are not known for each Mira. By the determination of the mean
absolute magnitude from a large sample of homogeneous and uniformly
distributed stars, we can expect that, to a certain extent, these factors
compensate for themselves.
On the other hand, errors in AV (r,b) and V (among other uncertainties)
fully contribute
to a scatter of estimated individual absolute magnitudes and, consequently,
to the rms errors of the mean absolute magnitudes
in Fig. 6 and Table 4.
In the next step we took this PLR to derive the
absolute magnitudes at maximum MV for the remaining stars of the kinematic
sample (
724 - 382 = 342 stars).
The distances r and extinctions AV (r,b) were computed from
(13) and (14).
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10095f6.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg115.gif) |
Figure 6:
Absolute magnitude versus period for the oxygen-rich Miras
(solid curve). For
comparison, the previous results obtained for Mira variables are
presented. Short-dashed curve: Osvald et al. (1961), dashed-dotted curve:
Clayton et al. (1969), long-dashed curve: Kharchenko (1992). |
| Open with DEXTER |
Due to large amplitudes of Mira variables, Hipparcos could not observe the
complete light curves for a number of these stars. Especially for
those with periods close to 1 year, the parallax determination was
rather difficult. We could find only 11 resolved stars with a relative
accuracy of the parallaxes better than 25% from 239 Miras observed by
Hipparcos. Nevertheless, these data are the best that are available
for Miras at the moment. The result of a comparison between the
Hipparcos parallaxes and parallaxes
obtained from the PLR as described in the previous paragraph
is shown in Fig. 7. The error bars for
 indicate
the rms errors estimated
by the propagation of the mean errors listed in Table 4
for a given group. Except for Mira itself (the point most on
the right in Fig. 7), the coincidence is quite good.
indicate
the rms errors estimated
by the propagation of the mean errors listed in Table 4
for a given group. Except for Mira itself (the point most on
the right in Fig. 7), the coincidence is quite good.
The "outlier behaviour'' of Mira may be a consequence
of a strong variability of its V magnitude at maximum. Though Mira becomes
occasionally as bright as
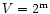 (GCVS-4), its average
magnitude at maximum is about
(GCVS-4), its average
magnitude at maximum is about
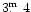 (GCVS-3). In the first case,
the statistical method yields a parallax
(GCVS-3). In the first case,
the statistical method yields a parallax
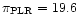 mas
(Fig. 7), in the second case
mas
(Fig. 7), in the second case
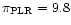 mas, which
is in a better agreement with the Hipparcos parallax (7.8 mas).
On the other hand, due to the binarity (=ADS 1778) and the pulsation
period close to 1 year (
mas, which
is in a better agreement with the Hipparcos parallax (7.8 mas).
On the other hand, due to the binarity (=ADS 1778) and the pulsation
period close to 1 year ( 332 days),
Mira was not an "easy'' object for Hipparcos, too.
This is indicated by large correlation coefficients (up to 39%) between
the astrometric parameters of Mira in the Hipparcos catalogue.
Note also that Mira was not used in the construction of the PLR which,
in this paper, was based on stars with V magnitudes at maximum
between 7.0 and 9.5.
332 days),
Mira was not an "easy'' object for Hipparcos, too.
This is indicated by large correlation coefficients (up to 39%) between
the astrometric parameters of Mira in the Hipparcos catalogue.
Note also that Mira was not used in the construction of the PLR which,
in this paper, was based on stars with V magnitudes at maximum
between 7.0 and 9.5.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10095f7.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg122.gif) |
Figure 7:
Comparison of
the Hipparcos parallaxes with parallaxes derived in this paper
from the PLR.
The solid line indicates zero parallax differences. |
| Open with DEXTER |
In order to compare the period-luminosity relation derived in this
paper with theoretical predictions of the pulsation theory and with the
relation for LMC Miras from Feast & Whitelock (1999), we must
convert the averaged visual magnitudes at maximum brightness into mean
bolometric magnitudes.
Since visual amplitudes of Miras tend to correlate with periods (Whitelock et al. 2000), we computed the averaged amplitudes for each group, separately.
We used all stars from our basic kinematic sample (724 Miras) with
amplitudes listed in the GCVS-4. The mean amplitudes (
 )
and their rms errors are given in Table 4. For each group,
the mean absolute visual magnitudes were derived as
)
and their rms errors are given in Table 4. For each group,
the mean absolute visual magnitudes were derived as
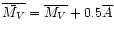 .
.
Figure 8 shows a BC-period relation for the Mira variables having
reliable Hipparcos data. Periods, Hipparcos parallaxes, extinction
data and bolometric (the average of the maximum and minimum)
magnitudes were taken from van Leeuwen et al. (1997); visual
magnitudes are averaged GCVS-4 data.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10095f8.eps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg124.gif) |
Figure 8:
BC - period relation for the Mira variables (open circles).
The stars excluded from further analysis are marked with crosses. |
| Open with DEXTER |
The following Miras listed in van Leeuwen et al. (1997) were excluded
from further analysis: the carbon-rich R Lep, the double-period R Cen,
two stars with decreasing periods (R Aql and R Hya) and R Leo (its
ground-based trigonometric parallax differs from the Hipparcos
result). These five stars are marked with crosses. For the remaining 11
Miras (indicated by circles), a linear fit to the data yields
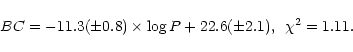 |
(15) |
Since the distribution of stars over the pulsation period is rather
inhomogeneous,
we checked the possibility whether the shape and slope of the
obtained relation is mainly determined by S Car, the shortest-period
star in our sample. A least squares solution without S Car yields
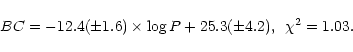 |
(16) |
Since the coefficients in (15) and (16) did not differ significantly, we
conclude that the obtained solution is sufficiently stable.
We may also assume that the derived relation is almost independent of
the mode of
pulsation:  Cyg and R Cas identified by van Leeuwen et al.
(1997) as fundamental pulsators match the relation as well as other
stars, presumably first overtone pulsators. We note, however,
that a reliable interpretation of the pulsation mode of Miras
is still a controversial and highly discussed problem (e.g., see discussion
in Feast 1999; Tuchman 1999; Percy & Bagry 1999).
Cyg and R Cas identified by van Leeuwen et al.
(1997) as fundamental pulsators match the relation as well as other
stars, presumably first overtone pulsators. We note, however,
that a reliable interpretation of the pulsation mode of Miras
is still a controversial and highly discussed problem (e.g., see discussion
in Feast 1999; Tuchman 1999; Percy & Bagry 1999).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10095f9.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg128.gif) |
Figure 9:
The (
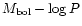 )
relation. Solid and dashed lines
represent our results and data from van Leeuwen et al. (1997),
respectively. )
relation. Solid and dashed lines
represent our results and data from van Leeuwen et al. (1997),
respectively. |
| Open with DEXTER |
The corresponding BCs were applied to the mean visual magnitudes
(see Table 4) computed
for eight groups of oxygen-rich Mira variables.
The resulting (
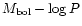 )
relation
is presented in Fig. 9 and in the bottom line of
Table 4.
)
relation
is presented in Fig. 9 and in the bottom line of
Table 4.
The results were compared with theoretical predictions of
Barthès (1998) for near-solar metallicity (Z = 0.02).
According to the model
grid by Barthès (1998), our (
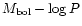 )
relation is compatible
with both fundamental mode and first overtone pulsations. Nevertheless,
Miras with shorter periods (P < 270 days) fit better the fundamental mode
with masses lower than
)
relation is compatible
with both fundamental mode and first overtone pulsations. Nevertheless,
Miras with shorter periods (P < 270 days) fit better the fundamental mode
with masses lower than
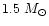 ,
whereas Miras with larger periods
pulsate probably on the first overtone with masses between
,
whereas Miras with larger periods
pulsate probably on the first overtone with masses between
 and
and
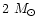 .
The mid-point of our sample at P = 285 days matches the
first overtone with a mass of about
.
The mid-point of our sample at P = 285 days matches the
first overtone with a mass of about
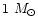 or alternatively,
the fundamental mode with a mass of about
or alternatively,
the fundamental mode with a mass of about
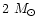 .
The model
of Barthès (1998) is based on a linear pulsation model assuming that
the pulsating envelope does not significantly differ from the static one.
However, further developments (Ya'ari & Tuchman 1996; Barthes & Luri 2001)
have provided indication that this assumption may not be correct.
.
The model
of Barthès (1998) is based on a linear pulsation model assuming that
the pulsating envelope does not significantly differ from the static one.
However, further developments (Ya'ari & Tuchman 1996; Barthes & Luri 2001)
have provided indication that this assumption may not be correct.
Recently, theoretical (
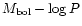 )
relations based on an improved
linear nonadiabatic pulsation model have been computed by
Barthès & Luri (2001) for different masses and pulsation modes but
only for a LMC metallicity (Z = 0.008). We have compared our data with
this model grid keeping in mind that a smaller metallicity leads to a higher
luminosity; e.g. metallicity
decreasing by a factor of 20 leads to an increase of about 0.43 mag in
luminosity (Barthès 1998). On the other hand, a metallicity
of Z = 0.008 may be a good compromise for Miras in the solar neighbourhood
provided that these stars belong to an older population.
From the comparison with the model grid by Barthès & Luri (2001) for
LMC metallicity, we can conclude that our (
)
relations based on an improved
linear nonadiabatic pulsation model have been computed by
Barthès & Luri (2001) for different masses and pulsation modes but
only for a LMC metallicity (Z = 0.008). We have compared our data with
this model grid keeping in mind that a smaller metallicity leads to a higher
luminosity; e.g. metallicity
decreasing by a factor of 20 leads to an increase of about 0.43 mag in
luminosity (Barthès 1998). On the other hand, a metallicity
of Z = 0.008 may be a good compromise for Miras in the solar neighbourhood
provided that these stars belong to an older population.
From the comparison with the model grid by Barthès & Luri (2001) for
LMC metallicity, we can conclude that our (
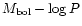 )
relation
is located in the region occupied by Miras pulsating in the fundamental mode
with masses from
)
relation
is located in the region occupied by Miras pulsating in the fundamental mode
with masses from
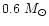 (shorter periods) and up to
(shorter periods) and up to
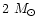 (larger periods). Though, taking into account the error bars of
(larger periods). Though, taking into account the error bars of
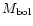 ,
Miras with periods larger than 315 days in our sample are also compatible
with the first overtone and masses of about
,
Miras with periods larger than 315 days in our sample are also compatible
with the first overtone and masses of about
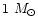 .
The mid-point
of the sample fits the fundamental mode with about
.
The mid-point
of the sample fits the fundamental mode with about
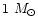 mass.
Due to relatively large rms errors of the bolometric magnitudes
(see Table 4), this interpretation will probably be valid also
if we could compare our results with model predictions for near-solar
metallicity. The nearly identical conclusions can be drawn from
comparing our results with the models by Wood & Sebo (1996) for the
asymptotic giant branch where Z = 0.008 was adopted, too.
mass.
Due to relatively large rms errors of the bolometric magnitudes
(see Table 4), this interpretation will probably be valid also
if we could compare our results with model predictions for near-solar
metallicity. The nearly identical conclusions can be drawn from
comparing our results with the models by Wood & Sebo (1996) for the
asymptotic giant branch where Z = 0.008 was adopted, too.
To compare our empirical (
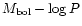 )
relation with other observations,
we plotted the PLR by van Leeuwen et al. (1997) in
Fig. 9. This relation adopts the slope derived for LMC Miras
(Feast et al. 1989) and the zero-point evaluated from the Hipparcos
data. The corresponding infrared (K) PLR were used by Feast & Whitelock
(2000) to study the kinematics of Miras measured by Hipparcos (see discussion
in Chapter 5). Although the differences between the PLRs in Fig. 9
are within error bars, our PLR is significantly steeper than the PLR
by van Leeuwen et al. (1997).
)
relation with other observations,
we plotted the PLR by van Leeuwen et al. (1997) in
Fig. 9. This relation adopts the slope derived for LMC Miras
(Feast et al. 1989) and the zero-point evaluated from the Hipparcos
data. The corresponding infrared (K) PLR were used by Feast & Whitelock
(2000) to study the kinematics of Miras measured by Hipparcos (see discussion
in Chapter 5). Although the differences between the PLRs in Fig. 9
are within error bars, our PLR is significantly steeper than the PLR
by van Leeuwen et al. (1997).
Several reasons for these differences may be considered.
Relatively large uncertainties in the Hipparcos parallaxes of
Miras (see, e.g., discussion in Feast & Whitelock 1999) can
introduce a systematic effect on the derived (
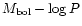 )
relation.
Also, the empirical amplitude-period relation used can yield a bias
in the calculation of mean absolute magnitudes, though the number of
stars is relatively large (from 23 in the last group to 112 in the third
group). To check this, we re-calculated the amplitude-period relation
for a subsample of bright stars (
)
relation.
Also, the empirical amplitude-period relation used can yield a bias
in the calculation of mean absolute magnitudes, though the number of
stars is relatively large (from 23 in the last group to 112 in the third
group). To check this, we re-calculated the amplitude-period relation
for a subsample of bright stars (
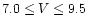 )
and obtained the
same results.
)
and obtained the
same results.
On the other hand, we have to recall that the considered sample of Miras
is by far not
homogeneous and may include stars of different populations and in a wide range
of metallicities and masses.
It may also be a mixture of fundamental mode pulsators, first overtone
pulsators and, probably, higher overtone pulsators.
Due to a different
evolution history, Miras in our Galaxy and in the LMC must not necessary
show the same PLR. A similar conclusion was inferred by
Barthès & Luri (1999) who also derived a considerably steeper
(
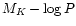 )
relation of their Group 1 of galactic oxygen-reach LPVs
(composed to about 66% of Miras) than usually observed in the LMC.
The steepness of the PLR in the solar neighbourhood can result from
a present mass distribution which may differ from the mass distribution
of Miras in the LMC. Additionally, an apparent bend of the PLR
at
)
relation of their Group 1 of galactic oxygen-reach LPVs
(composed to about 66% of Miras) than usually observed in the LMC.
The steepness of the PLR in the solar neighbourhood can result from
a present mass distribution which may differ from the mass distribution
of Miras in the LMC. Additionally, an apparent bend of the PLR
at
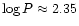 (Fig. 9)
may indicate distinct populations of Miras in the solar neighbourhood.
This suggestion is also supported by the kinematics of the Mira sample
studied (see Chapter 5). On the other hand, a more or less continuous
star formation may be characteristic of the LMC (see also Barthès & Luri
1999). However, at present,
there is no reliable observing basis for a conclusive answer.
(Fig. 9)
may indicate distinct populations of Miras in the solar neighbourhood.
This suggestion is also supported by the kinematics of the Mira sample
studied (see Chapter 5). On the other hand, a more or less continuous
star formation may be characteristic of the LMC (see also Barthès & Luri
1999). However, at present,
there is no reliable observing basis for a conclusive answer.
We used the distances, proper motions and radial velocities of the
Miras to compute the spatial velocity components U, V, W and their
dispersions in the Galactic Cartesian system with the axes directed
to the anticenter, along the rotation, and to the north pole of the
Galaxy, respectively. The spatial velocities were corrected for
the peculiar velocity of the Sun assuming
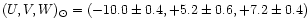 km s-1(Dehnen & Binney 1998).
The elements of Galactic box orbits, apocenter
and pericenter distances
km s-1(Dehnen & Binney 1998).
The elements of Galactic box orbits, apocenter
and pericenter distances 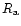 and
and 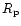 ,
eccentricity e and maximum
Z-distance from the Galactic plane
,
eccentricity e and maximum
Z-distance from the Galactic plane
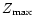 which a star can reach
in its orbital motion, were obtained by assuming the form of
the Galactic potential proposed by Saio & Yoshii (1979). The
distance of the Sun from the Galactic center is taken to be 8.5 kpc.
According
to the
which a star can reach
in its orbital motion, were obtained by assuming the form of
the Galactic potential proposed by Saio & Yoshii (1979). The
distance of the Sun from the Galactic center is taken to be 8.5 kpc.
According
to the 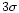 -criterion, 69 stars were excluded from the final
solution. The resulting values and their rms errors are presented
in Table 5.
-criterion, 69 stars were excluded from the final
solution. The resulting values and their rms errors are presented
in Table 5.
The kinematic data given in Table 5 indicate a
higher age for the oxygen-rich Miras with smaller periods.
Smaller
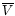 -velocities
and larger velocity dispersions
-velocities
and larger velocity dispersions
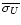 ,
,
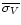 ,
,
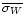 support the idea that
these stars belong to older Galactic subsystems. Also, the increasing
eccentricities and maximum Z-distances of the oxygen-rich Miras with
smaller periods prove that these stars move at higher eccentric orbits,
more inclined to the Galactic plane, that is typical for the older
population.
support the idea that
these stars belong to older Galactic subsystems. Also, the increasing
eccentricities and maximum Z-distances of the oxygen-rich Miras with
smaller periods prove that these stars move at higher eccentric orbits,
more inclined to the Galactic plane, that is typical for the older
population.
This conclusion is consistent with the results obtained by
Barthès et al. (1999) for oxygen-rich LPVs falling into their Groups
1 and 4 which are predominantly composed of Miras (102 Miras out of 121 stars
in Group 1 and 13 Miras out of 14 stars in Group 4). A direct comparison of the
kinematic parameters is rather difficult since LPVs in these Groups
cover larger ranges of periods P (from 225 to 500 days with
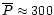 days in Group 1 and from 125 to 250 days
with
days in Group 1 and from 125 to 250 days
with
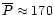 days in Group 4). However, the velocity
components derived by Barthès et al. (1999) for Groups 1 and 4 coincide
well with the corresponding values in Table 5 for Miras
with periods
days in Group 4). However, the velocity
components derived by Barthès et al. (1999) for Groups 1 and 4 coincide
well with the corresponding values in Table 5 for Miras
with periods
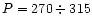 days and P < 165 days, respectively.
days and P < 165 days, respectively.
Recently, a kinematic study of field Miras with proper motions
measured by Hipparcos was published by Feast & Whitelock (2000). For
the determination of space velocities, the authors make use of
the infrared (K) PLR for LMC Miras (Feast et al. 1989) with the zero-point
derived from Hipparcos parallaxes (Whitelock & Feast 2000). The
kinematic parameters obtained by the authors are in good agreement with
our results for Miras with periods lager than 200 days![[*]](/icons/foot_motif.gif) .
For variables with periods between 145 and 200 days (17 stars), a
significant motion radially outwards from the Galactic Centre of
.
For variables with periods between 145 and 200 days (17 stars), a
significant motion radially outwards from the Galactic Centre of
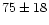 km s-1 was derived in Feast & Whitelock (2000).
km s-1 was derived in Feast & Whitelock (2000).
In our sample there are 77 stars with periods in the range
145-200 days. Out of them,
11 are in common with stars listed by Feast & Whitelock (2000) in
their group 2. The remaining 6 stars (SW Scl, RW Sgr, R Pic, X Mon, X Oct,
V CVn, S Acl) from this group are classified as Semiregulars in the GCVS-4
and were not included in our study. For the 11 stars in common, the individual
values of the velocity components
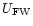 ,
,
 ,
,
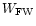 given in
Feast & Whitelock are consistent with our data
U, V, W (see Table 6).
The mean difference in the U component is
given in
Feast & Whitelock are consistent with our data
U, V, W (see Table 6).
The mean difference in the U component is
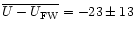 km s-1 (with the median value
for the ratio
km s-1 (with the median value
for the ratio
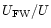 being 1.2).
Also the total space velocities in Feast & Whitelock (2000) are, on average,
by a factor of 1.2 higher then those derived in the present paper.
Most probably, this effect is a consequence of different distance estimations
(underestimated distances in the present paper, or overestimated in
Feast & Whitelock 2000, or both). Simple calculations support this
explanation. Let us assume that, on average, a relation between the transverse
being 1.2).
Also the total space velocities in Feast & Whitelock (2000) are, on average,
by a factor of 1.2 higher then those derived in the present paper.
Most probably, this effect is a consequence of different distance estimations
(underestimated distances in the present paper, or overestimated in
Feast & Whitelock 2000, or both). Simple calculations support this
explanation. Let us assume that, on average, a relation between the transverse
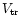 and radial
and radial
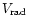 velocity components is
velocity components is
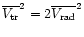 .
Then the given
difference in space velocities could arise due to distance estimations
differing by a factor 1.4. If a PLR was used to derive the distances,
an effect of this order would be
caused by a difference in the estimation of absolute magnitudes of
.
Then the given
difference in space velocities could arise due to distance estimations
differing by a factor 1.4. If a PLR was used to derive the distances,
an effect of this order would be
caused by a difference in the estimation of absolute magnitudes of
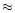 0.7 mag. The data in Fig. 9 suggest this explanation.
The direct comparison with the distances given in Whitelock et al. (2000)
and those used by Feast & Whitelock (2000) to compute the spatial velocities
for these stars confirms the effect of the same order (which
yields, finally, the difference by a factor of about 1.2 for the U component).
0.7 mag. The data in Fig. 9 suggest this explanation.
The direct comparison with the distances given in Whitelock et al. (2000)
and those used by Feast & Whitelock (2000) to compute the spatial velocities
for these stars confirms the effect of the same order (which
yields, finally, the difference by a factor of about 1.2 for the U component).
Nevertheless, we conclude from Table 6 that
11 common stars with periods between 145 and 200 days and at distances less
than 2 kpc from the Sun show a strong motion
outwards from the Galactic Center.
On the other hand, we must also stress that the subset considered
by Feast & Whitelock (2000) includes
only a small portion of Miras known in the Solar neighborhood.
Considering all 35 Miras identified within 2 kpc from the Sun and
assuming the possibility that the distances may be underestimated in our
study, we cannot completely exclude the hypothesis
of a net radial motion from the Galactic Centre for these stars,
although, the effect should be of a considerably less significance.
However, on the basis of all 77 known Miras with periods in the range
145-200 days, we must reject the finding of an outward motion.
Note also that the kinematic parameters
derived for Miras in the near (R < 2 kpc) and far (R > 2 kpc)
Solar neighborhood (see Table 6) do not justify a statistically
significant separation into two different groups. Therefore, it is likely
that the group 2 stars from Feast & Whitelock (2000), which were selected
on the basis of available Hipparcos proper motions, radial velocities and
K photometry, do not represent a
general motion of Miras with periods in the range 145-200 days
sufficiently well.
In order to construct the luminosity function for the Miras, we computed
absolute magnitudes MV for all 5042 stars with known periods by use
of the PLR derived in this paper (see Fig. 6).
A representative sample of Miras is accumulated in such a
volume Q where selection effects of observations and peculiarities
of the spatial distribution in the galactic coordinate system (XYZ) can be
compensated.
As a compromise, we adopted a maximum distance
from the Sun in the galactic plane
R = (X2 +Y2)1/2 to
be 0.5 kpc. Assuming an exponential decrease of the star density along the
Z coordinate, we defined the luminosity function as the
number of Mira variables in the volume
where the scale height hZ was taken from Kharchenko (1994) and
R = 0.5 kpc. In order to decide which Miras are located
within the volume Q, the distances were obtained
from the solution of (13) and (14) in the same way as described above.
Figure 10 shows the luminosity
function of Mira variables in comparison with the function by Kharchenko
(1994).
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10095f10.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg244.gif) |
Figure 10:
The luminosity function of Mira variables
based on the PLR which has been obtained in this paper (solid line) and
by Kharchenko (1994) (dashed line). |
| Open with DEXTER |
Furthermore, the luminosity function was used to derive the frequency
functions
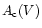 and
and
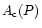 given in (1) and (2) and to predict the
numbers of Miras to be expected from an all-sky survey complete up to
a given limiting magnitude. The corresponding differential A(V) and
integrated N(V) numbers of Mira variables were computed, assuming a
distance of 8.5 kpc of the Sun from the Galactic center.
Figure 11 shows the predicted numbers of Miras per square degree in
the directions to the Galactic center and anticenter.
given in (1) and (2) and to predict the
numbers of Miras to be expected from an all-sky survey complete up to
a given limiting magnitude. The corresponding differential A(V) and
integrated N(V) numbers of Mira variables were computed, assuming a
distance of 8.5 kpc of the Sun from the Galactic center.
Figure 11 shows the predicted numbers of Miras per square degree in
the directions to the Galactic center and anticenter.
From Figs. 1 and 11, we conclude that the
proposed future astrometric space missions
with a limiting magnitude of
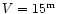 (DIVA, FAME) or
(DIVA, FAME) or
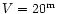 (GAIA)
will be able, in principle, to
observe about 70000 or 135000 field Miras in the Galaxy, respectively.
However, the number of Mira variables
with accurate trigonometric parallaxes will be much less and will depend
on the accuracy of the astrometric measurements. For example, DIVA
(Röser 1999) will provide parallaxes at the 10%-precision level
for about 200 Miras. At present, the distance of not even a single Mira
variable is known to this accuracy.
(GAIA)
will be able, in principle, to
observe about 70000 or 135000 field Miras in the Galaxy, respectively.
However, the number of Mira variables
with accurate trigonometric parallaxes will be much less and will depend
on the accuracy of the astrometric measurements. For example, DIVA
(Röser 1999) will provide parallaxes at the 10%-precision level
for about 200 Miras. At present, the distance of not even a single Mira
variable is known to this accuracy.
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10095f11.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg248.gif) |
Figure 11:
The predicted differential A(V) and integrated N(V)numbers of Miras versus magnitude in the directions to the Galactic
center (
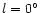 )
and anticenter ( )
and anticenter (
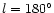 ). The
dotted, short-dashed, long-dashed, thin, normal and thick lines mark
the number of Miras at ). The
dotted, short-dashed, long-dashed, thin, normal and thick lines mark
the number of Miras at
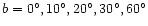 and
and
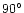 ,
respectively. ,
respectively. |
| Open with DEXTER |
We took the information on Mira variables given in the GCVS-4 and
selected a sample of stars for which new kinematic data were
obtained during the last decade. Based on the statistical parallaxes,
the mean absolute magnitudes and the spatial kinematic parameters
were determined as functions of the pulsation periods. The BCs were
derived for the oxygen-rich Miras and the PL relation was compared
with predictions from pulsation theory and with other observations.
The frequency of Mira
variables was computed as a function of the visual magnitude. The
following findings result from this analysis:
- With respect to Mira variables, the GCVS-4 is complete up to a
magnitude at maximum of V=9.
- The method of statistical parallaxes provides a
satisfactory distance scale.
- The BC-period relation of the oxygen-rich Miras shows a
rather small dispersion and, at this stage, there is no
evidence that it depends on the pulsation mode.
- The derived PLR (
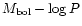 )
is significantly steeper than
the corresponding PLR found in the LMC (Feast et al. 1989) but in good
agreement with the findings of Barthes et al. (1999) who studied
galactic oxygen-rich LPVs from the Hipparcos Catalogue.
The derived shape of the PLR may be due to a significant dispersion of
present masses and due to the existence of Mira populations of
distinct ages in the solar neighbourhood.
)
is significantly steeper than
the corresponding PLR found in the LMC (Feast et al. 1989) but in good
agreement with the findings of Barthes et al. (1999) who studied
galactic oxygen-rich LPVs from the Hipparcos Catalogue.
The derived shape of the PLR may be due to a significant dispersion of
present masses and due to the existence of Mira populations of
distinct ages in the solar neighbourhood.
- The comparison with theoretical pulsation models yields
reasonable masses around
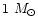 ,
consistent with previous
studies. The most probable pulsation mode is the
fundamental one.
,
consistent with previous
studies. The most probable pulsation mode is the
fundamental one.
- The kinematic parameters describing the spatial velocities and
orbital motion indicate a higher age for the oxygen-rich Miras
pulsating with smaller periods. That is in agreement with previous
findings.
- The analyzed data do not support the assumption (Feast & Whitelock
2000) of a significant
motion radially outwards in the Galaxy for Miras in the period range
145-200 days.
Acknowledgements
We are grateful to Olga Durlevich for providing necessary data from
the GCVS. N. Kharchenko and O. Malkov thank the Deutsche
Forschungsgemeinschaft for financial support that enabled their visit to AIP
Potsdam where this work has been done. E. Kilpio and
O. Malkov also acknowledge support from the RF President grant
99-15-96022, and the Russian Academy of Sciences for the help
provided in the frame of the "Young scientists support program''.
The authors also thank the anonymous referee for his/her very useful
comments and suggestions.
- Allen, C. W. 1973, Astrophysical quantities, 3d ed.
(Athlone Press, London)
In the text
- Alvarez, R., Mennessier, M. O., Barthès, D.,
Luri, X., & Mattei, J. A. 1997, Hipparcos Venice'97, ESA SP-402, 383
In the text
- Bahcall, J. N., & Soneira, R. M. 1980, ApJS, 44, 73
In the text
NASA ADS
- Barbier-Brossat, M., & Figon, P. 2000, A&AS, 142, 217
In the text
NASA ADS
- Barnes, T. G., & Fekel, F. C. 1977, The Observatory, 97, 1
In the text
NASA ADS
- Barthès, D. 1998, A&A, 333, 647
In the text
NASA ADS
- Barthès, D., Luri, X., Alvarez, R., & Mennessier, M. O.
1999, A&AS, 140, 55
In the text
NASA ADS
- Barthès, D., & Luri, X. 2001, A&A, 365, 519
In the text
NASA ADS
- Bastian, U., & Röser, S. 1993a, PPM Star Catalogue 3, 4 (Spektrum Academischer Verlag)
In the text
- Bastian, U., & Röser, S. 1993b, Veröffentlichungen
Astronomisches Rechen Inst. (Heidelberg)
- Bedding, T. R., & Zijlstra, A. A. 1998, A&A, 506, L47
In the text
- Carlsberg Meridian Catalogue La Palma Numbers 1 to 11,
Observations of positions of stars and planets: May 1984 to May 1998
(CMC11) 1999, Copenhagen University Observatory, Royal Greenwich
Observatory and Real Instituto y Observatorio de la Armada en San
Fernando, CD-ROM distribution
- Clayton, M. L., & Feast, M. V. 1969, MNRAS, 146, 411
In the text
NASA ADS
- Dean, C. A. 1976, AJ, 81, 364
In the text
NASA ADS
- Dehnen, W., & Binney, J. J. 1998, MNRAS, 298, 387
In the text
NASA ADS
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA
SP-1200
- Feast, M. W. 1963, MNRAS, 125, 367
In the text
NASA ADS
- Feast, M. W. 1966, MNRAS, 132, 495
In the text
NASA ADS
- Feast, M. 1999, in Asymptotic Giant Branch Stars, ed.
T. Le Bertre, A. Lèbre, & C. Waelkens, IAU Symp., 191, 109
In the text
- Feast, M. W., Robertson, B. S. C., & Black, C. 1980,
MNRAS, 190, 227
In the text
NASA ADS
- Feast, M. W., & Whitelock, P. 1997, MNRAS, 291, 683
In the text
NASA ADS
- Feast, M. W., & Whitelock, P. 1999, in Post-Hipparcos
Cosmic Candles, ed. A. Heck, & F. Caputo (Kluwer), 75
- Feast, M. W., & Whitelock, P. 2000, MNRAS, 317, 460
In the text
NASA ADS
- Feast, M. W., Woolley, R., & Yilmas, N. 1972, MNRAS, 158, 23
In the text
NASA ADS
- Høg, E., Kuzmin, A., Bastian, U., et al. 1998, A&A, 335, L65
In the text
NASA ADS
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000,
Astrometric and photometric reference catalogue of the 2.5 million
brightest stars covering the entire sky, Copenhagen,
CD-ROM distribution
In the text
- Ikaunieks, J. J. 1971, Long period
variable stars, Zinante, Riga
In the text
- Kharchenko, N. V. 1992, Kinemat. Phys.
Celest. Bodies, 8, 61
In the text
- Kharchenko, N. V. 1994, Kinemat. Phys.
Celest. Bodies, 10, 70
In the text
- Kholopov, P. N., Samus, N. N., Frolov, M. S., et al. 1985-1988,
General Catalogue of Variable Stars, 4th edition (Nauka Publishing
House, Moscow) (GCVS-4)
In the text
- Kilpio, E. Yu., & Malkov, O. Yu. 1997, Astron. Rep., 41, 10
In the text
NASA ADS
- Kukarkin, B. V., Kholopov, P. N., Efremov, Yu. N.,
et al. 1969, General Catalogue of Variable
Stars, 3rd edition (Nauka Publishing House, Moscow) (GCVS-3)
In the text
- Kukarkin, B. V., Kholopov, P. N., Artiukhina, N. M.,
et al. 1982, New Catalogue of Suspected Variable Stars (Nauka Publishing House, Moscow)
In the text
- Osvald, V., & Risley, A. M. 1961, Publ. Leander
McCormick Obs., 11, 147
In the text
- Percy, J. R., & Colivas, T. 1999, PASP, 111, 94
In the text
NASA ADS
- Perry, C. L., & Bidelman, W. P. 1965, PASP, 77, 214
In the text
NASA ADS
- Röser, S. 1999, in Reviews in Modern Astronomy 12,
ed. R. E. Schielicke (Astronomische Gesellschaft, Hamburg), 97
In the text
- Röser, S., & Bastian, U. 1991, PPM Star Catalogue
1, 2 (Spektrum Academischer Verlag)
In the text
- Saio, H., & Yoshii, Y. 1979, PASP, 91, 553
In the text
NASA ADS
- Sharov, A. S. 1963, Astron. Zh., 40, 900
In the text
NASA ADS
- Smak, J. I., & Preston, G. W. 1965, ApJ, 142, 943
In the text
NASA ADS
- Straizys, V. 1992, Multicolor stellar photometry (Pachart Publishing House, Tucson, Arizona)
In the text
- Tuchman, Y. 1999, in Asymptotic Giant Branch Stars, ed.
T. Le Bertre, A. Lèbre, & C. Waelkens, IAU Symp., 191, 122
In the text
- Urban, S. E., Corbin, T. E., & Wycoff, G. L. 1998, AJ, 115, 2161
In the text
NASA ADS
- van Leeuwen, F., Feast, M. W., Whitelock, P. A., & Yudin, B.
1997, MNRAS, 287, 955
In the text
NASA ADS
- Whitelock, P., & Feast, M. 2000, MNRAS, 319, 759
In the text
NASA ADS
- Whitelock, P., Marang, F., & Feast, M. 2000, MNRAS, 319, 728
In the text
NASA ADS
- Wood, P. R., & Sebo, K. M. 1996, MNRAS, 282, 958
In the text
NASA ADS
- Ya'ari, A., & Tuchman, Y. 1996, ApJ, 456, 350
In the text
NASA ADS
Copyright ESO 2002
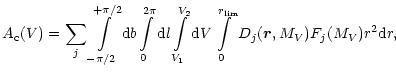
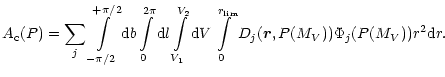
![\begin{figure}
\par\includegraphics[angle=270,width=7.1cm,clip]{10095f1.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg26.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.1cm,clip]{10095f2.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg27.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{10095f3.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg28.gif)
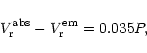
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10095f4.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg47.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10095f5.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg48.gif)
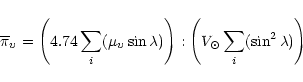
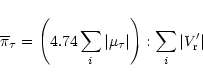
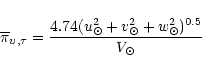

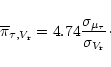
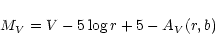
![\begin{displaymath}%
A_V(r,b) = a_V\,h_{\rm Za} [1 - \exp( - r \vert\sin b\vert / h_{\rm Za})] / \vert\sin b\vert
\end{displaymath}](/articles/aa/full/2002/12/aa10095/img111.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10095f6.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg115.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{10095f7.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg122.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10095f8.eps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg124.gif)
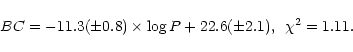
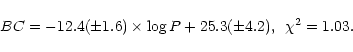
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{10095f9.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg128.gif)
![$\displaystyle %
Q {=} \pi R^2 \int\limits_{-Z}^{Z}
\exp ({-}z/h_{Z}) {\rm d}z
{=} 2\pi R^2 h_{Z}[1{-}\exp(-Z/h_{Z})].$](/articles/aa/full/2002/12/aa10095/img243.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10095f10.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg244.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.5cm,clip]{10095f11.ps}\par\end{figure}](/articles/aa/full/2002/12/aa10095/Timg248.gif)