A&A 384, 433-440 (2002)
DOI: 10.1051/0004-6361:20020019
Non-linear radial pulsation models for the early-type helium stars V652 Her and BX Cir
P. Montañés Rodríguez
- C. S. Jeffery
Armagh Observatory, College Hill,
Armagh BT61 9DG, Northern Ireland
Received 18 September 2001 / Accepted 2 January 2002
Abstract
We report new non-linear pulsation models of the helium stars
V652 Her and BX Cir. Linear theory has previously shown
their pulsations to be due to iron-group bump instability.
Recent high-resolution spectroscopic observations have provided
high-precision measurements of their radial velocity curves and of
their radii. Their masses remain less well determined.
A hydrodynamic code including recent OPAL opacity data has been
used to construct the models. These are compared with the observational
data. In particular, we attempt to reproduce accurately the observed radial
velocity
and luminosity curves.
The results impose additional constraints on those stellar dimensions,
including mass,
which remain poorly determined by observation. Final results show a model
for V652 Her which reproduce the observed velocity and luminosity curves with
0.7 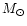 and 23 400 K.
For BX Cir, the mass must lie between 0.50 and 0.38
and 23 400 K.
For BX Cir, the mass must lie between 0.50 and 0.38 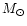 if the
temperature is in the range 22 400-24 000 K. However, the
luminosity of the models is smaller than that measured directly by
a factor of two.
if the
temperature is in the range 22 400-24 000 K. However, the
luminosity of the models is smaller than that measured directly by
a factor of two.
Key words: stars: helium -
stars: individual: V652 Her -
stars: individual: BX Cir -
stars: oscillations -
stars: early-type
Extreme helium early-type stars are located in a region on the H-R diagram
between 10 000 and 25 000 K and with
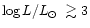 .
Although
this locus coincides with that of massive main sequence stars,
they are low mass stars (
.
Although
this locus coincides with that of massive main sequence stars,
they are low mass stars (
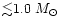 )
in an advanced stage
of evolution.
Their unusually low surface hydrogen abundance, less than 1% (Drilling et al. 1998; Jeffery et al. 2001) is a question not entirely solved by stellar evolution theory.
)
in an advanced stage
of evolution.
Their unusually low surface hydrogen abundance, less than 1% (Drilling et al. 1998; Jeffery et al. 2001) is a question not entirely solved by stellar evolution theory.
Several theories have been proposed to explain their origin.
The most recent hypothesis, explain the evolution of a merged binary helium white dwarf to
become a low-mass helium star (Saio & Jeffery 2000).
But evolution models strongly depend on the stellar parameters,
in particular, the stellar mass and metallicity have to be accurately known.
A few low-mass (early-type) helium stars show periodic light variations
due to stellar pulsations (Kilkenny & Koen 1995; Lynas-Gray et al. 1984;
Jeffery & Saio 1999; Kilkenny et al. 1999) which provide a direct way to measure their
mass, metallicity and position within the H-R diagram. At present
just two of these, V652 Her and BX Cir (BD + 13 3224 and LSS 3184) have been identified
as purely radial pulsators.
3224 and LSS 3184) have been identified
as purely radial pulsators.
The instability strip for extreme helium stars was first discovered,
using OPAL opacities and linear analysis, by Saio (1995). He found that
pulsation models become unstable due to the iron-group ionization opacity peak at around
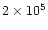 K (iron-group bump mechanism). For early-type helium
stars the instability boundaries were approximately located between
K (iron-group bump mechanism). For early-type helium
stars the instability boundaries were approximately located between
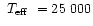 and 16 000 K and between
L =300 and
and 16 000 K and between
L =300 and
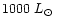 with small variations depending on stellar mass and metallicity.
with small variations depending on stellar mass and metallicity.
Non-linear analyses of V652 Her have been previously carried out by
Fadeyev & Lynas Gray (1996), providing radial
velocity and luminosity curves for 0.72 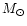 models in good agreement
with observational data. They also studied the variations of velocity
and luminosity amplitudes within the instability strip, finding
that the boundaries are close to those proposed by Saio (1995).
models in good agreement
with observational data. They also studied the variations of velocity
and luminosity amplitudes within the instability strip, finding
that the boundaries are close to those proposed by Saio (1995).
Recent observations of V652 Her (Jeffery et al. 2001) using higher
resolution have provided a lower value for its mass. Also a more
accurate measurement of its abundances gives a higher nitrogen
abundance than previous results, as well
as a carbon abundance smaller than solar. New observations have also provided
better estimates of the mass and effective temperature of BX Cir (Woolf & Jeffery 2000).
The goal of this paper is to constrain the stellar parameters
and in particular, the mass, effective temperature and metal abundances of V652 Her and
BX Cir, by comparing new non-linear models with the recent observational data,
as well as to analyze the variations of the light and velocity curves
for this range of masses and effective temperatures.
Since the discovery of V652 Her as a short period variable by Landolt (1975),
several observations have been carried out to determine its stellar properties
with better accuracy.
Initially, it was identified as a radially pulsating star by Hill et al. (1981).
A more precise measurement of its radius
was obtained by Lynas-Gray et al. (1984) by including ultraviolet
spectroscopy.
Subsequent studies of the light curves and
spectrum of V652 Her are summarized in Tables 1 and 2,
and Fig. 1. In particular, Table 1 shows the recent observed
parameters (Jeffery et al. 2001) measured (a) by visual magnitude and (b) by ultraviolet spectrophotometry,
although the unrealistically low mass obtained by the first method, causes us to choose
(b) parameters, where systematic errors are probably smaller.
A second pulsating helium star, BX Cir, was discovered by Drilling (1980) and, as V652 Her,
was predicted to pulsate due to its location in the instability region (Saio 1995).
Kilkenny & Koen (1995) measured a period of 0.1066 days.
An atmospheric analysis by Drilling et al. (1998) reported the dimensions and abundances
shown in Tables 1 and 2. Subsequent analysis by Woolf & Jeffery (2000)
measured BX Cir's radial velocity, angular radius and stellar mass, providing the results
also shown in Table 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F1.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg15.gif) |
Figure 1:
H-R diagram showing the location of V652 Her and BX Cir
according to references given in Table. 1. Stellar luminosity was calculated from the provided effective
temperature and radius. The boundaries of the region of pulsational instability
due to the iron-group bump mechanism for 0.5 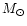 (solid line) and 0.7
(solid line) and 0.7 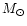 (dotted line)
for metallicity Z=0.01 are also shown.
(dotted line)
for metallicity Z=0.01 are also shown. |
| Open with DEXTER |
A non-linear pulsation code (Bridger 1984) based on the description by Christy (1967)
has been used to model radial oscillations. Equations of motion and continuity were solved
using the explicit finite-difference scheme, whereas the energy equation was treated
implicitly with the Crank-Nicholson scheme.
Each pulsation model represents a fundamental mode radial pulsator and is
characterized by four parameters,
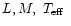 and chemical abundances.
and chemical abundances.
The initial model of the stellar envelope was calculated in hydrostatic equilibrium.
The equations were integrated inward from the surface, using approximately 5000 integration points,
after choosing an outer-zone mass and a zone mass ratio (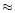 1.1).
The number of mass zones considered in the different hydrodynamic models varies between 70 and 80.
1.1).
The number of mass zones considered in the different hydrodynamic models varies between 70 and 80.
Convection was ignored and chemical composition was assumed to be constant.
The inner boundary of the pulsating envelope was considered to be a rigid sphere
radiating with constant luminosity.
At the surface, the standing wave or total reflection boundary condition was applied
(
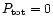 ). The inner boundary must be at a radius of less than one tenth of the stellar radius and must have a temperature
). The inner boundary must be at a radius of less than one tenth of the stellar radius and must have a temperature
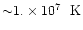 .
.
The static model was perturbed using a radius dependent velocity distribution,
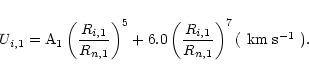 |
(1) |
Here Ri,1 is the initial radius in the
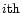 zone, Rn,1 is the initial radius at the surface and the amplitude A1, varies for different models and have typical values in the range
5-20
zone, Rn,1 is the initial radius at the surface and the amplitude A1, varies for different models and have typical values in the range
5-20
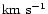 .
This was done to reduce computing time, rather than assume Ui,1=0.
.
This was done to reduce computing time, rather than assume Ui,1=0.
An artificial viscosity Qi was introduced as a dissipative pressure
following the Richtmyer-Morton method, with the equation described by Stellingwerf (1975).
The adopted viscosity parameters were
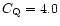 ,
following previous work for helium-rich envelopes (see Saio 1985),
and
,
following previous work for helium-rich envelopes (see Saio 1985),
and
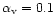 .
However, a deeper analysis of the propagation of shock waves in
such media would be interesting, since a different viscosity can modify
the shape, and the amplitude, of the velocity and luminosity curves.
.
However, a deeper analysis of the propagation of shock waves in
such media would be interesting, since a different viscosity can modify
the shape, and the amplitude, of the velocity and luminosity curves.
For temperatures lower than 10 kK
the radiative opacity was calculated using hydrogen-deficient Alexander's (1994) opacities,
with a standard solar mixture of metals (see http://web.physics.twsu.edu/alex/pub/G93.txt).
OPAL opacity tables (Iglesias & Rogers 1996) were used for temperatures higher than 10 kK.
These were initially generated in the OPAL web site (http://www-phys.llnl.gov/V_Div/OPAL/)
to have solar mixture of metals with enhanced nitrogen or carbon.
Final tables were smoothed and interpolated using adapted OPAL software.
The hydrodynamic models are characterized by their maximum kinetic
energy per pulsation cycle, E. For a model with n mass zones,
the kinetic energy for each temporal step I, is given by
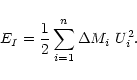 |
(2) |
E is the maximum value of EI over a pulsation cycle.
As a consequence of the initial perturbation, Edecreases initially in some models.
In contrast, in the case where Ui,1=0, E increases initially.
To ensure that our hydrodynamic calculations had converged, models
were continued until E reached a constant value and therefore the pulsation
had reached a limiting amplitude.
However, some unstable models which did not reach limiting amplitudes
were used to find the pulsation periods and to establish limits to the amplitudes
of the pulsation.
In general, the distribution of the pulsational work integral for models located within
the boundaries of the instability region, has a maximum value deeper in the envelope
than for models located in the Cepheid instability strip.
This is due to the effect of the iron-group bump, as is shown in Fig. 2.
The driving region, where the pulsation work is positive, coincides with the region of
maximum luminosity (around zone 40) and with the iron-group opacity peak.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F2.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg70.gif) |
Figure 2:
The distributions of pulsational work integral, divided by its
maximum value (thicker line W),
luminosity (L) and opacity (K) at luminosity maximum, for model 20. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F3.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg71.gif) |
Figure 3:
H-R diagram showing the models calculated. Different symbols show
chemical mixtures used in Table 3.
Boundaries of the instability region for this range of masses and chemical composition are also shown. |
| Open with DEXTER |
Homologous stellar pulsations obey the period-mean density relation
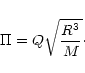 |
(3) |
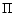 is the pulsation period, R and M are the stellar radius and
mass and Q is a factor depending on the structure of the stellar envelope.
is the pulsation period, R and M are the stellar radius and
mass and Q is a factor depending on the structure of the stellar envelope.
Since luminosity and effective temperature are related by the identity,
| L | = | 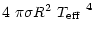 |
(4) |
| |
= |
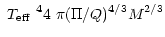 |
(5) |
then,
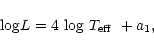 |
(6) |
where,
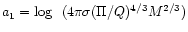 .
.
We note that models which have the measured radii and masses of V652 Her
and BX Cir do not give a period corresponding to that observed. However,
period is the best observed constraint. For this reason,
we have chosen to investigate families of models obeying Eq. (6),
with 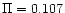 d to within
d to within 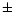 0.002 days and masses in the range 0.38-
0.002 days and masses in the range 0.38-
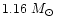 .
We have also investigated models with a range of chemical composition, including a
standard mixture
of 21 metals (Grevesse & Noels 1993) with Z=0.01 and Z=0.02 in both cases X=0.0
(z1 and z2 in Table 3) where X, Y, Z are mass fractions of hydrogen, helium and metals.
Mixtures with enhanced carbon and/or nitrogen (fv, n1, n2, c1
and c2 in Table 3) were also considered.
.
We have also investigated models with a range of chemical composition, including a
standard mixture
of 21 metals (Grevesse & Noels 1993) with Z=0.01 and Z=0.02 in both cases X=0.0
(z1 and z2 in Table 3) where X, Y, Z are mass fractions of hydrogen, helium and metals.
Mixtures with enhanced carbon and/or nitrogen (fv, n1, n2, c1
and c2 in Table 3) were also considered.
The models are described in Table 4 (see also Fig. 3).
One model (11) was computed for direct comparison with that of Fadeyev &
Lynas-Gray (1996).
This model has the same stellar parameters as the model they
consider to be in best agreement with observations at the time,
i.e.
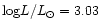 ,
,
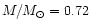 ,
,
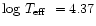 and mixture B13.002 (our
mixture fv in Table 3). Our model has velocity and luminosity
amplitudes similar to those obtained by them, showing smooth maxima in
velocity and luminosity and a characteristic spike after the maximum
in the luminosity curve.
Although this model was already in good agreement with observations,
new models were calculated specifically in an attempt to match the composition
of V652 Her and either the lower mass or the radius suggested by recent
observations (models 12-20).
and mixture B13.002 (our
mixture fv in Table 3). Our model has velocity and luminosity
amplitudes similar to those obtained by them, showing smooth maxima in
velocity and luminosity and a characteristic spike after the maximum
in the luminosity curve.
Although this model was already in good agreement with observations,
new models were calculated specifically in an attempt to match the composition
of V652 Her and either the lower mass or the radius suggested by recent
observations (models 12-20).
Another five models were computed to match the composition of BX Cir and either the mass or
the radius (models 21-25). Certain models were computed simply to explore further
certain areas of the parameters space.
Table 4 also gives the corresponding value for the factor Q, the surface gravity,
the pulsation period,  ,
and the amplitudes of the radial velocity,
,
and the amplitudes of the radial velocity,
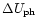 ,
and
logL/
,
and
logL/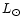 ,
,
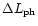 ,
at the stellar photosphere.
If the model is stable against pulsations (12, 13, 21, 22), as happens for those mixtures with very low iron abundances,
the latter values are omitted.
If the model was not computed until it reached a limiting amplitude, its
amplitudes are preceded by a < sign indicating an upper limit.
,
at the stellar photosphere.
If the model is stable against pulsations (12, 13, 21, 22), as happens for those mixtures with very low iron abundances,
the latter values are omitted.
If the model was not computed until it reached a limiting amplitude, its
amplitudes are preceded by a < sign indicating an upper limit.
The object of this investigation was to study whether the amplitudes and the shape of the stellar
radial velocity and luminosity variations could help to determine the stellar properties.
Because the period is the parameter most accurately determined by observation,
fixing it and assuming the factor Q approximately constant
allows us to fix the stellar luminosity and to compare
models in a small range of temperatures and masses around the measured values.
The changes in the light and velocity curves
for 0.42 and 0.90 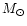 ,
as functions of temperature are shown in Fig. 4.
,
as functions of temperature are shown in Fig. 4.
For 0.42 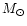 ,
we have found that for the higher effective temperature,
a characteristic bump appears after the luminosity maxima, which causes a flattening effect
over the light curve at log
,
we have found that for the higher effective temperature,
a characteristic bump appears after the luminosity maxima, which causes a flattening effect
over the light curve at log
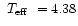 .
This shape is similar to the one observed for BX Cir.
Since this feature is almost negligible for higher masses (see luminosity curve for 0.52
.
This shape is similar to the one observed for BX Cir.
Since this feature is almost negligible for higher masses (see luminosity curve for 0.52 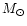 in Fig. 5) the hypothesis of BX Cir having mass less than (because luminosity
amplitudes increase with the mass) or equal to 0.40
in Fig. 5) the hypothesis of BX Cir having mass less than (because luminosity
amplitudes increase with the mass) or equal to 0.40 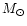 and effective temperatures around
log
and effective temperatures around
log
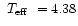 seems suitable. However, this feature disappears when varying the
chemical composition, as is shown in Fig. 6 models 25 and 4.
seems suitable. However, this feature disappears when varying the
chemical composition, as is shown in Fig. 6 models 25 and 4.
For 0.90 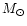 ,
both velocity and luminosity amplitudes increase when temperature decreases.
In the velocity curves, maxima and minima are rounder than for lower masses, whereas luminosity curves are, in
general, sharper. These effects can be observed in Fig. 5 for different stellar masses and approximately
constant effective temperature, around log
,
both velocity and luminosity amplitudes increase when temperature decreases.
In the velocity curves, maxima and minima are rounder than for lower masses, whereas luminosity curves are, in
general, sharper. These effects can be observed in Fig. 5 for different stellar masses and approximately
constant effective temperature, around log
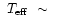 4.37.
4.37.
Our experiment to investigate the effect of increased carbon and/or nitrogen content within the metal component
was not entirely successful since in the cases with mixtures n1 and c1, closest to the measured ones, models were stable.
The reason is that the increase in carbon (or nitrogen) means a reduction in the iron-group
elements (for constant total metallicity 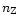 ).
Therefore in these mixtures n1 and c1,
).
Therefore in these mixtures n1 and c1,
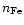 is approximately half the solar value.
When
is approximately half the solar value.
When
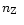 is increased to 0.0041 (for the nitrogen-rich mixture, n2) and
to 0.0066 (for the carbon-rich mixture, c2), the iron
abundance increase to
is increased to 0.0041 (for the nitrogen-rich mixture, n2) and
to 0.0066 (for the carbon-rich mixture, c2), the iron
abundance increase to
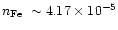 and the iron-group bump mechanism becomes effective.
In these cases, models were unstable and velocity and luminosity curves were consistent with the
observed ones.
and the iron-group bump mechanism becomes effective.
In these cases, models were unstable and velocity and luminosity curves were consistent with the
observed ones.
The behaviour of velocity and luminosity with increasing iron abundance is illustrated
in Fig. 6. The velocity curves show a faster growth
and sharper maxima and minima when the iron abundance is higher (models 4, 6 and 26). These models also
show a characteristic spike after the maximum in the luminosity curve.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F4.ps}\par\end{figure}](/articles/aa/full/2002/11/aah3161/Timg104.gif) |
Figure 4:
Variations of the velocity and luminosity curves with effective temperature,
for models with
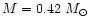 (1, 2 and 3) and
(1, 2 and 3) and
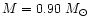 (7, 8 and 9). Model number in Table 4
is indicated in brackets. In Figs. 4-7 the vertical axes have been shifted by an arbitrary amount.
(7, 8 and 9). Model number in Table 4
is indicated in brackets. In Figs. 4-7 the vertical axes have been shifted by an arbitrary amount. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F5.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg106.gif) |
Figure 5:
Variations of the velocity and luminosity curves with stellar mass for effective
temperature approximately constant (log
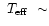 4.37).
4.37). |
| Open with DEXTER |
The observed radial velocity and luminosity curves for V652 Her and BX Cir are shown in
Fig. 7. The measured velocity and luminosity (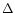 log
log
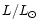 )
amplitudes are respectively
94
)
amplitudes are respectively
94
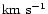 and 0.240 for V652 Her and 56
and 0.240 for V652 Her and 56
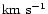 and 0.096 for BX Cir.
and 0.096 for BX Cir.
The observed radial velocities have been transformed into the stellar rest frame by multiplying
the projection factor for helium-rich early-type stars, p=-1.402
(Montañés Rodríguez & Jeffery 2001). Observational data have been taken from Jeffery et al. (2001: V652 Her) and
Woolf & Jeffery (2000: BX Cir).
Figure 7 also shows two models for each case, which fit quite well to the observed
velocity and light
curves, having not only a closer chemical composition to that observed but also similar
parameters. For V652 Her these models have 0.62
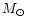 and 22 900 K
and 0.70
and 22 900 K
and 0.70
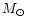 and 23 400 K. The second (model 20) shows the best fit and has a radius closer to that
given by observations, although a bigger mass.
and 23 400 K. The second (model 20) shows the best fit and has a radius closer to that
given by observations, although a bigger mass.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F6.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg110.gif) |
Figure 6:
Velocity and luminosity curves for models indicated into brackets.
Next to the model number: log
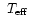 ,
stellar mass ( ,
stellar mass (
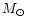 ), iron abundance ( ), iron abundance (
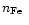 )
and total
abundance of metals ( )
and total
abundance of metals (
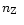 )
appear respectively. )
appear respectively. |
| Open with DEXTER |
For BX Cir, model 25 with
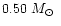 and 22 400 K presents a good fit
reproducing not only the measured velocity and luminosity amplitudes but also the observed shapes,
except for the flattening observed in the light curve which has not been reproduced in any case
for this composition.
Model 23 with a smaller mass,
and 22 400 K presents a good fit
reproducing not only the measured velocity and luminosity amplitudes but also the observed shapes,
except for the flattening observed in the light curve which has not been reproduced in any case
for this composition.
Model 23 with a smaller mass,
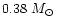 ,
and higher temperature, 24 000
K, is also quite close
to the observations for BX Cir.
The velocity and luminosity curves of these two models are
in remarkably good agreement with the observed ones. We emphasize
that, after the pulsation period, they are the most directly and reliably
measured properties of BX Cir.
,
and higher temperature, 24 000
K, is also quite close
to the observations for BX Cir.
The velocity and luminosity curves of these two models are
in remarkably good agreement with the observed ones. We emphasize
that, after the pulsation period, they are the most directly and reliably
measured properties of BX Cir.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{H3161F7.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg113.gif) |
Figure 7:
Velocity and luminosity curves for four selected models with mixtures n2
and c2. Next to the model number: log
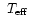 ,
stellar mass ( ,
stellar mass (
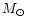 ), iron abundance ( ), iron abundance (
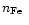 )
and total
abundance of metals ( )
and total
abundance of metals (
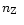 )
appear respectively. )
appear respectively. |
| Open with DEXTER |
In this paper we provide new non-linear radial pulsation models
computed within the iron-group instability strip where low-mass
extreme-helium stars are located. We attempt to reproduce the
observed light and velocity curves of V652 Her and BX Cir and,
hence, study their possible masses, luminosities and radii.
All the models have temperatures and masses close to those measured
for V652 Her and BX Cir. Their luminosities are chosen to ensure the pulsation period
matches that observed. The chemical composition was initially chosen
to be similar to the observed surface composition, but this produces
stable models. Metallicity was gradually increased to find unstable (overstable) models,
which provide a lower limit to the iron abundance of around
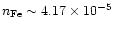 .
This indicates that the recently published iron
abundance BX Cir may be too small, although a more
detailed study of the dependence of the instability boundaries on the
iron abundance using a linear analysis is recommended. It is
evident that the pulsation properties (amplitude, light curve shape)
are very sensitive to the chemical composition.
.
This indicates that the recently published iron
abundance BX Cir may be too small, although a more
detailed study of the dependence of the instability boundaries on the
iron abundance using a linear analysis is recommended. It is
evident that the pulsation properties (amplitude, light curve shape)
are very sensitive to the chemical composition.
We have found that several models can reproduce with good accuracy the
observed velocity and luminosity curves for these two stars.
The parameters of the best fit model for V652 Her are close
to those previously provided by Fadeyev & Lynas-Gray (1996) but with
lower helium, carbon and iron abundances (model 20) more similar to those
reported in a recent spectroscopic analysis (Jeffery et al. 2001).
An attempt to reproduce the velocity and light curves with a lower mass (
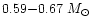 ), closer to that provided by recent observations, within
the range of temperatures 21 900-23 400
), closer to that provided by recent observations, within
the range of temperatures 21 900-23 400 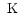 was not
successful. For
was not
successful. For
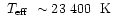 ,
a mass of at least
,
a mass of at least
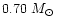 is necessary to reproduce the velocity and luminosity
curves. This value would be slightly higher for lower temperatures.
The white dwarf merger model (Saio & Jeffery 2000)
introduced to account for the origin of V652 Her
requires a final mass
between 0.6 and
is necessary to reproduce the velocity and luminosity
curves. This value would be slightly higher for lower temperatures.
The white dwarf merger model (Saio & Jeffery 2000)
introduced to account for the origin of V652 Her
requires a final mass
between 0.6 and
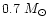 ,
which is in satisfactory agreement
with the results of our pulsation analysis.
,
which is in satisfactory agreement
with the results of our pulsation analysis.
As suggested by Jeffery et al. (2001), it remains a problem to reconcile fully
the optical line spectrum, the overall flux distribution and, as here,
the pulsation properties of V652 Her.
The pulsation period and velocity and luminosity amplitudes
of BX Cir could be
satisfactorily reproduced by a model (25) with a mass and temperature
within the observational errors. A minimum mass of
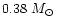 for 23 900
for 23 900 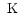 and a maximum mass of
and a maximum mass of
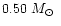 for 22 300
for 22 300 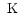 were found.
Between these limits, an increase in stellar mass requires a
corresponding decrease in effective temperature in order
to reproduce the observed velocity and luminosity amplitudes.
were found.
Between these limits, an increase in stellar mass requires a
corresponding decrease in effective temperature in order
to reproduce the observed velocity and luminosity amplitudes.
It is not possible to match the observed luminosity for
BX Cir, which seems too large by a factor of 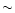 2.
The reason is far from clear because both temperature and
radius are well defined by observation (Woolf & Jeffery 2000).
Pulsation theory imposes
a very tight relation between pulsation period and mean density - or
mass-to-radius ratio. Small departures from this ratio do not significantly
alter the shapes of light and velocity curves. Thus we
believe that fixing the period is the most appropriate way to approach the
problem. There are several other possibilities. One is that the
radius of Woolf & Jeffery (2000) is too big, but their data do not seem to
allow this. Another is that systematic errors in the model atmospheres
overestimate the effective temperature and a smaller radius results.
A third is that similar errors led to an underestimate of the
surface gravity of Drilling et al. (1996) so that a higher mass would result.
Finally, systematic errors in the pulsation models could yield incorrect
amplitudes.
Such errors would have to be selective in order to modify the BX Cir
result more than the V652 Her result, and could occur if the composition
adopted for either star were incorrect. Further observational work
might yield evidence for a
solution with a higher mass. This would be easier to
reconcile with white dwarf merger models (Saio & Jeffery 2000), which
require masses in excess of
2.
The reason is far from clear because both temperature and
radius are well defined by observation (Woolf & Jeffery 2000).
Pulsation theory imposes
a very tight relation between pulsation period and mean density - or
mass-to-radius ratio. Small departures from this ratio do not significantly
alter the shapes of light and velocity curves. Thus we
believe that fixing the period is the most appropriate way to approach the
problem. There are several other possibilities. One is that the
radius of Woolf & Jeffery (2000) is too big, but their data do not seem to
allow this. Another is that systematic errors in the model atmospheres
overestimate the effective temperature and a smaller radius results.
A third is that similar errors led to an underestimate of the
surface gravity of Drilling et al. (1996) so that a higher mass would result.
Finally, systematic errors in the pulsation models could yield incorrect
amplitudes.
Such errors would have to be selective in order to modify the BX Cir
result more than the V652 Her result, and could occur if the composition
adopted for either star were incorrect. Further observational work
might yield evidence for a
solution with a higher mass. This would be easier to
reconcile with white dwarf merger models (Saio & Jeffery 2000), which
require masses in excess of
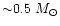 .
However the
conclusion of this paper is that the current pulsation models favour a
low-mass solution for BX Cir. Otherwise the theoretical
velocity amplitude is too large compared with that
observed.
.
However the
conclusion of this paper is that the current pulsation models favour a
low-mass solution for BX Cir. Otherwise the theoretical
velocity amplitude is too large compared with that
observed.
Acknowledgements
This research is supported by a grant to the Armagh Observatory from the
Northern Ireland Department of Culture, Arts and Leisure and by the British Council through
Collaborative Research Grant TOK/880/41/4. We are grateful to Prof. H. Saio (Tohoku University, Sendai)
for valuable advice, to Prof. Y. A. Fadeyev (Institute of Astronomy of the RAS, Moscow) for his comments,
to Dr. A. Bridger (UK Astronomy Technology Centre, Edinburgh) for his pulsation code and
to the referee Dr. T. Metcalfe for his review of the paper.
-
Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197
In the text
-
Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879A
In the text
NASA ADS
-
Bridger, A. 1984, Cepheids: Theory & Observations, IAU Coll., 82, 246
In the text
-
Christy, F. 1966, ARA&A, 4, 353
NASA ADS
-
Drilling, J. S., Jeffery, C. S., & Heber, U. 1998, A&A, 329, 1019
In the text
NASA ADS
-
Drilling, J. S. 1980, ApJ, 242, L43
In the text
NASA ADS
-
Fadeyev, Yu. A., & Lynas-Gray, A. E. 1996, MNRAS, 280, 427
In the text
NASA ADS
-
Grevesse, N., & Noel, A. 1993, Origin and Evolution of the Elements,
ed. N. Pratzo, E. Vangioni-Flam, & M. Casse (Cambridge: Cambridge
Univ. Press), 15 (GN93)
In the text
-
Hill, P. W., Kilkenny, D., Schönberner, D., & Walker, H. J. 1981,
MNRAS, 197, 81
In the text
NASA ADS
-
Holweger, H., Heise, C., & Kock, M. 1990, AA, 232, 510
In the text
NASA ADS
-
Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943
In the text
NASA ADS
-
Jeffery, C. S., & Heber, U. 1992, A&A, 260, 133
NASA ADS
-
Jeffery, C. S. 1996, ASP Conf. Ser., 96, 152
-
Jeffery, C. S., & Saio, H. 1999, MNRAS, 308, 221
NASA ADS
-
Jeffery, C. S., Hill, P. W., & Heber, U. 1999, A&A, 346, 491
NASA ADS
-
Jeffery, C. S., Woolf, V. M., & Pollacco, D. 2001, A&A, 376, 497
In the text
NASA ADS
-
Kilkenny, D., & Koen, C. 1995, MNRAS, 275, 327
In the text
NASA ADS
-
Kilkenny, D., Koen, C., Jeffery, C. S., Hill, N. C., & O'Donoghue, D. 1999, MNRAS, 310, 1119
In the text
NASA ADS
-
Landolt, A. U. 1975, ApJ, 196, 789
In the text
NASA ADS
-
Lynas-Gray, A. E., Schönberner, D., Hill, P. W., & Heber, U. 1984, MNRAS, 209, 387
In the text
NASA ADS
-
Montañés Rodríguez, P., & Jeffery, C. S. 2001, A&A, 375, 411
In the text
NASA ADS
-
Saio, H. 1985, ApJ, 295, 38S
NASA ADS
-
Saio, H. 1990, ASP Conf. Ser., 557
-
Saio, H. 1993, MNRAS, 260, 465
NASA ADS
-
Saio, H. 1995, MNRAS, 277, 1393
In the text
NASA ADS
-
Saio, H., & Jeffery, C. S. 2000, MNRAS, 313, 671
In the text
NASA ADS
-
Stellingwerf, R. F. 1975, ApJ, 195, 441
In the text
NASA ADS
-
Stürenburg, S., & Holweger, H. 1990, A&A, 237, 125
In the text
NASA ADS
-
Woolf, V. M., & Jeffery, C. S. 2000, A&A, 358, 1001
In the text
NASA ADS
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F1.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg15.gif)
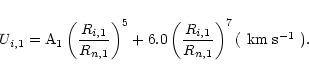
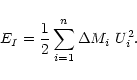
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F2.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F3.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg71.gif)
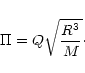
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F4.ps}\par\end{figure}](/articles/aa/full/2002/11/aah3161/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F5.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3161F6.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg110.gif)
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{H3161F7.ps}\end{figure}](/articles/aa/full/2002/11/aah3161/Timg113.gif)