A&A 384, 654-665 (2002)
DOI: 10.1051/0004-6361:20020028

Very Long Baseline Interferometer measurements of turbulence in the inner solar wind

S. R. Spangler 1,2 - D. W. Kavars 1 - P. S. Kortenkamp 1 - M. Bondi 2 - F. Mantovani 2 - W. Alef 3


1 - Dept. of Physics and Astronomy, University of Iowa, Iowa City, Iowa 52242, USA
2 - Istituto di Radioastronomia del CNR, Via Gobetti 101, 40129 Bologna, Italy
3 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany

Received 3 July 2001 / Accepted 4 January 2002

Abstract
Very Long Baseline Interferometry (VLBI) observations were made of six sources in September and October 1998. The observations were made at a time when the solar elongations of five of those sources ranged from 4 $.\!\!^\circ$4 to 6 $.\!\!^\circ$8, so that the lines of sight to these sources passed at distances of closest approach to the Sun of 16.5 to 25.3 $R_{\odot }$. The solar elongation of the sixth source was 16 $.\!\!^\circ$6, corresponding to a distance of $62.4~R_{\odot}$. The observations were made with the Medicina and Noto antennas of the Istituto di Radioastronomia, the Matera (Italy) antenna of the Agenzia Spaziale Italiana, and the Wettzell (Germany) antenna of the Bundesamt für Kartographie und Geodäsie. On two of the three days of observation (September 24 and October 15, 1998) simultaneous observations were made at 8.380 (X band) and 2.257 (S band) GHz. In the third observing session (September 25, 1998) observations were made at 4.981 GHz (C band). Temporal fluctuations in the interferometer phase, induced by the solar wind, were analysed to yield information on plasma turbulence in the inner heliosphere. The results of this investigation are as follows. (1) The measured interferometer phase power spectra are consistent with a theoretical expression which incorporates independent information on solar wind turbulence. (2) The values for  $C_{\rm N}^2$, the normalization constant of the density power spectrum, are reasonably consistent with a previously-determined expression for $C_{\rm N}^2(r)$, where r is the heliocentric distance, although the new values for $C_{\rm N}^2$ are systematically high with respect to this prior expression. (3) Our estimates for the speed at which the irregularities move with respect to the antennas, and in the radial direction from the Sun, are in the range of 190-340 kms-1 for heliocentric distances of 16-26 $R_{\odot }$. These values are in good agreement with observational estimates of the solar wind flow speed in this part of space based on coronagraph observations. The speeds are lower than the sum of the estimated solar wind flow speed and the local Alfvén speed. The potential significance of this result is discussed.

Key words: solar wind - Sun: corona- turbulence


1 Introduction

This paper is the latest in a series devoted to the investigation of the near-Sun solar wind plasma via Very Long Baseline Interferometry (VLBI) (Sakurai et al. 1992; Spangler & Sakurai 1995; Spangler et al. 1996; Grall et al. 1997). VLBI observations of this type are a subclass of radio propagation investigations of the solar wind plasma (Coles 1978; Bourgois 1993). The primary advantage of radio propagation investigations is that they provide information on the solar wind plasma at distances ranging from the solar surface to 60 $R_{\odot }$ and greater. They therefore provide information on a part of space in which there have been no in-situ plasma measurements.

1.1 Knowledge of the solar wind at heliocentric distances $\leq $62 R ${_{\odot }}$

The capability of radio propagation observations to provide information on the solar wind plasma at heliocentric distances $\leq62~R_{\odot}$ is particularly important because a number of processes crucial to the nature of the solar wind are believed to operate there. The acceleration of the slow speed solar wind is largely or entirely completed within $62~R_{\odot}$ (Schwenn et al. 1981; Sheeley et al. 1997; Breen et al. 1999, 2000). The high speed solar wind is almost certainly fully accelerated to its asymptotic speed much closer to the Sun. Radio propagation observations can provide information on the plasma properties of the inner solar wind, and thus provide important observational constraints for solar wind acceleration models.

Plasma turbulence is believed to play an important role in determining the overall flow characteristics and thermodynamics of the solar wind. For thirty years it has been speculated that dissipation and damping of turbulence is a heat source for the gas internal energy, and the gradient of the turbulent energy density constitutes a force on the solar wind fluid (e.g. Hollweg 1973, review in Hollweg 1978). Theoretical models incorporating these effects have been able to explain the acceleration of the solar wind, and account for its density, flow speed, and temperature in the region of space accessible to spacecraft measurement (e.g. Hollweg 1973; Hollweg 1978; Esser et al. 1986; Coles et al. 1991). However, these models are forced to invoke properties of turbulence in the heliocentric distance range $1~R_{\odot} < r < 62~R_{\odot}$ which are poorly constrained, or even totally unconstrained. Radio propagation observations provide information on the intensity and spatial power spectrum of plasma turbulence, and so provide input to theoretical models which invoke turbulence as an important agent.

1.2 Previous results from Very Long Baseline Interferometer phase scintillation measurements

In this section we describe the phenomenon of VLBI phase scintillations, and discuss results and conclusions from previous observations using this technique. A more in-depth discussion of the technical aspects of interferometer phase scintillations, utilizing the same data set used here, is in preparation.

Perhaps the most important difference between VLBI measurements and other radio propagation phenomena is that the VLBI observables are determined by irregularities with sizes of order the interferometer baseline, typically hundreds or thousands of kilometers, whereas intensity scintillations are determined by irregularities with sizes of order the Fresnel scale, which is 34 km at a fiducial frequency of 5 GHz. This is comparable to the value of approximately 30 km for the inner scale of solar wind turbulence at a heliocentric distance of $20~R_{\odot}$, as shown in Fig. 2 of Coles & Harmon (1989). Thus VLBI observations are providing information on irregularities more in the inertial subrange of the turbulence spectrum than the irregularities responsible for intensity scintillations.

The phenomenon of interferometer phase scintillations is described in pictorial form in Fig. 1.

 \begin{figure} \par\includegraphics[width=8.3cm,clip]{H2981F1.PS} \end{figure} Figure 1: Cartoon illustration of the principle of phase scintillations. Different radio refractive indices along the lines of sight to the two antennas cause a stochastic perturbation to be introduced in the interferometer phase. The moving solar wind causes this phase perturbation to vary with time. Parameters introduced in the text are graphically defined.
Open with DEXTER

A compact extragalactic radio source is used as a generator of radio waves far behind the corona and solar wind. The radio waves propagate through the solar wind, reaching a point of closest approach to the Sun (hereafter termed the impact parameter) at a radial distance R0 from the center of the Sun. The radio waves are then received on Earth at two antennas which are elements of a radio interferometer. These antennas are separated by a distance (termed the baseline) $\vec{P}$. The projection of the baseline on the plane of the sky is described by a vector $\vec{\rho}$. The component of the baseline in the radial direction, i.e. in the direction of the solar wind flow, is $\rho_{\parallel}$. The component perpendicular to the radial direction and the mean solar wind flow is $\rho_{\perp}$. In a radio interferometer the signals from the two antennas are correlated, producing a measurement of the complex visibility. If such an interferometer views a source far from the Sun, or if turbulence were absent from the solar wind, the interferometer amplitude and phase would be constant or slowly varying in time, except for the presence of radiometer noise. However, when the lines of sight from the radio source to the antennas pass through the turbulent solar wind, random phase variations are introduced due to turbulent fluctuations in the radio refractive index.

In this section, basic facts and definitions related to phase scintillations are introduced to permit description of previous results as well as those of the present paper. Radio propagation phenomena are interpreted in terms of the spatial power spectrum of density fluctuations in the solar wind plasma, $P_{n} ( \vec{q} )$, where $\vec{q}$ is the spatial wavenumber of the density fluctuations. The simplest and most commonly adopted model for this power spectrum is a power law which depends only on the magnitude of $\vec{q}$, i.e.

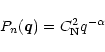\begin{displaymath}P_{n} ( \vec{q} ) = C_{\rm N}^2 q^{- \alpha} \end{displaymath} (1)

in the wavenumber range $\frac{2 \pi}{l_{\rm o}} < q < \frac{2 \pi}{l_{\rm i}}$ , i.e. between the wavenumbers corresponding to the outer scale $l_{\rm o}$ and the inner or smallest scale $l_{\rm i}$. Equation (1) also defines the coefficient $C_{\rm N}^2$, which is prominently featured in the scientific results of this paper. The parameter $C_{\rm N}^2$ determines the level of the density fluctuations, and can be loosely referred to as the "intensity of the turbulence''. It is directly related to the electron density variance (a consequence of the fact that the integral of the power spectrum equals the variance) by

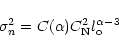\begin{displaymath}\sigma_n^2 = C(\alpha) C_{\rm N}^2 l_{\rm o}^{\alpha -3} \end{displaymath} (2)

where $l_{\rm o}$ is the outer scale to the turbulence, and $C(\alpha)$ is a numerical coefficient of order unity. For the case of a Kolmogorov spectrum in which $\alpha = 11/3$, $C(11/3) = \frac{6}{2^{2/3}}\pi^{1/3}$. Equation (2) then becomes

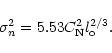\begin{displaymath}\sigma_n^2 = 5.53 C_{\rm N}^2 l_{\rm o}^{2/3}. \end{displaymath} (3)

Equations (2) and (3) show that since $C_{\rm N}^2$ is directly proportional to $\sigma_n^2$, it should have a strong dependence on heliocentric distance r, as well as heliographic longitude and latitude. Determination of the heliocentric distance dependence of $C_{\rm N}^2$ has been a major goal of this program of research.

Spangler & Sakurai (1995) and Spangler et al. (1996) found that $C_{\rm N}^2(r)$ could be modeled as

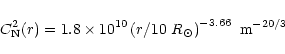\begin{displaymath}C_{\rm N}^2(r) = 1.8 \times 10^{10} \left( r/10~R_{\odot} \right)^{-3.66} \mbox{ m}^{-20/3} \end{displaymath} (4)

over the heliocentric distance range $10 {-} 60~R_{\odot}$. The form given in Eq. (4) is from Spangler et al. (1996), and corrects a factor of two arithmetic error in the value of the leading coefficient reported by Spangler & Sakurai (1995)[*]. As noted by Spangler & Sakurai (1995), Eq. (4) is in agreement with in-situ measurements made by the Helios spacecraft at $r > 62~R_{\odot}$. This expression appears to be valid for lines of sight which are dominated by dense, slow speed solar wind. Lines of sight which primarily pass through coronal holes and the high speed solar wind will have reduced radio wave scattering and a lower inferred value for  $C_{\rm N}^2$. In addition, observationally-obtained values for  $C_{\rm N}^2$ show a factor of three dispersion above and below the relationship given by Eq. (4) (Spangler et al. 1996).

Relation (4) is of interest in that it provides information on the intensity and (to the extent that Eq. (1) is found adequate) spatial power spectrum of turbulence in a part of the solar wind which lacks direct measurements. Spangler & Sakurai (1995) discuss the possibility that density fluctuations can be used as a proxy for magnetic field fluctuations in the heliocentric distance range $ r \leq 62~R_{\odot}$. If the amplitude of the density fluctuations is proportional to the amplitude of the magnetic field fluctuations (a proposition we consider plausible, but by no means firmly established), then (4) is consistent with a WKB (Wentzel-Kramers-Brillouin) law, as argued by Roberts (1989). Roberts used this result to contend that the turbulent energy density in the inner solar wind and corona is dynamically and thermodynamically insignificant, and therefore incapable of producing the high temperature and flow speed of the solar wind. These comments obviously cannot be used as an argument against efficient dissipation of turbulence, and associated heating and acceleration of the solar wind, within a few solar radii of the Sun. Such regions are interior to those probed by our radio propagation techniques.

The purpose of this paper is to present new and improved VLBI phase scintillation observations of solar wind turbulence. Observations were made of six compact radio sources on September 24 and 25, and October 15, 1998. The impact parameters for five sources were in the heliocentric distance range 16.5 to 25.3 $R_{\odot }$. The impact parameter for the sixth source was $62.7~R_{\odot}$, much further out in the solar wind, and at a heliocentric distance at which one can make the comparison between remote sensing and in-situ measurements. The outline of this paper is as follows. Section 2 discusses the observational details and the processing of the data. This section also presents the model which was fit to the phase power spectra. Section 3 presents the main observational results. In Sect. 4 we discuss the implications of those observations for the properties of solar wind turbulence in the inner solar wind, and the bulk properties of the solar wind. Section 5 summarizes and concludes.

2 Observations and data reduction

2.1 Details of observations

Table 1 contains a synopsis of the principal features of the observations. Observations were carried out on September 24, September 25, and October 15, 1998. The observations utilized the Medicina and Noto antennas of the Istituto di Radioastronomia, the Matera (Italy) antenna of the Agenzia Spaziale Italiana, and the Wettzell (Germany) antenna of the Bundesamt für Kartographie und Geodäsie. The diameter of the Medicina and Noto antennas is 32 meters; the Matera and Wetzell antennas have diameters of 22 meters. System temperatures were in the range 40 K-70 K for the frequencies and systems employed, and the Mark III VLBI recording system was used.

 
Table 1: Parameters of observing session.

Observational Parameter		 Value    

Date of Obs.		 24 September 1998 25 September 1998 15 October 1998
Duration of Session 7 $\hbox{$.\!\!^{\rm h}$ }$5-13$^{\rm h}$ UT 7 $\hbox{$.\!\!^{\rm h}$ }$5-16 $\hbox{$.\!\!^{\rm h}$ }$5 7$^{\rm h}$-16$^{\rm h}$
Stations Medicina, Wettzell, Matera Medicina, Noto Medicina, Noto, Matera
Range of baselines 340-970 km 640-900 km 220-850 km
Freq. of Observation 8.380 (X), 2.257 (S) GHz 4.981 (C) GHz 8.380, 2.257 GHz
Rec. Bandwidth 16 MHz (X), 12 MHz (S) 14 MHz 16 (X), 12 (S) MHz
Program Sources 3C273, 1055+018 3C273, 1148-001 1334-127 3C279
Number 13-min scans 13, 3 10, 4 11, 5
Source impact parameters 25.2, 62.4 $R_{\odot }$ 22.6, 16.5 $R_{\odot }$ 22.5, 25.3 $R_{\odot }$


The basic observational unit was a scan of thirteen minutes duration. The number of such scans for each source is listed in Table 1. For the most part, observations were conducted at antenna elevation angles in excess of 20$^{\circ}$. This restriction is important because atmospheric sources of phase fluctuations, and in particular tropospheric variations, are an important noise source in our observations. The data tapes were correlated at the processor of the Max-Planck-Institut für Radioastronomie in Bonn. Following processing, the data were fit for fringes and the fringes were "stopped''. This means that the visibility rotation due to residual antenna baseline uncertainties, atmospheric model errors, etc were removed. The fringe fitting time was three minutes, meaning that phase variations on longer timescales are filtered out. Shorter timescale variations, including the interplanetary scintillation (IPS) fluctuations of interest to us, are not filtered by this process.

The net output of the correlation and fringe fitting process was time series of fringe amplitude and fringe phase on each baseline for each scan. The coherent integration time for each data point was 2.0 s. The phase time series consisted of a measurement every two seconds for the scan duration of 13 min. For purposes of illustration, we show in Fig. 2 the X band phase time series on the Medicina-Noto baseline, while observing 1334-127 from 11:24 to 11:37 UT on October 15, 1998. The phase shows variations on all time scales from the sampling time to tens of seconds. Reference sources did not show such variations. Qualitatively and roughly, the intensity of turbulence along the line of sight determines the amplitude of the phase scintillations. The solar wind speed governs the rapidity of those fluctuations.

2.2 VLBI phase scintillations: the physical content of the phase power spectrum

In the present paper, the primary observable will be the interferometer phase power spectrum. Given a phase time series such as that shown in Fig. 2, $\phi(t)$, we can calculate the power spectrum $P_{\phi}(f) = \vert\tilde{\phi}\vert^2$, where $\tilde{\phi}(f)$ is the Fourier transform of $\phi(t)$. When corrected for a number of instrumental effects (see below), this measured spectrum can be fit to a theoretical expression for the phase power spectrum. We have utilized the theory of Mutel (1975), which is valid in the case of weak scintillations, i.e. the intensity modulation index being much less than unity.

The density power spectrum modeled in Mutel's theory is a generalization of (1) to describe a rollover at low wavenumbers comparable to the outer scale $l_{\rm o}$, and dissipative truncation of the spectrum at small scales comparable to the inner scale $l_{\rm i}$,

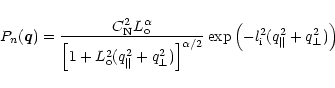\begin{displaymath}P_n(\vec{q}) = \frac{C_{\rm N}^2 L_{\rm o}^{\alpha}}{\left[ 1... ...p \left( -l_{\rm i}^2 (q_{\parallel}^2 + q_{\perp}^2 ) \right) \end{displaymath} (5)

with $L_{\rm o} \equiv l_{\rm o}/2 \pi$. In Eq. (5) the components of the spatial wavenumber of the density fluctuations $(q_{\parallel},q_{\perp})$ are defined such that parallel is along the radial direction from the Sun, which is assumed to be the same direction as the solar wind flow.

Given the spatial power spectrum of density, (5), one can derive the following expression for the phase power spectrum as a function of audio frequency f from the expression in Mutel (1975).

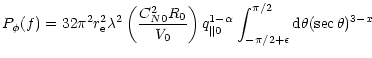$\displaystyle P_{\phi}(f) = 32 \pi^2 r_{\rm e}^2 \lambda^2 \left( \frac{C_{N0}^... ... - \alpha} \int^{\pi/2}_{- \pi/2 + \epsilon} {\rm d} \theta (\sec \theta)^{3-x}$      
$\displaystyle \times \int^{\infty}_{0} \frac{{\rm d}Q}{(\sec^2 \theta + Q^2)^{\... ...left[ \beta (\sec \theta b_{\parallel} +Q b_{\perp} ) \right] R(\vec{q},\theta)$        (6)

with
$\displaystyle R(\vec{q}, \theta) \equiv \cos^2 \left( \frac{q_{\parallel 0}^2 l... ...n \theta -1)\right) \exp [-l_{\rm i}^2 q_{\parallel 0}^2 (\sec^2 \theta +Q^2)].$     (7)

The expression is obtained by integrating through a spherically-diverging solar wind in which $C_{\rm N}^2 \propto r^{-x}$, and in which parcels of plasma have a reduced component of velocity perpendicular to the line of sight, $V_{0} \cos \theta$. The angle $\theta$ is defined as being between the direction from the Sun to the impact parameter, and that from the Sun to a given point along the line of sight (see Fig. 1). It serves as an alternate variable for position along the line of sight. We assume that the radial component of the solar wind velocity is constant throughout the region of interest, and noted by V0. As will be discussed in Sect. 4.2 and as may be seen in Fig. 6, this is a reasonable approximation.
 \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2981F2.PS} \end{figure} Figure 2: Interferometer phase fluctuations due to the solar wind. The baseline is Medicina-Noto, and the observing frequency is 8.380 GHz. The source being observed is 1334-127 on October 15, 1998. Each data point represents a 2 s integrated measurement of the interferometer phase. Sources far from the Sun show much smaller and slower phase fluctuations.
Open with DEXTER

The level of the spectrum is largely determined by  $C_{\rm N0}^2$, which is the value of $C_{\rm N}^2$ at a heliocentric distance equal to the impact parameter R0. The solar elongation of the source at the time of the observation is $\epsilon$, an angle which was between 4 and 7 degrees for most of our sources. The second variable of integration Q describes integration over wavenumber, with Q defined as $q_{\perp} = q_{\parallel 0} Q$, with $q_{\parallel 0} \equiv \frac{2 \pi f}{V_0}$. The quantity $\beta \equiv 10^6 q_{\parallel 0} \lambda/2$, where $\lambda$ is the wavelength of observation. The perpendicular and parallel components of the interferometer baseline are given by  $b_{\perp} \mbox{ and } b_{\parallel}$, respectively, and are in units of $10^6 \lambda$. Other variables appearing in Eqs. (6) and (7) are l, the distance from the observer to the point of closest approach to the Sun (very nearly 1 astronomical unit), $r_{\rm e}$, the classical electron radius, and $k=\frac{2 \pi}{\lambda}$, the wavenumber of the radio wave. Physically, the terms described by the function $R(\vec{q}, \theta)$ correspond to Fresnel filtering and truncation of the density power spectrum near the ion inertial scale. In the analysis of this paper, we will adopt a value of x=4 to describe the heliocentric distance dependence of $C_{\rm N}^2$.

It might appear from Eq. (6) that the level of the measured power spectrum is sensitive only to the ratio CN02/V0, or that retrieved values of CN02 and V0 would be highly correlated. However, a more complex dependence on V0 is introduced through the parameter $q_{\parallel 0}$. Thus the correlation between CN02 and V0 is much less than would appear through casual examination of (6), and in most cases of interest to this study, these two quantities could be retrieved independently or with slight correlation. This assertion is supported by simple analytic arguments as well as examination of $\chi^2$ spaces for the fits of (6) to the actual data. Further discussion of this matter will be given in a paper in preparation.

In Eq. (6) $C_{\rm N}^2$ is in the cgs system of units. The conversion from the conventional form of this coefficient in MKS units is given by

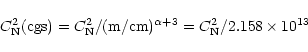\begin{displaymath}C_{\rm N}^2 (\mbox{cgs}) = C_{\rm N}^2 / (\mbox{m}/\mbox{cm})^{\alpha + 3} = C_{\rm N}^2 / 2.158 \times 10^{13} \end{displaymath} (8)

for a Kolmogorov spectrum.

2.3 Processing of phase power spectra

The power spectrum given by Eq. (6) is what would be measured by an ideal instrument. The available power spectrum is from a time series with a two second sampling and integration period, a total record length of 780 s, imposed distortions resulting from propagation through the Earth's atmosphere, and radiometer noise. A number of corrections were made to the measured phase power spectra before a fit of Eq. (6) was carried out. A detailed discussion of the processing of the power spectra will be presented in a paper in preparation. For the present, we note that the raw phase power spectra were corrected for the effects of radiometer noise, aliasing, the two second integration time, and tropospheric phase fluctuations. Estimates for these corrections were applied to the observed spectra before fitting Eq. (6).

Radiometer noise adds a white noise term which is readily calculated and verified in the observations. The effect of tropospheric phase fluctuations was estimated by interfeafing observations of control sources with the program sources. The control sources were compact radio sources in roughly the same part of the sky as the program sources, but sufficiently far from the Sun that coronal propagation effects were negligible. These control sources were observed and processed in the same way as the program sources, and a simple parameterized model was fit to their phase power spectra. The noise terms corresponding to radiometer noise and tropospheric fluctuations were subtracted from the raw spectra (i.e. such as obtained from the time series in Fig. 2), yielding an intermediate spectrum which still possessed the effects of aliasing and the two second integration time.

The correction for these latter two effects is problematical because the aliasing term is determined by the spectrum of the IPS process itself. The following describes the procedure employed in this paper. A portion of the intermediate spectrum was chosen which was at a relatively high frequency, but not so high that it was affected by aliasing and temporal averaging. A power law model was fit to this portion of the spectrum. The typical frequency interval employed in this model fitting was 0.05 to 0.15 Hertz. This model was used to estimate the spectrum above the Nyquist frequency (taking into account the effect of temporal averaging), and thus the error due to aliasing. This estimate of the error due to aliasing was subtracted from the measured spectrum. The spectrum resulting from this penultimate step was finally corrected for the two second averaging time, yielding the final, corrected spectrum which was fit to (6).

For the scans with high signal-to-noise ratio, it was found that the corrections due to aliasing and temporal integration were small and did not produce significant changes in the shape of the spectra. In the cases of scans in which phase fluctuations were weak compared to noise terms, an abbreviated version of the corrections was undertaken, in which the corrections for aliasing and integration time were omitted.

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2981F3.PS} \end{figure} Figure 3: Power spectrum of phase fluctuations such as those shown in Fig. 2. The data are again from the Medicina-Noto baseline at a frequency of 8.380 GHz. The solid line represents a fit of the theoretical expression (6) to the power spectrum. The model spectrum is defined by $R_{\rm CN} = 3.90~\mbox{ and } V_0 = 300$ kms-1. The solid triangles connected by a dotted line indicate the range of frequencies over which the model expression (6) was fit to the data, and for which this expression should be an accurate description of the power spectrum. The components of the baseline for this observation were 752 km in the parallel direction, and 9.0 km in the perpendicular direction.
Open with DEXTER

In addition to the effects described immediately above, estimates were made of the effect of the finite fringe fitting interval of 3 min and the process of "fringe stopping'' during the three minute interval. These latter two effects were found to be innocuous at frequencies $\geq 0.010$ Hz. Fits of Eq. (6) to the data were restricted to the part of the spectrum above 0.010 Hz.

Of the corrections made to the measured power spectra, the most uncertain is that due to tropospheric effects. In practice, we lumped all interferometer phase variations in the absence of the corona, and not attributable to radiometer noise, in this category. Although propagation effects through the neutral atmosphere are well-known to be present at the levels measured, there are other possible contributory culprits such as ionospheric effects (presumably small at these relatively high frequencies) and unidentified instrumental and electronics problems. Whatever their source, the tropospheric phase fluctuations were smaller and had different power spectra than those of the program sources viewed through the inner solar wind. This was invariably the case for the measurements of highest confidence. In some cases, on short baselines affected by tropospheric activity or instrumental problems, the tropospheric spectrum became comparable to the spectrum of the program source. In those cases, a statistically satisfactory fit of Eq. (6) to the spectrum was not possible, and those scans were not considered in subsequent analysis and interpretation.

2.4 Properties of the spectra and model fits

Figure 3 shows an observed power spectrum, corrected as described in Sect. 2.3, with a superposed, best fit spectrum of the form given by Eq. (6). The spectrum shown in Fig. 3 has had the effects of radiometer noise and tropospheric fluctuations removed. For purposes of reference, the raw spectrum reached a peak power spectral density of 12400 deg2/Hz at 0.010 Hz. By comparison, the power spectral density due to tropospheric fluctuations and radiometer noise at this time was estimated to be 1550 deg2/Hz (below about 7 mHz), and declined to about 100 deg2/Hz at the Nyquist frequency. For the fit to the spectrum in Fig. 3, the value of $C_{\rm N}^2$ at the impact parameter is parameterized by the ratio $R_{\rm CN}$, which is the ratio of $C_{\rm N}^2$ to that of the model expression (4), i.e. $R_{\rm CN} = \frac{C_{\rm N0}^2}{C_{\rm N0}^2(\rm model)}$, where $C_{\rm N0}^2(\rm model)$ is given in Eq. (4). In the case of the model spectrum shown in Fig. 3, $R_{\rm CN}=3.90$ and the effective solar wind speed V0= 300 kms-1. The fit is consistent with the data, and the retrieved values are in agreement with independent measurements.

Model spectra given by Eq. (6) were fit to the corrected power spectra by a least-squares grid search in the two parameters $R_{\rm CN}$ (effectively $C_{\rm N0}^2$) and V0. The errors shown in Fig. 3 and elsewhere were calculated via standard formulas (e.g. Blackman & Tukey 1958; Sentman 1974). The fits were carried out over a restricted frequency range of the power spectrum. The default spectral ranges for fitting were 0.010 to 0.150 Hz at X band and C band, and 0.030 to 0.20 Hz at S band. The fit interval at S band was restricted to higher audio frequencies because the data were more susceptible to $2 \pi$ ambiguities (see Spangler & Sakurai 1995 for discussion) which can distort the spectrum at the low frequencies $\simeq0.010$ Hz.

A fit was attempted of the power spectrum for each scan, or average of two consecutive spectra in most cases of back-to-back scans. A scan is here defined as a thirteen minute observation on a given baseline. To exemplify the results of this analysis, we discuss 1334-127 on October 15, 1998, which is one of the best observed sources. A total of 34 time series were analysed at X band, each time series resulting from a scan on a given baseline. The power spectra for some of the scans were averaged with a temporally-adjacent scan to give a total set of 21 power spectra analysed. At S band, 19 time series were analysed. Averaging of the S band power spectra from adjacent scans left 13 power spectra to be analysed. We thus had 34 power spectra from both bands to analyse for this source. Statistically acceptable fits of Eq. (6) were obtained for 12 of the X band spectra, and all 13 of the S band spectra. A successful fit was required to have a reduced $\chi^2 \leq 1.45$ for some combination of values of $R_{\rm CN} \mbox{ and } V_0$. An example of a successful fit on the Medicina-Noto baseline is shown in Fig. 3.

A few comments should be made as to probable reasons for the failure to obtain acceptable fits for some scans. We were unable to obtain acceptable fits for any of the X band spectra for 1334-127 on the Matera-Noto baseline. Visual inspections of the spectra showed that the corrected spectra were too steep for plausible model spectra, even with implausibly low solar wind speeds of 100-150 kms-1. These baselines tended to be relatively short (i.e. $\vert\rho\vert \sim 300 $ km), so they may be sensitive to turbulence in the dissipation range of the solar wind density power spectrum, which is known to depart from a pure power law (see Coles & Harmon 1989). In this case, Eq. (6) is not a good model for the phase power spectrum. The first two spectra from the Medicina-Matera baseline for 1334-127 were also impossible to fit; since these scans had projected baselines less than 300 km, they could also have been measuring turbulence in the dissipation range. We feel a more likely explanation for the failed fits is that the tropospheric correction was significant on these baselines, and uncertainty in the tropospheric model could produce a distorted spectrum which was poorly fit by Eq. (6). By contrast, the Medicina-Noto baselines had less problematical tropospheric characteristics, and the longer baselines produced larger solar wind fluctuations. Similar comments apply to some of the scans for the remaining sources.

The parameters $(R_{\rm CN},V_0)$ of the fits to the 1334-127 spectra are shown in Fig. 4.

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2981F4.PS} \end{figure} Figure 4: Values of $R_{\rm CN}$ and V0 (defined in text) retrieved from power spectra in the observations of 1334-127 on October 15, 1998. Although there is scatter in the measurements, well-defined mean values are readily discernible. Solid symbols represent measurements at X band (8.380 GHz) and open symbols represent data at S band (2.257 GHz). Different symbols are defined in the text.
Open with DEXTER

Each symbol corresponds to a spectrum which was successfully fit. Solid symbols represent X band spectra, while open symbols represent those at S band. Circles (filled and open) represent the best data, while those represented by other symbols are of lower fidelity. Stars represent symbols from the first three scans, which occurred when the source was below 20 degrees of elevation at one of the stations, so there are grounds for being concerned about tropospheric contamination. In support of this conjecture is the fact that the values of $R_{\rm CN}$ from X and S band for the first scan are not in agreement within a single standard deviation. Square symbols represent those scans for which the projected baseline $\vert\rho\vert < 300 $ km, and the measurement may be affected by fluctuations in the dissipation range.

The values for $R_{\rm CN}$ were averaged for all baselines which were longer than 300 km and were not from the first three scans of the session, i.e. all those represented by circular symbols in Fig. 4. The result was $\bar{R}_{\rm CN} = 2.89 \pm 0.16$ for the source 1334-127. The reader is reminded that $R_{\rm CN}=1.0$ would indicate perfect agreement with the model expression of Eq. (4). Since this description of the heliocentric-distance-dependence of $C_{\rm N}^2$ was considered to contain a factor of three variation above and below the best-fit curve (Spangler et al. 1996), our result can be considered consistent with (4).

With regard to the solar wind velocity, it can be seen from Fig. 4 that any individual measurement has a large associated error. This reflects the fact that a large range of solar wind speeds were statistically compatible with the data, whereas the fits were less tolerant of variations in $R_{\rm CN}$. Nonetheless, this plot shows that an average over the measurements leads to a more localized value for the solar wind speed. In calculating a mean value for V0, we used only X band data. This policy was due to the greater susceptibility of S band data to spectral flattening due to phase fluctuations exceeding the interval $(\pi, -\pi)$. The mean value of the speed $\bar{V_0} = 340 \pm 50$ kms-1 for 1334-127.

 
Table 2: Solar wind characteristics.

Parameter		 1148-001 3C273 (9-25) 3C273 (9-24) 1334-127 3C279 1055+018

RCN		 $3.01 \pm 0.76$ $2.45 \pm 0.58$ $2.61 \pm 0.26$ $2.89 \pm 0.16$ $2.97 \pm 0.52$ $1.68 \pm 0.35 $
V0 $188 \pm 50$ $275 \pm 50$ $266 \pm 50$ $340 \pm 50$ $188 \pm 50$ $480 \pm 200 $


3 Observational results

In this section we present our main observational results on the characteristics of solar wind turbulence. The data to be utilized are presented in Table 2, which gives the derived value of $R_{\rm CN}$ and V0 for each source.

3.1 Heliocentric distance dependence of the intensity of turbulence

The values of the parameter $R_{\rm CN}$ in Table 2, together with the model expression (4) for the heliocentric distance dependence of $C_{\rm N}^2$, allow us to compare our measurements of $C_{\rm N0}^2$ with previous ones. This is done in Fig. 5. With the exception of the solid star symbols, which represent the new measurements presented in this paper, this plot is identical to Fig. 1 of Spangler et al. (1996). Open circular data points represent radio propagation measurements and open triangles represent in-situ measurements by the spacecraft Helios.

From Fig. 5 we see that the new measurements in the range $16 {-} 26~R_{\odot}$ are consistently high relative to our previously-published model for $C_{\rm N}^2$ as a function of r. The measurement at $62~R_{\odot}$ is consistent with the previously reported relation. In Spangler et al. (1996) it was noted that there was a scatter of the observed points about the least-squares fit relationship by about a factor of three (above and below best-fit line). This scatter is indicated by the dashed lines that flank the solid line representing Eq. (4). The new points cluster near the upper limit, and are therefore not inconsistent with Eq. (4).

There are at least two possible explanations for the tendency of our new measurements to lie above the relationship (4) determined by the previous measurements reported in Spangler & Sakurai (1995) and Spangler et al. (1996).

1.
The techniques used in Spangler & Sakurai (1995) to retrieve the path integral of $C_{\rm N}^2$ and thereby values for $C_{\rm N0}^2$ differed from those used here. The methods used to process the phase scintillation data are described in detail in Sect. 2.3 of that paper. The difference in approach raises the possibility of a systematic bias which would cause values of $C_{\rm N}^2$ retrieved using the present techniques to be overestimates relative to the measurements of Spangler & Sakurai (1995). To fully assess this possibility would require an extensive analysis which is probably not worth the effort in view of the superiority of the analysis method reported in the present paper. However the following limited investigation was undertaken.
 \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2981F5.PS} \end{figure} Figure 5: Values of parameter $C_{\rm N}^2$ as a function of heliocentric distance. Open symbols are from Spangler et al. (1996). All are due to VLBI measurements with the exception of the triangles beyond 60 $R_{\odot }$, which represent direct spacecraft measurements. Solid stars represent new measurements reported in this paper. Two of the plotted points in the heliocentric distance range 20-30 $R_{\odot }$ have been adjusted downward by 20% in this figure to show that they are distinct from two other measurements. Errors are plotted for all five new measurements, but are comparable in size to the plot symbols.
Open with DEXTER

All X band power spectra for 1334-127 that yielded a value for $C_{\rm N0}^2 \mbox{ and } V_0$ were processed in the same manner as described in Spangler & Sakurai (1995) to yield a value for $C_{\rm N0}^2$. Specifically, the filtered variance method was used, with an adopted value of the R parameter of 2. The values for $C_{\rm N}^2$ so determined were in all cases less than the values emergent from the analysis described here. The mean value for the ratio of these latter values for $C_{\rm N}^2$ to those given in this paper was 0.56, with a relatively small dispersion. A similar result was obtained by comparing model power spectra described by Eq. (6) (and utilizing the published value for $C_{\rm N0}^2$) with the measured power spectra for the source 0735+178 observed on July 22, 1991. These exercises indicate that reduction to a common scale for  $C_{\rm N}^2$ would probably cause a slight downward adjustment of the current $C_{\rm N}^2$ values, and make them more consistent with those previously reported. However, by the same token it does not seem to be the case that data reduction bias is responsible for all of the difference between our measurements and the a priori model for $C_{\rm N}^2(r)$, Eq. (4). It should be noted that the measurement for the most distant source is consistent with the best-fit relation (4).

2.
The solar wind is obviously a variable medium on all spatial and temporal scales, and the content of Fig. 5 indicates that the lines of sight investigated in the present paper traversed denser or more turbulent parts of the solar wind than the average of the observations reported in 1996. In the autumn of 1998 the Sun was rising towards solar maximum, with a sunspot number over halfway between the value at solar minimum and the maximum of solar cycle 23 at the end of 2000. Under these circumstances, slow wind would probably dominate all the lines of sight discussed here. It was noted in Spangler & Sakurai (1995) and Spangler et al. (1996) that the bulk of radio wave scattering occurs in the slow solar wind. The same conclusion was reached independently by Pätzold et al. (1996) and Pätzold et al. (1997). The measurements reported in Spangler & Sakurai (1995) and Spangler et al. (1996) were from the period September 1989 to November 1992, and corresponded to the maximum phase of cycle 22. Based on this, we expect solar maximum conditions to be valid for both sets of observations.

In addition, for October 15, 1998, LASCO C3 coronagraph observations were available, and the C3 field of view contained both 1334-127 and 3C279. This coronagraph observation showed that the part of the sky interior to 30 $R_{\odot }$ was dominated by two streamers on opposite sides of the Sun, which were visible to the edge of the C3 field. Each of these streamers was roughly 50-60 degrees in angular width. Both 1334-127 and 3C279 were viewed through one of these streamers. The former source was offset from the brightest part of the streamer, but definitely in a region of enhanced scattered light, while 3C279 was on the axis of the other streamer, and beyond the brightest portion. This registration of our sources with the coronagraph images therefore corroborates our suggestion that the lines of sight to these two sources traversed, and were probably dominated by, slow speed solar wind.

In summary, it appears that the differences between the new values of $C_{\rm N}^2$ and Eq. (4) can be partially attributed to differences in data reduction approaches (less than a factor of 2) and partially to enhanced density or level of turbulence along some of the lines of sight analysed here (between 50 percent and a factor of 2).

3.2 Solar wind speed in the region 16 R ${_{\odot } \leq r \leq 26}$ R ${_{\odot }}$

The solar wind speed measurements reported here have substantial errors, but are still of considerable interest because existing evidence indicates that the slow solar wind is still accelerating in this part of space (Schwenn et al. 1981; Sheeley et al. 1997). Our speed measurements are shown as a function of heliocentric distance in Fig. 6. Although there is considerable scatter in these observations, and they do not of themselves show a discernible trend with heliocentric distance, these measurements support the contention that there is further acceleration of the slow wind outside of $25~R_{\odot}$. The wind speeds range from 188 to 340 kms-1, significantly below the typical slow solar wind at 1 AU. The solar wind is still picking up speed in the part of space probed by our measurements. The curves plotted with the data in Fig. 6 are described in Sect. 4.2.

 \begin{figure} \par\includegraphics[width=8.8cm,clip]{H2981F6.PS} \end{figure} Figure 6: Solar wind speed as a function of heliocentric distance. Plotted points represent our measurements (see Table 2). The solid line represents speed measurements from coronagraph data as reported by Sheeley et al. (1997) and modeled by Eq. (9). The dashed line represents a speed which is the sum of the solar wind speed as measured by Sheeley et al. (1997) and the estimated Alfvén speed at that heliocentric distance. It is at this speed that the irregularities responsible for the scintillations should be moving, according to plausible models for the nature of the density turbulence. Our measurements appear to be below this irregularity propagation speed.
Open with DEXTER

4 Implications for properties of solar wind turbulence at heliocentric distances of 16-26 solar radii

In this section, we discuss the implications of the measurements reported in this paper for our understanding of the plasma physics of the solar wind.

4.1 The heliocentric distance dependence of the intensity of turbulence

Figure 5 shows that the new measurements are consistent with the relation (4) for the dependence of $C_{\rm N}^2$ on heliocentric distance, although the new measurements are at the high end of the expected values. However, as discussed in Sect. 3.1, if the new values are multiplied by an adjustment factor of 0.56 to put them on the same scale as the Spangler et al. (1996) values, the degree of corroboration is much stronger. Our present observations therefore support and contribute to the determination of a mean relation for $C_{\rm N}^2(r)$.

Spangler & Sakurai (1995) noted that this relationship contains information on the evolution of turbulence with heliocentric distance. The arguments of Spangler & Sakurai (1995) will not be repeated here; the discussion of Sect. 4.2 of that paper remains current. Briefly, it pointed out that if the magnitude of density fluctuations is linearly proportional to the amplitude of magnetic field fluctuations, then the relationship (4) indicates that the magnetic field variations follow a WKB-like evolution with heliocentric distance from $\simeq 10~R_{\odot} \mbox{ to } \simeq 60~R_{\odot}$. This was the argument made by Roberts (1989). Roberts (1989) concluded that the energy density of magnetohydrodynamic turbulence in the corona could be inferred from its value at heliocentric distances of 0.3 AU and greater. As explained by Hollweg (1978) and re-iterated by Roberts (1989), the coronal turbulence is then too weak to furnish the heat and momentum source for the solar wind.

The contribution of Spangler & Sakurai (1995), Spangler et al. (1996), and the present work, is to use density fluctuations, detectable via their VLBI phase fluctuations, as a proxy for magnetic field fluctuations. Subject to a number of qualifications, the present paper supports our earlier work, and thus the arguments of Roberts (1989). Further discussion and elaboration of this matter is given in Spangler (2002).

4.2 The solar wind speed at heliocentric distances of 18-26 solar radii

As mentioned in Sect. 1.1, the solar wind at the perihelion distance of the Helios spacecraft is nearly entirely accelerated to its asymptotic value. All but a residual amount of the acceleration, and the physical processes responsible for acceleration, therefore occur interior to 60 $R_{\odot }$ (Schwenn et al. 1981). For this reason, remote sensing measurements of the velocity profile of the solar wind in the heliocentric distance range $ 0 \rightarrow 60~R_{\odot}$ provide important experimental input to theories of solar wind acceleration. The measurements presented in this paper allow extraction of estimates of the solar wind speed and therefore assist in this regard.

Of equal interest is the fact that scintillations are due to turbulence in the solar wind, and thus provide information on the characteristics of turbulence as much as the host plasma per se. When combined with other information on the solar wind profile, measurements such as these can provide new and interesting information on the nature of the solar wind turbulence interior to $60~R_{\odot}$. Such information can be highly valuable in assessing theories of solar wind acceleration and heating. Specific illustrations of these ideas will be given in the paragraphs below.

Information on the slow solar wind speed in the heliocentric distance range probed by our radio measurements is provided by the LASCO coronagraph on SOHO. Sheeley et al. (1997) have carried out a careful analysis of these data, and have established a velocity profile of the solar wind. This profile pertains to the slow solar wind, which provides more measurable features by virtue of its higher density. A subsequent study of the same sort was carried out by Tappin et al. (1999). An examination of the plots of Sheeley et al. shows that the solar wind velocity at 25 $R_{\odot }$ is about 300 kms-1. Referring to Table 2 and Fig. 6, we see that this value, determined from coronagraph measurements, is very similar to our speed measurements in the heliocentric distance range $16 {-} 26~R_{\odot}$.

A somewhat more rigorous analysis can be undertaken as follows. Sheeley et al. (1997) fit their velocity measurements with a simple model of the form

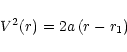\begin{displaymath}V^2(r) = 2a \left( r - r_1 \right) \end{displaymath} (9)

with V being the solar wind speed, r being the heliocentric distance, and $a \mbox{ and } r_1$ being model parameters. For the fit to velocity data shown in the middle panel of their Fig. 6, Sheeley et al. report values of $a = 3.4 \mbox{ m/s}^2$ and $r_1 = -0.4~R_{\odot}$. The velocity as a function of heliocentric distance given by Eq. (9) (which describes the motion of the density features seen in coronagraph data) may then be directly compared with our phase scintillation velocities V0. This comparison is made in Fig. 6.

In Fig. 6 the plotted symbols represent our V0 estimates from Table 2. The solid curve represents the relation (9) with the parameters described above. The dashed line is discussed below. Our phase-scintillation-derived solar wind speeds are not inconsistent with the velocity law obtained by Sheeley et al., and in fact fall slightly below that expression. An alternative method of determining solar wind speeds utilized by Sheeley et al. (which leads to the top panel of their Fig. 6) leads to somewhat lower speeds which are in even better agreement with our VLBI values. A similar conclusion was reached by Breen et al. (1999, 2000), i.e. that the speed which characterizes the density irregularities responsible for scintillations is in agreement with that determined from coronagraph observations. The technique of Breen et al. (1999, 2000) utilized cross correlation of intensity scintillations at separated antennas of the EISCAT facility, a technique developed by W.A. Coles and collaborators, and similar slow solar wind speeds could be extracted from the published papers of that group (e.g. Coles 1996).

The above comments contain our primary observational result on solar wind flow speeds, i.e. that the VLBI-deduced values are consistent with the bulk solar wind flow speeds as deduced from coronagraph data. In the remainder of this section we wish to briefly discuss a more speculative matter which is suggested by the data. The crux of this matter is that one actually expects a difference between the coronagraph and radio scintillation velocity measurements, not complete accord. The expectation is that the radio-determined speed V0 will exceed the speed determined from coronagraph measurements by an amount which is of the order of the local Alfvén speed. The reason for this and its quantitative elaboration is stated in the following paragraphs.

The structures studied by Sheeley et al. (1997) must have scales of several tenths of a solar radius to a solar radius or more in size. As such, they can be described as large scale gradients in the solar wind and may be considered part of the structure of the solar wind. It is difficult to think of these features as waves. The scale size of the irregularities measured with radio wave scintillations is orders of magnitude less. As mentioned in Sect. 1.2, the irregularities which make the dominant contribution to VLBI phase scintillations have spatial scales of the order of the interferometer baseline, which is hundreds of kilometers in the case of the present experiments. In the case of the intensity scintillations measured by Coles et al. (1991), Grall et al. (1997), and Breen et al. (1999, 2000), the scale size is even smaller, being the Fresnel scale at a frequency of 900 MHz, i.e. 90 km. The fluctuations responsible for radio propagation phenomena can therefore be accurately described as small-scale turbulence, and these turbulent fluctuations should move with respect to the fluid in which they are embedded.

There are two theoretical models for the nature of solar wind turbulence, and both have substantial observational support. It must be stressed that these models have been directed to the magnetic and velocity fluctuations in the solar wind, which contain most of the turbulent energy, rather than the density fluctuations which are so important to radio observers. In what follows we will assume that the density fluctuations are slaved to the magnetic and velocity fluctuations via the equations of magnetohydrodynamics, so that the density fluctuations share the statistical properties of the magnetic and velocity fluctuations. The first of the theoretical models envisions the solar wind turbulence as comprised of Alfvén waves. These waves would then propagate along the large scale magnetic field at the Alfvén speed. If the density fluctuations are associated with these waves, they should also propagate with respect to the solar wind plasma at the Alfvén speed.

The second common model for solar wind turbulence is based on the equations of reduced magnetohydrodynamics. Discussions of the viability of reduced magnetohydrodynamics as a model for solar wind turbulence have been made by Matthaeus & colleagues (e.g. Matthaeus & Ghosh 1999; Ghosh et al. 1998). A general property of the solutions of reduced MHD is the existence of strong spatial gradients across the large scale magnetic fields, and weak gradients along it. These solutions therefore differ from plane Alfvén wave solutions. However, these quasi-two dimensional structures propagate along the large scale field at the Alfvén speed. The nature of density fluctuations in such turbulence is not well understood. However, the natural and probable case is that the density perturbations propagate with respect to the background plasma at the Alfvén speed, $V_{\rm A}$. The point of the above ruminations is that for either of the best models for the physical nature of solar wind turbulence, one would expect the density irregularities to propagate with respect to the background plasma at the Alfvén speed. Thus while the coronagraph measurements of Sheeley et al. (1997) measure the bulk solar wind speed V, the scintillation measurements should refer to $V_0 = V + V_{\rm A}$. Thus the agreement of the two types of measurements is actually not expected.

To quantitatively assess the situation, we need an estimate of the Alfvén speed in the heliocentric distance range 16-26 $R_{\odot }$, where the present data pertain. We have used the expressions given in Eqs. (6) and (7) of Mancuso & Spangler (2000), which are valid for the slow solar wind. These models for the electron density and magnetic field strength match radio propagation delay and Faraday rotation measurements close to the Sun, as well as in-situ measurements at 1 AU.

The Alfvén speed computed in this way has been added to the model for the bulk solar wind speed, Eq. (9) and is plotted as the dashed line in Fig. 6. Clearly our speed measurements fall well below this curve, and suggest that density irregularities in the slow solar wind at heliocentric distances of 16-26 $R_{\odot }$ do not propagate at the Alfvén speed with respect to the solar wind plasma.

Coles (2001, and private communication) contends that a diagram such as Fig. 6 is inconclusive, and might be obtained even in the case where the irregularities are propagating at the Alfvén speed with respect to the background fluid. Coles identifies two effects that will bias the scintillations speed V0 toward the bulk flow speed V. (1) The derived speed V0 is a line-of-sight average of $V + V_{\rm A}$. As may be seen in Fig. 6, the Alfvén speed declines with heliocentric distance, while the bulk flow speed slowly approaches its asymptotic value. As a result, the measured, line-of-sight average of V0 will exceed the bulk flow speed by an amount which is less that the Alfvén speed at the impact parameter. If the amount is reduced sufficiently, it will be observationally indistinguishable from the bulk flow speed. (2) The slow speed wind is inhomogeneous in its plasma properties, and regions of higher density will make a disproportionate contribution to all scintillation observables. These higher density regions are also likely to have a lower Alfvén speed than the rest of the slow solar wind. The net effect is that the path-integrated, $C_{\rm N}^2$-weighted value of V0 may exceed the bulk flow speed by an amount which is less than the Alfvén speed model described above, and evaluated at r=R0.

We consider Coles' points as serious and plausible ones which must be thoroughly treated before one can confidently draw the conclusion that seems suggested by Fig. 6. For this reason we refrain, in the present paper, from definitely asserting that the irregularities are stationary in the solar wind frame. Nonetheless, in what follows, we present an approximate, analytic estimate of the first of the two effects, dealing with line-of-sight averaging.

In a preliminary phase of this project, the phase spectra were fit with a model spectrum which was simpler than (6), and approximated the solar wind by a slab of turbulence moving perpendicular to the line of sight with a velocity $\bar{V_0}$. This simpler model spectrum also produced excellent fits to the observed power spectra. It was obvious that $\bar{V_0}$ would underestimate the true V0 because of projection effects along the line of sight, as may be seen in Fig. 1. In correcting for this effect, we modeled $\bar{V_0}$ as the $C_{\rm N}^2(r)$-weighted value of the perpendicular (to the line of sight) component of the irregularity speed, i.e.

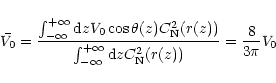\begin{displaymath}\bar{V_0} = \frac{\int^{+ \infty}_{- \infty} {\rm d}z V_0 \co... ...- \infty} {\rm d}z C_{\rm N}^2 (r(z))} = \frac{8}{3 \pi} V_0 \end{displaymath} (10)

where the last equality on the right is true when V0 is independent of heliocentric distance. The values of V0 obtained by this procedure were in excellent agreement with those presented in this paper, obtained by explicit integration of the phase power spectrum along the line of sight, thus supporting the validity of the procedure.

To estimate the effect of a line-of-sight averaged Alfvén speed, we evaluated (10) with $V_0 = V + V_{\rm A}(r)$, approximating V as constant as above, and with $V_{\rm A}(r)$ calculated from the model which produced the dashed line in Fig. 6. This permitted an analytic estimate for the upward bias in the scintillation speed due to propagating irregularities,

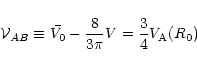\begin{displaymath}{\cal V}_{AB} \equiv \bar{V_0} - \frac{8}{3 \pi}V = \frac{3}{4}V_{\rm A}(R_0) \end{displaymath} (11)

where $V_{\rm A}(R_0)$ is the Alfvén speed at the impact parameter.

This exercise indicates that line-of-sight averaging does not substantially dilute the effect of propagating irregularities, and that irregularities propagating at the Alfvén speed with respect to the bulk solar wind would produce scintillation speeds V0 higher than measured. Nonetheless, a fully satisfactory resolution of this matter calls for explicit modeling of the line of sight. It is beyond the scope of this paper to treat point (2) raised by Coles (2001).

5 Summary and conclusions

The following results were presented in this paper.
1.
Very Long Baseline Interferometer observations at frequencies of 2.257, 4.981, 8.380 GHz were made of five compact radio sources when their lines of sight passed within $16 {-} 26~R_{\odot}$ of the Sun. An additional source was observed at 2.257 and 8.380 GHz at a greater solar elongation. Fluctuations in the interferometer phase (phase scintillations) due to the solar wind were measured, yielding information on the turbulence in the solar wind in this part of space.
2.
The measured phase power spectra are consistent with a theoretical expression for the spectrum due to Mutel 1975), thus enhancing the experimental utility of VLBI phase scintillations as a technique for solar wind and coronal plasma research.
3.
This experiment yielded new and superior measurements for the value of $C_{\rm N}^2$, the normalization coefficient of the density spatial power spectrum, as a function of heliocentric distance. The new measurements are consistent with a previously-determined relation for $C_{\rm N}^2(r)$, and thus contribute to the establishment of an empirical law for the heliocentric distance dependence of the intensity of turbulence.
4.
The phase scintillation power spectra provide estimates of the speed V0 at which the density fluctuations responsible for the phase scintillations move with respect to the antennas. The retrieved speeds are in the range of 188 to 340 kms-1 for the heliocentric distance range of 16-26 $~R_{\odot}$. These speeds are consistent with independent measurements of the flow speed V of the solar wind in this part of space. They are less than the sum of the wind speed and the local Alfvén speed, $V_0 < V + V_{\rm A}$, which would be the case if the irregularities responsible for scintillations propagate at the Alfvén speed with respect to the solar wind fluid. At the present, this result must still be considered tentative (see Sect. 4.2), but it should motivate further investigation of the matter.

Acknowledgements
This work was supported at the University of Iowa by grants ATM96-16721 and ATM99-86887 from the National Science Foundation. SRS wishes to express his sincere gratitude to the Consiglio Nazionale delle Ricerche for making possible an extended visit at Bologna in the Fall of 1998. We appreciate the thorough and insightful review by the referee of this paper, Professor William Coles.

References

 

Copyright ESO 2002