A&A 384, 568-584 (2002)
DOI: 10.1051/0004-6361:20011814

Nanodiamonds around HD 97048 and Elias 1

C. Van Kerckhoven1 - A. G. G. M Tielens2,3 - C. Waelkens1


1 - Instituut voor Sterrenkunde, K.U. Leuven, Celestijnenlaan 200B, 3001 Heverlee, Belgium
2 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen, The Netherlands
3 - SRON, PO Box 800, 9700 AV Groningen, The Netherlands

Received 5 June 2001 / Accepted 11 December 2001

Abstract
We present an analysis of ISO-SWS observations of the Herbig Ae/Be stars HD 97048 and Elias 1. Besides the well-known family of IR emission bands at 3.3, 6.2, "7.7'', 8.6 and 11.2 $\mu $m these objects show strong, peculiar emission features at 3.43 and 3.53 $\mu $m. The latter two features show pronounced substructure which is very similar in the two sources. Comparison of the spectra of HD 97048 and Elias 1 with laboratory spectra of H-terminated diamond surfaces show excellent and very convincing agreement in peak position and spectral detail (Guillois et al. 1999). The position of the 3.53 $\mu $m band indicates a temperature of $\sim$1000 K. An analysis of the radiative energy budget makes us conclude that the diamond carrier of the 3.53 $\mu $m feature has typical sizes of 1-10 nm for HD 97048. A fit of the 3.53 $\mu $m feature with a theoretical, calculated profile indicates that the emitting diamonds in HD 97048 see a FUV flux of 5.8 $\times $ 10-3 [W/cm2]. The derived diamond mass, 1.5 $\times $ 10-10 $M_{\odot}$, is only a tiny fraction of the total circumstellar dust mass and corresponds to only about 1 parts per billion relative to hydrogen. We discuss the origin of the diamond around these Herbig Ae/Be stars and conclude that most likely they are formed in situ. The implications for the nanodiamonds discovered in meteorites are also discussed.

Key words: circumstellar matter - infrared: ISM: lines and bands - ISM: general - ISM: molecules, dust - ISM: individual: HD 97048, Elias 1


1 Introduction

The spectra of the two Herbig Ae/Be stars HD 97048 and Elias 1 show, next to the well-known family of Infrared (IR) emission bands at 3.3, 6.2, "7.7'', 8.6 and 11.2 $\mu $m, attributed to Polycyclic Aromatic Hydrocarbons (PAHs), unique emission features at 3.43 and 3.53 $\mu $m (Aitken & Roche 1981; Allen et al. 1982; Baas et al. 1983; Whittet et al. 1984; Geballe et al. 1989; Geballe 1997).

The 3 $\mu $m spectra of some other PAH sources show spectral structure as well, but in these sources all features, in the 3 $\mu $m region, are dwarfed by the 3.3 $\mu $m feature and none of the emission bands falls at 3.43 and 3.53 $\mu $m. HR 4049 (Geballe et al. 1989) is the only other source showing the 3.53 $\mu $m feature next to PAH emission features. New reductions of HD 100546 and HD 142527 indicate that the (suggested) presence of a 3.53 $\mu $m feature (Waelkens et al. 1996) in these objects is rather doubtful. It has also been suggested that the spectrum of HD 52961, a post-AGB star similar to HR 4049 in various aspects, shows 3.43 and 3.53 $\mu $m bands (Oudmaijer et al. 1995), but the weakness of these bands precludes a detailed analysis.

Different origins of the 3.43 and 3.53 $\mu $m features have been proposed, all sought in C-H bonds, since the 3 $\mu $m region is the characteristic emission region for C-H stretches. At first the carriers were thought to be aldehydes frozen on ice grains (van der Zwet et al. 1985). However, the vicinity of the carriers to the central star (Roche et al. 1986) excluded this option. Later an explanation was sought in sidegroups on PAHs and overtone and combination bands of highly excited, large, dehydrogenated PAHs (Schutte et al. 1990). Finally, Guillois et al. (1999) noted the great resemblance of the emission structure in the 3 $\mu $m region with the absorption bands of hydrogenated diamonds; an identification which, because of the good match between laboratory and observed spectra, is very persuasive.

In this paper we will investigate in more detail the characteristics of the emitting diamonds and discuss the astrophysical implications. After a short description of the sources and the observations, we will have a close look at the 3 $\mu $m spectra of HD 97048 and Elias 1 and compare them with the spectra of other sources. Furthermore, we will discuss their spectral appearance in general. Moreover, we will discuss the location of the different emission components. In Sect. 6, a possible origin of the 3.43 $\mu $m and 3.53 $\mu $m features in emission by sidegroups of PAHs is shortly discussed. In Sect. 7, an overview of the characteristics of hydrogenated diamonds is given. We derive the characteristics of the observed diamonds in Sect. 8. In Sect. 9, we discuss the astrophysical implications and the connection to meteoritic diamond. In the last section, a summary of the results and conclusions is given.


  \begin{figure} \par\includegraphics[angle=90,width=12.2cm,clip]{h2907F1.ps}\end{figure} Figure 1: SWS AOT1 data of Elias 1 and HD 97048. Both Elias 1 and HD 97048 show clear "PAH'' emission at 3.3, 6.2, 7.6, 7.8 and 8.6 $\mu $m. The HI recombination lines characteristic for HAe/Be stars are also present in the two spectra. In addition Elias 1 has H2O-ice and CO2-ice in absorption and a 10 $\mu $m silicate feature in emission. The overall spectra of HD 97048 and Elias 1 are rather normal except for the 3 $\mu $m region. The 3 $\mu $m regions of HD 97048 and Elias 1 are completely dominated by features at 3.43 and 3.53 $\mu $m.
Open with DEXTER

   
2 The sources


 

 
Table 1: Source characteristics.
Source Sp.Type Association d [pc] Ref.
Elias 1 A0-A6 L1495 150 +10-10 1, 2
HD 97048 B9-A0 Cham I 180 +30-20 2, 3
HR 4049 A7   660 +140-140 4, 5
1 Haas et al. (1997) and reference therein, 2 Henning et al. (1998) and reference therein,
3 van den Ancker et al. (1998) and reference therein, 4 Lambert et al. (1988),
5 Bakker et al. (1998).


HD 97048

HD 97048 is a Herbig Ae/Be star, member of the Chameleon T association (Whittet et al. 1987). Thé et al. (1986) conclude that the IR excess of HD 97048 originates in a flattened shell structure or disk of dust particles seen pole-on. Later observations and investigations confirm this hypothesis: the invariable reddening (Davies et al. 1991) suggests that it is mostly intracloud and the unresolved SEST-image of HD 97048 taken by Henning et al. (1998) together with the measured mm-flux also point towards the presence of a flattened disk-like structure (Henning et al. 1998, 1993).

The object is extended in the mid-IR (Prusti et al. 1994) but not in the near-IR (Henning et al. 1998). The mid-IR emission is most probably due to an extended envelope consisting of transiently heated very small grains and PAHs. The object shows the peculiar 3.43 and 3.53 $\mu $m features (Baas et al. 1986), where the 3.53 $\mu $m emission is known to originate at <0.05'' from the star (Roche et al. 1986).

Elias 1

Elias 1 is an embedded young star illuminating a reflection nebula, located in the Taurus-Auriga complex (Elias 1978). The star is classified as a Herbig Ae/Be star (Thé et al. 1994). The extinction towards Elias 1 is uncertain inducing uncertainty on its spectral type, A6-A0 for AV = 3.9-8.8 (Leinert et al. 1997). A recent study of Teixeira & Emmerson (1999) gives however, a value of 10.5 for the visual extinction towards Elias 1. Next to PAH emission, silicate emission and ice absorption, the spectrum of Elias 1 shows the same 3.43 and 3.53 $\mu $m bands as HD 97048.

Elias 1 shows evidence for the presence of a disk. It is unresolved at 1.3 mm and in the mm-range (Di Francesco et al. 1997; Henning et al. 1998). Near-IR speckle interferometric observations show that the emission at J and H is resolved into a narrow east-west elongated halo while at K and L$^\prime$ a more circular symmetric, marginally resolved red structure is observed (with a radius $\leq$0.15''), interpreted as due to two lobes perpendicular to an optically thick disk (Haas et al. 1997).

HR 4049

The evolved star HR 4049 (= HD 89353) is the only source except the two HAe/Be stars Elias 1 and HD 97048, showing the 3.43 and 3.53 $\mu $m feature next to PAHs emission features (cf., Fig. 4; Geballe et al. 1989).

HR 4049 is a carbon rich post-AGB (Asymptotic Giant Branch) star with an unseen companion (Waelkens et al. 1991, 1995). The photosphere is strongly depleted in refractories and the star is surrounded by a circumbinary disk (Waters et al. 1989; Bakker et al. 1998), most probably originating from severe mass loss, experienced during the AGB phase (Parthasarathy & Pottasch 1986).

The circumstellar absorption is variable in the visual and the UV and, the variations in the UV and optical occur in phase (Monier et al. 1999). This is due to the geometry of the system. The binary system is situated in a circumbinary disk and the variable absorption is due to a variable amount of disk-dust between HR 4049 and the observer during its orbital motion (Waelkens et al. 1991; Bakker et al. 1998; Johnson et al. 1999).

   
3 The observations

We present observations taken with the Short Wavelength Spectrometer (SWS, de Graauw et al. 1996) on board the Infrared Space Observatory (ISO, Kessler et al. 1996) of HD 97048 (TDT61801318), Elias 1 (TDT67301306) and HR 4049 (TDT17100101). The spectra were taken using the AOT1 scanning mode at low (4), medium (3) and high (2) speed respectively. The data were processed using ESA's interactive analysis product; IA (de Graauw et al. 1996), using calibration files and procedures equivalent with pipeline version 7.0. Further data processing consisted of bad data removal, flatfielding, rebinning with a constant resolution and splicing the subbands to form a continuous spectrum. Up and down scans were reduced separately to check the reliability of the spectra. The resulting 2.5-14 $\mu $m spectra are shown in Fig. 1.

In addition we use a ground-based spectrum of Elias 1 (Geballe 1997) for comparison with HD 97048 around 3 $\mu $m. To construct the spectral energy distribution of HD 97048 we use the International Ultraviolet Explorer (IUE) archive spectra, LWP04906LL and SWP24590LL, for the UV. The optical data of HD 97048 are taken from Malfait et al. (1998) (and references therein). The 1.3 mm flux is taken from Henning et al. (1998) and for the FIR we use the ISO-LWS (Long Wavelength Spectrometer) spectrum (TDT26101305). For the IR spectral energy distribution of Elias 1, we use (sub)millimeter measurements of Mannings (1994) and Henning et al. (1998).

We compare the 3 $\mu $m spectra of our sources with the near-IR spectra of IRAS 05341+0852 (Joblin et al. 1996) and IRAS 21282+5050 (Geballe et al. 1994).

   
4 Spectral analysis


  \begin{figure} \par\includegraphics[angle=90,width=8.4cm,clip]{h2907F2.ps}\end{figure} Figure 2: The spectral energy distribution of HD 97048, corrected for extinction (see text for details), is compared with a Kurucz (1993) model atmosphere ( $T_{\rm eff}$=10000, $\log(g)$ = 4). The structure around 30 $\mu $m is not real and due to the difficult calibration of band 4 (29-45 $\mu $m).
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,height=8.5cm,width=8.5cm,clip]{h2907F3.ps}\end{figure} Figure 3: The spectral energy distribution of Elias 1 and HD 97048 from IR to millimeter. Next to the ISO data we show the IRAS data and (sub)millimeter measurements (Henning et al. 1998; Mannings 1994).
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,height=13.5cm,width=7.8cm,clip]{h2907F4.ps} \end{figure} Figure 4: The 3 $\mu $m spectra of HD 97048, Elias 1 (top panel). HR 4049 and IRAS 05341 (middle panel). A comparison of the 3 $\mu $m spectra of Elias 1 and the planetary nebula, IRAS 21282 (bottom panel).
Open with DEXTER

The Spectral Energy Distribution (SED) of HD 97048 (Fig. 2) has been corrected for extinction with the method of Cardelli et al. (1989), where we adopt AV = 1.24 (van den Ancker et al. 1998) and E(B-V)= 0.36 (Davies et al. 1991; Thé et al. 1986). The stellar flux, $F_{\rm\star}$, was determined by integration of the scaled Kurucz model atmosphere ( $T_{\rm eff}=$ 10000, log(g)= 4) and the IR flux, $F_{\rm IR}$, was determined by integrating the spectrum from IR to mm (Fig. 2) minus the Kurucz model. Obviously a large part of the stellar radiation is reprocessed by the circumstellar dust. The ratio $F_{\rm IR}$/ $F_{\rm\star}$ is 0.4 which is much larger than expected from a geometrically thin disc, and more characteristic for a flared disk (Meeuws et al. 2001 and references therein). The spectrum does not show evidence of silicate emission. The spectrum of Elias 1 is indicative of a (flared) disk as well. The spectrum seems to be steeper than HD 97048 in the 20-100 $\mu $m range (Fig. 3).

Both Elias 1 and HD 97048 show clear PAH emission features at 3.3, 6.2, "7.7'' and 8.6 $\mu $m (Fig. 1). The 11.2 and 12.7 $\mu $m bands are only seen in HD 97048; in Elias 1 these bands may well be hidden by the silicate emission (Fig. 1). The overall PAH spectra of HD 97048 and Elias 1 are rather normal (Sect. 6) except for the 3 $\mu $m region. In most PAH sources, the 3.3 $\mu $m band dwarfs any possible satellite features occurring around 3.4 and 3.5 $\mu $m (Fig. 4). In contrast, the unique 3 $\mu $m regions of HD 97048 and Elias 1 are totally dominated by features at 3.43 and 3.53 $\mu $m (Fig. 4). The 3 $\mu $m regions of these two are very rich in components and strikingly similar.

4.1 The incredibly rich 3 $\mu $m region of HD 97048 and Elias 1

Although the 3 $\mu $m region of HD 97048 and Elias 1 are peculiar because of their exceedingly strong 3.43 and 3.53 $\mu $m bands, some other sources show weak emission bands around these wavelengths as well. In Fig. 4 we compare the spectra of Elias 1 and HD 97048 with two post-asymptotic giant branch (post-AGB) stars, HR 4049 and IRAS 05341. The sources seem to show some related spectral structure in this wavelength region. First, HR 4049 shows bands around 3.4 and 3.5 $\mu $m, which - taking the difference in spectral resolution into account - are very similar to the bands in HD 97048 and Elias 1. The only difference between HR 4049 and the other two spectra is the strength of the components at 3.4 and 3.5 $\mu $m relative to the 3.3 $\mu $m PAH band. Because of the spectral resemblance of HR 4049, we will include this post-AGB object in our analysis of the characteristics of the carrier(s) of the 3.43 and 3.53 $\mu $m bands in the Herbig Ae/Be stars, HD 97048 and Elias 1. The second trend that may be discerned involves IRAS 05341. There seems to be a broad underlying component underneath the 3.4-3.5 complexes in HD 97048 and Elias 1, which resembles the broad feature - at $\sim$3.42 and $\sim$3.49 $\mu $m - in IRAS 05341 (Van Kerckhoven et al. 1999). This broad band in IRAS 05341 is generally attributed to methyl groups or extra hydrogen on PAHs (Joblin et al. 1996; Bernstein et al. 1996).

Some PAH sources show weak "satellite'' bands around 3.4 and 3.5 $\mu $m. In Fig. 4 we compare the 3 $\mu $m spectrum of Elias 1 with that of a prototypical source with spectral structure in this wavelength region: the planetary nebula IRAS 21282 (Geballe et al. 1994). This spectrum shows a strong emission band at 3.3 $\mu $m and some weaker structure around 3.4, 3.43, 3.46, 3.51, 3.56 $\mu $m. None of the spectral detail in IRAS 21282 really coincides with the dominant 3.43 and 3.53 $\mu $m features in HD 97048. We conclude that the strong 3.43 and 3.53 $\mu $m bands in HD 97048 and Elias 1 are independent of the "normal'' PAH features in this wavelength region. Moreover, while some of the broader underlying spectral structure in HD 97048 and Elias 1 may be present in other sources as well, the strong 3.43 $\mu $m and 3.53 $\mu $m bands have no counterpart in the interstellar PAH spectrum.

Component analysis

Perusing the 3 $\mu $m spectra, we recognize two complexes - centered at 3.43 and 3.53 $\mu $m, respectively - each of which consists of a number of spectral components. In order to make a detailed spectral comparison between these sources, we have decomposed the spectra in the 3 $\mu $m region using Lorentzian profiles. The peak frequency, width and relative strength of the profiles are determined using a least-square fitting routine. The high resolution spectra of HD 97048 and Elias 1 with their clear substructures are a good guideline for this decomposition. The resolution of the spectrum of HR 4049, on the contrary, is too low for such a detailed analysis and will not be used in this respect. We use Lorentzian profiles because of their simplicity and physical relevance.

Looking at the spectra of HD 97048 and Elias 1 it is clear that at least seven components have to be used; three components for the "3.53'' $\mu $m band and four for the "3.43'' $\mu $m band. It appears that an extra component is needed to fill up the fit around 3.48 $\mu $m. So, at least eight profiles are needed (see Fig. 5). Input values for the position of the components are easily found for the four and three components of respectively the "3.43'' $\mu $m and "3.53'' $\mu $m band. For the last component, at $\sim$3.48 $\mu $m, this is more difficult. Therefore the "3.43'' and "3.53'' $\mu $m features are first fitted separately. After subtraction of these fits, input parameters for the last profile are determined.

In total we have 8 profiles for which we fit the peak position, width and relative strength. The results of the fits are presented in Fig. 5 and Table 2.

As the spectrum of HR 4049 is too noisy to make the same decomposition, Table 2 gives only the strength and FWHM of the 3.53 $\mu $m feature, the intensity of the remaining emission is referred to as the "3.4'' band for this source.


  \begin{figure} \par\includegraphics[angle=90,height=8.2cm,width=8cm,clip]{h2907F5.ps} \end{figure} Figure 5: The Lorentz decomposition of the 3 $\mu $m spectra. The thick solid line compares the sum of the fitted Lorentzian profiles with the observations (thin line).
Open with DEXTER


 

 
Table 2: Fitting parameters of the fits presented in Fig. 5. See text for details on assignments.
$\lambda $ FWHM I assignments
$[\mu{\rm m}]$ $[\mu{\rm m}]$ $[10^{-18}~{\rm W}/{\rm cm}^2]$  
Elias 1
3.397 0.016 0.15  
3.414 0.020 0.34 C(100)-2$\times $ 1:H
3.431 0.016 0.38 C(100)-2$\times $ 1:H
3.452 0.023 0.21  
3.481 0.033 0.22  
3.503 0.021 0.32 C(110)-1$\times $ 1:H
3.518 0.014 0.23 C(110)-1$\times $ 1:H
3.533 0.012 0.72 C(111)-1$\times $ 1:H
HD97408
3.402 0.027 0.97  
3.416 0.014 1.13 C(100)-2$\times $ 1:H
3.431 0.014 1.43 C(100)-2$\times $ 1:H
3.450 0.029 1.04  
3.483 0.027 0.66  
3.503 0.022 2.38 C(110)-1$\times $ 1:H
3.519 0.015 1.33 C(110)-1$\times $ 1:H
3.532 0.012 3.84 C(111)-1$\times $ 1:H
HR 4049
"3.4'' ... 4.2 ($\pm$1.7)  
3.53 0.025 ($\pm$0.009) 3.0 ($\pm$1.5)  


Conclusion

Analyzing the fits, we conclude that the components in HD 97048 and Elias 1 are very similar in peak position, width and relative strength (cf., Table 2). This decomposition is not unique - in particular due the uncertainty on the parameters of the component at $\sim$3.48 $\mu $m, which mostly influences the strength of the components at $\sim$3.45 $\mu $m and $\sim$3.5 $\mu $m. But as long as the decomposition is done in a consistent way for the two sources, this conclusion stands.

   
4.2 An inventory of the PAH features

Apart from the 3 $\mu $m region, the IR spectra of HD 97048, Elias 1 and HR 4049 show fairly normal PAH spectra. The regular PAH features at 3.3, 6.2, "7.7'', 8.6 and 11.2 $\mu $m are present with relative intensities, very comparable to those in other sources (Table 3; Hony et al. 2001). The profiles of the 6.2 $\mu $m and the 11.2 $\mu $m bands - with a sharp blue rise and a red tail - very much resemble those in other sources. The profile of the "7.7'' $\mu $m bands are somewhat more special with a relatively strong 7.8 $\mu $m component. Most sources involving interstellar material have a 7.6 $\mu $m component which exceeds the 7.8 $\mu $m band in strength. However, many objects with circumstellar PAHs show "7.7'' $\mu $m complexes which differ similarly (Peeters et al. submitted). The 12.7 $\mu $m feature is present in the spectrum of HD 97048 as well.

A 15-20 $\mu $m emission plateau, ascribed to the C-C-C bending modes of large PAHs (Van Kerckhoven et al. 2000) is present in HD 97048 ( $I_{\rm plateau}= 9 \times 10^{-18}$ [W/cm2]). The intensity ratio of the 15-20 $\mu $m plateau compared to the total PAH intensity is 0.3. This is in the range of the ratios 0.1-0.6 for the sources discussed by Van Kerckhoven et al. (2000). In Elias 1 glitches around these wavelengths make the detection of a possible emission plateau difficult. Therefore no conclusions can be made concerning the presence of a 15-20 $\mu $m plateau in Elias 1.

In HD 97048 there is an additional feature at 6.8 $\mu $m, while weak features are also detected at 9.4, 10.2, 21 and 22 $\mu $m. In Elias 1 a clear feature is detected at 20.8 $\mu $m and other substructure is possibly present at these longer wavelengths.


 

 
Table 3: Integrated strength of the PAH features. The 8.6 $\mu $m feature is considered as superposed on the 7.7 $\mu $m feature. The uncertainty on the integrated strength of the features is mainly due to the uncertainty on the continuum (less true for the 6.2 $\mu $m feature).
Source $\lambda $ I
  [$\mu $m] [10-18 W/cm2]
Elias 1    
  3.3 0.48$^\ast$ ($\pm$0.03)
  6.2 4.0 ($\pm$0.2)
  "7.7'' 15 ($\pm$2)
  8.6 2.5 ($\pm$0.3)
HD 97048    
  3.3 1.1 ($\pm$0.3)
  6.2 5.3 ($\pm$0.5)
  "7.7'' 21.5 ($\pm$1)
  8.6 2.9 ($\pm$0.5)
  11.2 2.5 ($\pm$0.5)
HR 4049    
  3.3 9.2 ($\pm$0.7)
  6.2 25.2 ($\pm$5)
  "7.7'' 66.7 ($\pm$7)
  8.6 14.6($\pm$1)
  11.2 8.4 ($\pm$1)


$^\ast$ Measured in ground-based spectrum.


4.3 The silicate feature in Elias 1

Elias 1 shows a 10 $\mu $m silicate emission feature which presumably originates from the circumstellar environment. Such an emission feature is very unusual for interstellar material illuminated by a bright star (i.e. H II or reflection nebula, Peeters et al. in prep). However, isolated Herbig Ae/Be stars, as well as some AGB and Post-AGB objects sometimes show amorphous and/or crystalline silicate emission features (Malfait et al. 1998b; Bouwman et al. 2000; Meeuws et al. 2001; Waters & Molster 1999). This has been attributed to circumstellar dust disk material.

We conclude therefore, that the silicate emission feature in the spectrum of Elias 1 originates from a circumstellar disk.

   
5 Location of the different emission components

The PAH emission in HD 97048 is extended on a scale of at least 10'' (Siebenmorgen et al. 2000), which corresponds to about 1800 AU. In contrast, the emission at 3.53 $\mu $m originates in a region smaller than 0.1'' (Roche et al. 1986), ie. 18 AU, across. Likely the 3.53 $\mu $m band - and by inference the 3.43 $\mu $m band - originates in a circumstellar disk surrounding this young stellar object. We note that while the PAH emission originates from a much more extended region, it is likely still circumstellar. Indeed, the spectral details of the "7.7'' $\mu $m feature are reminiscent of other sources with circumstellar material, rather than interstellar material (Peeters et al. submitted; Van Kerckhoven et al. in prep.). Finally we note that the global spectral energy distribution (Fig. 2) is characteristic for stars with circumstellar dust disks (Fig. 2, Sects. 2 and 4).

Comparison of the SWS spectrum with the ground-based spectrum of Elias 1 (Geballe 1997) suggests that the 3.43 and 3.53 $\mu $m features are not extended on a 5 $^{\prime\prime}$ scale. We have already commented upon the likelihood that the silicate emission in this spectrum traces emission from a dust disk. Additionally, the near-IR speckle interferometric observations of Elias 1 are suggestive of an origin of the 3.43 and 3.53 $\mu $m emission close to the star (<0.15'' which corresponds to R < 22 AU) (Haas et al. 1997).

For HR 4049, the IR emission is generally thought to arise from a long-lived stable circumbinary disk at a distance of $\sim$10 AU (Dominik et al. in prep; Waelkens et al. 1991; Bakker et al. 1998)

In conclusion, both the 3.53 & 3.43 $\mu $m bands and the PAH emission arise in the immediate circumstellar environment of the central stars of HD 97048, Elias 1 and HR 4049. However, at least for HD 97048, the 3.43 & 3.53 $\mu $m bands arise from a very small region immediately ($\le$9 AU) around the illuminating star. It is clear that the 3.43 & 3.53 $\mu $m bands are carried by species other than the "normal'' PAHs carrying the bulk of the Aromatic InfraRed (AIR) bands in these objects or in other objects. This "decoupling'' of the carriers of the 3.43 & 3.53 $\mu $m band and the AIR bands is also obvious from the large variations in the relative strengths of these bands between the different sources (Tables 2 and 5). We also note that the 3.43 & 3.53 $\mu $m components are narrower ( $\Delta\lambda \simeq$ 0.01-0.03 $\mu $m) than the 3.3 $\mu $m band ( $\Delta\lambda \simeq$ 0.05 $\mu $m), pointing towards a different carrier than the PAHs for this bands.

   
6 PAHs

In the past the 3.43 and 3.53 $\mu $m features have been assigned to PAHs (Schutte et al. 1990). Recently (Guillois et al. 1999) new insights have pointed to hydrogenated diamonds as carriers of these emission bands. In this section a short overview will be given of the PAH assignments, in the next section the diamond hypothesis will be discussed.

It is known that the C-H stretches of molecular sidegroups (-CHO, -CH2, -CH3) attached to PAH molecules emit in the 3-4 $\mu $m region. The C-H stretches of -CHO sidegroups fall at 3.54 and 3.66 $\mu $m (Baas et al. 1986, Schutte et al. 1990). These do not match the 3.43 and 3.53 $\mu $m bands. In addition, the C-O stretch at 5.9 $\mu $m would be expected to be very strong (at least as strong as the 3.53 $\mu $m band, Schutte et al. 1990) but is at the very most 22% of the 3.53$\mu $m band (Fig. 1). Therefore it can be excluded that -CHO molecular sidegroups contribute significantly to the 3 $\mu $m complex.

Methyl (-CH3) and ethyl (-CH2-CH3) sidegroups emit at 3.4 $\mu $m (C-H stretch) and 6.8 $\mu $m (C-H bend), ethyl has an extra feature at 3.36 $\mu $m (Schutte et al. 1993; Pauzat et al. 1999; Joblin et al. 1996). Another candidate for the 3.4 $\mu $m feature are the so called super-hydrogenated PAHs or Hn-PAHs (Bernstein et al. 1996). In both cases the 3.4 $\mu $m band is attributed to an aliphatic C-H group associated with the molecule. A 6.8 $\mu $m feature is observed in HD 97048 with an intensity of 4.8 $\times $ 10-19 [W/cm2]. This is $\sim$0.5 times the intensity of the 3.4 $\mu $m feature (see Table 2). A feature at 3.36 $\mu $m is not observed. In Elias 1 no 6.8 $\mu $m feature is detected, but if the intensity is 0.5 times I 3.4, as is the case in HD 97048, this feature can easily be hidden in the noise (upper limit: $I_{ 6.8}= 4.5 \times 10^{-19}$ [W/cm2]).

Therefore, if we attribute the 6.8 $\mu $m feature in HD 97048 to methyl groups, such groups may also contribute to the 3.4 $\mu $m complex. However, we note that some sources show a strong emission band at 6.8 $\mu $m but not the peculiar 3.43 and 3.53 $\mu $m features characteristic for HD 97048 (Buss et al. 1993). Hence, we conclude that methyl groups attached to PAHs and Hn-PAHs are not the carriers of the 3.43 and 3.53 $\mu $m bands. Such groups may, however, be responsible for the "normal'' 3.4 $\mu $m band observed in sources such as IRAS 21282 or IRAS 05341 (cf., Fig. 4; Joblin et al. 1996; Bernstein et al. 1996).

   
7 Diamond

Comparison of the spectra of HD 97048 and Elias 1 with laboratory spectra of H-terminated diamond surfaces show excellent and very convincing agreement in peak position and spectral detail (Guillois et al. 1999) and therefore we believe that this is the correct assignment. In this section, diamond nanocrystallites and their IR properties will be discussed.

Perfect diamonds are IR inactive in the one-phonon region (6.25-25 $\mu $m) and only multi-phonon modes appear in the IR, but these are very weak (Braatz et al. 2000a; Edwards 1985). Impurities (i.e. presence of atoms other than C) or structural defects can enable one-phonon modes to become active (Andersen et al. 1998).

When diamond is exposed to an atomic hydrogen flux, the carbon surface atoms form C-H bonds. These C-H bonds are active in the 3 $\mu $m region. Hydrogen atoms attached to different facets of the diamond surface give rise to different emission bands (Chang et al. 1995; Lin et al. 1996; Cheng et al. 1997b). The peak frequency of these bands is determined by the crystallographic orientation of the surface plane, indicated by the Miller indices (e.g., (111)) and by the surface reconstruction (e.g. (1 $\times $ 2))[*] (nice representations of the different surface structures can be found in Zhigilei et al. 1997; summary on http://www.people.virginia.edu/~lz2n/Diamond.html and Su & Lin 1998). A band at 3.53 $\mu $m arises from the C-H stretch of H attached on a C(111)-(1 $\times $ 1) surface. Hydrogen attached to a C(100)-(2 $\times $ 1) surface is responsible for the 3.41 and 3.43 $\mu $m bands. The blue tail of the strong 3.53 $\mu $m feature is probably due to contributions of the C-H stretching modes on C(110)-(1 $\times $ 1) surfaces (Lin et al. 1996; Cheng et al. 1997b) (although the stretching mode of C(111)-(2 $\times $ 1)-H could contribute around 3.49 $\mu $m (Su & Lin 1998) as well). The shoulders and substructures are generally associated with H atoms bonded to surface defects, such as the corners and edges of the facets (Chang et al. 1995). The bending modes of the C-H bond on a C(111)-(1 $\times $ 1) facet fall around 7.5-7.9 $\mu $m (Chin et al. 1995; Sandfort et al. 1995) but are much fainter than the stretching mode ($\sim$$0.05\%$; Chin et al. 1995).

The surface structure of diamond is sensitive to the physical conditions and as H-atoms attached to different surface facets emit at different wavelengths, the structure of the 3 $\mu $m emission/absorption complex reflects the physical conditions during the formation and predominantly the hydrogenation of the diamond particles.

The C(111) is the most stable surface configuration. In a hydrogen rich environment a great part of the C(110)-(1 $\times $ 1) and C(100)-(2 $\times $ 1) surfaces are irreversibly converted to C(111) facets after prolonged heating to $\sim$1100 K (Cheng et al. 1997a). The C(111)-H band is also the best studied and therefore we will use this band to investigate the observed diamond emission bands in the following section.

At low temperatures the bare C(111) surface is organized in a $\pi$-bonded chain (2 $\times $ 1) structure. If the surface is hydrogenated the conversion from the $\pi$-bonded chain (2 $\times $ 1) to the bulk-terminated (1 $\times $ 1) structure starts around 800 K and is complete at 1000 K. Dehydrogenation at temperatures around 1300 K initiate a reconversion of the (1 $\times $ 1) to (2 $\times $ 1) structure (Su & Lin 1998) which is complete at 1450 K. If the diamond is further heated to about 2300 K, the bonds between the first and second double layer break and a graphite sheet is formed at the surface (Zhigilei et al. 1997). For nanodiamonds the conversion to graphite already starts at lower temperature (1400-2000 K depending on the size; Butenko et al. 2000; Braatz et al. 2000b) and proceeds from the diamond surface to the bulk. Small ($\sim$2 nm) nanodiamonds are rapidly, completely converted at $T \sim$ 1420 K, somewhat bigger ($\sim$5-6 nm) nanodiamonds convert completely only at $T \sim$ 1900 K (Butenko et al. 2000). For nanodiamonds, this process will thus lead to onion-like carbon surface layers.

We can thus conclude that the 3.53 $\mu $m band is characteristic for hydrogenated diamonds in the range from 800 to 1300 K.

   
8 Discussion: The characteristics of the observed diamonds

The exact position of the emission bands is sensitive to the temperature of the emitters (Lin et al. 1996). The 3.53 $\mu $m peak shifts to longer wavelengths, and the FWHM ( $\Delta \lambda $) of this band increases with increasing temperature (see Fig. 6).

8.1 Single temperature fit


  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{h2907F6.ps}\end{figure} Figure 6: The peak position, $\lambda $, and FWHM, $\Delta \lambda $, of the 3.53 $\mu $m band measured in the laboratory (Lin et al. 1996) (solid line). Thick marks indicate increasing temperature (in steps of 100 K). The dashed lines indicate the experimental uncertainty. The peak position and width of the 3.53 $\mu $m band observed in HD 97048 and Elias 1 are indicated with their uncertainty
Open with DEXTER

The position of the 3.53 $\mu $m feature in both Elias 1 and HD 97048 indicates a temperature of about 1000 K (see Fig. 6). Our best single temperature Lorentzian fit is obtained with a temperature of 950 K for HD 97048 (see Fig. 7). The 3.53 $\mu $m feature is slightly redder in Elias 1 than in HD 97048 ($\sim$0.001 $\mu $m; Table 2), consequently the best fit is obtained with the somewhat higher temperature of 1000 K. From Fig. 6 it is clear that the 3.53 $\mu $m profile in HD 97048 and Elias 1 is broader than expected from the laboratory measurements. This increased width likely reflects the presence of a temperature gradient. While more uncertain because of the low resolution of the observations the derived temperature in HR 4049 (1000 $\pm$ 100 K) is similar to that in Elias 1 and HD 97048.

8.2 Gaussian temperature distribution

As discussed in the previous section, single temperature profiles are narrower than the observed features (Fig. 6). Therefore in this section a temperature distribution is considered. We take a Gaussian temperature distribution (this distribution is comparable to the more physical distribution that will be considered in the next section). We assume that diamonds are dehydrogenated when their temperature exceeds 1300 K and that diamonds are fully hydrogenated below this temperature. The observed profile, $F(\lambda)$, is then given by

 \begin{displaymath}% F(\lambda)=\int_{0}^{T_{+}}\/\phi(\lambda_0(T),\Delta\lambda (T))\,B(\lambda,T) f(T,T_{\rm peak},\sigma ) {\rm d}T\, \end{displaymath} (1)

where $\phi(\lambda_0(T),\Delta\lambda (T))$ is the Lorentzian emission profile of diamonds at temperature T, $B(\lambda,T)$ is the Planck function, $ f(T,T_{\rm peak},\sigma)$ is a Gaussian centered on $T_{\rm peak}$ and T+ is taken to be 1300 K. The comparison between the calculated and observed profiles is evaluated with a least-square fit, where most weight is given to the peak of the profile and the red wing, as this wing is not - in contrast to the blue wing - influenced by the presence of other bands.


  \begin{figure} \par\includegraphics[angle=90,width=7.4cm,clip]{h2907F7.ps}\end{figure} Figure 7: Single temperature fit of the observed 3.53 $\mu $m feature of HD 97048.
Open with DEXTER

The results show that different temperature distributions can fit the 3.53 $\mu $m feature equally well (Fig. 8a). Lower peak temperatures require broader temperature distributions: The 3.53 $\mu $m feature of HD 97048 is fitted equally well by distributions with [$\sigma =$ 100 K, $T_{\rm peak}=$ 920 K] and [$\sigma =$ 190 K, $T_{\rm peak}=$ 820 K], for Elias 1 higher peak temperatures are needed: [$\sigma =$ 100 K, $T_{\rm peak}=$ 980 K] and [$\sigma =$ 200 K, $T_{\rm peak}=$ 890 K]. In Fig. 8c the relation between peak temperature and width of the distribution for the best fitting profiles is shown for HD 97048. For peak temperatures higher than respectively 950 K and 1000 K a good fit is not possible for HD 97048 and Elias 1 (cf., Fig. 7).

8.3 A physical model for HD 97048

In this section we will consider a more physical model, where we assume that the diamonds have a log-normal distribution, similar to diamonds found in meteorites (Lewis et al. 1989). We calculate their temperature assuming radiative equilibrium and use the measured relation between $\lambda_0$, $\Delta \lambda $ and T to construct the 3.53 $\mu $m profiles for comparison with the observed 3.53 $\mu $m features: We will concentrate here on the source HD 97048 where most information is available.


  \begin{figure} \par\includegraphics[angle=90,height=9.6cm,width=7.3cm,clip]{h2907F8.ps}\end{figure} Figure 8: a) Two normalized profiles, both build up with a Gaussian temperature distribution and fitting the observed 3.53 $\mu $m feature in HD 97048. The parameters of this distribution are respectively [$\sigma =$ 100 K, $T_{\rm peak}=$ 920 K] for profile A and [$\sigma =$ 190 K, $T_{\rm peak}=$ 820 K] for profile B. b) The temperature distributions multiplied by the Planck function (see Eq. (1)). c) The relation between peak temperature and width of the Gaussian temperature distribution, for distributions fitting the observed 3.53 $\mu $m feature the best.
Open with DEXTER

8.3.1 The temperature of emitting diamonds

Radiative equilibrium temperature

Under the assumption that the grains are in radiative equilibrium, the temperature of the hydrogenated nanodiamonds can be derived from the energy balance between absorption and emission:

 \begin{displaymath}% F_{\rm uv}\ \sigma_{\rm uv} \ N_{\rm C} = \sigma_{\rm ir} \ N_{\rm C-s} \ \theta\ B_{\nu}(T)\ 4\pi \end{displaymath} (2)

here $F_{\rm uv}$ is the UV flux at the position of the diamonds, $\sigma_{\rm uv}$ is the UV cross-section of diamond per C-atom, $N_{\rm C}$ is the number of C-atoms in a diamond grain, $\sigma_{\rm ir}$ is $\sigma_{\rm ir}$ = c  $\sigma_{\rm i}$ with $\sigma_{\rm i}$ the integrated IR cross-section per H-atom (1.8 $\times $ 10-18 cm, for a C-H bond on a C(111)-(1 $\times $ 1) surface; Cheng et al. 1997a), $\theta$ is the hydrogen coverage (number of surface H-atoms/number of surface C-atoms) and $B_{\nu}(T)$ is the Planck function at a temperature T and frequency $\nu$. The number of surface C-atoms, $N_{\rm C-s}$, is given by $\pi D^2/ a^2 $, with D the diameter of the diamond grain and a the average distance between neighboring surface C-atoms, a = 2.52 Å on a C(111)-(1 $\times $ 1) surface. Adopting a value of 2.3 [g/cm3] for the specific density of diamond, in accordance with Lewis et al. (1989), we can rewrite Eq. (2) as:

 \begin{displaymath}% B_{\nu}(T) = 5 \times 10^{-15} \frac{1}{\theta} \left(\fra... ...nm} \,\, \left[\frac{\rm W/cm^2}{\rm Hz\ sr}\right] \!\cdot\, \end{displaymath} (3)

For HD 97048, $F_{\rm uv}$ can be determined from the IUE spectrum (see Sect. 4). Diamonds only absorb substantially at frequencies higher than 6 $\mu $m-1 (Lewis et al. 1989), a spectral region where the stellar UV flux decreases rapidly. The calculated UV extinction cross section for small diamonds (Lewis et al. 1989) averaged over the extinction-corrected observed UV flux of HD 97048 gives a value of 5 $\times $ 10-19 cm2 per C-atom for $\sigma_{\rm uv}$. The emission of the 3.53 feature in HD 97048 arises from a region with a radius $\le$0.05'' (Roche et al. 1986) from the star. With an adopted distance of 180 pc (Van den Ancker et al. 1998) this gives a maximum radius, R, of 9 AU. The UV flux ( $\nu > 6~\mu{\rm m}^{-1}$) at a distance, R, from the star is then

 \begin{displaymath}% F_{\rm uv} = 5.8 \times 10^{-3} \left(\frac{\rm 9\ AU}{R}\right)^2 \qquad\left[\frac{\rm W}{\rm cm^2}\right]\cdot \end{displaymath} (4)

The solid line in Fig. 9 gives the relation between temperature and size of the emitting diamonds for this UV flux, where we adopt full hydrogen coverage ($ \theta=1$). Also shown is the relationship for an adopted FUV flux which is respectively twice an half this value.

We note that the temperature of hydrogenated nanodiamonds increases with their size. This is contrary to most dust materials, which show a constant or decreasing temperature with increasing grain size. The size dependence of the temperature for nanodiamonds reflects that, in this case, UV absorption scales with the bulk while IR emission scales with the surface area.

Stochastical heating

For very small grains and low FUV fluxes, stochastical heating can become important. We calculate the relation between the instantaneous temperature, $T_{\sigma}$, reached by a grain after the absorption of a photon with energy, $E_\phi $, and the grain diameter, D:

 \begin{displaymath}% E_{\phi} = \int_{T_{0}}^{T_{\sigma}}C(T) {\rm d}T \end{displaymath} (5)

T0 is the temperature of the grain prior to photon absorption which we assume to be the radiative equilibrium temperature.

Following the Debye theory the heat capacity of diamond, $C_{\rm D}$, per C-atom, can be expressed as:

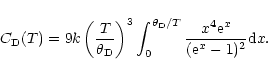
\begin{displaymath}C_{\rm D}(T) = 9 {k} \left(\frac{T}{\theta_{\rm D}}\right)^3 ... ...ta_{\rm D}/T} \frac{x^4 {\rm e}^x}{({\rm e}^x-1)^2} {\rm d}x.\ \end{displaymath}

We adopt a value of 2200 K for $\theta_{\rm D}$ (Spear & Frenklach 1994). To estimate the contribution, per H-atom, of the hydrogenated surface we use Einsteins approximation:

\begin{displaymath}C_{\rm H}(T) = {k} \sum_{i=1}^{3} \left(\frac{\theta_i}{T}\right)^2 \frac{\exp(\theta_i/T)}{[\exp(\theta_i/T)-1]^2} \end{displaymath}

with $k \theta_i = h \nu_i$ and where we assume that every H atom has one stretching (3.53 $\mu $m) and two bending modes (falling around 7.5 $\mu $m; the exact position is not important in this context). The heat capacity of a hydrogenated diamond with diameter D can then be express as

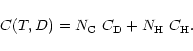
\begin{displaymath}C(T,D) =N_{\rm C}\ C_{\rm D}+ N_{\rm H}\ C_{\rm H}. \end{displaymath}

The relation between the stochastical temperature, $T_{\sigma}$, and the grain size is shown in Fig. 9 (dashed line), where a (maximum) photon energy, $E_\phi $, of 13.6 eV is adopted. The stochastical heating starts to be important for grains smaller than 2 nm.


  \begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{h2907F9.ps}\end{figure} Figure 9: The radiative equilibrium temperature, T, of fully hydrogenated diamonds is shown as a function of diamond diameter, D, (solid lines) for three values of $F_{\rm uv}$ (in units of 10-3 W/cm2). The dashed lines give the relationship for the peak temperature reached upon absorption of a single FUV photon, $E_\phi $ = 13.6 eV. The horizontal lines indicate the dehydrogenation temperature (1300 K) and the minimum temperature (800 K) required to convert a C(111)-(2 $\times $ 1) surface to the (1 $\times $ 1) structure responsible for the 3.53 $\mu $m band.
Open with DEXTER


  \begin{figure}\par\includegraphics[angle=90,width=8.2cm,clip]{h2907F10.ps}\end{figure} Figure 10: The size range of a log-normal size distribution contributing to the 3.53 $\mu $m emission feature (thick solid lines) for different values of $F_{\rm uv}$ (in units of 10-3 [W/cm2]) (see also Fig. 9).
Open with DEXTER

Size of the emitting diamonds

The temperature determines which size range contributes to the 3.53 $\mu $m feature (cf., Fig. 10). Diamonds with temperatures above 1300 K are dehydrogenated and will not contribute to the 3.53 $\mu $m feature (Chang et al. 1995). To convert the more relaxed C(111)-(2 $\times $ 1) surfaces to a (1 $\times $ 1) structure, temperatures exceeding 800 K are needed (Su & Lin 1998). Therefore, if we assume that the diamonds are hydrogenated in situ, only diamonds with a temperature higher than 800 K can contribute to the 3.53 $\mu $m feature. From this analysis, given the UV flux of HD 97048 (cf., Eq. (4)) we can draw the important conclusion that the diamond carrier of the 3.53 $\mu $m feature in HD 97048 has a very small size, typically 1-10 nm diameter. This is precisely the size range of the nanodiamonds isolated in carbonaceous meteorites (Lewis et al. 1989). This is a very robust result, which does not depend much on the detailed assumptions. Essentially, this small size reflects the poor emissivity of diamonds in the IR (ie., only the surfaces "emit'') coupled with the good FUV absorptivity (by the bulk) and the strong FUV flux within 9 AU of the central star. Any larger diamond which might have been present will have been dehydrogenated or even transformed into onion-like graphite.

8.3.2 The calculated emission profile

Adopting a log-normal size distribution, n(D), the profile of the 3.53 $\mu $m feature is given by,

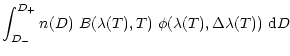$\displaystyle % \int_{D_{-}}^{D_{+}} n(D)\ B(\lambda(T),T)\ \phi(\lambda(T),\Delta\lambda (T))\ {\rm d}D$     (6)

with T = $T(F_{\rm uv},~D)$. The log-normal size distribution is defined by

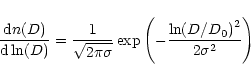
\begin{displaymath}\frac{{\rm d} n(D)}{{\rm d} \ln(D)}=\frac{1}{\sqrt{2\pi\sigma}} \exp\left({-\frac{{\ln(D/D_0)}^2}{2\sigma^2}}\right) \end{displaymath}

with the same parameters as meteoritic diamonds: D0 = 2.6 nm and $\sigma = 0.47$ (Lewis et al. 1989).

With a log-normal size distribution, a good fit to the observed 3.53 $\mu $m feature of HD 97048 can be obtained taking $F_{\rm uv}$ = 5.8 $\times $ 10-3 [W/cm2] (Fig. 11), which corresponds to the UV flux at 9 AU from HD 97048. When the diamonds are exposed to higher UV fluxes the feature shifts to longer wavelengths, as the average temperature of the diamonds becomes higher. The opposite is true for smaller UV fluxes. The profiles in Fig. 11 are evaluated assuming radiative equilibrium (full line in Fig. 9) and stochastical heating has not been taken into account. However, if we calculate the profiles assuming $T=T_{\sigma}$ (in this case we overestimate the influence of stochastical heating), the profile shifts slightly redwards but this shift is only about half the shift due to the variations in the UV field strength.

In Fig. 12 the fit to the 3.53 $\mu $m feature of Elias 1 is shown. As the 3.53 $\mu $m feature of Elias 1 is slightly redder than the 3.53 $\mu $m feature of HD 97048, a slightly higher UV flux, 6.4 $\times $ 10-3 [W/cm2], is needed to obtain a good fit. Assuming a similar intrinsic UV intensity for Elias 1 as for HD 97048, this intensity corresponds to a distance of 8.5 AU from the star.

The FUV flux of HR 4049, shortward 1666 Å, at 10 AU (the inner rim of the circumbinary disk, Dominik et al. in prep) and adopting a distance of 660 pc is 2 $\times $ 10-2 [W/cm2] (derived from the IUE spectrum SWP 44702, corrected for extinction following Buss et al. 1989). Correcting the UV cross-section per C-atom for the cooler spectral type ( $\sigma_{\rm uv}\simeq 2.5 \times 10^{-19}$ cm2) this corresponds to $F_{\rm uv}\ \sigma_{\rm uv} \sim 5 \times 10^{-21}$ W. Thus similarly to HD 97048 the carriers of the 3.53 $\mu $m band must be nanodiamonds (see top curve of Fig. 9) of about 1000 K, which is in good agreement with the peak position.


  \begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{h2907F11.ps}\end{figure} Figure 11: The emission profiles of diamonds with a log-normal size distribution exposed to $F_{\rm uv}$ = 2.9, 5.8 and 11.6 $\times $ 10-3 [W/cm2]. The profiles are compared to the spectrum of HD 97048. $F_{\rm uv}$ = 5.8 $\times $ 10-3 [W/cm2] gives a good fit.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{h2907F12.ps}\end{figure} Figure 12: The emission profile of diamonds with a log-normal size distribution exposed to $F_{\rm uv}$ of 6.4 $\times $ 10-3 [W/cm2]. The profile is compared to the spectrum of Elias 1.
Open with DEXTER

8.3.3 The mass in diamonds

When the grains are in radiative equilibrium we can write:

 
                $\displaystyle % F_{\rm obs}$ = $\displaystyle \frac{\sigma_{\rm ir}\ N_{\rm C-s}\ \theta\ B_{\nu}(T)\ 4\pi}{4\pi \/d^2}$  
  = $\displaystyle \frac{F_{\rm uv}\ \sigma_{\rm uv}\ N_{\rm C}}{4\pi d^2}\cdot$ (7)

Using Eq. (7) and $M=N_{\rm C} m_{\rm C} $ we can then express the mass as follows:
 
$\displaystyle M = 5\times 10^{-11} \left(\frac{\displaystyle F_{\rm obs}}{\disp... ...}\ F_{\rm uv}}\right) {\left(\frac{d^2}{180^2\ {\rm pc}^2}\right) {M}_{\odot}.}$     (8)

Equation (8) shows that the mass derived from the observed IR flux is independent of the size of the emitting grains (and thus of the size distribution), keeping in mind, of course, that this formula only probes hydrogenated diamonds.

With the UV fluxes of our fits, this gives a mass of 5 10-11 $M_{\odot}$for HD 97048. Similarly the 3.51 and 3.52 $\mu $m features (H on C(110)) and the 3.42 and 3.43 $\mu $m (H on C(100)) correspond to 4.5 $\times $ 10-11$M_{\odot}$ and 3.4 $\times $ 10-11 $M_{\odot}$ respectively, which gives a total mass of about 1.3 $\times $ 10-10 $M_{\odot}$. Of course an unknown mass of dehydrogenated diamonds might be present as well. For Elias 1 we obtain a total mass of 1.7 $\times $ 10-11 $M_{\odot}$. An estimate of the diamond mass present around HR 4049, with F3.53 = 3 $\times $ 10-18 [W/cm2] (Table 2) and $\sigma_{\rm uv}\ F_{\rm uv}$ similar to HD 97048 gives $M\sim 5.3 \times 10^{-10}$ $M_{\odot}$.

The total dust mass around HD 97048 and Elias 1 is estimated to be respectively $\sim$1.4 $\times $ 10 $^{-3}~M_\odot$ and $\sim$4 $\times $ 10 $^{-4}~M_\odot$(Henning et al. 1998) and the diamond carriers of the 3.53 $\mu $m bands are only minor dust components of these sources. Adopting a standard dust to gas fraction of 0.01, the hydrogenated diamonds around HD 97048 are only 1 ppb by mass relative to H.

   
9 Astrophysical implications

   
9.1 Meteoritic diamonds

Interstellar nanodiamonds were first discovered in meteorites (Lewis et al. 1989). Meteorites contain diamonds with isotopic anomalies, e.g., 15N depletions and likely p- and r-process Xe compositions, and enhanced D/H ratios, indicating an extra-solar origin of at least a part of the meteoritic diamond (Anders & Zinner 1993). The carbon isotopes are, however, mundane and there is no obvious stellar birth-site. Different models are proposed for the origin of meteoritic diamond (Anders & Zinner 1993): formation in interstellar shocks (Tielens et al. 1987), formation in exotic stellar locations (Jorgenson 1988), quantum heating of carbonaceous grains (Nuth & Allen 1992), but all of them face serious challenges (Anders & Zinner 1993).

While the characteristics of meteoritic diamonds do not have to be exactly the same as the diamonds around HD 97048, Elias 1 and HR 4049, they provide an important source of information on the possible birth-sites and residence-sites of diamond in space. We also realize that, while meteoritic diamonds contain isotopically enriched noble gases betraying an origin in supernova ejecta (Anders & Zinner 1993), this could be a contamination problem: only a very minute fraction (<10-6) of these diamonds needs to have been exposed to supernova ejecta (Clayton et al. 1995). In particular, the mundane C isotopes (Anders & Zinner 1993) suggest an origin from interstellar material.

The meteoritic diamonds have a median size of $\sim$3 nm (Lewis et al. 1989; Daulton et al. 1996) and are ten to one thousand times smaller than common interstellar grains. Their size distribution is log-normal rather than power-law, reflecting growth rather than fragmentation, and suggesting a short interstellar residence time (Lewis et al. 1989; Daulton et al. 1996). These meteoritic diamonds have a high hydrogen content (Lewis et al. 1989). A significant amount of this hydrogen must be intrinsic and not terrestrial in origin since the deuterium abundance is enriched (Braatz et al. 2000a). The high H content of presolar diamonds suggests that they originate from a H-rich region, an environment in which nanometer-sized diamonds may be more stable than graphite.

No indications have been found that presolar diamonds grew on a substrate or around a core of non-diamond material (Braatz et al. 2000a). Possibly, these diamonds formed through homogeneous nucleation. This process similar to the Chemical Vapor Deposition (CVD) process, depending on similar chemical reactions in the gas phase, but does not require a substrate (Frenklach et al. 1989; Braatz et al. 2000a; Buerki et al. 1996). However, laboratory experiments have shown that diamond forms much more efficiently when some silicon is added to the environment and yet the silicon leaves no trace in the diamonds grown this way (Frenklach & Feigelson 1997). So this issue is still open.

   
9.2 Diamonds in circumstellar disks

The 3.53 $\mu $m feature attests to the presence of hydrogenated diamond. The position of the 3.53 $\mu $m feature indicates a temperature of about 1000 K for these diamonds. From an analysis of the radiative energy budget, we therefore conclude that we are dealing with nanodiamonds.

The 3.53 $\mu $m feature in HD 97048 originates in a region with a projected diameter less than 0.1'' (Roche et al. 1986). In contrast, the PAH emission is spatially extended over 5-10'' (Siebenmorgen et al. 2000).

In Table 4 a summary is presented of the flux in different wavelength regions for the three objects. When we compare the flux emitted by the diamonds and PAHs in HD 97048 to the fraction of UV radiation they can absorb, we find a value of 4.8% for the UV fraction processed by the PAHs (Table 5). This is similar to the value of 5% for "typical'' sources (Allamandola et al. 1989). The diamonds reprocess about 3%, from which only 30% is radiated in the 3.53 $\mu $m feature. The fraction of UV radiation reprocessed by diamonds in HR 4049 is only slightly higher than in HD 97048. The PAHs, on the contrary, are a more important UV opacity source as they absorb about 36% of the FUV radiation (Table 5). As the extinction curve towards this source is anomalous - i.e., a linear rise is present, but no 2175 Å bump - the PAHs cannot be the carriers of the 2175 Å feature (Waters et al. 1989), although special geometrical arrangements of the circumstellar material could get around this conclusion (Waters et al. 1989).


 

 
Table 4: Extinction corrected UV fluxes and fluxes emitted in the different IR bands.
  $\log\frac{L_{\star}}{L_{\odot}}$ $F_{\rm UV} > 7.5 {\rm eV}^{(3)}$ $F_{\rm UV} > 6 {\rm eV}^{(3)}$ $F_{\rm diamond}^{(4)}$ $F_{\rm 3.53}^{(5)}$ $F_{\rm PAH}^{(6)}$ $F_{\rm IR}$ $T_{\rm eff}$
    $\left[ 10^{-18}\frac{\rm W}{\rm cm^2} \right] $ $\left[ 10^{-18}\frac{\rm W}{\rm cm^2} \right] $ $\left[ 10^{-18}\frac{\rm W}{\rm cm^2} \right] $ $\left[ 10^{-18}\frac{\rm W}{\rm cm^2} \right] $ $\left[ 10^{-18}\frac{\rm W}{\rm cm^2} \right] $ $\left[10^{-15}\frac{\rm W}{\rm cm^2}\right]$ $\left[ {\rm K} \right]$
HD97048 1.6(1) 340 650 10.1 3.8 31.5 1.4(1) 10000(1)
Elias 1 1.3(1) - - 2.0 0.7 19.8 3.3(1) 8000(1)
HR 4049 3.8(2) 100 340 (7.2) 3.0$^{\star}$ 124.1 8.4(7) 7500(2)
$^{\star}$ Integrated intensity of lorentzfit. Probably overestimated due to noisy spectrum.
(1) van den Ancker (1999); (2) Bakker et al. (1998); (3) Derived out of IUE data (for details see text);
(4) Summation over fitted diamond bands, see Table 2; (5) Strength of fit to the 3.53 $\mu $m feature;
(6) Summation over PAHs bands, see Table 3; (7) Waters et al. (1989).



 

 
Table 5: Fraction of the UV radiation emitted by different components.
  $f_{\rm diamond}^{(1)}$ f3.53(2) $f_{\rm PAH}^{(3)}$ F3.3/ $F_{\rm PAH}$(4)
HD 97048 3.0% 1.1% 4.8% 4.1%
HR 4049 7.0% 3.0% 36% 7.4%
(1) Fraction of UV radiation (>7.5 eV) processed by hydrogenated diamonds;
(2) fraction of UV radiation (>7.5 eV) radiated in the 3.53 $\mu $m band;
(3) fraction of UV radiation (>6 eV) processed by PAHs, $F_{\rm PAH}$;
(4) fraction of UV radiation absorbed by PAHs, emitted in the 3.3$\mu $m band.


One of the most striking aspects of the observed spectrum of HD 97048 is the absence of IR characteristics of other dust components in the disk. In particular, there is no evidence for small, warm silicates (cf., Sect. 4), which, if present, would attain $\sim$200 K in this UV radiation field and emit copiously in the 10 $\mu $m feature. If PAHs were present in the disk and would process 5% of the available FUV flux, the observed IR flux in the PAHs features would be 3 $\times $ 10-17 [W/cm2]. While the observed PAH flux is indeed this large, it originates from a much larger area (Siebenmorgen et al. 2000). Hence, we conclude that the PAHs are underabundant in the disk or perhaps even absent and that the near-IR emission from the disk is dominated by the diamond emission features.

The absence of small silicates and PAHs in the disk makes the presence of nanodiamonds even more puzzling. It suggests that the diamonds are a later addition; i.e., produced locally at later times after the silicates and PAHs have been removed and the coagulation process was well under way. The spectrum of Elias 1 shows a 10 $\mu $m silicate feature and this may suggest that (the disk dust of) this object is in a slightly earlier phase of evolution. The post-AGB object, HR 4049, has had a completely different history. However, its dust including the diamonds is located in a circumstellar disk and is newly formed from AGB ejecta. The disk is carbon rich and no silicate emission feature is present in the spectrum.

9.3 The origin of the nanodiamonds

The diamond spectral features around 3 $\mu $m observed in the spectra of these three stellar objects, together with the diamonds identified in meteorites clearly indicate that diamonds are present in space. There are two main, and related questions: why do we see the diamond bands only in these three objects? Are the diamonds produced in situ or are they present everywhere but only "activated'' in these systems?

Consider first the common characteristics of the three sources:

9.3.1 Formation in situ
As argued in Sect. 9.2, the circumstellar diamonds are likely a local product formed in situ in the disks of these systems. In short, the arguments in favor of a local origin are the absence of the diamond bands in the general ISM, their small sizes, the absence of the IR characteristics of other, common interstellar dust grains in the spectrum of HD 97048, and the very general conditions required for diamond formation (see below). Of course, the diamonds around HR 4049 have to be formed in situ from the AGB ejecta trapped in the disk. The meteoritic diamonds add to this the following arguments: the log-normal size distribution, which is characteristic for growth (rather than interstellar processing of grains) (Lewis et al. 1989; Daulton et al. 1996) and the normal carbon isotopes, which are easiest understood as formation from an interstellar reservoir. In fact, 12C and 13C are produced by different nucleosynthetic processes and their abundances in the ISM derive from different types of stars. Hence, it would be highly fortuitous if the average C-isotope ratio of stardust diamonds resembles that of the solar system as a whole. The very specific conditions required for diamond condensation compound this problem. Of course, HR 4049 is direct proof that some stardust sites form diamonds. But the C-isotope ratio in the ejecta is highly anomalous, with 12C/13C $\sim$ 1-2 (derived from the CO2 values measured by Cami & Yamamura 2001) as compared to solar abundances of 90, and typical abundances of 30-70 for carbon stars (Lambert et al. 1986), reemphasizing the problem of producing meteoritic diamonds in exotic stardust formation sites. The isotopically anomalous noble gasses measured in meteoritic diamonds must then reflect a small contamination of gas-rich SN-stardust or SN-processed stardust.

The most serious challenge facing the in-situ hypothesis is formation of a carbonaceous material in an O-rich gas. Laboratory experiments show that the sooting limit (ie., the onset of soot formation) is at a C/O ratio as low as 0.5 (Takahasi & Glassman 1984; Glassman 1988; Frenklach private communication). The interstellar C/O ratio in the gas phase is close to this value (Snow & Witt 1998). At the expected temperatures and pressures of protostellar disks, CH4 is the thermodynamically preferred compound (Fegley & Prinn 1989; Kress & Tielens 2001). However, in the molecular cloud in which these YSOs (and the solar system) formed, almost all of the C is locked up in CO (Langer et al. 2000), which is highly unreactive. The carbon in CO could be broken out either by an excess of H; eg., an H/H2ratio which is much larger than thermodynamics would indicate (Kress & Tielens 2001). Alternatively, the C can be broken out of CO through the Fischer-Tropsch reaction provided metallic iron is present in the nebula. The rate conversion depends solely on the total iron surface available (Kress & Tielens 2001). The formation of iron grains is expected in a cooling gas of solar composition (Latimer et al. 1978) and such iron grains were present in the solar nebula (Meibom et al. 1999). The presence of warm iron grains is consistent with the mid IR spectra of isolated Herbig Ae/Be stars (Bouwman et al. 2000).

Thus, the temperature, pressure, and composition (ie., molecular precursors) in these planetary disks and in the solar nebula would favor the condensation of carbonaceous compounds (Morgan et al. 1992; Frenklach & Wang 1991). Theoretical calculations show that the long residence time in such disks more readily allow carbon dust formation than in stellar outflows (Morgan et al. 1992). Now, generally, such a gas will form a condensate with an aromatic (sp2) character. Indeed, the physical conditions have to be carefully tuned in order to form diamonds in laboratory settings. Diamond is metastable under these conditions but graphite is the thermodynamically preferred compound. However, the actual carbonaceous condensation product formed is always a competition between different kinetic pathways available. In the laboratory experiments, diamond formation is favored by an overabundance of atomic H and by low C/O ratios (Frenklach, private communication). The presence of suitable substrates can be conducive for diamond formation as well - even in such minute quantities that they cannot be traced back in the products afterwards.

Within this framework, the presence of hydrogenated diamonds in only these three objects reflects then the careful tuning required for diamond formation. However, the existence of (solar)meteoritic diamond suggests that diamond is a common byproduct of starformation regions and that maybe the hydrogenated diamonds are only a minor component of the diamonds or only present during a short lived phase. In situ formation would also provide an explanation for the small size range (i.e., starvation: rapid nucleation coupled with running out of fuel) and the absence of other condensates (in the disk of HD 97048) including PAHs; ie., the conditions are just right for diamond formation but not for other compounds.

9.3.2 A stardust origin

In such a model, the diamonds are formed in stellar ejecta, and present everywhere. In order to escape detection in the ISM, their surfaces should not be hydrogenated. As the 3.43 and 3.53 $\mu $m features are not observed in the ISM, we can - following Tielens et al. (1999) - estimate that hydrogenated nanodiamonds cannot be more abundant than $\simeq$0.1 ppm in the interstellar medium.

If interstellar diamonds are not hydrogenated, they could be much more abundant. Analysis of the interstellar extinction observations shows that up to 10% of the interstellar carbon can be locked up in diamond and escape detection (Lewis et al. 1989). In these two YSO's, and only in these two YSO's, the conditions would then be right for hydrogenating diamond surfaces, revealing their presence. Hydrogenation requires the presence of atomic hydrogen and temperatures in the range 800-1300 K and as all three sources, showing the 3.53 $\mu $m band, have an associated long-lived stable disk, this may be the prerequisite for diamond hydrogenation. Since all circumstellar disks, which have not been cleared up by planets yet, would have zones appropriate for 1000 K diamonds, in this model, in other YSOs no atomic H should be present.

We note, however, that the surfaces of non hydrogenated diamonds will relax to an sp2 structure. In this regard it should be mentioned that the surfaces of meteoritic diamonds have relaxed to an sp2 structure (Bernatowicz et al. 1990).

As commented upon already, in order to explain the mundane 12C/13C ratio in solar system diamonds, diamonds must be formed in the ejecta of all types of stars. However, this is at variance with the special conditions required for diamond formation. Also, it would be curious if only very small diamonds would be formed in all such environments. The more since shock processing and coagulation are thought to play a major role in the history of interstellar grains and to dominate their size distribution (Bierman & Harwit 1980; Jones et al. 1994, 1996; Dominik & Tielens 1996).

9.4 Other tracers of nanodiamonds

The discovery of nanodiamonds in meteorites has lead to a flurry of activity by astronomers to "link'' them to various spectral characteristics of interstellar and circumstellar dust (Lewis et al. 1989; Hill et al. 1998; Braatz et al. 2000a; Allamandola et al. 1992; Jones & d'Hendecourt 2000). For example a feature at $\simeq$21 $\mu $m in some post-AGB objects has been attributed to a phonon mode of diamonds (Hill et al. 1998). However, this feature has now been attributed to TiC nanocrystals (von Helden et al. 2000). Moreover, HD 97048, Elias 1 and HR 4049 do not show this 21 $\mu $m feature and the diamond identification for the 21 $\mu $m band seems now untenable.

Jones & d'Hendecourt (2000) have suggested that the dehydrogenated surface layers of diamonds, which relax to an sp2 structure, would have a PAH-like character. In their view, such PAH-diamond structure would be responsible for the PAH emission features which dominate the IR emission spectra of the interstellar medium. In their model, the PAH-structure would be "perpendicular'' to the diamond surface and terminated by H's (to give rise to the C-H modes). In contrast, experiments on nanodiamonds show that the sp2-surface carbon forms an onion-like structure parallel to the surface. Furthermore, the nanodiamonds (with an sp2-surface) are too large, and do not get hot enough, to be responsible for the IR emission features in the interstellar medium. To phrase it differently, in terms of size, the 50 C-atom carrier characteristic for the IR bands can only have a PAH-like surface and no diamond core. Nevertheless, there may be a deeper interrelationship between (larger) PAHs or PAH cluster and nanodiamonds.

In particular, Duley & Grishko (2001) have suggested that chemical conversion of PAH clusters to nanodiamonds could occur in a sequence of full hydrogenation followed by dehydrogenation in the presences of UV photons and O-atoms. In their hypothesis the precursors of diamond are present in many sources. However, only in those sources where full hydrogenation occurred before exposure to FUV radiation can aromatic hydrocarbon material be converted into diamonds.

An absorption feature at 3.47 $\mu $m has been observed towards a large number of protostars and attributed to the C-H stretching mode of a H-atom bonded to a C-atom which is bonded to three other C-atoms (Allamandola et al. 1992). This is of course a diamond-like structure and this band has therefore been dubbed the diamond band. However, it is now known that the C-H modes of hydrogen bonded to diamond surfaces occur at somewhat different wavelengths. Moreover, observationally, the 3.47 $\mu $m band scales with the amount of H2O ice along the line of sight and, likely, this band is carried by a molecule in interstellar ices (Brooke et al. 1996, 1999).

Onion-like carbon particles have been proposed as the carrier of the 2175 Å bump (Ugarte 1995). Graphitization of carbon dust requires very high ($\sim$2300 K) temperatures (Ugarte 1995; Zhigilei et al. 1997). In contrast, graphitization of diamond particles already occurs at temperatures $\ge$1450 K (Butenko et al. 2000; Braatz et al. 2000b). A formation path, involving diamonds, would make the presence in the ISM of large amounts of carbon onion in the ISM possible.

The 2175 Å bump is not present in the extinction curve of HR 4049 (Waters et al. 1989; Monier et al. 1999). As the extinction towards this object is mainly circumstellar, this means that the carrier of the 2175 Å bump is not present in the disk, responsible for the CS extinction, around HR 4049. We see diamond emission around HR 4049. This means, accepting onion-like carbon as carrier of the 2175 Å band, that either diamonds around HR 4049 are not (yet) converted into carbon-onions, or the absorption is dominated by other dust components and therefore the 2175 Å band is not detected or diamonds are not situated in the light path to the observer.

10 Summary

We are convinced that the 3.43 and 3.53 $\mu $m features in the spectra of the two Herbig Ae/Be stars HD 97048 and Elias 1 can be assigned to H-terminated diamond surfaces (Guillois et al. 1999). The presence of a 3.53 $\mu $m feature in the spectrum of HR 4049 indicates that hydrogenated diamonds are present around this post-AGB object as well.

The 3 $\mu $m spectra of HD 97048 and Elias 1 are very similar, especially if one takes into account that the different bands originate on different diamonds facets. This indicates that the formation/hydrogenation mechanism has to be similar in both sources.

The position of the 3.53 $\mu $m band indicates a temperature of $\sim$1000 K, in the three sources. An analysis of the radiative energy budget indicates that the diamond carrier in HD 97048 has very small sizes, typically 1-10 nm: this high temperature reflects the poor emissivity of diamond in the IR coupled with the good FUV absorption and the strong FUV flux in the vicinity of the central star HD 97048. Any larger diamond which might have been present would have been dehydrogenated or even transformed into onion-like particles.

A theoretical fit to the profile of the 3.53 $\mu $m feature in HD 97048 shows that the carriers in HD 97048 are exposed to a $F_{\rm uv}$ flux of about 5.8 $\times $ 10-3 [W/cm2]. This is what is expected at radius of 9 AU from the star, the region where the 3.53 $\mu $m emission originates. The mass of hydrogenated diamond in the circumstellar environment of HD 97048 is estimated to be 1.3 $\times $ 10-10 $M_{\odot}$ and similar amounts are derived for HR 4049 and Elias 1. This is only a fraction of the total circumstellar mass.

We conclude that an in situ formation of diamonds in these objects is more likely than a stardust origin. The arguments in favor of a local origin are the absence of the diamond bands in the general ISM, their small sizes, the absence of the IR characteristics of other, common interstellar dust grains in the spectrum of HD 97048, and the very specific conditions required for diamond formation. The meteoritic diamonds add to this the following arguments: the log-normal size distribution, which is characteristic for growth (Lewis et al. 1989; Daulton et al. 1996) and the normal carbon isotopes, which are most easily understood as formed from an interstellar reservoir. The isotopically anomalous noble gasses measured in meteoritic diamonds must then reflect a small contamination of gas-rich SN-stardust or SN-processed stardust.While the deuterium fractionation may result from the somewhat stronger C-D bond (relative to the C-H bond) coupled with active exchange with H and D driven by FUV photolysis (cf., Allamandola et al. 1989).

Acknowledgements
We gratefully acknowledge stimulating and fruitful discussions with Michael Frenklach on the subject of diamond formation. We thank Thomas Henning for pointing out the importance of diamond graphitization at high temperatures. We are grateful to Tom Geballe for providing us with the spectra of Elias 1 and IRAS 21282. We tank the referee, Bruce Draine, for his insightful comments and suggestions. CVK is a Research Assistant of the Fund for Scientific Research - Flanders.

References

 

Copyright ESO 2002